基于物理信息嵌入的非固定长度电力系统暂态稳定快速评估

doi:10.16183/j.cnki.jsjtu.2023.452

基于物理信息嵌入的非固定长度电力系统暂态稳定快速评估

李湘¹, 陈思远^,¹, 张俊¹, 柯德平¹, 高杰迈¹, 杨欢欢²

1.武汉大学电气与自动化学院,武汉 430072

2.南方电网有限责任公司,广州 510663

Physics-Informed Fast Transient Stability Assessment of Non-Fixed Length in Power Systems

LI Xiang¹, CHEN Siyuan^,¹, ZHANG Jun¹, KE Deping¹, GAO Jiemai¹, YANG Huanhuan²

1. School of Electrical Engineering and Automation, Wuhan University, Wuhan 430072, China

2. Southern Power Grid Co., Ltd., Guangzhou 510663, China

通讯作者: 陈思远,博士后;E-mail:wddqcsy@whu.edu.cn.

责任编辑: 王历历

收稿日期: 2023-09-7 修回日期: 2023-12-20 接受日期: 2024-03-15

基金资助:

南方电网有限责任公司科技项目(0000002022030101XT00031)

Received: 2023-09-7 Revised: 2023-12-20 Accepted: 2024-03-15

作者简介 About authors

李湘(2000—),硕士生,从事人工智能在电力系统暂态稳定问题的应用.

摘要

在双碳目标下,构建以新能源为主体的新型电力系统是实现电力工业转型升级的主要方向和关键途径,新型电力系统背景下快速准确的暂态功角稳定评估研究具有重要意义.为此,基于物理信息嵌入序列到序列(PI-seq2seq)神经网络与级联卷积神经网络模型提出一种含构网型新能源的新型电力系统暂态功角稳定评估方法.首先,采用PI-seq2seq网络结构预测未来功角轨迹,通过构造含物理损失项的损失函数引导模型训练过程,避免时域仿真耗时过长影响快速暂态评估.其次,级联卷积神经网络以预测的功角轨迹作为输入评估暂态稳定情况及其置信度,并配置评估置信度阈值判断机制以实现非固定评估长度的暂态稳定判断,克服了固定功角曲线长度对评估结果的影响.最后,在Kundur系统中进行验证,仿真结果表明:所提方法在功角曲线预测与稳定评估方法均获得令人满意的结果.

关键词： 构网型新能源; 物理信息嵌入序列到序列神经网络; 功角轨迹预测; 级联卷积神经网络; 暂态功角稳定评估

Abstract

Against the backdrop of “dual carbon” goals, the construction of a new power system with new energy as the main component is the main direction and key way for the transformation and upgrading of the power industry. Research into fast and accurate evaluation of transient power angle stability in the context of new power systems is of great significance. To address this, a new transient power angle stability evaluation method is proposed for power systems with grid-forming new energy based on the physics-informed sequence-to-sequence (PI-seq2seq) neural networks and cascaded convolutional neural networks models. First, the PI-seq2seq network structure is used to predict the future power angle trajectory, and a loss function with physical loss terms is constructed to guide the model training process, which avoids the long-duration time-domain simulation to ensure fast transient evaluation. Then, predicted power angle trajectory is taken as input by the cascade convolutional neural networks to evaluate the transient stability and its confidence level. A threshold judgment mechanism for the evaluation confidence level is configured to realize the transient stability judgment of the non-fixed evaluation length, which overcomes the impact of the fixed power angle curve length on the evaluation results. Finally, the method proposed is verified in the Kundur system, and the simulation results show that it has obtained satisfactory results in both the power angle curve prediction and the stability evaluation.

Keywords： grid-forming new energy; physics-informed sequence-to-sequence (PI-seq2seq) neural networks; power angle trajectory prediction; cascade convolutional neural networks; transient power angle stability assessment

PDF (1706KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李湘, 陈思远, 张俊, 柯德平, 高杰迈, 杨欢欢. 基于物理信息嵌入的非固定长度电力系统暂态稳定快速评估[J]. 上海交通大学学报, 2025, 59(7): 962-970 doi:10.16183/j.cnki.jsjtu.2023.452

LI Xiang, CHEN Siyuan, ZHANG Jun, KE Deping, GAO Jiemai, YANG Huanhuan. Physics-Informed Fast Transient Stability Assessment of Non-Fixed Length in Power Systems[J]. Journal of Shanghai Jiaotong University, 2025, 59(7): 962-970 doi:10.16183/j.cnki.jsjtu.2023.452

截至2022年底,我国可再生能源新增装机152 GW,占全国新增发电装机的76.2%,可再生能源装机达到 1 213 GW,占全国发电总装机的47.3%,我国新型电力系统的建设和发展呈现势不可挡的态势^[1].可再生能源装机规模的不断扩大使电网变成低惯量的弱电网,近年来发生多起新能源电网停电事件^[2-4],含构网型新能源^[5-7]的新型电力系统暂态稳定问题变得日益复杂,因此深入探索新型电力系统暂态稳定评估方法对系统安全稳定运行具有重要意义.

随着人工智能的发展,以深度学习、迁移学习为代表的机器学习算法以其强大的高维特征挖掘和非线性关系映射能力有效契合以多因素强耦合、随机性和不确定性强、机理复杂等为特点的新型电力系统暂态功角稳定评估问题,弥补了传统方法难以对当前复杂电网进行物理建模的不足,为电力系统暂态功角稳定评估问题拓宽了技术思路.文献[8]中经过时域仿真生成数据,并以固定评估长度作为一维卷积神经网络的输入,通过多尺寸卷积核提取量测数据的多粒度时序信息,实现暂态稳定评估.文献[9]中同样基于时域仿真生成的固定长度数据,采用卷积神经网络和图注意力机制方法进行暂态功角稳定评估.文献[10]中采用双向长短期记忆网络的电力系统暂态功角稳定评估方法,并结合多粒度邻域粗糙集解决失稳样本与暂态稳定样本间的不平衡问题.文献[11]中提出一种基于卷积神经网络的集成主动学习和微调技术方法实现暂态功角稳定评估,降低分类器更新的计算成本,并采用3个不同尺寸卷积核的卷积神经网络(convolutional neural networks, CNN)共同进行暂态功角稳定评估.

然而,上述暂态功角稳定评估方法存在两方面问题.一是依赖时域仿真结果:暂态功角稳定评估需要基于时域仿真中发电机功角曲线进行判断,通过功角曲线的变化趋势来评估稳定或失稳情况,评估结果会受到仿真时效性的影响.二是评估方法采用固定功角曲线长度:暂态功角稳定评估往往采用故障清除后固定功角曲线长度,选取较短的曲线会导致特征信息太少使得评估准确性不高,而选取较长的曲线会导致特征信息冗余且影响评估的快速性,尤其是面对严重的故障,稳定评估时间长会影响制定紧急控制策略的及时性.

物理深度学习与多阶段评估的技术手段为应对上述问题提供了新思路.文献[12]中将物理约束嵌入神经网络中,提出命名为物理信息神经网络(physics-informed neural networks, PINN)的方法.近年来,物理信息嵌入神经网络的思路被广泛应用于传统数学、物理和工程领域的建模及计算,以物理数据双驱动的方式解决问题.在电力系统领域,PINN的思想还处于初步探索和简单应用的阶段.文献[13]中初步探索了将PINN引入单机无穷大系统,证明该方法能有效模拟转子运动方程;另外,PINN的思想在电力系统状态估计^[14-15]、系统动态建模与仿真^[16]等领域均有研究.对于变长的暂态功角稳定评估,文献[17 -19]中集成多个能处理时序数据的同类神经网络,如卷积神经网络、长短期记忆(long short-term memory, LSTM)神经网络,并根据鲁棒性、样本平衡性等需求,设计投票或代价灵敏等策略输出最终稳定评估结果.文献[20]中训练一个LSTM模型,以多个时间段的数据作为输入,结合可信度阈值筛选出不稳定结果.但只训练一个模型,模型为提升泛化性以适应变长输入,将会以同一时间长度的精确性降低为代价.

本文结合物理信息嵌入和多阶段评估的思想,构建物理层嵌入序列到序列-CNN(PI-seq2seq-CNN)模型,提出一种含构网型新能源的新型电力系统快速可靠暂态功角稳定评估方法,主要贡献与创新点如下:

(1) 采用物理信息嵌入神经网络预测未来功角轨迹的方式取代时域仿真计算,该方式既能克服时域仿真无法满足快速稳定评估的局限,又能保证预测结果满足物理一致性,有效结合了时域仿真方法与深度学习.具体而言,将转速与功角之间的微分关系转化为物理约束模块嵌入seq2seq模型,构建PI-seq2seq模型预测未来的功角轨迹,并设计包含物理损失和数据损失两部分的损失函数引导神经网络参数寻优过程,提升功角预测的准确性.

(2) 为了避免固定输入长度对评估结果快速性和可靠性的影响,采用级联CNN模型以逐级增长所输入的功角轨迹长度来实现非固定长度评估.级联CNN模型对不同长度的功角曲线进行逐级评估,对每个长度的功角曲线输出稳定评估结果及其置信度,并配置有阈值判断机制,若置信度大于阈值则提前判断其稳定性;若置信度小于阈值则进行下一级的暂态稳定判断,确保快速暂态功角稳定评估结果的可靠性.

1 暂态功角稳定模型及其转化处理

虚拟同步发电(virtual synchronous generator, VSG)技术控制方式下构网型新能源机组通过模拟同步发电机的转子运动方程实现,并由此获得虚拟转速和功角^[21],具有与传统发电机相似的电力特性.对于一个有g台发电机的多机系统,其暂态稳定分析的动态方程可以由经典二阶发电机转子运动方程表示:

(1)

\begin{array}{l} \frac{d δ_{i}}{d t} = ω_{i} \\ T_{j i} \frac{d ω_{i}}{d t} = - D ω_{i} + P_{m i} - P_{e i} \end{array}\}

式中:δ为发电机的功角;t为时间;ω为转速;T_j为惯性时间常数,T_j=2H,仿真软件中设置H表示惯性系数;D为阻尼系数;P_m、P_e分别为发电机的机械功率和电磁功率;下标i表示发电机编号, i∈[1,g].

时域仿真法是一种可靠的暂态稳定性判别方法,电力系统的转子运动动态方程可以表达为y'=f(x,y),首先对方程进行离散处理,并依据四阶龙格库塔法(fourth order Runge-Kutta,RK4)利用已知的初始条件和微分方程,依次迭代求解下一个时间点上的函数值,龙格库塔法计算公式见附录式(A1).

2 暂态功角稳定评估框架与方法

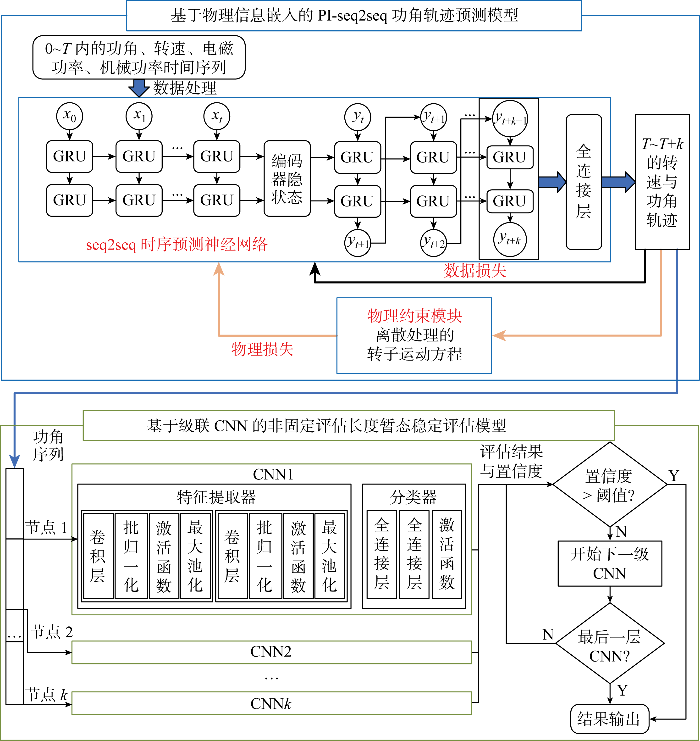
所提暂态功角稳定评估方法整体框架如图1所示,首先基于门控循环单元(gated recurrent unit,GRU)构建PI-seq2seq模型,以0~T时刻内的输入数据预测故障清除后系统在T~T+k时刻内未来功角曲线.然后,以得到的功角曲线作为输入,基于级联 CNN和阈值判断机制实现非固定曲线长度的快速暂态功角稳定评估.图中:x_t、y_t分别为t时刻输入和输出.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 PI-seq2seq-CNN暂态功角稳定评估框架

Fig.1 Framework of PI-seq2seq-CNN transient stability assessment

2.1 暂态功角稳定评估的特征选取

利用深度学习进行暂态功角稳定评估的首要任务是选择能表征暂态功角稳定性的特征量,从原始数据中构建最具灵敏性和准确性的判据指标体系.对于预测模型,依据式(1)中表达的机理关系与时序特性,选取故障清除之后0~T时刻的功角、转速、电磁功率、机械功率的时序数据作为输入特征量,以故障清除之后T时刻以后未来的功角和转速为输出特征,这里引入转速作为输出特征是为了辅助功角的准确预测;对于功角稳定评估模型,根据《电力系统安全稳定导则》^[22]对暂态稳定的定义,暂态稳定判别主要取决于系统发电机之间的功角轨迹是否出现失步情况,因此,选择故障清除之后发电机组的功角轨迹作为输入特征量.

2.2 基于PI-seq2seq的功角曲线预测方法

结合数据驱动和物理约束的方法构建功角曲线预测模型,引入物理信息来提高神经网络的拟合性能,物理约束模块和损失函数的设计将物理信息为额外的约束条件或先验知识来指导神经网络的学习过程,PI-seq2seq的模型框架见图1.

对于数据驱动部分,采用能够处理时序数据的编码器-解码器模型.以GRU网络构建编码器和解码器,seq2seq模型的编码器接受归一化处理后,将故障清除后的转速、功角、机械功率以及电磁功率作为输入,捕捉数据中的关键信息并转化为隐藏状态,作为解码器的初始隐状态.解码器的输入为上一时刻的功角和转速,最终通过全连接层输出未来时间的功角和转速序列.

对于物理约束部分,将描述转速与功角之间微分关系通过RK4进行处理,转化为物理约束模块嵌入进seq2seq网络结构中,要求数据驱动部分求得的功角和转速序列计算满足物理约束.设计包含物理损失和数据损失两部分的损失函数以引导神经网络参数寻优过程,损失函数的数据损失为神经网络预测值和真实值之间的均方根误差(root mean square error,RMSE),物理损失为物理约束结果与真实值之间的RMSE损失,损失函数如下:

(2)

\begin{array}{l} L = L_{1} + L_{2} \\ L_{1} = \sqrt{\frac{1}{N} \sum_{q - 1}^{N} (y_{q} - {\tilde{y}}_{q})} \\ L_{2} = \sqrt{\frac{1}{N} \sum_{q - 1}^{N} ({\tilde{δ}}_{q} - {\hat{δ}}_{q})} \end{array}\}

式中:L为总体损失;L₁为数据损失;L₂为物理损失;N为样本数量;y_q为第q个样本中功角和转速的实际观测值; ${\tilde{y}}_{q}$ 为预测值; ${\tilde{δ}}_{q}$ 为功角预测值; ${\hat{δ}}_{q}$ 为根据RK4计算得到的功角.L₂的加入要求模型训练优化方向满足功角与转速之间的微分关系,要求预测结果满足物理一致性,从而提升预测的准确性.

2.3 基于级联CNN的非固定评估时间暂态功角稳定评估方法

在故障清除后的早期阶段,某些处于临界稳定状态的样本功角曲线特征往往没有表现出明显的稳定或者失稳特性,需要观察曲线在更长仿真时间后的变化趋势才能判别,这给系统的快速功角稳定评估带来一定困难.针对这一问题,通过设置多个功角曲线截止点,对暂态功角稳定性进行多阶段评估,将从故障清除点到每个截止点之间的功角曲线视为神经网络的时序输入,分别输入到级联的多个CNN中,通过捕捉不同长度曲线的功角变化特征,输出评估结果及其置信度.单个CNN的计算公式见附录式(A2),其中置信度为softmax层输出的评估结果概率,置信度越高意味着评估模型预测出的评估结果概率越大.

在对一条功角曲线进行多阶段评估时,提出一种评估置信度阈值判断机制,逻辑伪代码如算法一所示.具体表现为:每个阶段的评估任务由各级的CNN模型承担,分别输出各阶段的稳定判断结果以及置信水平,当某一级的评估结果置信水平达到预设的稳定性阈值时或者已到达最末一级,其稳定判断结果被认为可信而输出结果,否则被认为该判断结果无效而进入下一个阶段的评估.在配置该阈值判断机制下,层级低的CNN能够及时分辨明显稳定或不稳定序列,层级高的CNN输入功角序列长,预测结果可靠性高,各级CNN之间通过阈值是否满足要求来配合运行.因此,基于所提机制的级联CNN模型能够兼顾暂态稳定评估的快速性和准确性需求.

算法一: 级联CNN运行逻辑

输入:级联CNN总级数M,对应M个阶段的功角序列,功角序列均储存在A数组,置信度阈值S

输出:评估结果z,置信度c,当前层级m

1. function CNN_m(A_m):

2. return z,c

3. end function

4. 初始化当前CNN级数m= 0,c=0

5. while m<M and c<S do

6. m← m+1

7. z,c ← CNN_m(A_m)

8. end while

3 仿真与结果

3.1 算例分析

3.1.1 算例描述

采用开源的电力系统暂态仿真软件ANDES^[23]作为时域仿真引擎,利用Python语言建立Kundur系统的仿真环境,通过生成包含多类暂态场景的样本集,对所提方法进行建模和效果验证.Kundur电力系统是典型的暂态稳定分析系统,在原系统上改进,共设置10个节点和4台发电机,系统的基准频率为60 Hz.在PI-seq2seq学习到基础暂态特性之后,将第4台传统同步机组替换为VSG控制的风电机组,如附录图A1所示.

3.1.2 场景数据生成方法

基于ANDES的时域仿真功能来获取数据,将第4台发电机替换为VSG控制的新能源发电机,暂态仿真设置情况如下:

(1) 初始运行条件.包括有功和无功功率的所有负荷在基准负荷水平的90%~120%范围内变化,并添加标准差为0.1的噪声,避免单一运行状态导致的算法拟合空间过小的情况,采用牛顿拉夫逊法计算潮流,确定运行条件.根据被替换的发电机组参数,设置VSG变流器的惯性系数H∈{10,12.5,15},阻尼系数D∈{0.1,0.5,0.9}.

(2) 故障设置.故障事件设置为于1.0 s任意母线、支路的三相接地故障,故障清除时间设置为{1.05 s,1.1 s,1.15 s,1.2 s,1.25 s,1.3 s}.仿真步长设置为0.01 s.

(3) 稳定判断.依据《电力系统安全稳定导则》,暂态稳定被定义为电网遭受扰动后,各机组之间功角相对摇摆,经过第1、第2振荡周期不失步的情况.故选取暂态稳定系数作为暂态功角稳定评估指标,如下:

(3)α_TSI=

\frac{360 ° - δ_{m a x}}{360 ° + δ_{m a x}}

式中 :δ_max为系统任意两台发电机之间的最大功角.设置仿真时长为20 s,以20 s时刻的功角情况计算α_TSI.当α_TSI>0,系统暂态稳定;当α_TSI<0,系统暂态失稳,据此对样本的暂态稳定情况标注.

3.1.3 数据处理

首先,对生成的样本进行数据筛选,排除未收敛的样本数据;另外,为避免暂态特征量之间的量纲差异,对功角采用正弦和余弦变换,对其他特征数据采用Z-score标准化.

在时域仿真过程中,ANDES在求解微积分时采用的隐形梯形积分算法会根据收敛情况调整步长,造成步长变小,采用固定步长容易导致不收敛的情况.因此,对非固定步长的数据进行线性插值处理,得到固定步长为0.01 s的暂态仿真数据.

3.2 基于PI-seq2seq的功角轨迹预测模型验证

3.2.1 功角预测模型参数配置与训练设置

功角轨迹预测模型的参数设置如表1所示,配置和训练设置如下:

表1 PI-seq2seq功角轨迹预测模型训练配置

Tab.1 Training configuration for PI-seq2seq angle trajectory prediction model

参数	含义	取值
Input_len	输入长度	5步长
Output_len	预测长度	20步长
Input_dim	输入特征数量	20
Output_dim	输出特征数量	2
Learning_rate	学习率	3×10^-4(预训练)/ 1×10^-4(微调)
Hidden_size	隐藏层大小	128
Epoch	训练轮次	80
Batch_size	训练批次大小	64
Optimizer	优化器	Adam
Loss function	损失函数	RMSE

新窗口打开| 下载CSV

(1) 获取有效样本数量共计 5 515 个,样本按照8∶2的比例划分为训练集和测试集,测试集复用为验证集.

(2) 在训练阶段,为了加速收敛速度并提高模型性能,将解码器设计为接收前一时刻的标签数据作为输入.这样,预测点前的实际标签信息被引入解码器,能够帮助模型训练时更准确地学习任务特征和模式.在验证和预测阶段,为了模拟真实应用场景,不引入实际标签数据,而是将前一时刻的预测结果作为解码器的输入,可评估模型的泛化能力以及其在未知数据上的预测效果.

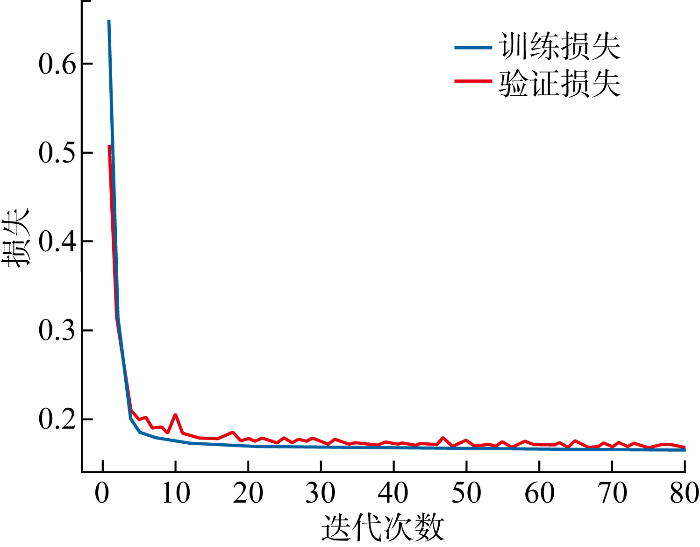
(3) 使用4个相同结构的模型分别预测4条发电机的功角轨迹,提升模型的准确性,通过数据汇总得到4条功角轨迹并输送至评估模型.算例后续结果均针对第1台发电机功角对应的模型展开.图2展示了使用RK4的PI-seq2seq模型,即PI-seq2seq(RK4)的损失曲线.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 PI-seq2seq (RK4) 功角轨迹预测模型损失曲线

Fig.2 Loss curves of angle trajectory prediction model PI-seq2seq (RK4)

3.2.2 功角轨迹预测模型效果对比分析

对比seq2seq、使用向前欧拉法处理的PI-seq2seq模型(PI-seq2seq(Euler))以及PI-seq2seq(RK4)共3种模型,各模型的配置相同见表1.比较平均绝对误差、均方误差、平均相对误差这3种指标,各模型在测试集中的误差如表2所示.可知所提PI-seq2seq(RK4)各项误差最低,表现最优,拟合的相对误差最小.模型2将向前欧拉法转化式(2)为物理约束模块的方式,其性能比没有引入物理约束的模型1高,验证了物理信息的嵌入能够引导模型的训练方向,提升模型的性能.而模型3采用更高精度的龙格库塔法,能够进一步模型拟合性能.

表2 不同功角轨迹预测模型的误差

Tab.2 Test errors of different angle trajectory prediction models

模型序号	模型	平均绝对误差	均方误差	平均相对误差/%
1	seq2seq	5.531×10^-3	8.412×10^-5	0.7226
2	PI-seq2seq(Euler)	5.199×10^-3	8.975×10^-5	0.4820
3	PI-seq2seq(RK4)	4.359×10^-3	7.117×10^-5	0.4189

新窗口打开| 下载CSV

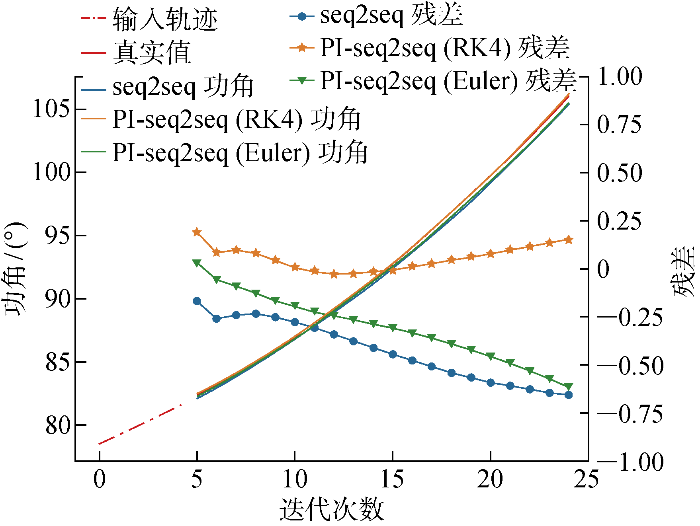
图3展示了功角预测结果及残差情况,可见,这几种模型都能够较准确地预测功角曲线,而所提方法的曲线紧靠真实曲线,误差最小,最能准确预测功角趋势.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 3种模型预测结果

Fig.3 Prediction results of three models

此外,在计算速度上,所提方法在保证预测精度的同时,相较于时域仿真大幅度降低计算耗时.表3对比了仿真软件ANDES和所提方法计算耗时情况.实验环境配置情况为Intel(R) Core(TM) i5-8250U CPU @1.60 GHz,1.80 GHz,4个内核,8个逻辑处理器,对比ANDES仿真软件和训练好的PI-seq2seq(RK4)模型在相同计算或预测长度下所耗时间.为避免偶然情况,以100次场景进行测试,取平均值为平均耗时.由表可见,所提方法耗时明显较短,计算速度相较于时域仿真方法显著提升.随着预测时长增加,时域仿真计算耗时较大程度增加,预测耗时增幅可忽略不计.

表3 对比时域仿真的耗时情况

Tab.3 Comparison of time consumption of time-domain simulations

计算长度	Andes时域仿真平均耗时/s	PI-seq2seq(RK4) 平均耗时/s
0.3 s功角曲线	0.3480	0.0199
0.5 s功角曲线	0.5300	0.0215

新窗口打开| 下载CSV

3.3 基于级联卷积神经网络的暂态功角稳定评估模型效果验证

3.3.1 级联CNN各级CNN的暂态稳定评估性能分析

暂态功角稳定评估模型以仿真数据进行训练,设置3个级联一维CNN,三级CNN的输入长度依次设置为故障清除后10、15、25步长的数据量,其他训练参数配置如表4所示,训练和测试数据同3.2.1节中的训练集、测试集数据.

表4 级联CNN暂态功角稳定评估模型训练配置

Tab.4 Training configuration for cascade CNN transient stability assessment model

参数	含义	取值
Kernal size	卷积核大小	3×3
Learning_rate	学习率	3×10^-4
Epoch	训练轮次	100
Batch_size	训练批次大小	64
Optimizer	优化器	Adam
Loss function	损失函数	交叉熵损失

新窗口打开| 下载CSV

准确率是评估分类模型性能的重要指标之一,但在暂态稳定评估(transient stability assessment, TSA)问题中,由于数据集具有样本不均衡性和非稳定情况错分代价大的特点,仅评估准确率可能不足以全面评判模型对失稳情况的辨识能力,所以针对失稳情况综合使用准确率(A_cc)、查准率(P_rec)、查全率(R_ecall)和F₁值(F_1-score)等指标对TSA模型的性能进行评估计,指标计算公式可表示为

(4)

\begin{array}{l} A_{c c} = \frac{T_{P} + T_{N}}{T_{P} + F_{P} + F_{N} + T_{N}} \\ P_{r e c} = \frac{T_{N}}{T_{N} + F_{N}} \\ R_{e c a l l} = \frac{T_{N}}{T_{N} + F_{P}} \\ F_{1 - s c o r e} = \frac{2 P_{r e c} R_{e c a l l}}{P_{r e c} + R_{e c a l l}} \end{array}\}

式中:T_P为标签为稳定的预测正确样本数量;F_P为标签为失稳的错误预测样本数量;F_N为标签为稳定的错误预测样本数量;T_N为标签为失稳的预测正确样本数量.

各级CNN的训练曲线和评估性能如附录图A2和表5所示,对比不同层级CNN的表现情况,随着CNN模型的层级增加,模型的准确性增加.这是因为随着层级的增加,模型能够获取更长的信息序列,捕捉到更多功角的动态和趋势特征,从而使评估结果更加准确可靠.表5表明随着层级的增加,CNN模型的各项指标表现越来越优异,进一步验证了设置的评估时间长度对准确性的影响.

表5 基于级联CNN的TSA模型的评估结果

Tab.5 Evaluation results of cascaded CNN TSA model %

层级	准确率	查准率	查全率	F₁
CNN1	97.28	90.74	95.14	92.89
CNN2	98.73	95.23	97.09	96.15
CNN3	99.27	98.05	98.05	98.05

新窗口打开| 下载CSV

3.3.2 配置置信度阈值判断机制的级联CNN模型暂态稳定评估效果验证

针对3.3.1节训练好的最优CNN1~CNN3模型,设置阈值为0.95,添加置信度阈值判断机制,统计得到各级CNN评估结果如表6所示.

表6 级联CNN评估结果

Tab.6 Results of cascade CNN assessment %

层级	满足阈值占比	准确率	查准率	查全率	F₁
CNN1	95.47	95.28	100	83.01	89.25
CNN2	97.37	97.83	97.22	98.91	98.04
CNN3	100	99.09	96.65	98.06	97.35

新窗口打开| 下载CSV

CNN1仅需要0.1 s的功角评估长度,能够对满足阈值的失稳样本实现完全正确的准确识别,能及时判断并提醒调度员快速采取措施,以确保系统的安全稳定运行.随着后续层级增加,对不满足阈值的样本进行暂态稳定评估,CNN3模型的准确率达到99.09%;模型F₁值较低的原因在于样本存在不平衡性,而失稳样本的查全率较高,失稳的误判率较低,证明所提阈值判断机制能够有效筛选出错误样本,实现准确性和快速性的平衡.

4 结论

根据物理数据双驱动、非固定评估长度等创新思想,提出一种基于PI-seq2seq与级联CNN的新型电力系统暂态功角稳定快速评估方法.通过仿真以及与其他算法的对比,得到如下结论:

(1) 通过构建基于PI-seq2seq的功角轨迹预测模型,可以模拟传统时域仿真预测未来功角曲线轨迹.该模型将物理信息集成到深度学习框架中,通过损失函数的物理损失项引导模型训练以满足物理一致性,相对于其他深度学习预测模型,所提方法的功角轨迹预测性能最优;且在低误差下能够快速预测出未来功角轨迹,避免了长时间时域仿真计算.物理信息与深度学习结合的方式为后续快速暂态功角稳定评估提供了有力支持.

(2) 采用级联CNN实现利用非固定长度功角曲线进行暂态稳定的快速准确评估.级联CNN结构可以有效地提取不同长度的暂态特征,且随着输入长度增加,评估性能越好.结合基于置信度阈值判断机制的多阶段评估构架,在满足预测结果可信度达标的情况下,能够尽早评估暂态稳定情况,有效平衡评估快速性与准确性的需求.

未来计划将所提方法应用至更大规模的电力系统以及真实电力系统;采取更精确的发电机模型,从输入特征以及物理信息的丰富角度提升模型的准确性和合理性;探索临界稳定和临界不稳定的数据增强方法,提升级联CNN的可辨识能力.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-7-962.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

中华人民共和国国家能源局.

国家能源局2023年一季度新闻发布会文字实录

[EB/OL]. (2023-02-13)[2023-8-28]. http://www.nea.gov.cn/2023-02/13/c_1310697149.htm.

URL [本文引用: 1]

National Energy Administration of the People’s Republic of China.

Transcript of the National Energy Administration’s press conference for the first quarter of 2023

[EB/OL]. (2023-02-13)[2023-8-28]. http://www.nea.gov.cn/2023-02/13/c_1310697149.htm.

URL [本文引用: 1]

[2]

何剑, 屠竞哲, 孙为民, 等.

美国加州“8·14” 、“8·15” 停电事件初步分析及启示

[J]. 电网技术, 2020, 44(12): 4471-4478.