单相高频逆变器无窄脉冲高质量调制方法

doi:10.16183/j.cnki.jsjtu.2023.426

单相高频逆变器无窄脉冲高质量调制方法

张国澎¹^,², 陈东安^,¹, 陶海军¹, 刘永辉³, 马原¹

1.河南理工大学电气工程与自动化学院,河南焦作 454003

2.河南省煤矿装备智能检测与控制重点实验室,河南焦作 454003

3.河南洛宁抽水蓄能有限公司,河南洛阳 471700

Single-Phase High Frequency Inverter Narrow Pulse High-Quality Modulation Method

ZHANG Guopeng¹^,², CHEN Dongan^,¹, TAO Haijun¹, LIU Yonghui³, MA Yuan¹

1. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454003, Henan, China

2. Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment, Jiaozuo 454003, Henan, China

3. Henan LuoningPumped Storage Co., Ltd., Luoyang 471700, Henan, China

通讯作者: 陈东安,硕士生;E-mail:cda4702160168@163.com.

责任编辑: 王一凡

收稿日期: 2023-08-28 修回日期: 2024-01-3 接受日期: 2024-01-17

基金资助:

国家自然科学基金(52267018)
河南省高校基本科研业务费专项资金(210423)

Received: 2023-08-28 Revised: 2024-01-3 Accepted: 2024-01-17

作者简介 About authors

张国澎(1974—),副教授,从事大功率电力电子变换器、电能质量等研究.

摘要

针对高频单相两电平逆变器运行于高调制比下存在的窄脉冲问题,分析了正弦脉宽调制(SPWM)策略下调制比、载波频率和死区对窄脉冲的影响,得出调制波周期内的窄脉冲分布规律.在此基础上提出一种无窄脉冲的高质量调制方法,消除了高频逆变器调制周期内的窄脉冲.同时,为了解决该方法在调制波峰谷处存在的波形畸变问题,设计一种三拍载波预测法,通过对窄脉冲区域内调制方法的修正,进一步改善了交流侧输出波形质量.最后,搭建了单相全桥逆变器实验平台,对所提无窄脉冲高质量调制方法的可行性和有效性进行验证.

关键词： 窄脉冲; 波形畸变; 高频逆变; 死区; 单相

Abstract

To analyze the narrow pulse issue of high-frequency single-phase two-level inverter running at high modulation ratio, the effects of modulation ratio, carrier frequency, and dead time on the narrow pulse under sinusoidal pulse width modulation (SPWM) strategy are examined, and the distribution law of the narrow pulse within the modulating wave period is derived. Based on this analysis, a high-quality modulation method without narrow pulses is proposed to eliminate narrow pulses within the modulation cycle of high-frequency inverters. To address the waveform distortion issue at the modulation peak and valley in this method, a three-beat carrier prediction method is designed to further improve the quality of the alternating current (AC) output waveform by modifying the modulation within the narrow pulse area. Finally, a single-phase full bridge inverter experimental platform is built to verify the feasibility and effectiveness of the proposed narrow pulse-free high-quality modulation method.

Keywords： narrow pulse; waveform distortion; high-frequency inverter; dead time; single phase

PDF (7288KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张国澎, 陈东安, 陶海军, 刘永辉, 马原. 单相高频逆变器无窄脉冲高质量调制方法[J]. 上海交通大学学报, 2025, 59(7): 952-961 doi:10.16183/j.cnki.jsjtu.2023.426

ZHANG Guopeng, CHEN Dongan, TAO Haijun, LIU Yonghui, MA Yuan. Single-Phase High Frequency Inverter Narrow Pulse High-Quality Modulation Method[J]. Journal of Shanghai Jiaotong University, 2025, 59(7): 952-961 doi:10.16183/j.cnki.jsjtu.2023.426

近年来,随着功率半导体器件的发展,超高速永磁发电机以其功率密度高、结构紧凑等特点,在航空航天、医疗等高性能要求领域需求急剧上升^[1-3].目前超高速永磁发电机多采用单相两电平逆变器结构^[4],且随着发电机转速的进一步提升,既要求逆变器输出波形质量最优,又要求较强的响应速度^[5].因此,行之有效的方式为提高逆变器开关频率.窄脉冲^[6]问题是高频逆变必须解决的核心问题之一,会严重影响逆变器的运行安全和输出波形质量,尤其是死区的加入^[7],会加剧窄脉冲的产生.因此,解决高频逆变器的窄脉冲问题是保证逆变器输出高质量波形的基础^[8].

为了解决窄脉冲问题,文献[9]中提出通过归一化扇区的调制策略来抑制窄脉冲产生,其原理是先对空间矢量调制下的扇区进行归一化后,通过抑制窄脉冲的产生来消除窄脉冲影响,但文献中没有解决合成矢量位于极限情况下的窄脉冲问题.文献[10]中设计了适用于虚拟空间矢量脉宽调制(space vector pulse width modulation,SVPWM)的窄脉冲抑制算法,根据开关矢量分配的基本原则,在窄脉冲区域优化开关矢量的分配时序和作用时间,从而消除窄脉冲;但该算法只能避免部分窄脉冲,使开关频率增加,且该文献并未分析死区对输出波形谐波畸变率(total harmonic distortion,THD)的影响^[11].文献[12-13]中通过向三相调制波同时注入零序分量展宽或剔除开关管开通时间,消除某一相的窄脉冲,保证了三相的对称性;但因为修改了三相调制波,可能会使原本没有窄脉冲的其他相产生新的窄脉冲.文献[14]中根据开关器件的触发脉宽,设置一个窄脉冲限值,令小于该限值的调制波占空比恒等于该限值,以达到消除窄脉冲的目的;但该方法会在窄脉冲限值区域内生成错误的占空比,且随着频率的提高,会导致输出波形畸变越发严重.文献[15]中为了消除窄脉冲提出了一种新型载波脉宽调制(carrier-based pulse width modulation,CBPWM)策略,通过分析开关管的开关状态与输出电压的关系,推导出了开关管的占空比,在窄脉冲区域内实现恒定占空比的变化,从而消除窄脉冲的影响;但该方法在高频调制时由于占空比恒定,会明显增大输出波形谐波含量.

针对上述问题,首先研究了高频逆变器两电平正弦脉冲宽度调制(SPWM)中,调制比、载波和死区对窄脉冲的影响,得出调制周期内的窄脉冲分布规律.在此基础上,提出了一种无窄脉冲的高质量调制方法,消除调制波峰谷值附近窄脉冲的同时,提高了输出波形质量.为解决该方法在调制波峰谷处存在的波形畸变问题,提出了一种三拍载波预测法,在不影响无窄脉冲调制效果的前提下,改善了交流侧输出波形畸变问题.所提方法在高频高调制区域内,有效地解决了单相两电平逆变器的窄脉冲问题,同时也降低了输出波形谐波含量.最后,搭建实验平台验证所提无窄脉冲调制方法的有效性.

1 高频逆变器窄脉冲产生机理

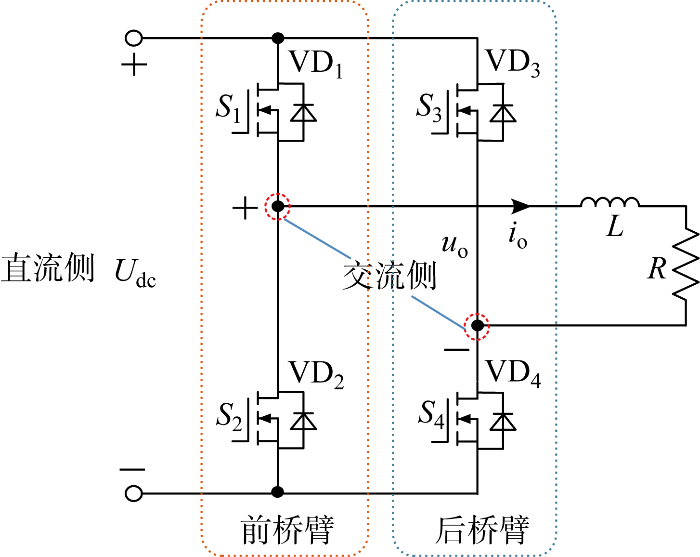
图1为电压源型单相全桥逆变器拓扑.图中:功率开关管S₁和S₂、S₃和S₄分别构成单相逆变桥前、后两个桥臂,其中S₁、S₂互补导通,S₃、S₄互补导通;VD₁~VD₄是开关管S₁~S₄的反并联二极管;U_dc为单相逆变桥直流侧输入电压;u_o、i_o分别为交流侧输出电压、电流;L为交流侧电感值;R为交流侧电阻值.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 单相全桥逆变器拓扑

Fig.1 Topology of voltage source single-phase full bridge inverter

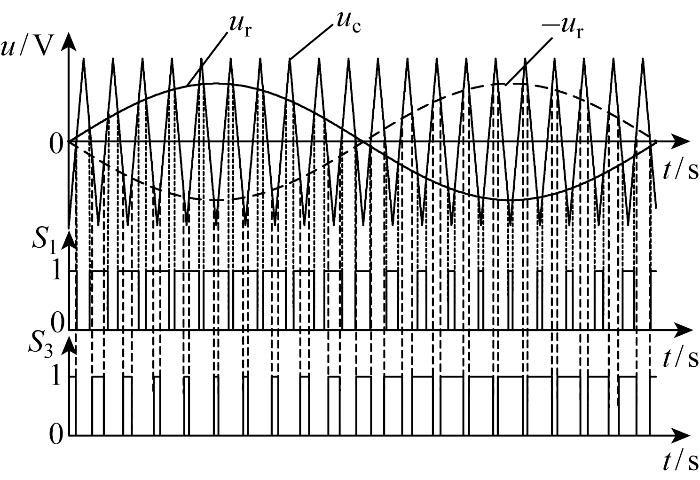
调制采用单极性SPWM,原理如图2所示.图中:u_c为载波;u_r为调制波,u_r=Msin ωt,调制比M为u_r与u_c的峰值之比,ω为调制波角频率.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 单极性SPWM原理

Fig.2 Principle of unipolar SPWM

图2中,当u_r>u_c时,功率半导体开关管S₁开通,S₂关断;反之S₁关断,S₂开通.同理可得,当-u_r>u_c时,S₃开通,S₄关断;反之S₃关断,S₄开通.

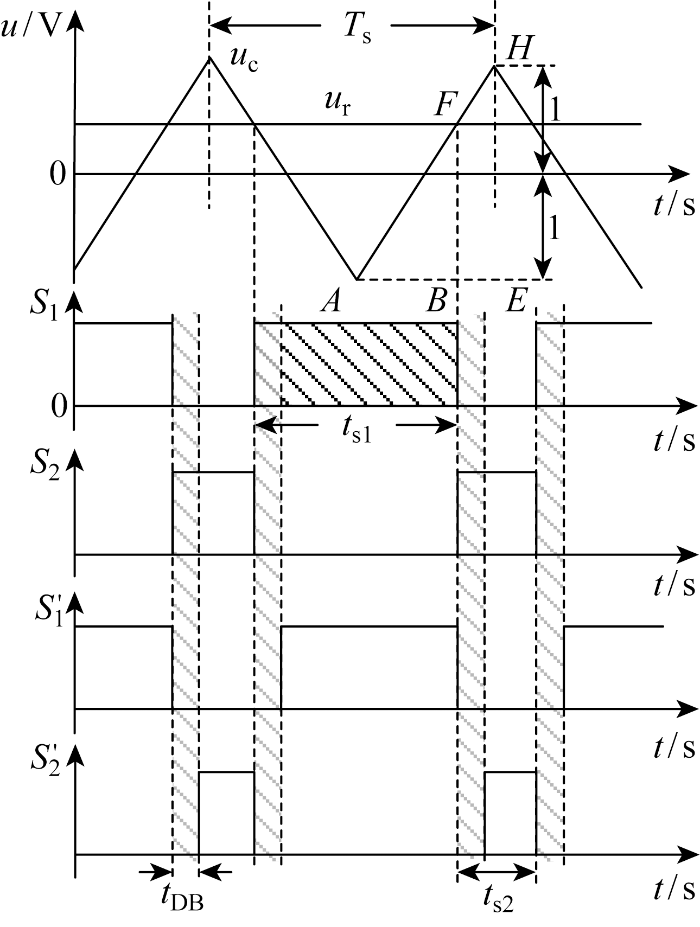
当载波频率f_c远远大于调制波频率f_r时,认为调制波u_r在一个载波周期内不变.以开关管S₁、S₂为例,载波与死区对开通时间的影响如图3所示.图中:T_s为载波周期;t_s1为开关管S₁的开通时间;t_s2为开关管S₂的开通时间;t_DB为死区时间;S'₁、S'₂为加入死区后的开关管触发脉冲.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 死区加入前后开关管工作状态

Fig.3 Working status of the switch before and after addition of dead time

根据图3中几何关系推导可得:

(1)

\frac{t_{s 1}}{T_{s}}

\frac{t_{A B}}{t_{A E}}

\frac{t_{B F}}{t_{E H}}

\frac{1 + u_{r}}{2}

\frac{1}{2}

(1+Msin ωt)

由式(1)可知,若T_s不变,随着M的增大,调制波在波峰附近时,会导致开关管S₁的关断时间过短,当该时间小于开关管允许的最小开关时间t_nar时,产生关断窄脉冲;同理调制波在波谷附近时,若t_s1< t_nar,会产生开通窄脉冲.

若M不变,随着T_s的减小,即载波频率的增大,导致开关管S₁的开通时间t_s1减小,当其小于t_nar时,产生窄脉冲.尤其是高调制比下,窄脉冲更容易产生.因此,高频逆变器在高调制比下,窄脉冲问题不可避免.

图3中死区加入方式为:将S₁上升沿延迟一个死区t_DB,下降沿不变,得到S'₁信号;S₂上升沿保持不变,将下降沿延迟一个死区t_DB,得到S'₂信号.可见,死区加入后t_s1、t_s2较加入前均减小了t_DB,使得开关管的开通时间提前t_DB进入窄脉冲区,相当于增加窄脉冲区域的判定区间,加剧窄脉冲的产生.

综上所述,通过分析单相两电平逆变器窄脉冲产生与调制比、载波周期死区的关系,得出窄脉冲区域并非固定不变,且死区在整个调制周期的占比也无法忽略.因此,窄脉冲区域内的调制策略将会极大地影响逆变器输出波形的质量.

2 单相高频逆变器无窄脉冲高质量

调制要保证逆变器输出波形质量,就要使SPWM后的输出波形在窄脉冲区域按正弦规律变化.而文献[13]中的窄脉冲消除采用一种载波周期固定的调制方法,以开关管S₁为例,固定载波周期的窄脉冲补偿原理如图4所示.图中:t_on为开关管的开通时间.

图4

新窗口打开| 下载原图ZIP| 生成PPT

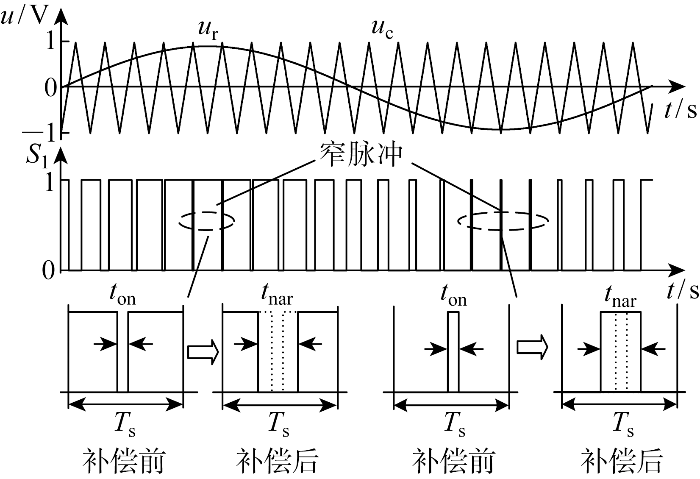
图4 固定载波周期变化的窄脉冲补偿示意图

Fig.4 Schematic diagram of narrow pulse compensation with fixed carrier period variation

由图4可知,在调制波峰值附近出现的窄脉冲为开关管关断窄脉冲,采用微机实现时,计算得开关管关断时间t_off,由于t_off<t_nar,需要将其展宽至t_nar;同理在调制波波谷值附近出现开通窄脉冲,此时计算出t_on,当t_on<t_nar时,将其展宽至t_nar.

文献[13]中的窄脉冲补偿方法通过将最小脉宽限制t_nar值来消除窄脉冲,单相高频应用中,因为载波周期和开关管导通、关断时间均固定不变,所以会在窄脉冲区域生成固定占空比,使输出波形失去正弦变化.为此,本文提出了一种变载波频率的无窄脉冲调制,通过调节T_s,使输出波形在窄脉冲区域内依然按其正弦规律变化,也就是将现有的SPWM中固定的载波周期变为可调载波周期.

2.1 无窄脉冲调制原理

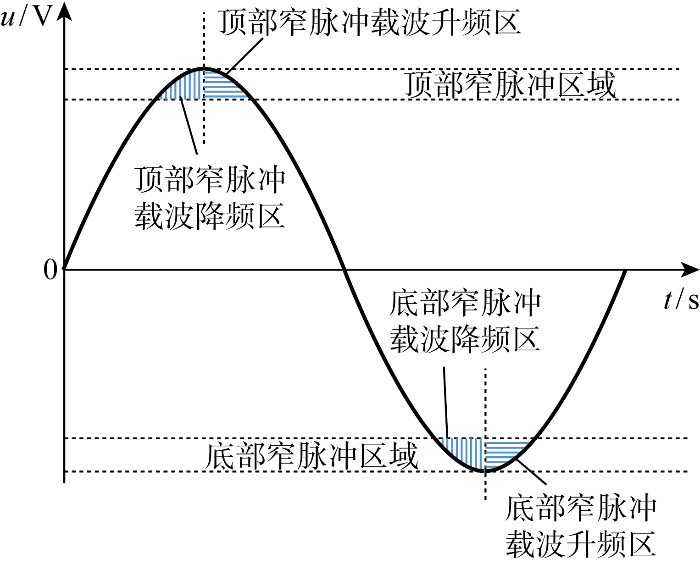
根据SPWM时窄脉冲出现的位置,将窄脉冲区域分为顶部窄脉冲区与底部窄脉冲区.根据在窄脉冲区域载波频率的变化趋势,又可将窄脉冲区域细分为:顶部窄脉冲载波升频区、顶部窄脉冲载波降频区、底部窄脉冲载波升频区、底部窄脉冲载波降频区,如图5所示.在调制过程中,若进入窄脉冲区域,按照t_nar作为功率半导体开关管的最小开关时间.通常应有t_nar≥2t_DB,为便于论述,以下均令t_nar=2t_DB.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 SPWM窄脉冲区域划分

Fig.5 Division of SPWM narrow pulse region

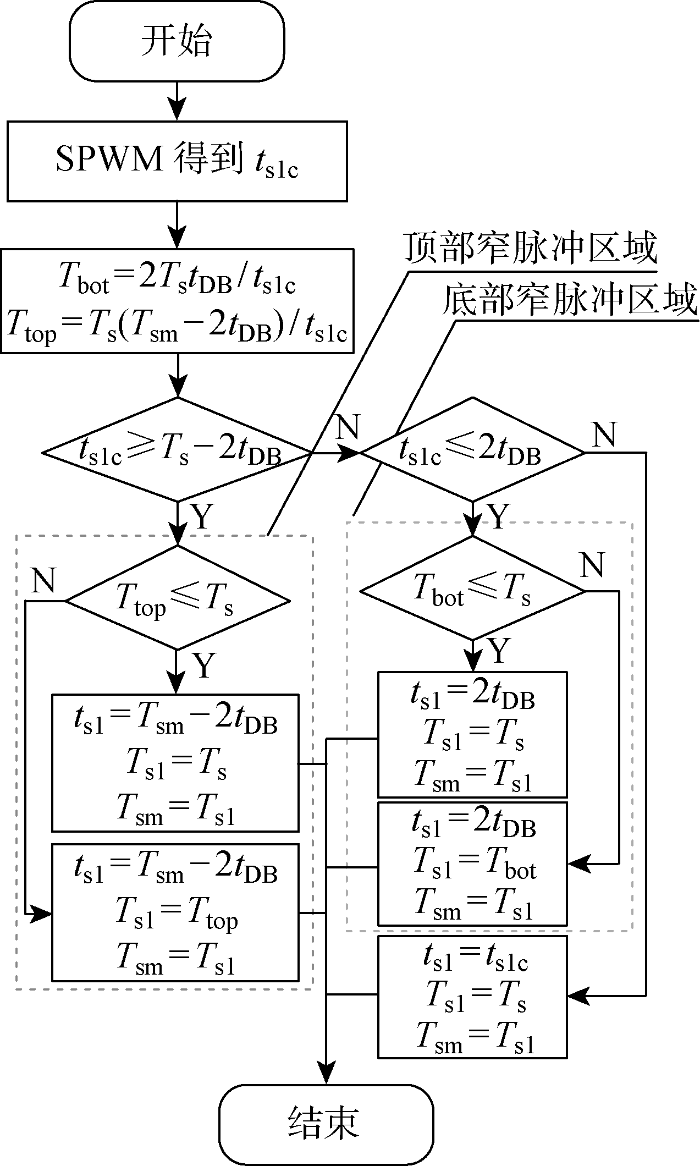
仅考虑功率半导体开关管S₁的执行信号,在控制上,通过计算当前载波周期的T_s1与t_s1,然后下一个载波周期时开始执行,其具体实施步骤如图6所示.图中:T_bot为底部窄脉冲区域的载波周期计算值;T_top为顶部窄脉冲区域的载波周期计算值;T_sm为存储的当前载波周期的载波周期执行值;T_s1为下一个载波周期实际执行的载波周期值;t_s1c为下一个载波周期S₁的开通时间.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 无窄脉冲高质量调制法流程图

Fig.6 Flow chart of high-quality modulation without narrow pulse

首先,通过SPWM得到开通时间t_s1c=T_s(1+Msin ωt)/2;并计算T_bot与T_top,计算方法如下所示.

调制波进入顶部窄脉冲区域,开关管S₁不产生窄脉冲的导通时间t_s1=T_sm-2t_DB,将t_s1代入式(1)可得载波周期由T_s变为T_top,其表达式如下:

(2)T_top=

\frac{2 (T_{s m} - 2 t_{D B})}{1 + M s i n ω t}

将式(2)中1+Msin ωt用式(1)中变量表述得到T_top的最终表达式:

(3)T_top=

\frac{T_{s} (T_{s m} - 2 t_{D B})}{t_{s 1 c}}

同理当调制波进入底部窄脉冲区域时,使得开关管S₁不产生窄脉冲的导通时间t_s1=2t_DB,将t_s1代入式(1)可得载波周期由T_s变为T_bot,其表达式如下:

(4)T_bot=

\frac{4 t_{D B}}{1 + M s i n ω t}

将式(2)中1+Msin ωt用式(1)中变量表述得到T_bot的最终表达式:

(5)T_bot=

\frac{2 T_{s} t_{D B}}{t_{s 1 c}}

当t_s1c≥T_s-2t_DB时,下一个载波周期调制进入顶部窄脉冲区域.在该区域内,载波周期会随着时间先增加后减小.若T_top>T_s,令t_s1=T_sm-2t_DB、T_s1=T_top;若T_top≤T_s,下一个载波周期调制结束顶部窄脉冲降频,进入正常区域.此时T_s1由T_top变为T_s,其他参数不变.T_sm一直存储T_s1的值,便于下一个载波周期调用计算.

当t_s1c≤2t_DB时,下一个载波周期调制进入底部窄脉冲区域.在该区域内,若T_bot>T_s,令t_s1=2t_DB、T_s1=T_bot;若T_bot≤T_s,下一个载波周期调制结束底部窄脉冲降频,进入正常区域.此时T_s1由T_bot变为T_s,其他参数不变.T_sm存储T_s1的值,便于下一个载波周期调用计算;当载波周期调制在非窄脉冲区域时,t_s1=t_s1c,T_s1=T_s,且T_sm存储T_s1的值.

由式(2)、(4)可知,在调制波峰谷值附近高调制比会导致相邻的两个载波周期值相差较大,以负半周期调制波为例,载波周期随调制波变化如图7所示.图中:k为调制周期.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 正半周期调制波与载波周期变化

Fig.7 Positive half-cycle modulation wave and carrier period variation

由图7可知,调制波波谷值处的载波周期值T_bot(k+2)与T_bot(k+1)和T_bot(k+3)的差值很大,较大的载波周期差值会使得输出波形的质量变差,从而影响调制效果.为了防止载波周期在调制波峰谷值附近出现较大差值,需要对调制波峰谷值附近处的载波进行修正.

2.2 调制波峰谷值处策略修正

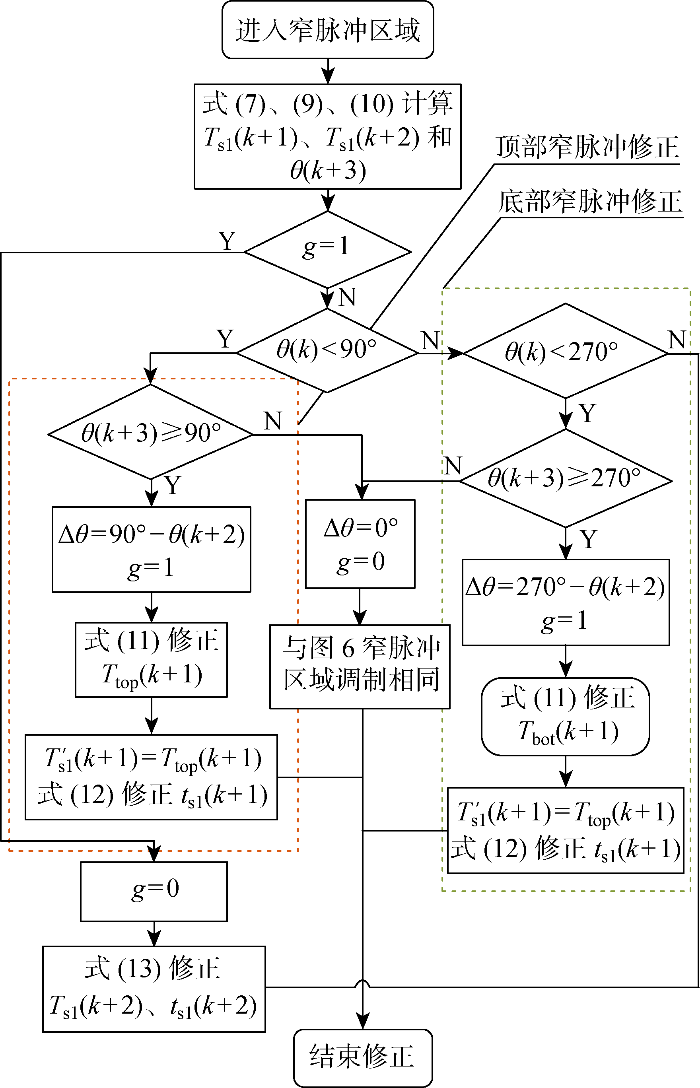
在窄脉冲区域内,载波周期T_s随着频率的降低而增大.为了解决T_s在调制峰谷值附近出现较大差值而影响正常的降频过程,采用三拍载波预测法,对跨过调制波峰谷值的当前载波周期和下一载波周期进行修正,防止载波周期的不正常变化,修正流程如图8所示.图中:Δθ为调制波峰谷值与θ(k+2)之差;g为标志位.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 调制波峰谷值修正策略流程图

Fig.8 Flow chart of correction strategy at modulation peak and valley

进入窄脉冲区域后,根据当前调制波起始角度θ(k)和载波周期值T_s1(k)的关系,计算下一个载波周期的调制波起始角度θ(k+1):

(6)θ(k+1)=θ(k)+ωT_s1(k)

将θ(k+1)代入式(2)、(4),得到载波周期T_s1(k+1)在顶、底部窄脉冲区域的变化:

(7)T_s1(k+1)=

\{\begin{array}{l} T_{t o p} (k + 1) = \frac{2 (T_{s m} - 2 t_{D B})}{1 + M s i n [θ (k + 1)]} \\ T_{b o t} (k + 1) = \frac{4 t_{D B}}{1 + M s i n [θ (k + 1)]} \end{array}

由θ(k+1)和T_s1(k+1)的值,计算调制波起始角θ(k+2):

(8)θ(k+2)=θ(k+1)+ωT_s1(k+1)

将θ(k+2)代入式(2)、(4)可得载波周期T_s1(k+2)在顶、底部窄脉冲区域的变化:

(9)T_s1(k+2)=

\{\begin{array}{l} T_{t o p} (k + 2) = \frac{2 (T_{s m} - 2 t_{D B})}{1 + M s i n [θ (k + 2)]} \\ T_{b o t} (k + 2) = \frac{4 t_{D B}}{1 + M s i n [θ (k + 2)]} \end{array}

根据计算出的θ(k+2)和T_s1(k+2)由式(6)计算θ(k+3):

(10)θ(k+3)=θ(k+2)+ωT_s1(k+2)

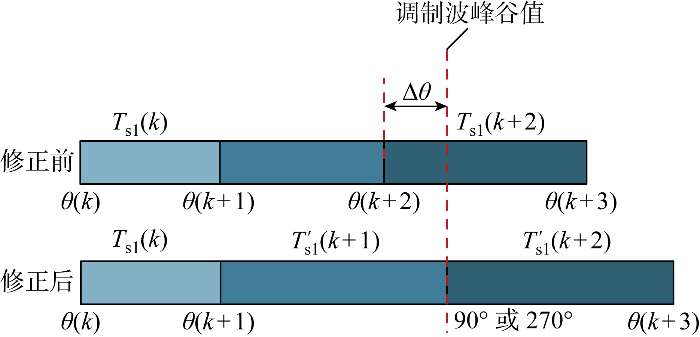
调制波在波峰、波谷值分别为90°、270°,判断起始角θ(k+3)与调制波峰谷值的关系,如图9所示.图中:T'_s1(k+1)为修正后的载波周期值.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 三拍载波预测法修正策略

Fig.9 Correction strategy for three-beat carrier prediction method

由图9可知,若调制波峰谷值在θ(k+2) 和 θ(k+3)之间,则修正载波周期T_s1(k+1),修正后的载波周期变为T'_s1 (k+1),相当于将T'_s1 (k+1)的调制波起始角θ(k+1)增加了Δθ,使得起始角θ(k+2)落在调制波峰谷值处.由式(7)可得,修正后的载波周期为

(11)T'_s1(k+1)=

\{\begin{array}{l} T_{t o p} (k + 1) = \frac{2 (T_{s m} - 2 t_{D B})}{1 + M s i n [θ (k + 1) + Δ θ]} \\ T_{b o t} (k + 1) = \frac{4 t_{D B}}{1 + M s i n [θ (k + 1) + Δ θ]} \end{array}

式中:Δθ的判别条件如表1所示.

表1 窄脉冲区域跨越判断

Tab.1 Judgment of narrow pulse area crossing

窄脉冲区域	Δθ
θ(k)<90°、θ(k+3)≥90°	90°-θ(k+2)
θ(k)<270°、θ(k+3)≥270°	270°-θ(k+2)
其他	0°

新窗口打开| 下载CSV

将修正后的T'_s1 (k+1)代入式(2),得到修正后的开关管导通时间t'_s1 (k+1)为

(12)t'_s1(k+1)=

\frac{T'_{s 1} (k + 1)}{2} [1 + M s i n θ (k + 1)]

当调制波过峰、谷值后第一个载波周期的起始角度等于90° 或270° 时,设定标志位g.判断标志位的取值,若g=1,则使过调制波峰谷值后的首个载波周期T'_s1(k+2)等于修正后的T'_s1(k+1),同时计算开关管导通时间t'_s1(k+2),计算公式如下:

(13)

\begin{array}{l} T'_{s 1} (k + 2) = T'_{s 1} (k + 1) \\ t'_{s 1} (k + 2) = t'_{s 1} (k + 1) \end{array}\}

根据修正公式,搭建仿真分析修正前后的载波周期随时间的变化,如图10所示.由图10可以看出,通过上述修正后,窄脉冲区域内,调制波峰谷值附近处载波周期最大值即为修正后的T_s1(k+1),且T_s1(k+1)的起始角距峰谷值较远,不会导致载波周期过大,保证了窄脉冲区域内的正常调制过程.

图10

新窗口打开| 下载原图ZIP| 生成PPT

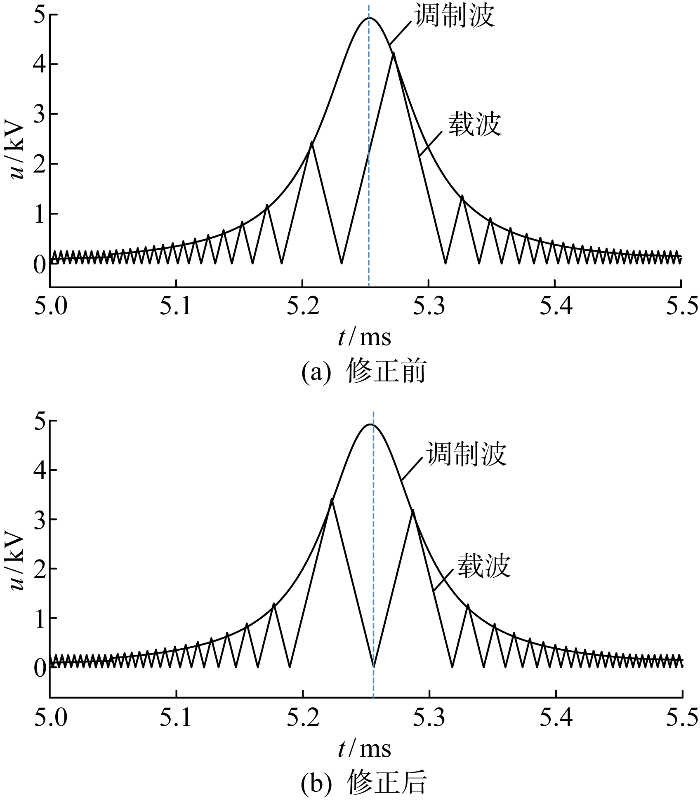
图10 修正前后载波周期随时间的变化

Fig.10 Changes in carrier period over time before and after correction

3 实验验证

为了验证所提无窄脉冲调制方法的正确性和有效性,搭建了单相全桥两电平逆变器实验平台,如图11所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 两电平逆变器实验平台

Fig.11 Two-level experimental platform

功率半导体开关器件为瞻芯电子公司的IV1Q12017T4G,主控制器采用TMS320F28377D数字信号处理芯片,直流侧采用直流源NXR75030H,交流测为阻感性负载,电阻20 Ω,电感800 μH.逆变器参数如表2所示.

表2 逆变器参数

Tab.2 Parameters of inverter

参数	取值
U_dc/V	500
f_c/kHz	100
f_r/kHz	1
t_nar/μs	2
t_DB/μs	1

新窗口打开| 下载CSV

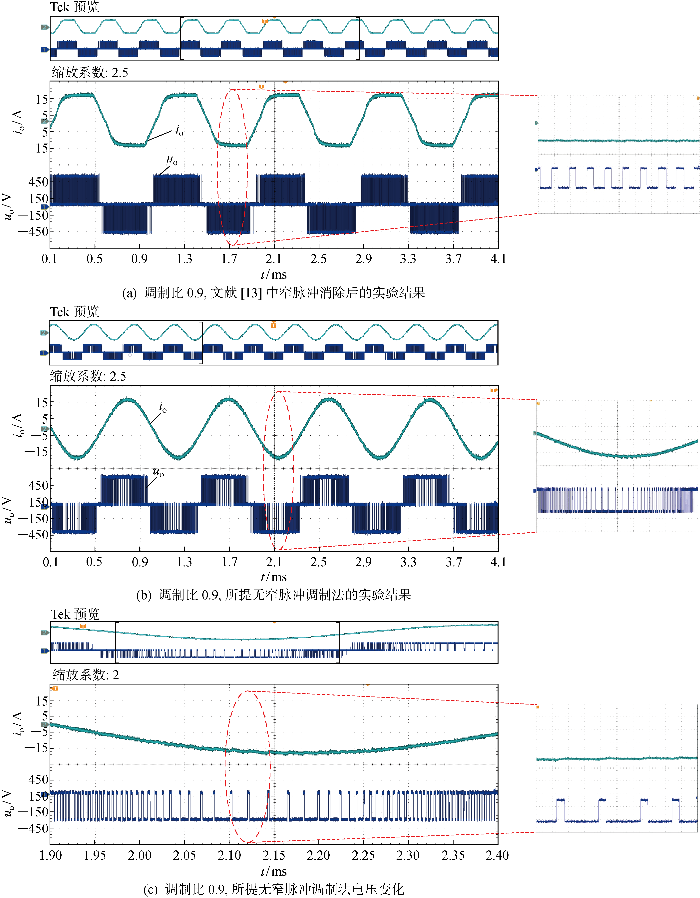
图12为文献[13]中的窄脉冲消除和本文所提无窄脉冲调制在高调制比区域的实验对比结果.分析可知,图12(a)中在调制波峰谷值附近处采用文献[13]中的窄脉冲消除法,将输出电压脉冲宽度拓展至最小脉宽值,使其占空比在窄脉冲区域维持在恒定值不变,会导致高频逆变器在高调制比情况下,输出电流的峰谷值处波形发生畸变问题,且交流侧输出波形失去正弦性.作为对比,图12(b)、12(c)采用本文所提的无窄脉冲调制法,在产生窄脉冲的调制波峰谷值附近,将固定周期的载波改为可调周期的载波,使交流侧输出电流波形保持较高正弦性的同时消除了窄脉冲的影响.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 逆变器高调制比下实验波形

Fig.12 Inverter experimental waveform at high modulation ratio

为了防止本文所提无窄脉冲调制法在载波周期横跨调制波峰谷值时造成的波形畸变问题,采用三拍载波预测法修正策略,改善交流侧输出波形质量,得到如图13所示实验结果.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 策略修正前后实验结果

Fig.13 Experimental results before and after strategy correction

图13(a)为修正前的交流侧输出波形,由图中可以看出,输出电流的峰谷值附近产生了波形畸变问题,使输出电压生成错误的占空比,影响了输出波形的正弦性;图13(b)为修正后的交流侧输出波形,可以看出,相比于修正前,输出电流在峰谷值附近的畸变问题得到明显改善,且修正了该位置错误的输出电压占空比,优化了交流侧输出波形质量.为直观分析文献[13]中窄脉冲消除法和所提无窄脉冲调制法对交流侧输出波形质量的影响,在调制比为0.9的情况下,分别对两种方法下交流侧的输出电流进行快速傅里叶变换(FFT)分析,得到如图14所示结果.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 交流侧输出电流FFT分析

Fig.14 FFT analysis of AC-side output current

对比分析结果可以发现,采用文献[13]中的窄脉冲消除方法其输出电流THD为16.08%,且3次谐波含量超过15%,其余奇次特征谐波含量超过1%;采用所提无窄脉冲调制法得到的输出电流THD仅为1.79%,相较于文献[13]中的方法下降了14.29个百分点,其余奇次特征谐波含量均不超过0.4%.说明本文所提的无窄脉冲调制法能有效降低输出波形谐波含量,消除窄脉冲的同时优化了交流侧的输出波形质量.

图15是文献[13]中的窄脉冲消除方法和所提方法在高调制比0.70~0.98下,逆变器交流侧输出电流的谐波含量对比图.由图可见,过高的调制比会产生严重的窄脉冲问题.采用文献[13]中的方法,输出电流的谐波含量受调制比影响较大,其变化趋势整体呈上升型,在调制比为0.98时谐波含量高达17.56%;而所提方法由于在窄脉冲区域降低了开关频率,使得输出电流的谐波含量在高调制比时趋于稳定,值均不超过4%,显著降低了调制比对输出电流谐波含量的影响.

图15

新窗口打开| 下载原图ZIP| 生成PPT

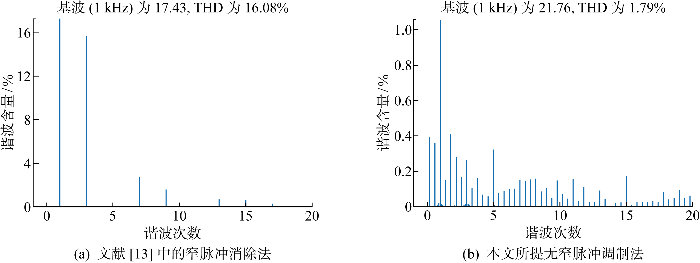
图15 不同调制比下输出电流FFT分析

Fig.15 FFT analysis of output current at different modulation ratios

4 结论

针对单相两电平高频逆变器高调制比下存在的窄脉冲问题,通过分析SPWM下窄脉冲的发生条件和分布规律,提出了一种无窄脉冲高质量调制方法,得出如下结论:

(1) 单相两电平逆变器在调制波峰谷值附近均可能有窄脉冲产生,其产生原因与调制比、载波频率和死区相关.逆变器高频工作中,会加剧窄脉冲现象的发生.

(2) 所提无窄脉冲高质量调制方法在保证抑制窄脉冲发生的同时,能有效提高交流侧输出波形质量,显著降低高调制比对输出波形谐波含量的影响.

(3) 所采用的三拍载波预测法解决了高调制比下交流侧输出波形在峰谷值处的畸变问题,优化了波形质量.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王晓琳, 李紫佳, 李正龙, 等.

超高速低载频比下永磁同步电机无差拍电流控制

[J]. 电机与控制学报, 2023, 27(4): 55-63.