单层网壳结构的局部加肋渐进式拓扑优化方法

doi:10.16183/j.cnki.jsjtu.2023.490

单层网壳结构的局部加肋渐进式拓扑优化方法

王润谷, 董骁, 龚景海^,

上海交通大学船舶海洋与建筑工程学院,上海 200240

Evolutionary Topological Optimization Method for Local Rib Addition in Single-Layer Shell Structures

WANG Rungu, DONG Xiao, GONG Jinghai^,

School of Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 龚景海,研究员,博士生导师;E-mail:gongjh@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-09-25 修回日期: 2023-12-13 接受日期: 2024-01-17

Received: 2023-09-25 Revised: 2023-12-13 Accepted: 2024-01-17

作者简介 About authors

王润谷(1997—),硕士生,从事空间结构拓扑优化研究.

摘要

研究单层网壳结构的局部加肋拓扑优化对提升其经济性与整体稳定性有重要意义.针对单层网壳结构,以结构用钢量为评价指标,基于渐进结构优化算法,提出局部加肋拓扑优化方法.根据结构中杆件的内力分布计算应变能,结合单层网壳结构的特点建立网格加强评价准则,在迭代运算中增加锥体加强应变能过大的网格,删除应变能过小的新增锥体,比较优化前后网壳结构的用钢量与整体稳定性,验证结构优化方法的可行性.经拓扑优化得到新的局部加肋单层网壳结构,相较于初始结构,优化后的结构用钢量减小,并且整体稳定性提高,结果可为单层网壳结构的局部加肋设计优化提供技术参考.

关键词： 单层网壳结构; 局部加肋; 渐进结构优化算法; 拓扑优化

Abstract

This paper investigates the topological optimization of locally reinforced single-layer reticulated shell structures to enhance their economy and overall stability. Using steel consumption as the evaluation index, a topological optimization method based on the evolutionary structural optimization algorithm is proposed for single-layer reticulated shell structures. The strain energy is calculated based on the internal force distribution of the structural members, and a grid strength evaluation criterion is established considering the specific characteristics of single-layer reticulated shell structures. In the iterative calculation, pyramids are added to strengthen the grid with excessive strain energy, while new pyramids with insufficient strain energy are removed. The steel consumption and the overall stability of the reticulated shell structure before and after optimization are compared to verify the effectiveness of the structural optimization method. After topological optimization, the locally reinforced single-layer reticulated shell structure exhibits a reduced steel consumption and improved overall stability compared to the initial structure. The results can provide technical references for optimizing the local reinforcement design of single-layer reticulated shell structures, and also provide references for similar structural optimization problems.

Keywords： single-layer reticulated domes; local rib augmentation; evolutionary structural optimization algorithm; topological optimization

PDF (30863KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王润谷, 董骁, 龚景海. 单层网壳结构的局部加肋渐进式拓扑优化方法[J]. 上海交通大学学报, 2025, 59(7): 1019-1028 doi:10.16183/j.cnki.jsjtu.2023.490

WANG Rungu, DONG Xiao, GONG Jinghai. Evolutionary Topological Optimization Method for Local Rib Addition in Single-Layer Shell Structures[J]. Journal of Shanghai Jiaotong University, 2025, 59(7): 1019-1028 doi:10.16183/j.cnki.jsjtu.2023.490

单层网壳结构具有造型优美和安装简捷等优点^[1-3],但通常平面外刚度低、用钢量高、整体稳定性差.对其局部加肋可增大平面外刚度,提高其经济性与整体稳定性.局部加肋的数量和位置对网壳结构用钢量与力学性能有较大影响,但单层网壳结构杆件与网格规模较大,可采用的加肋方式众多,实际工程中设计师难以确定加肋的最优布置形式.因此单层网壳结构的局部加肋拓扑优化在工程中有重要的意义^[4-5].

为了解决连续体结构的拓扑优化问题,谢亿民等^[6]提出了渐进结构优化(evolutionary structural optimization, ESO)算法,其基本原理是逐步删除最不起作用的材料,使剩余结构逐步达到最优解.该方法已被用于多种结构的优化^[7-9],在空间结构的拓扑优化中,才琪等^[10]基于双向渐进结构优化法对桁架结构进行拓扑优化;朱吉吉^[11]基于渐进式优化法对网架结构进行拓扑优化.对单层网壳结构,这种以连续实体结构作为初始结构,通过迭代运算逐步离散为非连续体结构的方法存在两个缺点:首先,难以对已确定基本拓扑形式的空间结构进行拓扑优化;其次,由连续实体结构优化出的非连续体结构虽然是理论上的优解,但可能不满足建筑的实用性和功能性要求,如出现优化结构在部分荷载较小的区域网格尺寸过大等问题.

为了改善ESO在单层网壳结构的拓扑优化中的缺点,本文提出了一种以ESO为基础的单层网壳结构局部加肋拓扑优化方法.根据单层网壳结构的特点,以非连续体结构作为初始结构进行优化,保留网壳结构原有的节点和杆件来保证单层网壳结构的合理性和适用性;根据基于应变能提出的准则在迭代过程中判断网格是否需要添加锥体以及新增锥体是否需要删除,获得结构的优解,提高结构的经济性与整体稳定性.

1 单层网壳结构的局部加肋渐进式拓扑优化方法

1.1 概述

渐进式拓扑优化方法由4个部分构成:评价指标、优化准则、ESO方案设计和运算流程.根据《空间网格结构技术规程: JGJ 7—2010》^[12]第4.3.1至4.3.5条的规定,用结构的失稳荷载因子衡量结构的整体稳定性;以结构用钢量为评价指标,结构的用钢量越小则结构越优.应变能代表在外力作用下,构件中以应变和应力形式储存的势能.对于单层网壳结构,构件作为梁单元进行运算时,其受力包括轴力、剪力和各方向的弯矩等.应变能的表达包含各种应力和应变情况,以应变能为基础的优化准则能够准确衡量构件承担内力的情况.根据单层网壳结构以网格为单元的特点,渐进式拓扑优化方法在优化过程中同样以网格为单元,将构件视为网格的组成部分.通过对构件的受力分析,判断其所在网格是否需要加强,以及新增锥体是否需删除.该方法以ESO为基础,需要根据ESO的理论设计相应的运算流程.

1.2 优化准则

为了确定以应变能为基础的网格加强评价准则,选用单位长度的应变能密度准则与等效轴力准则通过算例进行对比和取舍.两种准则都包含3个参数,分别为属性值R(包括杆件的属性值R_M与网格的属性值R_G)、上阙值L_U和下阙值L_M.属性值R为考察杆件发挥作用大小的参数,R在杆件局部坐标系下的y向分量R_y和z向分量R_z以及上阙值L_U判断结构中的网格是否需要添加锥体,下阙值L_M判断新增的锥体是否需要被删除.

第1种准则是单位长度的应变能密度准则,即直接计算杆件与网格的单位长度应变能作为杆件的属性值R_M与网格的属性值R_G.为了避免杆件的横截面积和长度对用应变能衡量构件承担内力的情况的准确度造成不良影响,如杆件应力很小但截面积或杆件长度很大导致该构件的应变能很大,采用构件的应变能密度(构件单位体积内储存的应变能)更准确.考虑到在每次进行迭代运算前,结构都会经过满应力优化设计,即在确保结构中的每根构件在符合相关规范要求的前提下使构件采用尽可能小的横截面,由于很少出现构件应力很小但横截面积很大的情况,所以研究最终采用构件的单位长度应变能,即杆件的应变能除以其几何长度.单层网壳结构的杆件的单位长度应变能密度计算公式为

(1)S=

\frac{1}{2} (\frac{N^{2}}{E A} + \frac{T^{2}}{G I_{x}} + \frac{M_{y}^{2}}{E I_{y}} + \frac{M_{z}^{2}}{E I_{z}})

式中:S为杆件的单位长度应变能密度;N为杆件所受轴力;E为杆件的弹性模量;A为杆件的横截面积;T为杆件所受扭矩;G为杆件的切变模量;I_x为杆件的x方向惯性矩;M_y为杆件所受y方向弯矩;I_y为杆件的y方向惯性矩;M_z为杆件所受z方向弯矩;I_z为杆件的z方向惯性矩.

在每次迭代计算过程中,当杆件长度方向沿结构全局坐标系的z轴方向时,选取(e¹⁰, 0, 0)作为参考点,在其他情况下选取(0, 0, e¹⁰)作为参考点.规定杆件局部坐标系的x轴由杆件起点指向杆件终点(杆件的起点与终点由有限元软件在创建杆件时决定),参考向量由杆件起点指向参考点,参考向量与x轴单位向量进行叉乘得到y轴方向,x轴单位向量与y轴单位向量进行叉乘得到z轴方向,如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 杆件局部坐标系示意图

Fig.1 Schematic diagram of local coordinate system of the member

计算每根构成网格的杆件在各工况下的单位长度应变能,以最大的单位长度应变能代表每根杆件的单位长度应变能,作为杆件的属性值R_M.出于考虑网格内力的组成以决定是否强化网格的需要,记录杆件的单位长度应变能中y向的分量S_y与z向的分量S_z作为R_M,_y与R_M,_z:

(2)

\begin{array}{l} S_{y} = \frac{M_{y}^{2}}{2 E I_{y}} \\ S_{z} = \frac{M_{z}^{2}}{2 E I_{z}} \end{array}\}

所有网格内杆件的单位长度应变能的总和为该网格的属性值R_G,所有网格内杆件的y向与z向单位长度应变能的总和作为该网格的y向与z向应变能,即网格的R_G,_y与R_G,_z.取每个网格的单位长度应变能与当前结构所有网格中最大的网格单位长度应变能的比值,当该比值大于上阙值L_U时,网格需要被强化;取杆件的单位长度应变能与当前结构所有杆件中最大的杆件单位长度应变能的比值,当该比值小于下阙值L_M且该杆件属于迭代过程中新增的锥体时,需要进一步考虑是否删除锥体.

第2种准则是等效轴力准则,即计算杆件和网格的等效轴力作为杆件的属性值R_M与网格的属性值R_G.等效轴力以应变能为基础,由梁单元杆件承受的所有内力转换而来,衡量杆件的受力状态.等效轴力N^E的计算公式^[13]为

(3)N^E=

\sqrt{E A (\frac{N^{2}}{E A} + \frac{T^{2}}{G I_{x}} + \frac{M_{y}^{2}}{E I_{y}} + \frac{M_{z}^{2}}{E I_{z}})}

在每次迭代计算过程中,杆件局部坐标系与第1种准则相同,计算每根构成网格的杆件在各工况下的等效轴力,以最大的等效轴力代表每根杆件的等效轴力,作为杆件的属性值R_M.计算出等效轴力后,记录杆件的单位长度应变能中y向分量 $N_{y}^{E}$ 与z向分量 $N_{z}^{E}$ :

(4)

\begin{array}{l} N_{y}^{E} = \sqrt{\frac{A M_{y}^{2}}{I_{y}}} \\ N_{z}^{E} = \sqrt{\frac{A M_{z}^{2}}{I_{z}}} \end{array}\}

所有网格内杆件的等效轴力的总和作为该网格的属性值R_G.所有网格内杆件的y向与z向等效轴力的总和作为该网格的y向与z向等效轴力.取每个网格的等效轴力与当前结构所有网格中最大的等效轴力的比值,当该比值大于上阈值L_U时,网格需要添加锥体;取杆件的等效轴力与当前结构所有杆件中最大的杆件等效轴力的比值,当该比值小于下阈值L_M且该杆件属于迭代过程中新增的锥体时,需要进一步考虑是否删除锥体.

1.3 基于ESO理论的方法设计

本研究采用ESO方法进行迭代计算,基于ESO方法的拓扑优化设计包括目标函数、设计变量和约束条件3个要素^[9],对于一般的最小化问题,其公式化表达^[14]为

(5)min f(x)

(6)g_j(x)≤0, j=1,2,…,p

(7)h_k(x)=0, k=1,2,…,l

(8)

{x^{D}}_{i}

≤x_i≤

{x^{U}}_{i}

, i=1,2,…,Z

式中:f(x)是目标函数,x是设计变量矢量;g_j(x)和h_k(x)分别为不等式和等式约束;p和l分别为不等式和等式约束个数; ${x^{U}}_{i}$ , ${x^{D}}_{i}$ 分别是设计变量x_i的上、下限;Z代表设计变量的总数.对于单层网壳结构的局部加肋拓扑优化问题,目标函数为应变能最小,设计变量为单元密度,约束条件为结构优化质量比和平衡方程:

(9)$ f(\boldsymbol{x})=\frac{1}{2} \boldsymbol{P}^{\mathrm{T}} \boldsymbol{Q}$

(10)$ h_{1}(\boldsymbol{x})=(1-\gamma) M_{0}-\sum_{b=1}^{D} M_{b} x_{b}$

(11)$ h_{2}(\boldsymbol{x})=\boldsymbol{K}^{\mathrm{T}} \boldsymbol{Q}-\boldsymbol{P}$

(12)x_b=0,1

式中:b表示单元号,b=1,2,…,D,D为单元总数;x_b表示第b个单元的单元密度,为二元设计变量,只能取0或1,其中,0代表单元不存在,1代表单元存在^[15];f(x)为结构应变能,是关于设计变量x_b的函数;P为结构承受的外荷载向量;Q为结构的位移向量;K为结构总刚度矩阵;M_b为第b个单元的质量;M₀为初始结构经过满应力优化后的质量;γ为质量优化系数.除此之外,针对实际工程中用有限数量锥体加强单层网壳结构的需要,该方法也支持指定锥体数量上限的局部加肋拓扑优化设计.

1.4 拓扑优化方法运算流程

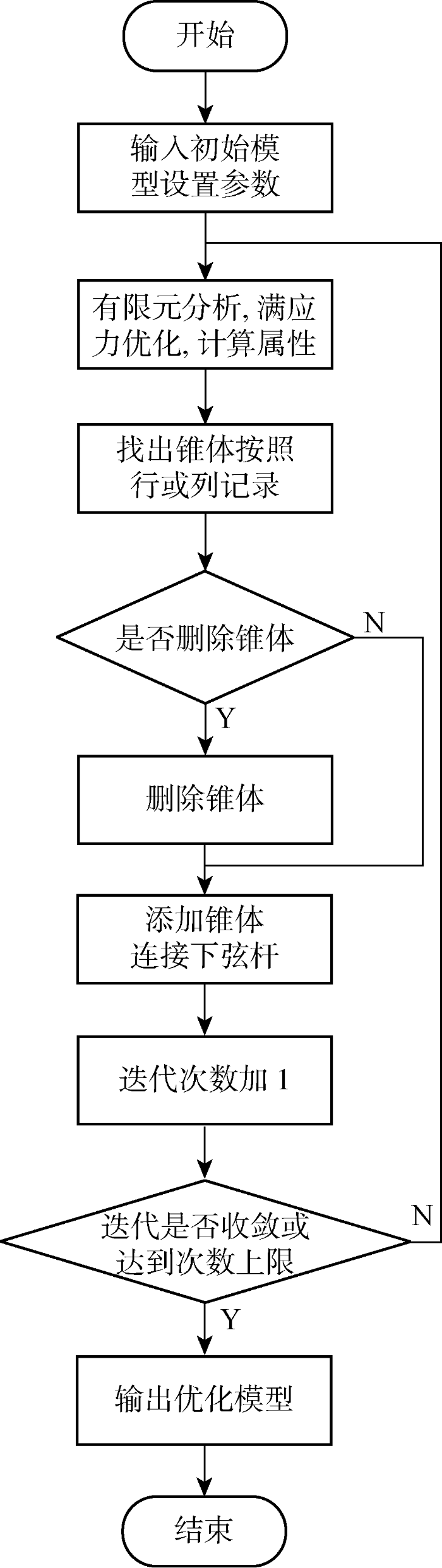
单层网壳结构的渐进式拓扑优化方法包括以下运算流程.

(1) 输入初始模型,设置参数(R, L_U, L_M).

(2) 建立有限元模型,进行有限元分析和满应力优化.

(3) 计算属性:计算杆件属性值R_M及杆件局部坐标系下的分量R_M,_y与R_M,_z,找出最大杆件属性值R_M,max;计算网格属性值R_G及R_G,_y与R_G,_z,找出最大网格属性值R_G,max.

(4) 找出锥体按照行或列记录:找出具有锥体的网格;根据网格中的索引将在同一行或列的具有锥体的网格记录在一起.

(5) 判断锥体是否删除:对具有锥体的行和列,计算该行或列的所有锥体的下弦杆属性值R_M的平均值R_M,ave;若R_M,ave<R_M,maxL_M,则删除该行或列的锥体(如果有锥体还关联其他列或行的锥体则不删除)及其关联的下弦杆;若此时锥体数量超过限制,则将有锥体的行和列按照它们的R_M,ave排序;依次删除R_M,ave最低的行和列的锥体及其关联的下弦杆直至锥体数量不超过数量限制.

(6) 添加锥体:对所有网格,若网格属性值 R_G≥R_G,maxL_U且R_G,_y≥R_G,_z且网格没有锥体且已有锥体数量未超过上限,则找出该网格所在的行和列,对该行该列添加锥体,对这些锥体添加记录所在行与列的索引;若网格为母网格且网格属性值R_G≥R_G,maxL_U且R_G,_y≥R_G,_z且网格有锥体且已有锥体数量未超过上限,则搜索该网格的子网格;若子网格存在则找出子网格周边可以添加锥体的网格,找出它们所在的行和列,对这些行和列添加锥体,对锥体添加记录所在行与列的索引;否则搜索母网格周边可以加锥体的网格,将它们记为母网格的子网格,找出它们所在的行和列,对这些行和列添加锥体,对锥体添加记录所在行与列的索引;所有添加的锥体高度为网格中所有上弦杆的几何长度的平均值的一半,由下弦节点用腹杆连接至网格中的各节点,腹杆初始截面均为⌀48 mm×3.5 mm圆钢管,后续会在满应力优化中更改.

(7) 连接下弦杆:对所有网格,若两个相邻(有公共边)的网格都具有锥体,则用一根下弦杆连接这两个锥体的下弦节点,所有下弦杆的初始截面均为⌀48 mm×3.5 mm圆钢管,后续会在满应力优化中更改.

(8) 迭代次数加1.

(9) 判断迭代是否收敛或达到次数上限:当该拓扑优化设计算法中的某次迭代运算没有对模型进行任何更改,或最近10次迭代运算的质量优化系数γ的方差小于1×10^-4,则认为迭代收敛,若迭代未收敛且未达到次数上限则返回步骤(2),否则进行步骤(10).

(10)输出优化后模型:输出用钢量最小的模型,结束优化.

渐进式拓扑优化方法流程图如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 单层网壳的渐进式拓扑优化方法流程图

Fig.2 Flow chart of evolutionary topology optimization method for single-layer reticulated shells

2 算例与分析

2.1 算例基本信息

确定单层网壳结构的局部加肋渐进式拓扑优化算法的准则与流程后,通过算例分析两种准则的优化效果、算法中的参数对拓扑优化效果的影响,以及算法在实际工程中的实用性.

由于联方型单层柱面网壳与椭球面网壳是拓扑形式较为简单且多采用四边形网格的单层网壳,在单层网壳中具有代表性,所以选取这两种类型的网壳作为初始模型进行算例分析.所有杆件在有限元运算中均为梁单元,所有杆件截面均采用圆钢管,可选杆件截面从直径89 mm、壁厚4 mm到直径 1 000 mm、壁厚25 mm不等,杆件材料为Q355钢材.对于拓扑优化设计算法中涉及的3个参数R, L_U与L_M,R与优化准则关联,由两种准则的取舍决定,L_U=0.5,0.6,0.7,0.8,0.9,L_M=0.1,0.2,0.3,0.4,0.5;将L_U与L_M的取值两两组合,以此研究两个参数对拓扑优化效果的影响.迭代次数上限取50次.

各算例中对模型施加的荷载符合《建筑结构荷载规范: GB 50009—2012》^[16]中的相关规定;结构的稳定性分析按弹塑性全过程分析,初始几何缺陷分布采用结构的最低阶屈曲模态,缺陷最大计算值按网壳跨度的1/300取值,计算结构在自重+恒荷载+满布活荷载组合工况下的失稳荷载因子判断结构的稳定性.以下为3个算例.

算例1 以图3所示的联方型单层柱面网壳为模型1.图中:A₁C长60 m,跨度30 m,矢高10 m;A₁C边网格数为15个.模型的支座在A₁C边与BD₁边的所有边界节点上.对模型整体施加0.3 kN/m²的恒荷载、0.5 kN/m²的活荷载和标准风压0.55 kN/m²,体型系数按回转面计算,地面粗糙度为B类,风振系数为1.5的风荷载.经对模型1进行满应力优化设计,结构杆件用钢量为35.42 t,该初步设计方案在自重+恒荷载+满布活荷载组合工况作用下且考虑材料非线性时的失稳荷载因子为1.43,不满足《空间网格结构技术规程: JGJ 7—2010》^[12]的相关要求.采用局部加肋方案提高结构经济性与稳定性,对其分别采用单位长度的应变能密度准则与等效轴力准则下的属性值R_M与R_G进行渐进式拓扑优化设计.该算例用于比较两种准则对拓扑优化效果的影响,选出一种优化准则为其他算例使用.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 模型1俯视图

Fig.3 Top view of Model 1

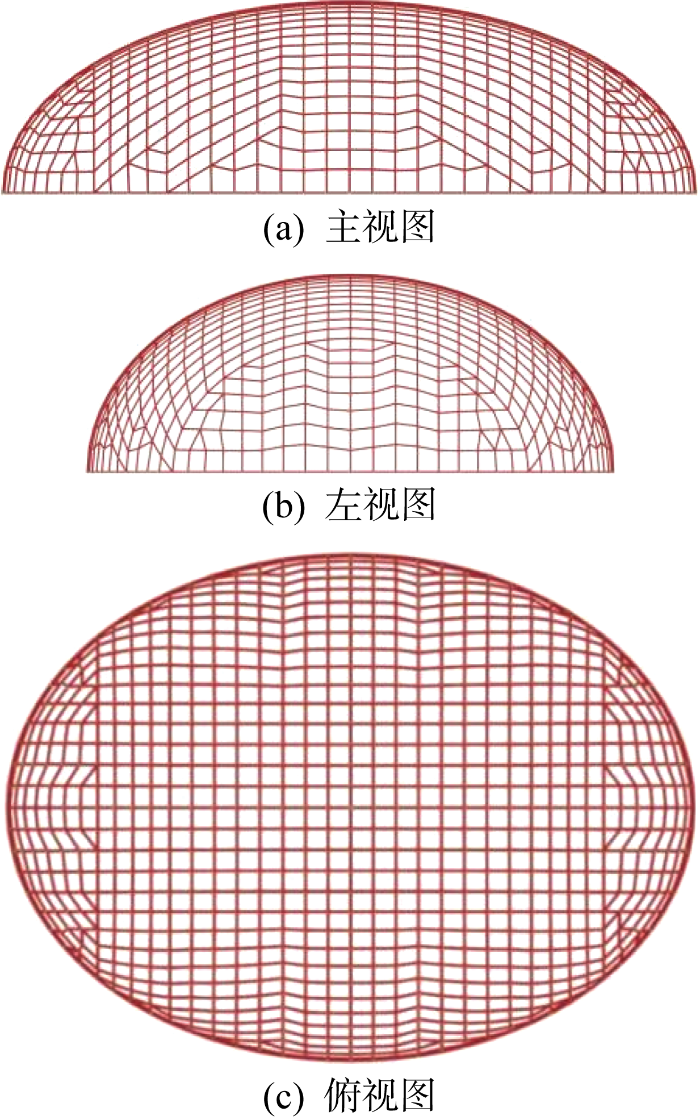
算例2 以图4所示的单层椭球网壳为模型2,该椭球壳取自大连某体育馆,其主要由四边形网格组成,在靠近网壳边缘处由三角形网格组成,所有杆件的初始截面均为⌀48 mm×3.5 mm圆钢管,后续会在满应力优化中更改.椭球网壳的长轴为152 m,平面椭圆短轴为112 m,网壳矢高为42 m,模型的边界节点每隔一个网格设置一个支座,考虑下部结构刚度,支座水平刚度取为25 MN/m.按照《建筑结构荷载规范: GB 50009—2012》^[16]中相关规定对该模型施加荷载,包括0.3 kN/m²恒荷载,考虑半跨布置与整体布置的0.5 kN/m²活荷载和6种雪荷载.风荷载沿荷载面法向施加,基本风压为0.75 kN/m²,体型系数按回转面计算,地面粗糙度为B类,风振系数为1.5.经对模型2进行满应力优化设计,结构杆件用钢量为 1 022.53 t,该初步设计方案在自重+恒荷载+满布活荷载组合工况作用下且考虑材料非线性时的失稳荷载因子为1.32,不满足《空间网格结构技术规程: JGJ 7—2010》^[12]的相关要求.采用局部加肋方案提高结构经济性与稳定性,验证算法在实际工程中的可行性.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 模型2三视图

Fig.4 Three views of Model 2

算例3 对算例2中的模型2,保持模型的支承条件与施加荷载不变,在优化算法中设置锥体数量限制为300,采用局部加肋方案进行运算.该算例将验证限制锥体数量时,拓扑优化算法在实际工程中的可行性.

在每个算例中,拓扑优化算法会在每次迭代运算中将优化后的模型的用钢量 $\sum_{b = 1}^{D}$ M_bx_b与初始模型经过满应力优化后的用钢量M₀做比较,计算质量优化系数γ=(M₀- $\sum_{b = 1}^{D}$ M_bx_b)/M₀,即以经过满应力优化的初始模型作为对照组考察算法的优化效果.

2.2 不同准则下的拓扑优化结果

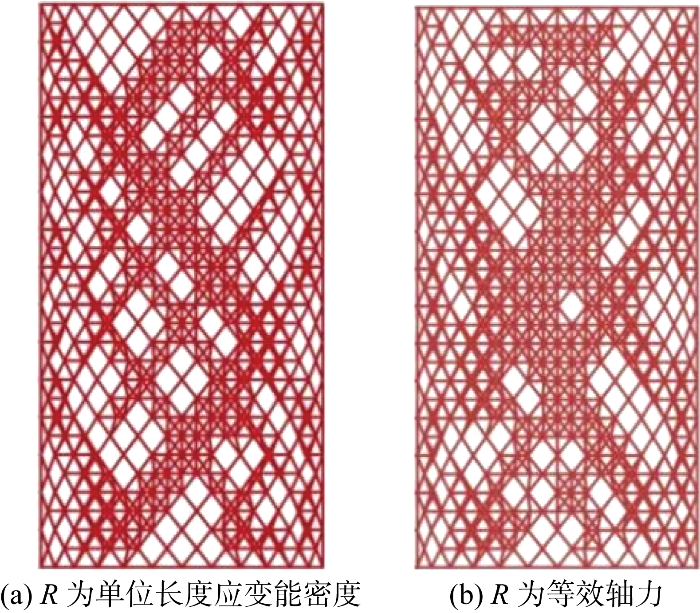
对于模型1采用应变能准则时,取上阙值L_U=0.6和下阙值L_M=0.1优化效果最好,进行50次迭代运算后,最优模型为第11次迭代运算后的结果,结构杆件用钢量为 25.77 t,质量优化系数γ=0.272 4;采用等效轴力准则时,取上阙值L_U=0.5,下阙值L_M=0.1优化效果最好,算法仅用12次迭代运算就完成了对初始模型的优化,最优模型为第12次迭代运算后的结果,结构杆件用钢量为 25.85 t,质量优化系数γ=0.270 2.两种R取值下优化后模型在自重+恒荷载+满布活荷载组合工况作用下且考虑材料非线性时的失稳荷载因子分别为3.51和3.55,均满足《空间网格结构技术规程: JGJ 7—2010》^[12]的相关要求.优化后的模型如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 两种R取值下的最优模型

Fig.5 Optimal models at two values of R

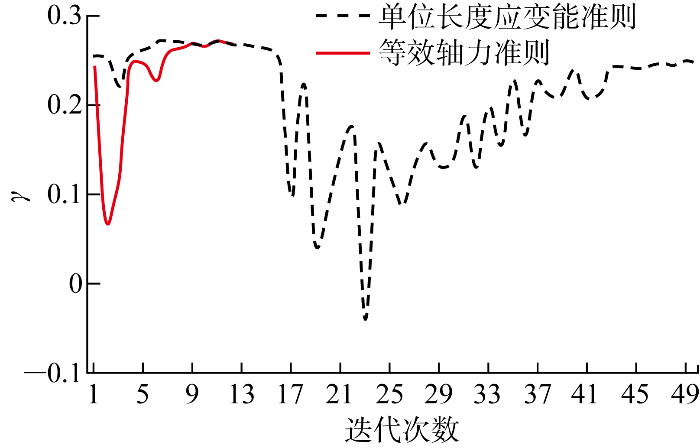
两种准则下的优化结果对比如图6所示.由对比可知,优化模型的失稳荷载因子与质量优化系数γ相差很小,采用等效轴力准则时迭代优化算法的运算效率远高于应变能准则.在结构对称且荷载对称的情况下,优化结构也应具有对称性,采用等效轴力准则时的最优优化结果对称性更好,因此选择等效轴力作为杆件的属性值R_M与网格的属性值R_G.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 两种准则的迭代运算结果对比

Fig.6 Comparison of the iterative operation results of two criteria

参考图5(b)的结构,绘制图7中的模型并进行线性分析与满应力优化,结构杆件用钢量为 28.70 t,质量优化系数γ=0.189 7,即节省用钢量18.97%;模型在自重+恒荷载+满布活荷载组合工况作用下且考虑材料非线性时的失稳荷载因子为3.70,比初始结构提高了158.7%,满足《空间网格结构技术规程: JGJ 7—2010》^[12]的相关要求.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 参考算例1优化结果绘制的模型

Fig.7 Model drawn from optimization result of Example 1

2.3 实际工程模型的拓扑优化结果

对模型2采用等效轴力准则时,取上阙值 L_U=0.5,下阙值L_M=0.1时优化效果最好,算法用21次迭代运算完成了对初始模型的优化,运算结果如图8所示.优化效果最优的是第14次迭代运算后的结果,结构杆件用钢量为632.54 t,质量优化系数 γ=0.381 4,即节省用钢量38.14%;模型在自重+恒荷载+满布活荷载组合工况作用下且考虑材料非线性时的失稳荷载因子为2.38,比初始结构提高了80.3%,满足《空间网格结构技术规程: JGJ 7—2010》^[12]的相关要求.优化后模型如图9所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 模型2迭代运算结果

Fig.8 Iterative calculation results of Model 2

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 优化后的模型2三视图

Fig.9 Three views of optimized Model 2

参考图9中的结构,绘制图10中的模型并进行线性分析与满应力优化,得出的结构杆件用钢量为733.77 t,质量优化系数γ=0.282 4,即节省用钢量28.24%;模型在自重+恒荷载+满布活荷载组合工况作用下且考虑材料非线性时的失稳荷载因子为2.24,比初始结构提高了69.7%,满足《空间网格结构技术规程: JGJ 7—2010》^[12]的相关要求.

图10

新窗口打开| 下载原图ZIP| 生成PPT

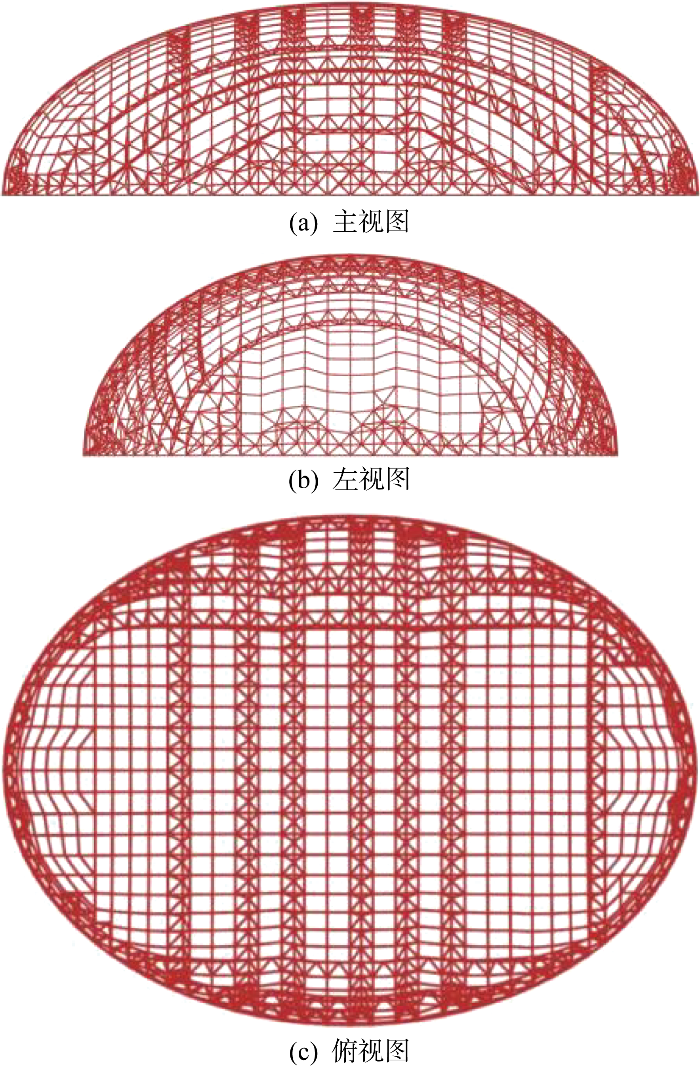
图10 参考算例2优化结果绘制的模型三视图

Fig.10 Three views of the model drawn from optimization results of Example 2

2.4 限制锥体数量时的拓扑优化结果

对模型2,采用等效轴力准则并限制添加锥体数量为300时,取上阙值L_U=0.5,下阙值L_M=0.1优化效果最好,算法用24次迭代运算完成了对初始模型的优化,运算结果如图11所示.优化效果最优的是第16次迭代运算后的结果,结构杆件用钢量为656.87 t,质量优化系数γ=0.357 6,即节省用钢量35.76%;模型在自重+恒荷载+满布活荷载组合工况作用下且考虑材料非线性时的失稳荷载因子为2.55,比初始结构提高了93.2%,满足《空间网格结构技术规程: JGJ 7—2010》^[12]的相关要求.优化后的模型如图12所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 限制锥体数量时模型2迭代运算结果

Fig.11 Iterative operation results of Model 2 with limited number of pyramids

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 限制锥体数量时优化后的模型2三视图

Fig.12 Three views of optimized Model 2 with limited number of pyramids

参考图12中的结构,绘制图13中的模型并进行线性分析与满应力优化,得出的结构杆件用钢量为674.05 t,质量优化系数γ=0.340 8,即节省用钢量34.08%;模型在自重+恒荷载+满布活荷载组合工况作用下且考虑材料非线性时的失稳荷载因子为2.53,比初始结构提高了91.7%,满足《空间网格结构技术规程: JGJ 7—2010》^[12]的相关要求.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 参考算例3优化结果绘制的模型三视图

Fig.13 Three views of model drawn from optimization result of Example 3

在以上算例的优化结果中,结构与荷载均对称的模型没有得到完全对称的优化结果.在迭代过程中计算机由于受浮点类型数据精度影响对杆件内力和下弦节点位置计算的误差可能导致对称位置的受力不均匀,截面选择不完全对称,影响了加肋的对称性.在连续体中运用渐进结构优化算法对施加对称荷载的对称结构进行优化时,优化结果也会出现不对称情况;本文的方法对非连续体使用渐进结构优化算法时,由于一个网格只有存在锥体或不存在锥体两种状态,所以这种误差被放大.如果限制添加锥体数量,还会出现因锥体数量已达上限无法在对称位置添加锥体的情况.以上原因都可能造成算法的优化结果不对称,在迭代算法中,有一次迭代结果中的结构不完全对称,都会导致后续结果不对称.

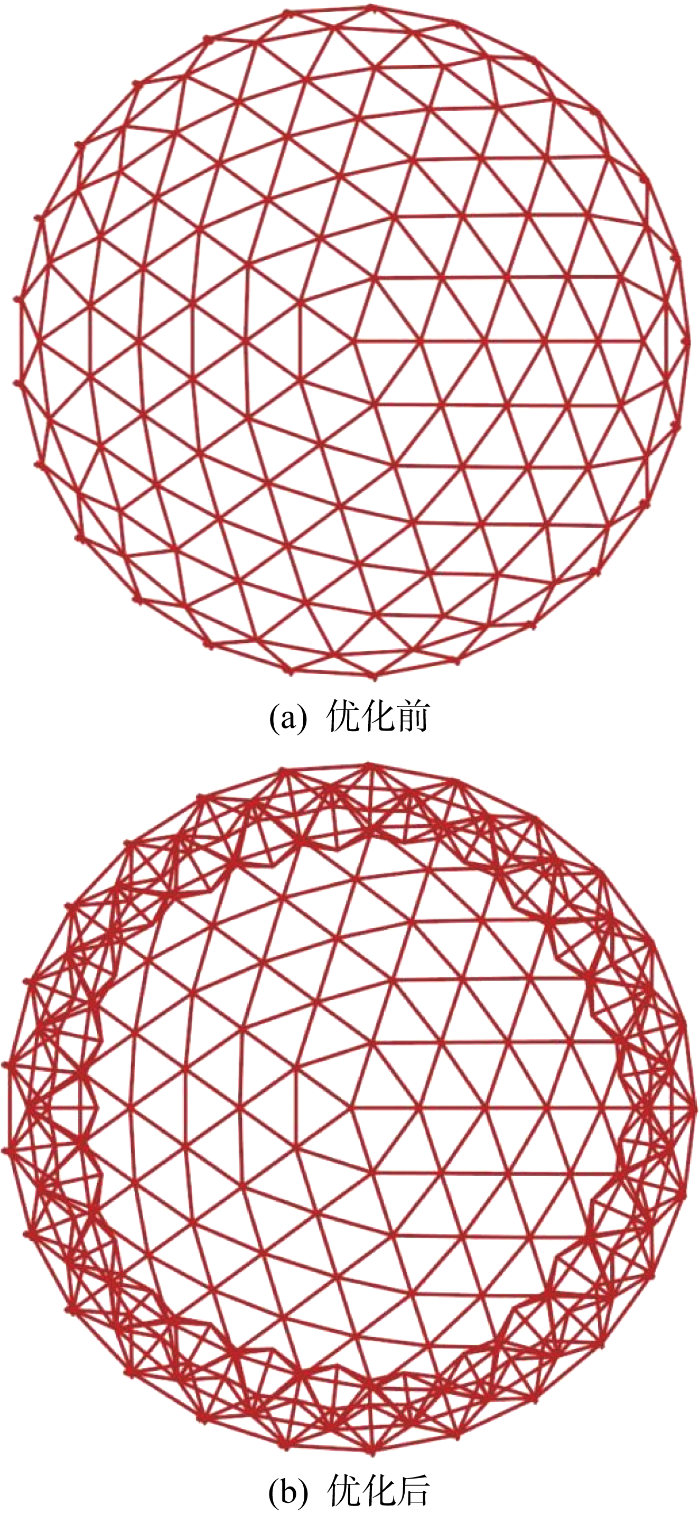
由于添加锥体的算法在设计时较为通用,单层网壳的局部加肋拓扑优化方法理论上可对采用三角形等其他多边形网格的单层网壳使用,如图14所示.采用四边形网格的网壳网格分布较规整,加肋路径易寻找,因此对其采用该方法效果最好.后续会改进该方法在其他多边形网格组成的单层网壳中应用的效果.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 对某短程线型单层球面网壳使用该拓扑优化方法的结果

Fig.14 Result of a short-range linear single-layer spherical reticulated shell using this topology optimization method

3 结论

针对单层网壳结构,引入渐进结构优化算法进行局部加肋拓扑优化,对比分析了实际工程案例优化前后结构的用钢量与整体稳定性.

(1) 以结构杆件用钢量为评价指标,基于杆件应变能计算的等效轴力为网格加强评价准则,通过增加和删除锥体,提出单层网壳结构局部加肋渐进结构优化方法与迭代运算流程.

(2) 单层网壳结构工程案例通过局部加肋拓扑优化后,结构用钢量可显著降低,同时结构整体稳定性得到显著提高.

(3) 通过限制局部加肋的锥体数量,拓扑优化后可得到不同的单层网壳结构局部加肋形式,供结构设计者选择.

(4) 借鉴优化后模型的拓扑关系,极易建立单层网壳结构实际工程设计模型,证明该方法得出的优化结果能为结构设计者提供技术参考,在工程中具有应用意义.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

梁汉奇, 张月强, 张峥.

异形单层网壳结构造型与关键问题研究

[J]. 建筑结构, 2023, 53 (Sup.1): 418-423.