提升弱网有功稳定输出能力的光伏逆变器Q-V下垂系数在线调整方法

doi:10.16183/j.cnki.jsjtu.2023.353

提升弱网有功稳定输出能力的光伏逆变器Q-V下垂系数在线调整方法

王语阳¹^,², 张琛^,¹^,², 张宇¹^,², 王一鸣³, 许颇³, 蔡旭¹^,²

1.上海交通大学电子信息与电气工程学院,上海 200240

2.上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240

3.锦浪科技股份有限公司,浙江宁波 315712

Reactive Power-Voltage Droop Gain Online Tuning Method of Photovoltaic Inverters for Improvement of Stable Output Power Capability in Weak Grids

WANG Yuyang¹^,², ZHANG Chen^,¹^,², ZHANG Yu¹^,², WANG Yiming³, XU Po³, CAI Xu¹^,²

1. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Key Laboratory of Control of Power Transmission and Conversion of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

3. Ginlong Technologies Co., Ltd., Ningbo 315712, Zhejiang, China

通讯作者: 张琛,副教授,博士生导师;E-mail:nealbc@sjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2023-07-28 接受日期: 2023-09-7

基金资助:

锦浪科技股份有限公司科技项目(22H010300150)
国家自然科学基金重点项目(51837007)

Received: 2023-07-28 Accepted: 2023-09-7

作者简介 About authors

王语阳(1999—),硕士生,从事光伏并网稳定性与自适应控制研究.

摘要

弱电网下静态有功输出与小扰动稳定能力是制约光伏可靠并网发电的关键因素.为提升弱电网下光伏发电系统有功稳定输出能力,提出一种基于无功功率-电压(Q-V)下垂系数自适应在线调整方法的光伏逆变器稳定控制方法.首先,为保障弱电网下的静态有功输出能力,提出计及电压、电流限制约束的Q-V下垂系数“一次优化”方法.然后,为进一步满足弱电网稳定性约束,开展光伏逆变器并网系统阻抗建模与稳定性分析,基于人工智能神经网络实现以闭环系统最弱极点为稳定性约束条件的“参数-最弱模式”映射关系和以有功稳定输出为目标的Q-V下垂系数“二次调整”方法;结合卡尔曼滤波器辨识的电网阻抗信息,最终实现所提Q-V下垂系数自适应在线调整方法.最后,利用远宽实时仿真平台对所提控制方法的有效性进行了分析与验证.

关键词： 自适应控制; 变换器; 稳定性; 光伏发电; 下垂控制; 弱电网; 人工智能

Abstract

The active power output capability and small signal stability in weak grids are key factors that limit stable photovoltaic (PV) power generation. To improve stably generating PV power in weak grids, an adaptive control method for PV inverters based on online tuning of the reactive power-voltage (Q-V) droop gain is proposed. First, to ensure active power output capability in weak grids, a “first optimization” method for the Q-V droop gain is proposed, considering voltage and current constraints. Then, to address stability constraints in weak grids, impedance modeling and stability analysis of the PV inverter system are conducted. A mapping relationship between the “parameter-weakest pole” is established with the weakest pole of the closed-loop system as a stability constraint based on the artificial neural network. A “second adjustment” method for the Q-V droop gain is developed at stably generating active power. Combined with the extended Kalman-filter-based grid impedance estimation, the proposed Q-V droop gain adaptive tuning method is realized. The effectiveness of the proposed adaptive control method is validated on the Modeling Tech real-time simulation platform.

Keywords： adaptive control; converter; stability; photovoltaic (PV) power generation; voltage droop control; weak grid; artificial intelligence

PDF (7800KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王语阳, 张琛, 张宇, 王一鸣, 许颇, 蔡旭. 提升弱网有功稳定输出能力的光伏逆变器Q-V下垂系数在线调整方法[J]. 上海交通大学学报, 2025, 59(6): 845-856 doi:10.16183/j.cnki.jsjtu.2023.353

WANG Yuyang, ZHANG Chen, ZHANG Yu, WANG Yiming, XU Po, CAI Xu. Reactive Power-Voltage Droop Gain Online Tuning Method of Photovoltaic Inverters for Improvement of Stable Output Power Capability in Weak Grids[J]. Journal of Shanghai Jiaotong University, 2025, 59(6): 845-856 doi:10.16183/j.cnki.jsjtu.2023.353

国家战略“双碳”目标下,构建以新能源为主体的新型电力系统提上日程^[1].风力发电、光伏发电是新能源发电的重要形式,故存在大量对风光电源并网的研究^[2-3].然而,风光电源通常远离负荷中心,需要长距离输电才能接入电网;同时,随着新能源不断取代常规电源,支撑电网基本运行的同步机组不断减少,这些都会导致电网强度下降^[4].新能源如光伏发电弱网稳定运行问题十分突出^[5].

光伏发电一般经过电压源型“并网变换器”接入电网,因此变换器的控制特性将主导光伏发电的并网特性.弱电网下变换器与电网存在显著的控制相互作用,极易引发以“宽频振荡”为特征的小扰动稳定问题^[6-8].针对该问题目前已有大量研究,主要有时域状态空间法和频域阻抗法两种,而后者因易于实测获取、稳定判据成熟以及可用于稳定性的黑箱和灰箱分析等特点,在新能源并网振荡中得到广泛应用.阻抗建模是进行基于阻抗稳定性分析的基础,文献[8]中给出电流环控制下考虑锁相环动态引起的频率耦合效应建立输出阻抗模型的方法,并基于广义奈奎斯特判据分析并弱网小干扰失稳的条件.文献[9]中在分析坐标变换、正负序分解的基础上,提出改进序坐标系并利用改进序域分析频率耦合效应产生的原因,并给出在dq坐标系和在改进序坐标系下进行扫频的方法.利用该方法可从较易推导的dq阻抗经简单数学变换和频率平移导出较难解析推导的正负序阻抗模型,便于实现不同坐标系的阻抗分析.文献[10]中研究了在两相静止复坐标系下的阻抗建模方法与验证,该模型本质上是序耦合模型的另一种表示.为更好地揭示振荡关键机理,文献[11]中建立简化模型,并以此为基础分析锁相环误差导致的逆变器-电网交互谐振产生的机理.文献[12]中建立并网变换器不同维度下的阻抗模型,并分析电网强度对稳定性的影响.利用这些方法可以得到光伏弱网稳定运行的条件与参数边界,为基于参数调优和附加阻尼的在线稳定控制设计等提供理论和分析基础.

在并网稳定自适应控制上,文献[13]中通过分析逆变器剩余容量调节虚拟阻抗,实现在微电网中谐波功率在不同逆变器中的合理分配,并根据稳定性确定虚拟阻抗的调节范围.文献[14]中针对海上二极管整流器-模块化多电平换流器混合直流电网场景,通过分析定电压-频率控制和下垂控制下的稳态传输特性,提出一种自适应下垂控制方法来降低交流电压波形范围.文献[15]中改进传统前馈环节,根据电网阻抗测量结果自适应调整前馈环节增益系数,提升变换器弱电网鲁棒性.文献[16]中利用拓展卡尔曼滤波方法辨识电网阻抗,并训练人工神经网络判断系统稳定性,通过缩小电流环控制器参数搜索空间优化电流环控制器参数,提升变换器稳定性.

除了平衡点附近的小干扰稳定分析与控制问题,非理想电网下光伏并网系统的平衡点存在性问题也是其并网稳定问题研究的另一个关键方面.分析该问题时,通常会对变换器控制动态进行简化,以更好地得到系统的静态工作区间.文献[17]中研究了由直流电压环、功率环和电流内环的变化率在不同并网点条件下发生变化而出现的静态稳定性问题.文献[18]中进一步考虑电流约束影响,讨论新能源并网变换器在弱网下的静态功率极限,并根据变换器直流电压控制环中有功功率相对于有功电流的变化率信息给出该系统的静态稳定条件,该分析对于弱电网下合理设定有功功率以确保存在静态工作点十分有用.上述分析表明,非理想电网下新能源并网有功功率会受到限制,因此合理的无功控制配合十分必要.在该方面,文献[19]中对极弱电网下光伏发电单元的功率传输特性进行分析,并提出自适应调整下垂控制参考电压的方法来提升有功功率传输能力,但该方法没有考虑弱网稳定性约束,有功能力的有效释放无法得到保障.

综上可知,弱电网下静态平衡点的存在,如多静态约束下的有功边界,和平衡点附近的小扰动稳定控制是影响光伏并网有功输出能力的两个重要方面,但同时满足两者的控制方法仍有待进一步研究.为此,提出一种无功功率-电压(Q-V)下垂系数的自适应调整方法,可保障光伏逆变器不同弱网下稳定输出给定有功功率.首先,介绍Q-V下垂系数一次优化过程,分析在并网电压电流限制下根据工作点范围求解Q-V下垂系数的方法,给出Q-V下垂系数优化结果和可行区间随电网强弱和输出功率大小的变化结果,并介绍其具体算法实现.然后,介绍Q-V下垂系数二次调整,对光伏并网系统进行小扰动分析、阻抗建模、稳定性分析以及利用人工神经网络(artificial neural network, ANN)拟合互联系统极点线上判断系统稳定性的方法,并介绍了Q-V下垂系数二次调整算法的实现.其次,介绍为实现电网适用性所采用的电网阻抗辨识方法.最后,在远宽实时仿真平台中进行算法实现和仿真分析,结果验证了方法的有效性.

1 面向静态有功能力提升的Q-V下垂系数一次优化方法

1.1 系统概述

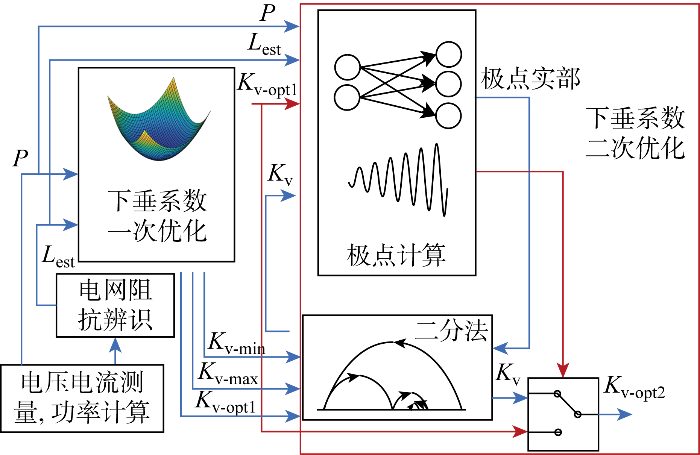
图1为整体控制结构框图,其中红色框为所提控制方法.可以看出,所提方法是在常规控制结构的基础上加入Q-V下垂系数的自适应调节,主要包括:根据输出电压电流限制对Q-V下垂系数进行一次优化并求解可行范围;根据ANN拟合系统极点进行稳定性判断并二次调整Q-V下垂系数.最终,结合电网阻抗辨识结果,实现Q-V下垂系数一次、二次自适应在线调整.图1中也展示了所考虑的典型光伏并网变换器电路结构,主要包括电压源型变换器、LC滤波器以及非理想电网.图中:EKF表示扩展卡尔曼滤波;U_s、U_c分别为并网点电压、变换器输出电压;I_s、I_c分别为输出电流、滤波电感电流;U_dc为直流电压;P_g、P_pv分别为电网侧输出功率与光伏(PV)侧发出功率;L_est为电网阻抗辨识结果;K_v为Q-V下垂系数;K_v-max、K_v-min分别为Q-V下垂系数最大、最小值;K_v-opt1、K_v-opt2分别为Q-V下垂系数一次优化与二次调整的结果;U_m为并网点电压幅值;U_n为设定电压基准;U_dc-ref为直流电压控制参考值;Q_ref为无功功率输出参考值; $I_{C_{f}}$ 为滤波电容上流过的电流;s_abc为abc三相开关控制脉冲;L_f为变换器滤波电感;C_f为交流滤波电容;L_g为电网等效电感.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 光伏并网自适应控制系统示意图

Fig.1 Scheme of proposed adaptive control of PV inverter system

1.2 静态可行域分析与工作点优化

通过分析电压、电流约束和有功输出求解Q-V下垂系数,实现Q-V下垂系数的一次优化.考虑到系统输出的稳态电压电流大小及其相位关系决定了系统所有的工作状态如有功、无功,故将其称为系统的“工作点”.

一个光伏变换器的输出电流受到变换器器件能够承受的最大电流限制,并网点电压受到电网的要求和变换器正常工作需要的限制.本文限制电压U_s的标幺值(p.u.)在0.95~1.1的范围内,I_s的标幺值在1.2以下.光伏发电侧通常采用最大功率点跟踪(maximum power point tracking, MPPT)控制,将功率作为其控制目标,而在并网逆变器侧将维持直流电压恒定作为控制目标^[20].故在逆变器控制中,所面临限制条件还包括输出的有功功率,由光伏侧boost电路MPPT控制指令决定.

得到工作点的限制之后,可对工作点进行优化.由于并网点电压对系统的正常运行较为重要,所以选取并网点电压与额定电压之差最小作为工作点的优化目标.同时,对工作点的约束也体现为对功率最大值的限制,对工作点和输出功率求解的优化问题可总结如下:第一个优化问题优化K_v,第二个优化问题求解并网点最大功率P_s,max.表示为

(1)

\begin{array}{l} \begin{array}{l} m i n (- | U_{s} - U_{n o m} |) \\ s . t . I_{s d}^{2} + I_{s q}^{2} \leq I_{l i m}^{2} \\ U_{s, m i n} \leq U_{s} \leq U_{s, m a x} \\ U_{s} I_{s d} = P_{o} \end{array}\} \\ \begin{array}{l} m i n (- P_{s}) \\ s . t . I_{s d}^{2} + I_{s q}^{2} \leq I_{l i m}^{2} \\ U_{s, m i n} \leq U_{s} \leq U_{s, m a x} \end{array}\} \\ U_{s} = \sqrt{U_{g}^{2} - (X_{g} I_{s d})^{2}} - X_{g} I_{s q} \end{array}\}

式中:U_nom为额定电压;U_s,min、U_s,max分别为并网点电压最小、最大值;I_s_d、I_s_q分别为输出电流在dq坐标系下的分量;P_o为光伏发电功率;X_g为电网等效阻抗;I_lim为电流限幅值;P_s为并网点输出有功功率;U_g为电网等效内电势.工作点优化的结果为系统的最优工作点,根据该工作点可计算出对应的Q-V下垂系数,计算公式为

(2)K_v=

\frac{Q}{U_{n} - U_{s}}

为使并网点电压标幺值能够达到1.1,设置电压基准设定值U_n标幺值为1.2.

在输出功率一定的条件下,通过求解以下优化问题可得约束下K_v最大值和最小值:第一个优化问题求解K_v最小值,第二个优化问题求解K_v最大值.表示为

(3)

\begin{array}{l} \begin{array}{l} m i n K_{v} \\ s . t . I_{s d}^{2} + I_{s q}^{2} \leq I_{l i m}^{2} \\ U_{s, m i n} \leq U_{s} \leq U_{s, m a x} \\ U_{s} I_{s d} = P_{o} \end{array}\} \\ \begin{array}{l} m i n (- K_{v}) \\ s . t . I_{s d}^{2} + I_{s q}^{2} \leq I_{l i m}^{2} \\ U_{s, m i n 2} \leq U_{s} \leq U_{s, m a x} \\ U_{s} I_{s d} = P_{o} \end{array}\} \\ U_{s} = \sqrt{U_{g}^{2} - (X_{g} I_{s d})^{2}} - X_{g} I_{s q} \\ U_{s - m i n 2} = m a x {U_{s, m i n}, U_{s, K_{v - m i n}}} \end{array}\}

式中: $U_{s, K_{v - m i n}}$ 为第一个优化问题求解出的K_v=K_v-min时对应的U_s值.绘制在不同电网短路比(short circuit ratio,SCR)和不同输出功率下K_v优化结果和边界求解结果,如图2所示.可以看出,随着SCR和P_s的增加,K_v的优化结果和可行区间端点值增大,并且当增大到一定程度后,K_v优化结果与K_v的下边界重合.值得一提的是,输出功率并不能无限增大,当输出功率过大,任意工作点都会导致电压或电流超限,在这种情况下,需要向光伏侧boost电路控制发出限制有功功率输出指令.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 K_v一次调整结果

Fig.2 Results of the first K_v regulation

1.3 Q-V下垂系数一次优化实现方法

过往研究对K_v一次调整原理介绍中的求解过程为求解多约束的优化问题,但对优化问题的迭代求解通常需要较多的计算资源,对线上计算不利.因此,对优化过程进行整理,将求解过程总结为算法求解来节省计算资源,示意图如图3所示.K_v最小值求解化归为对电压最小限幅和电流最大限幅工作点K_v求解结果的比较,K_v最大值求解化归为对电压最大限幅和电流最大限幅工作点K_v求解结果的比较,K_v-opt1求解化归为对电压最优值工作点处K_v求解结果与最大值最小值的比较.图中:P为光伏直流侧发出的功率.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 Q-V下垂系数一次优化算法示意图

Fig.3 First optimization algorithm of Q-V droop gain

通过以上过程可以得出满足有功输出以及上述电气约束的Q-V下垂系数一次优化结果与可行区间,但为保证该有功条件以及Q-V下垂系数下的并网稳定性,需要进行考虑稳定性约束的二次优化调整,具体如下.

2 考虑并网稳定约束的Q-V下垂系数二次调整

考虑并网稳定性对下垂系数调整的限制,对含有直流电压控制与Q-V下垂控制的逆变系统在dq坐标系下进行阻抗建模,考虑锁相环带来的频率耦合效应以及功率环节的非线性,建立完整的并网点端口阻抗模型;通过端口扫频验证理论建模的正确性;计算回率矩阵行列式零点判断互联系统稳定性,进一步作为线上稳定性判断的依据,并在此基础上介绍Q-V下垂系数二次调整方法及在线应用.

2.1 阻抗建模及验证

网侧变流器控制系统结构如图4所示,利用经典的锁相环对并网点电压进行锁相,外环采用直流电压控制和电压-无功下垂控制,内环采用电流环.图中:PI表示比例积分控制器;Droop表示无功下垂控制;Filter表示低通滤波器;I_d_,ref、I_q_,ref 分别为dq轴电流的控制参考值;U_s_d、U_s_q分别为并网点电压dq轴分量;U_sm为并网点电压幅值;Q_s为并网点处输出的无功功率; ω为电网角频率;L为滤波器电感.主电路为图1所示电路,由于含有交流电容,与电网电感共同构成了LCL电路结构,所以采用一种较为简单的有源阻尼方法对谐振峰进行抑制.当直流电容较大时,前端和网侧的耦合较小,可以忽略.机侧控制结构采用MPPT控制,因此将光伏侧等效为一个功率源.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 控制系统结构示意图

Fig.4 Structure of control system

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 小信号建模示意图

Fig.5 Diagram of small signal modelling

对图4中的系统进行小信号分析,绘制系统的小信号建模示意图.求解系统在给定工况下的工作点电压电流大小,在工作点附近对系统进行线性化,可得图5所示控制框图,对控制框图端口处扰动电压与扰动电流关系进行求解可得系统输出阻抗表达式.考虑频率耦合效应与功率非线性的完整阻抗模型推导过程见附录A.2×2输出阻抗矩阵表达式如下所示:

(4)Z_o=B^-1A

表达式中的矩阵均为s域的函数,为了简化表达式对拉普拉斯算子进行了省略,其中

(5)A=

B_{L_{f}}

+B_PI_{_i}-B_decpl-B_PI_{_i}C_PI_{_v}_dcR_dc_i
-B_PI_{_i}C_PI_{_v}_dcR_dc_v

B_{L_{f}}

-B_PI_{_i}C_PI_{_q}G_q_droopR_qi

(6)B=

B_{L_{f}} B_{C_{f}}

-B_pll_{_v}_c-
B_filter_v+B_filter_vB_pll_{_v}_o-
B_PI_{_i}B_pll_{_i}_o+B_decplB_pll_{_i}_o+K_v

B_{C_{f}}

-
B_PI_{_i}C_PI_{_v}_dcR_dc_v-B_PI_{_i}C_PI_{_v}_dcR_dc_i

B_{C_{f}}

-
B_PI_{_i}C_PI_{_v}_dcR_dc_i

B_{L_{f}} B_{C_{f}}

-
B_PI_{_i}C_PI_{_q}G_q_droopR_qv+B_PI_{_i}C_PI_{_q}G_q_droopR_qiB_pll_{_i}_c+
B_pll_{_v}_oB_PI_{_i}C_PI_{_q}G_q_droopR_qv-
B_PI_{_i}C_PI_{_q}G_q_droopK_v_droopR_v_t_v_o+I

式中:Z_o为输出阻抗;B表示矩阵,B_{pll_}_i_c、 $B_{L_{f}}$ 、 $B_{C_{f}}$ 、B_{PI_}_i、B_filter_v、B_decpl分别为变换器交流电流的锁相环扰动矩阵,滤波电感、滤波电容在dq坐标系下的电路矩阵,电流PI控制器传递函数构成的对角矩阵,电压滤波器构成的传递函数矩阵,交叉解耦控制构成的矩阵;R表示行向量,R_dc_i、R_dc_v、R_qi、R_qv、R_v_t_v_o分别为交流电流对直流电压,交流电压对直流电压,电流、电压对无功功率,交流电流对交流电压幅值的传递函数构成的行向量;C表示列向量,C_{PI_}_v_dc、C_{PI_}_q分别为直流电压、无功功率的控制传递函数构成的列向量;G、K分别表示传递函数与系数标量,K_v_droop为下垂控制系数,G_q_droop为Q-V下垂控制对应传递函数;I表示单位矩阵.图5、式(5)和式(6)中其余符号说明及推导过程见附录A.

为验证阻抗建模的正确性,利用仿真模型对其进行扫频验证,在改进序下注入不同频率的扰动电压并对扰动电压电流进行快速傅里叶(fast fourier transform,FFT)分析,利用文献[7]中提出的方法可以计算出扫频结果.图6给出扫频结果与理论结果的对比,横坐标频率为abc坐标系下的频率(f).由图可见,阻抗矩阵在1~1 000 Hz的频率范围内与理论几乎一致,从而验证了以上阻抗建模结果的正确性.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 扫频验证结果

Fig.6 Impedance scanning verification

2.2 互联系统极点求解与稳定性判断

基于前文的阻抗建模结果,可以对系统的小干扰稳定性进行分析和判断.一种被广泛采用的小干扰稳定性判断方法为广义奈奎斯特判据,对于采用跟网型控制的并网变换器而言,有回率矩阵:

(7)L=Z_g

Z_{o}^{- 1}

式中:Z_g为电网等效阻抗,和Z_o均为s域2×2矩阵,即上文中阻抗建模的结果.绘制L矩阵的特征根轨迹并判断其是否环绕(-1,0)点,可以验证系统的稳定性.

所提自适应控制策略需要对系统稳定性进行线上判断,故采用求解互联系统极点的方式对系统稳定性进行判断.事实上,对于采用跟网型控制的变流器,广义奈奎斯特判据等价于判断下式的零点是否均在左半平面^[21]:

(8)det(I'+Z_g

Z_{o}^{- 1}

)=0

式中:I'为2阶方阵的单位矩阵.式(8)中的零点即互联系统极点.式(8)为14阶方程,共有14个零点,求解上式的零点可得互联系统极点.

图7为互联系统的极点分布图.该系统的所有极点均分布在左半平面,故可判断该系统稳定.由于系统的稳定性判断可以归结为判断实部最大的极点是否分布在右半平面,故下文中涉及稳定性分析的部分仅展示该互联系统最弱极点,即实部最大的极点的分布规律.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 极点分布

Fig.7 Pole distribution of the system

2.3 面向在线应用的极点映射学习方法

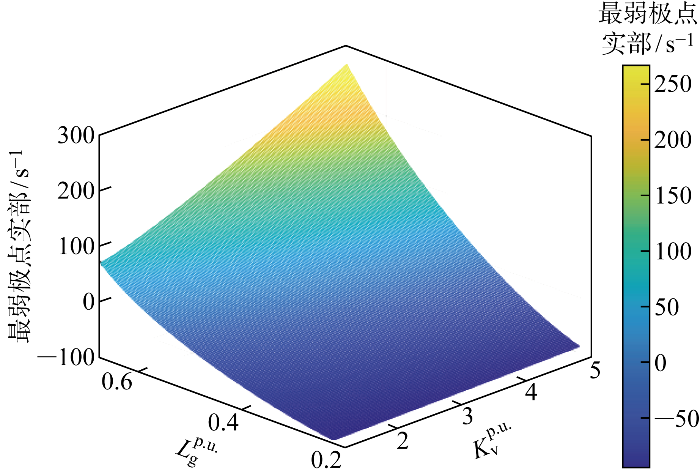
自适应控制方法需要对系统并网稳定性进行在线判断,而稳定性判断中对系统极点的求解涉及矩阵运算、特征根计算以及高次方程求解.为减轻控制器线上运算负荷,利用人工神经网络对该部分算法计算结果进行拟合.利用不同控制参数对应系统极点的数据集进行离线训练,并线上运用训练完成的人工神经网络对系统的小干扰稳定性进行预测.由于该部分神经网络仅完成对已有映射关系的拟合,且需要线上实时运算,数字信号处理器对算力的限制较大,故采用结构较为简单的3层全连接神经网络进行拟合.对人工神经网络给出的最弱极点绘制三维曲面如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 人工神经网络拟合最弱极点实部变化规律

Fig.8 Real part of weakest pole using fitted ANN

可以看出,随着电网电感增加即电网强度下降、下垂系数增加,系统最弱极点实部增加,系统由收敛逐渐变化为发散.人工神经网络得到正确的最弱极点实部与下垂系数、电网电感之间的变化规律.在研究的参数范围内,系统最弱极点实部与下垂系数为正相关关系,从而可以利用二分法来优化下垂系数,得到最接近稳定裕度的下垂系数设定值.

2.4 基于Q-V下垂系数二次调整的稳定控制方法

根据前文给出的最弱极点变化规律,K_v单调性不会发生变化,故K_v二次调整依据系统稳定性利用二分法来进行,具体如下.

Q-V下垂系数二次调整方法接受一次优化结果K_v-opt1作为稳定性调整的起始值并进行稳定性判断.如果其稳定性满足要求,则直接作为控制参数进行控制;如果其稳定性不满足要求,则求解可行区间端点的极点,取极点满足稳定性要求的端点和起始值K_v-opt1作为二分法的起始区间,利用二分法求解极点恰好满足稳定性要求的K_v-opt2,从而使得在满足稳定性要求的同时并网点电压尽量接近额定值.具体调整过程如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 自适应控制方法示意图

Fig.9 Diagram of adaptive control method

3 面向自适应控制的电网阻抗辨识

为实现上述一次、二次调整方法的电网适应性,需要对电网阻抗进行辨识.电网阻抗辨识包括注入脉冲法^[22]、注入M序列法^[23-24]、卡尔曼滤波法^[25]等多种方法,本文重点以卡尔曼滤波法为例,验证上述参数调整方法,具体实现方法如下.

对电网电路方程进行建模,得到αβ坐标系下的电网传输方程,选择流向电网为电流正方向,对其进行离散化,考虑电感和角频率等,从而有完整的卡尔曼滤波先验迭代方程:

(9)

[\begin{array}{l} Δ i_{α} (K + 1) \\ Δ i_{β} (K + 1) \\ Δ u_{s α} (K + 1) \\ Δ u_{s β} (K + 1) \\ ω_{c} (K + 1) \\ l (K + 1) \end{array}]

[\begin{array}{l} Δ i_{α} (K) - l T Δ u_{s α} (K) \\ Δ i_{β} (K) - l T Δ u_{s β} (K) \\ c o s (ω_{c} T) Δ u_{s α} (K) - s i n (ω_{c} T) Δ u_{s β} (K) \\ s i n (ω_{c} T) Δ u_{s α} (K) + c o s (ω_{c} T) Δ u_{s β} (K) \\ ω_{c} (K) \\ l (K) \end{array}]

式中:i为电流;u为电压,下标s表示并网点;K为第K步算法执行时变量的值;Δ表示相应物理量的变化量;l为电网电感的倒数;ω_c为电网角频率估计值;T为算法两次执行之间的时间间隔.利用完整的拓展卡尔曼滤波迭代算法,可在线辨识电网阻抗.

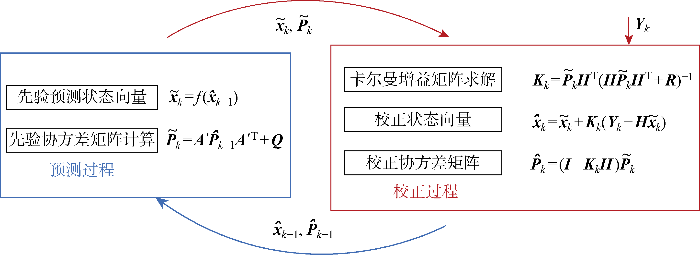
图10为卡尔曼滤波迭代算法示意图.图中:Q、R分别为过程噪声协方差矩阵和测量噪声协方差矩阵;P_k为第k步的协方差矩阵;x_k为状态向量迭代至第k步的值;f( )为上文建立的先验迭代方程;A'为f( )的雅可比矩阵;H为测量方程的系数矩阵;Y_k表示第k步输入的测量向量;K_k为第k步卡尔曼增益矩阵;上标^ 表示预测值,~表示估计值.通过不断输入测量αβ坐标系下电压电流值,并不断迭代计算,可得对电网阻抗的测量值.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 拓展卡尔曼滤波迭代过程示意图

Fig.10 Diagram of EKF algorithm

4 仿真验证

利用如图11所示的远宽(Modeling Tech)的实时仿真平台搭建模型并采用所提自适应控制方法对其在弱电网下进行控制,来验证本文分析的正确性以及所提方法的有效性.实时仿真系统额定功率为230 kW,额定电压为800 V,滤波电感为80 μH,滤波电容为21 μF,直流电压额定值为 1 500 V,直流电容为 2.19 mF,开关频率为 16 kHz.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 远宽实时仿真平台示意图

Fig.11 Real-time simulation platform of Modeling Tech

4.1 电网阻抗辨识验证

对电网阻抗的辨识结果如图12所示.变换器每0.5 s注入50 ms无功指令脉冲,变更系统状态.将两种系统状态的差值作为卡尔曼滤波算法的输入,通过迭代辨识当前电网阻抗,在dq坐标系下展示仿真结果.可以看出,电路中的电感在6.5 s时从4 mH下降至3 mH,每隔0.5 s进行初始化并执行辨识算法,拓展卡尔曼滤波算法基本正确地估计了电网阻抗的大小.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 电网阻抗辨识结果

Fig.12 Waveforms of grid impedance identification

4.2 Q-V下垂系数自适应调整控制方法验证

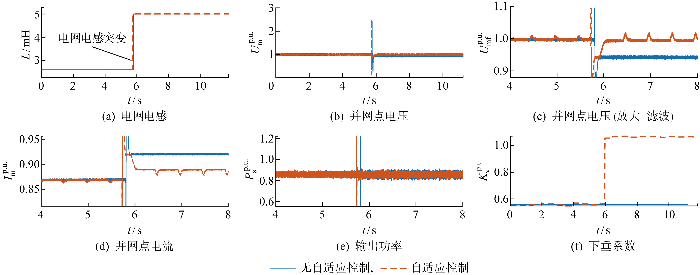
案例一系统参数如前文所述,电网等效电感从2.6 mH变化为5.0 mH,SCR从3.40变化为1.77,输出功率为200 kW,并网点电压限制标幺值为0.95~1.1,输出电流限幅标幺值为1.2,分别在加入自适应下垂系数调整控制和不加入自适应下垂系数调整控制的情况下进行实时仿真,从而展示所提自适应控制方法对并网点电压的优化.

图13(a)~13(f)分别展示了无自适应和自适应情况下的电网电感、并网点电压、电压幅值滤波值(U_mf)、电流幅值(I_m)、输出功率、下垂系数变化的情况.具体地,图13(c)展示了10 ms滤波时间常数下对并网点电压进行滤波的结果,可以看出所提自适应控制方法能够在电网条件发生变化的情况下调节下垂系数(见图13(f)),将并网点电压基本保持在了额定值.而未加入自适应控制的情况下并网点电压标幺值下降到0.95以下,低于系统限制,可能会进入异常工况.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 自适应调整Q-V下垂系数优化并网点电压结果

Fig.13 Waveforms of Q-V droop gain adaptive tuning for POC voltage optimization

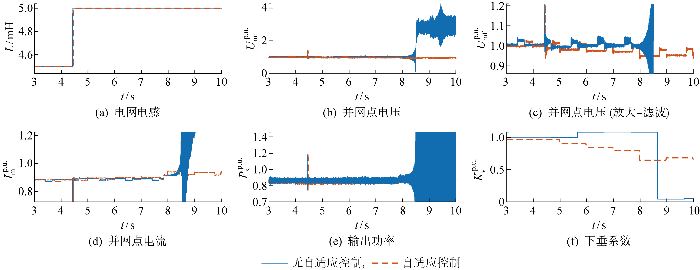
案例二系统参数如前文所述,电网等效电感从4.5 mH变化为5.0 mH,SCR从1.97变化为1.77,之后输出功率从200 kW变化为205 kW,并网点电压限制标幺值为0.95~1.1,输出电流限幅标幺值为1.2,调整控制参数至稳定裕度较小的情况,分别在考虑稳定性约束的自适应调整Q-V下垂系数和不考虑稳定性约束的自适应调整Q-V下垂系数的情况下进行实时仿真,从而展示所提自适应控制方法对系统稳定性的提升作用.

图14(a)~14(f)分别展示了无自适应和自适应情况下的电网电感、并网点电压、电流幅值、输出功率、下垂系数变化的情况,可以看出控制方法对稳定性的提升作用.具体地,图14(c)展示了10 ms滤波时间常数下对并网点电压进行滤波的结果.如图14(a)所示, 两种情况下电网电感在4.5 s左右完成切换.如图14(e)所示,输出功率在7.8 s左右增加了5 kW.增加稳定性约束的控制方法在电网强度下降和输出功率上升的同时降低了下垂系数来提升系统的稳定性,并保证了电压电流幅值在系统工作允许的范围内;而未加入稳定约束的控制方法仍然通过提升Q-V下垂系数来抬高并网点电压,从而导致系统在功率输出增加后失稳.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 自适应调整Q-V下垂系数提高稳定性结果

Fig.14 Waveforms of Q-V droop gain adaptive tuning for stability improvement

5 结论

提出考虑静态及稳定性约束的光伏逆变器Q-V下垂系数自适应在线调整方法,保障并网有功的稳定输出,具体结论如下:

(1) 该方法考虑并网电压允许范围、变流器电流限制以及无功电压控制影响,能够避免电网变弱出现并网点电压过低和功率过大导致的电流幅值超限情况,可给出考虑Q-V下垂系数调整、实际可行的有功功率优化限值,如上限值.

(2) 该方法考虑弱网稳定性约束及控制,通过对含Q-V下垂的光伏逆变器并网系统进行阻抗建模和人工智能神经网络学习,得到易于在线控制应用的参数化最弱极点映射,并基于此开发基于Q-V下垂系数二次调整的稳定控制算法,保障并网有功输出的稳定性.

(3) 开发了Q-V系数自适应在线控制方法,并基于远宽实时仿真平台进行了方法验证.

最后,值得指出的是,本方法未详细考虑光伏逆变器前段特性,在一些极端情况下可能存在光伏源端功率与网侧输出能力不匹配的情况,导致直流卸荷保护的投入,因此光伏发电系统全工作范围的控保方案及验证是后续需要进一步完善的内容.此外,所提方法具有一定通用性,理论上其也可迁移至构网型变换器,未来将对此作进一步研究.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-06-0845.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要

[N]. 人民日报, 2021-03-13(1).