大规模新能源并网和低效率火电机组的计划性退役增加了电力系统中净负荷波动的随机性和不确定性[1 -2 ] .为适应新能源电力系统的发展变化,我国进行了大规模的火电机组灵活性改造.改造后的火电机组深度调峰能力增强,可实现快速爬坡和快速启停.然而,随着调峰频率增加,机组的寿命损耗也随之加快.此外,为实现存量煤电机组转型发展,我国发布了延长煤电机组服役寿命的政策和文件.国际上火电机组的设计寿命一般为30 a,但由于我国严格执行环保、降耗等要求,不断推进火电落后产能的淘汰,使得许多机组达不到设计寿命就被关停,平均服役年限仅为12 a.为支撑我国能源转型,同时提高火电机组的利用效率,避免资源浪费,中国电力企业联合会牵头完成《煤电机组灵活性运行与延寿运行研究》调研报告(以下简称《研究》).《研究》指出2050年左右,“十二五”“十三五”投产机组将达到设计寿命,机组延寿对实现碳中和意义重大.
当前,火电机组采用不同调峰工况运行配合新能源消纳的频率提高,寿命损耗加快;同时,发展环境需要延长机组服役寿命.因此,为应对火电机组面临的寿命损耗加快与服役期限延长之间的矛盾,区分火电机组各类运行工况造成的损耗程度,研究如何在调度过程中考虑不同工况对机组寿命损耗的影响,从而优化机组组合运行结构,目前尤为重要.
国内外针对火电机组寿命损耗的研究主要集中在转子[3 6] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗.
另外,以往研究普遍采用Langer公式估算机组单次参与深调峰的平均损耗与深调峰次数乘积的形式计算机组寿命损耗[13 -14 ] .这种平均损耗叠加的计算方法以及较为固定的启停约束条件[14 16] 未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境.
鉴于此,基于当前火电机组寿命损耗理论,提出一种计及多工况对火电机组寿命损耗的机组组合优化模型.首先,对火电机组常规工况和特殊工况的损耗进行区分,比较分析不同运行工况的损耗程度;在此基础上采用线性损伤累计方法,建立多工况的火电机组寿命损耗成本模型,并从时序生产模拟的角度给出停机时长的计算方法;然后,改进对应的机组运行约束条件,考虑风电出力不确定性,构建含长短期风电出力模拟的机组组合模型;最终,通过3类递进的电力系统运行场景验证了所提模型的有效性.相比于已有研究,所提模型兼顾常规工况下的蠕变损耗和特殊工况下的综合损耗,建立不同工况对应的损耗率判定模型,能够判断机组不同类型的特殊工况并计算对应损耗和成本;进而丰富机组组合问题的运行可能性,为新能源发电提供更多可消纳区间,对实现机组延寿,助力碳减排意义重大.
1 火电机组多工况寿命损耗
火电机组常规运行工况下的寿命损耗可根据购机成本和预计使用年限分摊获得,但火电机组在特殊工况下的寿命损耗则需区分机组不同运行工况,结合对应损耗率进行计算.在分析火电机组不同运行工况对机组寿命损耗影响的基础上,从时序生产角度建立火电机组寿命损耗成本模型.
1.1 火电机组特殊工况对转子寿命损耗的影响
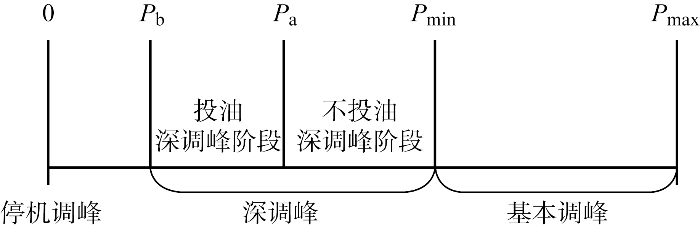
参与调峰作业的火电机组,除正常出力运行方式外,根据其出力状态可划分为基本调峰阶段、深度调峰阶段以及停机调峰阶段.在基本调峰阶段,机组可以通过快速爬坡响应净负荷波动.深度调峰阶段可以实现机组出力的进一步降低,可按照调峰能力和燃烧介质不同划分为不投油深调峰阶段和投油深调峰阶段,如图1 所示.图中:P max 为火电机组最大技术出力;P min 为基本调峰阶段最小技术出力;P a 为需要进行投油稳燃的技术出力界限;P b 为火电机组投油深调峰最小技术出力.
图1
图1
火电机组调峰阶段示意图
Fig.1
Diagram of peak shaving phase of thermal power unit
在实际工程中火电机组根据调度指令进行的调峰深度和爬坡速率各不相同,由此造成的转子损耗也不一致,因此每次机组进行调峰的损耗成本并不是一个固定值,需要结合不同工况的损耗率进行计算.同时,火电机组可以实现在不同时长停机后的再启动,对应的启停约束条件也应根据火电机组不同启动运行方式对应的停机时长加以区分.因此,在火电机组建模过程中应结合不同特殊工况的运行特点进行工况判别.
为直观说明各类特殊工况对火电机组寿命损耗的影响程度,表1 提供了美国通用电气公司某机型寿命分配数据,对寿命损耗的80%进行特殊工况下的预分配[8 ] .
机组各类特殊工况包括机组启停和变负荷运行.其中,不同启停工况的运行及损耗特点如下:
(1) 大型汽轮机冷态启动对应停机时长大于 72 h.冷态启动过程升温、升负荷速率较高,引起金属温度变化较为剧烈,转子受到较大应力,部分区域会产生明显塑性变形,因此会出现较大疲劳损伤[10 ] .
(2) 温态启动和热态启动对应的停机时长分别为[72 h]和[2 h,10 h).温态启动和热态启动时,汽轮机上下气缸温度较高,转子承受的温度变化较小,因此相比冷态启动损耗较小.
(3) 极热态启动对应的停机时长在2 h以内.进行极热态启动时,冲转的主蒸汽温度往往低于或者接近汽缸温度,冲转时汽缸进汽量很小,做功后温度下降;当机组进汽量增加后,汽缸温度又逐步回升.调节级处汽缸温度的反复变化造成转子表面先受冷再受热,产生的交变应力相比于温态和热态启动更大.
因此,在各类启停工况中,冷态启动的损耗最大,极热态第二,温态和热态相继次之,对应损耗率因机型不同而异.
由表1 可见,除不同时长的启停损耗外,机组通过快速爬坡进行大幅度变负荷运行的损耗同样不容忽视,其对机组寿命造成的损耗相当于一次温态启动或热态启动.同时,由于小幅度变负荷的损耗率略小且运行界限不易判定,故在本研究中忽略对小幅度变负荷损耗的考虑.
此外,在实际生产中,极热态启动具有一定的特殊性.文献[17 -18 ]中基于实际生产中的技术经验指出,极热态启动过程极为复杂,操作不当会出现人员伤亡或者设备损坏.文献[18 ]中说明了包括故障跳闸和机组停运在内的应用极热态启动场景.为使模型计算更加接近实际,在电力系统运行中保留足够的安全裕度,本文在进行后续研究时不再考虑极热态启动的情况.
综上,为准确模拟火电机组在电力系统调峰运行过程中各类工况下的损耗情况,针对冷态启动、温态启动、热态启动以及大幅度变负荷共4类主要特殊工况及常规工况建立适用于电力系统调度模拟的模型和约束,根据机组停机时长和功率变化判定机组实时工况并结合不同工况损耗率计算机组运行过程中的寿命损耗成本.
1.2 火电机组多工况寿命损耗成本模型
在对火电机组运行工况进行区分的基础上,考虑蠕变损耗和低周疲劳损耗对机组寿命的综合影响,为火电机组建立更加贴近实际的寿命损耗成本模型.
模型搭建过程中,认为单机组使用寿命为30 a,转子致裂损耗在常规运行中占20%,在特殊工况运行时占80%[3 6] .参考《中华人民共和国电力行业标准火电机组寿命评估技术导则》(DL/T 654—2022),沿用线性损伤累计法计算火电机组的寿命损耗成本.
(1) 常规工况运行损耗成本.火电机组在常规运行状态下的蠕变损耗成本可根据机组预计寿命年限计算各时段平均成本并结合机组在该时段运行状态获得:
(1) C U, i ζ u C u n i t , i T l i f e ∑ t = 1 T i , t ΔT
式中:i ∈{1,2,…,N }为火电机组编号,N 为参与系统运行的火电机组总数;ζ u 为常规运行工况下的寿命分配占比,如前所述为20%;C unit, i T life 为机组寿命损耗分摊系数;t ∈{1,2,…,T },T 为调度模拟过程中的时间节点数;xi , t i 在t 时段的运行状态量,xi , t xi , t T 为调度模拟中设定的时间步长,当时间步长为1 h时,ΔT =60,当数据时间步长为15 min时,ΔT =15.
(2) 特殊工况运行损耗成本.机组运行在特殊工况时,受到低周疲劳损耗和蠕变损耗的共同作用,这一过程中产生的损耗成本定义为特殊工况下的综合损耗成本:
(2) C V, i , t ζ v C unit, i ηk yi , t
式中:ζ v 为特殊运行工况下的寿命分配占比,如前所述为80%;ηk 为对应工况的损耗率,k ∈{1,2,3,4};yi , t yi , t yi , t .
火电机组在运行过程中不同工况对应的损耗率可由下式计算得出:
(3) η = η 1 , τ i , t > t 3 η 2 , t 2 < τ i , t ≤ t 3 η 3 , t 1 < τ i , t ≤ t 2 η 4 , τ i , t = 0 , P i , t - P i , t - 1 > Δ P i
式中:η 1 ~η 4 分别对应冷态启动、温态启动、热态启动和大规模变负荷的损耗率;τi , t t 1 ~t 3 为不同启动状态之间的停机时间界限;Pi , t i 在t 时段的计划出力;ΔPi 为机组大幅度变负荷判定值.
忽略极热态损耗以及小幅度变负荷损耗对机组寿命的影响,参考表1 中的预分配数据,理论上所建火电机组寿命损耗模型涵盖了机组寿命的90%,剩余10%的特殊工况分配寿命将作为实际生产过程中应对极端运行指令时的安全裕度.
(4) C S = ∑ i = 1 N U, i + ∑ i = 1 N ∑ t = 1 T V, i , t
1.3 火电机组停机时长
火电机组在运行过程中的多次停机时长无法直接获得,通过计算机组启停时刻的差值表征机组停机时长.机组停机时刻和机组启动时刻对应的时间节点可由下式获得:
(5) τ o f f , i , t = x i , t - 1 ( 1 - x i , t ) t τ o n , i , t = ( 1 - x i , t - 1 ) x i , t t
(6) $\begin{aligned} \tau_{i, t}= & \left(1-x_{i, t-1}\right) x_{i, t}\left(\max \left\{\tau_{\mathrm{on}, i, 1}, \tau_{\mathrm{on}, i, 2}, \cdots, \tau_{\mathrm{on}, i, t}\right\}-\right. \\ & \left.\max \left\{\tau_{\mathrm{off}, i, 1}, \tau_{\mathrm{off}, i, 2}, \cdots, \tau_{\mathrm{off}, i, t}\right\}\right) \end{aligned}$
式(6)结合机组启停时刻差值和机组运行状态得出机组各时段的停机时长,即仅在机组重启时输出该时段停机时长,否则为0.
2 考虑机组寿命损耗成本的机组组合优化模型
以含风电的电力系统为例,针对火电机组的调峰运行场景,在目标函数中考虑机组寿命损耗成本,改进因考虑火电机组多工况寿命损耗问题而产生变化的约束条件,并给出算例验证所需的风电典型日选取方法及中长期风电不确定性转化模型.
2.1 目标函数
目标函数包括煤耗成本、深调峰附加投油成本、寿命损耗折算成本和弃风惩罚成本4个部分,相关表达式如下:
(7) min F =C coal +C oil +C S +C W
(8) C coal = ∑ i = 1 N ∑ t = 1 T P i , t 2 i , t +c)
(9) C coal =γ wind ∑ t = 1 T wind, t
式中:F 为系统运行总费用;C coal 为火电机组发电的煤耗成本;C oil 为火电机组深调峰附加投油费用;C S 为火电机组在各类工况运行过程中的寿命损耗折算成本;C W 为弃风电量的弃风惩罚费用;a 、b 、c 为与机组特性相关的耗量系数;γ wind 为弃风惩罚系数;Q wind, t t 时刻系统弃风电量.
火电机组投油深调峰阶段需要进行投油稳燃,其附加投油成本可由下式计算:
(10) C oil = ∑ i = 1 N ∑ t = 1 T oil Qoil, i , t
(11) Q oil, i , t P i , a - P i , t , P i , t ≤ P i , a 0 , 其 他
式中:ρ oil 为单位调峰电量所需的燃料价格,与当季的油料价格相关;Q oil, i , t i 在投油深调峰期间t 时段发电低于不投油深调峰稳燃时的电量;Pi ,a 为机组i 的不投油深调峰最小技术出力.
陆上风力机运行维护成本主要包含定期检修维护和日常排故维护[19 -20 ] .风场的风速和风力机的出力不可控,风电场的运行维护成本不因火电机组运行状态的改变而发生变化,对本文需要验证的目标无影响,因此不考虑风电场的运行成本.
2.2 约束条件
与常规模型相比,由于考虑了多工况对机组的寿命损耗,所以机组运行状态决策变量的约束条件发生变化.因此,在目标函数优化求解的过程中除满足常规约束条件外,需根据火电机组多工况寿命损耗成本模型对机组启停约束进行修改.
(1) 机组开机时长约束.由于式(3)建立通过机组停机时长判定机组启动状态的模型,无需再对机组停机时长设置约束条件,所以仅考虑最小开机时长约束.表示为
(12) ∑ n = t t + T i , o n - 1 i , n ≥Ti ,on (xi , t -xi , t -1 )
(2) 机组日最大启停次数约束.式(2)~(4)通过区分不同工况下的停机时长建立火电机组多工况寿命损耗成本模型,因此,常规的火电机组最小停机时长将不再适用.为保证机组的安全运行,结合火电机组启动管理实践经验[21 ] 对机组短期启停次数进行限制.表示为
(13) ∑ n = t t + 1 440 / Δ T x i , n - x i , n - 1 i
2.3 风电典型日选取
选取电量偏差与功率偏差指标最小的单日运行数据作为风电场运行典型日,典型日所需的电量偏差Δσ M, d [22 ] 可以根据下式计算获得:
(14) Δσ M, d ∑ j = 1 J ( S w i n d , d - S w i n d , j ) ∑ j = 1 J S w i n d , j
(15) Δσ D, d 1 T w ∑ k = 1 T w P w i n d , d , k J - ∑ j = 1 J P w i n d , j , k ∑ j = 1 J P w i n d , j , k
式中:d 为假设典型日编号;S wind, j j 天的风力发电总量,j ∈{1,2,…,J };T w 为不同时间步长下的归算参数,当数据时间步长为1 h,T w =24,当数据时间步长为15 min时,T w =96;P wind, j , k j 天k 时段的风力发电功率,k ∈{1,2,…,T w }.
2.4 中长期风电预测不确定性转化
与能够稳定出力的火电机组相比,风电出力不确定性对功率平衡的影响较大,因此需设置旋转备用容量,以维持电力系统的稳定性和可靠性[23 -24 ] .
电力系统可提供的旋转备用容量受到各机组发电剩余容量和最大爬坡速率影响,可表示为
(16) R u p , t = ∑ i = 1 n m i n { P i , m a x - P i , t , S u p , i T 10 } x i , t R d n , t = ∑ i = 1 n m i n { P i , t - P i , b , S d n , i T 10 } x i , t
式中:R up, t R dn, t t 时段系统所能提供的正、负旋转备用容量;Pi ,max 为机组i 的最大技术出力;Pi ,b 为机组i 的投油深调峰最小技术出力;S up, i S dn, i i 最大上、下爬坡速率;T 10 为旋转备用响应时间,设定为10 min.
考虑风电出力不确定性,利用风电计划出力与实际出力期望之差的概率分布,设置电力系统旋转备用容量约束:
(17) P r R u p , t ≥ P w i n d , t - E ( P w p r e , t ) ≥ β 1 P r R d n , t ≥ E ( P w p r e , t ) - P w i n d , t ≥ β 2
式中:P wind, t P wpre, t β 1 、β 2 分别为根据风电预测误差概率分布函数确定的置信水平,β 1 =0. 95,β 2 =0. 95;E 表示期望值.
2.5 模型转化与求解
所建立模型的约束条件中包含随机变量,需要将式(17)中的随机约束转化为确定性约束.
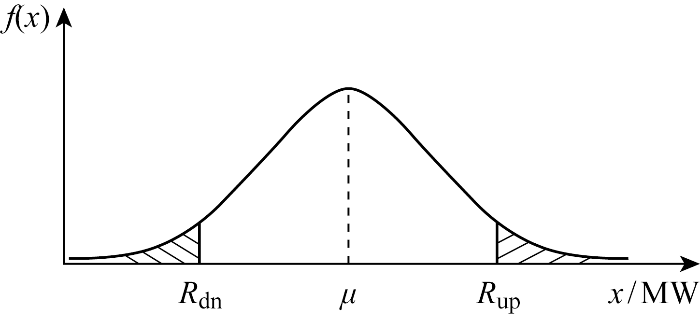
如图2 所示,风电预测误差概率密度函数可由正态分布拟合,可将式(17)中的含期望概率约束转化为
(18) ∫ μ R u p , t f ( x ) d x ∫ μ + ∞ f ( x ) d x 1 , ∫ - R d n , t μ f ( x ) d x ∫ - ∞ μ f ( x ) d x 2
式中:f (x )为风电预测误差的概率密度函数;x 为样本中风电预测值与实际值的误差;μ 为样本均值.
图2
图2
风电功率预测误差概率密度函数示意图
Fig.2
Probability density function of wind power prediction error
进而,借助正态分布函数的反函数,可将式(18)转化为确定性约束:
(19) R u p , t ≥ φ - 1 1 - 1 2 β 1 σ + μ R d n , t ≥ - φ - 1 1 - β 2 2 σ - μ
式中:φ -1 为正态分布函数的反函数;σ 为样本标准差,可通过风电预测历史数据得出.
电力系统运行成本求解属于混合整数线性规划问题,可通过MATLAB平台、YALMIP工具箱调用CPLEX求解器对模型进行求解.
3 算例验证
为验证所提模型的可行性,分别在风电出力较 大、波动性较小的春季和风电出力较小、波动性较大的夏季典型日验证,以及中比例风电中长期验证和高比例风电中长期验证3类递进的电力系统运行场景,模拟局部电力系统调峰运行过程并对比分析常规模型和多工况模型的运行数据.
此外,所提计及多工况对机组寿命损耗优化模型即多工况模型采用包含各类调峰过程的机组寿命损耗成本模型,相比平均化寿命损耗的常规模型,总成本计算流程存在差异.因此,将常规模型的仿真运行结果代入多工况模型的成本计算流程中,获得常规模型运行结果向多工况模型归算后的成本,以方便不同模型之间进一步比较分析.
算例收集北方某地相距较近的两个火电厂和风力发电站的运行数据,采用两台 1 000 MW(机组1、机组2)和两台350 MW(机组3、机组4)凝气式汽轮机组及日负荷曲线,陆上风电站五线50 台中型风力机的历史出力功率作为算例验证的支撑数据.机组特殊工况的寿命损耗率和停机时长界限值参考表1 ,各类运行参数值如表2 所示,弃风惩罚系数设置为336元/(MW·h).
3.1 典型日验证
本阶段研究参考华北地区风电总装机容量占比为26.9%,设置模拟系统中风电的容量占比为27%,装机容量为 1 000 MW.依照式(14)和(15)计算风电场运行典型日,根据计算结果,选取2月27日和7月26日作为春、夏典型日,见附录图A1、图A2.在此基础上进行常规模型和多工况模型的运行模拟,时间步长设置为15 min,共96个时间节点.
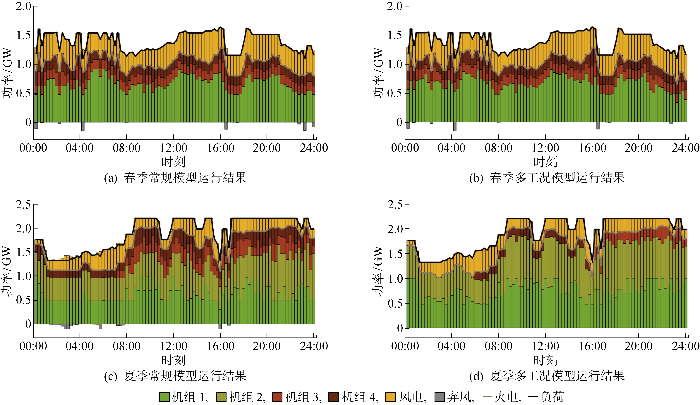
典型日场景下,两类模型在春、夏季运行结果如图3 所示.表3 给出不同模型下的电力系统各指标值,包括可供与实际电价对比的折算电价,以验证算例数据的有效性.表中:A~C分别代表常规模型结果、多工况模型结果、常规模型向多工况模型归算后的结果.
图3
图3
典型日运行情况
Fig.3
Operation of typical day
由图3(a) 和3(b) 可见,在春季典型日场景中,常规模型的3台机组均未进入深调峰状态,而多工况模型中仅机组1在93节点(23:00—23:15)和96
节点(23:45—24:00)进入深调峰状态,见附录图A3.结合图3(a) 和3(b) 可知,多工况模型相应时段的弃风功率较常规模型出现显著下降.由表3 可知,相比常规模型,多工况模型的春季典型日弃风电量减少了55.9 MW·h,表明在短期尺度下,多工况模型具有更强的调峰能力.
由图3(c) 和3(d) 可见,两类模型在夏季典型日运行结果存在较大不同,常规模型在自身约束条件下采用多机组运行提高系统调峰灵活性,受机组常规出力下限影响,弃风电量相对较高;多工况模型在保障供电的同时采用机组轮换启停以提高风电消纳量.在第64节点(15:45—16:00)负荷出现大幅度下降,常规模型的机组1进入投油深调峰最小技术出力,其余机组保持基本调峰最小技术出力以减少弃风;而多工况模型则采用机组3、4的轮换启停调峰,为风电消纳提供足够的容量.由表3 可知,相比常规模型,多工况模型夏季的弃风电量减少185.4 MW·h,弃风情况得到显著改善.
相比常规模型,多工况模型在春、夏季的运行总成本分别减少2.3万元和16.2万元.同时,春、夏季常规模型归算后的总成本较原有值分别增加了0.68万元和59.4万元.由于常规模型的春季调度过程中不含调峰工况,差值来源于对常规蠕变损耗的成本折算;而夏季机组调峰工况增多,使得机组综合损耗上升,成本差值增大.表3 中模型A、C对应总成本不同表明常规模型运行总成本低于实际值.
典型日短期调度模拟采用春、夏典型日两种场景,验证了在短期时间尺度下,多工况模型能够降低系统运行成本,提高风电消纳水平.
3.2 中比例风电电力系统算例验证
在春季算例验证中,保持算例供需结构不变,选取春季2月份共14日连续负荷和风电出力预测数据,时间步长为1 h,共计337个时间节点,各运行指标值如表4 所示.夏季算例场景选取夏季7月份共15日连续负荷和风电出力预测数据,时间步长设置为1 h,共360个时间节点,各运行指标值如表5 所示.机组1、2,机组3、4,两两之间生产参数相同,存在可替换性,故采用相同机型平均后的寿命损耗比例表征机组寿命损耗情况.
由表4 和表5 可知,在中比例风电电力系统场景验证中,相比常规模型,多工况模型在春夏季的运行总成本分别减少 1 630.4 万元和710.3万元,弃风电量分别下降 1 309.5和 1 035.5 MW·h,两类机型的机组寿命损耗均有下降.
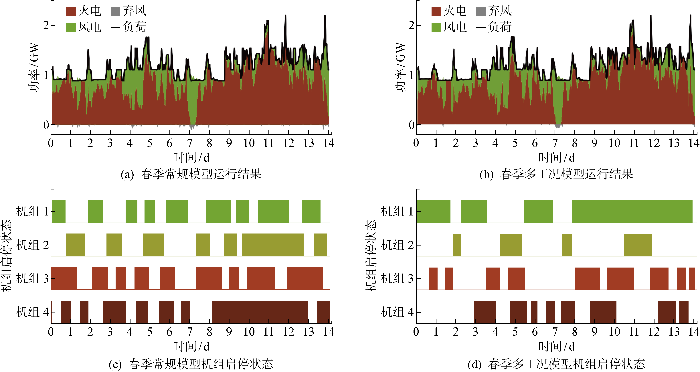
图4 和附录图A4~A7分别展示常规模型和多工况模型在春、夏季的机组出力和启停状态,表6 和7 给出不同模型在运行过程中出现的各类启停调峰次数及平均时长.
图4
图4
中比例风电电力系统春季运行结果及机组启停情况
Fig.4
Operation results and unit startup and shutdown status of medium-proportion wind power system in spring
由图4 、附录图A4~A7、表6 和7 可知,在多工况模型运行模拟时,4台机组采用不同时长的停机调峰,出现多次较长时间停机后的温态启动.其中,相比常规模型平均化的启停约束,多工况模型采用区分不同工况的火电机组停机模型大幅提升了温态 启停的时长,使得春、夏季机组累计停机调峰时长分别延长156 h和236 h.综合图4(a)、4(b) 、附录A4和A5可以看出,电网中停机调峰时间延长导致多工况模型优化调度图像的弃风面积显著减少,提高了风电消纳程度.该场景算例验证了中长期尺度下多工况模型能够优化调峰过程中的机组停机组合,延长机组损耗较小的温态启停停机时长,增加风电可消纳区间,并降低运行总成本.
3.3 高比例风电电力系统算例验证
为探索多工况模型在未来高比例新能源电力系统运行中的应用,将风电的装机占比提高至46%,装机容量为 2 000 MW,保持系统中最大负荷为 2 200 MW,并关停一台350 MW凝气式火电机组(机组4),调度时间尺度和时间步长与3.2节中比例风电电力系统算例验证保持一致.
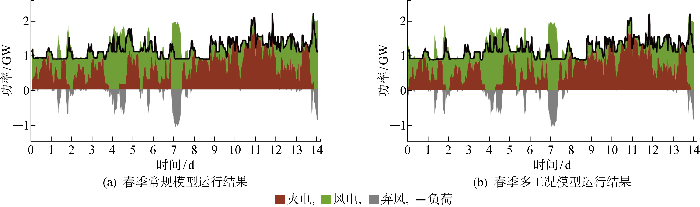
图5 和表8 分别展示了春季高比例风电电力系统运行结果和各指标值.
图5
图5
高比例风电电力系统春季运行结果
Fig.5
Operation results of high-proportion wind power system in spring
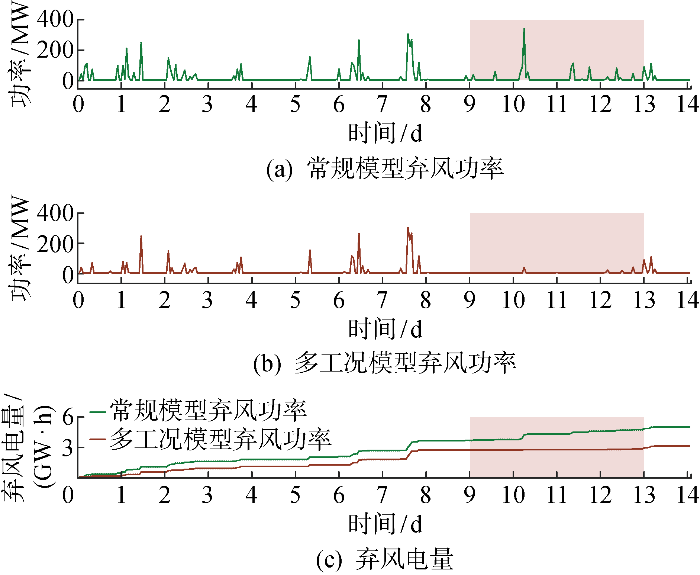
由图5 可知,在应对春季风电大发时段,两类模型都通过多次停机调峰消纳风电.由表8 可知,两类模型优化结果的总弃风电量差距较小,为了详细分析高比例风电电力系统场景下两类模型风电消纳能力的差异,图6 进一步给出春季场景中两类模型在负荷水平内的弃风功率和累计弃风电量.
图6
图6
春季负荷水平内的弃风曲线
Fig.6
Wind power curtailment within load level in spring
由图6 可知,相比常规模型,多工况模型在负荷水平内的弃风显著降低.结合图5 和图6 在9~13 d的弃风区域对比可知,多工况模型在系统消纳水平内消纳了更多风电,证明多工况模型能够进一步调动机组调峰能力,提高新能源消纳灵活性.
高比例风电电力系统夏季场景中风电出力水平较低且集中于负荷水平线以内,两类模型的调度弃风占比均小于1%,因此未对两类模型的弃风组成做进一步比较,高比例风电系统夏季调度运行结果详见附录B.
由表8 和附录表B1可知,在高比例风电电力系统场景验证中,相比常规模型,多工况模型在春、夏季的运行总成本分别减少 1 734.1 万元和723.4万元,弃风电量分别下降 1 580.6 和 3 808.1 MW·h,参与调峰的3台火电机组寿命损耗都有降低.在高比例风电电力系统春、夏场景中,两类模型因机组寿命损耗而产生的成本差值分别为179.3万元和334.3万元,这表明在风电出力波动较大的高比例新能源电力系统中,多工况模型仍能通过优化机组寿命损耗降低运行成本.
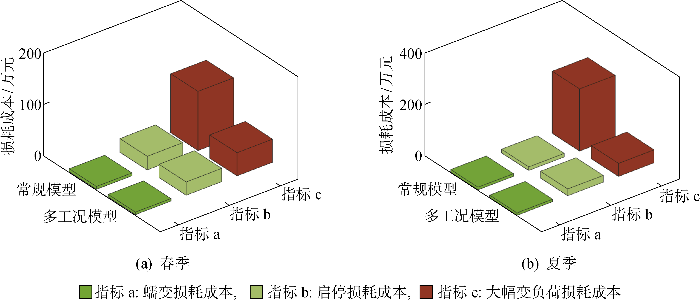
在高比例风电电力系统场景中,风电波动性增强,火电机组的运行工况也更加复杂,分析各类工况损耗在总损耗成本中的比例对研究不同模型之间差异具有重要意义.图7 进一步给出调度运行过程中火电机组各类工况的损耗成本.
图7
图7
火电机组各类工况寿命损耗成本
Fig.7
Life loss cost under various working conditions of thermal power unit
由图7 可知,火电机组的寿命损耗成本中占比最大为大幅度变负荷损耗成本.同时,大幅度变负荷损耗也是影响两类模型成本差值的主要指标,春季大幅度变负荷损耗成本差值为70.3万元,夏季对应差值为192万元,分别占成本总差值的39.2%和57.4%.因此,在对火电机组寿命损耗建模的过程中,不能忽视大幅度变负荷损耗的影响.而同时段下,不同工况对应的累计损耗成本不同,这也进一步说明本研究建立基于多工况的机组寿命损耗模型的必要性.
针对新能源电力系统分别在春季和夏季的典型日场景、中比例风电电力系统场景和高比例风电电力系统场景进行仿真模拟.算例结果表明,在不同场景下采用多工况模型进行调度模拟的总成本、弃风量和机组损耗指标值都优于常规模型结果及其归算后的结果.在提供更加全面机组寿命损耗计算方法的基础上,多工况模型能够提高春季高比例新能源电力系统负荷水平内的风电消纳程度,并在满足负荷需求的基础上减少高损耗工况出现次数,进而降低运行总成本.
4 结论
为适应电力系统发展方向,应对机组损耗频率加快而服役寿命延长的现实问题,使火电机组运行模型更加贴近实际,在考虑火电机组不同运行工况及对应损耗率的基础上提出一种计及多工况对机组寿命损耗影响的机组组合模型,并通过北方某地含风电局部电力系统多场景模拟验证模型必要性和有效性,主要内容包括:
(1) 为对火电机组不同工况的寿命损耗进行区别建模,在当前工程实验和研究理论的基础上,比较分析火电机组的各类特殊工况及其损耗成本,建立火电机组多工况寿命损耗成本模型,并基于此改进火电机组运行约束条件.
(2) 为验证多工况模型与常规模型相比能够减小机组寿命损耗,进一步调动火电机组的调峰潜力,设置3类递进运行场景并代入两种模型进行调度模拟和数据对比.根据模型仿真结果可知,所提计及多工况对机组寿命损耗影响的机组组合模型能够降低机组寿命损耗,减少弃风并降低调度运行成本.
(3) 为避免模型差异影响数据结果的可对比性,在进行算例验证时设置额外对照组,即在调度模拟结束后,将常规模型运行数据代入多工况模型的成本计算流程中,验证多工况模型更加接近实际的同时,使两类运行结果能够在同一计算流程下进行比较,进一步说明常规模型总成本计算值低于实际值的情况,以及采用多工况模型求解机组组合优化问题的必要性.
附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-06-0768.shtml)
参考文献
View Option
[1]
BROUWER A S VAN DEN BROEK M SEEBREGTS A , et al Operational flexibility and economics of power plants in future low-carbon power systems
[J]. Applied Energy 2015 , 156 : 107 -128 .
[本文引用: 1]
[2]
刘永奇 , 陈龙翔 , 韩小琪 . 能源转型下我国新能源替代的关键问题分析
[J]. 中国电机工程学报 2022 , 42 (2 ): 515 -524 .
[本文引用: 1]
LIU Yongqi CHEN Longxiang HAN Xiaoqi . The key problem analysis on the alternative new energy under the energy transition
[J]. Proceedings of the CSEE 2022 , 42 (2 ): 515 -524 .
[本文引用: 1]
[3]
金震杰 , 纪冬梅 , 吴凌轩 . 某超超临界汽轮机转子蠕变-疲劳损伤分析及寿命评估
[J]. 汽轮机技术 2022 , 64 (2 ): 123 -128 .
[本文引用: 2]
JIN Zhenjie JI Dongmei WU Lingxuan . Creep-fatigue damage analysis and life assessment for a ultra-supercritical stream turbine rotor
[J]. Turbine Technology 2022 , 64 (2 ): 123 -128 .
[本文引用: 2]
[4]
赵乃龙 , 吴穹 , 王炜哲 , 等 . 超超临界汽轮机高压转子低周疲劳及损伤分析
[J]. 上海交通大学学报 2015 , 49 (5 ): 590 -594 .
ZHAO Nailong WU Qiong WANG Weizhe , et al Numerical analysis of low-cycle fatigue and damage of a ultra-supercritical steam turbine high-pressure rotor
[J]. Journal of Shanghai Jiao Tong University 2015 , 49 (5 ): 590 -594 .
[5]
周新灵 , 田宇 , 李海霞 , 等 . 超超临界汽轮机高中压转子钢高温低周疲劳性能研究
[J]. 机械工程师 2013 (7 ): 51 -53 .
ZHOU Xinling TIAN Yu LI Haixia , et al Study on the high temperature low cycle fatigue behavior of ultra-supercritical turbine HP/IP rotor steel
[J]. Mechanical Engineer 2013 (7 ): 51 -53 .
[6]
ZHAO X RU D H WANG P , et al Fatigue life prediction of a supercritical steam turbine rotor based on neural networks
[J]. Engineering Failure Analysis 2021 , 127 : 105435 .
[本文引用: 2]
[7]
刘华锋 , 王炜哲 , 蒋浦宁 , 等 . 超超临界汽轮机转子蠕变对低周疲劳应变的影响
[J]. 动力工程学报 2010 , 30 (9 ): 715 -719 .
[本文引用: 1]
LIU Huafeng WANG Weizhe JIANG Puning , et al Influence of creep on low-cycle fatigue strain of ultra-supercritical steam turbine rotor
[J]. Journal of Chinese Society of Power Engineering 2010 , 30 (9 ): 715 -719 .
[本文引用: 1]
[8]
吴瑞康 , 华敏 , 秦攀 , 等 . 燃煤机组深度调峰对汽轮机设备的影响
[J]. 热力发电 2018 , 47 (5 ): 89 -94 .
[本文引用: 4]
WU Ruikang HUA Min QIN Pan , et al Influence of deep peak load regulation of coal-fired units on turbine equipment
[J]. Thermal Power Generation 2018 , 47 (5 ): 89 -94 .
[本文引用: 4]
[9]
JI D M SUN J Q SUN Q , et al Optimization of start-up scheduling and life assessment for a steam turbine
[J]. Energy 2018 , 160 : 19 -32 .
[本文引用: 1]
[10]
刘盛龙 . 汽轮机转子损伤分析与启动过程优化研究 [D]. 杭州 : 浙江大学 , 2020 .
[本文引用: 2]
LIU Shenglong . Steam turbine rotor damage analysis and startup process optimization study [D]. Hangzhou : Zhejiang University , 2020 .
[本文引用: 2]
[11]
程鹏 , 钟芳源 . 汽轮机转子蠕变-疲劳耦合寿命精细分析与传统方法的比较
[J]. 动力工程 1995 , 15 (6 ): 12 -17 .
[本文引用: 1]
CHENG Peng ZHONG Fangyuan . Rotor life expenditure under the concurrent action of creep and fatigue: A precise analysis as compared with the conventional
[J]. Journal of Chinese Society of Power Engineering 1995 , 15 (6 ): 12 -17 .
[本文引用: 1]
[12]
荆建平 , 孟光 . 汽轮机转子疲劳强度理论研究现状与展望
[J]. 汽轮机技术 2003 , 45 (5 ): 260 -264 .
[本文引用: 1]
JING Jianping MENG Guang . Survey of fatigue strength theory of turbine rotor
[J]. Turbine Technology 2003 , 45 (5 ): 260 -264 .
[本文引用: 1]
[13]
李一铭 , 李文沅 , 颜伟 , 等 . 基于机会约束规划模型降低机组寿命损耗的日调度计划
[J]. 电网技术 2014 , 38 (7 ): 1885 -1890 .
[本文引用: 1]
LI Yiming LI Wenyuan YAN Wei , et al Daily generation scheduling for reducing losses of unit’s lives based on the chance constrained programming model
[J]. Power System Technology 2014 , 38 (7 ): 1885 -1890 .
[本文引用: 1]
[14]
陟晶 , 张高航 , 邵冲 , 等 . 含大规模风电及光热电站的电力系统优化调度方法
[J]. 电力工程技术 2021 , 40 (1 ): 79 -85 .
[本文引用: 2]
ZHI Jing ZHANG Gaohang SHAO Chong , et al Optimal dispatching method for power system with large scale wind power and concentrated solar power plant
[J]. Electric Power Engineering Technology 2021 , 40 (1 ): 79 -85 .
[本文引用: 2]
[15]
邓婷婷 , 娄素华 , 田旭 , 等 . 计及需求响应与火电深度调峰的含风电系统优化调度
[J]. 电力系统自动化 2019 , 43 (15 ): 34 -41 .
DENG Tingting LOU Suhua TIAN Xu , et al Optimal dispatch of power system integrated with wind power considering demand response and deep peak regulation of thermal power units
[J]. Automation of Electric Power Systems 2019 , 43 (15 ): 34 -41 .
[16]
程韧俐 , 李江南 , 周保荣 , 等 . 含碳捕集-电转气的风光火储一体化系统优化运行
[J]. 上海交通大学学报 2024 , 58 (5 ): 709 -718 .
DOI:10.16183/j.cnki.jsjtu.2022.270
[本文引用: 1]
碳捕集、电转气装置能够利用系统富裕新能源捕集火电燃烧所产生的碳排放,并生成燃气,形成碳资源循环利用链.为降低系统碳排放,促进新能源消纳,提升系统运行灵活性,提出含碳捕集-电转气(CC-P2G)的风光火储一体化系统架构,并设计其优化运行模型.重点讨论该架构电能流和碳流的运行特性;考虑配额制下碳排放交易收益,以一体化系统综合效益最大化为目标,综合考虑各类设备运行特性,提出其优化运行模型.算例验证了CC-P2G系统在提升新能源消纳能力和系统运行效益方面的效用.结果表明,CC-P2G系统与碳排放配额交易等市场机制有效配合,能够在降低系统整体碳排放的同时提升运行效益.
CHENG Renli LI Jiangnan ZHOU Baorong , et al Operation optimization for integrated system of wind-PV-thermal-storage with CC-P2G
[J]. Journal of Shanghai Jiao Tong University 2024 , 58 (5 ): 709 -718 .
[本文引用: 1]
[17]
宋晓辉 , 李晓飞 , 蔺奕存 , 等 . 二次再热1 000 MW燃煤机组(极)热态启动过程切缸与并缸故障分析及处理
[J]. 热力发电 2022 , 51 (4 ): 141 -149 .
[本文引用: 1]
SONG Xiaohui LI Xiaofei LIN Yicun , et al Analysis and treatment of cylinder cutting and cylinder merging during(extremely)hot start-up in double-reheat 1 000 MW coal-fired unit
[J]. Thermal Power Generation 2022 , 51 (4 ): 141 -149 .
[本文引用: 1]
[18]
赵振锐 , 朱忠芳 . 350 MW超临界机组跳闸后极热态启动过程的探讨
[J]. 山西电力 2018 (1 ): 48 -51 .
[本文引用: 2]
ZHAO Zhenrui ZHU Zhongfang . Discussion on 350 MW supercritical unit extreme hot start-up process after tripping
[J]. Shanxi Electric Power 2018 (1 ): 48 -51 .
[本文引用: 2]
[19]
夏芹芹 , 罗永捷 , 王荣茂 , 等 . 考虑新能源爬坡的风光火耦合系统源荷匹配性分析及容量优化配置
[J]. 上海交通大学学报 2024 , 58 (1 ): 69 -81 .
DOI:10.16183/j.cnki.jsjtu.2022.260
[本文引用: 1]
风力发电、光伏发电与火力发电经同一点并网形成耦合系统,是我国北方地区发电侧灵活性调节电源与新能源间高效、低碳协同的一种形式.考虑区域新能源爬坡特性,结合源荷匹配分析,发掘和利用其规律,研究风光火耦合系统的容量优化配置方法,为耦合系统规划提供参考.首先,简述耦合系统运行模式和不确定性处理方法;其次,考虑耦合系统风光互补、爬坡事件和关键负荷特性,选取并提出相关指标用于源荷匹配评价;再次,考虑源荷特性、匹配、成本和收益等约束,建立耦合系统容量优化配置模型;最后,基于辽宁地区实际数据进行算例仿真,得到该地区耦合系统风、光的最优安装容量,并分析上述源荷相关因素与容量优化配置结果之间的相互影响,为新能源最优容量配置提供了参考与建议.
XIA Qinqin LUO Yongjie WANG Rongmao , et al Source-load matching analysis and optimal planning of wind-solar-thermal coupled system considering renewable energy ramps
[J]. Journal of Shanghai Jiao Tong University 2024 , 58 (1 ): 69 -81 .
[本文引用: 1]
[20]
赵振宙 , 王同光 , 郑源 . 风力机原理 [M]. 北京 : 中国水利水电出版社 , 2016 .
[本文引用: 1]
ZHAO Zhenzhou WANG Tongguang ZHENG Yuan . Wind turbine principle [M]. Beijing : China Water & Power Press , 2016 .
[本文引用: 1]
[21]
于强 . 新建火力发电厂精细化调试及管理 [D]. 南京 : 东南大学 , 2018 .
[本文引用: 1]
YU Qiang . Fine debugging and management of new thermal power plant [D]. Nanjing : Southeast University , 2018 .
[本文引用: 1]
[22]
郭力 , 杨书强 , 刘一欣 , 等 . 风光储微电网容量规划中的典型日选取方法
[J]. 中国电机工程学报 2020 , 40 (8 ): 2468 -2479 .
[本文引用: 1]
GUO Li YANG Shuqiang LIU Yixin , et al Typical day selection method for capacity planning of microgrid with wind turbine-photovoltaic and energy storage
[J]. Proceedings of the CSEE 2020 , 40 (8 ): 2468 -2479 .
[本文引用: 1]
[23]
刘子旭 , 米阳 , 卢长坤 , 等 . 计及需求响应和风力发电消纳的电-热系统低碳优化调度
[J]. 上海交通大学学报 2023 , 57 (7 ): 835 -844 .
DOI:10.16183/j.cnki.jsjtu.2022.056
[本文引用: 1]
针对热电联产机组存在热电耦合性大、火电机组碳排放量高和负荷侧资源灵活性未充分挖掘等问题,建立计及负荷需求响应和风力发电消纳的电-热系统低碳调度模型.首先,在源侧考虑增加储热和碳捕集设备,同时在负荷侧考虑电价型需求响应和供暖建筑热负荷惯性.然后,以机组运行成本、碳交易成本和弃风惩罚成本总和为目标函数,考虑相关约束,并调用Gurobi求解器进行求解.最后,针对不同案例下系统的经济成本、风力发电消纳量和碳排放速率等方面进行算例对比分析,证明该调度策略在提高系统风力发电消纳能力的同时兼顾经济性和低碳性.
LIU Zixu MI Yang LU Changkun , et al Low-carbon optimal dispatch of electric-thermal system considering demand response and wind power consumption
[J]. Journal of Shanghai Jiao Tong University 2023 , 57 (7 ): 835 -844 .
[本文引用: 1]
[24]
顾慧杰 , 周华锋 , 彭超逸 , 等 . 含抽水蓄能电站的高比例新能源发电系统多时间尺度调度模型
[J]. 上海交通大学学报 2024 , 58 (12 ): 1957 -1967 .
DOI:10.16183/j.cnki.jsjtu.2023.123
[本文引用: 1]
针对高比例新能源接入电网的消纳问题,提出一种含抽水蓄能电站的高比例新能源发电系统多时间尺度协调调度模型.依据风电、光伏、负荷功率预测精度随时间尺度缩短逐级提高的特点,以系统总运行成本最小为目标构建日前24 h、日内1 h、实时15 min三阶段协调调度模型.通过多时间尺度的协调配合,逐级修正发电计划,实现抽蓄、风电、光伏、火电出力良好跟踪负荷.基于CPLEX商业优化软件,利用混合整数线性规划法对含6台抽蓄机组的风光火抽蓄互补发电系统展开仿真分析.结果表明:抽水蓄能机组可发挥其负荷响应时间短、功率调节速度快的优势,减轻火电机组调节负担,有效缓解火电机组调节压力.通过多时间尺度的协调配合,可减少弃风弃光,提高新能源消纳水平.
GU Huijie ZHOU Huafeng PENG Chaoyi , et al A multi-time scale scheduling model for power generation system with high proportion of new energy including pumped storage power station
[J]. Journal of Shanghai Jiao Tong University 2024 , 58 (12 ): 1957 -1967 .
[本文引用: 1]
Operational flexibility and economics of power plants in future low-carbon power systems
1
2015
... 大规模新能源并网和低效率火电机组的计划性退役增加了电力系统中净负荷波动的随机性和不确定性[1 -2 ] .为适应新能源电力系统的发展变化,我国进行了大规模的火电机组灵活性改造.改造后的火电机组深度调峰能力增强,可实现快速爬坡和快速启停.然而,随着调峰频率增加,机组的寿命损耗也随之加快.此外,为实现存量煤电机组转型发展,我国发布了延长煤电机组服役寿命的政策和文件.国际上火电机组的设计寿命一般为30 a,但由于我国严格执行环保、降耗等要求,不断推进火电落后产能的淘汰,使得许多机组达不到设计寿命就被关停,平均服役年限仅为12 a.为支撑我国能源转型,同时提高火电机组的利用效率,避免资源浪费,中国电力企业联合会牵头完成《煤电机组灵活性运行与延寿运行研究》调研报告(以下简称《研究》).《研究》指出2050年左右,“十二五”“十三五”投产机组将达到设计寿命,机组延寿对实现碳中和意义重大. ...
能源转型下我国新能源替代的关键问题分析
1
2022
... 大规模新能源并网和低效率火电机组的计划性退役增加了电力系统中净负荷波动的随机性和不确定性[1 -2 ] .为适应新能源电力系统的发展变化,我国进行了大规模的火电机组灵活性改造.改造后的火电机组深度调峰能力增强,可实现快速爬坡和快速启停.然而,随着调峰频率增加,机组的寿命损耗也随之加快.此外,为实现存量煤电机组转型发展,我国发布了延长煤电机组服役寿命的政策和文件.国际上火电机组的设计寿命一般为30 a,但由于我国严格执行环保、降耗等要求,不断推进火电落后产能的淘汰,使得许多机组达不到设计寿命就被关停,平均服役年限仅为12 a.为支撑我国能源转型,同时提高火电机组的利用效率,避免资源浪费,中国电力企业联合会牵头完成《煤电机组灵活性运行与延寿运行研究》调研报告(以下简称《研究》).《研究》指出2050年左右,“十二五”“十三五”投产机组将达到设计寿命,机组延寿对实现碳中和意义重大. ...
The key problem analysis on the alternative new energy under the energy transition
1
2022
... 大规模新能源并网和低效率火电机组的计划性退役增加了电力系统中净负荷波动的随机性和不确定性[1 -2 ] .为适应新能源电力系统的发展变化,我国进行了大规模的火电机组灵活性改造.改造后的火电机组深度调峰能力增强,可实现快速爬坡和快速启停.然而,随着调峰频率增加,机组的寿命损耗也随之加快.此外,为实现存量煤电机组转型发展,我国发布了延长煤电机组服役寿命的政策和文件.国际上火电机组的设计寿命一般为30 a,但由于我国严格执行环保、降耗等要求,不断推进火电落后产能的淘汰,使得许多机组达不到设计寿命就被关停,平均服役年限仅为12 a.为支撑我国能源转型,同时提高火电机组的利用效率,避免资源浪费,中国电力企业联合会牵头完成《煤电机组灵活性运行与延寿运行研究》调研报告(以下简称《研究》).《研究》指出2050年左右,“十二五”“十三五”投产机组将达到设计寿命,机组延寿对实现碳中和意义重大. ...
某超超临界汽轮机转子蠕变-疲劳损伤分析及寿命评估
2
2022
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
... 模型搭建过程中,认为单机组使用寿命为30 a,转子致裂损耗在常规运行中占20%,在特殊工况运行时占80%[3 6 ] .参考《中华人民共和国电力行业标准火电机组寿命评估技术导则》(DL/T 654—2022),沿用线性损伤累计法计算火电机组的寿命损耗成本. ...
Creep-fatigue damage analysis and life assessment for a ultra-supercritical stream turbine rotor
2
2022
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
... 模型搭建过程中,认为单机组使用寿命为30 a,转子致裂损耗在常规运行中占20%,在特殊工况运行时占80%[3 6 ] .参考《中华人民共和国电力行业标准火电机组寿命评估技术导则》(DL/T 654—2022),沿用线性损伤累计法计算火电机组的寿命损耗成本. ...
超超临界汽轮机高压转子低周疲劳及损伤分析
0
2015
Numerical analysis of low-cycle fatigue and damage of a ultra-supercritical steam turbine high-pressure rotor
0
2015
超超临界汽轮机高中压转子钢高温低周疲劳性能研究
0
2013
Study on the high temperature low cycle fatigue behavior of ultra-supercritical turbine HP/IP rotor steel
0
2013
Fatigue life prediction of a supercritical steam turbine rotor based on neural networks
2
2021
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
... 模型搭建过程中,认为单机组使用寿命为30 a,转子致裂损耗在常规运行中占20%,在特殊工况运行时占80%[3 6 ] .参考《中华人民共和国电力行业标准火电机组寿命评估技术导则》(DL/T 654—2022),沿用线性损伤累计法计算火电机组的寿命损耗成本. ...
超超临界汽轮机转子蠕变对低周疲劳应变的影响
1
2010
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
Influence of creep on low-cycle fatigue strain of ultra-supercritical steam turbine rotor
1
2010
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
燃煤机组深度调峰对汽轮机设备的影响
4
2018
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
... 为直观说明各类特殊工况对火电机组寿命损耗的影响程度,表1 提供了美国通用电气公司某机型寿命分配数据,对寿命损耗的80%进行特殊工况下的预分配[8 ] . ...
... GE公司某机型寿命分配数据[8 ] ...
... Life distribution data of a thermal power unit of GE company[8 ] ...
Influence of deep peak load regulation of coal-fired units on turbine equipment
4
2018
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
... 为直观说明各类特殊工况对火电机组寿命损耗的影响程度,表1 提供了美国通用电气公司某机型寿命分配数据,对寿命损耗的80%进行特殊工况下的预分配[8 ] . ...
... GE公司某机型寿命分配数据[8 ] ...
... Life distribution data of a thermal power unit of GE company[8 ] ...
Optimization of start-up scheduling and life assessment for a steam turbine
1
2018
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
2
2020
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
... (1) 大型汽轮机冷态启动对应停机时长大于 72 h.冷态启动过程升温、升负荷速率较高,引起金属温度变化较为剧烈,转子受到较大应力,部分区域会产生明显塑性变形,因此会出现较大疲劳损伤[10 ] . ...
2
2020
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
... (1) 大型汽轮机冷态启动对应停机时长大于 72 h.冷态启动过程升温、升负荷速率较高,引起金属温度变化较为剧烈,转子受到较大应力,部分区域会产生明显塑性变形,因此会出现较大疲劳损伤[10 ] . ...
汽轮机转子蠕变-疲劳耦合寿命精细分析与传统方法的比较
1
1995
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
Rotor life expenditure under the concurrent action of creep and fatigue: A precise analysis as compared with the conventional
1
1995
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
汽轮机转子疲劳强度理论研究现状与展望
1
2003
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
Survey of fatigue strength theory of turbine rotor
1
2003
... 国内外针对火电机组寿命损耗的研究主要集中在转子[3 6 ] .转子是汽轮机最薄弱的部件,整机寿命与转子寿命密切相关.转子寿命损耗主要分为两大类:一是转子材料受到高温和工作定应力作用产生的常规蠕变损耗,约占总寿命的20%;二是因启动、变负荷等不稳定变工况中受到交变应力引起的低周疲劳损耗,约占总寿命的80%[7 -8 ] .在影响转子寿命的两类损耗中,蠕变损耗占比虽小但贯穿火电机组运行的始终;而在由不稳定变工况引发的机组寿命损耗当中,低周疲劳损耗占主要部分,蠕变损耗占次要部分,但两类损耗在特殊工况运行过程中具有同步性,且存在一定的相互影响[9 12 ] .如果仅在常规工况下考虑蠕变损耗,在特殊工况下考虑低周疲劳损耗,并简单叠加计算两类损耗,则会低估机组在实际运行中的损耗情况[10 -11 ] .因此,本研究在火电机组运行寿命损耗模型构建的过程中,同时考虑蠕变损耗和低周疲劳损耗对转子寿命的影响,即在常规工况下考虑蠕变损耗,在特殊工况下结合对应的损耗率计算蠕变损耗和低周疲劳损耗的综合损耗. ...
基于机会约束规划模型降低机组寿命损耗的日调度计划
1
2014
... 另外,以往研究普遍采用Langer公式估算机组单次参与深调峰的平均损耗与深调峰次数乘积的形式计算机组寿命损耗[13 -14 ] .这种平均损耗叠加的计算方法以及较为固定的启停约束条件[14 16 ] 未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境. ...
Daily generation scheduling for reducing losses of unit’s lives based on the chance constrained programming model
1
2014
... 另外,以往研究普遍采用Langer公式估算机组单次参与深调峰的平均损耗与深调峰次数乘积的形式计算机组寿命损耗[13 -14 ] .这种平均损耗叠加的计算方法以及较为固定的启停约束条件[14 16 ] 未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境. ...
含大规模风电及光热电站的电力系统优化调度方法
2
2021
... 另外,以往研究普遍采用Langer公式估算机组单次参与深调峰的平均损耗与深调峰次数乘积的形式计算机组寿命损耗[13 -14 ] .这种平均损耗叠加的计算方法以及较为固定的启停约束条件[14 16 ] 未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境. ...
... [14 16 ]未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境. ...
Optimal dispatching method for power system with large scale wind power and concentrated solar power plant
2
2021
... 另外,以往研究普遍采用Langer公式估算机组单次参与深调峰的平均损耗与深调峰次数乘积的形式计算机组寿命损耗[13 -14 ] .这种平均损耗叠加的计算方法以及较为固定的启停约束条件[14 16 ] 未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境. ...
... [14 16 ]未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境. ...
计及需求响应与火电深度调峰的含风电系统优化调度
0
2019
Optimal dispatch of power system integrated with wind power considering demand response and deep peak regulation of thermal power units
0
2019
含碳捕集-电转气的风光火储一体化系统优化运行
1
2024
... 另外,以往研究普遍采用Langer公式估算机组单次参与深调峰的平均损耗与深调峰次数乘积的形式计算机组寿命损耗[13 -14 ] .这种平均损耗叠加的计算方法以及较为固定的启停约束条件[14 16 ] 未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境. ...
Operation optimization for integrated system of wind-PV-thermal-storage with CC-P2G
1
2024
... 另外,以往研究普遍采用Langer公式估算机组单次参与深调峰的平均损耗与深调峰次数乘积的形式计算机组寿命损耗[13 -14 ] .这种平均损耗叠加的计算方法以及较为固定的启停约束条件[14 16 ] 未针对火电机组运行工况进行详细区分,因此对火电机组寿命损耗成本的计算并不准确,且无法充分发挥火电机组的调峰能力,将不再适用于当前的研究环境. ...
二次再热1 000 MW燃煤机组(极)热态启动过程切缸与并缸故障分析及处理
1
2022
... 此外,在实际生产中,极热态启动具有一定的特殊性.文献[17 -18 ]中基于实际生产中的技术经验指出,极热态启动过程极为复杂,操作不当会出现人员伤亡或者设备损坏.文献[18 ]中说明了包括故障跳闸和机组停运在内的应用极热态启动场景.为使模型计算更加接近实际,在电力系统运行中保留足够的安全裕度,本文在进行后续研究时不再考虑极热态启动的情况. ...
Analysis and treatment of cylinder cutting and cylinder merging during(extremely)hot start-up in double-reheat 1 000 MW coal-fired unit
1
2022
... 此外,在实际生产中,极热态启动具有一定的特殊性.文献[17 -18 ]中基于实际生产中的技术经验指出,极热态启动过程极为复杂,操作不当会出现人员伤亡或者设备损坏.文献[18 ]中说明了包括故障跳闸和机组停运在内的应用极热态启动场景.为使模型计算更加接近实际,在电力系统运行中保留足够的安全裕度,本文在进行后续研究时不再考虑极热态启动的情况. ...
350 MW超临界机组跳闸后极热态启动过程的探讨
2
2018
... 此外,在实际生产中,极热态启动具有一定的特殊性.文献[17 -18 ]中基于实际生产中的技术经验指出,极热态启动过程极为复杂,操作不当会出现人员伤亡或者设备损坏.文献[18 ]中说明了包括故障跳闸和机组停运在内的应用极热态启动场景.为使模型计算更加接近实际,在电力系统运行中保留足够的安全裕度,本文在进行后续研究时不再考虑极热态启动的情况. ...
... ]中基于实际生产中的技术经验指出,极热态启动过程极为复杂,操作不当会出现人员伤亡或者设备损坏.文献[18 ]中说明了包括故障跳闸和机组停运在内的应用极热态启动场景.为使模型计算更加接近实际,在电力系统运行中保留足够的安全裕度,本文在进行后续研究时不再考虑极热态启动的情况. ...
Discussion on 350 MW supercritical unit extreme hot start-up process after tripping
2
2018
... 此外,在实际生产中,极热态启动具有一定的特殊性.文献[17 -18 ]中基于实际生产中的技术经验指出,极热态启动过程极为复杂,操作不当会出现人员伤亡或者设备损坏.文献[18 ]中说明了包括故障跳闸和机组停运在内的应用极热态启动场景.为使模型计算更加接近实际,在电力系统运行中保留足够的安全裕度,本文在进行后续研究时不再考虑极热态启动的情况. ...
... ]中基于实际生产中的技术经验指出,极热态启动过程极为复杂,操作不当会出现人员伤亡或者设备损坏.文献[18 ]中说明了包括故障跳闸和机组停运在内的应用极热态启动场景.为使模型计算更加接近实际,在电力系统运行中保留足够的安全裕度,本文在进行后续研究时不再考虑极热态启动的情况. ...
考虑新能源爬坡的风光火耦合系统源荷匹配性分析及容量优化配置
1
2024
... 陆上风力机运行维护成本主要包含定期检修维护和日常排故维护[19 -20 ] .风场的风速和风力机的出力不可控,风电场的运行维护成本不因火电机组运行状态的改变而发生变化,对本文需要验证的目标无影响,因此不考虑风电场的运行成本. ...
Source-load matching analysis and optimal planning of wind-solar-thermal coupled system considering renewable energy ramps
1
2024
... 陆上风力机运行维护成本主要包含定期检修维护和日常排故维护[19 -20 ] .风场的风速和风力机的出力不可控,风电场的运行维护成本不因火电机组运行状态的改变而发生变化,对本文需要验证的目标无影响,因此不考虑风电场的运行成本. ...
1
2016
... 陆上风力机运行维护成本主要包含定期检修维护和日常排故维护[19 -20 ] .风场的风速和风力机的出力不可控,风电场的运行维护成本不因火电机组运行状态的改变而发生变化,对本文需要验证的目标无影响,因此不考虑风电场的运行成本. ...
1
2016
... 陆上风力机运行维护成本主要包含定期检修维护和日常排故维护[19 -20 ] .风场的风速和风力机的出力不可控,风电场的运行维护成本不因火电机组运行状态的改变而发生变化,对本文需要验证的目标无影响,因此不考虑风电场的运行成本. ...
1
2018
... (2) 机组日最大启停次数约束.式(2)~(4)通过区分不同工况下的停机时长建立火电机组多工况寿命损耗成本模型,因此,常规的火电机组最小停机时长将不再适用.为保证机组的安全运行,结合火电机组启动管理实践经验[21 ] 对机组短期启停次数进行限制.表示为 ...
1
2018
... (2) 机组日最大启停次数约束.式(2)~(4)通过区分不同工况下的停机时长建立火电机组多工况寿命损耗成本模型,因此,常规的火电机组最小停机时长将不再适用.为保证机组的安全运行,结合火电机组启动管理实践经验[21 ] 对机组短期启停次数进行限制.表示为 ...
风光储微电网容量规划中的典型日选取方法
1
2020
... 选取电量偏差与功率偏差指标最小的单日运行数据作为风电场运行典型日,典型日所需的电量偏差Δσ M, d [22 ] 可以根据下式计算获得: ...
Typical day selection method for capacity planning of microgrid with wind turbine-photovoltaic and energy storage
1
2020
... 选取电量偏差与功率偏差指标最小的单日运行数据作为风电场运行典型日,典型日所需的电量偏差Δσ M, d [22 ] 可以根据下式计算获得: ...
计及需求响应和风力发电消纳的电-热系统低碳优化调度
1
2023
... 与能够稳定出力的火电机组相比,风电出力不确定性对功率平衡的影响较大,因此需设置旋转备用容量,以维持电力系统的稳定性和可靠性[23 -24 ] . ...
Low-carbon optimal dispatch of electric-thermal system considering demand response and wind power consumption
1
2023
... 与能够稳定出力的火电机组相比,风电出力不确定性对功率平衡的影响较大,因此需设置旋转备用容量,以维持电力系统的稳定性和可靠性[23 -24 ] . ...
含抽水蓄能电站的高比例新能源发电系统多时间尺度调度模型
1
2024
... 与能够稳定出力的火电机组相比,风电出力不确定性对功率平衡的影响较大,因此需设置旋转备用容量,以维持电力系统的稳定性和可靠性[23 -24 ] . ...
A multi-time scale scheduling model for power generation system with high proportion of new energy including pumped storage power station
1
2024
... 与能够稳定出力的火电机组相比,风电出力不确定性对功率平衡的影响较大,因此需设置旋转备用容量,以维持电力系统的稳定性和可靠性[23 -24 ] . ...