微电网功率预测与调度端到端协同优化方法

doi:10.16183/j.cnki.jsjtu.2024.224

微电网功率预测与调度端到端协同优化方法

张理¹, 王宝¹, 贾健雄¹, 宋竹萌¹, 叶钰童¹, 余跃¹, 林嘉庆², 徐潇源^,²

1.国网安徽省电力有限公司经济技术研究院,合肥 230000

2.上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240

End-to-End Collaborative Optimization Method for Microgrid Power Prediction and Optimal Scheduling

ZHANG Li¹, WANG Bao¹, JIA Jianxiong¹, SONG Zhumeng¹, YE Yutong¹, YU Yue¹, LIN Jiaqing², XU Xiaoyuan^,²

1. Economic and Technological Research Institute, State Grid Anhui Electric Power Co., Ltd., Hefei 230000, China

2. Key Laboratory of Control of Power Transmission and Conversion of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 徐潇源,副教授;E-mail:xuxiaoyuan@sjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2024-06-13 接受日期: 2024-10-28

Received: 2024-06-13 Accepted: 2024-10-28

作者简介 About authors

张理(1989—),副高级工程师,从事电力系统调度与控制工作.

摘要

作为消纳新能源的有效方式之一,微电网是新型电力系统的重要组成部分.以高比例新能源注入的微电网为背景,针对新能源功率预测和微电网优化调度目标不一致的问题,建立以微电网运行效益最高为目标的功率组合预测与微电网日前、日内调度端到端优化模型,并提出求解优化问题的方法.首先,构建双层优化问题,上层为功率预测模型训练,设计为组合预测问题;下层为微电网运行成本最小,其运行成本优化结果设为上层组合权重优化问题的损失函数.然后,利用启发式算法迭代求解上下层问题,获得使运行成本最低的预测结果和调度方案.最后,在由IEEE 33节点和IEEE 123节点系统扩展的微电网中接入真实的新能源数据,验证了该方法对提升微电网运行效益的有效性.

关键词： 微电网调度; 新能源预测; 组合预测; 端到端优化

Abstract

Microgrids, as one of the effective methods for integrating new energy sources, play a crucial role in the new-type power systems. In microgrids with high renewable energy penetration, the objectives of renewable energy power forecasting and microgrid optimal scheduling may be misaligned. To address this issue, this study proposes an end-to-end optimization model which combines power forecasting with day-ahead and intraday scheduling to maximize the operational benefits of the microgrid. It also provides a corresponding solution method. Initially, a bi-level optimization framework is established. The upper level focuses on training the power forecasting model, formulated as a combined forecasting problem, while the lower level aims to minimize microgrid operational costs. The result of the lower-level optimization is used as the loss function to optimize the forecasting weights in the upper level. Subsequently, a heuristic algorithm iteratively is employed to solve the upper and lower level problems, thereby obtaining forecasting results and scheduling schemes which minimize the operational costs. Finally, the effectiveness of the proposed method in enhancing microgrid operational benefits is validated by integrating real renewable energy data into a typical microgrid extended from the IEEE 33-node and IEEE 123-node systems.

Keywords： microgrid scheduling; new energy prediction; composite forecasting; end-to-end optimization

PDF (2364KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张理, 王宝, 贾健雄, 宋竹萌, 叶钰童, 余跃, 林嘉庆, 徐潇源. 微电网功率预测与调度端到端协同优化方法[J]. 上海交通大学学报, 2025, 59(6): 720-731 doi:10.16183/j.cnki.jsjtu.2024.224

ZHANG Li, WANG Bao, JIA Jianxiong, SONG Zhumeng, YE Yutong, YU Yue, LIN Jiaqing, XU Xiaoyuan. End-to-End Collaborative Optimization Method for Microgrid Power Prediction and Optimal Scheduling[J]. Journal of Shanghai Jiaotong University, 2025, 59(6): 720-731 doi:10.16183/j.cnki.jsjtu.2024.224

“双碳”战略目标要求建设以清洁低碳为主要特征的新型电力系统,因此风光为主的新能源在能源结构中的比例逐渐上升^[1].微电网是新能源接入电网的有效途径^[2-3],面对新能源出力的波动性给电力系统安全性和经济性带来的挑战^[4],微电网运营商需要通过新能源预测和调度方案优化工作提高能源利用率与运行效益^[5].日前调度根据负荷需求预测和新能源出力预测求解微电网各单元的日前出力计划;日内调度根据新能源实时波动和微电网运行状态在日前调度的基础上进行再调度,维持微电网日内的平衡.

关于微电网的预测和调度已有大量研究.文献[6]中针对微电网新能源和负荷的不确定性建立两阶段鲁棒优化模型,通过求解对偶问题得到最劣场景下成本最低的调度方案;文献[7]中把日前和日内调度模型转化成一个可用启发式算法求解的混合整数线性规划问题,减小日内调度对日前调度的调整,降低微电网的运营成本并且最大化新能源消纳率.在这些研究中,上游的新能源预测以精度为导向,以误差更小的预测结果为目标;下游的优化调度以运行效益更好的调度方案为目标,功率预测与优化调度目标不一致,信息从预测层向调度层单向传输.新能源功率预测误差分为正误差(实际发电量高于预测值)和负误差(实际发电量低于预测值),负误差引起的缺电需要立即启用备用发电资源,从市场高价购电或切除部分负荷,且火力发电机组的燃料成本关于发电功率是二次曲线关系,因此负误差会比正误差引起更高的再调度成本^[8].电力系统的非线性和再调度成本关于预测误差的不对称性导致精度更高的预测结果不一定在调度中使微电网的运行成本更低^[9].

在电力系统的新能源功率预测和电网运行优化领域,端到端方法是指从原始气象数据、历史发电数据和负荷数据到调度决策的整个流程由一个完整的模型来处理.现有的端到端预测-调度模型中,在上层预测中使用下层调度的目标,使预测结果具有靶向性^[10-11].文献[12]中建立以降低网络约束机组组合成本为导向的预测与调度闭环优化模型,用拉格朗日松弛法构造约束条件的凸包,模型松弛后的解是原优化问题解的下界^[13].文献[14]中在风电预测增长回归树模型中用成本导向的损失函数代替无偏预测损失函数,得到使供应商收益更高的预测结果.文献[15 -17]中构建集成功率预测与优化调度的高比例新能源微电网运行成本最小化问题,利用深度学习和强化学习算法求解运行成本最低的预测结果与调度方案,得到原始预测结果与成本最小导向的预测结果之间的线性关系.然而,基于机器学习的方法没有对电力系统的精确建模和数值求解,黑箱问题使这些方法只有输出结果而缺少对预测误差关于运行成本不对称性的解析^[18].

为了解决微电网中以精度为导向的预测工作和以效益为导向的优化调度工作之间目标不一致的问题,本文提出一种基于组合预测的微电网功率预测与日前、日内调度端到端协同优化模型.该模型以预测子模型的组合权重系数为优化变量,以微电网运行成本最低为优化目标,在日前调度阶段以微电网运行效益为目标进行优化生成调度方案;在日内阶段通过再调度平衡新能源预测值与实际值的偏差,然后调度层反馈结果到预测层,利用启发式算法更新预测权重至结果收敛,实现功率预测与优化调度的端到端闭环.最后,在IEEE 33节点和IEEE 123节点配电网系统中接入光伏电站、燃气轮机和储能设备等分布式电源,模拟大小系统的微电网,通过仿真验证所提方法的有效性.与计及不确定性的鲁棒优化、随机优化等方法相比,所提调度模型隶属确定性优化模型,考虑了预测结果的误差但没有对不确定性进行建模,使调度结果欠适应性和鲁棒性,但对于数据量和计算资源的需求更小.与现有关于端到端预测优化的研究相比,所提方法把组合预测权重优化问题的损失函数改为微电网的运行成本,没有改变基础预测子模型的学习目标,使预测模型训练和预测结果的靶向性优化解耦,预测结果的可解释性更强,使用对模型的线性和凸性要求更低的启发式算法,适用于复杂的优化问题.

1 微电网日前-日内调度模型

设计一个计及微电网内部自平衡的最小化运行成本的日前-日内优化模型.在日前阶段,根据微电网的拓扑信息、资源配置信息和光伏电站功率预测结果,求解运行成本最低的微电网日前调度方案;在日内阶段,对于光伏预测与日内实际出力的偏差,以最小化再调度惩罚为目标,求解出日内调度方案.

1.1 日前调度模型

微电网由分布式新能源发电单元(本模型以光伏电站为例)、储能单元、微型燃气轮机和负荷组成^[19-20].以微电网的运行成本最小为目标,网络功率平衡、潮流不越限、设备稳定运行为约束条件,各单元的功率调度方案为变量建立日前调度优化模型:

(1)$\begin{aligned} \min & \sum_{t \in T}\left(C_{\mathrm{b}, t} P_{\mathrm{DA}, \mathrm{~b}, t}-C_{\mathrm{s}, t} P_{\mathrm{DA}, \mathrm{~s}, t}\right)+ \\ & \sum_{m \in N_{\mathrm{MT}}} \sum_{t \in T}\left(a_{m} P_{\mathrm{DA}, \mathrm{MT}, m, t}^{2}+b_{m} P_{\mathrm{DA}, \mathrm{MT}, m, t}+c_{m}\right)+ \\ & \sum_{t \in T} C_{\mathrm{L}, \text { cut }} P_{\mathrm{DA}, \mathrm{~L}, \mathrm{cut}, t}+ \\ & \sum_{p \in N_{\mathrm{PV}}} \sum_{t \in T} C_{\mathrm{PV}, \text { cut }} P_{\mathrm{DA}, \mathrm{PV}, \mathrm{cut}, p, t} \end{aligned}$

式中:T为优化调度的时间段t集合; C_b,_t为t时段的单位电量购电成本;P_DA,b,_t为各时段购电功率;C_s,_t为t时段的单位电量售电收益;P_DA,s,_t为t时段售电功率;P_DA,MT,_m_,_t为t时段燃气轮机的发电功率;N_MT、N_PV分别为燃气轮机机组和光伏电站集合;m、p 分别为燃气轮机机组和光伏电站的编号; a_m、b_m、c_m分别为燃气轮机的二次、一次和常数成本系数;C_L,cut 为切除负荷惩罚系数;P_DA,L,cut,_t为t时段切除的负荷;C_PV,cut为弃光惩罚系数;P_DA,PV,cut,_p_,_t为日前t时段光伏电站的弃光量.

日前调度的约束条件如下:

(1) 与上级电网交互功率限制约束:

(2)

\begin{array}{l} 0 \leq P_{D A, b, t} \leq f_{D A, b, t} P_{b, m a x, t} \\ 0 \leq P_{D A, s, t} \leq f_{D A, s, t} P_{s, m a x, t} \\ f_{D A, b, t} + f_{D A, s, t} \leq 1 \\ \forall t \in T \end{array}\}

式中:f_DA,b,_t、f_DA,s,_t分别为指示微电网处于购电或售电状态的0-1变量,微电网向上级电网购电与售电交易不同时进行,因此f_DA,b,_t、f_DA,s,_t不同时为1;P_b,max,_t、P_s,max,_t分别为t时段购电与售电功率上限.

(2) 分布式电源约束.新能源电站约束:假设新能源电站均为光伏电站.

(3)

\begin{array}{l} 0 \leq P_{D A, P V, p, t} \leq P_{f o r e, P V, p, t} \\ Q_{D A, P V, p, t} = K_{Q P, p} P_{D A, P V, p, t} \\ P_{D A, P V, c u t, p, t} = P_{f o r e, P V, p, t} - P_{D A, P V, p, t} \\ \forall p \in N_{P V}, \forall t \in T \end{array}\}

式中:P_DA,PV,_p_,_t、Q_DA,PV,_p_,_t为t时段各个光伏输出的有功功率、无功功率;P_fore,PV,_p_,_t为t时段各光伏电站的预测有功出力值;K_QP,_p为光伏逆变器恒定功率因数运行下无功和有功功率的比值.

燃气轮机约束:

(4)

\begin{array}{l} P_{D A, M T, m, t}^{2} + Q_{D A, M T, m, t}^{2} \leq S_{M T, m a x, m}^{2} \\ - Δ_{d o w n, m} \leq P_{D A, M T, m, t} - P_{D A, M T, m, t - 1} \leq Δ_{u p, m} \\ \forall m \in N_{M T}, \forall t \in T \end{array}\}

式中:Q_DA,MT,_m_,_t为t时段各个燃气轮机机组的无功出力;S_MT,max,_m为该机组的容量上限;-Δ_down,_m、Δ_up,_m分别为该机组的爬坡速率下、上限.

储能约束:

(5)

\begin{array}{l} B_{D A, e, 1} = B_{D A, e, 24} \\ 0 \leq P_{D A, d i s, e, t} \leq d_{D A, d i s, e, t} P_{d i s, m a x, e} \\ 0 \leq P_{D A, c h a, e, t} \leq d_{D A, c h a, e, t} P_{c h a, m a x, e} \\ d_{D A, d i s, e, t} + d_{D A, c h a, e, t} \leq 1 \\ B_{D A, e, t + 1} = B_{D A, e, t} + \frac{P_{D A, c h a, e, t} η_{2}}{E_{m a x, e}} - \frac{P_{D A, d i s, e, t}}{η_{1} E_{m a x, e}} \\ B_{m i n, e} \leq B_{D A, e, t} \leq B_{m a x, e} \\ \forall e \in N_{E s s}, \forall t \in T \end{array}\}

式中:e为储能单元编号;N_Ess为储能单元集合;P_DA,cha,_e_,_t、P_DA,dis,_e_,_t分别为t时段各储能单元的充、放电有功功率;η₁、η₂分别为放电、充电效率;P_dis,max,_e、P_cha,max,_e分别为各储能单元的最大放电和充电功率;d_DA,cha,_e_,_t、d_DA,dis,_e_,_t分别为t时段指示各储能单元充放电状态的0-1变量;B_DA,_e_,_t为各储能单元在各时段的荷电状态; B_min,_e、B_max,_e分别为各储能单元的荷电状态的下、上限;E_max,_e为各储能单元的额定容量.

(3) 切负荷约束:

(6)

\begin{array}{l} P_{D A, L, t} = P_{L, t, 0} - P_{D A, L, c u t, t} \\ 0 \leq P_{D A, L, c u t, t} \leq P_{L, t, 0} \\ \forall t \in T \end{array}\}

式中:P_DA,L,_t为切除部分负荷后t时段的微电网负荷;P_L,_t_,0为微电网切负荷前的负荷;P_DA,L,cut,_t为被切除的负荷.

(4) 线路热约束:

(7)

\begin{array}{l} P_{D A, i j, t}^{2} + Q_{D A, i j, t}^{2} \leq S_{i j, m a x}^{2} \\ \forall t \in T, (i, j) \in ε \end{array}\}

式中:P_DA,_ij_,_t、Q_DA,_ij_,_t分别为日前t时段支路(i,j)传输的有功功率和无功功率;ε为网络的支路集合;S_ij_,max为支路(i,j)的最大传输容量.

(5) 潮流约束.用支路流模型对微电网建立潮流数学模型^[21]:

(8)

\begin{array}{l} l_{i j} = | I_{i j} |^{2}, v_{j} = | V_{j} |^{2} \\ p_{j} = \sum_{k : j \to k}^{} P_{j k} - \sum_{i : i \to j}^{} (P_{i j} - r_{i j} l_{i j}) \\ q_{j} = \sum_{k : j \to k}^{} Q_{j k} - \sum_{i : i \to j}^{} (Q_{i j} - x_{i j} l_{i j}) \\ v_{j} = v_{i} - 2 (r_{i j} P_{i j} + x_{i j} Q_{i j}) + (r_{i j}^{2} + x_{i j}^{2}) l_{i j} \\ l_{i j} \geq \frac{P_{i j}^{2} + Q_{i j}^{2}}{v_{i}} \\ \forall (i, j) \in ε, \forall j \in N \end{array}\}

式中:l_ij为支路(i,j)电流I_ij的平方;v_i、v_j为节点i、j电压V_i、V_j的平方;p_j、q_j分别为节点j注入的有功、无功功率;P_ij和Q_ij为支路(i,j)流过的有功功率和无功功率;r_ij、x_ij分别为支路(i,j)的电阻和电抗;N为网络的节点集合.

对于PQ节点,电能供需平衡为

(9)

\begin{array}{l} p_{j, t} = P_{L, j, t} - P_{P V, j, t} - P_{M T, j, t} + \\ P_{c h a, j, t} - P_{d i s, j, t} \\ q_{j, t} = Q_{L, j, t} - Q_{P V, j, t} - Q_{M T, j, t} \\ \forall t \in T, \forall j \in N \end{array}\}

式中:p_j_,_t、q_j_,_t分别为t时段节点j的有功注入功率、无功注入功率;P_L,_j_,_t、Q_L,_j_,_t 分别为t时段节点j的有功负荷、无功负荷;P_PV,_j_,_t、Q_PV,_j_,_t 分别为t时段节点j的光伏注入有功功率、无功功率;P_MT,_j_,_t、Q_MT,_j_,_t分别为 t时段节点j的燃气轮机注入有功功率、无功功率;P_cha,_j_,_t、P_dis,_j_,_t分别为t时段节点j的储能充电功率、放电功率.

对于与大电网相连的平衡节点(j=1),电能供需平衡为

(10)

\begin{array}{l} p_{1, t} = P_{L, 1, t} - P_{P V, 1, t} - P_{M T, 1, t} + P_{c h a, 1, t} - \\ P_{d i s, 1, t} - P_{b, 1, t} + P_{s, 1, t} \\ q_{1, t} = Q_{L, 1, t} - Q_{P V, 1, t} - Q_{M T, 1, t} \\ \forall t \in T \end{array}\}

式中:P_b,1,_t、P_s,1,_t分别为t时段平衡节点的购电功率、售电功率.

电压约束为

(11)

\begin{array}{l} v_{m i n} \leq v_{j} \leq v_{m a x} \\ \forall t \in T, \forall j \in N \end{array}\}

式中:v_min、v_max分别为各节点电压平方v_j的下、上限.

1.2 日内调度模型

日内调度根据光伏预测值与实际值偏差调整微电网各单元的调度方案,包括燃气轮机机组出力的调整、向上级电网购售电量的调整和日内弃光量的调整;储能单元的日内调度方案不变.

在日内调度,以再调度成本最小为目标函数:min C_RE,其中

(12)$\begin{aligned} C_{\mathrm{RE}}= & \sum_{t \in T} \sum_{m \in N_{\mathrm{MT}}}\left(C_{\mathrm{RE}, \mathrm{MT}, m}^{+} P_{\mathrm{RE}, \mathrm{MT}, m, t}^{+}+\right. \\ & \left.C_{\mathrm{RE}, \mathrm{MT}, m}^{-} P_{\mathrm{RE}, \mathrm{MT}, m, t}^{-}\right)+\sum_{t \in T}\left(C_{\mathrm{RE}, \mathrm{~b}}^{+} P_{\mathrm{RE}, \mathrm{~b}, t}^{+}+\right. \\ & \left.C_{\mathrm{RE}, \mathrm{~b}}^{-} P_{\mathrm{RE}, \mathrm{~b}, t}^{-}+C_{\mathrm{RE}, \mathrm{~s}}^{+} P_{\mathrm{RE}, \mathrm{~s}, t}^{+}+C_{\mathrm{RE}, \mathrm{~s}}^{-} P_{\mathrm{RE}, \mathrm{~s}, t}^{-}\right)+ \\ & \sum_{t \in T} \sum_{p \in N_{\mathrm{PV}}} C_{\mathrm{PV}, \mathrm{cut}} P_{\mathrm{ID}, \mathrm{PV}, \mathrm{cut}, p, t} \end{aligned}$

式中:C_RE为微电网的再调度成本; $C_{R E, M T, m}^{+}$ 、 $C_{R E, M T, m}^{-}$ 分别为燃气轮机机组日内增加出力和减少出力的单位成本; $P_{R E, M T, m, t}^{+}$ 、 $P_{R E, M T, m, t}^{-}$ 分别为燃气轮机机组日内各时段增加或减少的出力; $C_{R E, b}^{+}$ 、 $C_{R E, b}^{-}$ 分别为日内增加和减少的购电的惩罚系数; $P_{R E, b, t}^{+}$ 、 $P_{R E, b, t}^{-}$ 分别为各时段增加和减少的购电量; $C_{R E, s}^{+}$ 、 $C_{R E, s}^{-}$ 分别为日内增加和减少售电的惩罚系数; $P_{R E, s, t}^{+}$ 、 $P_{R E, s, t}^{-}$ 分别为增加和减少的售电量;P_ID,PV,cut,_p_,_t为日内各时段光伏电站的弃光量.

日内调度的约束条件如下:

(1) 与上级电网的交互约束.交互功率限制约束与式(2)一致.购售电量增减约束为

(13)

\begin{array}{l} P_{R E, b, t}^{+} = m a x \{P_{I D, b, t} - P_{D A, b, t}^{*}, 0\} \\ P_{R E, b, t}^{-} = m a x \{P_{D A, b, t}^{*} - P_{I D, b, t}, 0\} \\ P_{R E, s, t}^{+} = m a x \{P_{I D, s, t} - P_{D A, s, t}^{*}, 0\} \\ P_{R E, s, t}^{-} = m a x \{P_{D A, s, t}^{*} - P_{I D, s, t}, 0\} \end{array}\}

式中: $P_{D A, b, t}^{*}$ 、 $P_{D A, s, t}^{*}$ 分别为t时段日前调度决策的购电量和售电量;P_ID,b,_t、P_ID,s,_t分别为日内t时段的购入和出售电量.

(2) 分布式电源约束.光伏约束为

(14)

\begin{array}{l} 0 \leq P_{I D, P V, p, t} \leq P_{m a x, P V, p, t} \\ Q_{I D, P V, p, t} = K_{Q P, p} P_{I D, P V, p, t} \\ P_{I D, P V, c u t, p, t} = P_{m a x, P V, p, t} - P_{I D, P V, p, t} - \\ P_{D A, P V, c u t, p, t}^{*} \end{array}\}

式中:P_ID,PV,_p_,_t、Q_ID,PV,_p_,_t分别为日内t时段光伏单元p输出的有功功率、无功功率;P_max,PV,_p_,_t为各时段各光伏单元实际可用最大功率; $P_{D A, P V, c u t, p, t}^{*}$ 为日前调度决策的弃光量.

燃气轮机约束的功率约束与式(4)一致,表示为

(15)

\begin{array}{l} P_{R E, M T, m, t}^{+} = m a x {P_{I D, M T, m, t} - P_{D A, M T, m, t}^{*}, 0} \\ P_{R E, M T, m, t}^{-} = m a x {P_{D A, M T, m, t}^{*} - P_{I D, M T, m, t}, 0} \end{array}\}

式中:P_ID,MT,_m_,_t为日内t时段各个燃气轮机机组的有功出力;P^*_DA,MT,_m_,_t为日前调度决策t时段燃气轮机有功出力.

储能约束中,储能设备的日内调度方案服从日前调度决策结果.

(3) 切负荷约束与式(6)一致.

(4) 线路热约束与式(7)一致.

(5) 潮流约束与式(8)~(11)一致.

2 微电网新能源组合预测方法

组合预测是新能源预测中常见的方法,预测子模型利用天气数据和光伏电站信息训练后输出子预测结果,根据各子模型的权重加权组合,求出输入日前调度模型的功率预测值^[22].不同预测权重使组合预测结果的导向性不同,传统的组合预测以精度为导向^[23],用解析方法或启发式算法求解权重,预测结果的精度至少是子模型精度的下限.基于组合预测的方法,以组合预测权重系数为优化变量,提出以微电网运行效益(即运行成本)为导向的预测权重优化方法.

2.1 精度导向的组合预测模型

以训练集数据预测结果的误差最小为优化目标,各预测子模型的权重系数为优化变量,求解使预测精度最高的权重系数.选取均方误差(mean squared error,MSE)作为预测精度的度量指标,可以得到如下的组合预测优化模型:

(16)

\begin{array}{l} k_{a c}^{*} = a r g \underset{k_{a c}}{m i n} \frac{1}{N_{T}} \sum_{t \in T}^{} (k_{a c} {\hat{y}}_{t} - y_{t})^{2} \\ s . t . k_{a c} \geq 0 \\ {‖k_{a c}‖}_{1} = 1 \end{array}\}

式中:k_ac为精度导向的组合预测权重向量变量; $k_{a c}^{*}$ 为使预测精度最高的最优预测权重向量;N_T为每个样本日的时段数; ${\hat{y}}_{t}$ 为t时段的各预测子模型的预测结果;y_t为t时段光伏出力的真实值.

2.2 收益导向的预测与调度端到端优化模型

以微电网的运行成本最小为优化目标,各预测子模型的权重系数为优化变量,建立功率预测与日前日内调度端到端的闭环优化模型.上层权重优化模型求解收益导向的组合预测权重,下层优化调度模型求解微电网运行成本最低的日前与日内调度方案,采用启发式算法在上下层之间迭代求解.

2.2.1 端到端模型的分层优化形式

该模型的分层数学形式如本节后续公式组所示.

组合预测权重优化:

(17)

\begin{array}{l} k_{v a}^{*} = a r g \underset{k_{v a}}{m i n} \frac{1}{N_{T}} \sum_{t \in T}^{} c_{D A, t} x_{t}^{*} (k_{v a} {\hat{y}}_{t}) + \\ c_{I D, t} z_{t}^{*} (x_{t}^{*}) \\ s . t . k_{v a} \geq 0 \\ {‖k_{v a}‖}_{1} = 1 \end{array}\}

式中:k_va为收益导向的组合预测权重向量变量; $k_{v a}^{*}$ 为使运行收益最好的最优预测权重向量;c_DA,_t为日前调度成本系数; $x_{t}^{*}$ (k_va ${\hat{y}}_{t}$ )为日前调度结果;c_ID,_t为日内调度成本系数; $z_{t}^{*}$ ( $x_{t}^{*}$ )为日内调度结果.

日内调度层:

(18)

\begin{array}{l} z_{t}^{*} (x_{t}^{*}) = a r g \underset{z_{t}}{m i n} \sum_{t \in T}^{} c_{I D, t} z_{t} \\ s . t . A_{I D, t} z_{t} + B_{I D, t} x_{t}^{*} \leq b_{I D, t} \\ f (z_{t}, x_{t}^{*}) \leq 0 \end{array}\}

式中:A_ID,_t、B_ID,_t、b_ID,_t为日内调度优化模型中线性约束的系数矩阵;f(z_t, $x_{t}^{*}$ ) 为日内调度优化模型中的非线性约束;z_t为日内调度优化变量.

日前调度层:

(19)

\begin{array}{l} x_{t}^{*} (k_{v a} {\hat{y}}_{t}) = a r g \underset{x_{t}}{m i n} \sum_{t \in T}^{} c_{D A, t} x_{t} \\ s . t . A_{D A, t} x_{t} + B_{D A, t} k_{v a} {\hat{y}}_{t} \leq b_{D A, t} \\ f (x_{t}, k_{v a} {\hat{y}}_{t}) \leq 0 \end{array}\}

式中:A_DA,_t、B_DA,_t、b_DA,_t为日前调度优化模型中线性约束的系数矩阵;f(x_t, k_va ${\hat{y}}_{t}$ )为日前调度优化模型中的非线性约束;x_t为日前调度优化变量.

式(17)为上层的组合预测权重求解层;式(18)对应1.2节的日内调度模型;式(19)对应1.1节的日前调度模型.

2.2.2 端到端模型的算法求解

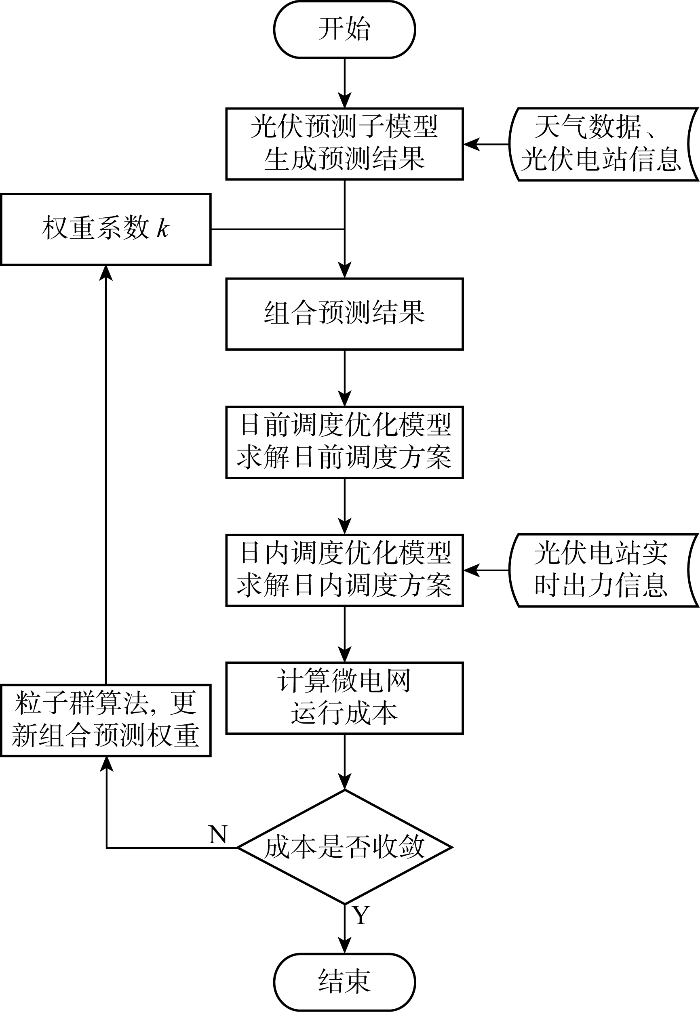
端到端的微电网功率预测与优化调度闭环优化模型流程如图1所示.用粒子群算法求解最优组合预测权重^[24],生成一定数量随机位置和速度的粒子,每个粒子是一个组合预测权重向量,根据每个粒子的权重组合子模型的预测结果得到光伏功率预测值.日前和日内调度模型根据功率预测值求解出微电网运行成本,粒子群算法根据成本高低对粒子进行适应度评价,更新粒子的速度和位置.粒子的位置更新后,以新的组合权重求出新的运行成本,重复上述步骤,直至结果的适应度不大于收敛条件,此时粒子的位置为最优组合预测权重向量.粒子群算法的收敛性取决于粒子的初始分布、速度更新规则、学习因子及惯性权重,设置合适的算法参数,避免局部最优陷阱,粒子群可以收敛到全局最优解^[25].

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 微电网预测-日前-日内闭环运行模型的流程

Fig.1 Process of microgrid closed-loop operation model with prediction day-ahead, and intraday

3 算例分析

3.1 组合预测子模型

选用4种常见的机器学习预测模型进行光伏功率预测,分别为支持向量回归^[26](support vector regression, SVR)、多层感知器^[27](multilayer perceptron,MLP)、随机森林回归^[28](random forest regression, RFR)与直方梯度提升^[29](histogram of oriented gradients,HGB),各子模型以精度为目标进行训练.上述模型的主要参数如表1所示.

表1 预测子模型参数设置

Tab.1 Parameter settings of prediction sub-model

模型	参数
SVR	kernel为poly, C=0.5, γ=0.03
MLP	hidden_layer_size为75, max_iter为30
RFR	n_estimators为5, max_depth为5, min_samples_leaf为7
HGB	max_iter为20, max_leaf_nodes为20, min_samples_leaf为7

新窗口打开| 下载CSV

3.2 IEEE 33节点小系统算例

在IEEE 33节点配电网系统^[30]中接入3个光伏电站,位于3节点、20节点、28节点;2个储能单元,位于10节点、30节点;2个燃气轮机机组,位于4节点、15节点.设定每日最大购电和售电量为 3 MW·h,弃光惩罚为0.4元/(kW·h),切除负荷的惩罚为1.2元/(kW·h).表2给出微电网分布式电源的参数;表3 给出日内再调度成本参数^[31],微电网的节点1作为松弛节点与大电网相连;表4给出分时购售电价.

表2 微电网分布式电源参数

Tab.2 Parameters of microgrid distributed power source

分布式电源类型	参数	取值
燃气轮机1,2	最大容量/kW	600
	向上爬坡速率/(kW·h^-1)	125
	向下爬坡速率/(kW·h^-1)	125
	成本系数,a/(元·kW^-2)	0.0002
	成本系数,b/(元·kW^-2)	0.386
	成本系数,c/元	0
光伏电站1	最大容量/(kV·A)	2000
光伏电站2	最大容量/(kV·A)	2400
光伏电站3	最大容量/(kV·A)	1800
储能设备1,2	电池容量/(kW·h)	1600
	最大充放电功率/kW	500
	充放电效率	0.95
	荷电状态下限	0.1
	荷电状态上限	0.95

新窗口打开| 下载CSV

表3 日内再调度成本参数

Tab.3 Parameters of intraday redispatch costs 元/kW

对象	参数	取值
燃气轮机	向上再调度成本	0.412
	向下再调度成本	0.386
电力交易	购电量增加的成本	1.200
	购电量减少的成本	0.400
	售电量增加的成本	0.280
	售电量减少的成本	0.400

新窗口打开| 下载CSV

表4 分时购售电价

Tab.4 Time-of-use electricity purchase and selling price 元/(kW·h)

时段	购电价格	售电价格
峰时段(8:00—11:00, 13:00—16:00, 18:00—22:00)	1.189	0.352
谷时段(0:00—7:00, 22:00—24:00)	0.423	0.352
平时段(7:00—8:00, 11:00—13:00, 16:00—18:00)	0.738	0.352

新窗口打开| 下载CSV

光伏预测数据来源于全球能源预测竞赛2014(GEFCom2014),时间分辨率为1 h,选用ZONEID为1的predictor15数据^[32].使用2012年4月1日至2014年5月31日,总计790个样本日整点的光伏出力数据,以前590 d的数据为训练集,后200 d的数据为测试集.

算例在一台配置为Intel Core i7-11800H八核CPU、32 GB内存的个人计算机运行,使用的编程软件为MATLAB2022b,优化求解器为CPLEX.

3.2.1 精度导向的光伏组合预测模型仿真验证

(1) 预测精度评价指标.MSE用于计算预测值与真实值之差的平方的平均值,MSE 越小,预测结果的误差越小.表示为

(20)e_MSE=

\frac{1}{n} \sum_{w = 1}^{n}

(y_w-

{\hat{y}}_{w}

)²

平均绝对误差(mean absolute error,MAE)用于计算预测值与实际值之差的绝对值的平均值,MAE反映预测值与实际值之间的平均偏差程度.表示为

(21)e_MAE=

\frac{1}{n} \sum_{w = 1}^{n} |y_{w} - {\hat{y}}_{w}|

决定系数(R²)用于衡量模型的预测性能,R²越接近 1,预测结果越接近实际值.表示为

(22)R²=1-

\frac{\sum_{w = 1}^{n} (y_{w} - {\hat{y}}_{w})^{2}}{\sum_{w = 1}^{n} (y_{w} - {\bar{y}}_{w})^{2}}

式中:y_w、 ${\hat{y}}_{w}$ 、 ${\bar{y}}_{w}$ 分别是第w个预测对象的实际值、预测值和实际值的平均值;n为预测对象集合.

(2) 预测性能分析.选用4种光伏预测子模型SVR、MLP、RFR、HGB,以均方误差为评价预测精度的指标,根据式(16)求解组合预测权重系数.SVR、MLP、RFR、HGB各预测子模型的权重分别为 0.188 8、0.030 9、0.465 6、0.314 6.

表5展示了各预测子模型与组合预测结果在各精度评价指标下的预测性能.由表可知:MSE越大的预测子模型在组合预测的权重中越小;精度导向组合预测的结果在MSE评价指标下,相较精度最好的预测子模型降低14.1%;在MAE评价指标下,精度导向组合预测结果相较精度最好的预测子模型升高1.0%,但较其余3个预测子模型降低明显;在R²评价指标下,精度导向组合预测结果相较精度最好的预测子模型降低0.1%,但较其余3个子模型有提升.该结果说明以某种精度指标为优化目标的组合预测在该指标下精度显著提升,在其余评价指标下,也优于大部分预测子模型,但略差于精度指标最优的子模型.组合预测性能的下限为单个预测子模型性能的上限.

表5 预测模型精度

Tab.5 Accuracy of forecast model

模型	e_MSE	e_MAE	R²
SVR	0.00978	0.0482	0.8243
MLP	0.00984	0.0672	0.8410
RFR	0.00889	0.0605	0.7979
HGB	0.00927	0.0622	0.8504
精度导向组合预测	0.00764	0.0487	0.8497
收益导向组合预测	0.00931	0.0568	0.8025

新窗口打开| 下载CSV

3.2.2 收益导向的预测——调度端到端模型仿真验证

以微电网运行收益最大化即运行成本最低为优化目标,根据式(17)~(19)求解组合预测权重系数.各预测子模型SVR、MLP、RFR、HGB的权重分别为 0.662 4、0.014 1、0.183、0.140 5.

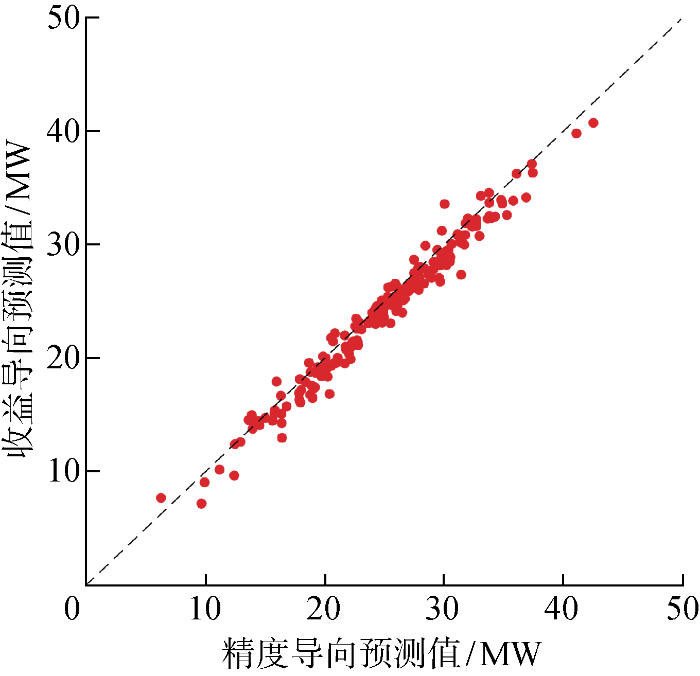
在测试集中以精度导向和收益导向的权重系数组合各子模型,得到光伏预测值分布如图2所示.在200个样本日中,共有161个样本日的收益导向组合预测值小于精度导向组合预测值,占总样本量的80.5%.收益导向预测值平均比精度导向预测值小3.1%.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 精度导向与收益导向的预测值分布

Fig.2 Distributions of forecast values based on precision-oriented and profit-oriented predictions

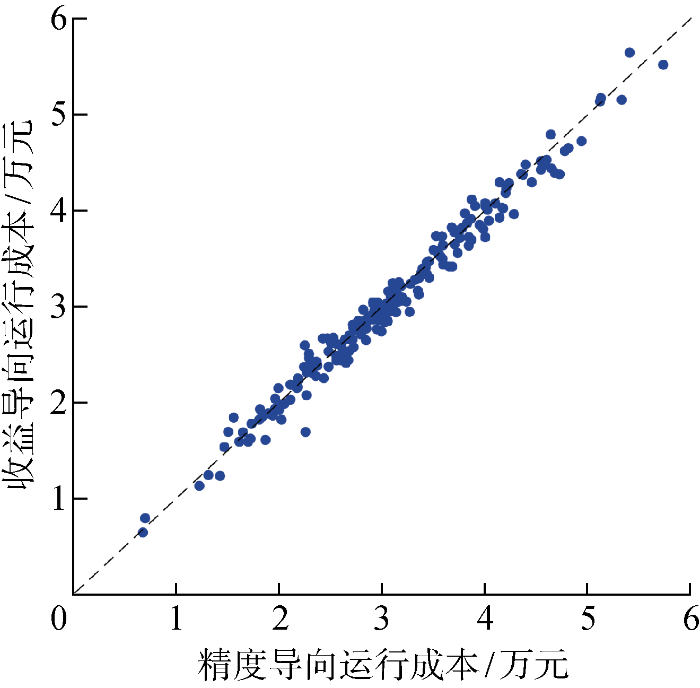
在测试集中,基于精度导向和收益导向预测结果求解得到的微电网运行成本如图3所示.在200个样本日中,119个样本日的端到端模型求解出的运行成本低于精度导向模型的运行成本,占总样本量的59.5%.表6给出根据各预测子模型的预测结果以及两种不同导向的组合预测结果进行日前和日内调度的微电网运行成本.端到端收益导向模型的最大日运行成本、最小日运行成本与平均成本相比,精度导向模型分别减少1.53%、4.62%和1.45%.两种组合预测方法的微电网运行平均成本都低于单个预测子模型.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 精度导向与收益导向的运行成本分布

Fig.3 Distributions of operating costs based on precision-oriented and profit-oriented predictions

表6 精度导向与收益导向运行成本对比

Tab.6 Comparison of precision-oriented and profit-oriented operating costs 元

预测模型	最大日运行成本	最小日运行成本	平均成本
精度导向组合预测	57159	6629	30815
收益导向组合预测	56283	6323	30368
SVR	59066	6917	31253
MLP	57806	6482	31657
RFR	58241	6315	30942
HGB	57278	6489	30888

新窗口打开| 下载CSV

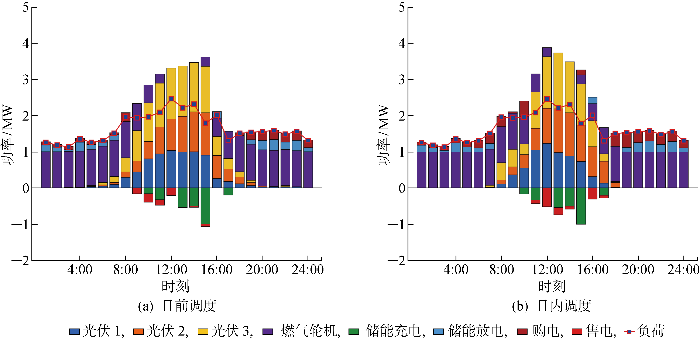
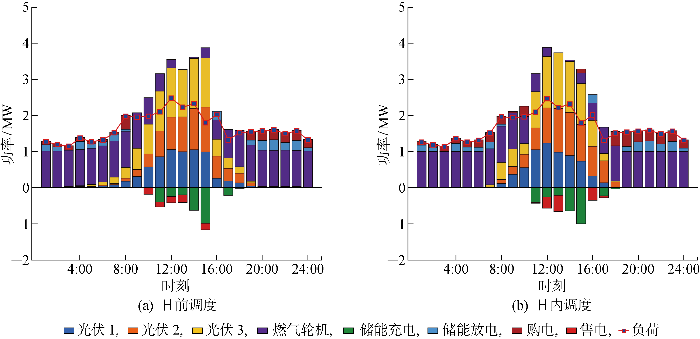
选取样本日(2014年3月30日)研究两种不同预测导向下的预测结果与调度方案的区别以及与微电网参数的联系,图4和图5分别为精度和收益导向下的日前与日内调度方案.日前调度模型生成基于光伏预测的机组出力方案,日内调度对日前方案进行实时调整以修正光伏预测误差导致的功率缺额或超额,包括更改与上级电网的购售电量,调整燃气轮机机组与弃光、弃负荷调度计划.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 基于精度导向预测的微电网调度策略

Fig.4 Microgrid scheduling strategy based on precision-oriented prediction

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 基于收益导向预测的微电网调度策略

Fig.5 Microgrid scheduling strategy based on profit-oriented prediction

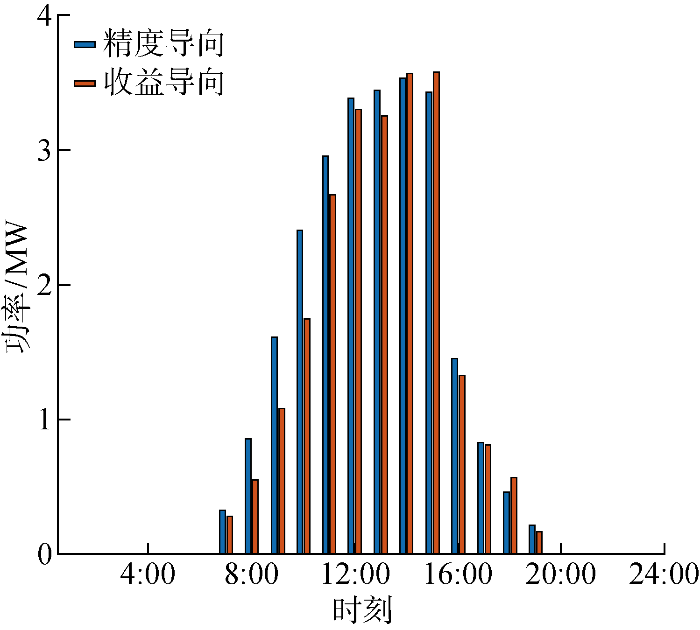
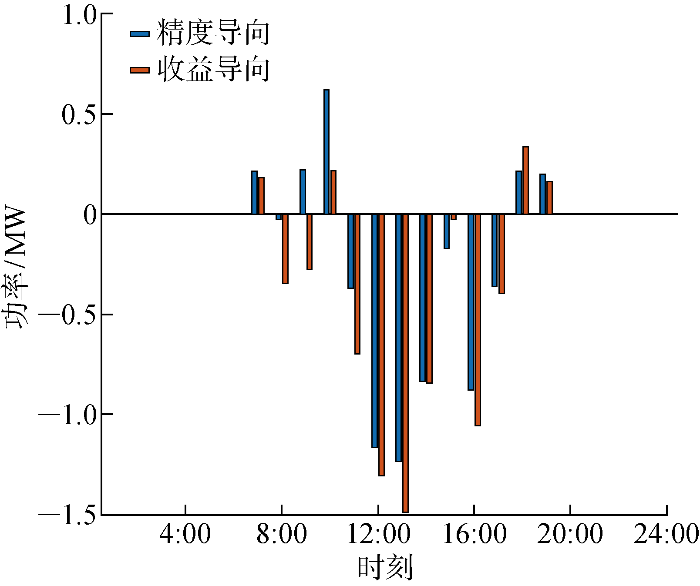
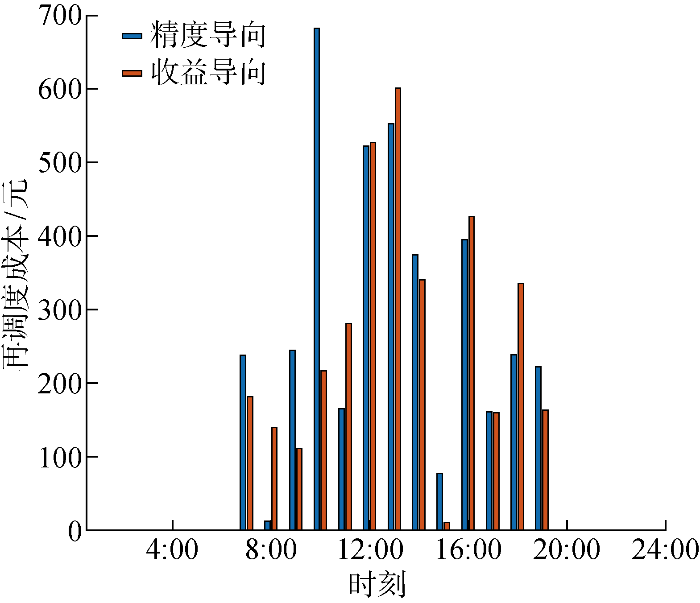
图6~8分别为精度与收益导向下样本日(2014年3月30日)各时段的光伏预测值、预测值与实际值的偏差、偏差导致的再调度成本.该日精度导向的调度成本为 42 131.8元,其中日前为 37 691.5元,日内为 4 440.3元;收益导向的调度成本为 42 058.4元,其中日前为 37 739.0元,日内为 4 319.4元.精度导向预测的均方误差较小,但在10:00时出现较大的正误差,当光伏实际出力低于预测值时,要通过向上再调度补偿功率缺额.表3所示日内再调度成本参数说明燃气轮机和电力交易的向上再调度比向下再调度惩罚更高, 10:00出现的误差尖峰导致高额的再调度成本.由于微电网的再调度成本关于预测误差有不对称性,所以尽管收益导向的组合预测结果偏小,略微降低了准确性,但同时减少了功率缺额尖峰出现场景的概率,更有效地规避了高额的再调度惩罚.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 精度导向和收益导向模型的预测结果对比

Fig.6 Comparison of forecasting results between precision-oriented and profit-oriented models

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 精度导向和收益导向模型的预测误差对比

Fig.7 Comparison of prediction errors between precision-oriented and profit-oriented models

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 精度导向和收益导向模型的再调度成本对比

Fig.8 Comparison of redispatch costs between precision-oriented and profit-oriented models

3.3 IEEE 123节点大系统算例

在低压配电网IEEE 123节点系统中接入分布式电源、储能单元等装置,验证端到端协同优化模型在低压复杂网络下的优化性能^[33].该系统中配置的分布式电源如表7所示,其余算例参数与表2~4一致.

表7 IEEE 123节点系统分布式电源配置

Tab.7 Distributed power configuration of IEEE 123-node system

分布式电源类型	所在节点	容量/(MV·A)
光伏电站	15,68,88	0.6
	35,114,121	0.8
	8,41	1.0
燃气轮机	22,100,111	0.8
	38,76	1.2
储能设备	48,107	1.5
	9,26	2.0

新窗口打开| 下载CSV

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 精度导向与收益导向的大系统运行成本

Fig.9 Operating costs of large-scale systems in precision-oriented and profit-oriented approaches

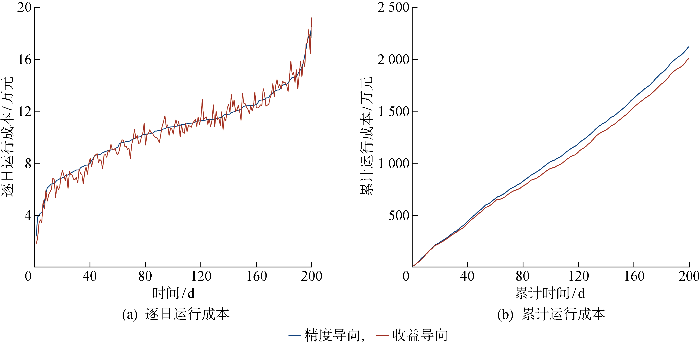
在测试集的200个样本日中,分别以预测精度和运行收益为导向计算两种优化方法下123节点微电网的运行成本,并根据精度导向下的运行成本进行升序排列,结果如图9(a)所示.图9(a)表明端到端收益导向的预测调度协同优化模型并非在所有样本日都能缩减运行成本,但都分布在以精度导向为目标的运行成本附近,未造成导致某一日成本突变的运行事故.

把200个样本日的运行成本逐日累加,得到两种优化方法在时间上累计的运行成本,结果如图9(b)所示. 图9(b)表明在长时间尺度上,端对端协同优化方法能有效缩减成本,且效益随时间尺度的延长而递增.

4 结论

针对高比例新能源的微电网运行成本关于预测误差的非对称性问题,提出基于组合预测的以微电网运行收益为导向的新能源预测与日前日内调度端到端联合优化模型.通过在算例分析中与传统的以预测精度为导向的方法进行对比,得到以下结论:

(1) 与单个预测子模型的预测结果相比,精度导向与运行收益导向的组合预测结果在多种评价指标下有优势;预测子模型的性能上限是组合预测的性能下限.

(2) 由于微电网日内再调度成本关于功率缺额和超额呈现不对称性,对功率缺额的惩罚更高,与精度导向模型的预测值相比,端到端优化模型解出的功率预测值大于实际值的场景更少,功率缺额场景减少,从而降低了微电网的运行成本.

(3) 微电网的运行成本和功率预测模型参数之间的关系难以用数学解析表达,采用启发式算法迭代求解组合预测权重系数,即可获得使微电网运行效益较高的预测结果.

未来研究将关注并网型微电网在无功支撑和调峰两方面与大电网的交互.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

韩肖清, 李廷钧, 张东霞, 等.

双碳目标下的新型电力系统规划新问题及关键技术

[J]. 高电压技术, 2021, 47(9): 3036-3046.