大规模电网机组组合状态迭代路径搜索优化方法

doi:10.16183/j.cnki.jsjtu.2024.301

大规模电网机组组合状态迭代路径搜索优化方法

崔一阳^a, 潘斗南^a, 黎灿兵^,^b, 刘健哲^b

上海交通大学 a. 国家电投智慧能源创新学院; b. 电子信息与电气工程学院,上海 200240

An Optimization Method for Iteration Path Search of Large-Scale Power Grid Unit Commitment State

CUI Yiyang^a, PAN Dounan^a, LI Canbing^,^b, LIU Jianzhe^b

a. College of Smart Energy; b. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 黎灿兵,教授,博士生导师;E-mail:licanbing@sjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2024-07-29 接受日期: 2024-09-12

基金资助:

国家重点研发计划资助项目(2022YFB2404200)

Received: 2024-07-29 Accepted: 2024-09-12

作者简介 About authors

崔一阳(2000—),硕士生,从事电力系统优化调度研究.

摘要

针对大规模电网机组组合问题中传统分支定界法计算量随计算规模指数级增长的“维数灾”问题,提出一种机组组合状态迭代路径搜索优化方法.为避免简化问题和缩减可行域导致最优解丢失,将机组状态方案的确定划分为深度遍历与广度迭代双阶段进行;在优选初始解的基础上,以机组动态优先顺序表作为机组状态迭代路径的搜索方向,通过深度遍历确定最佳关停冗余机组及对应关停时刻,并利用广度迭代拓展问题可行域以提高解的最优性.IEEE 118和ACTIVSg10k系统上的测试结果表明,所提方法能够缩小问题规模,减少机组状态尝试数,实现机组状态的高效搜索迭代,计算速度快、效率高,对大规模机组组合优化问题求解具有一定实用性和有效性.

关键词： 机组组合; 优先顺序法; 深度遍历; 广度迭代; 可行域

Abstract

To address the computational challenge posed by the “curse of dimensionality” inherent in traditional branch and bound algorithms for large-scale power grid unit commitment problems, an optimization method for iteration path search of unit commitment state is proposed. To prevent the loss of the optimal solution due to the simplification of the problem and the reduction of the feasible region, the determination of the unit state scheme is divided into a two-stage process of depth traverse and breadth iteration. Based on an initial solution, the unit dynamic priority list is used as the search direction for the unit state iteration path. In deep traverse stage, the optimal shutdown redundant units and their corresponding shutdown time are determined. Breadth iteration is then used to expand the feasible region of the problem to improve the optimality of the solution. The results of a comparative case study conducted on the IEEE 118 system and ACTIVSg10k system indicate that the proposed method effectively reduces the scale of the problem, minimizes the number of unit state attempts, and achieves efficient search and iteration of unit states, exhibiting fast computational speed, high efficiency, which has practical applicability for solving problems of large-scale unit commitment.

Keywords： unit commitment; priority list; depth traverse; breadth iteration; feasible region

PDF (1544KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

崔一阳, 潘斗南, 黎灿兵, 刘健哲. 大规模电网机组组合状态迭代路径搜索优化方法[J]. 上海交通大学学报, 2025, 59(6): 711-719 doi:10.16183/j.cnki.jsjtu.2024.301

CUI Yiyang, PAN Dounan, LI Canbing, LIU Jianzhe. An Optimization Method for Iteration Path Search of Large-Scale Power Grid Unit Commitment State[J]. Journal of Shanghai Jiaotong University, 2025, 59(6): 711-719 doi:10.16183/j.cnki.jsjtu.2024.301

电力系统机组组合(unit commitment, UC)是指在一定调度周期内,以成本最小为目标来制定机组的启停和发电计划,实现系统有功功率平衡并满足一定的约束条件和备用要求.作为市场出清的关键环节,高性能的机组组合计算是构建新型电力系统和实现“双碳”目标的重要支撑^[1-2].

机组组合是非凸、非线性的混合整数规划问题,其计算量与决策变量维度之间呈指数关系,大规模机组组合通常存在“维数灾”问题,难以在合理时间内找出理论上的全局最优解^[3].因此,求解效率问题一直是制约机组组合理论发展的技术瓶颈,同时也是机组组合领域的研究重点^[4].随着新型电力系统建设,机组组合问题规模变大、时段耦合性变强,计算面临物理量倍增、离散变量比例增加、求解实时性要求提高的挑战^[5].

目前,主流的机组组合算法普遍采用基于分支定界的迭代方法求解.在求解大规模机组组合问题时,由于机组数量庞大,机组状态方案将呈指数级增长,所以难以在短时间内获取机组组合问题的最优解^[6].文献[7]中将启发式算法嵌入混合整数规划法以确定部分整数变量,缩减计算规模;文献[8]中采用量子叠加态表示机组0-1状态,实现对机组组合状态空间的高效全局搜索;文献[9]中利用数学松弛手段将机组组合模型转化为等效的二阶锥规划模型;文献[10]中建立机组组合的双重凸包模型,将混合整数规划近似转化为线性规划,降低了计算复杂度.采用基于分支定界的数学解析优化算法求解机组组合问题,忽略了机组组合问题中由机组模型、电网物理约束所决定的变量之间的部分关联,一方面初始解选取的随机性导致问题收敛所需的迭代次数增加,影响求解的速度和效率;另一方面求解过程中机组状态迭代的方向选取缺少直观依据,产生较多无效迭代次数和方案.

与求解混合整数规划问题的分支定界法相比,优先顺序法作为求解机组组合问题的典型启发式算法,具有物理意义明确、实用性强和计算速度快等优点,可以避免数学变量规模增加导致的计算量指数级增长问题,通过设定排序指标确定机组的优先顺序,进而获取初始解和决策机组状态迭代方向.文献[11]中将机组排序作为新增约束纳入混合整数规划问题求解;文献[12]中综合灵敏度、可靠性和经济性指标,确定机组调度顺序以调整机组出力;文献[13]中依据机组开机排序确定中间时段边际机组,并进行深度优先遍历确定机组状态.优先顺序法引入机组排序对机组组合问题进行重新建模,将影响原机组组合问题的可行域,导致算法易丢失全局最优解.

针对上述问题,以市场模式下机组报价机制为排序指标,根据负荷需求得到分时段机组平均报价,形成动态优先顺序表,决策遍历和迭代方向;根据历史解规律确定特定边界条件下的必开必停机组,减小问题规模,避免无效迭代;根据数据驱动模型预测机组状态并进行修正提高初始可行解质量,减少遍历和迭代次数;在初始解基础上,优先进行深度遍历,在较优方案的基础上进行广度迭代,扩展问题的可行域,提高解的最优性,保证优化的深度.在IEEE 118节点系统进行算例验证,结果表明所提方法能够实现机组状态迭代路径的高效搜索,计算速度快,解的质量高.

1 机组动态优先顺序表

1.1 市场模式机组组合模型

机组组合的优化目标通常为系统成本最小,包括机组的启停成本和运行成本等,在电力市场中,机组组合以购电成本最小为目标函数:

(1)$\begin{array}{l} \min C=\sum_{t=1}^{T} \sum_{i=1}^{N} \sum_{j=1}^{n_{i}} u_{i, t} p_{i, j, t} c_{i, j}, \\ u_{i, t} \in\{0,1\}, \quad i=1,2, \cdots, N, \\ t=1,2, \cdots, T \end{array}$

式中:C为购电成本之和;T为调度周期内总时段数;N为机组总数量;n_i为机组i报价总分段数;u_i_,_t为机组i在t时段的状态,0为关机状态,1为开机状态;p_i_,_j_,_t为机组i在t时段位于报价段j的出力;c_i_,_j为机组i在报价段j的报价.

对于机组组合问题的约束条件,考虑系统功率平衡约束、机组出力上下限约束、机组爬坡约束、最小启停时间约束、旋转备用约束和潮流安全约束,具体形式和表达式参见文献[14].由于机组分段出力为决策变量,所以还需考虑机组的分段出力约束:

(2)

\sum_{j = 1}^{n_{i}}

p_i_,_t_,_j=P_i_,_t

式中:P_i_,_t为机组i在t时段的总出力.

为了延长机组的运行寿命,避免机组的频繁启停,添加机组启停次数约束^[15]:

(3)

\sum_{t = 1}^{T} |u_{i, t} - u_{i, t - 1}|

≤1

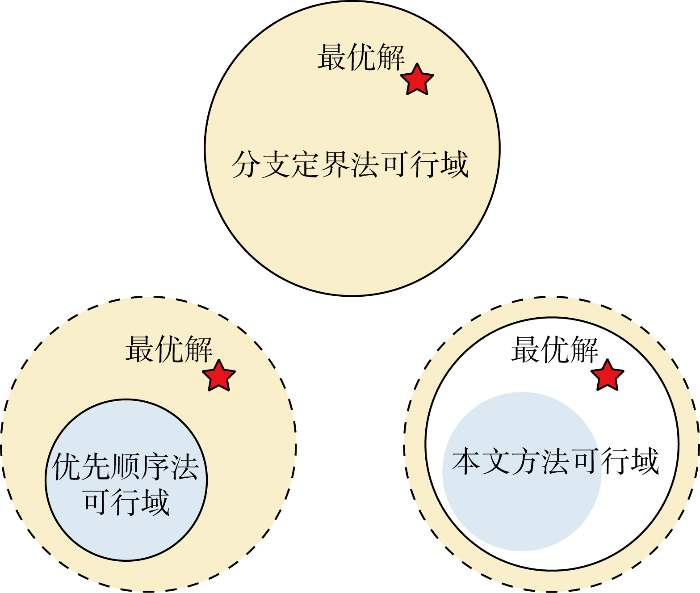
作为混合整数规划问题,机组组合问题的求解通常分为机组状态方案确定和机组出力优化分配两个环节.采用阶梯报价机制下的机组平均报价作为排序指标,得到机组动态优先顺序表,决策机组状态迭代的路径搜索方向,排除机组状态与机组排序不符的绝大多数非最优迭代方向,如排序极为靠后机组不可能优先于排序极为靠前机组进行开机出力.通过大幅缩减机组组合状态可行域,提升机组状态方案确定环节的效率和速度,同时一定程度上拓展可行域,避免丢失更优的机组状态方案,提高解的最优性,实现对大规模机组组合问题的高效求解,所提方法可行域对比如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 所提方法可行域对比

Fig.1 Comparison of feasible regions of method proposed

1.2 机组平均报价排序指标

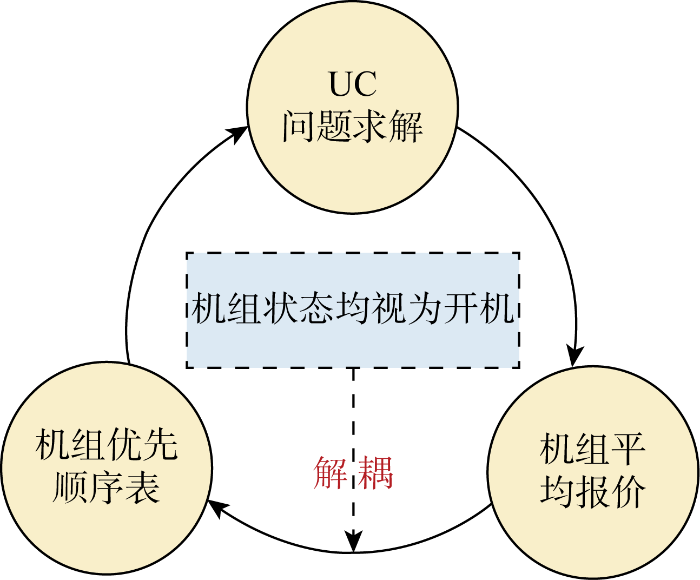
由于机组组合问题的目标函数主要涉及机组报价,所以机组优先顺序表的确定取决于机组的平均报价.机组的平均报价由机组的出力情况确定,而得到机组的出力情况则需先求解机组组合问题,因此机组的优先顺序表与机组组合问题求解间存在强耦合,如图2所示.为将二者解耦,可将所有机组在各时段均视为开机状态,保证所有机组均可出力;然后根据机组组合问题的目标函数,将优先报价较低的机组出力,进而衡量机组的平均报价指标.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 耦合关系与解耦方式

Fig.2 Coupling relationship and decoupling method

在机组状态方案确定的前提下,若忽略潮流安全约束、最小启停时间约束和启停次数约束,则机组的出力优化分配问题简化为线性规划问题.将所有机组均视为开机状态,确定机组平均报价指标的过程称为机组的初始出力优化分配,问题简化条件如下:

(4)u_i_,_t=1, i=1, 2, …, N, t=1, 2, …, T

采用内点法进行机组的出力优化分配,为保证机组的初始出力优化分配阶段始终有解,对机组出力下限约束进行松弛.根据机组初始出力优化分配结果,计算机组的平均报价如下:

(5)$I_{i, t}=\sum_{j=1}^{n_{i}} p_{i, j, t} c_{i, j} \Big / \sum_{j=1}^{n_{i}} p_{i, j, t} $

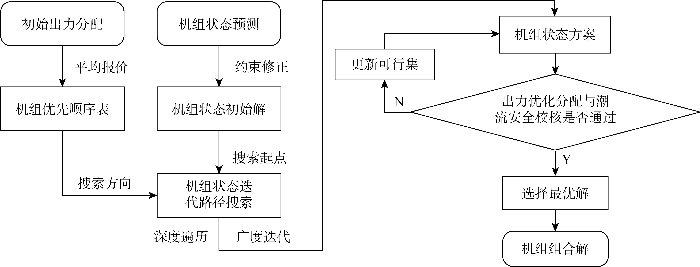
对于出力小于出力下限的机组,将其平均报价视为无穷大,以机组的平均报价作为排序指标得到各时段的机组动态优先顺序表.以机组动态优先顺序表作为机组状态迭代路径的搜索方向,在初始解的基础上依次进行深度遍历和广度迭代,得到机组状态方案,进行出力优化分配和潮流安全校核,所提方法的技术路线框架如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 所提方法技术路线框架

Fig.3 Technical framework of method proposed

2 机组状态初始解优选

2.1 机组状态预测

机组状态作为机组组合问题中的整数决策变量,是导致计算量指数级增长的主要因素.机组组合问题作为特定的数学优化问题,在相似的输入边界条件下输出的结果也相似.因此,基于历史解数据驱动的方法可以实现对机组状态的初步预测.

循环神经网络(recurrent neural network,RNN)是一种用于学习时间特征的深度学习模型,在处理时序数据时具有明显优势.由于机组组合问题在时段上具有强耦合性,所以采用RNN模型预测机组状态.将系统负荷需求、负荷爬坡率以及上一调度周期时段的机组状态作为特定的边界条件输入,当前调度周期时段的机组状态作为输出结果,训练RNN模型实现对机组状态的预测.

在某些特定的边界条件下,部分机组的启停状态可以直接确定,称为必开必停机组.机组的检修计划以及最小启停时间约束作为确定性因素可以直接确定部分必开必停机组.根据机组动态优先顺序表,按一定比例取排序靠后且预测状态为关机状态,即满足下式的机组视为必停机组:

(6)

\begin{array}{l} {\hat{u}}_{i, t} = 0, t = 1, 2, \dots, T \\ R_{i, t} \geq r_{1} N, t = 1, 2, \dots, T \end{array}\}

式中: ${\hat{u}}_{i, t}$ 为机组i在t时刻的预测状态;R_i_,_t为机组i在t时刻的排序编号;r₁为必停机组的划分比例.

按一定比例取排序靠前且预测状态为开机状态,即满足下式的机组视为必开机组:

(7)

\begin{array}{l} {\hat{u}}_{i, t} = 1, t = 1, 2, \dots, T \\ R_{i, t} \leq r_{2} N, t = 1, 2, \dots, T \end{array}\}

式中:r₂为必开机组的划分比例.

通过确定必开必停机组可以缩小机组组合问题规模,减少机组状态决策变量,避免机组状态方案的无效遍历迭代.

2.2 初始解修正

机组状态的初始解作为状态方案遍历和迭代的初始值,要在保证可行的前提下尽可能接近机组组合问题的最终解,从而减少迭代次数,缩短计算时间,提升计算效率.

根据日前负荷预测数据和上一调度周期时段的机组状态,输入训练好的RNN模型得到机组状态预测值.由于机组状态预测值由神经网络根据输入条件直接得到,无法确保满足约束条件,所以需对机组状态预测值依次进行如下修正:

(1) 根据确定的必开必停机组修正不同时段的机组状态:

(8)

\begin{array}{l} u_{i, t} = 0, i \in S_{1}, t = 1,2, \dots, T \\ u_{i, t} = 1, i \in S_{2}, t = 1,2, \dots, T \end{array}\}

式中:S₁、S₂分别为必停机组和必开机组的集合.

(2) 根据旋转备用约束核验机组状态:

(9)

\sum_{i = 1}^{N}

P_max,_iu_i_,_t≥(1+α)P_L,_t

式中:P_max,_i为机组i的出力上限;α为旋转备用系数;P_L,_t为t时刻的系统负荷需求.对于不满足式(9)的时段,按照机组动态优先顺序表依次开启排序靠前的机组,直至各时段均满足式(9).

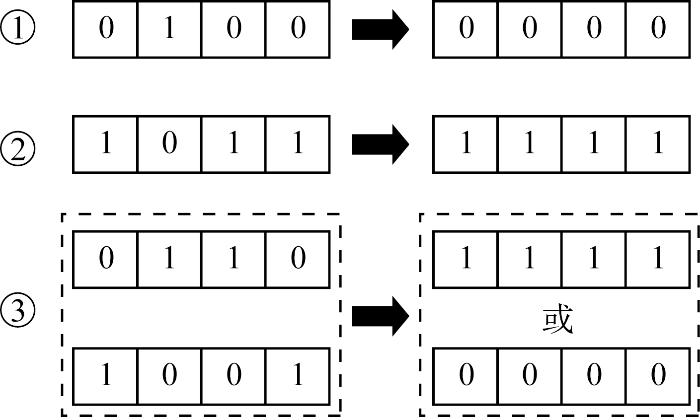
(3) 根据式(3)修正机组状态,对于调度周期内多次启停的机组,通过将相邻的持续时长较短的机组状态时段并入持续时长较长的机组状态时段,减少机组不必要的启停次数.根据启停状态持续时长,分3种情形考虑,如图4所示.情形①中,若机组保持当前启停状态的持续时长小于其改变状态前和后持续时段的时长之和,则将当前时段的机组状态修改为与前后时段一致,机组不进行该次启停动作指令;情形②中,若机组保持当前启停状态的持续时长大于其改变状态前和后持续时段的时长之和,则将前后时段的机组状态修改为与当前时段一致,整个时段机组不进行启停操作;情形③中,若机组保持当前启停状态的持续时长等于其改变状态前和后持续时段的时长之和,则将整个时段的机组状态修改为调度周期内持续时长占比较高的机组状态.根据上述情况重复修正机组状态,直至满足式(3).

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 机组状态修正

Fig.4 Correction of unit state

(4) 根据最小启停时间约束修正机组状态:

(10)

\begin{array}{l} ({X^{u}}_{i, t - 1} - {T^{u}}_{i}) (u_{i, t - 1} - u_{i, t}) \geq 0 \\ ({X^{d}}_{i, t - 1} - {T^{d}}_{i}) (u_{i, t} - u_{i, t - 1}) \geq 0 \end{array}\}

式中: ${X^{u}}_{i, t - 1}$ 、 ${X^{d}}_{i, t - 1}$ 分别为机组i在t时段前已连续开机和停机的时间; ${T^{u}}_{i}$ 、 ${T^{d}}_{i}$ 分别为机组i的最小连续开机和停机时间.考虑上一调度周期内的机组状态,保证当前调度周期内机组启停状态的持续时间不小于最小启停时间.

(5) 再次对机组状态进行旋转备用约束的核验,若不满足式(9),则转入步骤(2),重复上述操作,直至通过核验.

对机组状态预测值进行上述修正后,既保证了初始解的可行性,也使得初始解充分接近机组组合问题的实际最优解,实现机组组合问题的初始解优选.

3 机组状态迭代路径搜索

3.1 机组状态深度遍历

机组状态的深度遍历可以保证问题优化的深度,在机组组合问题初始解的基础上通过深度遍历,可以避免绝大多数无效迭代步骤,快速收敛到接近最优解的机组状态方案.以深度遍历的方式确定并关停各时段冗余机组,可以减少因冗余机组运行产生的额外购电成本,降低机组组合问题的目标函数值.

在满足式(9)的前提下,依次在各时段选择机组动态优先顺序表中排序靠后的机组作为需关停的冗余机组.由于调度周期内的机组状态方案处于逐步过渡的阶段,且考虑机组的最小启停时间与爬坡能力,使调度周期内总经济成本最低的方案中,机组启停时间不一定位于目标时刻,所以需采用时段回推的方式,比较各方案的目标函数值,选取最优方案为机组启停动作发生的时间.为保证遍历深度,对冗余机组的关停动作时刻进行回推遍历,选择最为合适的时间点执行关停指令.进行关停操作前,需进行式(10)的核验,判断该时段是否可以进行关停动作,且关停后在当前调度周期内不再进行开机操作.

为在保证遍历深度的同时提高遍历速度和效率,避免每台机组进行多时段关停动作时刻的回推导致过多机组状态方案的遍历,对于确定需关停的冗余机组,设定合适的回推时段数,在该时段范围中选择当前机组排序最为靠后的时段作为关停指令的执行时刻,因为同一机组在排序靠后的时段更具有关停的倾向,如下:

(11)u_i_,_t-u_i_,_t₊₁=1, R_i_,_t=max R_i

3.2 机组状态广度迭代

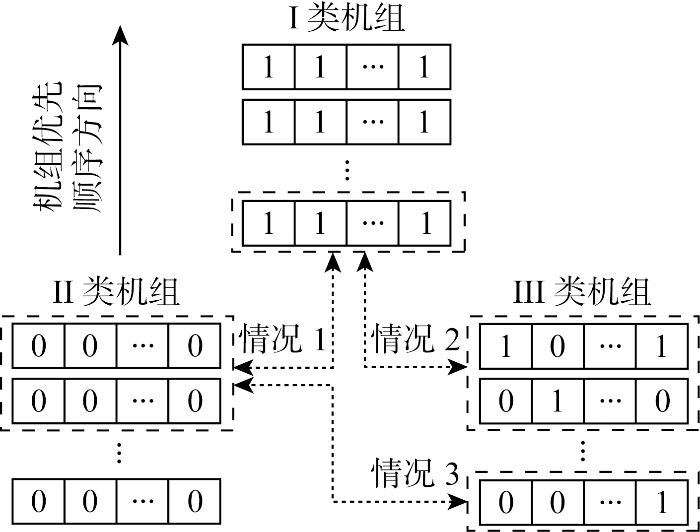
由于机组组合问题在时段上具有强耦合性,每一时刻的机组排序结果将依赖于上一时刻的机组运行状态,如上一时刻运行机组的总体爬坡性能不优,则下一时刻发生爬坡时,爬坡性能较优的机组将排序靠前,所以部分时段机组状态与机组排序结果可能存在差异.为避免求解过程中丢失更优的机组状态方案,需对机组状态方案进行广度迭代.对于所有投运机组,除必开必停机组外,其余机组均视为边际机组.根据机组状态初始解,将边际机组分为 I、II 和 III 类机组,其中 I 类机组指整个调度周期内始终处于开机状态的边际机组,该类机组倾向于在调度周期的所有时段处于开机状态;II 类机组指整个调度周期内始终处于关机状态的边际机组,该类机组倾向于在调度周期内的所有时段处于关机状态;III 类机组指调度周期内存在启停动作的边际机组,该类机组由于存在启停,需对其启停时间节点进行回推尝试,通过出力优化分配比较各方案,确定最优启停动作时刻,更新机组状态方案.

针对上述3类机组,以机组动态优先顺序表为依据,I 类机组中排序靠后的部分有向 II 类和 III 类机组转换的倾向,II 类机组中排序靠前的部分有向 I 类和 III 类机组转换的倾向,III 类机组中排序靠前的部分有向 I 类机组转换的倾向、排序靠后的部分有向 II 类机组转换的倾向.因此,分别考虑如下3种情况进行机组状态方案的广度迭代,如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 机组状态广度迭代

Fig.5 Breadth iteration of unit state

情况1,尝试用排序靠前的 II 类机组替代排序靠后的 I 类机组;情况2,尝试用排序靠前的 III 类机组替代排序靠后的 I 类机组,由于 III 类机组存在启停,所以替代后的 I 类机组同样需进行启停时间节点的回推尝试,确定最优启停动作时刻;情况3,尝试用排序靠前的 II 类机组替代排序靠后的 III 类机组,替代后的 II 机组进行启停时间节点的回推尝试,确定最优启停动作时刻.

对于上述3种情况的迭代尝试,需考虑从单台机组到多台机组发生替代的所有情形,直至所有目标机组均经历相应的替代尝试.多台机组的替代尝试需首先进行可选机组方案的排列组合,枚举所有可能组合方案并依次进行替代尝试,避免丢失更优的机组状态方案.

3.3 机组状态双阶段路径搜索

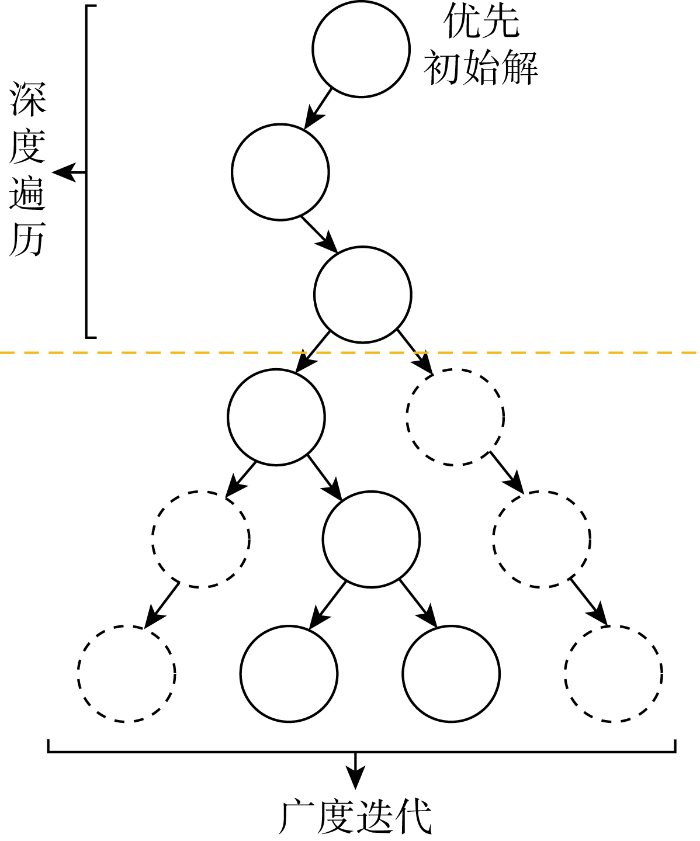
大规模机组组合问题中机组数量的增加和时间尺度的扩展导致机组状态方案的组合数量呈指数级增长,成为制约机组组合问题求解优化效率和速度的主要因素.为在保证机组组合问题求解速度和效率的同时,避免因可行域缩减丢失更优的机组状态方案,分双阶段对机组状态的迭代方向进行路径搜索,如图6所示,其中实线圆表示机组状态迭代的搜索路径,虚线圆表示根据机组动态优先顺序表排除的不优迭代方向.通过深度遍历高效搜索得到机组组合问题的局部最优解,随后进行广度迭代扩展问题的可行域,极大缩小了机组状态方案所需遍历和迭代的组合数量,同时保证了求解速度和解的质量.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 机组状态路径搜索迭代

Fig.6 Path search iteration of unit state

在深度遍历阶段,以机组状态优选初始解作为起点,根据机组动态优先顺序表依次关停各时段冗余机组,直至满足以下遍历终止条件:

(12)

\sum_{i = 1}^{N}

P_max,_iu_i_,_t≤(1+β)(1+α)P_L,_t

式中:β为最大允许冗余系数.

若深度遍历终止时存在多个满足约束的可行解,则对各可行解进行出力优化分配,选择其中目标函数最优的机组状态方案作为下一阶段广度迭代的初始值.

在广度迭代阶段,以深度遍历后的机组状态方案作为起点,假设为U₀,根据机组动态优先顺序表分情况进行状态方案的迭代,终止条件为所有情况的边际机组的排列组合方案均被考虑充分.每次迭代均需对产生的机组状态方案进行旋转备用约束的校核,满足式(9)的机组状态方案纳入可行集中,得到机组状态的可行集矩阵U=[U₀U₁ … U_Z],对应的购电成本矩阵为f=[f₀f₁ … f_Z],其中Z为机组状态可行方案的总数量.

若对由广度迭代得到的机组状态方案可行集中所有机组状态方案均进行潮流安全校核,将影响计算效率和求解时间,因此,按目标函数矩阵f从小到大排序,按比例选取排序靠前的对应机组状态方案作为进行潮流安全校核求解的目标集.

依次对目标集的机组出力优化分配结果进行潮流安全校核及结果修正.经潮流核验后,若存在潮流越限支路,则将该支路的直流潮流约束纳入出力分配优化阶段的不等式约束中,再次进行出力优化分配,并重复进行上述操作,直至不存在潮流越限支路.比较目标可行集经潮流安全校核修正后的出力优化分配结果,选择其中的最优方案作为机组组合问题的最终解.

4 算例分析

4.1 IEEE 118节点系统

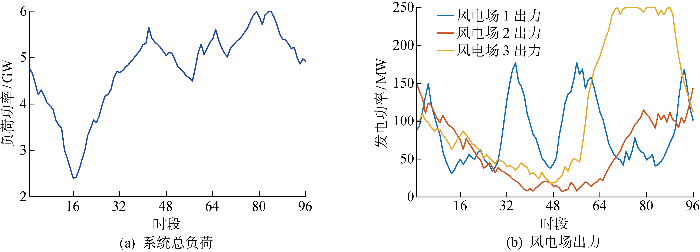
采用IEEE 118节点96时段系统作为测试算例,验证所提方法效果.含新能源出力的IEEE 118节点系统包含54台火电机组、3个风电场和186条支路,3个风电场分别位于节点14、54和98.详细的节点、机组和支路数据参见文献[16].按每15 min为一个时段进行划分,将1 d的24 h划分为96个时段.96时段的负荷和风电场出力数据根据文献[16]的24时段数据拓展得到,如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 IEEE 118系统负荷和风电场出力96时段数据

Fig.7 Load and wind farm output data of 96 time periods in IEEE 118 system

依据经济学原理,影响机组报价的因素包括机组类型和规模、燃料和设备成本以及竞争和市场需求等,机组报价曲线呈非递减的阶梯段形式.测试算例数据不含机组报价曲线信息,因此根据机组报价的制定规律,以燃料类型、成本系数、出力上下限和最小启停时间等机组参数作为特征值对机组进行聚类分析,将测试算例的54台火电机组划分为16个类别,并根据其成本曲线模拟报价曲线,如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 16类火电机组报价

Fig.8 Bids of 16 categories of thermal units

将机组组合历史解数据按照7:3比例划分训练集和测试集,采用均方误差作为标准评估模型性能,模型在测试集上的预测准确率为 0.973 2,机组状态预测的准确度较高.

调用Gurobi对测试算例进行优化求解,并与优先顺序法^[13]和所提方法进行结果对比,所提方法求解结果见附录图A1,优化结果和计算时间如表1所示.测试环境均为i5-12600KF@3.70 GHz、16.0 GB RAM硬件条件下的MATLAB R2023b平台,计算时间均为CPU时间.

表1 IEEE 118节点系统优化结果和计算时间对比

Tab.1 Comparison of optimization results and calculation time in IEEE 118-node system

优化方法	优化结果/美元	迭代次数	计算时间/s
Gurobi	3813579.9227	56288	34.13
优先顺序法^[13]	3815193.7850	78	14.55
所提方法	3808357.7889	117	16.88

新窗口打开| 下载CSV

由表1结果对比发现,在IEEE 118节点系统上,所提方法相较于Gurobi的计算结果更优,减少了99.79%的迭代次数,目标函数值减小 0.136 9%,计算时间缩短50.54%,具有较高的求解效率;与优先顺序法相比,通过广度迭代阶段扩展问题的可行域,目标函数值即优化结果减小 0.179 2%,提高了解的最优性.

4.2 ACTIVSg10k系统

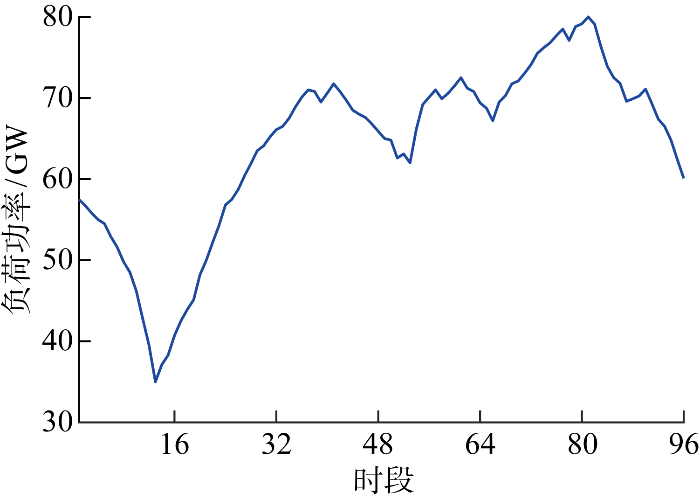
ACTIVSg10k系统包含1万个节点、1 474 台机组以及 12 706 条支路,在原有ACTIVSg10k系统的基础上,保持网络拓扑结构不变,进行同节点机组合并,得到含324台火电机组的测试算例.96时段的负荷曲线如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 ACTIVSg10k系统负荷和风电场出力96时段数据

Fig.9 Load and wind farm output data of 96 time periods in ACTIVSg10k system

对于测试算例的324台机组,根据成本曲线,分别模拟其报价曲线,机组报价的分段规则根据每台机组的出力上下限范围按固定比例确定.所提方法求解结果见附录图A2,优化结果和计算时间对比如表2所示.

表2 ACTIVSg10k系统优化结果和计算时间对比

Tab.2 Comparison of optimization results and calculation time in ACTIVSg10k system

优化方法	优化结果/美元	迭代次数	计算时间/s
Gurobi	63450681.8119	104735	783.21
优先顺序法^[13]	63623767.8846	2048	185.60
所提方法	63499492.3275	4586	405.47

新窗口打开| 下载CSV

由表2结果对比发现,在ACTIVSg10k系统上,所提方法相较于Gurobi迭代次数减少95.62%,计算时间缩短48.23%,同时目标函数值仅相差 0.076 9%;与优先顺序法相比,目标函数值减小 0.195 3%,得到的解更优.

5 结语

提出一种机组组合状态迭代路径搜索优化方法,将机组状态方案的求解划分为深度遍历和广度迭代尝试两个阶段,实现了对大规模电网机组组合问题的高效优化求解.在IEEE 118系统和ACTIVSg10k系统上的测试结果表明,所提方法以机组动态优先顺序表作为机组状态迭代的路径搜索方向,大幅缩小了问题的可行域,减少95%以上求解所需迭代次数,缩短近50%的求解时间,通过广度迭代拓展问题可行域,避免求解过程中丢失更优机组状态方案,与优先顺序法相比目标函数值更优,提高了解的最优性.在大规模、多时段机组组合问题的求解中,所提方法能够缩小问题规模,减少迭代次数,实现机组状态的高效搜索迭代,求解结果优化程度与商业求解器Gurobi基本一致,且较优先顺序法结果更优,计算时间大幅缩短,为大规模电网机组组合问题的求解降低经济成本,提高求解效率.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-06-0711.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

夏清, 钟海旺, 康重庆.

安全约束机组组合理论与应用的发展和展望

[J]. 中国电机工程学报, 2013, 33(16): 94-103.