数据驱动的流场稀疏数据建模

doi:10.16183/j.cnki.jsjtu.2023.213

数据驱动的流场稀疏数据建模

王鸿鑫¹^,², 徐德刚^,¹, 周楷文³, 李林文², 温新³

1.中南大学自动化学院,长沙 410083

2.上海飞机设计研究院,上海 201210

3.上海交通大学机械与动力工程学院,上海 200240

Data-Driven Method of Modeling Sparse Flow Field Data

WANG Hongxin¹^,², XU Degang^,¹, ZHOU Kaiwen³, LI Linwen², WEN Xin³

1. School of Automation, Central South University, Changsha 410083, China

2. Shanghai Aircraft Design and Research Institute, Shanghai 201210, China

3. School of Mechanical and Power Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 徐德刚,教授,博士生导师;E-mail:dgxu@csu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-05-29 修回日期: 2023-07-4 接受日期: 2023-08-22

Received: 2023-05-29 Revised: 2023-07-4 Accepted: 2023-08-22

作者简介 About authors

王鸿鑫(1979—),正高级工程师,从事民用飞机设计集成、试验验证、建模仿真及数字孪生研究.

摘要

流场实时感知与预测在航空航海等领域具有十分重要的应用价值,但是往往面临流场维度高和实时测量信息少等挑战.针对该问题,提出一种数据驱动的流场建模方法,通过线下建立稀疏数据与高维流场映射,实现线上流场实时重构.线下建模中,针对流场高维度挑战,使用本征正交分解等方法对数据进行降维,提取主要流场空间模态.采用正交三角(QR)分解方法,挖掘流场模态敏感性特征,优化测点位置.利用时间延迟的动态模态分解,显著降低测点数量.在线上重构中,基于实时稀疏测量数据与数据驱动模型,实现对当前和未来时刻全场流场的预测.在圆柱尾涡流场测试中,使用该方法并采用20个稀疏测点,得到的全场重构误差可达10%以下.

关键词： 数据驱动; 降阶模型; 动态模态分解; 位置优化; 稀疏数据; 流场重构

Abstract

Real-time perception and prediction of flow field have very important application value in aviation and navigation, and pose challenges such as high flow field dimension and less real-time measurement information. To solve such problem, a data-driven flow field modeling method framework is proposed, which realizes real-time reconstruction of online flow field by establishing sparse data and high-dimensional flow field mapping offline. In offline modeling, aimed at the high-dimensional challenge of the flow field, the eigenortho decomposition and other methods are used to reduce the dimensionality of the data and extract the spatial mode of the main flow field. The QR decomposition method is used to mine the modal sensitivity characteristics of the flow field and optimize the measurement point position. Dynamic modal decomposition with time delay significantly reduces the number of measurement points. In the online reconstruction, based on real-time sparse measurement data and data-driven models, the prediction of the current and future full-field flow field is realized. In the test of cylinder wake flow, using this method and using 20 sparse measurement points, the full-field reconstruction error obtained can reach less than 10%.

Keywords： data-driven; reduced order model; dynamic mode decomposition; location optimization; sparse data; flow field reconstruction

PDF (22276KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王鸿鑫, 徐德刚, 周楷文, 李林文, 温新. 数据驱动的流场稀疏数据建模[J]. 上海交通大学学报, 2025, 59(5): 684-690 doi:10.16183/j.cnki.jsjtu.2023.213

WANG Hongxin, XU Degang, ZHOU Kaiwen, LI Linwen, WEN Xin. Data-Driven Method of Modeling Sparse Flow Field Data[J]. Journal of Shanghai Jiaotong University, 2025, 59(5): 684-690 doi:10.16183/j.cnki.jsjtu.2023.213

流场环境感知在实际工程应用中具有重要的意义,尤其是在飞机和船舶的航行^[1]、深海探测^[2]、风力发电^[3]等领域极为关键.例如,飞行器需要根据外部流场环境的变化,做出飞行姿态的调整以保证飞行器的正常运行,这就需要对实时的流场环境进行感知.但是,流场演化具有强非线性、高纬度、多因素耦合的特点,在实际应用中,采用需要大量消耗计算资源的仿真是不现实的.因此,使用离散测量数据实现对流场全貌的感知、预测具有重要的意义.

近年来,许多学者研究了如何使用有限的测量数据实现流场的感知预测.在利用稀疏数据的过程中,离散测量点位置的选取极为重要.Willcox^[4]使用间断本征正交分解(POD)的方法,利用条件数约束来实现现有离散测量点的选取,从而少量的测量点的使用就可以实现流场的重构.Manohar等^[5]提出了基于数据驱动的方法,利用已知的数据模式来选取最优传感器位置并验证了其优越性.在稀疏数据的应用研究领域,涌现出了许多方法.Willcox^[4]使用了间断POD 的方法实现了稀疏数据对翼型非稳态流场的估计.Zhou等^[6]使用POD和k最近邻(kNN)的方法实现了对不同工况下翼型周围流场参数的感知.Deng等^[7]使用了长短时记忆(LSTM)神经网络,利用POD模态实现了从离散测量数据到全场数据的重构.这些方法都存在一定的缺陷,比如使用神经网络会带来过拟合、过于消耗计算资源、受噪声影响较大等问题;许多方法只着眼于流场的空间特性,并没有关注流场的时空间演化特性,难以对流场的动力学特性进行建模.因此,动态模态分解(DMD)作为无需方程的动力学系统建模方法可以用来把流场分解成时空间连续的结构,并且拥有对系统进行预测的能力^[8].刘余丹等^[9]将DMD和压缩感知结合实现了翼型表面压力的实时重构.一般来说,标准的DMD方法难以对离散测量数据进行建模,因为该方法是基于对有限维非线性系统的无限维近似,难以对稀疏的强非线性数据准确构建动力学模型.为了解决这一问题,扩展DMD^[10]和核DMD^[11]的方法被提出,引入新观测变量,使得其在新的空间内表现为线性.延时嵌入的方法通过把未来的数据嵌入当前的测量来对有限的离散测量数据进行增维,从而使得更多信息被捕捉来构建线性算子.Yuan等^[12]使用延时嵌入的DMD实现了对局部流场的高时空间分辨率的预测.Shi等^[13]使用延时嵌入DMD实现了动态翼型的强非线性压力场的预测.一般地,稀疏数据和全场流场模态存在线性关系的情况下,可以较为容易地实现从稀疏数据到全场数据的重构.流场的非线性则要求必须建立离散测量的稀疏数据和流场模态的线性关系.在本文中,延时嵌入DMD方法则是用来建立这一线性关系的方法.

本文所提出的数据驱动的稀疏流场建模方法,主要分为线上和线下两部分.线上对高分辨率的流场数据采用随机奇异值分解的方法实现了快速高效的流场特征提取,根据流场的特征使用正交三角(QR)分解寻找最优的传感器位置,利用这些传感器位置的高时间分辨率数据进行延时嵌入DMD建模,可以对离散测量点进行实时预测,再根据离散点的数据实现对未来时刻全场流场的预测.

1 建模方法

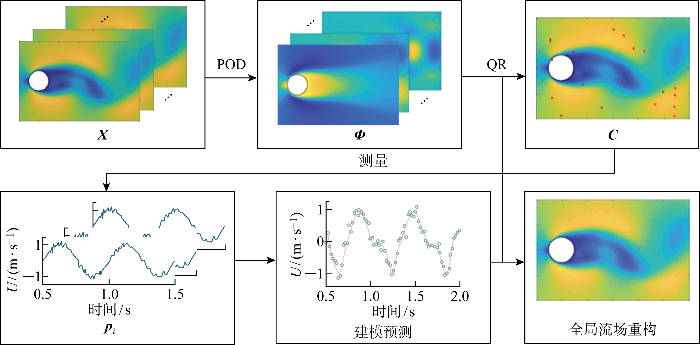
该数据驱动的稀疏数据建模方法主要包括全场特征提取,监测点位置优化选择以及动态模态分解,主要流程如图1所示.图中: X=[x₁x₂ … x_i]∈R^m^×ⁿ为全部流场数据,x_i代表第i时刻的流场数据,m代表每个数据样本的数据点数,即流场数据的网格点数,n代表采集的数据样本的数量,即流场数据的总时间步数;Φ 为POD模态; C为代表测量位置矩阵;p_i为对流场稀疏测量的数据;U 为流场速度.本文以流场数据为例,实现流场建模和监测.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 建模框架总览

Fig.1 Overview of the modeling framework

1.1 特征提取

POD是分析流场和提取流场特征的常见方法^[14].使用POD方法将全场数据 X分解成空间模态ϕ_i和对应的时间系数a_i 的线性组合形式:

X=a₁ϕ₁+a₂ϕ₂+a₃ϕ₃+a₄ϕ₄+…+a_iϕ_i

(1)

POD过程可以利用奇异值分解(SVD)来实现:

$(Φ, \sqrt{δ}, a) = S V D (X)$

(2)

式中: Φ=[φ₁φ₂ … φ_i];δ代表不同空间模态的能量占比;a=[a₁a₂ … a_i]. 可以选取较少的模态实现流场数据的高效重构并去除原数据中的噪声.但是高保真度的流场仿真会产生海量的数据,其流场数据矩阵维度巨大,使用POD会消耗大量的计算机资源.因此本文使用随机奇异值分解(RSVD)的方法来实现大尺度数据矩阵的快速奇异值分解,以及流场主要特征的提取^[15-16].

首先,构建随机投影矩阵 P∈R^p^×^q对数据X 的列向量空间进行采样:

Z=XP

(3)

所得矩阵Z远小于X,且可以近似表示X的列向量空间.因此,可以对矩阵Z进行QR分解来获取矩阵X的一组正交基Q_Z:

Z=Q_ZR_Z

(4)

利用低秩的Q_Z,将X投影到一个更小的空间上:

$Y = Q_{Z}^{T} X$

(5)

由于X≈Q_ZY,可以对Y进行奇异值分解:

$Y = U_{Y} \sum_{Y} V_{Y}^{T}$

(6)

因为Q_Z与X的列向量空间近似,根据SVD的酉变换性质可以得出,X和Y的奇异值分解结果中的Σ和V是相同的.所以,可以得出X的左奇异矩阵:

U_X=QU_Y

(7)

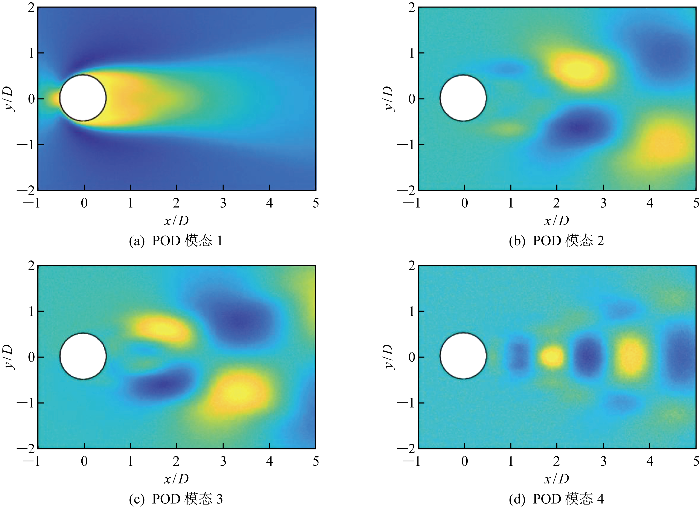
式中:U_X中的列向量即为式(1)中的空间模态ϕ_i.通过选取前r个向量ϕ_i来代表流场的主要特征,得到矩阵Φ_r.

1.2 监测点位置优化选取

合理的传感器位置对于流场的监测极为重要.人工智能和数据驱动技术为从稀疏的传感器数据重构出全场数据提供了有利的支撑.利用得到的全场数据的特征矩阵Φ_r,可以寻找一个优化的传感器位置.QR分解方法提供了一种简单有效的传感器位置优化方式.如果需要选取 s个传感器位置,而s = r, 则QR分解过程可以表示成:

$Φ_{r}^{T} C^{T} = Q R$

(8)

式中:Q为酉矩阵;R为上三角矩阵.由于流场数据仅使用较少模态就可以表征,即 m≫r,需要通过最小化矩阵体积来控制条件数.一般情况下,s≠r, 所以在本文中,使用过采样的模态进行QR分解:

$(Φ_{r} Φ_{r}^{T}) C^{T} = Q R$

(9)

式中:C中每一列不为0的元素的位置即对应传感器在测量节点上的位置.选取矩阵C的前s列得矩阵C_s,则在i时刻传感器的稀疏测量数据p_i为

$p_{i} = C_{s}^{T} x_{i}$

(10)

测量矩阵C代表着测量点的位置信息,在实际应用中可以通过约束矩阵C中非零项的位置来设定传感器测量点的布置区域.

1.3 动态模态分解

DMD是一种建立基于数据的动力学系统模型的有效方法,可以对非线性系统进行线性近似,在本文中可以表示成:

X₁=AX₂

(11)

式中: X₁ = [p₁p₂ … p_n_-1];X₂ = [p₂p₃ … p_n];A 是线性近似矩阵,即Koopman算子,可以实现利用过去和当前时刻的数据对未来的预测.DMD算法的核心在于获得A的低秩形式 $\tilde{A}$ :

$\tilde{A} = U_{X}^{T} A U_{X} = U_{X}^{T} X_{2} V_{X} Σ_{X}^{- 1}$

(12)

式中:U_X,Σ_X,V_X由对X进行SVD降维所得.本文工作中使用离散或稀疏的数据难以实现强非线性系统的线性近似.因此,使用延时嵌入的方法来解决该问题,其将未来的数据嵌入当前的空间观测量中来捕获更多的信息构建线性Koopman算子.延时嵌入的矩阵H₁和H₂可以由X₁和X₂得:

$H_{1} = [\begin{array}{l} x_{1} & x_{2} & \dots & x_{n - n_{d}} \\ x_{2} & x_{3} & \dots & x_{n - n_{d} + 1} \\ ︙ & ︙ & ⋱ & ︙ \\ x_{n_{d}} & x_{n_{d} + 1} & \dots & x_{n - 1} \end{array}] = [\begin{array}{l} h_{1} & h_{2} \dots & h_{n - n_{d}} \end{array}]$

(13)

$H_{2} = [\begin{array}{l} x_{2} & x_{3} & \dots & x_{n - n_{d} + 1} \\ x_{3} & x_{4} & \dots & x_{n - n_{d} + 2} \\ ︙ & ︙ & ⋱ & ︙ \\ x_{n_{d} + 1} & x_{n_{d} + 2} & \dots & x_{n} \end{array}] = [\begin{array}{l} h_{2} & h_{3} & \dots & h_{n - n_{d} + 1} \end{array}]$

(14)

式中: n_d是延时嵌入的时间步数;h_i是研究嵌入后的新快照.所得的H₁和H₂的维度都为n_d×(n-n_d).当n_d =1时,H₁和H₂即为X₁和X₂.因此,H₁和H₂ 之间的线性关系可以写成:

H₂≈BH₁

(15)

式中:B为反应动力学关系的Koopman算子,可以使用式(12)中的标准DMD的方法来求得.利用B就可以实现对未来数据的预测.

2 方法验证

2.1 数据准备

采用格子玻尔兹曼方法模拟了圆柱绕流的流场,雷诺数Re设置为100.采用了一组圆柱绕流的速度场数据来进行实验测试,圆柱的直径为D,该流场数据的时间间隔Δt=0.02 s,其时间分辨率可以捕捉到准确的动态特性.流场数据选取了一个6D×4D的区域.

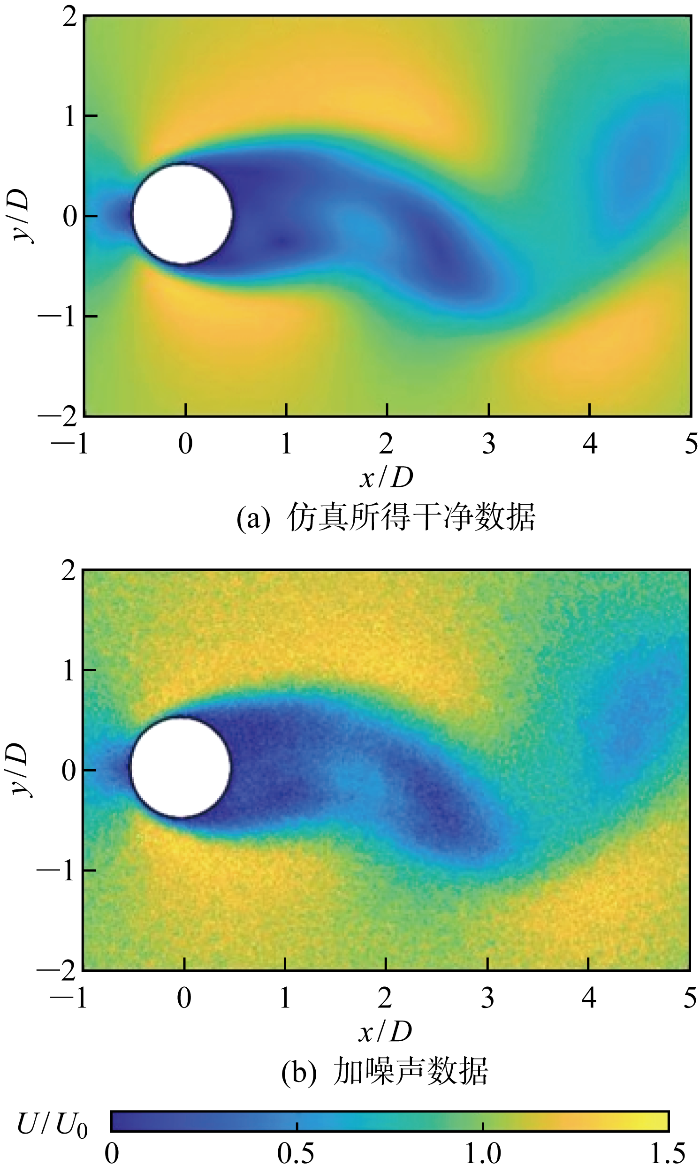
为模拟线下全场采样中可能产生的噪声问题,同时检测本文算法对噪声的鲁棒性,对所得流场速度场加入标准差为流场参数均值10%的高斯噪声,所得无噪声与含噪声速度场如图2所示.图中:x和y代表数据点的位置;U₀为仿真设置的来流速度.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 流场数据

Fig.2 Flow field data

2.2 特征提取结果

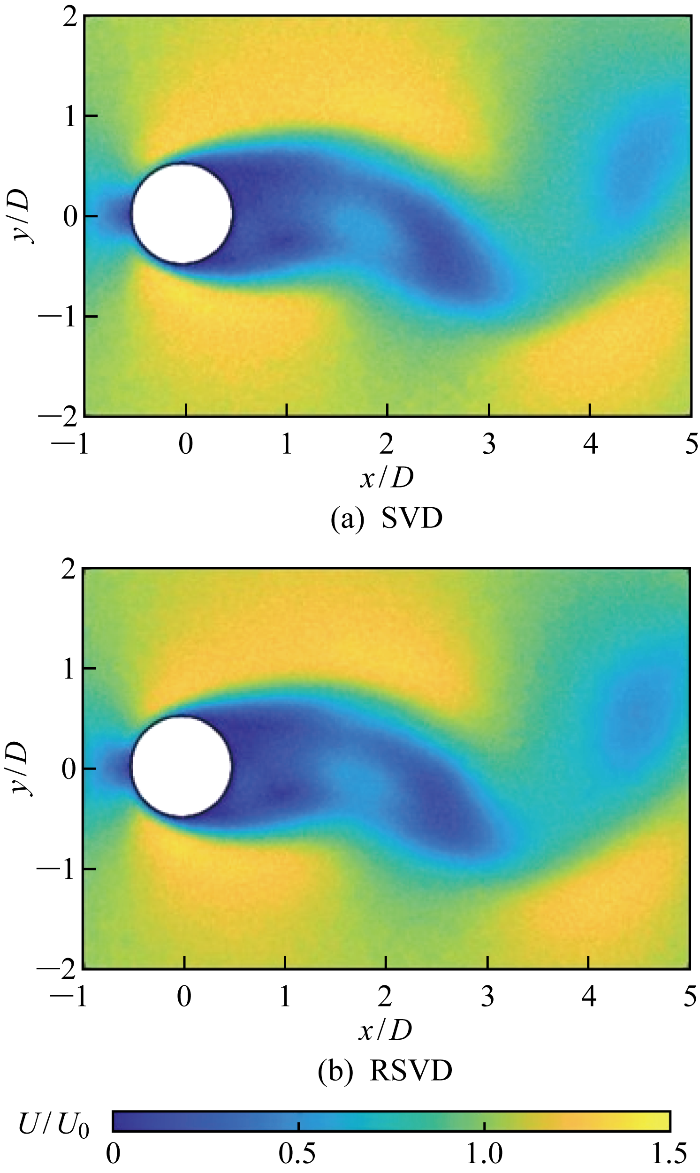
对包含噪声的流场数据分别进行SVD和RSVD分解获取流场主要空间模态.图3展示了采用两种不同分解方法后,使用前10阶模态重构的流场.为量化流场的重构效果,定义重构误差为

$e_{1} = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} \frac{(x_{i}^{r e} - x_{i}^{t r})^{2}}{(x_{i}^{t r})^{2}}}$

(16)

式中: $x_{i}^{r e}$ 代表i时刻的重构流场; $x_{i}^{t r}$ 代表i 时刻的真实流场.经与原始数据对比,使用SVD方法的相对误差为0.93%,使用RSVD方法的相对误差为0.94%,两种方法提取流场模态的效果类似.但是,经统计计算时间,发现相比SVD,RSVD只需要使用约20%的计算时间,因此使用RSVD可以大大提升大尺度流场数据模态分解的效率.使用RSVD所得前4阶模态如图4所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 重构流场

Fig.3 Reconstruction of flow field using SVD and RSVD

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 使用RSVD得出的POD前4阶模态

Fig.4 First 4 POD modes obtained by RSVD

2.3 传感器位置优化

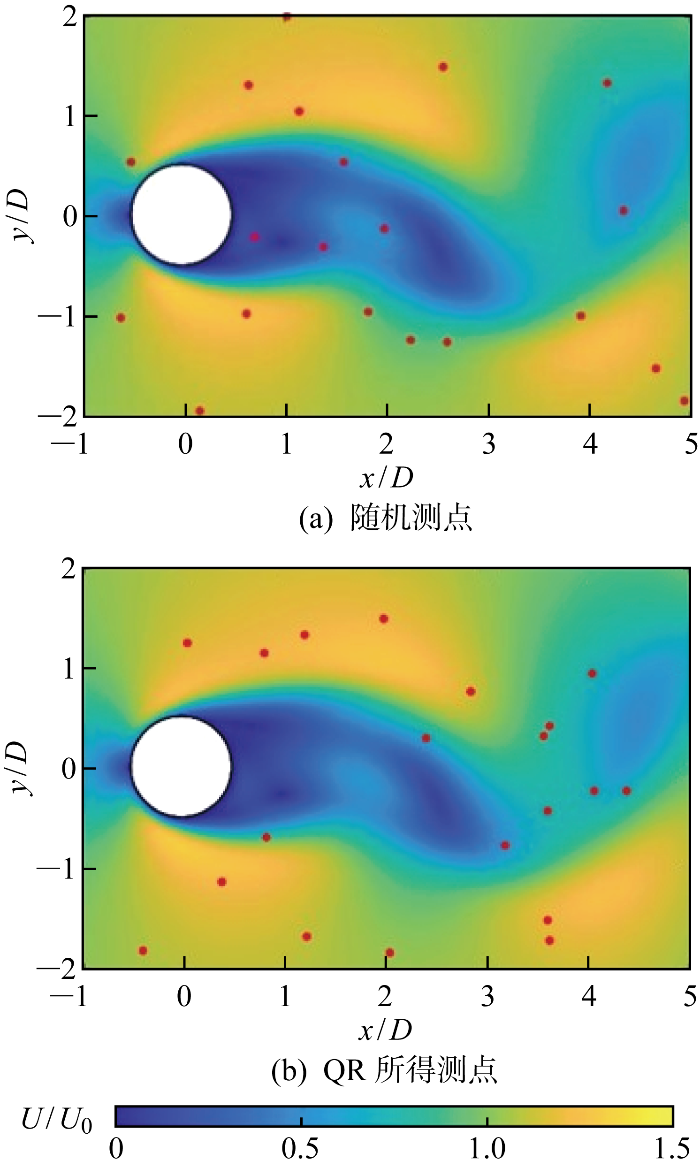
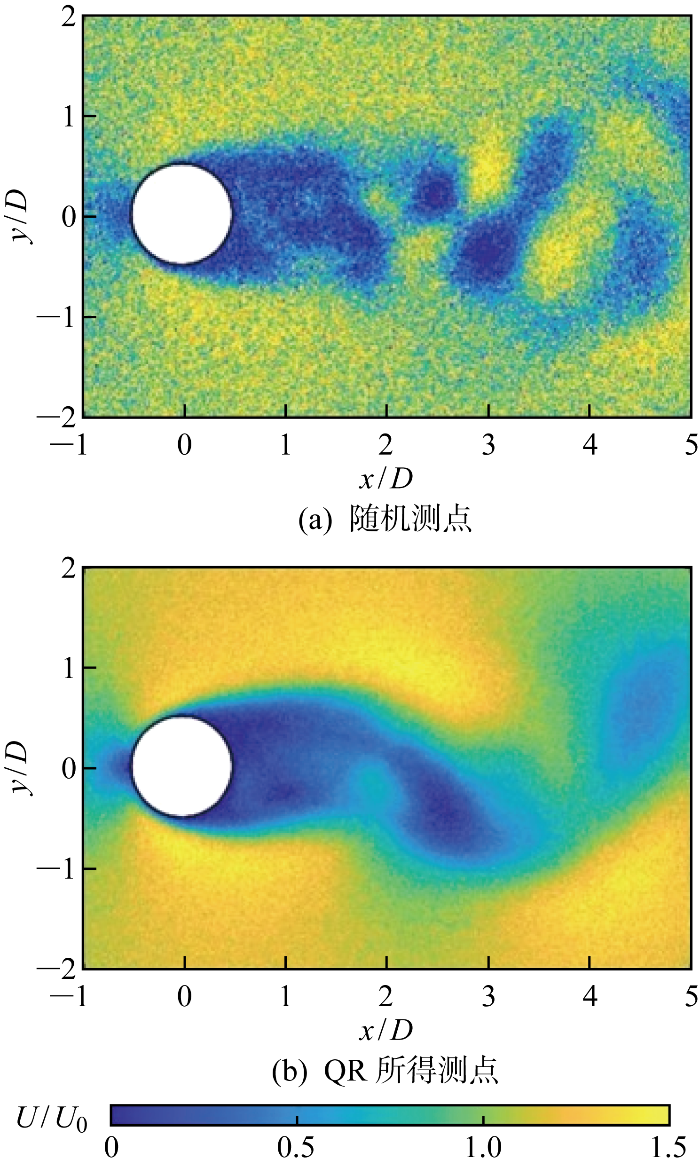
在得到流场数据的空间模态后,即可利用空间模态 Φ_r 进行QR分解.在本文中,使用前20阶模态来获取20个优化传感器的位置.为验证QR分解寻找最优传感器位置方法的有效性,采用相同传感器数量的随机传感器位置分布作为对比,两种传感器位置在流场中的分布如图5所示.将传感器位置的时序数据投影到全场时序数据上,可以得到一组基于传感器数据的基, 利用这组基和每个时刻的传感器数据就可以得到每个时刻全场流场数据.两种传感器分布所得的流场分布如图6所示.可以发现,随机的传感器分布无法得到准确的流场分布,与原始流场数据对比其误差率高达39.91%.而使用QR分解所得的传感器分布,可以较为准确地得到全场流场,其误差率约为4.86%.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 两种传感器在流场中的分布

Fig.5 Two different sensor distributions in flow field

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 两种传感器分布的流场重构效果

Fig.6 Flow field reconstruction with two different sensor distributions

2.4 建模效果

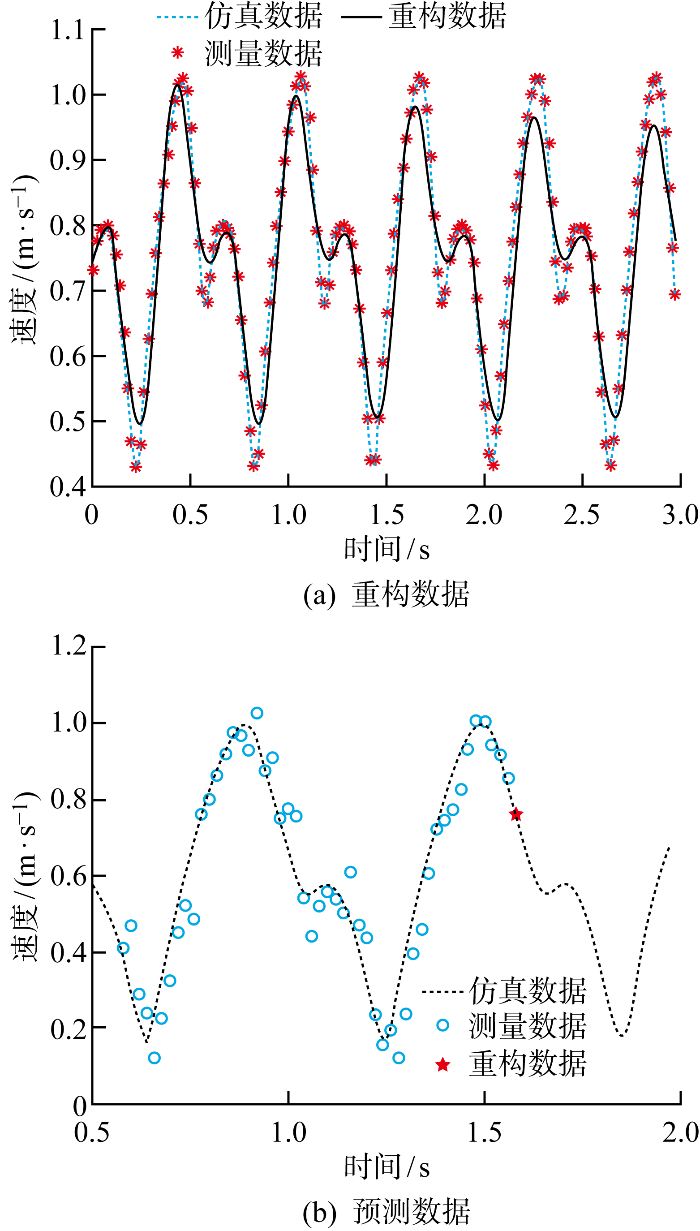
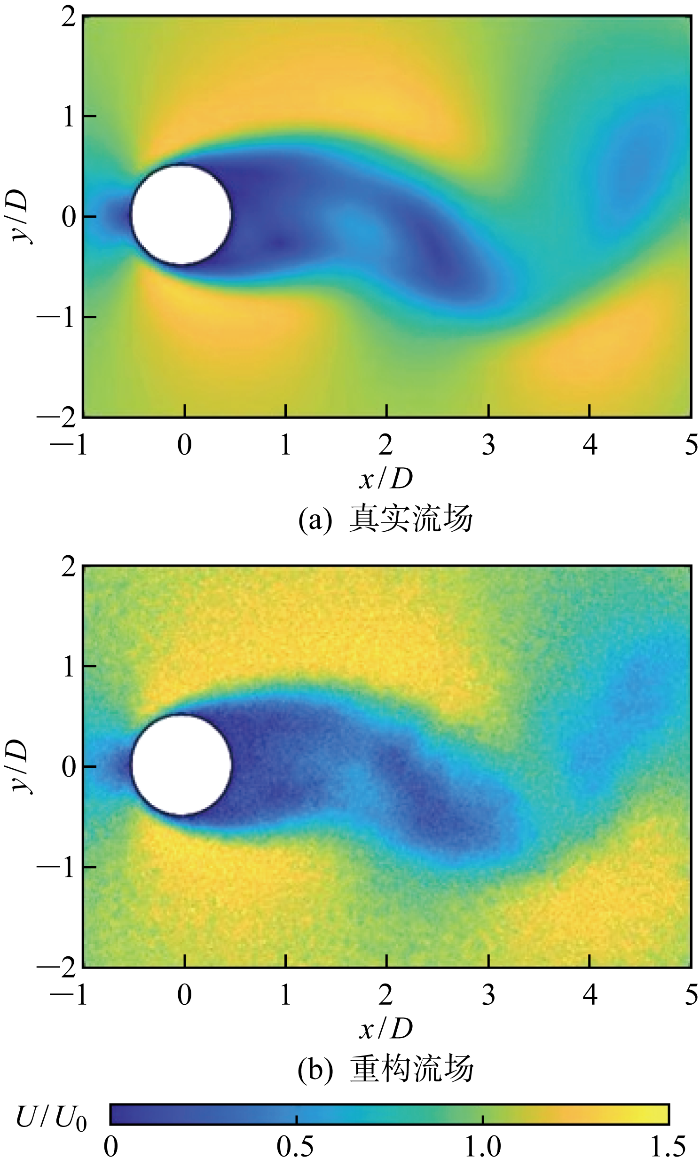
经过上述的实验可以发现,优化的传感器位置处信息可以有效反映全场流场.因此可以使用这些传感器的高时间分辨率的数据建立动力学系统模型,利用稀疏数据实现对全场的监测和预测.首先使用延时嵌入DMD对时间序列建模的效果如图7所示.标准DMD无法准确重构数据时,使用延时嵌入DMD可以更加准确地重构出稀疏数据序列.准确的重构可以得到较为准确的Koopman算子,利用该算子可以使用过去的数据实现对未来数据的预测,其预测效果如果图7(b)所示.在得到未来时刻的稀疏数据后,利用基于稀疏传感器时间序列的基可实现未来时刻全场流场的重构,其重构结果以及仿真中的流场对比如图8所示,可以看到预测效果较好,相对误差约为10.1%.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 延时嵌入DMD的建模和预测效果

Fig.7 Modeling and prediction using time delay embedding DMD

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 预测稀疏数据重构流场

Fig.8 Flow field reconstruction using prediction of sparse data

3 结语

本文提出了一种基于数据驱动的流场数据建模框架,可以实现从有限的稀疏数据实现非线性稀疏数据的建模以及全场流场的预测.用RSVD的方法来进行流场特征的提取在保证有效性的前提下大大节省了计算时间.使用QR分解选取优化传感器位置可以实现从稀疏数据到全场数据的重构,与随机的传感器分布相比,极大提升了重构结果的准确性.在建模过程中使用延时嵌入DMD的方法解决了稀疏非线性数据的准确建模问题,并利用得到的模型对未来时刻的流场进行了较为准确的预测.在实际应用中的流场状态更加复杂多变,需要引入新的方法来提升全场流场预测的准确性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

VOGEL

J M

, KELKAR

A G

Aircraft control augmentation and health monitoring using flush air data system feedback

[C]// AIAA Applied Aerodynamics Conference. Hawaii, USA: AIAA, 2008: 1-16.