基于全局灵敏度分析的综合能源设备响应价值量化方法

doi:10.16183/j.cnki.jsjtu.2023.590

基于全局灵敏度分析的综合能源设备响应价值量化方法

黄逸翔¹, 窦迅¹, 李林溪¹, 杨函煜^,¹, 于建成², 霍现旭³

1.南京工业大学电气工程与控制科学学院,南京 211816

2.国网天津市电力公司电力科学研究院,天津 300384

3.国网天津市电力公司,天津 300010

Quantitative Method of Response Value of Integrated Energy Equipment Based on Global Sensitivity Analysis

HUANG Yixiang¹, DOU Xun¹, LI Linxi¹, YANG Hanyu^,¹, YU Jiancheng², HUO Xianxu³

1. College of Electrical Engineering and Control Science, Nanjing Tech University, Nanjing 211816, China

2. State Grid Tianjin Electric Power Company Electric Power Research Institute, Tianjin 300384, China

3. State Grid Tianjin Electric Power Company, Tianjin 300010, China

通讯作者: 杨函煜,讲师;E-mail:hyang73@outlook.com.

责任编辑: 王历历

收稿日期: 2023-11-20 修回日期: 2024-01-3 接受日期: 2024-01-24

基金资助:

国家电网公司总部科技项目(5108-202218280A-2-244-XG)

Received: 2023-11-20 Revised: 2024-01-3 Accepted: 2024-01-24

作者简介 About authors

黄逸翔(1999—),硕士生,从事综合能源系统研究.

摘要

综合需求响应作为提升能源利用效率,促进可再生清洁能源消纳的有效途径之一,其本质是通过综合能源设备的多能耦合能力引导用户参与源荷双向互动.为提升综合能源系统的运行控制水平,需要准确评估综合能源设备的响应价值.因此,提出一种基于Sobol全局灵敏度分析的综合能源设备响应价值量化方法.首先,以总运行成本最小为目标函数,考虑多类型需求响应,建立综合能源系统泛化优化模型,并构建基于粒子群-反向传播神经网络的综合能源系统优化代理模型.然后,采用Sobol全局灵敏度方法量化设备效率参数对成本、用户满意度、综合能源利用率以及电能替代率的全局灵敏度指标,用于评估综合能源设备的响应价值并且辨识影响系统状态的关键设备.最后,通过对江苏省某商业园区进行仿真,获得各综合能源设备效率的全局灵敏度系数,分析不同设备效率对系统状态的影响,准确量化综合能源设备的响应价值,验证了所提方法的有效性.

关键词： 全局灵敏度分析; 综合需求响应价值; 综合能源设备; 综合能源系统; 粒子群-反向传播神经网络

Abstract

Integrated demand response is an effective strategy for improving energy efficiency and facilitating the integration of renewable clean energy, of which the essence is to guide users into bidirectional interactions between source and load by the multi-energy coupling capabilities of integrated energy devices. Accurately evaluating the response values of integrated energy devices is essential for improving the operational control level of integrated energy systems. Therefore, this paper proposes a method for quantifying the response value of integrated energy devices based on Sobol’s global sensitivity analysis. First, an integrated energy system generalized optimization model is developed with the objective function of minimizing total operating costs while considering multiple types of integrated demand response. A surrogate model for the integrated energy system is conducted based on particle swarm optimization-backpropagation (PSO-BP) neural network. The Sobol’s global sensitivity analysis is then applied to quantify the global sensitivity indices of device efficiency parameters in terms of cost, user satisfaction, integrated energy utilization rate, and electricity substitution rate, which are used to assess the response value of integrated energy devices and identify key devices influencing system states. Finally, simulations based on a commercial park in Jiangsu Province are conducted to determine the global sensitivity coefficients of the efficiency for each integrated energy device. The effect of various device efficiencies on system states is investigated with the response value of integrated energy devices calculated precisely, and the effectiveness of the proposed method is verified.

Keywords： global sensitivity analysis; value of integrated demand response; integrated energy equipment; integrated energy system; particle swarm optimization-backpropagation (PSO-BP) neural network

PDF (2893KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄逸翔, 窦迅, 李林溪, 杨函煜, 于建成, 霍现旭. 基于全局灵敏度分析的综合能源设备响应价值量化方法[J]. 上海交通大学学报, 2025, 59(5): 569-579 doi:10.16183/j.cnki.jsjtu.2023.590

HUANG Yixiang, DOU Xun, LI Linxi, YANG Hanyu, YU Jiancheng, HUO Xianxu. Quantitative Method of Response Value of Integrated Energy Equipment Based on Global Sensitivity Analysis[J]. Journal of Shanghai Jiaotong University, 2025, 59(5): 569-579 doi:10.16183/j.cnki.jsjtu.2023.590

构建新型能源系统,持续推进能源绿色低碳转型是实现“双碳”目标的关键环节.单一、独立的能源系统难以应对当前系统稳定性与能源供需平衡方面的挑战^[1-2],因此区域能源的重心将逐步转为以多能互补互济的综合能源系统(integrated energy system,IES)^[3-4].IES由区域能源管理系统、配电网、热网等多能源网络耦合构成,一方面IES可有效促进风光等可再生源的消纳^[5];另一方面可利用综合需求响应(integrated demand response,IDR)调动供需两侧灵活性资源,合理配置综合能源设备以实现多种能源网络的协同优化与集成运行,进一步提高能源利用效率^[6].

IDR是传统需求响应在IES架构下的延伸与拓展.目前,对于IES与IDR的研究主要侧重于考虑IDR的IES优化调度,通过设定某一目标函数或某具体场景,利用优化模型实现IES的最优能流分配.文献[7]中构建了一个能源供需双侧耦合的园区IES架构,并推导建立了考虑冷、热、电需求耦合响应特性的IDR模型以及园区IDR优化运行模型;文献[8]中提出一种基于价格激励的需求响应不确定性模型,基于能源枢纽模型,构建考虑需求响应的综合社区能源系统能量耦合矩阵,以最小化运行成本为目标进行优化.文献[9]中提出一种计及电、气、热、氢的IDR,引入阶梯式碳排放费用机制,在多时间尺度下对IES运行进行优化.文献[10]中考虑到IES内部不同时间尺度下的分布式资源不确定性,提出一个考虑多种IDR模型的园区级IES多时间尺度博弈优化调度模型.从日前、实时两个角度分别优化调度,引入改进的粒子群优化算法构建数据驱动模型提高优化效率.文献[11]中考虑楼宇结构的特点,计及围护结构传热系数、太阳辐射、遮阳系数等参数,构建包含多能柔性负荷的楼宇IES,兼顾IDR与用户舒适度进行能量优化管理.

IDR依赖综合能源设备的多能耦合与能源转换能力,本质是利用IES中不同能源转换设备的能流分配不同来实现不同能源形式的互换.在实际生产中,不同IES往往包含不同能源转换设备,其IDR潜力也不尽相同,量化设备的响应价值并且识别关键设备可以为综合能源服务商进一步提供决策支撑.尽管目前已有较多文献针对需求响应灵活性资源响应潜力评估开展研究,譬如,文献[12]中认为需求响应潜力对于促进可再生能源消纳和提高电力系统灵活性起到关键作用,该文献通过流程图的方案设计问卷调查,基于电力负荷曲线的定性分析和与当地企业访谈的方法研究需求响应潜力并通过统计的方式量化响应潜力;文献[13]中提出一种快速量化建筑空调系统需求响应潜力的方法,通过构建需求响应潜力的数据驱动模型实现需求响应潜力测算,该文献从系统最大功率削减、平均功率削减、最大功率回弹以及需求响应持续时间几个角度量化需求响应潜力;文献[14]中利用层次分析法和熵权法,利用熵权可拓物元模型建立区域综合能源需求响应评估模型,从多个角度对区域IES的需求响应进行全面评估.文献[15]中考虑当前需求响应评估不够灵活的问题,以聚合商为主体,构建综合考虑静态、动态过程的需求响应评估体系.但上述研究普遍关注灵活性资源响应容量的整体测算,针对IES中各综合能源设备响应价值的量化研究仍处于空白.

针对当前综合能源设备的响应价值缺乏量化方法的问题,提出基于Sobol全局灵敏度分析的综合能源设备需求响应价值量化方法,对综合能源设备的需求响应价值进行量化评估,进而为IES的规划运行提供指导与决策依据.首先,构建考虑IDR的IES能源枢纽优化运行模型,对模型中设备的关键参数效率、空调制冷效率等参数进行建模;然后,提出基于Sobol法的全局灵敏度分析方法,计算各个设备关键参数对综合能源设备多维价值的全局灵敏度指标,得到综合能源设备关键性参数对目标函数影响的量化结果;最后,以江苏省某商业园区IES为例,验证了该价值量化方法的有效性.

1 IES泛化优化模型

1.1 目标函数

泛化模型的优化目标通常为IES总运行成本最小、碳排放量最小、综合能源利用率最高、风光消纳率最高等的一种或多种的组合,如下式所示:

(1)

O = \{\begin{array}{l} m i n f_{I E S} \\ m i n f_{C O_{2}} \\ m a x η_{I E S} \\ m a x ν_{I E S} \end{array}

式中:O为目标函数;f_IES、 $f_{C O_{2}}$ 、η_IES、ν_IES分别为总运行成本、碳排放量、综合能源利用率、风光消纳率.

1.2 约束条件

(1) 电、冷、热负荷可削减和平移需求响应约束.考虑把可时移电负荷与可中断电负荷作为调控手段参与需求响应^[16],表示为

(2)

P_{t, i}^{L *} = {P^{L}}_{t, i} + P_{t, i}^{m o v e} - P_{t, i}^{c u t} + Δ L_{i, A L}^{t}, i \in {e, c, h}

式中:{e,c,h}表示能量种类集合,分别为电能、冷能、热能; ${P^{L}}_{t, i}$ 、 $P_{t, i}^{L *}$ 分别为第i种能源形式负荷在t时刻计及需求响应前后的负荷总量; $P_{t, i}^{m o v e}$ 、 $P_{t, i}^{c u t}$ 分别为第i种能源形式在t时刻的可时移负荷与可削减负荷; $Δ L_{i, A L}^{t}$ 为第i种能源形式负荷在t 时刻的替代响应量.

可时移负荷是指通过暂时改变用户的能源使用习惯,以减少或推迟能源使用高峰期的负荷.其特点在于用能时间灵活和用能总量恒定,可用如下所示条件表述:

(3)

\sum_{t = 1}^{24} P_{t, i}^{m o v e} = 0, 0 \leq P_{t, i}^{m o v e} \leq P_{t, i}^{m o v e . m a x}, i \in {e, c, h}

式中: $P_{t, i}^{m o v e . m a x}$ 为系统t时刻可时移负荷最大值;设置t时刻最大可时移电负荷为t 时刻电负荷总量的5%,最大可时移气负荷为t时刻气负荷总量的10%,最大可时移热负荷为t时刻热负荷总量的10%.

可中断负荷是指在不影响用能侧正常生活、工作的前提下,可进行削减的部分负荷.描述为如下式所示条件:

(4)

0 \leq P_{t, i}^{c u t} \leq P_{t, i}^{c u t . m a x}

式中: $P_{t, i}^{c u t . m a x}$ 为系统t时刻可中断负荷最大值,设置t时刻最大可中断负荷为t 时刻负荷总量5%.

(2) 替代型需求响应.综合考虑电、冷相互替代以及电、热相互替代,用户可根据能源间的价格相对关系选择满足其同等用能质量需求的能源种类.在构建多能源替代型需求响应数学模型时,需考虑能源间的替代方向.设置以下替代方向为正方向:电负荷被冷、热负荷替代.此外,能源间有效热值转化系数以被替代能源为基准.替代型需求响应数学模型如下:

(5)

\begin{array}{l} Δ L_{e, A L}^{t} = - θ_{e c} Δ L_{e c}^{t} - θ_{e h} Δ L_{e h}^{t} \\ Δ L_{c, A L}^{t} = θ_{e c} μ_{e c} Δ L_{e c}^{t} \\ Δ L_{h, A L}^{t} = θ_{e h} μ_{e h} Δ L_{e h}^{t} \\ 0 \leq Δ L_{i j}^{t} \leq Δ L_{i j}^{t, m a x}, Δ L_{i j}^{t} > 0 \\ 0 \leq | μ_{i j} Δ L_{i j}^{t} | \leq Δ L_{i j}^{t, m a x'}, Δ L_{i j}^{t} < 0 \\ 0 \leq |Δ L_{i, A L}^{t} | \leq Δ L_{i, A L}^{t, m a x} \end{array}\}

式中: $i, j \in {e, c, h}, i \neq j; Δ L_{i, A L}^{t, m a x}$ 为t时刻替代型需求响应后负荷总变化量上限; $Δ L_{e c}^{t}$ 、 $Δ L_{e h}^{t}$ 为t 时刻两能源间负荷替代量,其值为正时,代表前一能源被后一能源替代,反之代表后一能源被前一能源替代;θ_ec、θ_eh代表两能源间的替代状态,当负荷替代方向为正时,取1,否则取 -1;μ_ec、μ_eh为能源间有效热值转化系数,分别取3.2、2.8; $Δ L_{i j}^{t, m a x}$ 、 $Δ L_{i j}^{t, m a x'}$ 分别为负荷被替代量上限和替代量上限.

此外,参与IDR的负荷总量应处于一定区间内:

(6)

L_{i, I D R}^{t, m i n} \leq L_{i, I D R}^{t} \leq L_{i, I D R}^{t, m a x}, i \in {e, c, h}

式中: $L_{i, I D R}^{t} = {P_{t}^{L *}, V_{t}^{L *}, H_{t}^{L *}}$ 为t时刻计及IDR后的负荷量, $P_{t}^{L *}$ 、 $V_{t}^{L *}$ 、 $H_{t}^{L *}$ 分别为计及IDR后的电、冷、热负荷量; $L_{i, I D R}^{t, m a x}$ 、 $L_{i, I D R}^{t, m i n}$ 分别为计及IDR后负荷量上下限;电、冷负荷区间取 $[0.6 {P^{L}}_{t}, 1.4 {P^{L}}_{t}]$ 、 $[0.6 {V^{L}}_{t}, 1.4 {V^{L}}_{t}]$ ,热负荷区间取 $[0.7 {H^{L}}_{t}, 1.3 {H^{L}}_{t}]$ , ${P^{L}}_{t}$ 、 ${V^{L}}_{t}$ 、 ${H^{L}}_{t}$ 分别为计及IDR前的电、冷、热负荷量.

(3) 输入-输出约束.能量枢纽实质上是在描述多能源系统输入到输出的函数关系,由于系统中只存在能源传输、转换和存储等设备,所以可以利用一个耦合矩阵来描述二者之间的关系,记为C,则有

(7)

[\begin{array}{l} L_{1} \\ L_{2} \\ ︙ \\ L_{n} \end{array}] = [\begin{array}{l} c_{11} & c_{12} & \dots & c_{1 m} \\ c_{21} & c_{22} & \dots & c_{2 m} \\ ︙ & ︙ & ⋱ & ︙ \\ c_{n 1} & c_{n 2} & \dots & c_{n m} \end{array}] [\begin{array}{l} P_{1} \\ P_{2} \\ ︙ \\ P_{m} \end{array}]

式中: L=[L₁L₂ … L_n]、P=[P₁P₂ … P_m]分别为能源枢纽的输出与输入;c_nm为耦合因子,表示第m种形式能源输出与第n 种形式能源输入的比值.

(4) 其他约束.各能源转换设备均需要满足上下限约束以及爬坡率约束.对于储能装置,其需要满足功率上下限约束和爬坡率约束之外,还需满足容量约束和互斥约束,并且蓄电池还需满足充、放电频率约束,具体如下所示:

(8)

\begin{array}{l} 0 \leq P_{a}^{t} \leq u_{a}^{t} P_{a}^{m a x} \\ P_{a}^{d o w n} \leq P_{a}^{t} - P_{a}^{t - 1} \leq P_{a}^{u p} \end{array}\}

(9)

\begin{array}{l} I_{k, c h r}^{t} P_{k, c h r}^{m i n} \leq P_{k, c h r}^{t} \leq P_{k, c h r}^{m a x} I_{k, c h r}^{t} \\ I_{k, d i s}^{t} P_{k, d i s}^{m i n} \leq P_{k, d i s}^{t} \leq P_{k, d i s}^{m a x} I_{k, d i s}^{t} \\ P_{k, d i s}^{d o w n} \leq P_{k, d i s}^{t} - P_{k, d i s}^{t - 1} \leq P_{k, d i s}^{u p} \\ P_{k, c h r}^{d o w n} \leq P_{k, c h r}^{t} - P_{k, c h r}^{t - 1} \leq P_{k, c h r}^{u p} \\ I_{k, c h r}^{t} + I_{k, d i s}^{t} \leq 1 \\ S_{k}^{m i n} \leq S_{k}^{t} \leq S_{k}^{m a x} \\ S_{k}^{1} = S_{k}^{24} \\ \sum_{t = 1}^{24} (I_{k, c h r}^{t} + I_{k, d i s}^{t}) \leq T \end{array}\}

式中:下标 a表示能源转换设备,k表示储能设备; $P_{a}^{m a x}$ 为能源转换设备a的输出功率上限; $u_{a}^{t}$ 为t时刻能源转换设备的运行状态标志位; $P_{a}^{d o w n}$ 、 $P_{a}^{u p}$ 分别为能源转换设备a输出功率 $P_{a}^{t}$ 的最小、最大爬坡值; $P_{k, c h r}^{t}$ 、 $P_{k, d i s}^{t}$ 分别为t时刻储能设备的充、放能功率; $P_{k, c h r}^{m a x}$ 、 $P_{k, c h r}^{m i n}$ 分别为储能设备k充能功率上下限; $P_{k, d i s}^{m a x}$ 、 $P_{k, d i s}^{m i n}$ 分别为储能设备k放能功率上下限; $S_{k}^{t}$ 为储能设备的容量状态; $S_{k}^{m i n}$ 、 $S_{k}^{m a x}$ 分别为储能设备k的容量最小、最大值; $S_{k}^{1}$ 、 $S_{k}^{24}$ 分别为储能设备k在周期内初始和最终时刻的容量状态; $P_{k, c h r}^{u p}$ 、 $P_{k, c h r}^{d o w n}$ 分别为储能设备k充能爬坡率上下限; $P_{k, d i s}^{u p}$ 、 $P_{k, d i s}^{d o w n}$ 分别为储能设备k的放能爬坡率上下限; $I_{k, c h r}^{t}$ 、 $I_{k, d i s}^{t}$ 分别为储能设备k的充、放功率状态标志位;T 为蓄电池的最大充放电频率次数.

(5) 功率平衡约束

(10)

\sum_{m_{f}}^{M} {P^{g}}_{i, t, m_{f}} = P_{i, t}^{L *}

式中: m_f为设备编号;M为功能设备集合; $\sum_{m_{f}}^{M} {P^{g}}_{i, t, m_{f}}$ 为第i种能源形式t 时刻的供能总量.

2 基于Sobol全局灵敏度分析的综合能源设备需求响应价值量化模型

2.1 效率参数建模

不同多能耦合设备往往具有不同效率,效率参数的差异性意味着设备能源转换的深度不同,进而对IDR产生影响.

现有IES模型中通常对多能设备效率进行简化处理.具体来说,多能耦合设备的能量转换效率以及能量存储设备的能量存储效率被认为是固定值^[17],为了充分衡量设备效率大小对IDR的影响,认为综合能源设备效率取值在一定区间内服从均匀分布^[18]:

(11)

U : = \{\begin{array}{l} u = [η_{1} η_{2} \dots η_{r} η_{r + 1} \dots η_{n}] ∣ \\ η_{r} \in [{\hat{η}}_{r} - Δ η_{r}^{-}, {\hat{η}}_{r} + Δ η_{r}^{+}] \end{array}

式中: u为设备效率向量;η_r为第r种综合能源设备的效率, $[{\hat{η}}_{r} - Δ η_{r}^{-}, {\hat{η}}_{r} + Δ η_{r}^{+}]$ 为其效率分布区间,其中 ${\hat{η}}_{r}$ 为标准工况下该设备的基准效率,Δ $η_{r}^{-}$ 、Δ $η_{r}^{+}$ 分别为基准效率的负偏差量和正偏差量.

2.2 多能设备需求响应价值评价指标定义

2.2.1 用能成本

用能成本指标如下:

(12)C=C_G+C_P+C_IDR

式中:C_G、C_P、C_IDR分别为机组运行成本、与电网交互成本、参与需求响应成本.用能成本是衡量IDR经济性的重要指标.

2.2.2 用户综合满意度

(1) 用户用电方式满意度.当终端用户在不参与IDR时,其用电方式的满意度最高,记作ζ_SEU=1.参与IDR后,由于用电方式改变及新的负荷曲线产生,新的负荷曲线与原本的负荷曲线改变量越大,ζ_SEU数值越低.表示为

(13)

S_{1} = ζ_{S E U} = 1 - \frac{1}{4} \sum_{i \in I} [\sum_{t = 1}^{T} |L_{i, I D R}^{t} - L_{i, 0}^{t}| / \sum_{t = 1}^{T} L_{i, 0}^{t}]

式中: S₁∈[0,1],为用户用电方式满意度; $L_{i, 0}^{t}$ 为第i种能源形式的用户t 时刻参与IDR前的负荷量.

(2) 用户电费支出的满意度.当终端用户参与IDR时,其电费支付的变化情况会影响用户的满意度水平.具体定义方式如下:

(14)

S_{2} = 1 - \frac{1}{2} (\frac{\sum_{t = 1}^{T} Δ {c^{e}}_{t}}{\sum_{t = 1}^{T} {c^{e}}_{t}} + \frac{\sum_{t = 1}^{T} Δ {c^{g}}_{t}}{\sum_{t = 1}^{T} {c^{g}}_{t}})

式中: S₂∈[0,1],为用户电费支出的满意度;Δ ${c^{e}}_{t}$ 、Δ ${c^{g}}_{t}$ 分别为用户用能调整前后每一时段用户支出的电费、气费变化量; ${c^{e}}_{t}$ 、 ${c^{g}}_{t}$ 分别为用户用能调整前每一时段电费支出和气费支出.S₂ 越大表明用户减少的用能费用支出越多,用户用能支出费用满意度水平越高.

(3) 用户综合满意度.用户综合满意度由用电方式满意度及电费支出满意度的加权平均数表示,其测量模型如下:

(15)S=α₁S₁+α₂S₂

(16)α₁+α₂=1

式中: S为用户综合满意度;α₁、α₂分别为S₁、S₂ 的权重系数.

用户对用电方式和电费支出的重视程度不同时,反映到权重系数上会产生不同数值的 α₁、α₂.比如部分居民用户对于电费支出的重视程度要大于用户的用电方式,此时α₂的数值更大;对于一些工序严苛、用电方式可变性小的负荷,其用户对于用电方式的重视程度将更大,此时α₁ 的数值更大.当用户用电方式和支出费用超过用户预期,其满意度水平可能面临下降的风险,进而影响用户下一次参与IDR的积极性,因此综合满意度是评价IDR的重要指标之一.

2.2.3 综合能源利用率

综合能源利用率是指系统产出的能量总和与系统非可再生能源消耗量的比值,又称能源利用率或者综合能效.由于区域IES输入输出多为异质能源,所以为考虑不同能源的差异和能源转换环节的转换效率,利用能源间有效热值转化系数将不同能源折算至同一能级水平.能源间有效热值转化系数反映能源做功的能力,在同一标准环境下,不同能源的能源间有效热值转化系数是一个固定值.表示为

(17)

η_{e x} = \frac{\sum_{i \in Ω_{o u t}} E'_{i, o u t} λ_{i}}{\sum_{i \in Ω_{i n}} E_{i, i n} λ_{i}} = \frac{\sum_{t}^{T} \sum_{i \in {e, h, c}} (P_{t, i}^{b a s e} λ_{i} + μ_{t, i} P_{t, i}^{I D R} λ_{i})}{\sum_{t}^{T} (P_{e, t}^{n e t} λ_{e} + P_{g, t}^{n e t} λ_{g})}

式中: η_ex为综合能源利用率;Ω_out、Ω_in分别为输出、输入能源种类;E'_i_,out、E_i_,in分别为输出、输入的能量总量;λ_i为第i种能源形式量的转化系数; $P_{t, i}^{b a s e}$ 为t时刻园区基础负荷量;μ_t_,_i为IDR参与状态; $P_{t, i}^{I D R}$ 为第i种负荷在t时刻的IDR参与功率;λ_e、λ_g分别为电、气利用效率; $P_{e, t}^{n e t}$ 、 $P_{g, t}^{n e t}$ 分别为电、气输入至网络的功率.

2.2.4 电能替代率

电能替代是指能源消费端更多使用电能满足负荷需求而非其他化石能源,最终反映在终端的电能替代率上.IES中包含灵活的多能耦合设备,考虑IDR并对系统进行优化调度可以显著提升系统的电能替代水平.因此,选取电能替代率作为考察综合能源设备响应价值的指标之一:

(18)

η_{e s r} = \frac{\sum_{t}^{T} P_{e, t}^{n e t}}{\sum_{t}^{T} (P_{t, e}^{b a s e} + μ_{t, e} P_{t, e}^{I D R})}

式中:η_esr为IES电能替代率;μ_t_,e为t时刻IDR参与状态; $P_{t, e}^{I D R}$ 为在t时刻的IDR参与电功率; $P_{t, e}^{b a s e}$ 为t 时刻园区基础电负荷.

2.3 基于PSO-BP的Sobol全局灵敏度分析方法

基于前述IES优化模型及设备响应价值指标,将设备的效率参数作为系统的输入,将经过优化得到的设备响应价值指标作为系统的输出.Sobol全局灵敏度分析方法通过将系统输出的总方差分解为单个系统输入的方差和多个输入之间的方差,来计算综合能源设备效率参数对于响应价值指标的一阶全局灵敏度系数(first-order global sensitivity coefficient,FSC)和总全局灵敏度系数(total global sensitivity coefficient,TSC)^[19].通常上述系数需要借助基于蒙特卡罗模拟的数值积分获得,具体的表达式如下:

(19)

S_{i} = \frac{1}{\hat{V}} [\frac{1}{N_{m c}} \sum_{j = 1}^{N_{m c}} (f (x^{(j)}) f (x_{i}^{(j)}, x_{~ i}^{(j)})) - {\hat{f}}_{0}^{2}]

(20)

S_{T i} = 1 - \frac{1}{\hat{V}} \times [\frac{1}{N_{m c}} \sum_{j = 1}^{N_{m c}} (f (x^{(j)}) f (x_{i}^{' (j)}, x_{~ i}^{' (j)})) - {\hat{f}}_{0}^{2}]

式中: S_i、S_T_i分别为一阶全局灵敏度指标和总体全局灵敏度指标;{x⁽¹⁾, x⁽²⁾, …, $x^{(N_{m c})}$ }和{x^'⁽¹⁾, x^'⁽²⁾, …, $x^{' (N_{m c})}$ }为通过简单随机采样生成的N_mc个独立样本集;x_~i表示在向量x中除去元素x_i后得到的子向量;f(·)为输出设备的响应价值指标; ${\hat{f}}_{0}$ 、 $\hat{V}$ 分别为输出的期望和方差的估计值.

Sobol全局灵敏度分析的迭代计算过程中,需要大量输入和输出数据样本.综合能源设备效率参数可以通过在效率分布区间内进行随机采样的方式获得.然而,设备响应价值指标是IES优化模型优化的结果,因此在获取方面存在一定难度.为了解决这一问题,引入粒子群-反向传播(particle swarm optimization-back propagation,PSO-BP)神经网络代理模型来提高全局灵敏度指标的计算效率.

PSO-BP神经网络是以减小损失函数为优化目标,基于粒子群优化算法与反向传播算法训练的一种多层前馈神经网络模型.将BP神经网络各层权重设置为粒子,将神经网络输出的均方误差设置为适应度值,采用PSO算法随机初始化粒子的位置和速度,引入粒子的速度更新公式与位置更新公式并且更新迭代过程中粒子的历史最优位置进而获取群体的历史最优位置^[20].表示为

(21)

v_{q}^{(l + 1)} = ω v_{q}^{(l)} + c_{1} r_{1} (p_{q, p b e s t}^{(l)} - x_{q}^{(l)}) + c_{2} r_{2} (p_{g b e s t}^{(l)} - x_{q}^{(l)})

(22)

x_{q}^{(l + 1)} = x_{q}^{(l)} + v_{q}^{(l + 1)}

式中: $v_{q}^{(l)}$ 为第q个粒子在第l次迭代中的速度; $x_{q}^{(l)}$ 为第q个粒子在第l次迭代中的位置; $p_{q, p b e s t}^{(l)}$ 为粒子q在第l次迭代中个体最优位置; $p_{g b e s t}^{(l)}$ 为粒子群体在l次迭代过程中历史最优位置;ω、c₁、c₂分别为粒子惯性权重、个体学习因子和群体学习因子,用来衡量粒子寻优过程中惯性方向、个体最优方向以及群体最优方向对粒子寻优的影响;r₁、r₂ 为区间[0,1]内的随机数.

3 基于PSO-BP神经网络代理模型的响应价值指标计算流程

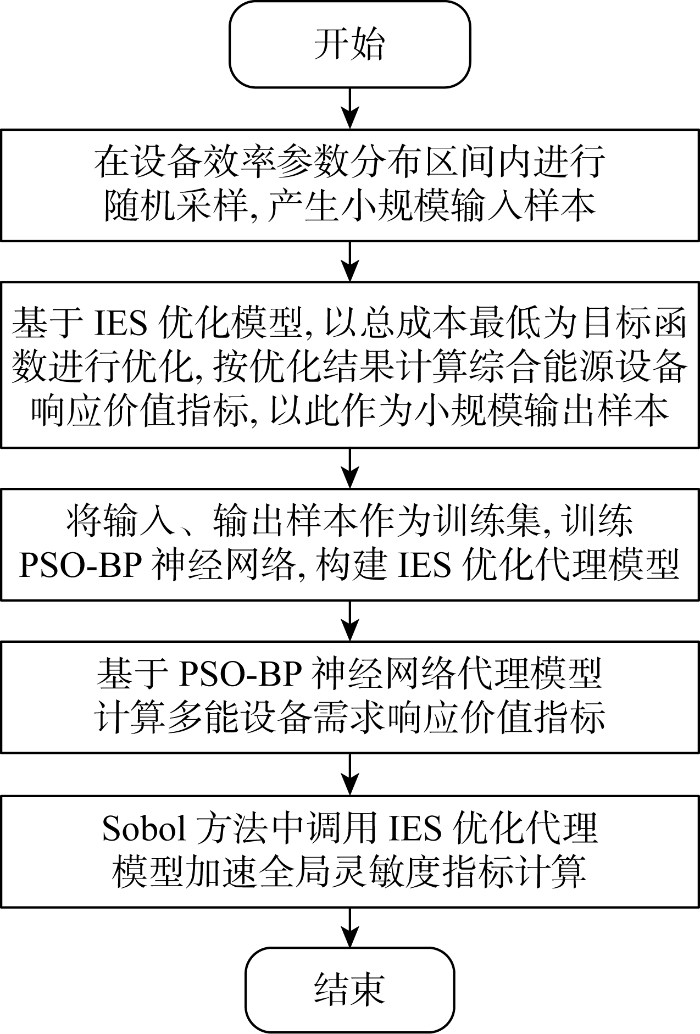
构建上述基于PSO-BP神经网络的IES优化代理模型,表征IES架构中综合能源设备效率与设备响应价值指标间的映射关系.通过代理模型替代初始IES优化模型的优化过程,降低大规模随机取样后指标的计算时间,可以显著提高计算效率.图1为基于PSO-BP神经网络代理模型的响应指标计算流程.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 基于PSO-BP神经网络代理模型的响应指标计算流程示意图

Fig.1 Flow chart of response index calculation process based on PSO-BP neural network surrogate model

4 算例分析

4.1 基础数据

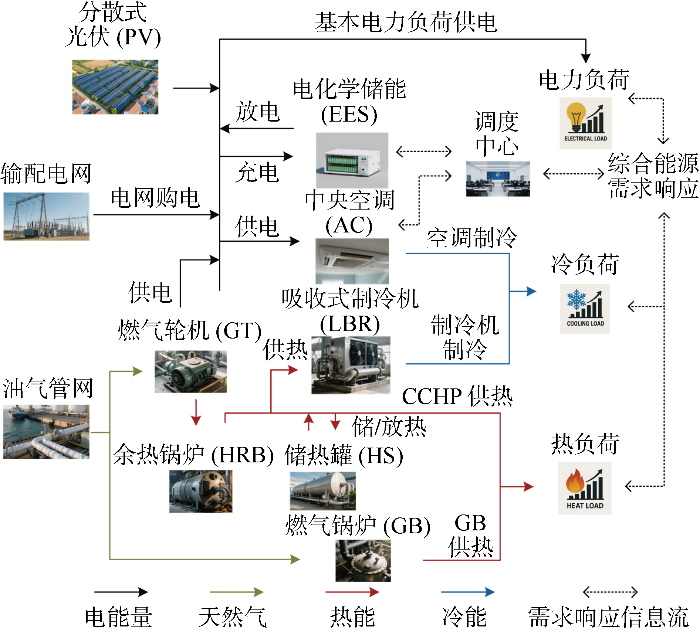
以江苏省某多能商业园区为例,构建如图2所示的IES架构.该园区夏季典型日内部负荷和光伏出力参见文献[16];园区设备具体参数如表1所示,μ_ec、μ_eh分别取3.2、2.8.表中: $P_{m a x}^{G T}$ 、 $H_{m a x}^{G T}$ 、 $H_{m a x}^{G B}$ 分别为燃气轮机(gas turbine,GT)的电功率、热功率和燃气锅炉(gas boiler, GB)的热功率; $P_{m a x}^{c E E S}$ 、 $P_{m a x}^{d E E S}$ 分别为电化学储能(electrochemical energy storage,EES)最大充、放电功率; $H_{m a x}^{c H S}$ 、 $H_{m a x}^{d H S}$ 分别为储热(heat storage,HS)最大蓄、放热功率;[ $E_{m i n}^{b a t t}$ , $E_{m a x}^{b a t t}$ ]和[ $θ_{m i n}^{H S}$ , $θ_{m a x}^{H S}$ ]分别为设备EES、HS存储电量和热量的容量区间; $P_{m a x}^{P G}$ 、 $V_{m a x}^{G a s}$ 分别为IES向电网和气网购能容量上限;Δ $P_{m a x}^{G T}$ 表示燃气轮机出力爬坡上限;η表示设备运行效率,其中LBR表示溴化锂制冷机;η^GTe为燃气轮机发电效率.需求响应相关参数如表2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 IES示意图

Fig.2 Schematic diagram of IES

表1 园区设备参数

Tab.1 Parameters of campus equipment

参数	取值	参数	取值
$P_{m a x}^{G T}$ , $H_{m a x}^{G T}$ , $H_{m a x}^{G B}$ /MW	2,3,4	η^GB	[0.7,0.9]
$P_{m a x}^{c E E S}$ , $P_{m a x}^{d E E S}$ /MW	0.2	η^LBR	[0.8,1]
$H_{m a x}^{c H S}$ , $H_{m a x}^{d H S}$ /MW	0.5	η^AC	[3,4]
[ $E_{m i n}^{b a t t}$ , $E_{m a x}^{b a t t}$ ]/(MW·h)	[0.2,2]	η^HRB	[0.8,1]
[ $θ_{m i n}^{H S}$ , $θ_{m a x}^{H S}$ ]/(MW·h)	[0.5,2]	η^ESS	[0.8,1]
Δ $P_{m a x}^{G T}$ , $P_{m a x}^{P G}$ /MW	0.3,5	η^HS	[0.8,1]
$V_{m a x}^{G a s}$ /m³	500	η^GTe	0.35

新窗口打开| 下载CSV

表2 需求响应相关参数

Tab.2 Parameters related to demand response

负荷种类	$P_{t, i}^{m o v e . m a x}$ /%	$P_{t, i}^{c u t . m a x}$ /%	[ $L_{i, I D R}^{t, m i n}$ , $L_{i, I D R}^{t, m a x}$ ]
电负荷	5	5	[0.6,1.4]
热负荷	10	5	[0.7,1.3]
冷负荷	10	5	[0.6,1.4]

注:表中百分比数值指占响应前的负荷比例.

新窗口打开| 下载CSV

4.2 考虑IDR的IES优化调度结果

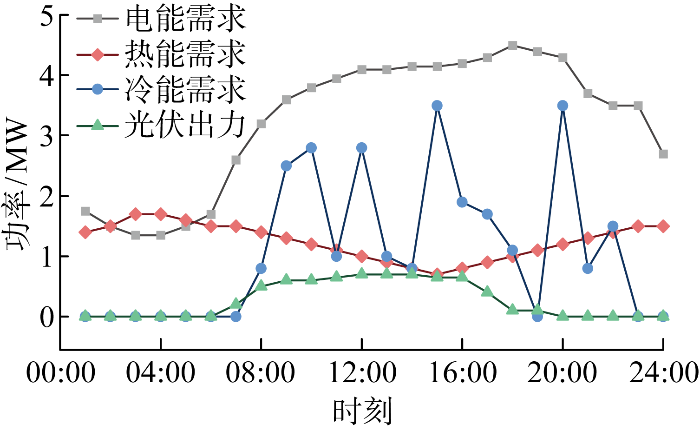
假定综合能源设备在标准工况下运行,具体参数如表3所示.夏季典型日光伏出力、电负荷、热负荷、冷负荷预测如图3所示.

表3 设备标准工况下效率参数

Tab.3 Efficiency parameters of equipment under standard operating conditions

设备效率	取值	设备效率	取值
η^GTe	0.35	η^GB	0.8
η^LBR	0.9	η^AC	3.5
η^HRB	0.9	η^ESS	0.9
η^HS	0.9

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 光伏及各类负荷预测出力

Fig.3 Forecasted output of photovoltaics at different loads

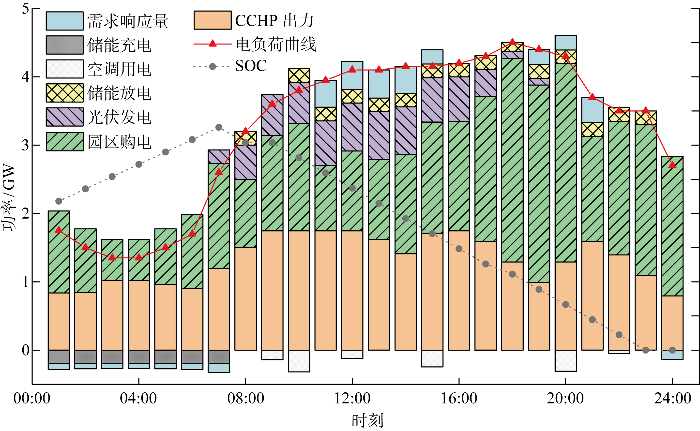
基于通用代数建模系统(general algebraic modeling system,GAMS)用成熟的商业求解器CPLEX求解IES经济优化模型,IES优化结果如图4所示.图中:SOC表示荷电状态;CCHP表示冷热电联产系统.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 电负荷平衡及电储能荷电状态变化

Fig.4 Power load balance and SOC variation curves of electrical energy storage

4.3 考虑综合能源设备效率偏差的全局灵敏度分析

以图2所示园区中的能量转换设备与储能设备即中央空调、溴化锂制冷机、燃气锅炉、储热、电化学储能、余热锅炉的随机效率为输入变量,以日运行成本最小为目标求解模型,分别以成本、用能满意度、用能支出满意度、综合满意度以及综合能源利用效率等指标为输出变量,利用所提基于Sobol法的全局灵敏度分析方法计算各个设备对于上述指标的全局灵敏度指标.为提高全局灵敏度指标的计算效率,所引入PSO-BP模型的输入变量维度为6(AC、LBR、GB、HS、EES、HRB的随机效率),输出变量维度为3(最小日运行成本、用户综合满意度、综合能源利用效率),设置10层隐含层(神经元数目为3),粒子群算法设置种群规模为20,种群更新次数为50次.PSO-BP模型的训练样本集由 1000 组输入-输出样本组成,经过22次迭代训练最终所得模型的均方误差为8.69×10^-7,满足所需精度需求.全局灵敏度指标计算时,采用蒙特卡罗抽样方法对上述3个输出变量进行次数为5万的采样.

通过蒙特卡罗抽样,得到样本容量为5万的6个设备的随机效率输入样本,基于GAMS调用成熟的商业求解器CPLEX求解IES经济优化模型,分析各个输入变量针对不同输出结果的灵敏度.

(1) 最小日运行成本.对于园区运营商而言,如何降低运行成本是其应考虑的首要问题,因此有必要分析各输入变量针对日运行成本的全局灵敏度.设备AC、LBR、GB、HS、EES以及HRB对最小日运行成本的FSC和TSC的具体数值如表4所示.由表可知,在所选取的6个设备中,园区最小日运行成本受LBR的运行效率影响最大,其次为HRB,然后是AC,受到GB、HS、EES的影响均较小.这是由于在本文所设置的能量枢纽参数条件下,系统冷负荷主要由CCHP系统中的LBR进行供冷,AC辅助供冷,所以园区运行成本对LBR的效率变化最为敏感.其次,HRB作为CCHP中重要的余热回收装置,其回收效率不仅对热能供应产生直接影响,也可通过LBR对冷能供应产生间接影响,因此其对于园区运行成本的贡献度也较高.接着,AC作为直接供冷设备之一,其性能系数(coefficient of performance,COP)将对冷能供应产生直接影响,尽管有LBR参与供冷可实现“多能互补”,但在冷能高峰期仍需AC参与供能,因此AC的COP变化也对成本有一定影响.EES作为园区中唯一的电储能,可通过电力高峰期放电、低谷期充电作为灵活性资源来降低成本,因此对于成本的影响显著.而对于GB而言,在本文所设置IES中,GB的作用属于备用供热源,仅在CCHP供热不足时参与供应热能,因此其对于运行成本的影响较为微弱.作为储能设备,HS受限于自身容量,并且也并非为主要供能设备,同时由于网络中的“多能互补”效应进一步削弱了其对园区运行成本的影响,所以对于园区最小运行成本的影响最小.

表4 输入变量对最小日运行成本的FSC和TSC

Tab.4 Input variables for minimum daily operating costs of FSC and TSC

设备	FSC	TSC
AC	0.1267	0.1215
LBR	0.2975	0.3214
GB	0.0025	0.0027
HS	0.0257	0.0206
EES	0.2695	0.2690
HRB	0.2766	0.2862

新窗口打开| 下载CSV

(2) 用户综合满意度.综合能源设备效率偏差对园区用户综合满意度α₁=0.6、α₂=0.4情形的FSC与TSC如表5所示.由表可知,园区用户综合满意度受到综合能源设备效率影响由大到小分别为HRB、LBR、AC、HS、GB与EES.其中,用户综合满意度主要受到HRB的影响最大,TSC值为0.8684.

表5 输入变量对用户综合满意度的FSC和TSC

Tab.5 Input variables for user overall satisfaction of FSC and TSC

设备	FSC	TSC
AC	0.0561	0.0651
LBR	0.0529	0.0929
GB	0.0037	0.0093
HS	0.0050	0.0223
EES	0.0006	0.0023
HRB	0.8329	0.8684

新窗口打开| 下载CSV

进一步,分别针对α₁=0.8、α₂=0.2和α₁=0.2、α₂=0.8两种情形的用户满意度,各设备效率偏差的FSC如表6所示.对比综合能源设备效率偏差对α₁=0.6、α₂=0.4情况与其他情况的FSC可知,在IES中,不同组成的用户综合满意度受到设备的影响程度不同.HRB作为主要的多能供能机组CCHP的重要组成设备,相较于其他可参与耦合供能的“多能互补”设备,参与供能方式较为单一,无法通过多种供能方式互补改变供应成本,而用户对于能源供应价格较敏感,供能价格的变动会极大地影响用户参与需求响应的满意度,进而影响用户用能支出费用,因此HRB对于综合满意度的影响最大.

表6 输入变量对不同构成的用户综合满意度的TSC

Tab.6 Input variables for user overall satisfaction with different constituents of TSC

设备	α₁=0.8, α₂=0.2	α₁=0.2, α₂=0.8
AC	0.0890	0.0598
LBR	0.1094	0.0765
GB	0.0502	0.0082
HS	0.0390	0.0069
EES	0.0495	0.0022
HRB	0.6238	0.9160

新窗口打开| 下载CSV

(3) 综合能源利用效率.对于该指标,各设备的效率偏差的FSC如表7所示.由表可知,综合能源利用效率主要受到LBR、HRB与AC的影响较大,受到其他设备的效率变化影响较小.LBR、HRB与AC的TSC之和为 0.971 2,而GB、HS、EES的TSC之和仅为 0.074 6,其影响程度相较于前三者可忽略不计.

表7 输入变量对综合能源利用效率的FSC和TSC

Tab.7 Input variables for comprehensive energy utilization efficiency of FSC and TSC

设备	FSC	TSC
AC	0.1893	0.1944
LBR	0.4333	0.4840
GB	0.0124	0.0245
HS	0.0430	0.0452
EES	0.0108	0.0049
HRB	0.2877	0.2928

新窗口打开| 下载CSV

(4) 电能替代率.考虑各设备效率偏差情况下,电能替代率的FSC和TSC如表8所示.由算例结果可知电能替代率主要受到设备HRB的影响,相比于其他设备HRB一方面可以通过余热回收作为热负荷的供能设备,另一方面给LBR提供热量间接影响冷负荷供应.其余热回收效率一定程度上反应CCHP机组的供热、供冷能力,HRB效率下降意味着CCHP机组需要更高的出力水平来满足冷、热负荷,系统的购气水平将上升,用户侧电能替代率明显下降.

表8 输入变量对电能替代率的FSC和TSC

Tab.8 Input variables for electric energy substitution rate of FSC and TSC

设备	FSC	TSC
AC	0.0127	0.0085
LBR	0.0529	0.0468
GB	0.0132	0.0092
HS	0.0149	0.0040
EES	0.0553	0.0447
HRB	0.8988	0.8932

新窗口打开| 下载CSV

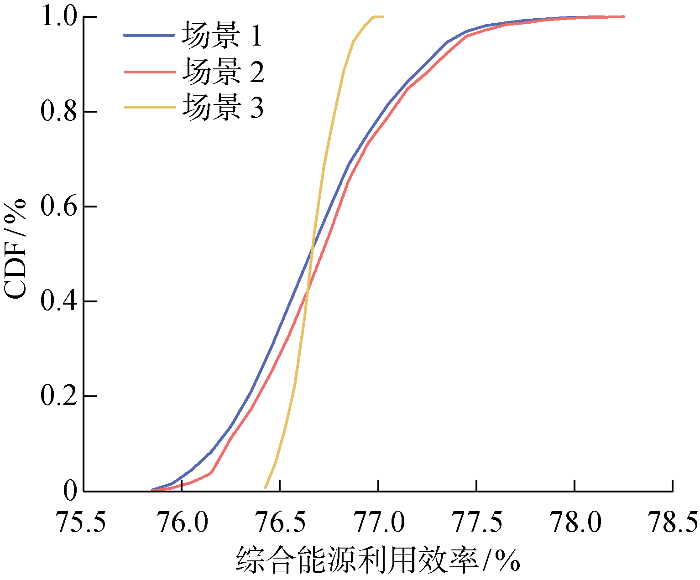
进一步,为验证基于Sobol法的FSC用于辨识系统关键因素的有效性,设置如下3种场景:场景1,6类综合能源设备效率均产生随机偏差;场景2,仅关键设备LBR、HRB与AC产生随机偏差,其余设备分别取其概率分布的均值;场景3,关键设备LBR、HRB与AC取其概率分布的均值,而非关键设备GB、HS、EES产生随机偏差.

通过累积概率分布(cumulative distribution function,CDF)可以体现上述指标取值与其概率之间的映射关系,两个近似系统的CDF曲线也会呈现相似变化趋势.针对以上3种场景,计算综合能源利用效率的累积概率分布如图5所示.由图可知,当仅考虑重要输入变量(场景2)时,其结果与考虑所有随机输入变量(场景1)的CDF基本一致;反之仅考虑不重要的随机输入变量(场景3)时,其CDF与场景1相差很大,且场景1与场景2的综合能源利用效率变化范围远大于场景3.因此,基于Sobol法计算得到的FSC能有效地辨识出影响系统输出变量概率分布的重要输入随机变量.仅考察某一指标时,可以不考虑非关键设备的影响,从而降低IES随机问题的输入变量维度,提高计算效率.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 场景1、2和3的累积概率分布

Fig.5 Cumulative probability distribution in Scenarios 1,2, and 3

4.4 综合能源设备经济价值分析

场景1~3从累积概率分布的角度证明所选取的综合能源设备对综合能源利用效率的影响程度,为更进一步分析选取的综合能源设备多维度价值分析,从系统运行角度,验证各综合能源设备对IES总运行成本的影响程度.

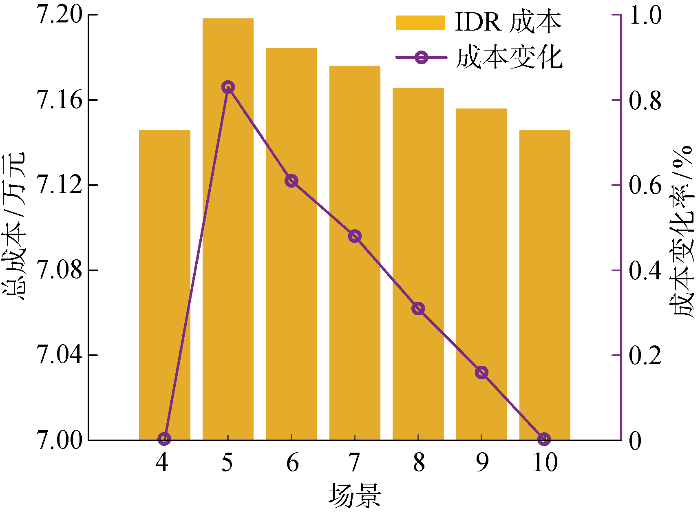
按照设备的参与优化情况设置如下优化场景:场景4,所有设备均以基础效率值参与优化;场景5,仅HRB以最低效率参与优化;场景6,仅LBR以最低效率参与优化;场景7,仅EES以最低效率参与优化;场景8,仅AC以最低效率参与优化;场景9,仅HS以最低效率参与优化;场景10,仅GB以最低效率参与优化.表9给出了上述各个场景的各部分成本组成情况.

表9 各场景成本变化情况

Tab.9 Cost variations in different scenarios

场景	运行成本/元				变化率/%
场景	购电成本	购气成本	IDR成本	总成本	变化率/%
4	42410.38	26148.94	2825.77	71385.09	0
5	41310.18	27827.83	2844.77	71982.79	0.83
6	43064.70	25913.03	2844.77	71822.51	0.61
7	42754.38	26148.94	2825.77	71729.09	0.48
8	42610.02	26148.94	2852.42	71611.38	0.31
9	42480.52	26194.22	2825.77	71500.51	0.16
10	42806.76	25752.60	2825.77	71385.14	0

新窗口打开| 下载CSV

图6进一步给出各场景成本变化率.由图可知,场景5~10的系统总运行成本呈下降趋势,且场景5与场景6的总成本上升最高,符合表4结果,其他场景大体按照输入变量对最小日运行成本的FSC大小排序情况,证明了4.3节中各设备对于成本的影响程度排序.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 各场景成本变化率

Fig.6 Change rate of costs in different scenarios

5 结论

针对综合能源设备的响应价值量化评估,计及综合能源设备变工况场景下的效率偏差,提出基于Sobol全局灵敏度分析的综合能源设备需求响应价值量化方法.首先,构建考虑IDR的IES优化运行模型;其次,考虑综合能源设备的变工况运行,对模型中设备的COP进行建模;然后,提出评估输入随机变量影响的全局灵敏度方法,得到综合能源设备关键性参数对综合能源设备价值指标的量化结果以辨识关键的综合能源设备,并应用于江苏省某商业园区,验证了该价值量化方法的有效性.主要结论如下:

(1) 同一设备的价值在不同指标上有所侧重,且对于不同构成的用户综合满意度指标也展现出不同价值,Sobol全局灵敏度系数准确辨识了影响多维度响应价值的关键设备和非关键设备.

(2) 对于待关注的某方面价值,如果某设备的效率偏差的全局灵敏度系数相对较小,则表明该设备的效率偏差对结果的影响近似为0,可以将其效率视作确定性因素,从而降低系统变量维数,简化模型.

(3) 对于全局灵敏度较高的设备,其效率偏差会对系统产生较明显影响,需要对关键设备加强监控管理以增强系统运行的稳定性.

所提PSO-BP的代理模型对全局灵敏度方法的计算效率与准确度有一定提升,未来将研究如何提高代理模型的准确度与效率,并进一步分析全局灵敏度的实际应用.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

辛保安, 陈梅, 赵鹏, 等.

碳中和目标下考虑供电安全约束的我国煤电退减路径研究

[J]. 中国电机工程学报, 2022, 42(19): 6919-6931.

[本文引用: 4]

XIN

Baoan

, CHEN

Mei

, ZHAO

Peng

, et al.

Research on coal power generation reduction path considering power supply adequacy constraints under carbon neutrality target in China

[J]. Proceedings of the CSEE, 2022, 42(19): 6919-6931.

[本文引用: 4]

[2]

司方远, 张宁, 韩英华, 等.

面向多元灵活资源聚合的区域综合能源系统主动调节能力评估与优化: 关键问题与研究架构

[J]. 中国电机工程学报, 2024, 44(6): 2097-2119.