结构损伤识别是结构动力学的反问题,在土木、机械、航空和海洋等诸多领域应用广泛,是一个重要的热点研究课题.结构损伤会导致结构动力特性发生改变,可通过分析动力特性的改变量来确定结构的损伤程度和损伤位置.基于振动的结构损伤识别方法因物理意义明确且在实践中操作简单得到了广泛关注.目前,国内外学者已发展了诸多适用于结构损伤识别的动力指纹,包括模态参数、柔度矩阵、频响函数、传递比函数等.柔度矩阵[1 ] 能提供丰富的结构损伤信息,且对损伤信息敏感,显示出更好的应用前景.
近年来,国内外学者提出了诸多基于柔度矩阵的结构损伤识别方法.Wang等[2 ] 将传统的位移振型替换为对损伤更为敏感的应变振型,提出应变柔度矩阵的概念,用于结构的损伤定位研究;Bernagozzi等[1 ] 提出基于比例柔度矩阵的结构损伤定位方法,解决了环境激励下实际工程结构振型归一化的难题;Khatir等[3 ] 提出适用于复杂结构的柔度损伤定位指标;Wickramasinghe等[4 ] 提出了分量形式的柔度矩阵损伤指标,并应用于悬索桥的损伤识别研究中,研究结果表明,分量形式的柔度矩阵损伤指标在实际工程中对多种不同工况有更好的识别能力.
理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法.
本文提出一种改进的广义柔度矩阵灵敏度损伤识别方法,建立广义柔度矩阵的高阶灵敏度展开式.相较于传统的广义柔度矩阵一阶灵敏度展开式,进一步减小了因矩阵摄动带来的误差,提高了结构损伤识别结果的精度.在求解上述高阶广义柔度矩阵的灵敏度损伤识别方程时,考虑结构损伤识别的物理意义,将损伤识别方程转换为有约束的最优化问题,并采用序列二次规划算法进行求解,得到优化的损伤识别结果,避免了负损伤系数的情况.最后,利用一个空间桁架结构有限元数值模型和7层框架结构试验,检验了所提算法的有效性和优越性.
1 广义柔度矩阵灵敏度方法
简单回顾文献[5 -6 ]中提出的广义柔度矩阵损伤识别方法.考虑一个具有n 个自由度的结构,质量矩阵记为M,维度为n ×n .通常假定结构的损伤仅导致刚度的降低而不会引起质量的改变,损伤前, 结构的刚度矩阵和柔度矩阵分别记为K u F u K d F d d 和u 分别为损伤后和损伤前的状态.损伤前后,结构整体刚度矩阵的改变量为
(1) Δ K = K u - K d
(2) Δ K = ∑ i = 1 n a i K u i
式中: K u i a i ( 0 ≤ a i ≤ 1 )
对式(1)求导可得损伤后的刚度矩阵关于损伤系数的灵敏度:
(3) ∂ K d ∂ a i = - K u i
(4) F d K d = I
(5) ∂ F d ∂ a i K d + F d ∂ K d ∂ a i = 0
将式(3)代入式(5),并右乘F d ,可得柔度矩阵关于损伤系数的一阶灵敏度:
(6) ∂ F d ∂ a i = F d K u i F d
为减小高阶模态对于柔度矩阵的影响,Li等[8 ] 提出了广义柔度矩阵的概念,即
(7) f d = F d ( M F d ) l
式中: f l l = 0 f l = 1 f d = F d M F d .
(8) f d ≈ ∑ i = 1 m 1 λ d i l + 1 φ d i φ d i T
式中: m 为实际测试获得的模态阶数,通常mn ;λ 为频率的平方;φ 是关于质量矩阵归一化的振型.由此可知, f d λ 的l + 1 l l = 1 , l 并不能一直提高损伤识别结果的精度.杨秋伟等[8 ] 的研究表明,随着广义柔度矩阵次数的增加,广义柔度矩阵本身的精度更高,但会导致灵敏度方程组的系数矩阵条件数也显著增大,使得方程组的病态性变得更严重,出现基于高次广义柔度矩阵计算所得的损伤系数的精度反而低于低次广义柔度矩阵的情况.数值算例分析结果也表明,单纯增大广义柔度的阶次,识别结果会先提高后降低.因此,在应用中建议l 取1或2即可,本文取l =1.
(9) Δ f = f d - f u = ∑ i = 1 m 1 λ d i l + 1 φ d i φ d i T - ∑ i = 1 m 1 λ u i l + 1 φ u i φ u i T
式中:Δf 为广义柔度矩阵的改变量.Δf 也可由广义柔度矩阵关于损伤系数的一阶导数进行线性叠加近似表述为
(10) Δ f ≈ ∑ i = 1 n a i ∂ f d ∂ a i | a i = 0
式中:∂ f d ∂ a i
(11) ∂ f d ∂ a i = F d K u i F d M F d + F d M F d K u i F d
整合式(9)~(11)得到基于广义柔度矩阵的结构损伤识别方程为
(12) ∑ i = 1 m 1 λ d i l + 1 φ d i φ d i T - ∑ i = 1 m 1 λ u i l + 1 φ u i φ u i T ≈ ∑ i = 1 n a i ( F u K u i F u M F u + F u M F u K u i F u )
式(12)为线性矩阵方程,可采用矩阵拉直运算[12 ] 求解.
求解得出各个单元的ai ,即可确定结构的损伤位置和损伤程度.
2 改进的广义柔度矩阵灵敏度方法
不考虑测试模态数据误差的情况下,基于广义柔度矩阵的结构损伤识别方法,计算误差主要由模态截断和广义柔度矩阵改变量关于损伤系数的展开式两部分组成.受限于实际振动测量技术,实际结构的模态分析仅能得到部分低阶模态数据,不能完全消除因模态截断产生的误差.因此,减小广义柔度矩阵改变量关于损伤系数展开式的误差,成为提高基于广义柔度矩阵的损伤识别方法精度的潜在途径.
虽然基于广义柔度矩阵的损伤方法与传统的柔度法相比精度更高,但由于广义柔度矩阵改变量关于损伤系数展开式的误差过大,导致其不适用于大损伤的情况.数值分析表明,当结构单元损伤系数大于15%时,识别误差可达20%以上,其根本原因是式(10)展开时仅考虑了线性项,而忽略了高阶项的影响.当式(10)应用于大损伤工况时,会产生更大的误差,进而影响损伤识别结果的精度.为提高基于广义柔度矩阵结构损伤识别方法的精度,进一步推导广义柔度矩阵改变量关于损伤系数的高阶灵敏度项,通过增加灵敏度阶数,减小广义柔度矩阵改变量展开式的误差,进而提高结构损伤识别结果的误差.
(13) ∂ 2 f d ∂ a i 2 = ∂ ( F d K u i F d M F d + F d M F d K u i F d ) ∂ a i = ∂ F d ∂ a i K u i F d M F d + F d K u i ∂ F d ∂ a i M F d + F d K u i F d M ∂ F d ∂ a i + ∂ F d ∂ a i M F d K u i F d + F d M ∂ F d ∂ a i K u i F d + F d M F d K u i ∂ F d ∂ a i
将式(6)代入式(13),可得广义柔度矩阵改变量关于损伤系数的二阶灵敏度系数:
(14) $\begin{array}{l}\frac{\partial^{2} f_{d}}{\partial a_{i}^{2}}=2\left[\left(F_{d} K_{u}^{i}\right)^{2} F_{d} M F_{d}+\right. \\\left.\quad\left(F_{d} K_{u}^{i}\right) F_{d} M F_{d}\left(K_{u}^{i} F_{d}\right)+F_{d} M F_{d}\left(K_{u}^{i} F_{d}\right)^{2}\right]\end{array}$
同理,为求得广义柔度矩阵关于ai 的三阶导数,对式(14)进一步求导并结合式(6)可得:
(15) $\begin{array}{l}\frac{\partial^{3} f_{d}}{\partial a_{i}^{3}}=6\left[\left(F_{d} K_{u}^{i}\right)^{3} F_{d} M F_{d}+\right. \\\left(F_{d} K_{u}^{i}\right)^{2} F_{d} M F_{d}\left(K_{u}^{i} F_{d}\right)+ \\\left.\left(F_{d} K_{u}^{i}\right)^{1} F_{d} M F_{d}\left(K_{u}^{i} F_{d}\right)^{2} F_{d} M F_{d}\left(K_{u}^{i} F_{d}\right)^{3}\right]\end{array}$
(16) ∂ p f d ∂ a i p = p ! ∑ j = 0 p ( F d K u i ) j F d M F d ( K u i F d ) p - j
利用Taylor级数将广义柔度矩阵改变量进行展开,则
(17) Δ f ≈ ∑ i = 1 n a i ∂ f d ∂ a i | a i = 0 + … + 1 p ! ∑ i = 1 n a i p ∂ p f d ∂ a i p | a i = 0
(18) ∑ i = 1 m 1 λ d i l + 1 φ d i φ d i T - ∑ i = 1 m 1 λ u i l + 1 φ u i φ u i T ≈ ∑ i = 1 n ∑ j = 0 1 a i ( F u K u i ) j F u M F u ( K u i F u ) 1 - j + ∑ i = 1 n ∑ j = 0 2 a i 2 ( F u K u i ) j F u M F u ( K u i F u ) 2 - j + … ∑ i = 1 n ∑ j = 0 p a i p ( F u K u i ) j F u M F u ( K u i F u ) p - j
式(18)是无穷级数,实际应用中需选定灵敏度阶数进行截断.当仅考虑1阶灵敏度时,式(18)退化为式(12),即传统的广义柔度损伤识别方法.由于考虑了高阶灵敏度项,式(18)中ai 不再为线性,所以需要采用非线性方程求解方法.
工程结构损伤识别的结果具有明确的物理意义,即a i ( 0 ≤ a i ≤ 1 ) .
(19) m i n J ( a ) = D Δ f - g ( a ) 2 , a i ∈ [ 0 , 1 ]
式中: D 为放大系数,由于柔度矩阵值都很小,通过D 放大目标函数值,避免最优化算法提前停止搜索; Δ f g ( a ) [13 ] 进行求解,可在MATLAB中用fmincon函数实现.SQP是求解约束非线性优化问题的一种极为有效的方法,相较于其他优化算法,最为突出的优点在于其拥有良好的收敛性、高效的计算效率及强大的边界搜索能力.
改进算法在实际工程结构损伤识别的基本流程可归纳为如下步骤:
(1) 对损伤前后的结构进行模态分析,得到低阶模态数据,根据式(9)计算Δf .
(2) 确定损伤识别方程式(18)的灵敏度阶数,形成Δf 的理论表达式.
(3) 将Δf 实测值和理论表达式代入式(19),利用MATLAB的fmincon函数求解各损伤系数.
3 数值模拟
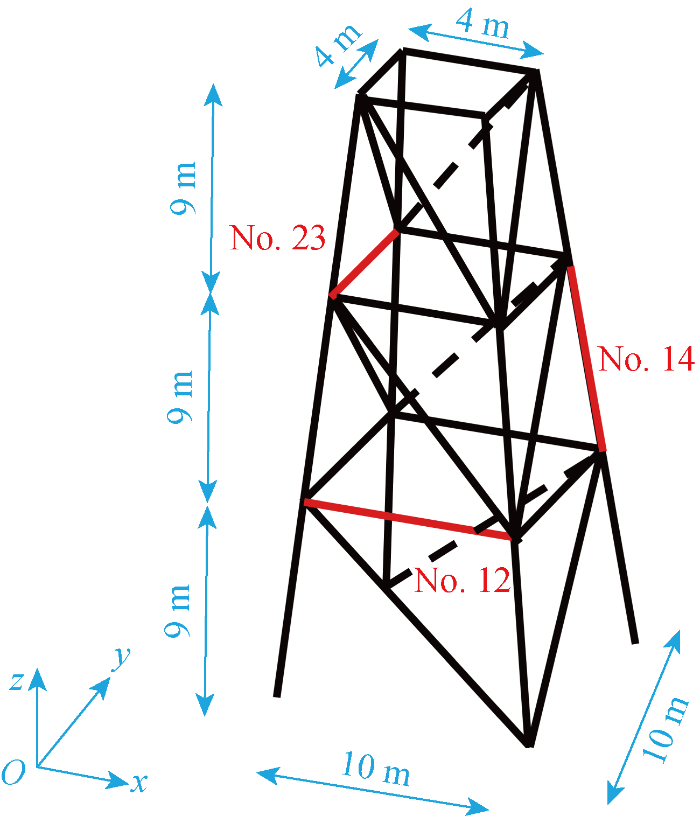
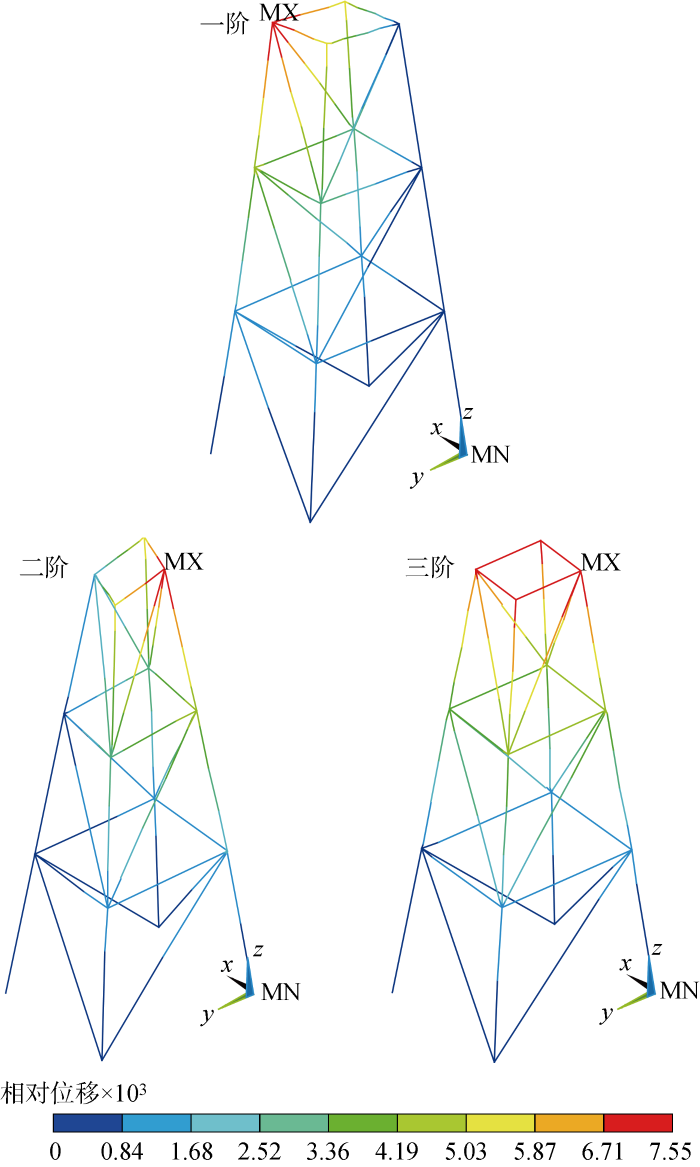
采用一个36杆的空间桁架结构有限元模型验证算法的有效性.模型借鉴了Fathi等[14 ] 数值算例的研究成果.模型基本参数如下:杆件弹性模量E =210 GPa,密度ρ =7 860 kg/m3 ,泊松比ν =0.3,所有杆件截面均为矩形,面积为0.028 m2 .模型几何形式如图1 所示,底部与基础固结.初始的有限元模型在ANSYS 2021R1中建立,杆件采用Link 8单元模拟,并设定为健康状态.提取健康状态有限元模型的质量矩阵M 和单元刚度矩阵K u i K d .通过对损伤前的刚度矩阵K u 求逆矩阵,即可确定损伤前的结构柔度矩阵F u .在获得结构的刚度矩阵和质量矩阵后,通过特征值分解可得到频率和振型.通过ANSYS分析,健康状态的结构振型如图2 所示,图中,MX为最大值,MN为最小值.
图1
图1
空间桁架结构示意图
Fig.1
3D truss structure
图2
图2
健康模型的前3阶振型
Fig.2
The first three modals of intact model
为验证算法的有效性,设置了3种损伤工况.工况D1为单个小损伤情况,工况D2为单个大损伤情况,工况D3为多个单元损伤情况,具体损伤单元如表1 所示.
在MATLAB中分析得到结构的自振频率如表2 所示.由表可知,结构的自振频率非常密集,由损伤引起的频率改变很小.
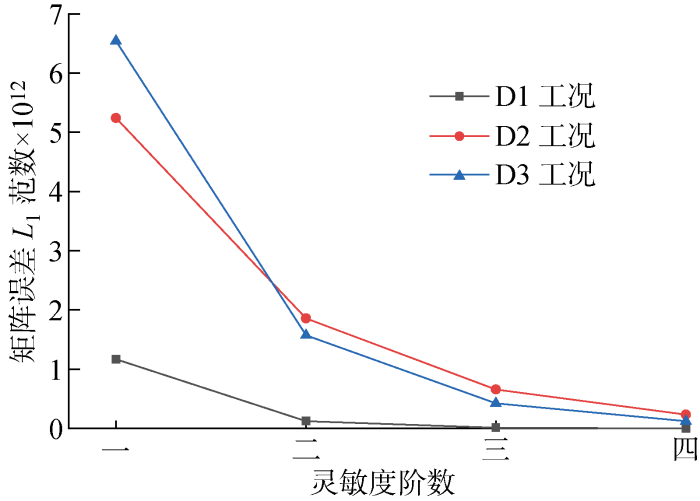
损伤导致的Δf 随灵敏度阶数的变化规律如图3 所示.由图可知,增加灵敏度阶数可显著减小损伤识别方程的截断误差.以工况D3为例,仅采用一阶灵敏度方程即原方法时,产生的截断误差是采用四阶灵敏度方程截断误差的52.6倍. 可见, 采用一阶灵敏度的广义柔度矩阵方法所建立的损伤识别方程本身有巨大的截断误差,加之模态参数不完备,应用于大损伤工况时将产生较大的误差.
图3
图3
广义柔度矩阵改变量随灵敏度阶数的误差规律
Fig.3
Variation of generalized flexibility matrix with respect to sensitivity orders
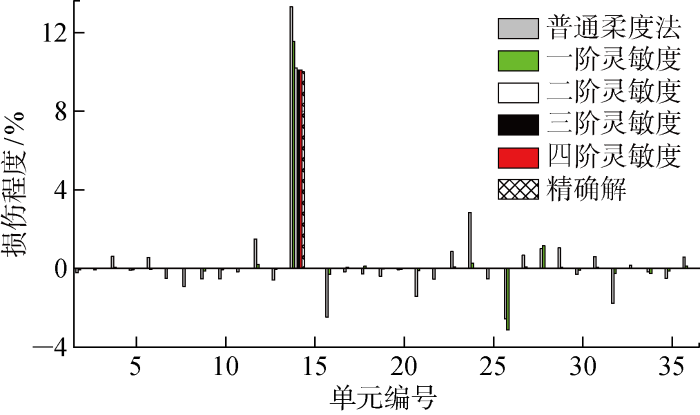
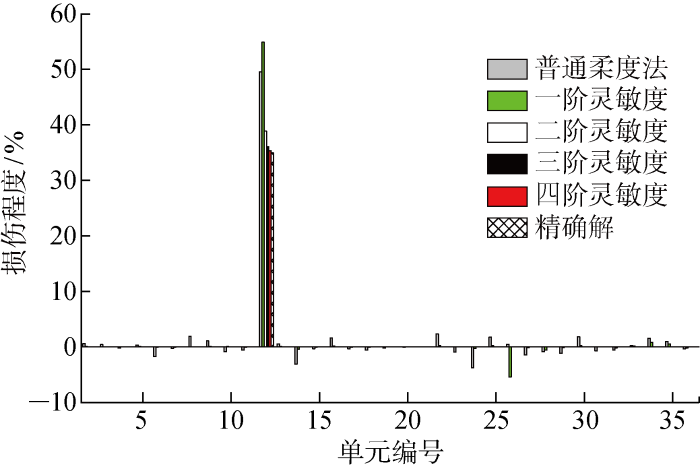
由于结构自振频率密集,采用前5阶理论计算得到的模态参数表述广义柔度矩阵.分别考虑普通柔度法建立的损伤识别方程和前4阶灵敏度建立结构的损伤识别方程,各工况的损伤识别结果如图4 ~6 所示.
图4
图4
数值模拟工况D1损伤识别结果
Fig.4
Damage detection results for D1 in simulation
图5
图5
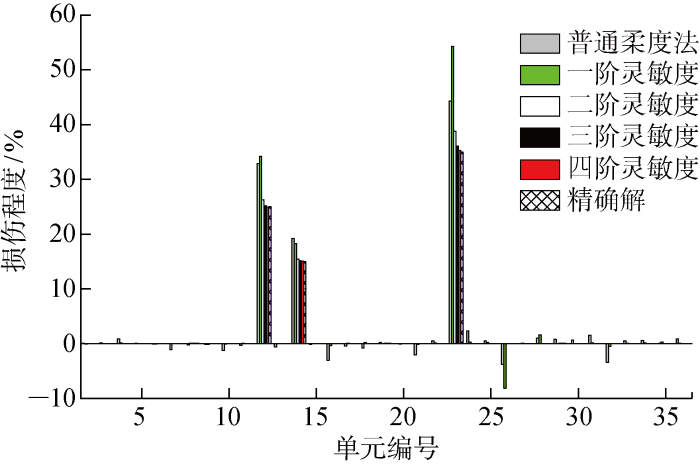
数值模拟工况D2损伤识别结果
Fig.5
Damage detection results for D2 in simulation
图6
图6
数值模拟工况D3损伤识别结果
Fig.6
Damage detection results for D3 in simulation
计算结果表明,采用普通柔度法和广义柔度矩阵一阶灵敏度建立的损伤识别方程,计算结果会出现负损伤系数.普通柔度法相较于广义柔度矩阵一阶灵敏度建立的损伤识别方法,出现负损伤系数的单元更多,但这两者都过高估计了损伤单元的损伤程度,识别精度在不同工况下各有不同.采用一阶灵敏度建立的损伤识别方程是线性矩阵方程,方程的系数矩阵条件数很大,属于病态方程.以工况D1为例,系数矩阵的条件数为418万,因此当方程有微小扰动时,会引起解向量很大的偏差,导致损伤单元与理论损伤有较大误差,未损伤单元出现负值,但这一情况在改进的方法中没有出现.此外,增加灵敏度阶数将显著提高识别结果的精度并伴有渐进收敛于精确值的趋势,其原因是增加损伤识别方程中灵敏度阶数,显著减小了广义柔度矩阵展开式的表述误差.但值得注意的是,模态截断的误差仍在其中,会降低识别精度.以工况D1为例,损伤单元14的识别误差按照一、二、三、四阶随灵敏度阶数的变化,分别为15.49%、1.99%、1.02%、0.93%;工况D2中,损伤单元12的识别误差按照一、二、三、四阶随灵敏度阶数的变化,分别为56.84%、11.05%、3.11%、0.88%.可见,损伤程度增大同时增加了损伤识别结果的误差.因此,针对大损伤工况,需要高阶的灵敏度项以减小损伤识别方程自身的截断误差来提高损伤识别精度.对于多损伤工况D3,其识别结果与单损伤工况有相似的规律.
为检验算法的抗噪性,在理论获取的振型数据中添加噪声[15 ] ,即
(20) φ ~ i j = φ i j ( 1 + r q φ m a x , j / 100 )
式中: φ i j φ ~ i j r 是均值为0、均方差为1的随机数; φ m a x , j j 振型的绝对最大分量;q 为噪声水平,例如q = 3 ,
分别考虑3%、5%、7%的噪声水平.曹晖等[15 ] 的研究表明,当噪声水平为2.64%时,噪声的能量与信号的能量相当.因此,所采取的噪声水平和噪声能量高于信号能量.采用前5阶模态参数,改进算法在各工况中都采用四阶灵敏度损伤识别方程.
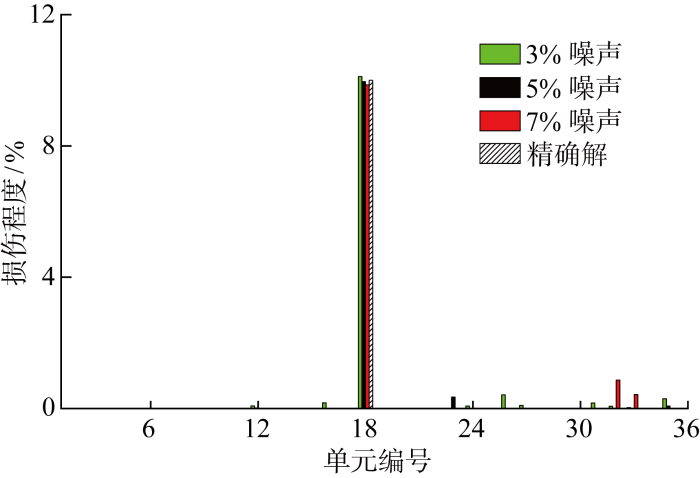
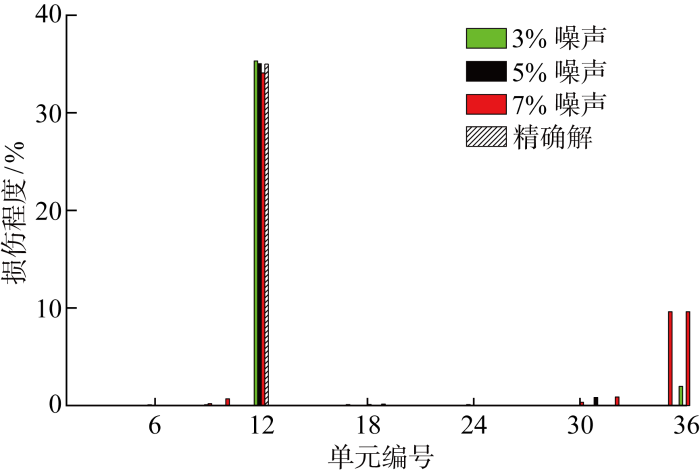
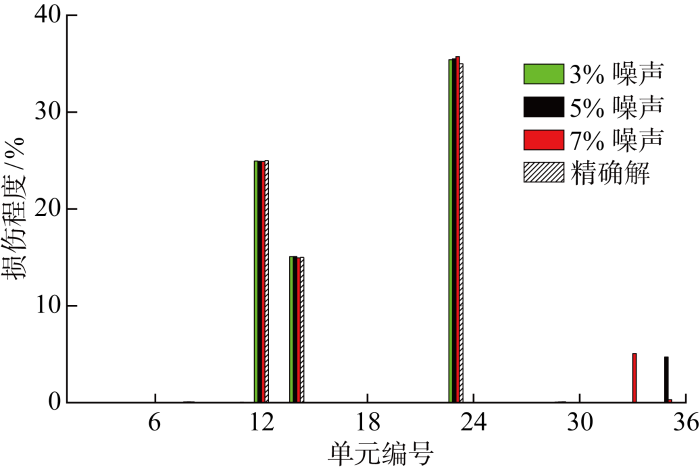
添加噪声后的各工况损伤识别结果如图7 ~9 所示.由图可知,损伤识别结果偏离精确解的趋势随噪声水平增加而增大,且在非损伤单元出现伪损伤的结果.不同工况下,损伤识别结果都为正数.数值模拟结果表明,所提算法具有一定的抗噪声性能.
图7
图7
工况D1噪声影响下的损伤识别结果
Fig.7
Damage detection results for D1 with noise
图8
图8
工况D2噪声影响下的损伤识别结果
Fig.8
Damage detection results for D2 with noise
图9
图9
工况D3噪声影响下的损伤识别结果
Fig.9
Damage detection results for D3 with noise
在MATLAB 2021a平台,CPU为AMD Ryzen 2600@3.4 GHz, 得到采用不同阶灵敏度项的计算效率如表3 所示.由表可知,仅采用一阶灵敏度时,计算时间不会发生显著波动,原因是一阶灵敏度损伤识别方程为线性矩阵方程,且不随工况发生改变.考虑高阶灵敏度时,计算时间随灵敏度项增加而增大,且不同工况间有显著差异.采用高阶灵敏度项的损伤识别方法结合了有约束的最优化求解算法,虽损伤识别过程计算量增大,但计算时间的消耗仍在可接受范围内.
4 试验验证
进一步采用一个7层的框架结构模型试验验证所提方法的有效性.框架结构模型的高×宽×厚尺寸为 1 330 mm×440 mm×40 mm,如图10 所示.模型基础至顶端分别为1~7层,由7根钢梁和14根钢柱组成.每两层的横梁都用螺栓固定在一对柱子上,底层与基础通过刚性的螺栓连接.经测试,各梁和柱的质量分别为3.73和0.22 kg.梁和柱的尺寸分别为300 mm×40 mm×40 mm和150 mm×40 mm×3.5 mm.材料的E =210 GPa,柱和梁的材料性能相同.
图10
图10
框架结构模型试验
Fig.10
Frame structure experiment
为确定柱的侧向刚度,开展了静力试验,如图11 所示.试验中,对横梁施加水平力,利用电子测力计测量水平力的大小,利用千分表测量柱在水平力作用下的位移.结构的损伤通过降低柱的刚度实现,共设置4种不同的损伤程度,如图12 所示.损伤通过在柱的表面刻蚀不同数量和深度的凹槽来实现,忽略柱质量的损失.
图11
图11
柱子抗弯刚度静力试验
Fig.11
Static experiment of the column stiffness
图12
图12
柱的损伤模拟
Fig.12
Simulation of damage
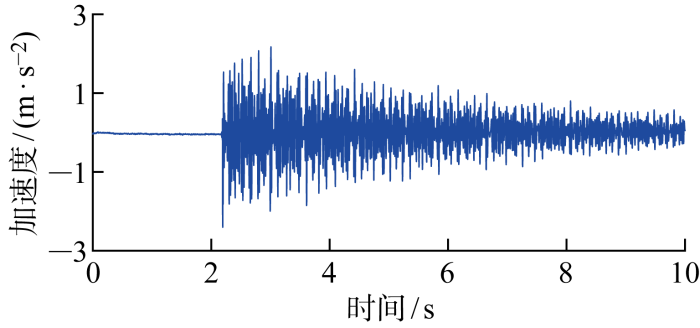
共设置3种结构损伤方案,如表4 所示.各工况通过替换健康的柱为B1~B4实现损伤的模拟.为确定各工况结构的模态参数,采用力锤激励结构在水平方向振动,同时在每一层布置水平方向的加速度传感器记录加速度信号,采样频率为500 Hz.仅考虑结构水平方向的运动自由度,因此结构共7个自由度,对应7阶模态.健康工况下敲击第6层时在第6层测量的加速度时程曲线如图13 所示.
图13
图13
典型的加速度响应时程
Fig.13
Typical acceleration response measured
由于模型的质量主要集中于各层横梁上,均可视为刚性质量块,而柱子提供结构的侧向刚度.因此,采用集中质量模型建立结构的动力分析模型.结构的自由度共7个,呈水平方向运动.
据测量的结构各层加速度响应时程,采用特征系统实现算法[16 ] 识别各工况下结构损伤前后的自振频率和振型,拾取的自振频率如表5 所示.由表5 可知,损伤导致结构的自振频率下降且高阶模态的改变更为明显.进一步采用所提算法识别结构损伤,损伤识别方程采用前4阶灵敏度.考虑到高阶模态参数的识别误差较大,应用中仅考虑前2阶模态数据表述广义柔度矩阵.
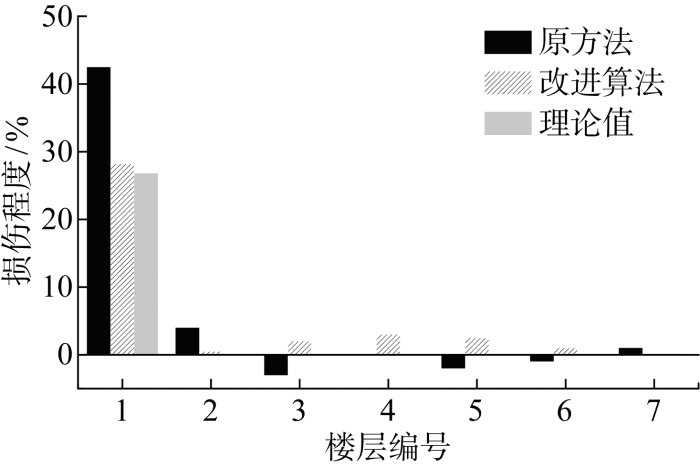
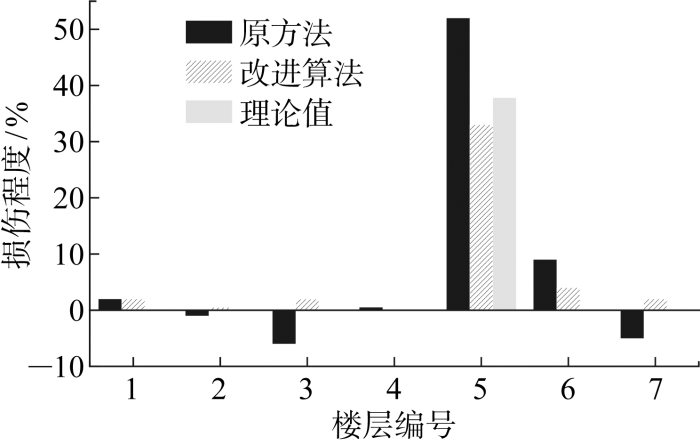
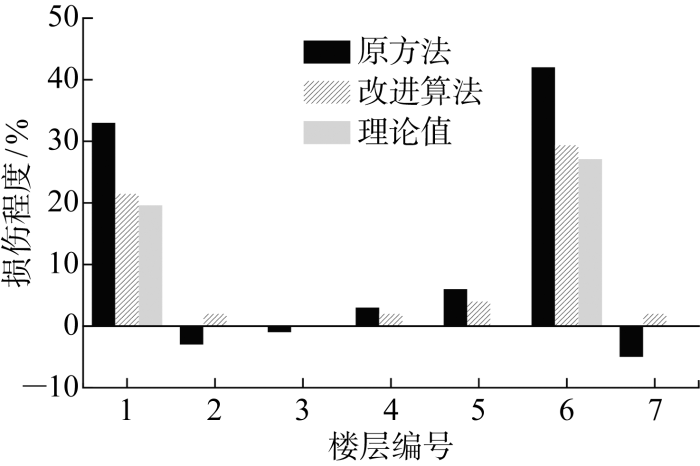
各工况的损伤识别结果如图14 ~16 所示. 由图可知,所提改进算法相较于原方法的识别精度大幅度提高且不会出现负数.以工况D1为例,原方法和所提改进算法识别出第1层的误差分别为56.72%和4.48%,前者是后者的12.66倍,D2和D3有类似的结论.各工况的识别结果都表明,所提算法能准确识别结构损伤位置和损伤程度,与原方法相比识别精度更高,且不会出现负损伤系数.
图14
图14
工况D1损伤识别结果
Fig.14
Damage detection results for D1
图15
图15
试验工况D2损伤识别结果
Fig.15
Damage detection results for D2 in test
图16
图16
试验工况D3损伤识别结果
Fig.16
Damage detection results for D3 in test
5 结论
提出一种改进的广义柔度矩阵灵敏度算法用于工程结构损伤识别.该算法在原有方法基础上增加了高阶灵敏度项,并将损伤识别方程转换为最优化问题求解,提高了损伤识别结果的精度,避免了负损伤系数的情况.通过一个空间桁架结构数值算例和框架结构模型试验对所提算法进行了验证.结论如下:
(1) 算例结果表明,不同工况下,所提改进算法较原有方法所得的损伤识别结果精度更高,且不会出现负损伤系数的情况.
(2) 针对大损伤工况,应至少采用三阶灵敏度的损伤识别方程,以确保损伤识别结果的精度.
(3) 增加损伤识别方程的灵敏度项数会增大求解的计算量,但在可接受的范围内.
(4) 噪声对损伤识别结果有显著的影响,过大的噪声水平会使得识别结果误差增大.
应用所提方法识别结构损伤,需知道其健康状态的质量矩阵和单元刚度矩阵.对于实际工程结构而言,可综合分析其设计资料和实测振动数据,并结合一定的模型修正技术建立对应的力学分析模型,进而得到所需的质量矩阵和单元刚度矩阵.由于所建力学模型与实际工程的差异将影响到损伤识别结果的精度,所以,所提方法更适用于框架结构和几何形式简单的桁架结构,对于复杂的结构形式,所提方法有一定限制.
参考文献
View Option
[1]
BERNAGOZZI G MUKHOPADHYAY S BETTI R et al Proportional flexibility-based damage detection for buildings in unknown mass scenarios: The case of severely truncated modal spaces
[J]. Engineering Structures 2022 , 259 : 114145 .
[本文引用: 2]
[2]
WANG F LI R XIAO Y et al A strain modal flexibility method to multiple slight damage localization combined with a data fusion technique
[J]. Measurement 2021 , 182 : 109647 .
[本文引用: 1]
[3]
KHATIR S TIACHACHT S LE THANH C et al A new robust flexibility index for structural damage identification and quantification
[J]. Engineering Failure Analysis 2021 , 129 : 105714 .
[本文引用: 1]
[4]
WICKRAMASINGHE W R THAMBIRATNAM D P CHAN T H Damage detection in a suspension bridge using modal flexibility method
[J]. Engineering Failure Analysis 2020 , 107 : 104194 .
[本文引用: 1]
[5]
LI J WU B S ZENG Q et al A generalized flexibility matrix based approach for structural damage detection
[J]. Journal of Sound and Vibration 2010 , 329 (22 ): 4583 -4587 .
[本文引用: 2]
[6]
李晶 , 吴柏生 . 基于广义柔度矩阵的结构损伤识别方法
[J]. 吉林大学学报: 理学版 2009 , 47 (4 ): 737 -739 .
[本文引用: 2]
LI Jing WU Baisheng A structural damage identification method based on generalized flexibility matrix
[J]. Journal of Jilin University (Science Edition) 2009 , 47 (4 ): 737 -739 .
[本文引用: 2]
[7]
赵博 , 徐自力 , 阚选恩 . 拉杆转子界面局部脱开识别的改进广义柔度矩阵法
[J]. 振动工程学报 2017 , 30 (5 ): 724 -729 .
[本文引用: 1]
ZHAO Bo XU Zili KAN Xuanen Method of detection of partial separation of interface in rod-fastened rotors with modified generalized flexible matrix
[J]. Journal of Vibration Engineering 2017 , 30 (5 ): 724 -729 .
[本文引用: 1]
[8]
杨秋伟 , 王学航 , 李翠红 . 基于高次广义柔度灵敏度的结构损伤识别
[J]. 固体力学学报 2019 , 40 (2 ): 157 -168 .
[本文引用: 3]
YANG Qiuwei WANG Xuehang LI Cuihong Structural damage assessment using the high-order generalized flexibility sensitivity method
[J]. Chinese Journal of Solid Mechanics 2019 , 40 (2 ): 157 -168 .
[本文引用: 3]
[9]
周卫东 , 杨秋伟 , 赵卫 . 环境激励下结构损伤识别广义柔度扰动法
[J]. 振动与冲击 2013 , 32 (23 ): 166 -169 .
[本文引用: 1]
ZHOU Weidong YANG Qiuwei ZHAO Wei Damage identification with generalized flexibility perturbation method under ambient excitation
[J]. Journal of Vibration and Shock 2013 , 32 (23 ): 166 -169 .
[本文引用: 1]
[10]
LIU H WU B LI Z The generalized flexibility matrix method for structural damage detection with incomplete mode shape data
[J]. Inverse Problems in Science and Engineering 2021 , 29 (12 ): 2019 -39 .
[本文引用: 1]
[11]
MASOUMI M JAMSHIDI E BAMDAD M Application of generalized flexibility matrix in damage identification using Imperialist Competitive Algorithm
[J]. KSCE Journal of Civil Engineering 2015 , 19 (4 ): 994 -1001 .
[本文引用: 1]
[12]
杨秋伟 , 孙斌祥 . 结构损伤识别的改进柔度灵敏度方法研究
[J]. 振动与冲击 2011 , 30 (5 ): 27 -31 .
[本文引用: 1]
YANG Qiuwei SUN Binxiang An improved flexibility sensitivity method for structural damage detection
[J]. Journal of Vibration and Shock 2013 , 30 (5 ): 27 -31 .
[本文引用: 1]
[13]
马昌凤 . 最优化方法及其Matlab程序设计 [M]. 北京 : 科学出版社 , 2022 .
[本文引用: 1]
MA Changfeng Optimization method and Matlab program [M]. Beijing : Science Press , 2022 .
[本文引用: 1]
[14]
FATHI A ESFANDIARI A FADAVIE M et al Damage detection in an offshore platform using incomplete noisy FRF data by a novel Bayesian model updating method
[J]. Ocean Engineering 2020 , 217 : 108023 .
[本文引用: 1]
[15]
曹晖 , 林秀萍 . 结构损伤识别中噪声的模拟
[J]. 振动与冲击 2010 , 29 (5 ): 106 -109 .
[本文引用: 2]
CAO Hui LIN Xiuping Noise simulation in structural damage identification
[J]. Journal of Vibration and Shock 2010 , 29 (5 ): 106 -109 .
[本文引用: 2]
[16]
洪彧 . 基于振动信号的桥梁结构模态参数识别与模型修正研究 [D]. 成都 : 西南交通大学 , 2019 .
[本文引用: 1]
HONG Yu Research on modal identification and model updating of bridge structure based on dynamic response [D]. Chengdu : Southwest Jiaotong University , 2019 .
[本文引用: 1]
Proportional flexibility-based damage detection for buildings in unknown mass scenarios: The case of severely truncated modal spaces
2
2022
... 结构损伤识别是结构动力学的反问题,在土木、机械、航空和海洋等诸多领域应用广泛,是一个重要的热点研究课题.结构损伤会导致结构动力特性发生改变,可通过分析动力特性的改变量来确定结构的损伤程度和损伤位置.基于振动的结构损伤识别方法因物理意义明确且在实践中操作简单得到了广泛关注.目前,国内外学者已发展了诸多适用于结构损伤识别的动力指纹,包括模态参数、柔度矩阵、频响函数、传递比函数等.柔度矩阵[1 ] 能提供丰富的结构损伤信息,且对损伤信息敏感,显示出更好的应用前景. ...
... 近年来,国内外学者提出了诸多基于柔度矩阵的结构损伤识别方法.Wang等[2 ] 将传统的位移振型替换为对损伤更为敏感的应变振型,提出应变柔度矩阵的概念,用于结构的损伤定位研究;Bernagozzi等[1 ] 提出基于比例柔度矩阵的结构损伤定位方法,解决了环境激励下实际工程结构振型归一化的难题;Khatir等[3 ] 提出适用于复杂结构的柔度损伤定位指标;Wickramasinghe等[4 ] 提出了分量形式的柔度矩阵损伤指标,并应用于悬索桥的损伤识别研究中,研究结果表明,分量形式的柔度矩阵损伤指标在实际工程中对多种不同工况有更好的识别能力. ...
A strain modal flexibility method to multiple slight damage localization combined with a data fusion technique
1
2021
... 近年来,国内外学者提出了诸多基于柔度矩阵的结构损伤识别方法.Wang等[2 ] 将传统的位移振型替换为对损伤更为敏感的应变振型,提出应变柔度矩阵的概念,用于结构的损伤定位研究;Bernagozzi等[1 ] 提出基于比例柔度矩阵的结构损伤定位方法,解决了环境激励下实际工程结构振型归一化的难题;Khatir等[3 ] 提出适用于复杂结构的柔度损伤定位指标;Wickramasinghe等[4 ] 提出了分量形式的柔度矩阵损伤指标,并应用于悬索桥的损伤识别研究中,研究结果表明,分量形式的柔度矩阵损伤指标在实际工程中对多种不同工况有更好的识别能力. ...
A new robust flexibility index for structural damage identification and quantification
1
2021
... 近年来,国内外学者提出了诸多基于柔度矩阵的结构损伤识别方法.Wang等[2 ] 将传统的位移振型替换为对损伤更为敏感的应变振型,提出应变柔度矩阵的概念,用于结构的损伤定位研究;Bernagozzi等[1 ] 提出基于比例柔度矩阵的结构损伤定位方法,解决了环境激励下实际工程结构振型归一化的难题;Khatir等[3 ] 提出适用于复杂结构的柔度损伤定位指标;Wickramasinghe等[4 ] 提出了分量形式的柔度矩阵损伤指标,并应用于悬索桥的损伤识别研究中,研究结果表明,分量形式的柔度矩阵损伤指标在实际工程中对多种不同工况有更好的识别能力. ...
Damage detection in a suspension bridge using modal flexibility method
1
2020
... 近年来,国内外学者提出了诸多基于柔度矩阵的结构损伤识别方法.Wang等[2 ] 将传统的位移振型替换为对损伤更为敏感的应变振型,提出应变柔度矩阵的概念,用于结构的损伤定位研究;Bernagozzi等[1 ] 提出基于比例柔度矩阵的结构损伤定位方法,解决了环境激励下实际工程结构振型归一化的难题;Khatir等[3 ] 提出适用于复杂结构的柔度损伤定位指标;Wickramasinghe等[4 ] 提出了分量形式的柔度矩阵损伤指标,并应用于悬索桥的损伤识别研究中,研究结果表明,分量形式的柔度矩阵损伤指标在实际工程中对多种不同工况有更好的识别能力. ...
A generalized flexibility matrix based approach for structural damage detection
2
2010
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
... 简单回顾文献[5 -6 ]中提出的广义柔度矩阵损伤识别方法.考虑一个具有n 个自由度的结构,质量矩阵记为M,维度为n ×n .通常假定结构的损伤仅导致刚度的降低而不会引起质量的改变,损伤前, 结构的刚度矩阵和柔度矩阵分别记为 K u F u K d F d d 和u 分别为损伤后和损伤前的状态.损伤前后,结构整体刚度矩阵的改变量为 ...
基于广义柔度矩阵的结构损伤识别方法
2
2009
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
... 简单回顾文献[5 -6 ]中提出的广义柔度矩阵损伤识别方法.考虑一个具有n 个自由度的结构,质量矩阵记为M,维度为n ×n .通常假定结构的损伤仅导致刚度的降低而不会引起质量的改变,损伤前, 结构的刚度矩阵和柔度矩阵分别记为 K u F u K d F d d 和u 分别为损伤后和损伤前的状态.损伤前后,结构整体刚度矩阵的改变量为 ...
A structural damage identification method based on generalized flexibility matrix
2
2009
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
... 简单回顾文献[5 -6 ]中提出的广义柔度矩阵损伤识别方法.考虑一个具有n 个自由度的结构,质量矩阵记为M,维度为n ×n .通常假定结构的损伤仅导致刚度的降低而不会引起质量的改变,损伤前, 结构的刚度矩阵和柔度矩阵分别记为 K u F u K d F d d 和u 分别为损伤后和损伤前的状态.损伤前后,结构整体刚度矩阵的改变量为 ...
拉杆转子界面局部脱开识别的改进广义柔度矩阵法
1
2017
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
Method of detection of partial separation of interface in rod-fastened rotors with modified generalized flexible matrix
1
2017
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
基于高次广义柔度灵敏度的结构损伤识别
3
2019
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
... 为减小高阶模态对于柔度矩阵的影响,Li等[8 ] 提出了广义柔度矩阵的概念,即 ...
... 式中: m 为实际测试获得的模态阶数,通常mn ;λ 为频率的平方;φ 是关于质量矩阵归一化的振型.由此可知, f d λ 的 l + 1 l l = 1 , l 并不能一直提高损伤识别结果的精度.杨秋伟等[8 ] 的研究表明,随着广义柔度矩阵次数的增加,广义柔度矩阵本身的精度更高,但会导致灵敏度方程组的系数矩阵条件数也显著增大,使得方程组的病态性变得更严重,出现基于高次广义柔度矩阵计算所得的损伤系数的精度反而低于低次广义柔度矩阵的情况.数值算例分析结果也表明,单纯增大广义柔度的阶次,识别结果会先提高后降低.因此,在应用中建议l 取1或2即可,本文取l =1. ...
Structural damage assessment using the high-order generalized flexibility sensitivity method
3
2019
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
... 为减小高阶模态对于柔度矩阵的影响,Li等[8 ] 提出了广义柔度矩阵的概念,即 ...
... 式中: m 为实际测试获得的模态阶数,通常mn ;λ 为频率的平方;φ 是关于质量矩阵归一化的振型.由此可知, f d λ 的 l + 1 l l = 1 , l 并不能一直提高损伤识别结果的精度.杨秋伟等[8 ] 的研究表明,随着广义柔度矩阵次数的增加,广义柔度矩阵本身的精度更高,但会导致灵敏度方程组的系数矩阵条件数也显著增大,使得方程组的病态性变得更严重,出现基于高次广义柔度矩阵计算所得的损伤系数的精度反而低于低次广义柔度矩阵的情况.数值算例分析结果也表明,单纯增大广义柔度的阶次,识别结果会先提高后降低.因此,在应用中建议l 取1或2即可,本文取l =1. ...
环境激励下结构损伤识别广义柔度扰动法
1
2013
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
Damage identification with generalized flexibility perturbation method under ambient excitation
1
2013
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
The generalized flexibility matrix method for structural damage detection with incomplete mode shape data
1
2021
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
Application of generalized flexibility matrix in damage identification using Imperialist Competitive Algorithm
1
2015
... 理论上,结构的柔度矩阵需由全部模态参数进行表述.然而,高阶模态参数在实际测试中难以准确辨识,传统的柔度矩阵方法仅能利用低阶模态参数进行近似,这一误差必然影响结构损伤识别结果的准确性.为减小模态截断的影响,文献[5 -6 ]中提出了广义柔度矩阵的概念.在广义柔度矩阵中,模态参数的参与度随频率的2n [7 ] 基于振型约束的方式提出改进的广义柔度矩阵结构损伤识别方法,改进后的方法能使用任意单阶模态参数对界面脱开进行识别;杨秋伟等[8 ] 系统分析了广义柔度矩阵的次数与损伤识别精度的关系,研究发现,损伤识别结果精度随广义柔度矩阵次数增加先提高后降低,由此可知,通过简单增加广义柔度矩阵阶数不能有效提高损伤识别结果的精度;周卫东等[9 ] 提出环境激励下的广义柔度矩阵损伤识别方法,解决了环境激励下振型不能归一化的难题;Liu等[10 ] 通过引入新变量并对广义柔度矩阵进行分块计算,考虑了模态振型不完备的影响;Masoumi等[11 ] 将广义柔度矩阵转换为有约束的优化问题,提出了基于最优化算法的损伤识别方法. ...
结构损伤识别的改进柔度灵敏度方法研究
1
2011
... 式(12)为线性矩阵方程,可采用矩阵拉直运算[12 ] 求解. ...
An improved flexibility sensitivity method for structural damage detection
1
2013
... 式(12)为线性矩阵方程,可采用矩阵拉直运算[12 ] 求解. ...
1
2022
... 式中: D 为放大系数,由于柔度矩阵值都很小,通过D 放大目标函数值,避免最优化算法提前停止搜索; Δ f g ( a ) [13 ] 进行求解,可在MATLAB中用fmincon函数实现.SQP是求解约束非线性优化问题的一种极为有效的方法,相较于其他优化算法,最为突出的优点在于其拥有良好的收敛性、高效的计算效率及强大的边界搜索能力. ...
1
2022
... 式中: D 为放大系数,由于柔度矩阵值都很小,通过D 放大目标函数值,避免最优化算法提前停止搜索; Δ f g ( a ) [13 ] 进行求解,可在MATLAB中用fmincon函数实现.SQP是求解约束非线性优化问题的一种极为有效的方法,相较于其他优化算法,最为突出的优点在于其拥有良好的收敛性、高效的计算效率及强大的边界搜索能力. ...
Damage detection in an offshore platform using incomplete noisy FRF data by a novel Bayesian model updating method
1
2020
... 采用一个36杆的空间桁架结构有限元模型验证算法的有效性.模型借鉴了Fathi等[14 ] 数值算例的研究成果.模型基本参数如下:杆件弹性模量E =210 GPa,密度ρ =7 860 kg/m3 ,泊松比ν =0.3,所有杆件截面均为矩形,面积为0.028 m2 .模型几何形式如图1 所示,底部与基础固结.初始的有限元模型在ANSYS 2021R1中建立,杆件采用Link 8单元模拟,并设定为健康状态.提取健康状态有限元模型的质量矩阵M 和单元刚度矩阵 K u i K d .通过对损伤前的刚度矩阵K u 求逆矩阵,即可确定损伤前的结构柔度矩阵F u .在获得结构的刚度矩阵和质量矩阵后,通过特征值分解可得到频率和振型.通过ANSYS分析,健康状态的结构振型如图2 所示,图中,MX为最大值,MN为最小值. ...
结构损伤识别中噪声的模拟
2
2010
... 为检验算法的抗噪性,在理论获取的振型数据中添加噪声[15 ] ,即 ...
... 分别考虑3%、5%、7%的噪声水平.曹晖等[15 ] 的研究表明,当噪声水平为2.64%时,噪声的能量与信号的能量相当.因此,所采取的噪声水平和噪声能量高于信号能量.采用前5阶模态参数,改进算法在各工况中都采用四阶灵敏度损伤识别方程. ...
Noise simulation in structural damage identification
2
2010
... 为检验算法的抗噪性,在理论获取的振型数据中添加噪声[15 ] ,即 ...
... 分别考虑3%、5%、7%的噪声水平.曹晖等[15 ] 的研究表明,当噪声水平为2.64%时,噪声的能量与信号的能量相当.因此,所采取的噪声水平和噪声能量高于信号能量.采用前5阶模态参数,改进算法在各工况中都采用四阶灵敏度损伤识别方程. ...
1
2019
... 据测量的结构各层加速度响应时程,采用特征系统实现算法[16 ] 识别各工况下结构损伤前后的自振频率和振型,拾取的自振频率如表5 所示.由表5 可知,损伤导致结构的自振频率下降且高阶模态的改变更为明显.进一步采用所提算法识别结构损伤,损伤识别方程采用前4阶灵敏度.考虑到高阶模态参数的识别误差较大,应用中仅考虑前2阶模态数据表述广义柔度矩阵. ...
1
2019
... 据测量的结构各层加速度响应时程,采用特征系统实现算法[16 ] 识别各工况下结构损伤前后的自振频率和振型,拾取的自振频率如表5 所示.由表5 可知,损伤导致结构的自振频率下降且高阶模态的改变更为明显.进一步采用所提算法识别结构损伤,损伤识别方程采用前4阶灵敏度.考虑到高阶模态参数的识别误差较大,应用中仅考虑前2阶模态数据表述广义柔度矩阵. ...