多场景多目标动态变化下船舶小组立装焊重调度

doi:10.16183/j.cnki.jsjtu.2023.274

多场景多目标动态变化下船舶小组立装焊重调度

张澳圆^a, 胡小锋^,^a, 张亚辉^b

上海交通大学 a. 机械与动力工程学院;b.海洋装备研究院,上海 200240

Rescheduling of Multi-Scenario and Multi-Objective Dynamic Changes of Ship Group Construction

ZHANG Aoyuan^a, HU Xiaofeng^,^a, ZHANG Yahui^b

a. School of Mechanical Engineering;b. Institute of Marine Equipment, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 胡小锋,研究员,博士生导师,电话(Tel.):021- 34205694;E-mail:wshxf@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-06-28 修回日期: 2023-08-20 接受日期: 2023-08-28

基金资助:

国家自然科学基金面上资助项目(51975373)
上海交通大学新进青年教师启动计划项目(22X010503668)

Received: 2023-06-28 Revised: 2023-08-20 Accepted: 2023-08-28

作者简介 About authors

张澳圆(1999—),硕士生,从事船舶小组立装焊过程大数据分析、优化调度算法研究.

摘要

针对船舶小组立装焊过程中物料配送延迟、设备故障等异常状况频发导致的生产进度滞后、生产计划需重新调整问题,提出一种多场景多目标动态变化重调度算法.首先,根据生产阶段和异常扰动的不同选取目标函数,并构建包含场地约束、任务先序约束和人力资源约束的数学模型;其次,引入场地配置算法,采用改进的基于参考点的非支配排序算法求解,增加交叉检查机制,设计基于任务序列的变异算子,融合多染色体机制,与场地配置算法相结合进行求解;之后,提出了面向船舶小组立装焊重调度的染色体序列距离计算方法,描述重调度算法解与初始计划的差异大小,与R2指标结合,定义Pareto-R2双标准选择算子,兼顾算法多样性和收敛性;最后,基于工程案例设计对比实验,验证了提出的重调度算法的有效性.

关键词： 船舶小组立; 重调度; 多目标优化; 多场景

Abstract

A multi-scenario and multi-objective dynamic change rescheduling algorithm is proposed to address the production schedule delays and the need for adjustments caused by frequent abnormal conditions, such as material delivery delays and equipment failures in the vertical assembly welding process of shipbuilding teams. First, the objective function is selected based on different production stage and abnormal disturbance, and a mathematical model is then developed, incorporating site constraints, task precedence constraints, and human resource constraints. Next, a site allocation algorithm is introduced, and an improved non-dominated sorting algorithm based on reference points is adopted to solve the problem. A cross-checking mechanism implemented, alongside a task-sequence-based mutation operator, and the multi-chromosome mechanism is integrated with the site allocation algorithm. Afterwards, a method for calculating the chromosome sequence distance in the ship group vertical assembly welding rescheduling is proposed, and the difference between the rescheduling algorithm solution and initial plan is described. An R2 indicator is combined with a Pareto-R2 double standard selection operator, which ensures both diversity and convergence of the algorithm. Finally, comparative experiments are conducted based on engineering cases to validate the effectiveness of the proposed rescheduling algorithm.

Keywords： small assembly of ship; reschedule; multi-objective optimization; multi-scenario

PDF (2668KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张澳圆, 胡小锋, 张亚辉. 多场景多目标动态变化下船舶小组立装焊重调度[J]. 上海交通大学学报, 2025, 59(4): 476-488 doi:10.16183/j.cnki.jsjtu.2023.274

ZHANG Aoyuan, HU Xiaofeng, ZHANG Yahui. Rescheduling of Multi-Scenario and Multi-Objective Dynamic Changes of Ship Group Construction[J]. Journal of Shanghai Jiaotong University, 2025, 59(4): 476-488 doi:10.16183/j.cnki.jsjtu.2023.274

船舶小组立是船舶制造过程的最小作业单元,其数量多、任务紧,对装配节奏与正确性要求较高,对船舶整体生产制造效率有着重要影响^[1].但小组立结构复杂,装焊作业过程涉及到多种工人配合,场地、设备等多种制造资源配置约束,因此在实际生产过程中时常会出现如物料配送延迟、机器故障、零件质量不合格需要返工等异常状况,导致原有生产计划停滞,甚至不再可行.传统的人工修改计划的方式效率低下,仅从经验出发对空间资源和人力资源重新配置,常常出现在资源空闲的情况下任务还会延期,工人不得不通过加班等方式弥补滞后的进度,增加了工人负担的同时,对企业造成极大的经济损失和资源浪费^[2].而且,依据人工经验调整的方法优化范围有限,往往需要反复调整,不断优化,通常也会额外增加工人负担和生产成本.此时需要一种方法在异常发生时自适应地调整生产计划,重调度算法旨在通过更改生产计划达到尽快恢复生产的目的,且在此过程中尽量不降低生产效率,不增加额外成本.

船舶小组立装焊作业重调度问题属于资源约束型项目调度问题(resource constrained project scheduling problem,RCPSP),优化调度过程中需要考虑各工序开工时间、工人资源和场地资源的合理分配.目前船舶制造领域的研究大多以船舶分段为研究对象,小组立装焊作业重调度问题的研究资料较少.

在目标选取上,杨志^[3]对船舶平面分段建造过程中的不确定性进行研究,以满足精益生产要求和提高生产效率为目标,分别提出了单流水线调度方法和并行流水线调度方法; 李敬花等^[4]针对船舶分段装配序列优化问题,以装配时间和消耗成本为目标,综合考虑分段装配过程中的几何约束等建立了问题模型;Kwon等^[5]针对造船行业大型装配工件空间调度问题,以最小化最大完工时间和负载平衡为目标函数建立了一种混合整数规划模型;侯金伟等^[6]使用智能算法优化船舶装焊任务序列和资源配置,但其未考虑多个异常场景,且仅考虑最小化装焊作业完工时间这一目标,难以有效应对异常频发的实际生产现场;此外部分研究将重调度目标设定为各项任务总开工时间的偏差最小^[7-9].以上研究的问题在于:① 对于目标函数的选取缺乏合理解释,且未考虑生产阶段变化对生产目标的影响,例如,在船舶小组立装焊前期,企业期待使用最少的资源尽早完成生产,随着生产进程的推进,生产计划稳定性、任务延期率最小等逐渐成为企业的关注重点;② 在船舶生产制造过程中,生产计划以时间窗的形式制定,各项任务需要在规定的时间窗内完成,将重调度目标设定为各项任务总开工时间的偏差最小,未考虑任务序列的变动对生产计划的冲击.

在调度策略上,高丽等^[10]设计了一种具有多重资源约束的多目标集成优化方法,融入了多规则资源分配的集成调度思想,通过调整规则概率使概率大的规则被优先选中;田启华等^[11]针对产品开发任务调度问题对多个目标进行决策优化,提出了学习遗忘效应矩阵,有助于指导产品设计开发;何小妹等^[12]针对混合流水车间紧急插单重调度问题进行研究,提出了基于事件驱动的重调度策略,建立了多目标多约束模型,采用非支配排序算法(non-dominated sorting genetic algorithm,NSGA)进行求解.以上文献主要针对某一异常干扰进行研究,未考虑不同的异常干扰对于生产计划的不同影响.

在求解方法上,安晓亭等^[13]基于改进的蚁群算法求解多目标资源受限调度问题,基于标准数据集进行测试分析得到帕累托(Pareto)解集,验证了算法的有效性;Bao等^[14]提出了一种船舶装配数据驱动方法,通过数据聚类识别计划变更导致的相关因素调整,识别机器、设备和人力等造船厂资源的未来可用性,以获得最佳生产性能;张亚辉^[15]针对双边装配线再平衡问题建立了多目标双边装配线再平衡问题的数学模型,基于改进的遗传算法获得了以优化产能和再平衡成本为目标的双边装配线再平衡最优解集;汤洪涛等^[16]提出一种基于变邻域搜索的自适应候鸟迁徙优化算法,实现了最小化完工时间与最小平均在制品数量的多目标优化.以上文献对于多目标组合优化问题求解得到的大多是Pareto解集,没有考虑如何从Pareto解集中选取一个最优方案.

综合以上分析,船舶小组立装焊作业的重调度研究需制定符合场景的目标函数,针对不同异常场景动态调整应对策略,关注整个任务序列的变动,从而使得重调度带来的物流计划、空间布局调整最小,保证各项任务如期交付更加契合企业生产实际与需求,更具研究价值.本文首先分析船舶小组立装焊作业过程中涉及的典型生产阶段和几种不同异常干扰模式,并为其设计相应的多个目标函数.分析船舶小组立装焊作业过程所受的关键约束,构建问题数学模型;其次,采用改进的基于参考点的非支配排序算法(non-dominated sorting genetic algorithm based on reference points,NSGA-III),融合多染色体机制,与场地配置算法相结合对模型进行求解;最后,定义了重调度解与初始计划的序列距离,并设计了Pareto-R2两阶段式迭代求解方法^[17],使得迭代过程朝着趋向原始序列的方向发展,同时兼顾了算法的多样性和收敛性.

1 船舶小组立装焊作业的多目标重调度模型

1.1 问题描述及场景定义

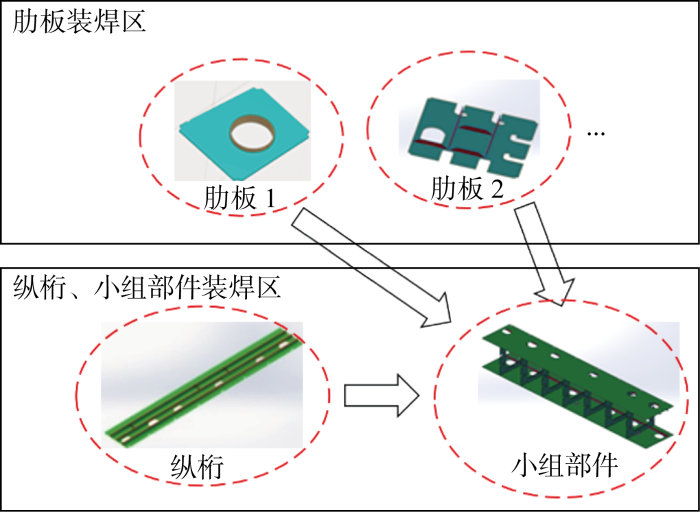
小组立的制造过程是将多个零件(肋板、纵桁)组成一个构件(小组立)的过程.装焊过程中先分别完成肋板和纵桁的装焊,然后将这些肋板与纵桁焊接在一起,完成一个小组立的装焊,如图1所示.其中,一个肋板或一个纵桁的装焊,乃至肋板与纵桁的组合装焊均称为一个任务组.船舶小组立装焊过程中存在多个装焊工位,每个装焊工位负责一个装焊任务组,对应一个小组立的装焊过程.每个任务组内往往包含多个具有严格先序约束的工序.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 肋板、纵桁和小组部件关系

Fig.1 Relationship between ribs, longitudinal, and group components

装焊作业开始的前提条件是:场地和工人资源有空余、前序工序均已完成、所需物料已送达.小组立装焊过程涉及到装焊工人和打磨工人两个工种,当前时刻计划工人配置总数不能超过相应工种的工人总数;场地资源也是小组立装焊调度过程中的关键要素,通常为一矩形空间,按照工艺不同可分为肋板、纵桁以及小组部件装焊场地,其中纵桁装焊完成后不需要释放场地资源,等待需要的肋板装焊完成后运送至该场地进行组合装焊作业,构成小组部件,如图1所示.小组立占用的场地资源描述为其部件主板形成的包络凸多边形面积.

装焊作业执行过程中,经常发生如物料供应不及时、机器故障、工人操作失误等异常状况,经过文献调研和生产现场的实地考察,主要有以下3种情况.

(1) 异常1:开工时间延迟.由于物料供应不及时、员工未到位等导致当前时刻应当开始工作的任务组无法正常开始,此时零件物料等尚未搬运至场地空间中,可以通过相应对策排除异常直至达到开工条件后继续执行.

(2) 异常2:工序时间增加.由于零部件质量不合格需要返工或者任务组作业过程中设备故障需要暂停作业,此时任务组已经放置在场地中,难以重新配置任务组空间布局,所以必然会导致相应工序时间增加.针对此类异常,在不改变该任务组初始场地配置方式的基础上,调整工人配置方式以使生产尽快回归正常轨道.

(3) 异常3:交付期变动.生产过程中有时会遇到客户要求部分关键部件提前交付,此时需优先调度交付期提前的任务组.

显然在不同的异常干扰场景下,所需实现的优化目标有所差异,重调度算法需要根据不同的优化指标,通过改变任务序列、工人配置模式和场地配置模式,对后续任务重新进行规划配置,使其尽快恢复稳定、高效生产,降低异常干扰对生产进度造成的影响.

1.2 条件假设

船舶小组立装焊多场景多目标重调度模型包含以下假设:

(1) 船舶小组立装焊过程中涉及到的各种物料零件、设备工装供应充足.

(2) 不同类型的任务组所需工人类型及工人数量不同,设定了多种工人执行模式可选,同一类型任务组也有多种工人执行模式,可以根据现场工人占用情况进行调整,不同的执行模式所需的作业时间不同,小组立执行模式确定后,整个作业过程不会改变.

(3) 装焊场地为二维空间矩形,高度无限制,场地内部均可占用,小组立可以放置在场地内任意位置,小组立之间位置不能重叠.

(4) 小组立形状采用小组立主板的平面投影来表示,其形状为各种凸多边形,且能以任意角度在装焊平台内放置.

(5) 小组立的放置姿态一经确定,在其开始作业,直至其完成作业并释放场地资源期间,均不可改变.

(6) 任务一旦开始,直至完工不会中断.

1.3 数学模型

1.3.1 符号说明

$t$ 为模拟时钟, $t = 1, 2, \dots, T$ ,其中T为模拟时钟可达最大范围,1个模拟时钟为10 min;n为小组立总数;i为任务组编号, $i = 1, 2, \dots, I$ ; j为任务编号, $j = 1, 2, \dots, J$ ; $G_{i}$ 为任务组i的集合; $A_{i, j}$ 为任务组i中的j任务; M为工人执行模式集合;m为工人执行模式,是枚举类型的值, $m \in M$ ;K为工人类型集合;k为工人类型,类型同工人执行模式, $k \in K$ ; $Q_{k}$ 为k型工人数量; $q_{m k}$ 为m型执行模式下k型工人数量;s为场地类型;S为场地类型集合; $L_{s}$ 为场地s的长度; $W_{s}$ 为场地s的宽度; $G_{i s}$ 为任务组i占用的场地区域; $R_{i}$ 为任务组i的区域范围; $R_{s}$ 为场地s的区域范围; $T_{i j, e s t}$ 为任务 $A_{i, j}$ 的最早开工时间; $T_{i j, l s t}$ 表示任务 $A_{i, j}$ 的最晚开工时间; $T_{i j m}$ 为任务 $A_{i, j}$ 在m型工人配置下的作业时间; $T_{i, d e l i}$ 为任务组i的交付时间; $T_{i, f i n i}$ 为任务组i的实际完工时间; $T_{f i n i}$ 为最大完工时间; $P_{i j}$ 为任务 $A_{i, j}$ 的紧前工序集; $x_{i j m} \in {0, 1}$ ,任务 $A_{i, j}$ 以工人配置m进行作业则 $x_{i j m} = 1$ ,否则 $x_{i j m} = 0; y_{i j t} \in {0, 1}$ ,任务 $A_{i, j}$ 在t时刻开始执行则 $y_{i j t} = 1$ ,否则 $y_{i j t} = 0; z_{i s} \in {0, 1}$ ,任务组 $G_{i}$ 在场地s上进行作业则 $z_{i s} = 1$ ,否则 $z_{i s} = 0$ ; $T_{j, s t}^{0}$ 表示计划调整前第j个任务的开始作业时间, $T_{j, s t}$ 表示计划调整后第j个任务的开始作业时间.

1.3.2 多场景下的目标函数定义

多场景下的小组立重调度目标函数受生产过程不同阶段的影响.在船舶小组立装焊前期,计划调整空间较大,着重需要关注异常扰动是否会影响生产效率,因此重调度计划应当尽量使得最大完工时间最短、工人利用率和空间利用率最高,以提高生产效率,降低成本;在装焊中期,工人排班计划、物流配送计划已经确定,场地资源大部分被占用,大部分任务正在进行中或已经完成,此时更加关注计划稳定性,减少计划调整带来的损失;在装焊后期,大部分任务组已经进入交付阶段,此时企业则更关注异常扰动对任务延期时间的影响,通常目标是使任务延期时间最短.

异常干扰的类型也会影响重调度的目标函数.当任务开工时间延迟时,当前等待任务尚未进行配置,其配置方式仍然可以变化,但会影响后续任务及其他任务的进行,此时应考虑尽可能维持计划稳定性,同时兼顾最小化最大完工时间;当任务的工序时间增加时,该任务已经在进行中,可以通过调整工人配置等缩短作业时间,对原计划的调整较小,重点关注工人利用率;当任务的交付期发生变动时,例如客户要求生产订单提前完成时,应当首先满足该任务的交付需求,且尽可能使其他任务准时交付.

综合上述分析,在船舶小组立装焊作业过程中主要关注最大完工时间、开工时间总偏差、空间利用率、工人利用率、延期时间和紧急任务是否如期交付6项指标.以完工任务数占任务组总数的比例定义不同的生产阶段,将小组立装焊过程分为前、中、后期3个阶段,完工任务数占任务组总数不足50%属于装焊前期,50%~75%属于装焊中期,大于75%属于装焊后期.基于不同生产阶段、不同的异常干扰对于目标函数的影响分析,可得到不同阶段不同异常场景下的重调度所关注的目标函数,如表1所示.

表1 多场景下目标函数的定义

Tab.1 Definition of objective function in multi-scenarios

目标函数	前期			中期			后期
目标函数	异常1	异常2	异常3	异常1	异常2	异常3	异常1	异常2	异常3
最小化最大完工时间	√	√	√	√			√
最小化开工时间偏差	√			√	√	√	√
最大化空间利用率	√	√	√
最大化工人利用率	√	√	√		√			√
最小化延期时间						√	√	√	√
最大化紧急任务如期交付			√			√			√

新窗口打开| 下载CSV

各个目标函数的定义及计算公式如下.

(1) 最大完工时间.最大完工时间定义为任务组序列中最后一个任务组的完工时间.该目标体现了装焊系统能力,最大完工时间越短,生产效率越高,记为f₁:

(1)

f_{1} = m i n (\underset{i \in I}{m a x} \sum_{m = 1}^{M} \sum_{t = T_{i (J + 1), e s t}}^{T_{i (J + 1), l s t}} t x_{i (J + 1) m} y_{i (J + 1) t})

(2) 开工时间偏差.当发生设备故障、物流延迟、紧急插单等异常状况,需要重新调整生产计划时,在保证关键任务及时交付的前提下,需考虑减少计划变动,进而减少因计划调整增加的成本,因此,计划调整前后的任务作业开始时间差越小越好.本文使用计划调整前后的任务作业开始时间差表征计划稳定性,记为f₂:

(2)

\begin{matrix} f_{2} = m i n \sum_{j = 1}^{J} |T_{j, s} - T_{j, s}^{0}| \end{matrix}

(3) 延期时间.船舶小组立装焊作业过程中,可能发生由于船舶零部件数量众多,堆积严重导致查找时间长,进而导致生产计划推进延后.任务延期时间记为f₃:

(3)

\begin{array}{l} f_{3} = m i n \sum_{i = 1}^{I} |\sum_{m = 1}^{M} \sum_{t = T_{i (J + 1), e s t}}^{T_{i (J + 1), l s t}} t x_{i (J + 1) m} y_{i (J + 1) t} - T_{i, d e l i}| \times \\ m a x \{\frac{\sum_{m = 1}^{M} \sum_{t = T_{i (J + 1), e s t}}^{T_{i (J + 1), l s t}} t x_{i (J + 1) m} y_{i (J + 1) t} - T_{i, d e l i}}{|\sum_{m = 1}^{M} \sum_{t = T_{i (J + 1), e s t}}^{T_{i (J + 1), l s t}} t x_{i (J + 1) m} y_{i (J + 1) t} - T_{i, d e l i}|}, 0\} \end{array}

任务延期完成会造成工期、资源方面的损失,某些关键任务的延期还会影响后续许多任务的进行.

(4) 空间利用率.空间资源是制约小组立装焊过程中的关键要素,其成本昂贵且可用量有限,对于空间资源进行合理利用能够提高整体造船效率.计算公式如下:

(4)

\begin{array}{l} f_{4} = \\ m a x \frac{\sum_{m = 1}^{M} \sum_{i = 1}^{I} \sum_{j = 1}^{J} z_{i s} R_{i} T_{i j m}}{\sum_{s}^{} L_{s} W_{s} \underset{i \in I}{m a x} \sum_{m = 1}^{M} \sum_{t = T_{i (J + 1), e s t}}^{T_{i (J + 1), l s t}} t x_{i (J + 1) m} y_{i (J + 1) t}} \end{array}

(5) 工人利用率.提高工人利用率,有助于减少生产成本,加快生产进度.计算公式如下:

(5)

\begin{array}{l} f_{5} = \\ m a x \sum_{k = 1}^{K} \frac{\sum_{m = 1}^{M} \sum_{j = 1}^{J} \sum_{i = 1}^{I} x_{i j m} T_{i j m} q_{m k}}{Q_{k} \underset{i \in I}{m a x} \sum_{m = 1}^{M} \sum_{t = T_{i (J + 1), e s t}}^{T_{i (J + 1), l s t}} t x_{i (J + 1) m} y_{i (J + 1) t}} \end{array}

(6) 紧急任务提前交付.实际生产过程中,有时会遇到订单交期提前的情况,此时需要调整生产计划,满足紧急任务需求.计算公式如下:

(6)

\begin{matrix} f_{6} = m a x (T_{i, f i n i} - T_{i, d e l i}) \end{matrix}

1.3.3 约束定义

主要包括以下几项约束.

(1) 任务先序约束.每一个任务组中的每项任务必须在其所有先序任务均完成后才能开始,如果操作1优先于操作2,则操作1的结束时间应不晚于操作2的开始时间:

(7)

\begin{array}{l} \sum_{m = 1}^{M} \sum_{t = T_{i j, e s t}}^{T_{i j, l s t}} t x_{i j m} y_{i j t} - \\ \sum_{m' = 1}^{M} \sum_{t = T_{i j', e s t}}^{T_{i j', l s t}} t x_{i j' m'} y_{i j' t} \geq T_{i j' m'} \\ A_{i j'} \in P_{i j}, i \in I, j, j' \in G_{i}, m, m' \in M \end{array}\}

每项任务的开始时间需要在最早开始时间之后:

(8)

\begin{matrix} \begin{array}{l} \sum_{m = 1}^{M} \sum_{t = T_{i j, e s t}}^{T_{i j, l s t}} t x_{i j m} y_{i j t} \geq T_{i j, e s t} \\ i \in I, j \in G_{i}, m, m' \in M \end{array}\} \end{matrix}

(2) 人力资源约束.任意时刻同时开工任务的工人配置要满足各工种工人总数约束:

(9)

\begin{matrix} \begin{array}{l} \sum_{i = 1}^{I} \sum_{j = 1}^{J} \sum_{m = 1}^{M} x_{i j m} y_{i j t} q_{m k} \leq Q_{k} \\ \forall t \in (0, T], k \in K \end{array}\} \end{matrix}

(3) 场地资源约束.任意时刻,同时开工任务的场地资源配置要满足面积约束:

(10)

\begin{matrix} \begin{array}{l} \sum_{i = 1}^{I} \sum_{j = 1}^{J} y_{i j t} R_{i} \leq L_{s} W_{s} \\ \forall t \in (0, T], s \in S, z_{i s} = 1 \end{array}\} \end{matrix}

场地中不能有出现交叠:

(11)

\begin{matrix} R_{i} ⋂ R_{i'} = ⌀, \forall i, i' \in I, i \neq i' \end{matrix}

场地内的部件不能超出场地边界:

(12)

\begin{matrix} R_{i} \subseteq R_{s}, z_{i s} = 1 \end{matrix}

2 基于改进的NSGA-III的船舶小组立多目标重调度问题求解

2.1 算法描述

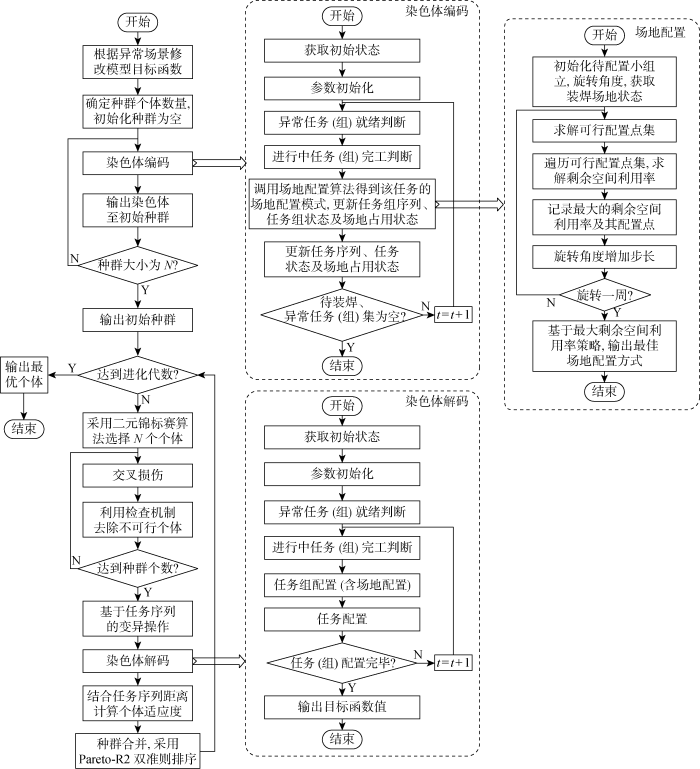
NSGA-III在传统遗传算法的基础上,引入了增强精英保留策略,相较于公认的多目标求解算法NSGA-II使用拥挤度进行前沿内部解排序的方法,NSGA-III引入了参考点机制,更适用于多维目标优化问题,通过引入广泛的参考点能够保证种群多样性和解的均匀性;采用基于顺序搜索策略的高效非支配排序(efficient nondominated sort using the sequential search strategy,ENS-SS)进行快速非支配层级划分排序^[18],计算效率高.为了更好地解决小组立多目标重调度问题,本文在原始NSGA-III算法的基础上增加如下改进:① 增加染色体交叉后的检查机制,保证船舶小组立约束规则下可行解的数量,提高遗传效率;② 设计基于任务序列的变异算子,在保证种群多样性的基础上增加可行解数量;③ 定义不同解之间的任务序列距离计算方法,确保解的搜索向着靠近初始序列的方向,减少变动成本;④ 设计Pareto-R2双标准选择算子,兼顾算法多样性和收敛性,算法整体流程如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 改进的NSGA-III算法流程图

Fig.2 Flow chart of the improved NSGA-III algorithm

2.2 编解码规则

船舶小组立重调度过程涉及到任务序列、工人资源和场地资源3种关键要素,采用多染色体混合编码,每个个体包含3条染色体,均采用实值编码方式,编码后的染色体即为对应的决策变量.

第1条染色体为小组立任务组号排列,各个小组立在装焊过程中需要按顺序放置在对应装焊场地中,并且占据一定的工人资源和场地资源,小组立任务组号染色体形式为 $C_{1} = {i_{1}, i_{2}, \dots, i_{n}}$ .对第1条染色体进行解码,可以得到该小组立对应的场地配置方式和开始作业时间,其形式为 ${(c_{x 1}, c_{y 1}, θ_{1}, t_{1}), (c_{x 2}, c_{y 2}, θ_{2}, t_{2}), \dots, (c_{x n}, c_{y n}, θ_{n}, t_{n})} .$

第2条染色体为小组立工序任务序号排列,小组立首任务信息已包含在第1条染色体中,因此第2条染色体为不包含首任务的其他未完成任务集,其形式为 $C_{2} = {o_{1}, o_{2}, \dots, o_{m}, o_{- 1}}$ ,其中 $o_{- 1}$ 为添加的虚拟结束任务,当执行到 $o_{- 1}$ 时表示所有任务均已完成.对第2条染色体进行解码可以得到各个工序的开始时间以及装焊作业全部完成的最大完工时间,其形式为 ${t_{1}, t_{2}, \dots, t_{m}, t_{n}} .$

第3条染色体为各任务对应的工人执行模式集合,长度为第1条和第2条染色体的长度之和,其形式为 $C_{3} = {m_{1}, m_{2}, \dots, m_{n}, m_{n + 1}, \dots, m_{n + m}, m_{- 1}}$ ,前半段 ${m_{1}, m_{2}, \dots, m_{n}}$ 为对应任务组的工人执行模式,后半段 ${m_{n + 1}, \dots, m_{n + m}}$ 为各工序的工人执行模式,均采用正整数表示.特别地,虚拟任务的工人执行模式 $m_{- 1}$ 设置为0.对第3条染色体进行解码,可以得到各任务在对应工人执行模式下所需工人数量和作业时间,其形式为 ${(q_{k 1}, t_{1}), (q_{k 2}, t_{2}), \dots, (q_{k n}, t_{n}), 0} .$

2.3 种群初始化

在遗传算法执行前,基于编解码规则对任务序列、工人资源和场地资源进行编码,并通过下方流程对种群进行初始化.

步骤1 获取初始状态,获取异常发生时刻场地占用情况、各个任务组及工序的执行情况、异常任务的异常处理时间、待配置任务组集合和工序集合.

步骤2 初始种群参数,初始种群为空,输入种群大小.

步骤3 异常任务释放判断,调度时刻加上异常任务的异常处理时间为异常任务的释放时间,当前时刻下判断异常任务是否已经处理完毕并释放,若已经释放,则将异常任务加入到待配置任务集合当中.

步骤4 当前作业任务是否完工判断,对于当前作业中的任务,判断当前时刻下该任务是否已经完成,若已完成,则将其从活动任务组中移至已完工集合.

步骤5 初始化第1条染色体,同时初始化第3条染色体,随机从待配置任务组中取出一个序号,并为其随机指定工人执行模式,调用场地配置算法得到该任务的场地配置模式,判断其是否满足任务组装焊条件,若满足则将该任务加入到第1条染色体中,反之,跳过该任务组.其中,任务组装焊条件为:该任务组的所有前序工序均已完成、该任务组的工人执行模式满足工人总数约束、该任务组的场地配置方式满足场地约束.

步骤6 初始化第2条染色体,同时初始化第3条染色体,从待配置的满足先序约束的工序中随机取出一个,并为其随机指定工人执行模式,判断其是否满足工序装焊条件.其中,工序装焊条件为:该工序的所有前序工序均已完成、该工序的工人执行模式满足工人总数约束,同时需要判断该工序是否需要释放场地,并更新场地占用情况.

步骤7 判断所有任务是否均已配置完成,若完成,输出染色体集合,转步骤8,否则,转步骤4.

步骤8 种群数量加1,判断是否已达到种群规模,若是,种群初始化结束,否则,转步骤3.

2.4 遗传操作

2.4.1 选择算子

采用二元锦标赛选择算子,随机从父代种群中选择两个个体竞争,选择适应度值大的作为父体,重复两次,进行后续交叉操作.二元锦标赛算子不需要对所有的适应度值进行排序处理,复杂度为O(n),并且能够防止最优个体支配种群,避免算法陷入局部最优.

2.4.2 增加检查机制的交叉算子

重调度模型中任务先序约束、场地约束和工人约束严格,采用随机交叉策略得到的染色体大概率违反约束,因此交叉后的种群中的可行解大部分来自父代,需要制定新的交叉策略增加可行解的多样性.对于第1条和第2条染色体采用部分匹配交叉算子^[19],对于第3条染色体采用模拟二进制交叉算子^[20].在交叉操作之后增加检查机制,舍弃违反任务先序约束的个体,直至获得足够数量的子代再进入下一步操作.

2.4.3 基于任务序列的变异算子

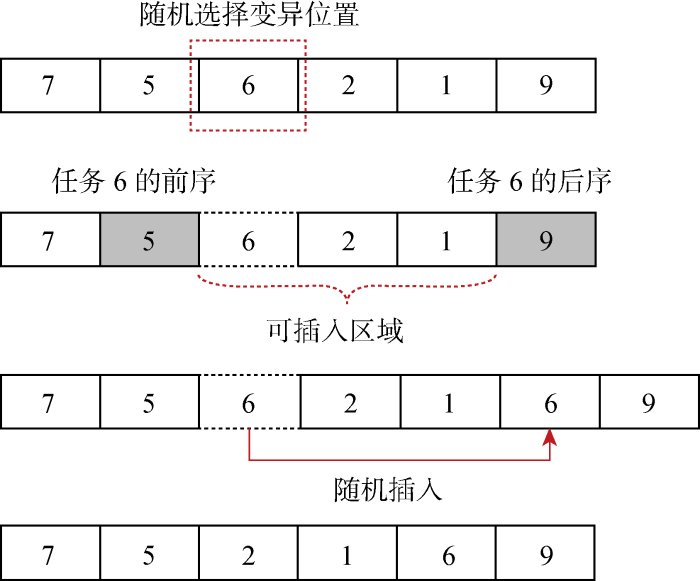
对于第1条和第2条染色体,现有的变异算子得到的绝大多数是不可行解,因此提出了基于任务序列的变异算子,和邻域搜索策略相结合以获得可行的个体,如图3所示,在交叉获得的可行任务序列上随机选择一个任务,将其插入到该任务的前序节点和后续节点之间的任意位置.第3条染色体采用多项式变异算子^[21].

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 基于任务序列的变异算子

Fig.3 Mutation operator based on task sequence

2.4.4 基于Pareto-R2的两阶段式迭代

本文采用Pareto-R2双准则排序,前期搜索过程中基于Pareto准则对解进行不同层次的排序,得到的解具有更高的多样性,后期搜索过程中基于R2指标进行排序获得指标值更好的解,提高算法收敛速度,兼顾算法多样性和收敛性的目的.

基于ENS-SS的Pareto排序方法进行快速非支配层级划分,计算效率高,空间复杂度是O(1),时间复杂度可以达到 $O (M N l g N) .$ 而传统的R2指标对于贡献度为0的解无法决策,本文提出一种基于序列距离的R2指标计算方法,继承了R2指标效用函数的概念,通过计算解序列和原始序列的序列距离得到每个解的权重,距离原始序列越近的解赋予更高的权重系数,利用效用函数和权重系数计算每个解的适应度大小,每一轮迭代结束后选择适应度更小的解进入下一轮.

首先计算解x的效用函数u(x):

(13)

f_{m i n i} = m i n f_{i} (\cdot), f_{m a x i} = m a x f_{i} (\cdot)

(14)

\begin{array}{l} u (x) = \sum_{1 \leq i \leq m}^{} \frac{f_{i} (x) - f_{m i n i}}{f_{m a x i} - f_{m i n i}} \end{array}

解x序列距离D(x)定义为重调度前后序列中各个任务位置变动的距离之和,单位为模拟时钟,然后根据序列距离计算解的权重ω(x):

(15)

\begin{array}{l} \begin{matrix} D (x) = \sum_{1 \leq i \leq n}^{} \frac{|x_{i'} - x_{i}|}{n} \end{matrix} \end{array}

(16)

ω (x) = \frac{D (x)}{\sum_{x \in A}^{} D (x)}

解x的适应度计算公式如下:

(17)

\begin{matrix} F (x) = ω (x) u (x) \end{matrix}

2.5 场地配置算法

场地配置算法采用文献[22-23]中的空间配置理论,在求得配置空间内的可行配置点集之后,依次遍历并计算出最大剩余空间利用率的方案作为配置方案并输出.

3 工程案例验证

3.1 案例说明

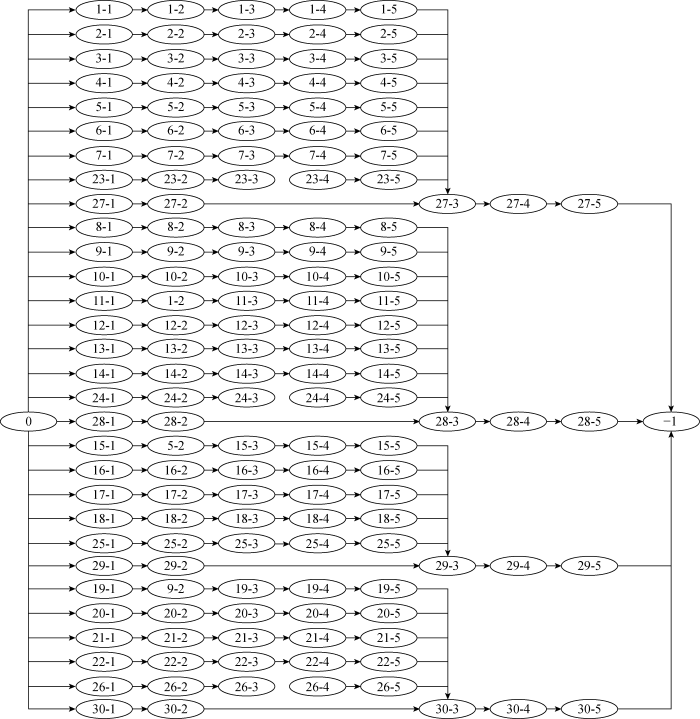
以某船厂小组立装焊作业车间为例开展研究.该车间共有两块装焊场地:肋板装焊区和纵桁、小组部件装焊区,两块区域均可视为长矩形,其中肋板装焊区作业面积为28 m×12 m,纵桁、小组部件装焊区作业面积为44 m×12 m.车间内共有两种工人:装焊工和打磨工,其中装焊工为主要工种,共有16人,打磨工为辅助工种,共有8人.船舶小组立部件形状可以抽象为14种凸多边形,其形状数据如表2所示,车间内某阶段生产订单如表3所示,共需生产30个小组立,每个小组立包含5道主要工序,5道生产工序之间存在着严格的先后顺序,部分小组立之间也存在先序约束,具体约束关系如图4所示.

表2 船舶小组立部件形状数据

Tab.2 Shape data of vertical parts of ship group

形状编号	形状	顶点坐标集
1	直角三角形	{(0, 0), (5, 0), (0, 3)}
2	正方形	{(0, 0, )(3, 0)(3, 3), (0, 3)}
3	直角梯形	{(0, 0), (5, 0), (3, 3)(0, 3)}
4	等腰梯形	{(0, 0), (5, 0), (3.9, 3), (1.1, 3)}
5	五边形	{(0, 0), (5, 0), (3.9, 3), (1.1, 3) (0, 1.5)}
6	四边形	{(0, 0), (3.0), (3.4, 1), (0, 3)}
7	一般三角形	{(0, 0), (5, 0), (4.2, 3)}
8	矩形1	{(0, 0), (14, 0), (14, 3), (0, 3)}
9	矩形2	{(0, 0), (14, 0), (14, 5), (0, 5)}
10	平行四边形1	{(0, 0), (12.3, 0), (14, 3), (1.7, 3)}
11	平行四边形2	{(0, 0), (13.1, 0), (14, 5), (0.9, 5)}
12	六边形	{(0, 0), (10.5, 0), (14, 2), (14, 5), (3.5, 5), (0, 3)}
13	横躺等腰梯形	{(0, 0), (14.4, 0), (15, 3), (1.4, 7.9)}
14	不规则五边形	{(0, 0), (14.4, 0), (15, 3), (9.6, 4.9), (0.9, 4.9)}

新窗口打开| 下载CSV

表3 船舶小组立装焊部件订单数据

Tab.3 Order data of ship group assembly welding operation

部件类型	部件编号	部件形状
肋板	1, 2, 3, 4, 5, 6, 7	五边形
	8, 9, 10, 11, 12, 13, 14	等腰梯形
	15, 16, 17, 18	直角梯形
	19, 20, 21, 22	直角三角形
纵桁	23	横躺等腰梯形
	24	不规则五边形
	25	六边形
	26	平行四边形2
小组部件	27	横躺等腰梯形
	28	不规则五边形
	29	六边形
	30	平行四边形2

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 船舶小组立装焊作业订单任务先序图

Fig.4 Order sequence diagram of ship group assembly welding operation

3.2 实验方案及分析

使用本文提出的改进的NSGA-III算法对问题进行求解,并将其求解结果与原始NSGA-III算法结果进行对比,从目标函数值、解均匀性、解多样性以及重调度计划与原始计划的序列距离4个方面进行分析.其中本文算法根据基于任务序列的R2指标计算后,最终得到一个最优方案,而NSGA-III得到的是一个Pareto解集.用原始NSGA-III算法得到的Pareto解集中各个目标函数达到最优的解,即Pareto前沿各个坐标短点的解与本文算法得到的解进行对比.

船舶小组立装焊作业车间的原始计划的甘特图如图5所示,计划完成总计需要96个模拟时钟,方块中的第1个数字代表部件编号,第2个数字代表该部件的工序编号,每个任务组均包含5道工序,5个工序用5种颜色进行区分.实验选取两个场景进行验证,不同场景包含不同的异常扰动.不同场景下的目标函数、算法的参数定义如下,不同算法的种群大小均为60,迭代均为100次.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 船舶小组立装焊原始计划的甘特图

Fig.5 Gantt chart of original assembly welding plan of ship group

场景1t=35模拟时刻,由于相关零件物料供应不及时,导致装焊任务A_1,3开工延迟,重新配送需要13个单位时间,此时属于生产前期发生的异常1.重调度目标是最小化最大完工时间、最小化开工时间偏差、最大化空间利用率和最大化工人利用率.针对该场景进行重调度,结果如表4所示,本文算法得到的解各个目标函数值均优于NSGA-III.

表4 场景1下不同算法的求解结果对比

Tab.4 Comparison of solution results of different algorithms in Scenario 1

算法	最大完工时间	开工时间偏差	空间利用率	工人利用率
改进前的NSGA-III	94	398	0.41	0.65
	97	287	0.39	0.58
	99	490	0.43	0.59
	94	398	0.41	0.65
本文算法	93	256	0.43	0.68

新窗口打开| 下载CSV

场景2t=49模拟时刻,任务组27需要提前10单位时间交付,且零件质检不合格,在不改变小组立当前位置的前提下,任务A_{1, 5}需要重做,此时属于生产中期发生的异常2和异常3.重调度目标是最小化开工时间偏差、最大化工人利用率、最小化延期时间和最大化紧急任务如期交付.针对该场景进行重调度,结果如表5所示,本文算法得到的解工人利用率、延期时间、紧急任务提前交付3个目标函数值均优于改进前的NSGA-III,开工时间偏差略差,但本文算法求得的解与原始序列的距离更小,因此计划变更更小.

表5 场景2下不同算法的求解结果对比

Tab.5 Comparison of solution results of different algorithms in Scenario 2

算法	开工时间偏差	工人利用率	延期时间	紧急任务提前交付
改进前的NSGA-III	39	0.60	95	5
	63	0.63	93	9
	72	0.62	92	6
	65	0.56	94	11
	56	0.55	96	11
	69	0.56	97	11
本文算法	57	0.65	91	11

新窗口打开| 下载CSV

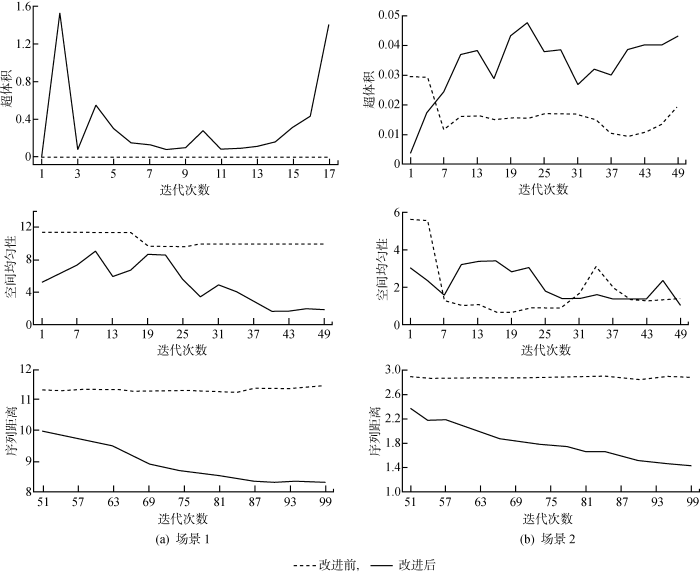
为了进一步说明本文所提出的检查机制、基于任务序列的变异算子以及Pareto-R2两阶段迭代过程的有效性,选取超体积(hypervolume,HV)^[24]指标和空间均匀性指标(Spacing)来衡量迭代过程解的多样性和均匀性,HV值越大,Spacing值越小,表示解的多样性和均匀性越好.采用所提出的序列距离来衡量计划稳定性,序列距离越小,对原始计划的变动越小,计划稳定性越好,重调度造成的额外成本越小.在两种场景下,迭代过程中各项指标的变化如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同场景下不同算法迭代过程的超体积、空间均匀性及序列距离指标变化

Fig.6 Variation of HV, Spacing, and distance during iteration of different algorithms in different scenarios

本文改进的NSGA-III算法在场景1下所获得的HV指标和Spacing指标均优于原始NSGA-III算法,在场景2的大部分迭代过程中,HV指标和Spacing指标优于原始的NSGA-III算法,说明了本文对NSGA-III算法的改进能够提升解的多样性和均匀性.另外,改进的NSGA-III算法在迭代前期倾向于获得多样性更好、更均匀的种群,以更好地探索解空间,在迭代后期,采用基于R2指标的方法,加速算法收敛,并且趋向于获得与原始计划距离更近的方案.

4 结语

本文开展了多场景多目标动态变化下的船舶小组立装焊作业重调度问题研究.首先根据生产阶段与异常干扰模式的不同定义场景并设计相应的重调度策略,动态调整目标函数,构建包含场地约束、任务先序约束和人力资源约束的数学模型,使其更加适用于实际现场;其次,提出改进的NSGA-III算法,并融合场地配置算法对重调度问题求解,在染色体交叉操作中增加检查机制,并设计基于任务序列的变异算子,保证遗传操作生成可行解的数量,并进一步定义了解的序列相似度计算方法,提出Pareto-R2两阶段式迭代求解方法,保证解的多样性、均匀性,确保使用最少的变动实现方案优化;最后根据实际现场设计对比实验,对比了两种场景下所提出的改进NSGA-III算法和原始NSGA-III的求解结果,实验结果表明改进的NSGA-III算法在不同场景下的多目标重调度问题上得到的解的目标函数值更优、与原始序列距离更小,同时兼顾了迭代过程中解的均匀性和多样性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

周泽麟, 单小芬, 张红伟,

等.

基于模型轮廓识别注册的船舶小组立装配指导技术

[J]. 船舶工程, 2022, 44 (Sup.1): 561-564.