在船舶与海洋工程领域,结构物在海浪中的运动和受力是设计人员关心的问题[1 ] .海浪的生成和传播特性分析是研究海浪与结构物相互作用的基础.实际海浪往往以连续几个大波的形式成群出现,构成不规则波群.相对于不规则波,不规则波群更能表征真实的海浪特征.为了使波群理论更好地用于船舶与海洋结构物设计,有必要开发数值波浪水池实现不规则波群生成和传播模拟.
基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率.
边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响.
关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道.
为了拓展波群理论在海洋工程领域的应用,本研究采用去奇异边界元法建立势流波浪水池模拟单向不规则波群的生成和传播,采用半混合欧拉-拉格朗日方法追踪自由面.针对势流波浪水池模拟不规则波精度和稳定性问题,讨论了消波阻尼层参数、源点去奇异距离、源点分布和时间步长等参数对模拟结果的影响,验证了所开发的势流波浪水池模拟不规则波群生成和传播的有效性.
1 势流波浪水池理论
1.1 流体运动方程
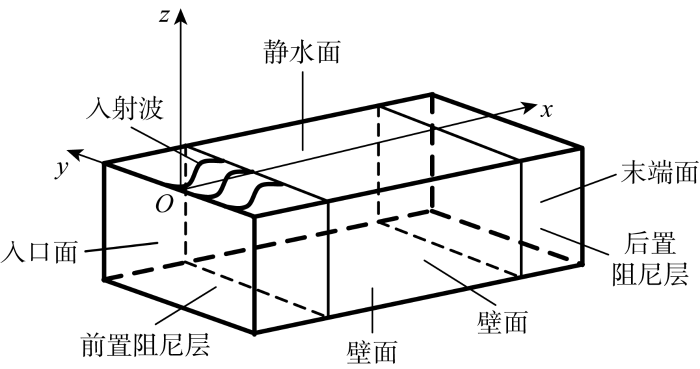
假设流体为理想流体,流动无旋,建立如图1 所示的波浪水池,坐标原点位于入口面和静水面的交线上.采用半混合欧拉-拉格朗日方法追踪瞬态自由面,将自由面边界条件改写为半拉格朗日形式[19 ] .在笛卡尔坐标系下,速度势满足以下方程:
(1) $\begin{array}{l}\nabla^{2} \phi(x, y, z, t)=0 \text { ,在流域内 }\end{array}$
(2) $\begin{array}{l}\frac{\mathrm{D} \eta}{\mathrm{D} t}=\frac{\phi}{z}-\frac{\phi}{x} \frac{\eta}{x}-\frac{\phi}{y} \frac{\eta}{y},\\\text { 自由面运动学条件 }\end{array}$
(3) $\begin{array}{l}\begin{aligned}\frac{\mathrm{D} \phi}{\mathrm{D} t}= & -g_{\eta}-\frac{1}{2} \mathbf{\nabla}_{\phi} \cdot \mathbf{\nabla}_{\phi}+ \\& \frac{\phi}{z}\left(\frac{\phi}{z}-\frac{\phi}{x} \frac{\eta}{x}-\frac{\phi}{y} \frac{\eta}{y}\right),\end{aligned}\\\text { 自由面动力学条件 }\end{array}$
(4) $\frac{\phi}{n}=v_{n} \text { ,在人口面,侧面,底面和末端面上 }$
式中: ϕ x、y 和z 分别为纵向、横向和垂向位置坐标;t 为时间;η 为自由面高度;g 为重力加速度;n 为流域外界外法向的单位向量;v n 为边界处的法向速度;$ \boldsymbol{\nabla}=\left[\begin{array}{llll}/ x & / y & / z\end{array}\right]^{\mathrm{T}}$ . 在入口面处, v n v n = 0 .
图1
图1
数值波浪水池示意图
Fig.1
Sketch of numerical wave tank
1.2 不规则波群生成理论
本研究结合海浪谱和波包谱理论生成单向不规则波群.海浪谱为改进的JONSWAP谱[20 ] :
(5) S η ( f ) = 0.062 38 ( 1.094 - 0.019 15 l n γ ) 0.23 + 0.033 6 γ - 0.185 ( 1.9 + γ ) - 1 × H 1 / 3 2 T P - 4 f - 5 e x p - 5 4 ( T P f ) - 4 γ e x p [ - ( f / f P - 1 ) 2 / ( 2 σ 2 ) ]
式中: S η H 1 / 3 T P f P γ σ f f ≤ f P σ
(6) S A ( f ) = 0.085 π e - 1 3.1 ( f / f P A ) m 0 G F H 2 / f P A , f f P A [ 0.042 + 0.019 ( f / f P A ) ] π m 0 G F H 2 / f P A , 0 ≤ f ≤ f P A
(7) f P f P A = G L F = 5 ~ 15 , G F H 0.7 10 ~ 28 , G F H ≥ 0.7
式中:S A 为波包谱函数;G FH 和G LF 分别为群高和群长参数;f PA 为波包谱的谱峰频率;m 0 为海浪谱Sη 的零阶矩.
单向不规则波群理论生成步骤[17 ] 如下:① 给定海浪的有义波高、谱峰周期、群高和群长等参数;②以海浪谱S η S A η ' ( t ) η A ( t ) η A ( t ) A ( t ) η ' ( t ) φ ( t ) η ( t ) = A ( t ) × c o s φ ( t ) η ( t )
1.3 数值造波和消波
为了在数值水池中模拟不规则波群的生成和传播,首先采用1.2节所述的理论方法生成单向不规则波列;然后通过快速傅里叶变换对该波列进行分析,得到相应的成分波要素;再结合线性叠加原理,假设波浪沿x 方向传播,便得到满足特定群性的不规则波列的速度势和波面升高:
(8) ϕ ( t ) = ∑ i = 1 M { π H i k i T i c o s h [ k i ( z + h ) ] s i n h ( k i h ) s i n [ k i ( x - x 0 ) - 2 π f i t + ε i ] }
(9) η ( t ) = ∑ i = 1 M [ H i 2 c o s [ k i ( x - x 0 ) - 2 π f i t + ε i ] ]
式中: H i 、 T i 、 f i 、 k i 、 ε i i 个成分波的波高、周期、频率、波数和相位;h 为水深;M 为频率等分区间数,取值200;x 0
由入射波速度势(式(8))可求得数值水池入口边界上的流体速度,即式(4)的右端项,便能实现速度入口造波功能.为了减少水池末端波浪反射对造波精度的影响,分别在水池首、末两端设置前置和后置阻尼层,则自由面边界条件式(2)和(3)改写为
(10) D η D t = ∂ ϕ ∂ z - ∂ ϕ ∂ x ∂ η ∂ x - ∂ ϕ ∂ y ∂ η ∂ y - b ( x ) ( η - η e )
(11) D ϕ D t = - g η - 1 2 Δ ϕ · Δ ϕ + ∂ ϕ ∂ z ( ∂ ϕ ∂ z - ∂ ϕ ∂ x ∂ η ∂ x - ∂ ϕ ∂ y ∂ η ∂ y ) - b ( x ) ( ϕ - ϕ e )
(12) $b(x)=\left\{\begin{array}{ll}\alpha_{1} \cos \frac{\pi\left(x-x_{1}\right)}{2 L_{1}}, & x_{1} \leq x \leq x_{1}+L_{1} \\0, & x_{1}+L_{1} x x_{2}-L_{2} \\\alpha_{2} \cos \frac{\pi\left(x_{2}-x\right)}{2 L_{2}}, & x_{2}-L_{2} \leq x \leq x_{2}\end{array}\right.$
式中: x 1 x 2 L 1 L 2 α 1 α 2 ϕ e 和η e 分别为速度势和波面升高的参考值.前置阻尼只允许入射波通过,ϕ e 和η e 分别取入射波速度势和波面升高的理论值(式(8)和(9));后置阻尼阻止任何波通过,ϕ e 和η e 取值均为0.
1.4 去奇异边界元法
流场内任意一点的速度势可用边界上分布的奇点积分来计算.采用Rankine源格林函数,则速度势的表达式为
(13) ϕ ( q , t ) = ∫ ∫ S 0 σ ( p , t ) 1 r ( p , q ) d S
式中: S 0 q = ( x q , y q , z q ) p = ( x p , y p , z p ) r 为场点与源点的距离;σ 为源强密度.将式(13)代入流域边界方程,采用面元法对积分方程进行离散,得到以源强密度为未知数的线性代数方程组:
(14) x q 1 - x p 1 r 3 [ q 1 p 1 ] … x q 1 - x p N r 3 [ q 1 p N ] ︙ ︙ ︙ x q N I - x p 1 r 3 [ q N I p 1 ] … x q N I - x p N r 3 [ q N I p N ] 1 r [ q N I + 1 p 1 ] … 1 r [ q N I + 1 p N ] ︙ ︙ ︙ 1 r [ q N I + N F p 1 ] … 1 r [ q N I + N F p N ] n q N I + N F + 1 · [ q N I + N F + 1 p 1 ] r 3 [ q N I + N F + 1 p 1 ] … n q N I + N F + 1 · [ q N I + N F + 1 p N ] r 3 [ q N I + N F + 1 p N ] ︙ ︙ ︙ n q N · [ q N p 1 ] r 3 [ q N p 1 ] … n q N · [ q N p N ] r 3 [ q N p N ] σ 1 ︙ σ N I σ N I + 1 ︙ σ N I + N F σ N I + N F + 1 ︙ σ N = ∂ ϕ i n ∂ x 1 ︙ ∂ ϕ i n ∂ x N I ( ϕ f s ) N I + 1 ︙ ( φ f s ) N I + N F 0 N I + N F + 1 ︙ 0 N
式中:N 为边界上的面元总数,包括入口面、自由面、底面、侧面和末端面的面元数;N I 为入口面的面元数;N F 为自由面的面元数;[q p ]表示q 点与p 点组成的向量;ϕ in 为入口面处的速度势,由式(8)求得;ϕ fs 为自由面处的速度势,由式(11)求得.当源点与场点距离过近时,式(14)奇异性增强,导致数值解精度下降.为了解决该问题,将源点布置在流域边界以外一定距离处,该距离称为去奇异距离(L d ),由下式确定[21 ] :
(15) $L_{\mathrm{d}}=l_{\mathrm{d}}\left(D_{\mathrm{m}}\right)^{\beta}$
式中:l d 和β 为常数,其大小会影响去奇异效果;D m 为面元的面积.
在每一个时间步内,采用四阶Adams-Bashforth-Moulton(ABM)预测-修正法求解自由面边界条件式(10)和(11),求得自由面升高和自由面上的速度势.为了提高自由面计算的稳定性,根据水池不同位置的波面抬升,采用三次样条插值法得到当前时间步的波面抬升函数表达式,波面抬升的空间导数通过对样条函数求导来获取,而速度势的空间导数通过对式(13)求导来获取.此外,每隔5个时间步,采用五点光顺法对自由面进行平滑处理以进一步提高计算稳定性.求得自由面位置、入口面和自由面上的速度势后,对式(14)系数矩阵进行更新.采用高斯消去法对式(14)进行求解,得到当前时刻面元上的源强密度.
1.5 不规则波群模拟实现
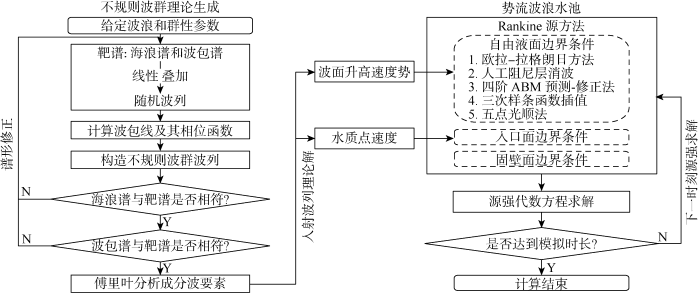
综合上述势流理论和不规则波群生成理论,在Visual Studio平台上采用C++语言编写相关代码,并在程序中调用OpenMP并行库以提高计算效率,实现势流波浪水池的不规则波群生成和传播模拟,数值计算流程如图2 所示.
图2
图2
不规则波群数值模拟流程
Fig.2
Simulation procedure of irregular wave group
2 模型参数影响分析
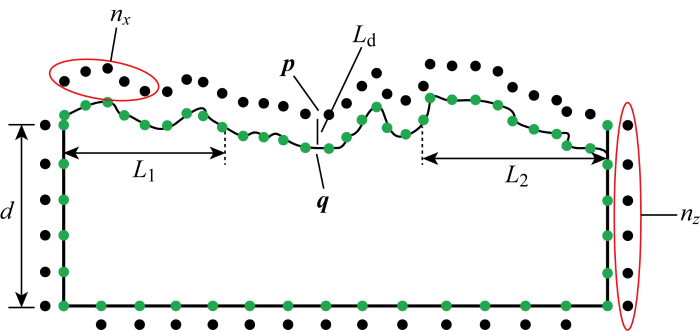
不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 .
图3
图3
数值波浪水池模型布置示意图
Fig.3
Schematic layout of numerical wave tank
L 1 α 1 L 2 α 2 L 1 = 3 λ 0 L 1 缩短, 波浪参数计算误差增大.与L 1 = λ 0 , 2 λ 0 L 1 = 3 λ 0 L 2 = λ 0 2 λ 0 和 4 λ 0 L 2 = 2 λ 0 L 2 = 4 λ 0 α 1 和 α 2 α 1 α 2 L 1 、 L 1 、 α 1 α 2 3 λ 0 、 4 λ 0 、 4
源点外移距离会影响数值求解的稳定性,而源点外移距离由去奇异距离参数β 和l d 共同决定(见式(15)).当β =0.1~0.4时,有义波高和平均周期计算误差均低于1%;其中β =0.3时,有义波高和平均周期误差相对较小,分别为-0.5%和0.1%.当β =0.5 时,源点与配置点距离较近,方程奇异性增强导致计算误差增大.当β >0.5时,源点与配置点过于接近导致方程奇异性过大,计算无法进行.当l d <0.5时,源点与配置点之间距离太近,奇异性增强导致计算无法进行.当l d =0.5,0.6时,源点与配置点之间距离减小,有义波高和平均周期计算误差有所增加.分析表明,β 和l d 分别取0.3和1能保证波浪模拟精度和稳定性.
越深位置处的流场所受波浪扰动越小,故水池垂直边界面(入口面、侧壁面和末端面)的源点可仅布置在离水面一定深度(d )的区域,以提高计算效率.对于有义波高误差,当d =λ 0 /20时,源点在垂直方向上的分布范围过小,导致计算误差超过10%.在源点分布密度相同情况下,源点分布范围增大,对应有义波高误差能降至2%以内.当d =λ 0 /10时,计算得到的有义波高误差约为-0.5%,有义周期计算误差为0.1%.随着d 进一步增加,计算精度变化不大,故d =λ 0 /10便能满足精度要求.
n z 、 n x Δ t d = λ 0 / 10 n z = 4 ~ 8 nx =20,25的情况相比,当nx =15时的有义波高和平均周期计算误差较大,分别为-4.5%和2.5%.当nx =20时,有义波高误差和平均周期误差均小于1%.当nx >25时,源点间的水平距离过小导致积分方程奇异性增强,计算无法进行.对于时间步长分析,相比Δt =T 0 /150,T 0 /200,Δt =T 0 /100得到的有义波高和平均周期计算误差较大,分别为4.5%和8.3%.随着Δt 减小,计算误差逐渐缩小.当Δt =T 0 /200时,有义波高和平均周期计算误差分别为-0.5% 和0.1%.综合考虑计算精度和稳定性,n z 、 n x 和 Δ t T 0 /200.
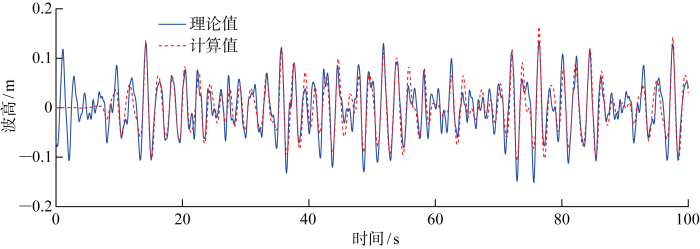
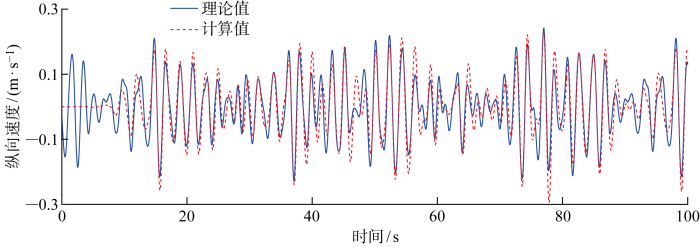
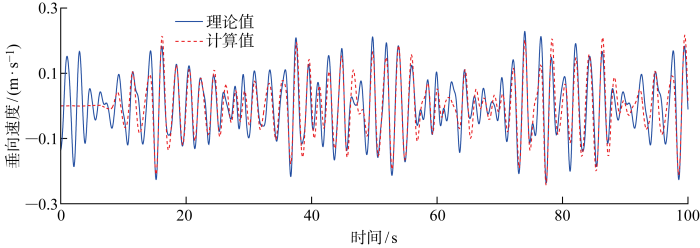
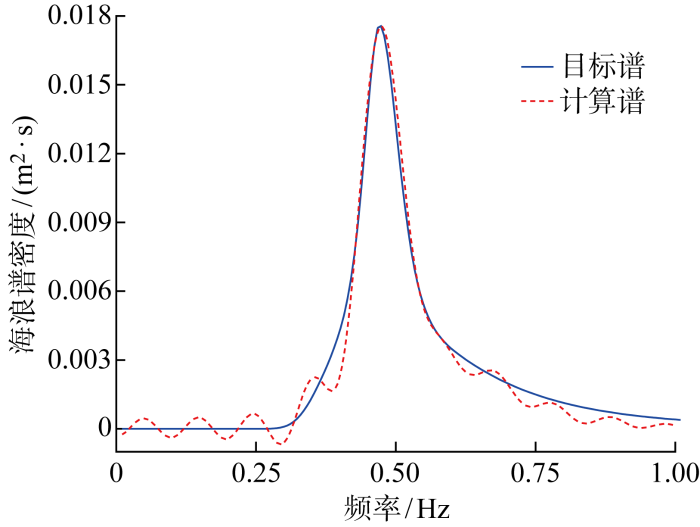
基于上述分析结果,不规则波浪水池模型参数最终选择如下:L 1 = 3 λ 0 , L 2 = 4 λ 0 , α 1 = 4 , α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 , n z = 8 , n x = 20 , Δ t = T 0 / 200 . 图4 ~7 分别给出该组模型参数计算得到的波高时历、流场速度时历、海浪谱与理论值的比较.对于波高和流速时历对比,在初始15 s内,波浪尚未完全发展,计算时历与理论结果相差较大;在15 s后,波浪传播逐渐趋于稳定,波高和流速时历计算值除了在峰、谷附近与理论值有所偏差外,总体上与理论值吻合良好.波高时历计算值和理论值之间的均方根误差为0.023 m,两者相关系数为0.81,基本属于强相关.取稳定后的时历数据进行统计,有义波高和周期分别为0.199 m和2.223 s,误差分别为-0.5%和0.1%.本研究采用自相关函数法估算海浪谱值,在主要能量分布频率范围内计算谱与理论谱吻合良好,在低频和高频区域计算谱出现振荡.研究发现,随着成分波个数(式(8)中的M )增加,低频和高频段海浪谱会变得光滑,但模拟耗时会增加.考虑到计算效率,本文选取成分波个数为200,从波浪场时历和波浪统计特性来看,已满足工程应用中的不规则波模拟精度的需求.上述结果表明,本研究所建立的数值水池及其参数设置能有效模拟不规则波的生成和传播.
图4
图4
波高时历计算值与理论值对比
Fig.4
Comparison of calculated and theoretical values of time series of wave elevations
图5
图5
纵向流速时历计算值与理论值对比
Fig.5
Comparison of calculated and theoretical values of time series of longitudinal velocities of flow
图6
图6
垂向流速时历计算值与理论值对比
Fig.6
Comparison of calculated and theoretical values of time series of vertical velocities of flow
图7
图7
海浪谱计算值与理论目标值对比
Fig.7
Comparison of calculated and theoretical target values of wave spectrums
3 不规则波群模拟验证
为了验证所建立的数值水池模拟单向不规则波群的有效性,采用物理水池试验工况[23 ] 作为测试算例,数值水池模型参数与上节论证得到的参数一致.波浪的H 1/3 =0.07 m,T 1/3 =1.5 s.模拟3组波群传播,群性如下:① G FH =0.6,G LF =15;② G FH =0.7,G LF =15;③ G FH =0.8,G LF =15.目标波群出现位置选在数值水池工作区中点处,并在该处设置一个波高监测点.
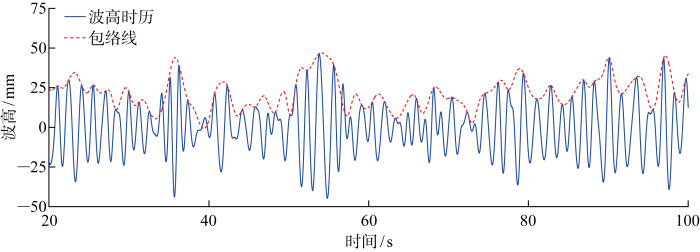
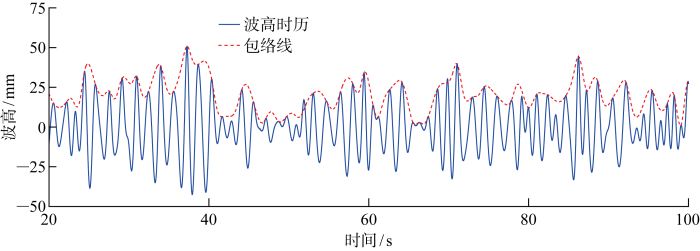
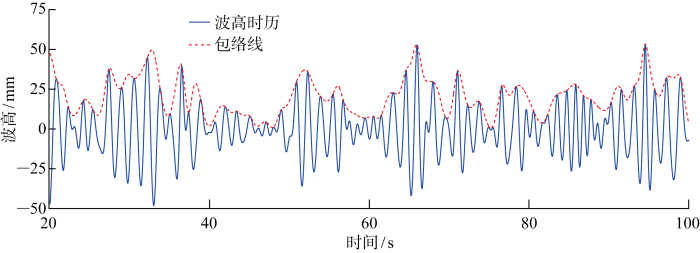
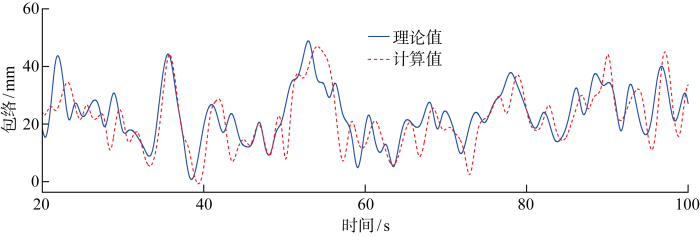
图8 给出了3组波群成分波相位随频率分布.图9 ~11 给出了数值模拟得到的3组波群的波高时历.随着G FH 增大,波面起伏程度变大,表现为包络线波动幅度增大.表2 给出了3组波群波高时历计算值与理论值之间误差和相关性统计,其中均方根误差约为8 mm,相关系数接近0.8.对波高时历进行分析得到波浪特征参数和群性参数,并与物理试验结果和理论目标值进行比较,结果列于表3 和表4 .在波浪要素相同情况下,随着群高参数增大,物理试验测得的有义波高和有义周期与目标值偏差较大.数值模拟得到的波浪特征值随群性变化波动较小,有义波高计算值低于目标值,最大误差约为 -7%;有义周期计算值与目标值吻合良好,最大误差约为4%.对于波浪群性,计算值与目标值基本吻合,群高和群长参数最大误差分别约为7%和6%,误差范围与试验结果相近.G FH 由波包线的方差和均值两者比值决定[17 ] ,图12 给出了数值模拟不规则波群波包线与理论波包线对比,发现数值模拟的波包线与理论值在整体趋势上吻合,但在波峰和波谷位置存在局部偏差,这造成计算所得群高参数与目标值出现较大误差.
图8
图8
不规则波群成分波相位随频率分布
Fig.8
Phases of irregular wave group components with different frequencies
图9
图9
不规则波群波高时历计算值(G FH =0.6,G LF =15)
Fig.9
Time series of calculated wave elevation of irregular wave group (G FH =0.6, G LF =15)
图10
图10
不规则波群波高时历计算值(G FH =0.7,G LF =15)
Fig.10
Time series of calculated wave elevation of irregular wave group (G FH =0.7, G LF =15)
图11
图11
不规则波群波高时历计算值(G FH =0.8,G LF =15)
Fig.11
Time series of calculated wave elevation of irregular wave group (G FH =0.8, G LF =15)
图12
图12
数值模拟不规则波群波包线与理论波包线对比(G FH =0.6,G LF =15)
Fig.12
Comparison of calculated and theoretical wave envelopes (G FH =0.6, G LF =15)
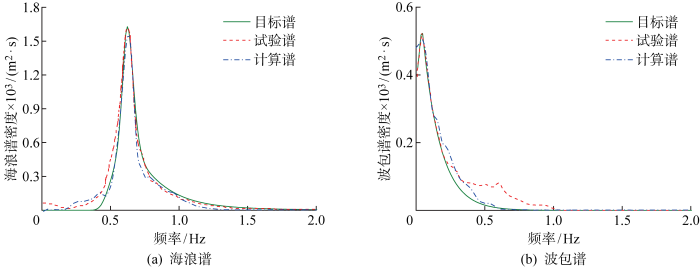
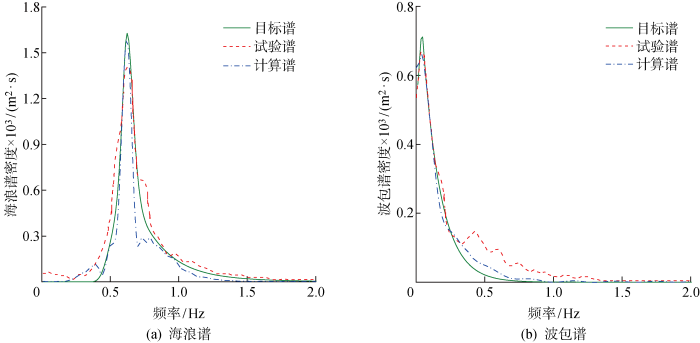
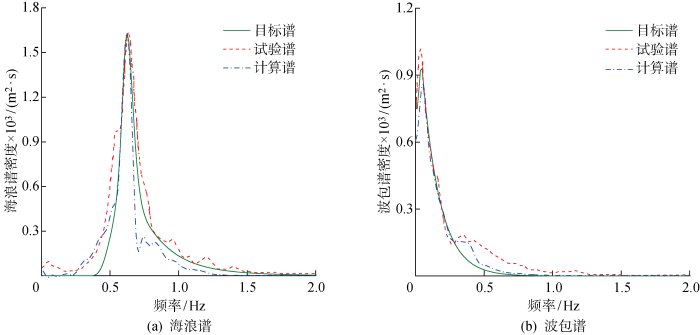
图13 ~15 给出了数值模拟、物理试验和理论生成得到的3组波群的海浪谱和波包谱对比.海浪谱主要能量分布在0.5~1 Hz,该频率范围内计算值和试验值与理论值基本吻合.在波包谱主能量频段范围内(0~0.5 Hz),波包谱的计算值与试验值和理论值基本吻合.可以观察到,波包谱的谱峰频率很低(约为0.04 Hz),而海浪谱的谱峰频率较高(约为0.62 Hz),由式(7)可知G LF 的误差对波包谱的谱峰频率十分敏感.成分波的频率间隔难以同时兼顾波包谱和海浪谱的能量分布,仅在0~2 Hz区间内采用等分频率法,这造成波包谱峰频附近的频率间隔偏大,导致数值模拟得到的波包谱峰值偏小,使得G LF 的误差偏大.
图13
图13
数值计算、物理试验和理论目标谱对比(G FH =0.6,G LF =15)
Fig.13
Comparison of calculated, experimental, and target spectrum (G FH =0.6, G LF =15)
图14
图14
数值计算、物理试验和理论目标谱对比(G FH =0.7,G LF =15)
Fig.14
Comparison of calculated, experimental, and target spectrum (G FH =0.7, G LF =15)
图15
图15
数值计算、物理试验和理论目标谱对比(G FH =0.8,G LF =15)
Fig.15
Comparison of calculated, experimental, and target spectrum (G FH =0.8, G LF =15)
总体来说,本研究方法对不规则波群特征参数计算误差为1%~7%,每组工况计算耗时约为 10 h.若采用黏性计算流体力学(computational fluid dynamics,CFD)方法对相同工况进行模拟[18 ] ,波浪特征参数计算误差为3%~13%,每组工况计算耗时约为85 h.与黏性CFD方法相比,本研究方法在计算精度和效率上展示出较大的优势.上述分析表明,本研究开发的数值水池能生成符合指定波浪要素和群性特征的单向不规则波.
4 结论
(1) 开发了基于半混合欧拉-拉格朗日自由面追踪方法和去奇异边界元法的数值波浪水池,用于不规则波群的生成和传播模拟.结合不规则波群理论生成方法,在水池入口面给定流速分布实现波群的生成.在首、末端区域设置人工阻尼层抑制波浪反射,改善波浪模拟精度.采用四阶ABM预测-修正法更新自由面,并采用三次样条插值法和五点光顺法对自由面进行平滑处理,以提高数值计算稳定性.
(2) 以四级海况不规则波作为测试工况,分析了计算模型参数对波浪模拟精度、稳定性和效率的影响,给出了不规则波模拟的模型参数建议值.随着前置和后置阻尼层长度的增加,波浪模拟精度逐渐提高,而阻尼项缓冲函数系数对求解精度影响不大;当前置和后置阻尼层长度分别取平均波长的3倍和4倍时,可兼顾波浪模拟精度和效率.适当的源点外移距离能改善波浪传播的稳定性,而去奇异距离过小会导致计算失效,去奇异距离参数β 和l d 分别在[0.1,0.4]和[0.5,1.0]区间内选取时能保证计算精度.将源点布置在距离自由面一定深度的区域内能够兼顾计算精度和效率,而水深方向源点数的增加对精度提升有限.单个平均波长范围内源点数适当增加可提高波浪模拟精度,但源点数过多会使奇异性增大导致计算失效.波浪计算精度随计算时间步长减小而提高.建议沿水深方向离静水面1/10平均波长范围内布置8个源点,沿波长方向单位平均波长范围内布置20个源点,时间步长取波浪平均周期的1/200.
(3) 采用比选后的模型参数模拟了3组单向不规则波群,在海浪谱和波包谱主要能量频段范围内,计算谱、试验谱和目标谱基本吻合.与目标值相比,有义波高、有义周期、群高和群长参数计算误差均在7%以内.研究表明,所开发的数值水池能生成符合指定波浪要素和群性特征的单向不规则波.
参考文献
View Option
[1]
TANG H HUANG C Bragg reflection in a fully nonlinear numerical wave tank based on boundary integral equation method
[J]. Ocean Engineering 2008 , 35 (17/18 ): 1800 -1810 .
[本文引用: 1]
[2]
李裕龙 , 朱仁传 , 缪国平 . 基于全时域势流理论的船舶与液舱晃荡耦合运动的数值计算
[J]. 船舶力学 2016 , 20 (11 ): 1369 -1380 .
[本文引用: 1]
LI Yulong ZHU Renchuan MIU Guoping Numerical method of ship motions coupled with tank sloshing based on fully time domain potential flow theory
[J]. Ship Mechanics 2016 , 20 (11 ): 1369 -1380 .
[本文引用: 1]
[3]
卜淑霞 , 鲁江 , 顾民 . 基于三维时域混合源法的顶浪不规则波参数横摇研究
[J]. 船舶力学 2018 , 22 (8 ): 926 -934 .
[本文引用: 1]
PU Shuxia LU Jiang GU Min Research on parameter roll of irregular top wave based on three-dimensional time-domain mixed source method
[J]. Ship Mechanics 2018 , 22 (8 ): 926 -934 .
[本文引用: 1]
[4]
WANG L X TANG H WU Y H Simulation of wave-body interaction: A desingularized method coupled with acceleration potential
[J]. Journal of Fluids & Structures 2015 , 52 : 37 -48 .
[本文引用: 1]
[5]
ZHANG X T KHOO B C LOU J Application of desingularized approach to water wave propagation over three-dimensional topography
[J]. Ocean Engineering 2007 , 34 (10 ): 1449 -1458 .
[本文引用: 1]
[6]
沈王刚 . 基于FMBEM的数值波浪水池及非线性波浪重构方法 [D]. 上海 : 上海交通大学 , 2018 .
[本文引用: 1]
SHENG Wanggang A numerical wave pool and nonlinear wave reconstruction method based on FMBEM [D]. Shanghai : Shanghai Jiao Tong University , 2018 .
[本文引用: 1]
[7]
XU G BAI X MA X et al Numerical simulation of fully nonlinear NWT by DBIEM method with MTF for the downstream boundary
[J]. Journal of Ship Mechanics 2017 , 21 (9 ): 1062 -1070 .
[本文引用: 1]
[8]
XU G ZHAO G CHEN J et al The numerical analysis of the flow on the smooth and nonsmooth boundaries by IBEM/DBIEM
[J]. Mathematical Problems in Engineering 2019 , 2019 (3 ): 1 -14 .
[本文引用: 1]
[9]
FENG A CHEN Z PRICE W G A desingularized Rankine source method for nonlinear wave-body interaction problems
[J]. Ocean Engineering 2015 , 101 (1 ): 131 -141 .
[本文引用: 1]
[10]
杨师宇 , 吴静萍 , 汪敏 , 等 . 基于去奇异边界元法的二维数值波浪水池计算参数影响分析
[J]. 武汉理工大学学报: 交通科学与工程版 2021 , 45 (5 ): 912 -918 .
[本文引用: 2]
YANG Shiyu WU Jingping WANG Min et al Influence analysis of calculation parameters in two-dimensional numerical wave tank based on Dbiem
[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering 2021 , 45 (5 ): 912 -918 .
[本文引用: 2]
[11]
吴明 , 应荣熔 , 蔡烽 , 等 . 不规则波数值模拟精度影响因素分析
[J]. 舰船科学技术 2020 , 42 (9 ): 75 -81 .
[本文引用: 2]
WU Ming YING Rongrong CAI Feng et al Analysis of factors affecting the accuracy of irregular wave numerical simulation
[J]. Ship Science and Technology 2020 , 42 (9 ): 75 -81 .
[本文引用: 2]
[12]
SCOLAN Y M Some aspects of the flip-through phenomenon: A numerical study based on the desingularized technique
[J]. Journal of Fluids and Structures 2010 , 26 (6 ): 918 -953 .
[本文引用: 1]
[13]
RYE H Ocean wave groups [R]. Trondheim, Norway : Department of Marine Technology, University of Trondheim , 1982 .
[本文引用: 1]
[14]
GODA Y On wave groups
[C]// Proceeding of the Behaviour of Offshore Structures Conference Trondheim, Norway : Norwegian Institute of Technology , 1976 , 1 : 115 -128 .
[本文引用: 1]
[15]
FUNKE E R MANSARD E On the synthesis of realistic sea states in a laboratory flume
[J]. Report, NRC of Canada 1979 , 66 : 2974 -2991 .
[本文引用: 1]
[16]
XU D HOU W ZHAO M et al The statistical simulation of wave groups
[J]. Applied Ocean Research 1993 , 15 : 217 -226 .
[本文引用: 1]
[17]
刘思 . 多向不规则波群的模拟研究 [D]. 大连 : 大连理工大学 , 2012 .
[本文引用: 5]
LIU Si Simulation study of multi-directional irregular wave groups [D]. Dalian : Dalian University of Technology , 2012 .
[本文引用: 5]
[18]
王文杰 . 基于高阶造波理论的单向不规则波群RANS模拟研究 [D]. 武汉 : 武汉理工大学 , 2022 .
[本文引用: 2]
WANG Wenjie Research on RANS simulation of unidirectional irregular wave groups based on higher-order wave theory [D]. Wuhan : Wuhan University of Technology , 2022 .
[本文引用: 2]
[19]
宁德志 . 快速多极子边界元方法在完全非线性水波问题中的应用 [D]. 大连 : 大连理工大学 , 2005 .
[本文引用: 1]
NING Dezhi The application of fast multipole boundary element method in completely nonlinear water wave problems [D]. Dalian : Dalian University of Technology , 2005 .
[本文引用: 1]
[20]
GODA Y Random seas and design of maritime structures [M]. London,UK : World Scientific Publishing Company , 2010 .
[本文引用: 1]
[21]
CAO Y SCHULTZ W W BECK R F Three-dimensional desingularized boundary integral methods for potential problems
[J]. International Journal for Numerical Methods in Fluids 1991 , 12 (8 ): 785 -803 .
[本文引用: 1]
[22]
俞聿修 . 随机波浪及其工程应用 [M]. 大连 : 大连理工大学出版社 , 1999 .
[本文引用: 1]
YU Yuxiu Random waves and their engineering applications [M]. Dalian : Dalian University of Technology Press , 1999 .
[本文引用: 1]
[23]
刘思 , 柳淑学 , 李金宣 , 等 . 单向不规则波群的实验室模拟和分析
[J]. 水道港口 2011 , 32 (5 ): 305 -312 .
[本文引用: 1]
LIU Si LIU Shuxue LI Jinxuan et al Laboratory simulation and analysis of unidirectional irregular wave groups
[J]. Waterway Port 2011 , 32 (5 ): 305 -312 .
[本文引用: 1]
Bragg reflection in a fully nonlinear numerical wave tank based on boundary integral equation method
1
2008
... 在船舶与海洋工程领域,结构物在海浪中的运动和受力是设计人员关心的问题[1 ] .海浪的生成和传播特性分析是研究海浪与结构物相互作用的基础.实际海浪往往以连续几个大波的形式成群出现,构成不规则波群.相对于不规则波,不规则波群更能表征真实的海浪特征.为了使波群理论更好地用于船舶与海洋结构物设计,有必要开发数值波浪水池实现不规则波群生成和传播模拟. ...
基于全时域势流理论的船舶与液舱晃荡耦合运动的数值计算
1
2016
... 基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率. ...
Numerical method of ship motions coupled with tank sloshing based on fully time domain potential flow theory
1
2016
... 基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率. ...
基于三维时域混合源法的顶浪不规则波参数横摇研究
1
2018
... 基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率. ...
Research on parameter roll of irregular top wave based on three-dimensional time-domain mixed source method
1
2018
... 基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率. ...
Simulation of wave-body interaction: A desingularized method coupled with acceleration potential
1
2015
... 基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率. ...
Application of desingularized approach to water wave propagation over three-dimensional topography
1
2007
... 基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率. ...
1
2018
... 基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率. ...
1
2018
... 基于势流理论的数值水池凭借计算高效,广泛应用于海洋工程水动力问题研究[2 ] .势流理论分为频域理论和时域理论.受限于线性和周期性假设,频域方法主要用于规则波问题的求解.时域方法能对瞬态自由面进行追踪,适用于不规则波问题的研究[3 ] .目前,追踪瞬态自由面质点的主流方法为混合欧拉-拉格朗日法[4 ] ,该方法将自由面边界条件写成随体导数形式,便于计算迭代各个时间步内的流体质点速度.根据自由面网格节点速度选取方式不同,混合欧拉-拉格朗日法分为半拉格朗日法和物质节点法.半拉格朗日法[5 ] 认为网格节点只存在垂向速度,网格的水平坐标无需更新,适用于波浪传播模拟研究.物质节点法[6 ] 则认为节点速度等于该处流体速度,自由面网格坐标需频繁更新;该方法避免了局部网格节点堆积,但频繁的网格更新也降低了计算效率. ...
Numerical simulation of fully nonlinear NWT by DBIEM method with MTF for the downstream boundary
1
2017
... 边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响. ...
The numerical analysis of the flow on the smooth and nonsmooth boundaries by IBEM/DBIEM
1
2019
... 边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响. ...
A desingularized Rankine source method for nonlinear wave-body interaction problems
1
2015
... 边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响. ...
基于去奇异边界元法的二维数值波浪水池计算参数影响分析
2
2021
... 边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响. ...
... 不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为 L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度 L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 . ...
Influence analysis of calculation parameters in two-dimensional numerical wave tank based on Dbiem
2
2021
... 边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响. ...
... 不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为 L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度 L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 . ...
不规则波数值模拟精度影响因素分析
2
2020
... 边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响. ...
... 不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为 L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度 L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 . ...
Analysis of factors affecting the accuracy of irregular wave numerical simulation
2
2020
... 边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响. ...
... 不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为 L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度 L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 . ...
Some aspects of the flip-through phenomenon: A numerical study based on the desingularized technique
1
2010
... 边界元方法是一种高效求解势流问题的数值方法.然而,传统边界元法的源点与配置点距离过近,易导致积分奇异性增强,影响自由面的求解精度和稳定性.为处理奇异性问题,可将源点布置在流场边界之外,发展出去奇异边界元方法,该方法实施简单又能提高求解精度.Xu等[7 -8 ] 采用去奇异方法结合多次透射公式进行消波,处理了自由面法向速度变化剧烈区域的奇异性,提高了波浪的模拟精度.Feng等[9 ] 基于去奇异边界元法处理了波浪与结构物相互作用时交界区域的奇异性问题,分析了结构物波浪中的运动和受力.杨师宇等[10 ] 讨论了去奇异距离、源点分布和时间步长等参数对规则波模拟精度的影响.吴明等[11 ] 讨论了网格尺寸、时间步长、欠松弛因子和频率间隔量等因素对不规则波模拟精度的影响.Scolan[12 ] 讨论了去奇异距离和关于速度势的附加时间项对非线性波浪模拟精度的影响. ...
1
1982
... 关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道. ...
On wave groups
1
1976
... 关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道. ...
On the synthesis of realistic sea states in a laboratory flume
1
1979
... 关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道. ...
The statistical simulation of wave groups
1
1993
... 关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道. ...
5
2012
... 关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道. ...
... 波包谱采用刘思[17 ] 提出的经验公式: ...
... 单向不规则波群理论生成步骤[17 ] 如下:① 给定海浪的有义波高、谱峰周期、群高和群长等参数;②以海浪谱 S η S A η ' ( t ) η A ( t ) η A ( t ) A ( t ) η ' ( t ) φ ( t ) η ( t ) = A ( t ) × c o s φ ( t ) η ( t )
... 不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为 L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度 L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 . ...
... 图8 给出了3组波群成分波相位随频率分布.图9 ~11 给出了数值模拟得到的3组波群的波高时历.随着G FH 增大,波面起伏程度变大,表现为包络线波动幅度增大.表2 给出了3组波群波高时历计算值与理论值之间误差和相关性统计,其中均方根误差约为8 mm,相关系数接近0.8.对波高时历进行分析得到波浪特征参数和群性参数,并与物理试验结果和理论目标值进行比较,结果列于表3 和表4 .在波浪要素相同情况下,随着群高参数增大,物理试验测得的有义波高和有义周期与目标值偏差较大.数值模拟得到的波浪特征值随群性变化波动较小,有义波高计算值低于目标值,最大误差约为 -7%;有义周期计算值与目标值吻合良好,最大误差约为4%.对于波浪群性,计算值与目标值基本吻合,群高和群长参数最大误差分别约为7%和6%,误差范围与试验结果相近.G FH 由波包线的方差和均值两者比值决定[17 ] ,图12 给出了数值模拟不规则波群波包线与理论波包线对比,发现数值模拟的波包线与理论值在整体趋势上吻合,但在波峰和波谷位置存在局部偏差,这造成计算所得群高参数与目标值出现较大误差. ...
5
2012
... 关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道. ...
... 波包谱采用刘思[17 ] 提出的经验公式: ...
... 单向不规则波群理论生成步骤[17 ] 如下:① 给定海浪的有义波高、谱峰周期、群高和群长等参数;②以海浪谱 S η S A η ' ( t ) η A ( t ) η A ( t ) A ( t ) η ' ( t ) φ ( t ) η ( t ) = A ( t ) × c o s φ ( t ) η ( t )
... 不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为 L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度 L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 . ...
... 图8 给出了3组波群成分波相位随频率分布.图9 ~11 给出了数值模拟得到的3组波群的波高时历.随着G FH 增大,波面起伏程度变大,表现为包络线波动幅度增大.表2 给出了3组波群波高时历计算值与理论值之间误差和相关性统计,其中均方根误差约为8 mm,相关系数接近0.8.对波高时历进行分析得到波浪特征参数和群性参数,并与物理试验结果和理论目标值进行比较,结果列于表3 和表4 .在波浪要素相同情况下,随着群高参数增大,物理试验测得的有义波高和有义周期与目标值偏差较大.数值模拟得到的波浪特征值随群性变化波动较小,有义波高计算值低于目标值,最大误差约为 -7%;有义周期计算值与目标值吻合良好,最大误差约为4%.对于波浪群性,计算值与目标值基本吻合,群高和群长参数最大误差分别约为7%和6%,误差范围与试验结果相近.G FH 由波包线的方差和均值两者比值决定[17 ] ,图12 给出了数值模拟不规则波群波包线与理论波包线对比,发现数值模拟的波包线与理论值在整体趋势上吻合,但在波峰和波谷位置存在局部偏差,这造成计算所得群高参数与目标值出现较大误差. ...
2
2022
... 关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道. ...
... 总体来说,本研究方法对不规则波群特征参数计算误差为1%~7%,每组工况计算耗时约为 10 h.若采用黏性计算流体力学(computational fluid dynamics,CFD)方法对相同工况进行模拟[18 ] ,波浪特征参数计算误差为3%~13%,每组工况计算耗时约为85 h.与黏性CFD方法相比,本研究方法在计算精度和效率上展示出较大的优势.上述分析表明,本研究开发的数值水池能生成符合指定波浪要素和群性特征的单向不规则波. ...
2
2022
... 关于不规则波群的理论生成方法主要有3种.早期研究认为只需要严格模拟海浪频谱的谱型[13 -14 ] 并结合线性叠加原理即可模拟波群,但该方法需要进行多次重复模拟.学者们随后提出同时模拟海浪频谱和相位谱,并用平滑的波面位移过程线描述波群[15 ] ,该方法引入的群性参数只能描述波群的高度特征.为了兼顾波群高度和长度两方面特征,第3种方法用波包线代替波面位移过程线来模拟相位谱[16 ] ,波群特征由海浪频谱和波包谱共同决定.目前,结合波包谱理论进行不规则波群数值模拟研究方面,主要有刘思[17 ] 基于有限元方法求解布辛尼斯克方程和王文杰[18 ] 基于有限体积法求解雷诺时均纳维-斯托克斯方程开展过工作,而基于边界元方法求解拉普拉斯方程的不规则波群模拟研究仍未见报道. ...
... 总体来说,本研究方法对不规则波群特征参数计算误差为1%~7%,每组工况计算耗时约为 10 h.若采用黏性计算流体力学(computational fluid dynamics,CFD)方法对相同工况进行模拟[18 ] ,波浪特征参数计算误差为3%~13%,每组工况计算耗时约为85 h.与黏性CFD方法相比,本研究方法在计算精度和效率上展示出较大的优势.上述分析表明,本研究开发的数值水池能生成符合指定波浪要素和群性特征的单向不规则波. ...
1
2005
... 假设流体为理想流体,流动无旋,建立如图1 所示的波浪水池,坐标原点位于入口面和静水面的交线上.采用半混合欧拉-拉格朗日方法追踪瞬态自由面,将自由面边界条件改写为半拉格朗日形式[19 ] .在笛卡尔坐标系下,速度势满足以下方程: ...
1
2005
... 假设流体为理想流体,流动无旋,建立如图1 所示的波浪水池,坐标原点位于入口面和静水面的交线上.采用半混合欧拉-拉格朗日方法追踪瞬态自由面,将自由面边界条件改写为半拉格朗日形式[19 ] .在笛卡尔坐标系下,速度势满足以下方程: ...
1
2010
... 本研究结合海浪谱和波包谱理论生成单向不规则波群.海浪谱为改进的JONSWAP谱[20 ] : ...
Three-dimensional desingularized boundary integral methods for potential problems
1
1991
... 式中:N 为边界上的面元总数,包括入口面、自由面、底面、侧面和末端面的面元数;N I 为入口面的面元数;N F 为自由面的面元数;[q p ]表示q 点与p 点组成的向量;ϕ in 为入口面处的速度势,由式(8)求得;ϕ fs 为自由面处的速度势,由式(11)求得.当源点与场点距离过近时,式(14)奇异性增强,导致数值解精度下降.为了解决该问题,将源点布置在流域边界以外一定距离处,该距离称为去奇异距离(L d ),由下式确定[21 ] : ...
1
1999
... 不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为 L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度 L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 . ...
1
1999
... 不规则波群是具有特定群性的不规则波,故不规则波的有效模拟是准确模拟不规则波群的前提.本节针对不规则波模拟精度问题,依次分析模型参数(阻尼层参数、去奇异距离、源点分布和时间步长)对计算结果的影响,空间参数示意如图3 所示.考虑到对波群模拟使用的波包谱公式(6)和(7)是由三至四级海况下实测波浪数据分析所得[17 ] ,因此本节模型参数依赖性分析选择四级海况为测试工况,波浪有义波高(H 1/3 )为2 m,有义周期(T 1/3 )为7.02 s,平均波长(λ 0 )为31 m.数值模拟缩尺比为1∶10,对应有义波高为0.2 m,有义周期为2.22 s,平均波长为3.1 m.数值波浪水池见图1 ,波浪沿x 方向传播,水池沿x 方向被划分为前置阻尼区、工作区和后置阻尼区3个区域,长度分别为 L 1 、 3 λ 0 L 2 . 水池宽度为0.5 m,水深为2.5 m.由于波浪为单向不规则波,故沿水池宽度方向仅布置3个面元.在水池工作区中点,设置一个波高监测点,并在静水面以下0.5 m处设置一个流速监测点.参照其他学者关于模型参数讨论分析[10 -11 ] ,本文模型参数取值讨论范围如表1 所列.在对某一参数进行分析时,仅改变该参数的取值,其他参数均取默认值:前置阻尼层长度 L 1 = 3 λ 0 L 2 = 4 λ 0 α 1 = α 2 = 4 , β = 0.3 , l d = 1 , d = λ 0 / 10 n z = 8 n x = 20 Δ t = T 0 / 200 . [22 ] 得到波列的有义波高和有义周期汇总于表1 . ...
单向不规则波群的实验室模拟和分析
1
2011
... 为了验证所建立的数值水池模拟单向不规则波群的有效性,采用物理水池试验工况[23 ] 作为测试算例,数值水池模型参数与上节论证得到的参数一致.波浪的H 1/3 =0.07 m,T 1/3 =1.5 s.模拟3组波群传播,群性如下:① G FH =0.6,G LF =15;② G FH =0.7,G LF =15;③ G FH =0.8,G LF =15.目标波群出现位置选在数值水池工作区中点处,并在该处设置一个波高监测点. ...
Laboratory simulation and analysis of unidirectional irregular wave groups
1
2011
... 为了验证所建立的数值水池模拟单向不规则波群的有效性,采用物理水池试验工况[23 ] 作为测试算例,数值水池模型参数与上节论证得到的参数一致.波浪的H 1/3 =0.07 m,T 1/3 =1.5 s.模拟3组波群传播,群性如下:① G FH =0.6,G LF =15;② G FH =0.7,G LF =15;③ G FH =0.8,G LF =15.目标波群出现位置选在数值水池工作区中点处,并在该处设置一个波高监测点. ...