电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义.
目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解.
为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略.
电力系统的运行方式影响其频率动态过程的模型参数.在电力系统运行状态变化的场景下,基于固定参数的二次调频策略可能导致ACE的偏移量超出预期.此外,集中式的二次调频控制策略在进行优化决策时,需要全网的模型和监测信息,对数据传输时效性和可靠性依赖程度较高,通信系统延迟和错误数据将限制其控制效果[18 ] .分散式二次调频控制策略由于各控制器间缺乏协调交流而影响优化结果的全局最优性[19 ] .相较之下,分布式的二次调频控制策略能够减少系统的数据交互量,在保障全局最优的同时提高可靠性,降低通信成本[20 ] .如何在分布式的二次调频控制中计及系统参数变化的影响,是亟待解决的问题.
针对上述问题,面向电力系统二次调频控制策略开展研究.首先,提出一种基于分布式模型预测控制(distributed model predictive control,DMPC)的自适应二次调频策略,通过辨识及更新各控制区域模型参数来提升二次调频性能;然后,建立电力系统各控制区域的频率响应参数辨识模型,采用递推最小二乘法(recursive least square,RLS)求解,以实现二次调频模型参数的在线更新;最后,基于DMPC调节机组出力,利用纳什均衡将系统二次调频控制分解为各区域的分布式优化问题,通过滚动求解来最小化ACE.算例分析证实了所提控制策略的有效性.
1 区域二次调频模型参数在线辨识
1.1 多区域互联系统模型
多区域互联电力系统由多个控制区域组成,某区域内的扰动将经联络线传递给其他区域,二次调频主要由各区域内的火电机组承担[21 ] .区域i的二次调频模型如图1 所示.图中:N为区域个数;s为拉普拉斯算子; βi 为区域i的频率偏移系数; Ai 、 Δ fi 、Δ Px ,i 分别为区域i对应的ACE 、频率偏移量和联络线功率偏移量;Rg Δ fj 为区域j对应的频率偏移量;Hi 、Di 分别为区域i的惯性系数和阻尼系数;Tij 为区域i和j之间的联络线同步系数;Δ Pl ,i 、Δ Pm ,i 和Δ Pg ,i 分别为区域i的负荷变化量、控制器输出指令和机组输出功率变化;vi 为区域i与其他区域间的接口量.
图1
图1
区域i 的频率响应模型
Fig.1
Frequency response model of Area i
(1) Δfi = 1 2 H i s + D i g ,i -ΔPl ,i -ΔPx ,i )
(2) ΔPx ,i = 2 π s ∑ j = 1 , j ≠ i N T i j Δ f i - ∑ j = 1 , j ≠ i N T i j Δ f j
(3) Ai =Δ Px ,i +βi Δ fi
区域i的惯性系数Hi 、阻尼系数Di 和频率偏移量Δ fi 可由机组参数计算[22 ] ,表示为
(4) Hi = ∑ k = 1 N m i,k Sg ,i,k / ∑ k = 1 N m g ,i,k
(5) Di = ∑ k = 1 N m i,k Sg ,i,k / ∑ k = 1 N m g ,i,k
(6) 1 R i ∑ k = 1 N m S g , i , k R i , k ∑ k = 1 N m g ,i,k
(7) Δfi = 1 H i ∑ k = 1 N m i,k Δfi,k
式中:Nm i 为区域i的下垂系数;Hi,k 、Di,k 、Ri,k 、Sg ,i,k 分别为机组k的惯性系数、阻尼系数、下垂系数和容量.
1.2 二次调频参数辨识模型
考虑各控制区域机组输入量Δ Pm ,i 和输出量Δ Pg ,i 间的传递特性,将频率响应模型表示为
(8) Gi (s)= Δ P g , i Δ P m , i Q i s P i s
式中:Qi (s)为传递函数Gi (s)的分子多项式;Pi (s)为传递函数Gi (s)的分母多项式.
(9) y(t)P(z)=u(t)Q(z)+o(t)
(10) P(z)=1+a1 z-1 +a2 z-2 +…+ a n 1 z - n 1
(11) Q(z)=b1 z-1 +b2 z-2 +…+ b n 2 z - n 2
式中:P(z)、Q(z)为对应的离散传递函数;ap 、bq 分别为离散后的分母和分子多项式系数,且p=1,2,…,n1 ,q=1, 2, …, n2 ;u(t)、y(t)分别为输入和输出数据序列,分别对应Δ Pm ,i 和Δ Pg ,i ;o(t)为白噪声,且均值为0,方差为σ v 2 .
针对机组频率响应模型,传递函数的分子和分母多项式一般均为1阶[23 -24 ] .因此,式(10)和(11)可简化为
(12) P(z)=1+a1 z-1
(13) Q(z)=b1 z-1
1.3 基于RLS的参数辨识方法
(14) yt = u T t
式中:yt 为第t 次迭代时的输出量;ut 为第t 次迭代时的输入向量;θ 为参数向量.
利用RLS 求解式(14)中的参数向量[25 ] ,表示为
(15) K t = P t - 1 u t 1 + u T t P t - 1 u t y ^ t = u T t θ ^ t - 1 e t = y t - y ^ t θ ^ t = θ ^ t - 1 + K t e t P t = P t - 1 + K t u T t P t - 1
式中:Kt 为第t 次迭代时的中间向量;Pt 为第t 次迭代时的协方差矩阵;y ^ t t 次迭代时的估计值;θ ^ t t 次迭代时的估计值;et 为第t 次迭代时的估计偏差.
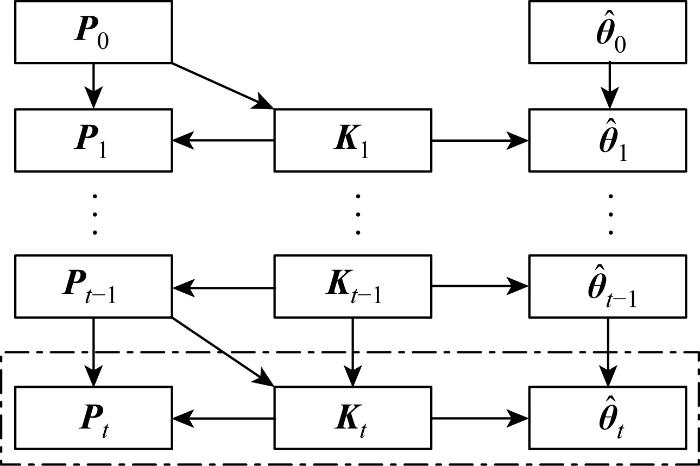
基于RLS 的参数辨识方法的迭代过程如图2 所示. 由参数量估计值θ ^ 0 P 0 的初始化开始,利用式(15)计算每步迭代时的中间向量Kt ,更新参数量的估计值θ ^ t Pt . 在迭代过程中,RLS计算当前的估计偏差et ,将θ ^ t - 1 et 作为第t 次迭代时的修正值,对参数量的估计值θ ^ t - 1 θ ^ t [26 ] . 随着时间的推移,RLS基于监测数据yt 和ut 估计当前时刻的参数量θ ^ t i 的频率响应模型Gi (s ).
图2
图2
基于RLS的参数辨识方法迭代过程示意图
Fig.2
Schematic diagram of iteration process of RLS-based parameter identification method
2 区域二次调频模型参数在线辨识
2.1 预测模型
联立式(1)~ (8)并整理可得,区域i的连续状态方程为
(16) Δ x · i = A c , i Δ x i + B c , i Δ u i + F c , i Δ d i + ∑ i ≠ j A c , a , i j Δ x j y i = C c , i Δ x i
式中:Δxi 、Δxj 分别为区域i 和j 的状态变量;Δui 、Δdi 、yi 分别为区域i 的控制变量、扰动变量和输出变量;A c, i B c, i F c, i A c,a, ij C c, i
(17) Δxi =[Δ f i Δ P x , i Δ P g , i T
(18) Δui =[ΔP m, i
(19) Δdi =[ΔP l, i
(20) yi =[Ai ]
(21) Δ x i ( t + t r ) = A r , i Δ x i ( t ) + B r , i Δ u i ( t ) + F r , i Δ d i ( t ) + ∑ i ≠ j A r , a , i j Δ x j ( t ) y i ( t ) = C r , i Δ x i ( t )
式中:t r 为离散化的步长;Δxi (t )、Δxj (t )分别为区域i 和j 在t 时刻的离散状态变量;Δui (t )、Δdi (t )、yi (t )分别为区域i 在t 时刻的离散控制变量、扰动变量和输出变量;A r, i B r, i F r, i A r,a, ij C r, i
(22) Ar, i = e A c , i t r
(23) Br, i = ∫ 0 t r e A c , i t r c, i dt
(24) Fr, i = ∫ 0 t r e A c , i t r c, i dt
(25) Ar,a, ij = ∫ 0 t r e A c , i t r r,a, ij dt
(26) C r, i C c, i
2.2 滚动优化
(27) Yi (k )= [yi (k +1|k ) yi (k +2|k ) … yi (k +N P |k )]T
(28) ΔUi (k )=[Δui (k ) Δui (k +1) … ui (k +N C -1|k )]T
以区域i 的输出序列Yi 和控制序列ΔUi 的平方加权和最小为优化目标,则目标函数Ji (k )可表示为
(29) $\begin{aligned}\min _{\Delta u_{i}\left(k+N_{\mathrm{C}} \mid k\right)} J_{i}(k)= & \sum_{\tau=1}^{N_{\mathrm{P}}}\left[\left\|\boldsymbol{y}_{i}(k+\tau \mid k)\right\|_{Q_{i}}^{2}+\right. \\& \left.\left\|\Delta \boldsymbol{u}_{i}(k+\tau \mid k)\right\|_{\boldsymbol{R}_{i}}^{2}\right]\end{aligned}$
式中:Qi 、Ri 分别为区域i 的输出变量和控制变量的加权矩阵.
(30) $P_{\mathrm{g}, i, \min } \leqslant P_{\mathrm{g}, i}(k-1)+\Delta P_{\mathrm{g}, i}(k) \leqslant P_{\mathrm{g}, i, \max }$
(31) $\Delta P_{\mathrm{g}, i, \min } \leqslant \Delta P_{\mathrm{g}, i}(k) \leqslant \Delta P_{\mathrm{g}, i, \max }$
式中:P g, i ,max 、P g, i ,min 分别为区域i 有功功率输出的最大值和最小值;ΔP g, i ,max 、ΔP g, i ,min 分别为区域i 爬坡功率的最大值和最小值;P g, i k )为区域i 在k 时刻的有功功率输出.
(32) ΔP x, i ,min ≤ΔP x, i k )≤ΔP x, i ,max
式中:ΔP x, i ,max 、ΔP x, i ,min 分别为区域i 联络线功率偏差的最大值和最小值.
综上可得,区域i的预测模型为式(21),优化模型为式(29)~ (32). 采用纳什均衡对各区域的优化模型进行分布式求解,其通过子优化问题间的信息交互来更新各子问题的边界条件,在迭代收敛的过程中保障问题求解的最优性[27 ] . 因此,针对区域i,将其他区域上次迭代求解的最优解作为边界条件,计算本次的最优解并与其他区域进行信息交互. 若在某次迭代后,各区域的最优解均能够满足纳什最优性条件,则分布式算法收敛,可表示为
(33) Ji (Δ U 1 * ( k ) … Δ U i * ( k ) … Δ U N * ( k ) i (Δ U 1 * ( k ) … Δ U i ( k ) … Δ U N * ( k )
式中:ΔU i * ( k )为区域i 在k 时刻的最优控制序列.
2.3 自适应反馈校正
利用纳什均衡将系统二次调频控制分解为各区域系统的分布式滚动优化问题. 在k时刻,由预测模型式(21)和优化模型式(29)~ (32)计算区域i 的最优控制序列ΔU i * ( k ),并将第1个控制量Δu i * ( k )施加于系统,如图3 所示.
图3
图3
考虑模型参数辨识的DMPC控制框架
Fig.3
Framework of DMPC with model parameter identification
为了提高DMPC 的控制性能,基于N 个区域的状态反馈量进行模型校正,利用Δu i * ( k )和Δxi (k )更新参数辨识模型式(14)的输入向量ut 和输出量yt ,并采用RLS求解更新后模型的参数向量θ. 由计算得到的参数向量θ ,更新预测模型式,并将Δxi (k )作为下一个控制时刻的初始条件,以计算下一个时刻的最优控制量Δu i * ( k +1).
3 算例分析
以WSCC 3机9节点系统为算例进行分析,如图4 所示,主要参数见文献[24 ]. 将WSCC 3机9节点系统划分为3个区域,其间通过5条联络线互联. 负荷1的变化情况如图5 所示,其中,负荷数据的时间分辨率为1 min ,总时长为300 min.
图4
图4
WSCC 3机9节点系统
Fig.4
WSCC 3-machine 9-bus system
图5
图5
区域1负荷曲线
Fig.5
Load of Area 1
RLS 方法的迭代步长设置为1 min ,DMPC 的步长设置为1 min ,控制时域NC P . 在未施加二次调频的场景下,各区域的频率波动情况如图6 所示.
图6
图6
不同区域的频率波动
Fig.6
Frequency variation of different areas
3.1 模型参数辨识验证
分析不同场景下所提参数辨识方法的性能,其中,场景1的系统参数保持不变. 在场景1下,区域1模型实际的输入和输出数据序列u (t )和y (t )如图7 所示.
图7
图7
场景1下的输入和输出序列
Fig.7
Input and output series in Scenario 1
将基于前200 min 观测数据的离线参数辨识方法作为对比方法,对应的输出数据序列的观测值和估计值如图8 所示. 所提方法能够较好地辨识模型参数,估计的输出序列与观测序列较为符合. 由于场景1的系统参数保持不变,且所提方法与离线对比方法所采用的模型和求解算法均相同,所以在该场景下所提方法与对比方法具有基本相同的性能.
图8
图8
场景1输出数据序列的观测值和估计值
Fig.8
Measured and estimated values of output series in Scenario 1
利用估计结果的均方根误差(root mean squared error ,RMSE )、平均绝对误差(mean absolute error ,MAE )和最大误差(maximum error ,ME )来衡量参数辨识的性能. 所提方法在场景1下估计结果的RMSE 、MAE 和ME 分别为5. 8×10-4 、3. 3×10-4 和4. 0×10-3 ,均在较小的范围内验证了所提参数辨识方法的性能.
在场景2下,系统在200 min 时运行方式发生变化,区域1的模型参数减小20% ,输入和输出数据序列u (t )和y (t )如图9 所示,对应的输出数据序列的观测值和估计值如图10 所示.
图9
图9
场景2下的输入和输出序列
Fig.9
Input and output series in Scenario 2
图10
图10
场景2输出数据序列的观测值和估计值
Fig.10
Measured and estimated values of output series in Scenario 2
由图10 可得,相较于对比方法,所提方法输出序列与观测序列的相似程度更高. 由于依据在线数据进行模型参数辨识,所以所提方法能够较好地计及系统运行方式的变化. 在场景2下,对比方法估计值的RMSE 为1. 6×10-3 ,MAE 为1. 3×10-3 ,ME 为4. 9×10-3 . 而所提方法对应的RMSE 为1. 2×10-3 ,MAE 为9. 5×10-4 ,ME 为4. 2×10-3 . 所提方法的RMSE 、MAE 和ME 均小于对比方法,验证了其能够适应系统参数的在线变化.
3.2 二次调频策略验证
通过对比分析验证所提二次调频策略的性能,其中,方法1未施加二次调频控制;方法2为基于比例- 积分(proportional-integral ,PI )控制的二次调频策略;方法3为未考虑系统参数变化的DMPC 策略. 在场景1下,不同方法对应的区域1频率轨迹和ACE 曲线分别如图11 和12 所示.
图11
图11
场景1下区域1的频率轨迹
Fig.11
Frequency trajectory of Area 1 in Scenario 1
图12
图12
场景1下区域1的ACE曲线
Fig.12
ACE of Area 1 in Scenario 1
由图11 和12 可得,二次调频能够平抑系统的频率波动,减小区域ACE 的数值. 由于未施加二次调频控制,所以方法1对应的频率波动最强,ACE 的数值最大. 方法2采用PI 控制进行二次调频,能够降低系统频率偏移量,但相比之下,DMPC 的控制效果更好. 在系统参数未发生变化的场景下,方法3与所提方法的控制对应的频率轨迹和ACE 曲线相同,均优于方法1和2. 计算不同方法作用下的频率最大偏差、频率偏差均方根、ACE 最大偏差和ACE 均方根,如表1 所示. 可知所提方法具有较好的二次调频性能指标,验证了其有效性.
对比分析不同方法在场景2下的控制性能,对应的区域1频率轨迹和ACE曲线分别如图13 和14 所示,计算得到的对应指标如表2 所示.与场景1类似,方法1作用下的频率偏移量和ACE最大,导致频率偏差达到-0.1319 Hz.方法2能够将最大频率偏差缩减到-0.1043 Hz,但是方法3对应的最大频率偏差更小,为-0.0882 Hz.由于未考虑系统参数变化,方法3的控制性能在200 min后受到限制.相较之下,所提方法在系统参数变化后仍然具有较好性能,验证了其在参数变化场景下的适应性.
图13
图13
场景2下区域1的频率轨迹
Fig.13
Frequency trajectory of Area 1 in Scenario 2
图14
图14
场景2下区域1的ACE轨迹
Fig.14
ACE of Area 1 in Scenario 2
4 结语
为提升二次调频对电力系统参数变化的适应性,提出一种基于DMPC的自适应控制策略.基于多区域互联系统的频率响应轨迹构建参数辨识模型,利用RLS方法在线辨识区域系统的模型参数.以ACE最小为目标,利用DMPC优化机组出力,依据辨识出的区域频率响应模型在预测时域内进行滚动优化,通过反馈校正形成闭环,实现二次调频控制.算例分析表明,所提方法能够适应系统参数的在线变化,降低模型参数的偏差,减小系统频率偏差和ACE.在下一步研究中,将分析二次调频控制策略在大规模电力系统中的计算效率.
参考文献
View Option
[1]
赵霞 , 梁钰 , 孙名轶 , 等 . AGC机组动态优化调度模型的凸松弛及其双层迭代算法
[J]. 电力系统自动化 2022 , 46 (17 ): 228 -238 .
[本文引用: 1]
ZHAO Xia LIANG Yu SUN Mingyi , et al Convex relaxation and bi-level iterative algorithm for dynamic optimal dispatch model of automatic generation control units
[J]. Automation of Electric Power Systems 2022 , 46 (17 ): 228 -238 .
[本文引用: 1]
[2]
FANG X YUAN H Y TAN J . Secondary frequency regulation from variable generation through uncertainty decomposition: An economic and reliability perspective
[J]. IEEE Transactions on Sustainable Energy 2021 , 12 (4 ): 2019 -2030 .
[本文引用: 1]
[3]
李文升 , 刘晓明 , 曹永吉 , 等 . 考虑电力系统灵活性的网-储联合规划
[J]. 智慧电力 2023 , 51 (4 ): 30 -37 .
[本文引用: 1]
LI Wensheng LIU Xiaoming CAO Yongji , et al Joint planning of energy storage and transmission line considering power system flexibility
[J]. Smart Power 2023 , 51 (4 ): 30 -37 .
[本文引用: 1]
[4]
ZHANG Y F WU S Y LIN J , et al Frequency reserve allocation of large-scale RES considering decision-dependent uncertainties
[J]. IEEE Transactions on Sustainable Energy 2024 , 15 (1 ): 339 -354 .
[本文引用: 1]
[5]
曹永吉 , 张恒旭 , 施啸寒 , 等 . 规模化分布式能源参与大电网安全稳定控制的机制初探
[J]. 电力系统自动化 2021 , 45 (18 ): 1 -8 .
[本文引用: 1]
CAO Yongji ZHANG Hengxu SHI Xiaohan , et al Preliminary study on participation mechanism of large-scale distributed energy resource in security and stability control of large power grid
[J]. Automation of Electric Power Systems 2021 , 45 (18 ): 1 -8 .
[本文引用: 1]
[6]
席星璇 , 熊敏鹏 , 袁家海 . 风电场发电侧配置储能系统的经济性研究
[J]. 智慧电力 2020 , 48 (11 ): 16 -21 .
[本文引用: 1]
XI Xingxuan XIONG Minpeng YUAN Jiahai . Economy analysis of energy storage system in wind farm generation side
[J]. Smart Power 2020 , 48 (11 ): 16 -21 .
[本文引用: 1]
[7]
崔俊涛 , 许岩 , 文福栓 . 基于H2 和H∞ 鲁棒优化的双馈感应发电机的二次调频策略
[J]. 智慧电力 2022 , 50 (6 ): 22 -27 .
[本文引用: 1]
CUI Juntao XU Yan WEN Fushuan . Secondary frequency control policy of doubly-fed induction generators based on H2 and H∞ robust optimization
[J]. Smart Power 2022 , 50 (6 ): 22 -27 .
[本文引用: 1]
[8]
RODRIGUES Y R ABDELAZIZ M WANG L W . D-PMU based secondary frequency control for islanded microgrids
[J]. IEEE Transactions on Smart Grid 2020 , 11 (1 ): 857 -872 .
[本文引用: 1]
[9]
周一辰 , 覃露 , 李永刚 . 基于多求和不等式输出反馈Lyapunov判据的时变时滞电力系统二次调频控制
[J]. 电网技术 2021 , 45 (8 ): 3247 -3258 .
[本文引用: 1]
ZHOU Yichen QIN Lu LI Yonggang . Secondary frequency modulation control of power system with time-varying delay based on Lyapunov criterion of multi-summation inequality output feedback
[J]. Power System Technology 2021 , 45 (8 ): 3247 -3258 .
[本文引用: 1]
[10]
KHALGHANI M R SOLANKI J KHUSHALANI SOLANKI S , et al Stochastic secondary frequency control of islanded microgrid under uncertainties
[J]. IEEE Systems Journal 2021 , 15 (1 ): 1056 -1065 .
[本文引用: 1]
[11]
李滨 , 王靖德 , 梁水莹 , 等 . 基于长短期记忆循环神经网络的AGC实时控制策略
[J]. 电力自动化设备 2022 , 42 (3 ): 128 -134 .
[本文引用: 1]
LI Bin WANG Jingde LIANG Shuiying , et al AGC real-time control strategy based on LSTM recurrent neural network
[J]. Electric Power Automation Equipment 2022 , 42 (3 ): 128 -134 .
[本文引用: 1]
[12]
李嘉文 , 余涛 , 张孝顺 , 等 . 基于改进深度确定性梯度算法的AGC发电功率指令分配方法
[J]. 中国电机工程学报 2021 , 41 (21 ): 7198 -7212 .
[本文引用: 1]
LI Jiawen YU Tao ZHANG Xiaoshun , et al AGC power generation command allocation method based on improved deep deterministic policy gradient algorithm
[J]. Proceedings of the CSEE 2021 , 41 (21 ): 7198 -7212 .
[本文引用: 1]
[13]
韩锐 , 吴军 , 廖清芬 , 等 . 基于NSGA-III算法的光-水-火电机组AGC协调优化策略
[J]. 智慧电力 2022 , 50 (1 ): 45 -52 .
[本文引用: 2]
HAN Rui WU Jun LIAO Qingfen , et al AGC coordination and optimization strategy of photovoltaic-hydropower-thermal power units based on NSGA-III algorithm
[J]. Smart Power 2022 , 50 (1 ): 45 -52 .
[本文引用: 2]
[14]
孙东磊 , 郑志杰 , 马逸然 , 等 . 储能与AGC机组协同的鲁棒调度
[J]. 电力自动化设备 2021 , 41 (6 ): 142 -149 .
[本文引用: 2]
SUN Donglei ZHENG Zhijie MA Yiran , et al Robust dispatching of energy storage coordinated with AGC units
[J]. Electric Power Automation Equipment 2021 , 41 (6 ): 142 -149 .
[本文引用: 2]
[15]
TAN Y J MUTTAQI K M CIUFO P , et al Enhanced frequency regulation using multilevel energy storage in remote area power supply systems
[J]. IEEE Transactions on Power Systems 2019 , 34 (1 ): 163 -170 .
[本文引用: 2]
[16]
KASIS A TIMOTHEOU S POLYCARPOU M . Optimal secondary frequency regulation with ON-OFF loads in power networks
[J]. IEEE Transactions on Control Systems Technology 2022 , 30 (6 ): 2490 -2505 .
[本文引用: 2]
[17]
张圣祺 , 袁蓓 , 季振东 , 等 . 基于分布式控制原理的电池储能系统二次调频控制
[J]. 电工技术学报 2019 , 34 (Sup.2) : 637 -645 .
[本文引用: 2]
ZHANG Shengqi YUAN Bei JI Zhendong , et al Secondary frequency modulation control of battery energy storage system based on distributed control principle
[J]. Transactions of China Electrotechnical Society 2019 , 34 (Sup.2) : 637 -645 .
[本文引用: 2]
[18]
YI Z K XU Y L GU W , et al Distributed model predictive control based secondary frequency regulation for a microgrid with massive distributed resources
[J]. IEEE Transactions on Sustainable Energy 2021 , 12 (2 ): 1078 -1089 .
[本文引用: 1]
[19]
孙舶皓 , 汤涌 , 仲悟之 , 等 . 基于分布式模型预测控制的包含大规模风电集群互联系统超前频率控制策略
[J]. 中国电机工程学报 2017 , 37 (21 ): 6291 -6302 .
[本文引用: 1]
SUN Bohao TANG Yong ZHONG Wuzhi , et al Multi-area interconnected power system advanced frequency control strategy considering large scale wind power cluster integration based on DMPC
[J]. Proceedings of the CSEE 2017 , 37 (21 ): 6291 -6302 .
[本文引用: 1]
[20]
杨冬锋 , 朱军豪 , 姜超 , 等 . 基于分布式模型预测的高比例风电系统多源协同负荷频率控制策略
[J]. 电网技术 2024 , 48 (7 ): 2804 -2814 .
[本文引用: 1]
YANG Dongfeng ZHU Junhao JIANG Chao , et al Multi-area interconnected power system advanced frequency control strategy considering large scale wind power cluster integration based on DMPC
[J]. Power System Technology 2024 , 48 (7 ): 2804 -2814 .
[本文引用: 1]
[21]
PATHAK N BHATTI T S VERMA A , et al AGC of two area power system based on different power output control strategies of thermal power generation
[J]. IEEE Transactions on Power Systems 2018 , 33 (2 ): 2040 -2052 .
[本文引用: 1]
[22]
徐清文 , 曹永吉 , 张恒旭 , 等 . 考虑暂态调频能力的虚拟电厂预防控制方法
[J]. 电力系统自动化 2022 , 46 (18 ): 83 -89 .
[本文引用: 1]
XU Qingwen CAO Yongji ZHANG Hengxu , et al Preventative control method for virtual power plant considering transient frequency regulation capability
[J]. Automation of Electric Power Systems 2022 , 46 (18 ): 83 -89 .
[本文引用: 1]
[23]
曹永吉 , 张恒旭 , 谢宇峥 , 等 . 暂态低频高压驱动的直流馈入电网减负荷紧急轮配置方案
[J]. 电力系统自动化 2019 , 43 (6 ): 156 -162 .
[本文引用: 1]
CAO Yongji ZHANG Hengxu XIE Yuzheng , et al Configuration scheme of emergency load shedding for HVDC receiving-end power grid based on transient low-frequency and high-voltage features
[J]. Automation of Electric Power Systems 2019 , 43 (6 ): 156 -162 .
[本文引用: 1]
[24]
CAO Y J ZHANG H X ZHANG Y , et al Extending SFR model to incorporate the influence of thermal states on primary frequency response
[J]. IET Generation, Transmission & Distribution 2020 , 14 (19 ): 4069 -4078 .
[本文引用: 2]
[25]
刘校销 , 郑涛 , 黄婷 . 基于等效漏电感参数辨识的磁控式并联电抗器匝间故障保护方案
[J]. 电工技术学报 2020 , 35 (1 ): 134 -145 .
[本文引用: 1]
LIU Xiaoxiao ZHENG Tao HUANG Ting . Protection scheme based on the identification of equivalent leakage inductance against turn-to-turn fault of magnetically controlled shunt reactor
[J]. Transactions of China Electrotechnical Society 2020 , 35 (1 ): 134 -145 .
[本文引用: 1]
[26]
黄依婷 , 沈建新 , 王云冲 , 等 . 基于递推最小二乘法观测器的永磁同步伺服电机变参数滑模控制
[J]. 中国电机工程学报 2022 , 42 (18 ): 6835 -6846 .
[本文引用: 1]
HUANG Yiting SHEN Jianxin WANG Yunchong , et al Variable parameter sliding mode control of permanent magnet synchronous servo machine based on recursive least square observer
[J]. Proceedings of the CSEE 2022 , 42 (18 ): 6835 -6846 .
[本文引用: 1]
[27]
叶林 , 陈超宇 , 张慈杭 , 等 . 基于分布式模型预测控制的风电场参与AGC控制方法
[J]. 电网技术 2019 , 43 (9 ): 3261 -3270 .
[本文引用: 1]
YE Lin CHEN Chaoyu ZHANG Cihang , et al Wind farm participating in AGC based on distributed model predictive control
[J]. Power System Technology 2019 , 43 (9 ): 3261 -3270 .
[本文引用: 1]
AGC机组动态优化调度模型的凸松弛及其双层迭代算法
1
2022
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
Convex relaxation and bi-level iterative algorithm for dynamic optimal dispatch model of automatic generation control units
1
2022
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
Secondary frequency regulation from variable generation through uncertainty decomposition: An economic and reliability perspective
1
2021
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
考虑电力系统灵活性的网-储联合规划
1
2023
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
Joint planning of energy storage and transmission line considering power system flexibility
1
2023
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
Frequency reserve allocation of large-scale RES considering decision-dependent uncertainties
1
2024
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
规模化分布式能源参与大电网安全稳定控制的机制初探
1
2021
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
Preliminary study on participation mechanism of large-scale distributed energy resource in security and stability control of large power grid
1
2021
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
风电场发电侧配置储能系统的经济性研究
1
2020
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
Economy analysis of energy storage system in wind farm generation side
1
2020
... 电力系统二次调频是将频率和联络线功率偏差维持在合理范围内的重要手段[1 -2 ] .风电、光伏等可再生能源具有随机性和不可控性,大规模接入下电力系统发电侧出力的不确定性增加,等效惯量降低[3 ⇓ -5 ] .为了保持发电和负荷间有功功率的平衡,电力系统运行方式的变化更加频繁,给二次调频的适应性带来严峻的挑战[6 ] .因此,提升二次调频控制在模型参数变化场景下的适应性,对于新型电力系统的安全运行具有重要意义. ...
基于H2 和H∞ 鲁棒优化的双馈感应发电机的二次调频策略
1
2022
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
Secondary frequency control policy of doubly-fed induction generators based on H2 and H∞ robust optimization
1
2022
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
D-PMU based secondary frequency control for islanded microgrids
1
2020
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
基于多求和不等式输出反馈Lyapunov判据的时变时滞电力系统二次调频控制
1
2021
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
Secondary frequency modulation control of power system with time-varying delay based on Lyapunov criterion of multi-summation inequality output feedback
1
2021
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
Stochastic secondary frequency control of islanded microgrid under uncertainties
1
2021
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
基于长短期记忆循环神经网络的AGC实时控制策略
1
2022
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
AGC real-time control strategy based on LSTM recurrent neural network
1
2022
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
基于改进深度确定性梯度算法的AGC发电功率指令分配方法
1
2021
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
AGC power generation command allocation method based on improved deep deterministic policy gradient algorithm
1
2021
... 目前,二次调频主要以区域控制偏差(area control error,ACE)最小为目标,通过调节可控有功源出力来实现无差控制.其中,文献[7 ]中设计了基于H2 /H∞ 的二次调频控制器,并转化为含线性矩阵不等式(linear matrix inequality,LMI)约束的优化问题求解.文献[8 ]中以降低频率波动和偏移程度为目标,利用时变下垂特性来改善二次调频的性能.文献[9 ]中计及通信网络时滞的影响,通过构造衡量系统输出反馈增益的LMI来优化二次调频控制器的参数.文献[10 ]中将系统二次调频表示为线性二次型最优控制问题,提出一种鲁棒控制方法.文献[11 ]中考虑不同工况下二次调频最优控制策略的差异性,基于长短期记忆循环神经网络构建深度学习模型,提出数据驱动的控制方法.文献[12 ]中以ACE最小为目标,构建二次调频指令优化分配模型,并利用改进深度确定性梯度算法求解. ...
基于NSGA-III算法的光-水-火电机组AGC协调优化策略
2
2022
... 为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
... ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
AGC coordination and optimization strategy of photovoltaic-hydropower-thermal power units based on NSGA-III algorithm
2
2022
... 为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
... ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
储能与AGC机组协同的鲁棒调度
2
2021
... 为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
... ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
Robust dispatching of energy storage coordinated with AGC units
2
2021
... 为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
... ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
Enhanced frequency regulation using multilevel energy storage in remote area power supply systems
2
2019
... 为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
... ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
Optimal secondary frequency regulation with ON-OFF loads in power networks
2
2022
... 为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
... ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
基于分布式控制原理的电池储能系统二次调频控制
2
2019
... 为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
... ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
Secondary frequency modulation control of battery energy storage system based on distributed control principle
2
2019
... 为了提升二次调频的性能,文献[13 ⇓ ⇓ ⇓ -17 ]中研究了多类型可控资源间的协调问题.其中,文献[13 ]中构建光-水-火电机组二次调频的多目标优化模型,并利用基于第三代非支配排序遗传算法的多目标进化算法求解.文献[14 ]中利用储能系统响应速度快的特点来弥补火电机组爬坡能力的不足,提出两阶段协调优化策略.文献[15 ]中考虑频率调节过程中不同阶段控制的差异,采用超级电容器、铅蓄电池和风电机组依次响应的方式来平抑频率波动.文献[16 ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
... ]中以频率偏移量最小为目标,构建混合整数规划模型,提出可控负荷参与下的二次调频策略.文献[17 ]中采用调频电源损耗函数衡量火电机组和储能系统在二次调频过程中的损耗,并以损耗最小为目标提出协调控制策略. ...
Distributed model predictive control based secondary frequency regulation for a microgrid with massive distributed resources
1
2021
... 电力系统的运行方式影响其频率动态过程的模型参数.在电力系统运行状态变化的场景下,基于固定参数的二次调频策略可能导致ACE的偏移量超出预期.此外,集中式的二次调频控制策略在进行优化决策时,需要全网的模型和监测信息,对数据传输时效性和可靠性依赖程度较高,通信系统延迟和错误数据将限制其控制效果[18 ] .分散式二次调频控制策略由于各控制器间缺乏协调交流而影响优化结果的全局最优性[19 ] .相较之下,分布式的二次调频控制策略能够减少系统的数据交互量,在保障全局最优的同时提高可靠性,降低通信成本[20 ] .如何在分布式的二次调频控制中计及系统参数变化的影响,是亟待解决的问题. ...
基于分布式模型预测控制的包含大规模风电集群互联系统超前频率控制策略
1
2017
... 电力系统的运行方式影响其频率动态过程的模型参数.在电力系统运行状态变化的场景下,基于固定参数的二次调频策略可能导致ACE的偏移量超出预期.此外,集中式的二次调频控制策略在进行优化决策时,需要全网的模型和监测信息,对数据传输时效性和可靠性依赖程度较高,通信系统延迟和错误数据将限制其控制效果[18 ] .分散式二次调频控制策略由于各控制器间缺乏协调交流而影响优化结果的全局最优性[19 ] .相较之下,分布式的二次调频控制策略能够减少系统的数据交互量,在保障全局最优的同时提高可靠性,降低通信成本[20 ] .如何在分布式的二次调频控制中计及系统参数变化的影响,是亟待解决的问题. ...
Multi-area interconnected power system advanced frequency control strategy considering large scale wind power cluster integration based on DMPC
1
2017
... 电力系统的运行方式影响其频率动态过程的模型参数.在电力系统运行状态变化的场景下,基于固定参数的二次调频策略可能导致ACE的偏移量超出预期.此外,集中式的二次调频控制策略在进行优化决策时,需要全网的模型和监测信息,对数据传输时效性和可靠性依赖程度较高,通信系统延迟和错误数据将限制其控制效果[18 ] .分散式二次调频控制策略由于各控制器间缺乏协调交流而影响优化结果的全局最优性[19 ] .相较之下,分布式的二次调频控制策略能够减少系统的数据交互量,在保障全局最优的同时提高可靠性,降低通信成本[20 ] .如何在分布式的二次调频控制中计及系统参数变化的影响,是亟待解决的问题. ...
基于分布式模型预测的高比例风电系统多源协同负荷频率控制策略
1
2024
... 电力系统的运行方式影响其频率动态过程的模型参数.在电力系统运行状态变化的场景下,基于固定参数的二次调频策略可能导致ACE的偏移量超出预期.此外,集中式的二次调频控制策略在进行优化决策时,需要全网的模型和监测信息,对数据传输时效性和可靠性依赖程度较高,通信系统延迟和错误数据将限制其控制效果[18 ] .分散式二次调频控制策略由于各控制器间缺乏协调交流而影响优化结果的全局最优性[19 ] .相较之下,分布式的二次调频控制策略能够减少系统的数据交互量,在保障全局最优的同时提高可靠性,降低通信成本[20 ] .如何在分布式的二次调频控制中计及系统参数变化的影响,是亟待解决的问题. ...
Multi-area interconnected power system advanced frequency control strategy considering large scale wind power cluster integration based on DMPC
1
2024
... 电力系统的运行方式影响其频率动态过程的模型参数.在电力系统运行状态变化的场景下,基于固定参数的二次调频策略可能导致ACE的偏移量超出预期.此外,集中式的二次调频控制策略在进行优化决策时,需要全网的模型和监测信息,对数据传输时效性和可靠性依赖程度较高,通信系统延迟和错误数据将限制其控制效果[18 ] .分散式二次调频控制策略由于各控制器间缺乏协调交流而影响优化结果的全局最优性[19 ] .相较之下,分布式的二次调频控制策略能够减少系统的数据交互量,在保障全局最优的同时提高可靠性,降低通信成本[20 ] .如何在分布式的二次调频控制中计及系统参数变化的影响,是亟待解决的问题. ...
AGC of two area power system based on different power output control strategies of thermal power generation
1
2018
... 多区域互联电力系统由多个控制区域组成,某区域内的扰动将经联络线传递给其他区域,二次调频主要由各区域内的火电机组承担[21 ] .区域i的二次调频模型如图1 所示.图中:N为区域个数;s为拉普拉斯算子; βi 为区域i的频率偏移系数; Ai 、 Δ fi 、Δ Px ,i 分别为区域i对应的ACE 、频率偏移量和联络线功率偏移量;Rg Δ fj 为区域j对应的频率偏移量;Hi 、Di 分别为区域i的惯性系数和阻尼系数;Tij 为区域i和j之间的联络线同步系数;Δ Pl ,i 、Δ Pm ,i 和Δ Pg ,i 分别为区域i的负荷变化量、控制器输出指令和机组输出功率变化;vi 为区域i与其他区域间的接口量. ...
考虑暂态调频能力的虚拟电厂预防控制方法
1
2022
... 区域i的惯性系数Hi 、阻尼系数Di 和频率偏移量Δ fi 可由机组参数计算[22 ] ,表示为 ...
Preventative control method for virtual power plant considering transient frequency regulation capability
1
2022
... 区域i的惯性系数Hi 、阻尼系数Di 和频率偏移量Δ fi 可由机组参数计算[22 ] ,表示为 ...
暂态低频高压驱动的直流馈入电网减负荷紧急轮配置方案
1
2019
... 针对机组频率响应模型,传递函数的分子和分母多项式一般均为1阶[23 -24 ] .因此,式(10)和(11)可简化为 ...
Configuration scheme of emergency load shedding for HVDC receiving-end power grid based on transient low-frequency and high-voltage features
1
2019
... 针对机组频率响应模型,传递函数的分子和分母多项式一般均为1阶[23 -24 ] .因此,式(10)和(11)可简化为 ...
Extending SFR model to incorporate the influence of thermal states on primary frequency response
2
2020
... 针对机组频率响应模型,传递函数的分子和分母多项式一般均为1阶[23 -24 ] .因此,式(10)和(11)可简化为 ...
... 以WSCC 3机9节点系统为算例进行分析,如图4 所示,主要参数见文献[24 ]. 将WSCC 3机9节点系统划分为3个区域,其间通过5条联络线互联. 负荷1的变化情况如图5 所示,其中,负荷数据的时间分辨率为1 min ,总时长为300 min. ...
基于等效漏电感参数辨识的磁控式并联电抗器匝间故障保护方案
1
2020
... 利用RLS 求解式(14)中的参数向量[25 ] ,表示为 ...
Protection scheme based on the identification of equivalent leakage inductance against turn-to-turn fault of magnetically controlled shunt reactor
1
2020
... 利用RLS 求解式(14)中的参数向量[25 ] ,表示为 ...
基于递推最小二乘法观测器的永磁同步伺服电机变参数滑模控制
1
2022
... 基于RLS 的参数辨识方法的迭代过程如图2 所示. 由参数量估计值 θ ^ 0 P 0 的初始化开始,利用式(15)计算每步迭代时的中间向量Kt ,更新参数量的估计值 θ ^ t Pt . 在迭代过程中,RLS计算当前的估计偏差et ,将 θ ^ t - 1 et 作为第t 次迭代时的修正值,对参数量的估计值 θ ^ t - 1 θ ^ t [26 ] . 随着时间的推移,RLS基于监测数据yt 和ut 估计当前时刻的参数量 θ ^ t i 的频率响应模型Gi (s ). ...
Variable parameter sliding mode control of permanent magnet synchronous servo machine based on recursive least square observer
1
2022
... 基于RLS 的参数辨识方法的迭代过程如图2 所示. 由参数量估计值 θ ^ 0 P 0 的初始化开始,利用式(15)计算每步迭代时的中间向量Kt ,更新参数量的估计值 θ ^ t Pt . 在迭代过程中,RLS计算当前的估计偏差et ,将 θ ^ t - 1 et 作为第t 次迭代时的修正值,对参数量的估计值 θ ^ t - 1 θ ^ t [26 ] . 随着时间的推移,RLS基于监测数据yt 和ut 估计当前时刻的参数量 θ ^ t i 的频率响应模型Gi (s ). ...
基于分布式模型预测控制的风电场参与AGC控制方法
1
2019
... 综上可得,区域i的预测模型为式(21),优化模型为式(29)~ (32). 采用纳什均衡对各区域的优化模型进行分布式求解,其通过子优化问题间的信息交互来更新各子问题的边界条件,在迭代收敛的过程中保障问题求解的最优性[27 ] . 因此,针对区域i,将其他区域上次迭代求解的最优解作为边界条件,计算本次的最优解并与其他区域进行信息交互. 若在某次迭代后,各区域的最优解均能够满足纳什最优性条件,则分布式算法收敛,可表示为 ...
Wind farm participating in AGC based on distributed model predictive control
1
2019
... 综上可得,区域i的预测模型为式(21),优化模型为式(29)~ (32). 采用纳什均衡对各区域的优化模型进行分布式求解,其通过子优化问题间的信息交互来更新各子问题的边界条件,在迭代收敛的过程中保障问题求解的最优性[27 ] . 因此,针对区域i,将其他区域上次迭代求解的最优解作为边界条件,计算本次的最优解并与其他区域进行信息交互. 若在某次迭代后,各区域的最优解均能够满足纳什最优性条件,则分布式算法收敛,可表示为 ...