随着电力电子变换技术在配电网中的快速发展和普及应用,配电网中的负荷种类不断丰富,如电动汽车、变频空调、发光二极管(LED)照明等.然而,基于电力电子变换技术的负荷通常伴有非线性和冲击性特征,给配电网的电能质量带来较大挑战[1 ] .例如,非线性负荷所产生的非线性电流易造成电网电压畸变;而冲击性负荷易造成电网电压暂降或升高.同时,电压畸变、暂降、升高问题会互相叠加,呈现出复合形式的电能质量问题,不仅影响用户的用电体验,还可能对电力系统的安全稳定产生影响[2 ] .为此,开发一种综合电能质量治理装置,能在治理电力电子负荷对配电网电压污染的同时,抑制电网电压问题对负荷的影响,从而满足重要负荷对高质量供电的需求.
电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] .
作为一种综合治理装置,统一电能质量调节器(UPQC)[9 ⇓ -11 ] 因其能克服上述装置的缺点,满足对电压和电流相关电能质量问题同时治理的多任务要求,而受到国内外学术界及工业界的广泛关注.但在以工频变压器进行电压补偿的UPQC中,工频变压器存在质量重和体积大的缺点,不利于装置模块化生产,降低了系统的灵活性,更重要的是,变压器可能出现的磁饱和问题将会影响系统安全稳定运行[12 ] .
为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度.
综上可知,目前无工频变压器UPQC存在拓扑结构复杂、控制难度较大的缺点.为克服这些缺点,提出一种基于两桥臂拓扑的无变压器型统一电能质量调节器(TLTT-UPQC),以期促进UPQC的进一步发展与应用.TLTT-UPQC不但具有含工频变压器UPQC的电能质量综合治理功能,还具有轻量化和高灵活性的优势.首先,从电路拓扑角度分析TLTT-UPQC的工作原理;其次,结合理论分析研究不同工况场景下,多种电能质量治理功能的运行机理,并以此为依据设计系统的控制策略;最后,通过仿真结果验证TLTT-UPQC的多功能运行性能.
1 TLTT-UPQC拓扑与工作原理
1.1 系统拓扑
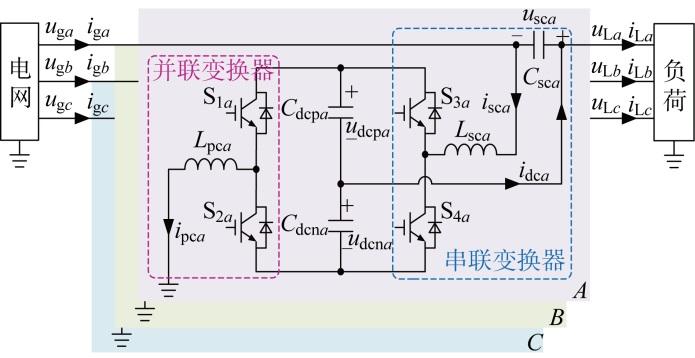
三相TLTT-UPQC拓扑结构如图1 所示,并联与串联变换器采用共直流母线背靠背连接形式.由于A 、B 、C 三相中的并联和串联变换器拓扑相同,所以图1 中主要给出了系统A 相的电路拓扑.A 相并联变换器由电力电子开关器件S1 a 2 a L pc a B 相和C 相并联变换器分别由S1 b 2 b L pc b 1 c 2 c L pc c i L a i L b i L c i g a i g b i g c 3 a 4 a L sc a C sc a 3 b 4 b L sc b C sc b 3 c 4 c L sc c C sc c u g a u g b u g c u L a u L b u L c C sc a C sc b C sc c
图1
图1
三相TLTT-UPQC拓扑结构
Fig.1
Topology structure of three-phase TLTT-UPQC
图1 中,u sc a u sc b u sc c C sc a C sc b C sc c i pc a i pc b i pc c i sc a i sc b i sc c C dcp a C dcp b C dcp c C dcn a C dcn b C dcn c u dcp a u dcp b u dcp c u dcn a u dcn b u dcn c i dc a i dc b i dc c .C sc a C sc b C sc c
(1) i g a = i s c a , i L a = i d c a = i s c a + i p c a i g b = i s c b , i L b = i d c b = i s c b + i p c b i g c = i s c c , i L c = i d c c = i s c c + i p c c
由式(1)可知,i g a i g b i g c
以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征.
1.2 工作原理
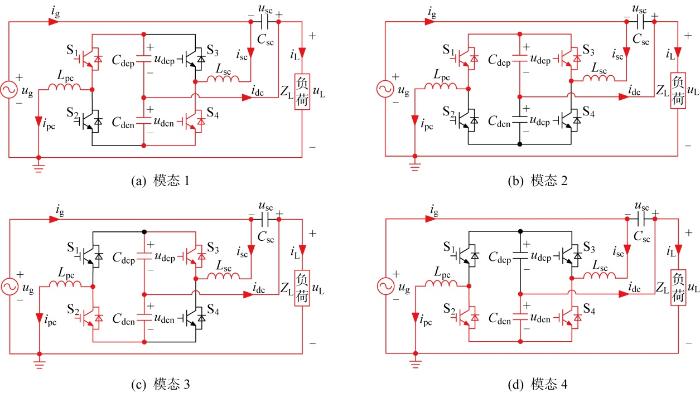
三相中的UPQC拓扑相同,因此以单相为例对TLTT-UPQC的工作原理进行分析,同时可省略表示3个相序的下标a 、b 和c. 在并联和串联变换器中,同一桥臂开关管S1 与S2 、S3 与S4 互补导通,以防止桥臂直通损坏装置.根据4个开关管的导通与关断状态,可得到TLTT-UPQC的4个工作模态,如图2 所示.图中,Z L 为负荷阻抗.
图2
图2
TLTT-UPQC工作模态
Fig.2
Working modes of TLTT-UPQC
模态1为S1 与S4 导通,S2 与S3 关断.如图2(a) 所示,电网电流i g 只为负荷提供有功电流i Lp ,经串联变换器后传输至负荷;而负荷电流中的谐波和无功分量由并联变换器电流i pc 补偿.此外,由电网电压u g 波动引起的网侧与负荷侧压差由电容C sc 补偿.
对模态2~4的分析与模态1类似,但电流传输路径有所不同.模态2为S1 与S3 导通,S2 与S4 关断;模态3为S2 与S3 导通,S1 与S4 关断;模态4为S2 与S4 导通,S1 与S3 关断.根据图2 所示的运行原理,不同工作模态下串联和并联变换器的状态方程总结如表2 所示.
2 多场景电能质量治理功能
TLTT-UPQC具备多种场景电能质量治理功能,如网侧电压波动与畸变补偿、负荷侧无功与畸变电流补偿等,为负荷提供高质量电能的同时,抑制负荷对电网电能质量的影响.本节主要对TLTT-UPQC的电能质量治理原理进行研究,揭示不同工况场景下系统的运行机理.
2.1 理论分析
考虑电网电压跌落、升高与畸变以及补偿负荷无功与畸变电流等工况,从负荷侧、电网侧、串联和并联变换器角度对系统的运行机理进行理论分析.应说明的是,电压和电流的大写形式表示均方根值,而下标p、q、f和h分别表示有功、无功、基波和谐波分量.
2.1.1 负荷侧
TLTT-UPQC为负荷提供稳定的交流输出电压,可表示为
(2) u L =u Lf = 2 Lf sin(ωt)
式中:u Lf 为u L 的基波分量瞬时值;U Lf 为u L 的基波分量均方根值;ω 为角频率.
(3) i L =i Lfp +i Lfq +i Lh = 2 Lf sin(ωt+φL )+ ∑ h = 3 , 5 , 7 , … ∞ 2 Lh sin(hωt+φLh )
式中:i Lfp 、i Lfq 和i Lh 分别为i L 中基波有功电流、基波无功电流和谐波电流的瞬时值;I Lf 和I Lh 分别为i L 中基波和谐波电流的均方根值;φ L 为i Lf 与u L 之间的相位角;φ Lh 为i Lh 与u L 之间的相位角;h 为谐波次数.
(4) $\begin{aligned}p_{\mathrm{L}}= & u_{\mathrm{L}} i_{\mathrm{L}}=P_{\mathrm{Lf}}(1-\cos (2 \omega t))+ \\& Q_{\mathrm{Lf}} \sin (2 \omega t)+D_{\mathrm{Lh}} \sin (\omega t) \sin \left(h \omega t+\varphi_{\mathrm{Lh}}\right)\end{aligned}$
$P_{\mathrm{Lf}}=U_{\mathrm{Lf}} I_{\mathrm{Lf}} \cos \varphi_{\mathrm{L}}=U_{\mathrm{Lf}} I_{\mathrm{Lfp}}$
$Q_{\mathrm{Lf}}=U_{\mathrm{Lf}} I_{\mathrm{Lf}} \sin \varphi_{\mathrm{L}}=U_{\mathrm{Lf}} I_{\mathrm{Lfq}}$
$D_{\mathrm{Lh}}=\sum_{h-3,5,7, \ldots}^{\infty} U_{\mathrm{Lf}} I_{\mathrm{Lh}} \cos \varphi_{\mathrm{Lh}}$
2.1.2 电网侧
(5) u g =u gf +u gh = 2 gf sin(ωt)+ ∑ h = 3 , 5 , 7 , … ∞ 2 gh sin(hωt+φgh )
式中:U gf 和U gh 分别为u g 的基波分量和谐波分量的均方根值;φ gh 为i g 与u gh 之间的相位角.
忽略损耗,在TLTT-UPQC控制下负荷有功功率由电网提供,同时说明系统可实现网侧单位功率因数校正.由此可知,网侧与负荷侧的有功功率P gf 和P Lf 保持相等,即:
(6) $P_{\mathrm{gf}}=P_{\mathrm{Lf}} \quad U_{\mathrm{gf}} I_{\mathrm{gf}}=U_{\mathrm{Lf}} I_{\mathrm{Lfp}}$
(7) i g = i g f = 2 I g f s i n ( ω t ) I g f = U L f / U g f I L f p = k g I L f p
式中:i gf 为i g 的基波分量瞬时值;k g 为电网电压变化度.
(8) $\begin{aligned}p_{\mathrm{g}}= & u_{\mathrm{g}} i_{\mathrm{g}}=P_{\mathrm{Lf}}(1-\cos (2 \omega t))+ \\& D_{\mathrm{gh}} \sin (\omega t) \sin \left(h \omega t+\varphi_{\mathrm{gh}}\right)\end{aligned}$
$D_{\mathrm{gh}}=\sum_{h-3,5,7, \ldots}^{\infty} U_{\mathrm{gh}} I_{\mathrm{gf}} \cos \varphi_{\mathrm{gh}}$
由式(8)可知,当u g 畸变时,p g 由P Lf 和D gh 构成;而当u g 无畸变时,p g 仅由P Lf 构成.此外,无论u g 是否波动,电网输入的有功功率始终与负荷有功功率相等.
2.1.3 串联变换器
电容C sc 补偿u g 与u L 之间的电压差值,其两端电压
(9) $\begin{array}{c}u_{\mathrm{sc}}=u_{\mathrm{g}}-u_{\mathrm{L}}=\sqrt{2}\left(U_{\mathrm{gf}}-U_{\mathrm{Lf}}\right) \sin (\omega t)+ \\\infty \quad \sqrt{2} U_{\mathrm{gh}} \sin \left(h \omega t+\varphi_{\mathrm{gh}}\right) \\h=5,7,11, \ldots\end{array}$
(10) $\begin{aligned}p_{\mathrm{sc}}= & u_{\mathrm{sc}} i_{\mathrm{g}}=P_{\mathrm{scf}}(1-\cos (2 \omega t))+ \\& D_{\mathrm{sch}} \sin (\omega t) \sin \left(h \omega t+\varphi_{\mathrm{gh}}\right)\end{aligned}$
$P_{\mathrm{scf}}=\left(1-k_{\mathrm{g}}\right) P_{\mathrm{Lf}}$
$D_{\mathrm{sch}}=D_{\mathrm{gh}}=\sum_{h-5,7,11, \ldots}^{\infty} U_{\mathrm{gh}} I_{\mathrm{gf}} \cos \varphi_{\mathrm{gh}}$
2.1.4 并联变换器
并联变换器主要用于补偿负荷的无功和畸变电流,以及由电网电压波动导致的i g 和i L 之间的有功电流差值,并联变换器输出电流可表示为
(11) i pc =i pcfp +i pcfq +i pch =(i g -i Lfp )+i Lfq +i Lh = 2 g -1)ILfp sin(ωt)+ 2 Lfq cos(ωt)+ ∑ h = 5 , 7 , 11 , … ∞ 2 Lh sin(hωt+φLh )
式中:i pcfp 、i pcfq 和i pch 分别为i pc 中基波有功电流、基波无功电流和谐波电流的瞬时值.
(12) $\begin{array}{l}p_{\mathrm{pc}}=u_{\mathrm{L}} i_{\mathrm{pc}}=P_{\mathrm{pcf}}(1-\cos (2 \omega t))+ \\\quad Q_{\mathrm{Lf}} \sin (2 \omega t)+D_{\mathrm{Lh}} \sin (\omega t) \sin \left(h \omega t+\varphi_{\mathrm{Lh}}\right)\end{array}$
式中:并联变换器输出的有功功率P pcf =(k g -1)P Lf .
对比式(10)和式(12)中的P scf 和P pcf 项,可得:
(13) $P_{\mathrm{scf}}=-P_{\mathrm{pcf}}=\left(1-k_{\mathrm{g}}\right) P_{\mathrm{Lf}}$
由式(13)可知,当电网电压跌落/升高,即k g ≠1时,串联与并联变换器之间将存在有功功率的传输行为.根据k g >1或k g <1情况,串联和并联变换器将分别工作于吸收或发出有功功率状态,其所传输的有功功率方向分别由u sc 和i pc 决定.
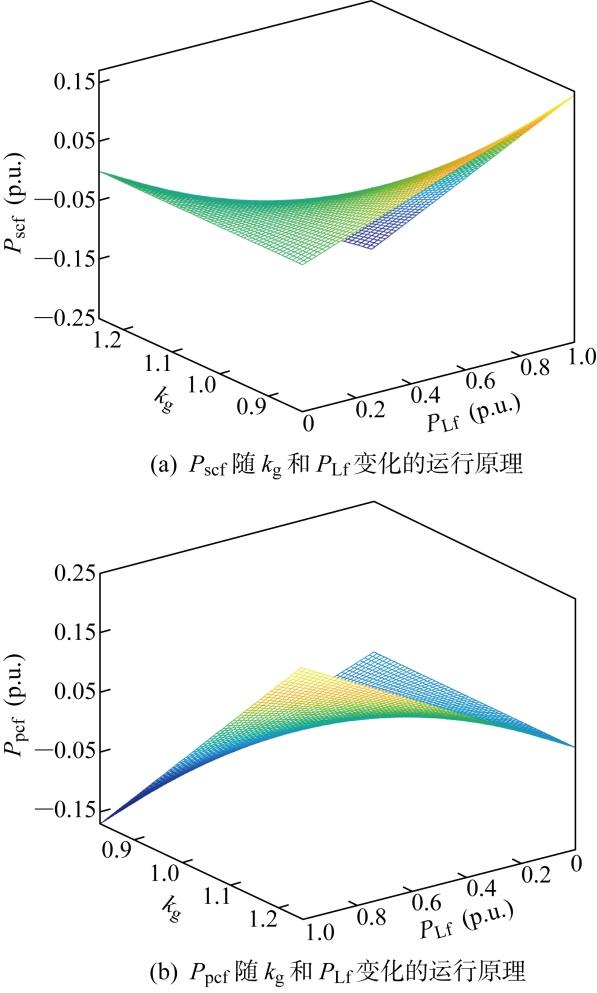
根据式(13),串联和并联变换器有功功率P scf 和P pcf 随k g 和P Lf 变化的运行原理如图3 所示.其中,P scf 、P pcf 和P Lf 均取标幺值(p.u.):电网电压u g 波动范围为-20%~+20%,即 k g =0.83~1.25;负荷有功功率P Lf 变化范围为0~1.可见,当两变换器之间传输有功功率时,一个吸收功率,另一个输出功率.以P Lf =1为例,虽然u g 上下波动均为20%,但两变换器所传输的功率情况有所不同.当u g 下降20%,即k g =1.25时,P scf =-0.25,P pcf =0.25;当u g 升高20%,即k g =0.83时,P scf =0.167,P pcf =-0.167.
图3
图3
串联和并联变换器有功功率运行原理
Fig.3
Active power operation of series and parallel converters
2.2 多功能运行分析
TLTT-UPQC中,串联和并联变换器分别用于补偿网侧电压与负荷侧电流相关的电能质量问题.对于不同电能质量治理功能,两变换器之间的功率流传递形式有所不同,具体分析如下.
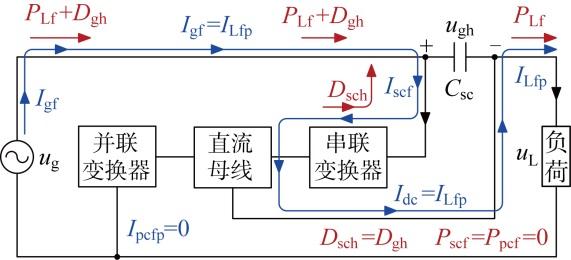
2.2.1 电网电压平衡/跌落/升高补偿功能
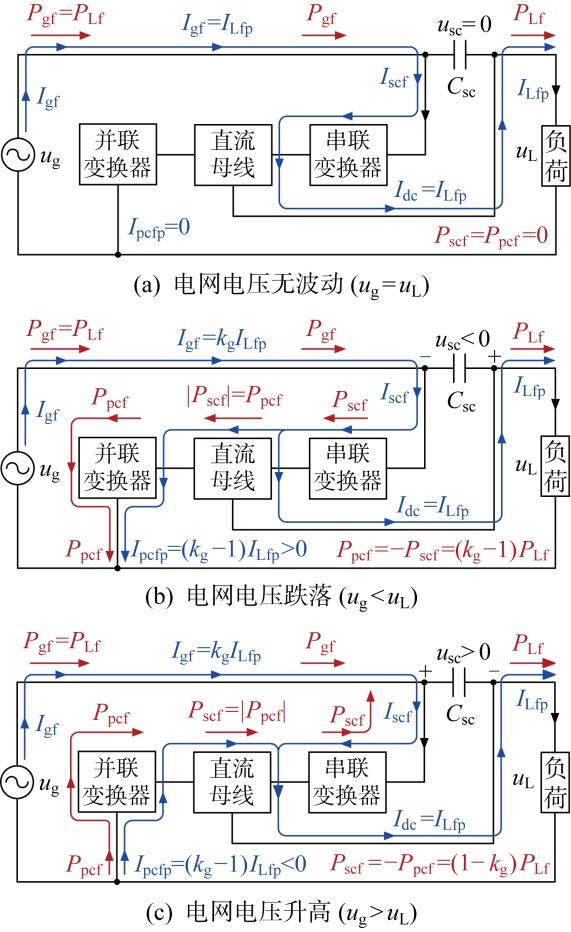
为分析电网电压跌落/升高的补偿功能,首先分析阻性负荷下电网电压平衡, 即u g =u L 且k g =1时的系统运行原理,如图4(a) 所示.电网电流i g 经串联变换器后传输至负荷,满足I gf =I scf =I dc =I Lfp .虽然i g 流经串联变换器,但由于电容C sc 两端电压u sc 为0,所以串联变换器传输的有功功率P sc 为0,负荷有功功率只由电网提供,P gf =P Lf .进一步,串联与并联变换器之间不存在有功功率的互动行为,并联变换器所传输的有功功率P pc 同样为0.
图4
图4
电网电压平衡/跌落/升高补偿功能
Fig.4
Compensation function of grid voltage balance/drop/rise
电网电压跌落工况下,即u g <u L 且k g >1时,为实现电网与负荷两侧的有功功率相等,电网电流均方根值I g 需增加至k g I Lfp ,超出了负荷所需电流I Lfp ,超出部分由并联变换器实施补偿,如图4(b) 所示.根据式(9)和式(11)可知,两变换器所补偿的电压和电流分别为:u sc =(U Lf /k g )-U Lf <0,I pcfp =(k g -1)I Lfp >0.由于u sc ≠0和I pcfp ≠0,所以两变换器将传输有功功率.根据式(10)和式(12)可知,P scf =(1-k g )P Lf <0和P pcf =(k g -1)P Lf >0,说明串联变换器吸收有功功率,而并联变换器输出该功率.
电网电压升高工况下,即u g >u L 且k g <1时,TLTT-UPQC功率流动分析过程与u g <u L 类似,此处不再赘述.不同之处在于,并联变换器从电网获取有功功率并通过直流母线传输至负荷,见图4(c) .
2.2.2 电网电压畸变补偿功能
电网电压u g 畸变工况下的系统运行原理如图5 所示,u g 中的畸变部分u gh 由电容C sc 补偿,从而保证负荷电压u L 不受u g 畸变影响.进一步由式(8)和式(10)可知,串联变换器将补偿电网输入的畸变功率,则有D sch =D gh .
图5
图5
电网电压畸变补偿功能
Fig.5
Compensation function of grid voltage distortion
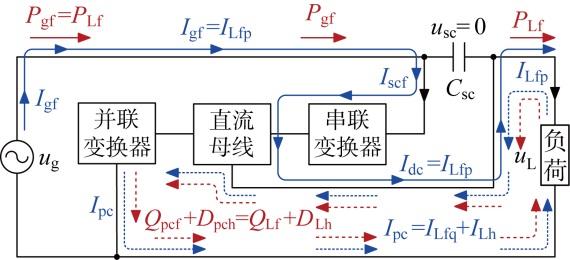
2.2.3 负荷无功与畸变电流补偿功能
当负荷特性表现为阻感性、阻容性或非线性时,并联变换器将补偿负荷的无功和畸变电流,而电网侧只输入负荷所需的有功电流,如图6 所示.
图6
图6
负荷无功与畸变电流补偿功能
Fig.6
Compensation functions of load reactive and distortion current
综上所述,与含工频变压器UPQC相比,TLTT-UPQC不但具有多种工况场景下的电能质量治理功能,同时还能克服工频变压器所带来的体积、质量和磁饱和等问题.因此,TLTT-UPQC能以轻量化、高灵活性形式实现对配电网电能质量改善,满足负荷高质量用电需求.
3 系统控制策略
根据第1章中所论述的TLTT-UPQC运行功能,设计串联和并联变换器控制策略.首先,推导出TLTT-UPQC的数学模型,然后基于该模型给出串联变换器、并联变换器和锁相环的控制设计过程.三相TLTT-UPQC是由3个单相TLTT-UPQC构成,因此三相系统之间的控制相对独立,可以由A 、B 、C 3个单相控制分别予以体现.
3.1 串联变换器控制策略设计
3.1.1 控制模型
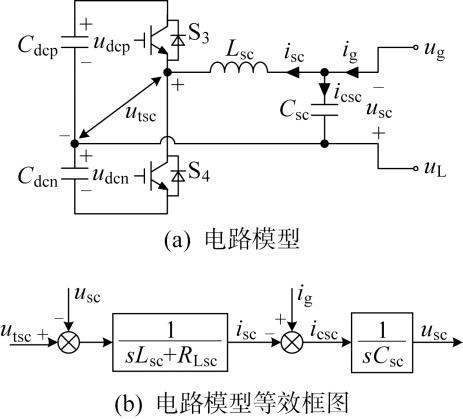
根据图1 所示,单相串联变换器电路模型见图7(a) .图中,u tsc 为串联变换器桥臂电压;i csc 为流过电容C sc 的电流.进一步,根据基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)可建立单相串联变换器的数学模型为
(14) u t s c = L s c d i s c d t + R L s c i s c + u s c i g = i s c + i c s c = i s c + C s c d u s c d t
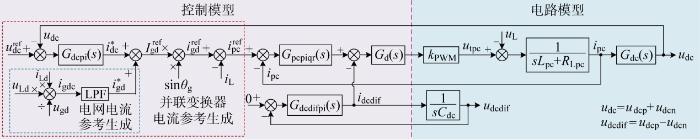
根据式(14),可得串联变换器的电路模型等效框图见图7(b) .以该图为被控对象,所设计的单相串联变换器控制策略如图8 所示,其控制目标为补偿电网电压的波动和畸变,从而保证负荷电压稳定且正弦.图中,θ g 为电网电压相位角;G scpiqr (s )为比例积分(PI)+准谐振控制器(PIQR);G scpi (s )为PI控制器;G d (s )=1/(τ d s +1)表示延迟环节,τ d 为延迟环节的时间常数;k PWM 为串联变换器桥臂等效增益.根据图8 ,串联变换器所需补偿的电压参考为
(15) u s c r e f u L r e f g =311sin θ g -ug
由式(15)可知,串联变压器主要用于补偿电网电压的波动和畸变分量.
图7
图7
单相串联变换器电路模型及其等效框图
Fig.7
Circuit model and equivalent block of single-phase series converter
图8
图8
单相串联变换器控制策略
Fig.8
Control strategy of single-phase series converter
3.1.2 电流环控制设计
串联变换器电流控制框图如图9 所示.其中,电流参考i s c r e f
图9
图9
串联变换器电流控制
Fig.9
Current control of series converter
(16) G sc-iol (s )= k P W M ( k s c - i p s + k s c - i i ) s ( L s c s + R L s c ) ( τ d s + 1 )
式中:k sc-ip 和k sc-ii 分别为G scpi (s )的比例系数和积分系数.
(17) G sc-iol (s )= k s c k P W M s ( τ d s + 1 ) k s c - i o p s ( τ d s + 1 )
式中:k sc =k sc-p /k sc-i 为PI控制器中比例系数与积分系数的比值;k sc-iop =k sc k PWM 为电流环开环增益.
由式(17)可知,电流环控制为一个I型系统.ω sci 表示电流环的穿越频率,根据I型系统幅频特性可得:
(18) $k_{\mathrm{sc}-\mathrm{iop}}=k_{\mathrm{sc}} k_{\mathrm{PWM}}=\omega_{\mathrm{sci}}$
(19) $k_{\mathrm{sc}}=k_{\mathrm{sc} \cdot \mathrm{ip}} / L_{\mathrm{sc}}=k_{\mathrm{sc} \mathrm{ii}} / R_{\mathrm{Lsc}}$
联立式(18)和式(19),可得G scpi (s )的参数k sc-ip 和k sc-ii 为
(20) k s c - i p = ω s c i L s c / k P W M k s c - i i = ω s c i R L s c / k P W M
3.1.3 电压环控制设计
串联变换器电压控制如图10 所示,其中G sc-icl (s )=k sc-opi /(s +k sc-opi )为电流闭环传递函数.
图10
图10
串联变换器电压控制
Fig.10
Voltage control of series converter
考虑电网电压畸变情况,采用PIQR控制器实现对电网电压波动和畸变的补偿.由于谐波次数越低,其含量越高,所以主要选择对3次、5次、7次和9次电压谐波进行抑制.因此,PIQR控制器可表示为
(21) G scpiqr (s )= k s c - v p s + k s c - v i s ∑ h = 1 , 3 , 5 , 7 , 9 2 k r ω c s s 2 + 2 ω c s + ( h ω o ) 2
式中:k sc-vp 为比例系数;k sc-vi 为积分系数;k r 为谐振增益;ω c 为截止频率;ω o 为谐振频率.PI控制器为(k sc-vp s +k sc-vi )/s ;准谐振控制器为
$\sum_{h-1,3,5,7,9} \frac{2 k_{\mathrm{r}} \omega_{\mathrm{c}} s}{s^{2}+2 \omega_{\mathrm{c}} s+\left(h \omega_{\mathrm{o}}\right)^{2}}$
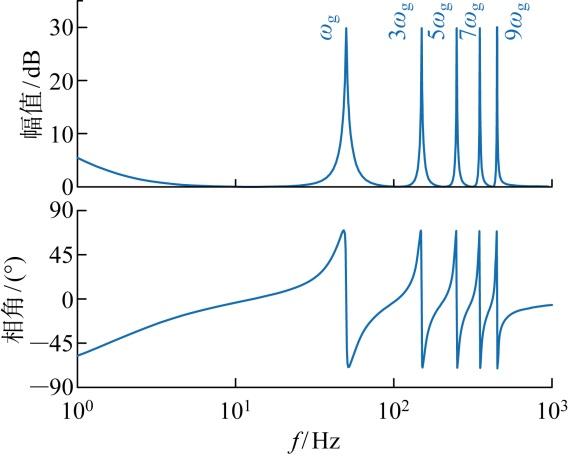
根据式(21)可得到G scpiqr (s )的伯德图,如图11 所示.由图可知,在调节过程中PI控制器起主要作用,而准谐振控制器在特定谐振点位置具有较大增益.因此,电压环中主要考虑对PI控制器的设计,而对准谐振控制器的k r 和ω c 参数设计可参考文献[21 ].
图11
图11
PIQR控制器伯德图
Fig.11
Bode diagram of PIQR controller
(22) G sc-vol (s )=k sc-vop ( k s c - v p / k s c - v i ) s + 1 s 2 ( τ s c v s + 1 )
式中:k sc-vop =k sc-vi /C sc 为电压开环增益;τ scv =1/k sc-iop 为时间常数.
由式(22)可知,电压环控制为一个 II 型系统.选取ω sci 的1/10作为电压环穿越频率ω scv ,令ω scv =ω sci /10,由II型系统幅频特性可得:
(23) $k_{\mathrm{sc}-\mathrm{vop}}=\omega_{\mathrm{scv}} k_{\mathrm{sc} \mathrm{vi}} / k_{\mathrm{sc}-\mathrm{vp}}$
此外,根据设定电压环相角裕度γ scv ≥45°,可得:
(24) $\begin{aligned}\gamma_{\mathrm{scv}}= & \arctan \left(\omega_{\mathrm{scv}} k_{\mathrm{sc}-\mathrm{vp}} / k_{\mathrm{sc} \mathrm{vi}}\right)- \\& \arctan \left(\tau_{\mathrm{scv}} \omega_{\mathrm{scv}}\right) \geqslant 45^{\circ}\end{aligned}$
根据式(23)和式(24)可对参数k sc-vp 和k sc-vi 进行计算.
3.1.4 三相串联变换器控制策略
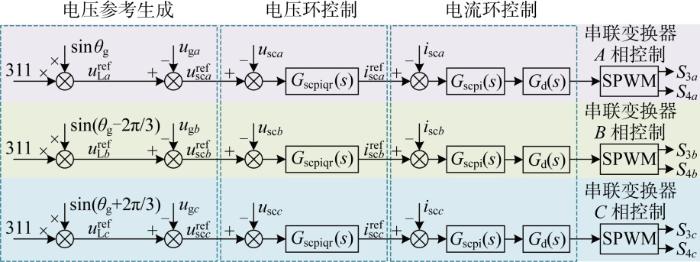
基于上述控制原理,三相串联变换器的总体控制策略如图12 所示,主要由电压参考生成环节、电压环控制和电流环控制组成.负荷电压参考量u L a r e f u L b r e f u L c r e f u g a u g b u g c C sc 的电压补偿参考量u s c a r e f u s c b r e f u s c c r e f . 之后,u s c a r e f u s c b r e f u s c c r e f u sc a u sc b u sc c G scpiqr (s )后得到串联变换器输出电流参考量i s c a r e f i s c b r e f i s c c r e f . 进一步,i s c a r e f i s c b r e f i s c c r e f i sc a i sc b i sc c G scpi (s )调节后得到串联变换器的调制信号,最后由正弦脉宽调制(SPWM)模块生成驱动信号S 3 a S 4 a S 3 b S 4 b S 3 c S 4 c .θ g 由锁相环(PLL)得到,关于PLL的控制设计见后文.
图12
图12
三相串联变换器总体控制策略
Fig.12
Overall control strategy of three-phase series converter
3.2 并联变换器控制策略设计
3.2.1 电路模型 主要包括以下几种模型.
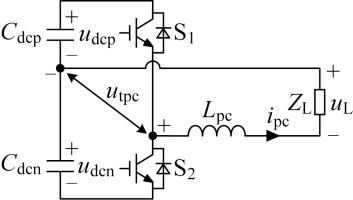
(1) 并联变换器模型.单相并联变换器电路模型如图13 所示,其中,u tpc 为并联变换器桥臂电压.
图13
图13
单相并联变换器电路模型
Fig.13
Circuit model of single-phase parallel converter
根据KVL可建立用于表示u tpc 、电感L pc 端电压和u L 之间关系的数学模型为
(25) u tpc =L pc d i p c d t Lpc ipc +uL
(2) 直流母线电压模型.基于交流瞬时变化功率与直流母线瞬时变化功率相等原则,推导直流母线侧的数学模型,具体过程如下:
令C dcp =C dcn =C dc ,直流母线瞬时变化功率为
(26) Δp dc = 1 2 dc Udc Δudc d Δ u d c d t
(27) $p_{\mathrm{ac}}=u_{\mathrm{L}}\left(i_{\mathrm{sc}}-i_{\mathrm{L}} \cos \varphi_{\mathrm{L}}\right)$
(28) $\Delta p_{\mathrm{ac}}=u_{\mathrm{L}} \Delta i_{\mathrm{sc}}+\Delta u_{\mathrm{L}}\left(I_{\mathrm{sc}}-2 I_{\mathrm{L}} \cos \varphi_{\mathrm{L}}\right)$
式中:Δi sc 为i sc 的瞬时变化量;Δu L 为u L 的瞬时变化量.
根据i sc 、i pc 和i L 之间的三角函数关系i p c 2 i s c 2 i L 2 -2 i sc i L cos φ L ,可得:
(29) Δi sc = I p c I s c - I L c o s φ L pc - I L - I s c c o s φ L I s c - I L c o s φ L L
式中:Δi pc 为i pc 的瞬时变化量;Δi L 为i L 的瞬时变化量.
(30) Δp ac = I p c I s c - I L c o s φ L pc uL
根据前文所述系统功率流转换原理可知,Δp dc 与Δp ac 的关系为
(31) $\Delta p_{\mathrm{dc}}=\Delta p_{\mathrm{ac}}$
对式(31)进行拉普拉斯(Laplace)变换,并整理可得直流母线的数学模型为
(32) G dc (s )= Δ u d c ( s ) Δ i p c ( s ) 2 u L I p c s C d c u d c ( I s c - I L c o s φ L )
(3) 正负直流母线电压模型.当正负直流母线电压处于不平衡状态时,u dcp 与u dcn 之间将存在电压差值u dcdif =u dcp -u dcn .令C dcp =C dcn =C dc ,u dcdif 所对应的电流为
(33) $i_{\mathrm{dcdif}}(t)=C_{\mathrm{dc}} \mathrm{~d} u_{\mathrm{dcdif}}(t) / \mathrm{d} t$
对式(33)进行Laplace变换后,可得正负直流母线数学模型为
(34) G bal (s )= Δ u d c d i f ( s ) Δ i d c d i f ( s ) 1 s C d c
3.2.2 控制模型
基于式(25)、式(32)和式(34),可得单相并联变换器控制策略如图14 所示,其控制目标为补偿负荷电流中的无功和畸变分量.
图14
图14
单相并联变换器控制策略
Fig.14
Control strategy of single-phase parallel converter
为主动适应电网电压变化,根据网侧与负荷侧有功功率相等原则,加入电网电流参考i g d *
(35) i g d * Ld iLd GLPF (s)/ugd
式中:G LPF (s )为二阶低通滤波器(LPF)的传递函数,选取其截止频率为5 Hz,用于提取i g d *
并联变换器电流参考i p c r e f i g d * i d c * i L 组成,可表示为
(36) i p c r e f i g d r e f L =(i g d * i d c * g -iL = I g d r e f g -iL
式中:第1项I g d r e f θ g 为基波有功电流;第2项负荷电流i L 可能同时含有有功、无功和谐波电流.因此,两项之差即为并联变换器所需补偿的电流.由于所提并联变换器控制方法无需检测负荷电流中的无功和谐波电流,所以可简化对控制策略的设计.
3.2.3 电流环控制设计
并联变换器控制策略设计过程与串联变换器类似,故对并联变换器控制参数设计进行简述.并联变换器电流环控制如图15 所示,考虑非线性负载条件,电流环控制器G pcpiqr (s )同样采用PIQR控制器,可表示为
(37) G pcpiqr (s )=(k pc-ip s +k pc-ii )/s + ∑ h = 1 , 3 , 5 , 7 , 9 2 k r ω c s s 2 + 2 ω c s + ( h ω o ) 2
式中:k pc-ip 和k pc-ii 为分别为比例系数和积分系数.
图15
图15
并联变换器电流控制
Fig.15
Current control of parallel converter
(38) G pc-iol (s )= k P W M ( k p c - i p s + k p c - i i ) s ( L p c s + R L p c ) ( τ d s + 1 )
利用零点与极点对消原理,可将式(38)进一步表示为
(39) G pc-iol (s )= k p c k P W M s ( τ d s + 1 ) k p c - i o p s ( τ d s + 1 )
式中: k pc =k sc-p /k sc-i 为比值系数;k pc-iop =k pc k PWM 为电流环开环增益.
根据I型系统幅频特性及零极点对消原理,可得k pc-ip 和k pc-ii 的表达式为
(40) k p c - i p = ω p c i L p c / k P W M k p c - i i = ω p c i R L p c / k P W M
3.2.4 直流母线电压环设计
由图14 和式(32)可得到直流母线电压环,如图16 所示.其中,G dcpi (s )=k d c p s + k d c i s G pc-icl (s )=k p c - o p i s + k p c - o p i
图16
图16
直流母线电压控制
Fig.16
DC bus voltage control
(41) G pc-vol (s )=k pc-vop ( k d c p / k d c i ) s + 1 s 2 ( τ p c v s + 1 )
式中:k pc-vop =2k dci u L I pc / [C dc u dc (I sc -I L cos φ L )]为电压开环增益;τ pcv =1/k pc-iop 为时间常数.
(42) k p c - v o p = ω p c v k d c i / k d c p a r c t a n ( ω p c v k d c p / k d c i ) - a r c t a n ( τ p c v ω p c v ) ≥ 45 °
根据式(42),可对直流母线电压控制中PI控制器的参数k dcp 和k dci 进行计算.
3.2.5 正负直流母线均压环设计
根据式(34),直流母线均压控制如图17 所示,其中G dcdifpi (s )为PI控制器.
图17
图17
直流母线均压控制
Fig.17
DC bus voltage balance control
(43) $G_{\mathrm{dif}-\mathrm{vol}}(s)=\left(k_{\mathrm{difp}} s+k_{\mathrm{difi}}\right) /\left(s^{2} C_{\mathrm{dc}}\right)$
设ω dif 为G dif-vol (s)的穿越频率,根据G dif-vol (s )在ω dif 处的幅频特性为单位增益可得:
(44) k d i f p 2 k d i f i 2 ω d i f 2 ω d i f 2 C d c 2
(45) $\tan \gamma_{\mathrm{dif}}=k_{\mathrm{difi}} \omega_{\mathrm{dif}} / k_{\mathrm{difp}}$
由式(44)和式(45)可计算出参数k difp 和k difi .
3.2.6 三相并联变换器控制策略
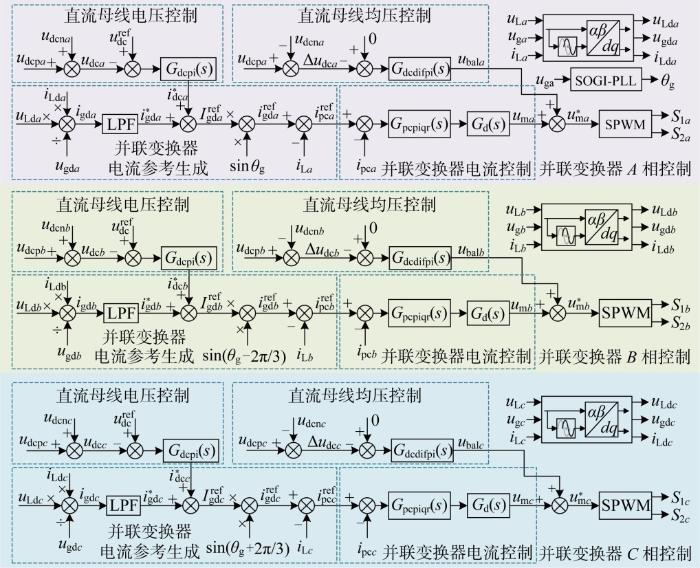
三相并联变换器总体控制策略如图18 所示,主要由直流母线电压控制、直流母线均压控制、并联变换器电流参考生成和并联变换器电流控制构成.
图18
图18
三相并联变换器总体控制策略
Fig.18
Overall control strategy of three-phase parallel converter
直流母线控制用于控制直流母线电压稳定于750 V,以A 相为例说明直流母线控制作用如下:
(1) 当u dc a u d c r e f i d c a * i p c a r e f
(2) 当u dc a u d c r e f i d c a * i p c a r e f u dc a
(3) 当u dc a u d c r e f i d c a * i p c a r e f u dc a
直流母线平衡控制用于控制正负直流母线电压分别为±375 V,同样以A 相为例直流母线平衡控制的具体控制原理如下:
(1) 当u dcp a u dcn a u bal a u m a * .
(2) 当u dcp a u dcn a u bal a u m a * i pc a C dcp a u dcp a C dcn a C dcn a u dcn a u dcp a u dcn a
(3) 当u dcp a u dcn a u bal a u m a * i pc a C dcn a u dcn a C dcp a C dcp a u dcp a u dcp a u dcn a
3.3 锁相环控制策略设计
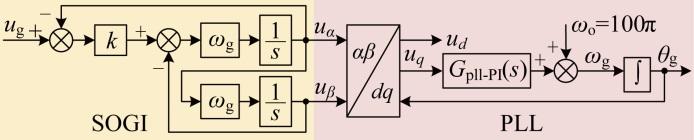
考虑电网电压u g 畸变工况,利用二阶广义积分器(SOGI)提取出u g 中的基波分量.u g 经SOGI后生成正交量uα 和uβ ,再通过PLL实现对u g 的相位跟踪.基于上述原理,SOGI-PLL控制原理如图19 所示,其中,G pll-PI (s )=k pll-p +k pll-i /s 为PI控制器.
图19
图19
SOGI-PLL控制框图
Fig.19
Control block of SOGI-PLL
阻尼系数k 与SOGI的滤波性能和动态响应有关,即k 越小SOGI滤波性能越好,但动态响应越慢,反之亦然.因此考虑SOGI的滤波性能和动态响应,选取k =2 . 基于文献[22 ],SOGI-PLL的等效控制框图如图20 所示,其中利用一阶惯性环节 1/(τ p s +1) 等效SOGI环节和派克(dq )变换.
图20
图20
SOGI-PLL等效控制
Fig.20
Equivalent control of SOGI-PLL
(46) $G_{\mathrm{PLL}-\mathrm{cl}}(s)=\frac{\theta_{\mathrm{g}}(s)}{\theta(s)}=\frac{1}{\tau_{\mathrm{p}} s+1} \frac{k_{\mathrm{pll}-\mathrm{p}} s+k_{\mathrm{pll-i}}}{s^{2}+k_{\mathrm{pll-p}} s+k_{\mathrm{pll-i}}}=\underbrace{\frac{1}{\tau_{\mathrm{p}} s+1}}_{\text {一阶惯性环节 }} \frac{2 \xi \omega_{\mathrm{n}} s+\omega_{\mathrm{n}}^{2}}{\underbrace{s^{2}+2 \xi \omega_{\mathrm{n}} s+\omega_{\mathrm{n}}^{2}}_{\text {二阶振荡环节 }}}$
(47) k p l l - p = 2 ξ ω n k p l l - i = ω n 2
对于二阶振荡环节,希望系统振荡程度较小且过渡时间较短,一般选择ξ =0.707和ω n =2π×18 rad/s,则有k pll-p =160和k pll-i =12 791.
4 仿真验证
为验证多工况电能质量治理效果及所设计控制策略的有效性,建立基于MATLAB的TLTT-UPQC 仿真模型,仿真参数如表3 所示.针对多种电能质量治理功能,仿真场景具体如下:①电网电压平衡/跌落/升高;②电网电压畸变补偿;③负荷无功功率补偿;④负荷畸变电流补偿.
4.1 电网电压跌落/平衡/升高
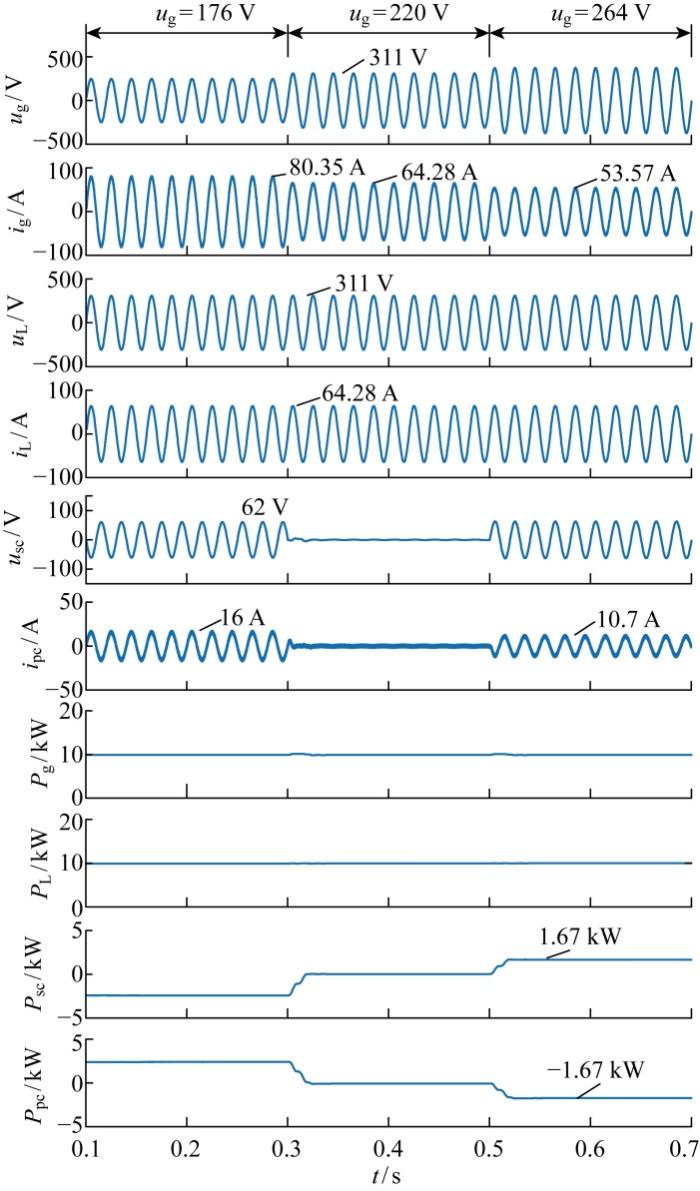
在每相额定功率10 kW条件下,TLTT-UPQC在电网电压跌落、平衡和升高3种工况下的仿真结果如图21 所示.
图21
图21
电网电压跌落/升高的补偿功能仿真结果
Fig.21
Simulation results of compensation function for grid voltage drop/rise
(1) 0.1~0.3 s范围内电网电压跌落20%:u g =176 V且k g =1.25时,系统控制电流i g 使其增加至2 P g =P L =10 kW.由于电网输入电流幅值2 I sc =2 I g =80.35 A,大于负荷电流幅值2 I L =64.28 A,所以并联变换器将串联变换器多吸收的电流馈送至电网,则并联变换器电流幅值为 2 I pc =16 A.电容C sc 补偿u g 跌落部分,进一步可知C sc 两端电压幅值为 2 u sc =62 V.由于u sc 与i g 相位相反,所以串联变换器吸收有功功率P sc =-2.5 kW.同时,并联变换器输出电流i pc 与u L 同相位,则并联变换器输出有功功率P pc =2.5 kW.
(2) 0.3 s~0.5 s范围内电网电压平衡:u g =u L =220 V且k g =1时,i g 的幅值由80.35 A降至64.28 A,满足i g =i L .由于u sc =0和i pc =0,所以 P sc =P pc =0,说明两变换器之间不存在有功功率的互动.
(3) 0.5 s~0.7 s范围内电网电压升高20%:u g =264 V且k g =0.83时,i g 的幅值由64.28 A降至53.57 A,小于负荷电流幅值64.28 A,因此并联变换器从电网吸收电流2 I pc =10.7 A并传输至负荷.由于u sc 与i g 同相位,而i pc 与u L 相位相反,所以有P sc =1.67 kW和P pc =-1.67 kW.
上述仿真结果与第2章理论分析一致,证明了TLTT-UPQC对电网电压跌落和升高的补偿功能.
4.2 电网电压畸变
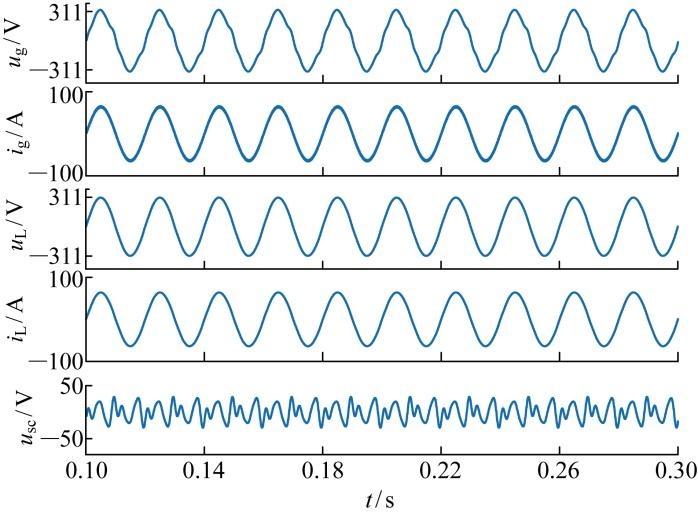
通常,电网电压畸变受低次谐波影响较大,因此在电网电压中加入了3次、5次、7次和9次谐波,其含量分别为6.4%、4.8%、3.2%和1.6%,电网电压畸变工况下的仿真结果图如图22 所示.u g 虽发生了明显的畸变,但在TLTT-UPQC控制下,i g 和u L 依然保持正弦,不受u g 畸变影响,而u g 畸变部分由C sc 补偿.
图22
图22
电网电压畸变补偿功能仿真结果
Fig.22
Simulation results of compensation function for grid voltage distortion
4.3 负荷无功电流补偿
以S L =8 kW+j6 kvar的阻感性负荷为例,对系统的负荷无功功率补偿进行仿真验证,仿真结果如图23 所示.i g 与u g 同相位,说明电网只为负荷提供有功电流;而i pc 滞后u L 为90°,说明并联变换器补偿负荷无功电流,从而使网侧实现单位功率因数.
图23
图23
负荷无功电流补偿功能仿真结果
Fig.23
Simulation results of compensation function for load reactive current
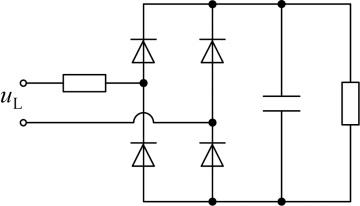
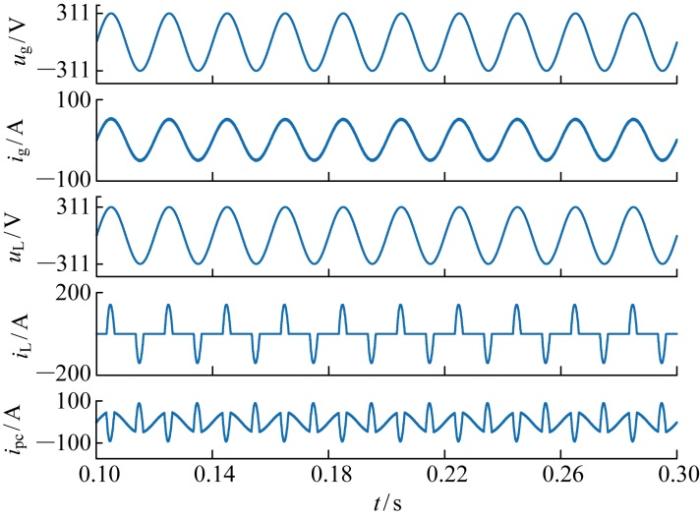
4.4 负荷畸变电流补偿
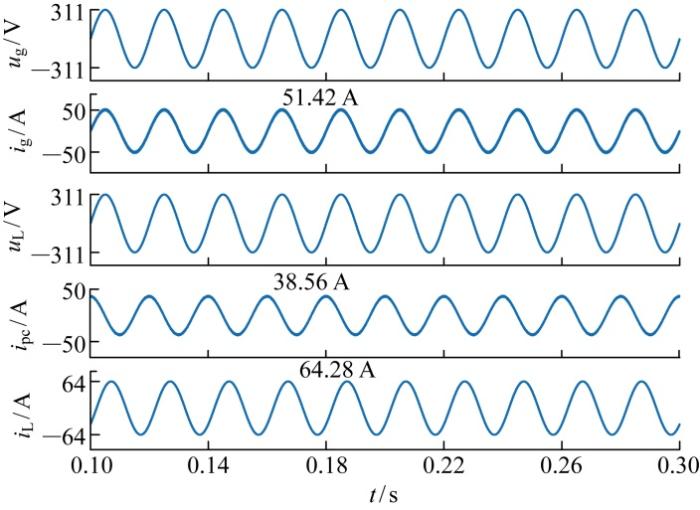
参照国标GB/T 7260.3—2003,TLTT-UPQC所带非线性负荷为二极管不控整流容性负荷,如图24 所示;非线性负荷工况下的负荷畸变电流补偿仿真如图25 所示.由图25 可知,i L 因含有大量谐波导致畸变较为严重,但i g 不受非线性负荷影响,只为负荷提供所需基波分量,i L 中的谐波分量由并联变换器补偿.此外,在非线性负荷工况下,u L 保持较好的正弦度,能实现对负荷的高质量供电.
图24
图24
非线性负荷
Fig.24
Nonlinear load
图25
图25
负荷畸变电流补偿功能仿真结果
Fig.25
Simulation results of compensation function for load distortion current
5 结论
所提TLTT-UPQC能解决UPQC中工频变压器体积、质量与磁饱和问题,以轻量化、高灵活性形式实施对多工况场景下电能质量问题的治理,在改善配电网电能质量的同时,满足负荷高质量用电需求,结论如下:
(1) TLTT-UPQC无需使用工频变压器,大大降低了系统的体积和质量,有助于实现UPQC的模块化生产及增强装置安装的灵活性.
(2) 电网电压跌落/升高工况下,电网输入电流相应增加或降低,串联与并联变换器之间存在有功功率互动,以平衡系统内部功率,实现网侧与负荷侧有功功率相等.
(3) 电网电压畸变工况下,电容C sc 补偿畸变电压,负荷电压不受电网电压畸变影响,实现了对负荷的高质量供电.
(4) 阻感性负荷与非线性负荷工况下,并联变换器补偿负荷无功和谐波电流,实现了对电网输入电流的无畸变控制,能在确保网侧单位功率因数的同时,不对电网造成谐波污染.
参考文献
View Option
[1]
张林林 , 胡熊伟 , 李鹏 , 等 . 基于极限学习机的电力系统暂态稳定评估方法
[J]. 上海交通大学学报 2019 , 53 (6 ): 749 -756 .
[本文引用: 1]
ZHANG Linlin HU Xiongwei LI Peng et al Power system transient stability assessment based on extreme learning machine
[J]. Journal of Shanghai Jiao Tong University 2019 , 53 (6 ): 749 -756 .
[本文引用: 1]
[2]
查鹏程 , 甘雅丽 , 高海祐 , 等 . 电动汽车充电站接入配电网的电能质量评估
[J]. 电测与仪表 2022 , 59 (6 ): 69 -75 .
[本文引用: 1]
ZHA Pengcheng GAN Yali GAO Haiyou et al Quality assessment of electric vehicle charging stations accessing distribution network
[J]. Electrical Measurement & Instrumentation 2022 , 59 (6 ): 69 -75 .
[本文引用: 1]
[3]
徐艳春 , 樊士荣 , 谢莎莎 , 等 . 一种适用于高渗透率主动配电网的电能质量调节器
[J]. 电机与控制学报 2022 , 26 (1 ): 46 -56 .
[本文引用: 1]
XU Yanchun FAN Shirong XIE Shasha et al Power quality regulator designed for high permeability active distribution network
[J]. Electric Machines and Control 2022 , 26 (1 ): 46 -56 .
[本文引用: 1]
[4]
高本锋 , 王飞跃 , 于弘洋 , 等 . 应用静止同步串联补偿器抑制风电次同步振荡的方法
[J]. 电工技术学报 2020 , 35 (6 ): 1346 -1356 .
[本文引用: 1]
GAO Benfeng WANG Feiyue YU Hongyang et al The suppression method of wind power sub-synchronous oscillation using static synchronous series compensator
[J]. Transactions of China Electrotechnical Society 2020 , 35 (6 ): 1346 -1356 .
[本文引用: 1]
[5]
FEI J T LIU L CHEN Y Finite-time disturbance observer of active power filter with dynamic terminal sliding mode controller
[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics 2023 , 11 (2 ): 1604 -1615 .
[本文引用: 1]
[6]
D$\dot{\mathrm{I}}$R$\dot{\mathrm{I}}$K H GEZEG$\dot{\mathrm{I}}$N C D$\dot{\mathrm{I}}$R$\dot{\mathrm{I}}$K H S Reactive power compensation with hybrid compensator combining a synchronous motor and switched capacitors
[J]. Electric Power Systems Research 2023 , 216 : 109010 .
[本文引用: 1]
[7]
LEITE J C ABRIL I P DE LIMA TOSTES M E et al Multi-objective optimization of passive filters in industrial power systems
[J]. Electrical Engineering 2017 , 99 (1 ): 387 -395 .
[本文引用: 1]
[8]
陶海军 , 周犹松 , 张国澎 , 等 . LCL型并网逆变器并联谐振机理分析及抑制方法
[J]. 上海交通大学学报 2020 , 54 (10 ): 1065 -1073 .
[本文引用: 1]
TAO Haijun ZHOU Yousong ZHANG Guopeng et al Parallel resonance mechanism analysis and suppression method for LCL type grid-connected inverter
[J]. Journal of Shanghai Jiao Tong University 2020 , 54 (10 ): 1065 -1073 .
[本文引用: 1]
[9]
SANJENBAM C D SINGH B Modified adaptive filter based UPQC for battery supported hydro driven PMSG system
[J]. IEEE Transactions on Industrial Informatics 2023 , 19 (7 ): 8018 -8028 .
[本文引用: 1]
[10]
YADAV S K PATEL A MATHUR H D Study on comparison of power losses between UPQC and UPQC-DG
[J]. IEEE Transactions on Industry Applications 2022 , 58 (6 ): 7384 -7395 .
[本文引用: 1]
[11]
张震霄 , 年珩 , 李培 , 等 . 储能型统一电能质量调节器电压补偿能力分析及提升方法
[J]. 电力系统自动化 2022 , 46 (23 ): 151 -159 .
[本文引用: 1]
ZHANG Zhenxiao NIAN Heng LI Pei et al Voltage compensation capability analysis and improvement method for unified power quality conditioner with energy storage
[J]. Automation of Electric Power Systems 2022 , 46 (23 ): 151 -159 .
[本文引用: 1]
[12]
陈国栋 , 宋晋峰 , 张亮 , 等 . 动态电压恢复器注入变压器的直流偏磁抑制策略
[J]. 中国电机工程学报 2014 , 34 (28 ): 4983 -4989 .
[本文引用: 1]
CHEN Guodong SONG Jinfeng ZHANG Liang et al Control strategy for eliminating DC magnetic flux in the injection transformer of a dynamic voltage restorer
[J]. Proceedings of the CSEE 2014 , 34 (28 ): 4983 -4989 .
[本文引用: 1]
[13]
HAN J LI X JIANG Y et al Three-phase UPQC topology based on quadruple-active-bridge
[J]. IEEE Access 2020 , 9 : 4049 -4058 .
[本文引用: 2]
[14]
HAN J LI X SUN Y et al Optimal design and decoupling control of series DC-link voltages for quadruple-active-bridge based UPQC
[J]. International Journal of Electrical Power & Energy Systems 2022 , 140 : 108038 .
[本文引用: 2]
[15]
ZHAO X J BAI P S ZHANG C J et al Analysis and validations of operation behaviors for dual active bridge-based unified power quality conditioner under different working conditions
[J]. International Journal of Circuit Theory and Applications 2023 , 51 (2 ): 541 -556 .
[本文引用: 2]
[16]
FELINTO A S CUNHA M F JACOBINA C B Three-phase unified power quality conditioner based on high-frequency link
[J]. IEEE Transactions on Industry Applications 2022 , 58 (5 ): 6397 -6407 .
[本文引用: 2]
[17]
张秀娟 , 姜齐荣 , 韩英铎 . 一种新型的单相统一电能质量调节器
[J]. 电力系统自动化 2004 , 28 (23 ): 76 -80 .
[本文引用: 2]
ZHANG Xiujuan JIANG Qirong HAN Yingduo A novel single phase unified power quality conditioner
[J]. Automation of Electric Power Systems 2004 , 28 (23 ): 76 -80 .
[本文引用: 2]
[18]
张晓明 , 于庆广 , 张秀娟 , 等 . 基于直流隔离单元的新型统一电能质量调节器
[J]. 电力电子技术 2007 , 41 (1 ): 7 -9 .
[本文引用: 2]
ZHANG Xiaoming YU Qingguang ZHANG Xiujuan et al Implementing of the unified power quality conditioner based on the DCI unit
[J]. Power Electronics 2007 , 41 (1 ): 7 -9 .
[本文引用: 2]
[19]
LU Y XIAO G C WANG X F et al Control strategy for single-phase transformerless three-leg unified power quality conditioner based on space vector modulation
[J]. IEEE Transactions on Power Electronics 2016 , 31 (4 ): 2840 -2849 .
[本文引用: 2]
[20]
XU C Q ZHOU M LIU Y L et al Transformer-less single-phase unified power quality conditioner of no circulating current
[J]. IET Power Electronics 2020 , 13 (5 ): 970 -980 .
[本文引用: 2]
[21]
CHEN Z Y CHEN Y D GUERRERO J M et al Generalized coupling resonance modeling, analysis, and active damping of multi-parallel inverters in microgrid operating in grid-connected mode
[J]. Journal of Modern Power Systems and Clean Energy 2016 , 4 (1 ): 63 -75 .
[本文引用: 1]
[22]
GOLESTAN S MOUSAZADEH S Y GUERRERO J M et al A critical examination of frequency-fixed second-order generalized integrator-based phase-locked loops
[J]. IEEE Transactions on Power Electronics 2017 , 32 (9 ): 6666 -6672 .
[本文引用: 1]
基于极限学习机的电力系统暂态稳定评估方法
1
2019
... 随着电力电子变换技术在配电网中的快速发展和普及应用,配电网中的负荷种类不断丰富,如电动汽车、变频空调、发光二极管(LED)照明等.然而,基于电力电子变换技术的负荷通常伴有非线性和冲击性特征,给配电网的电能质量带来较大挑战[1 ] .例如,非线性负荷所产生的非线性电流易造成电网电压畸变;而冲击性负荷易造成电网电压暂降或升高.同时,电压畸变、暂降、升高问题会互相叠加,呈现出复合形式的电能质量问题,不仅影响用户的用电体验,还可能对电力系统的安全稳定产生影响[2 ] .为此,开发一种综合电能质量治理装置,能在治理电力电子负荷对配电网电压污染的同时,抑制电网电压问题对负荷的影响,从而满足重要负荷对高质量供电的需求. ...
Power system transient stability assessment based on extreme learning machine
1
2019
... 随着电力电子变换技术在配电网中的快速发展和普及应用,配电网中的负荷种类不断丰富,如电动汽车、变频空调、发光二极管(LED)照明等.然而,基于电力电子变换技术的负荷通常伴有非线性和冲击性特征,给配电网的电能质量带来较大挑战[1 ] .例如,非线性负荷所产生的非线性电流易造成电网电压畸变;而冲击性负荷易造成电网电压暂降或升高.同时,电压畸变、暂降、升高问题会互相叠加,呈现出复合形式的电能质量问题,不仅影响用户的用电体验,还可能对电力系统的安全稳定产生影响[2 ] .为此,开发一种综合电能质量治理装置,能在治理电力电子负荷对配电网电压污染的同时,抑制电网电压问题对负荷的影响,从而满足重要负荷对高质量供电的需求. ...
电动汽车充电站接入配电网的电能质量评估
1
2022
... 随着电力电子变换技术在配电网中的快速发展和普及应用,配电网中的负荷种类不断丰富,如电动汽车、变频空调、发光二极管(LED)照明等.然而,基于电力电子变换技术的负荷通常伴有非线性和冲击性特征,给配电网的电能质量带来较大挑战[1 ] .例如,非线性负荷所产生的非线性电流易造成电网电压畸变;而冲击性负荷易造成电网电压暂降或升高.同时,电压畸变、暂降、升高问题会互相叠加,呈现出复合形式的电能质量问题,不仅影响用户的用电体验,还可能对电力系统的安全稳定产生影响[2 ] .为此,开发一种综合电能质量治理装置,能在治理电力电子负荷对配电网电压污染的同时,抑制电网电压问题对负荷的影响,从而满足重要负荷对高质量供电的需求. ...
Quality assessment of electric vehicle charging stations accessing distribution network
1
2022
... 随着电力电子变换技术在配电网中的快速发展和普及应用,配电网中的负荷种类不断丰富,如电动汽车、变频空调、发光二极管(LED)照明等.然而,基于电力电子变换技术的负荷通常伴有非线性和冲击性特征,给配电网的电能质量带来较大挑战[1 ] .例如,非线性负荷所产生的非线性电流易造成电网电压畸变;而冲击性负荷易造成电网电压暂降或升高.同时,电压畸变、暂降、升高问题会互相叠加,呈现出复合形式的电能质量问题,不仅影响用户的用电体验,还可能对电力系统的安全稳定产生影响[2 ] .为此,开发一种综合电能质量治理装置,能在治理电力电子负荷对配电网电压污染的同时,抑制电网电压问题对负荷的影响,从而满足重要负荷对高质量供电的需求. ...
一种适用于高渗透率主动配电网的电能质量调节器
1
2022
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
Power quality regulator designed for high permeability active distribution network
1
2022
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
应用静止同步串联补偿器抑制风电次同步振荡的方法
1
2020
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
The suppression method of wind power sub-synchronous oscillation using static synchronous series compensator
1
2020
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
Finite-time disturbance observer of active power filter with dynamic terminal sliding mode controller
1
2023
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
Reactive power compensation with hybrid compensator combining a synchronous motor and switched capacitors
1
2023
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
Multi-objective optimization of passive filters in industrial power systems
1
2017
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
LCL型并网逆变器并联谐振机理分析及抑制方法
1
2020
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
Parallel resonance mechanism analysis and suppression method for LCL type grid-connected inverter
1
2020
... 电能质量治理装置一般分为有源、无源及有源-无源混合3种形式.其中,常见的有源装置包括动态电压恢复器[3 ] 、静止同步串联补偿器[4 ] 、有源电力滤波器[5 ] 等;无源装置包括电感器、电容器及其组合形式[6 -7 ] .上述有源和无源装置通常只是单一治理电压或电流相关的电能质量,而有源-无源混合型装置虽能同时对电压和电流电能质量问题进行治理,但电感器和电容器仍存在增加系统体积与谐振振荡的问题[8 ] . ...
Modified adaptive filter based UPQC for battery supported hydro driven PMSG system
1
2023
... 作为一种综合治理装置,统一电能质量调节器(UPQC)[9 ⇓ -11 ] 因其能克服上述装置的缺点,满足对电压和电流相关电能质量问题同时治理的多任务要求,而受到国内外学术界及工业界的广泛关注.但在以工频变压器进行电压补偿的UPQC中,工频变压器存在质量重和体积大的缺点,不利于装置模块化生产,降低了系统的灵活性,更重要的是,变压器可能出现的磁饱和问题将会影响系统安全稳定运行[12 ] . ...
Study on comparison of power losses between UPQC and UPQC-DG
1
2022
... 作为一种综合治理装置,统一电能质量调节器(UPQC)[9 ⇓ -11 ] 因其能克服上述装置的缺点,满足对电压和电流相关电能质量问题同时治理的多任务要求,而受到国内外学术界及工业界的广泛关注.但在以工频变压器进行电压补偿的UPQC中,工频变压器存在质量重和体积大的缺点,不利于装置模块化生产,降低了系统的灵活性,更重要的是,变压器可能出现的磁饱和问题将会影响系统安全稳定运行[12 ] . ...
储能型统一电能质量调节器电压补偿能力分析及提升方法
1
2022
... 作为一种综合治理装置,统一电能质量调节器(UPQC)[9 ⇓ -11 ] 因其能克服上述装置的缺点,满足对电压和电流相关电能质量问题同时治理的多任务要求,而受到国内外学术界及工业界的广泛关注.但在以工频变压器进行电压补偿的UPQC中,工频变压器存在质量重和体积大的缺点,不利于装置模块化生产,降低了系统的灵活性,更重要的是,变压器可能出现的磁饱和问题将会影响系统安全稳定运行[12 ] . ...
Voltage compensation capability analysis and improvement method for unified power quality conditioner with energy storage
1
2022
... 作为一种综合治理装置,统一电能质量调节器(UPQC)[9 ⇓ -11 ] 因其能克服上述装置的缺点,满足对电压和电流相关电能质量问题同时治理的多任务要求,而受到国内外学术界及工业界的广泛关注.但在以工频变压器进行电压补偿的UPQC中,工频变压器存在质量重和体积大的缺点,不利于装置模块化生产,降低了系统的灵活性,更重要的是,变压器可能出现的磁饱和问题将会影响系统安全稳定运行[12 ] . ...
动态电压恢复器注入变压器的直流偏磁抑制策略
1
2014
... 作为一种综合治理装置,统一电能质量调节器(UPQC)[9 ⇓ -11 ] 因其能克服上述装置的缺点,满足对电压和电流相关电能质量问题同时治理的多任务要求,而受到国内外学术界及工业界的广泛关注.但在以工频变压器进行电压补偿的UPQC中,工频变压器存在质量重和体积大的缺点,不利于装置模块化生产,降低了系统的灵活性,更重要的是,变压器可能出现的磁饱和问题将会影响系统安全稳定运行[12 ] . ...
Control strategy for eliminating DC magnetic flux in the injection transformer of a dynamic voltage restorer
1
2014
... 作为一种综合治理装置,统一电能质量调节器(UPQC)[9 ⇓ -11 ] 因其能克服上述装置的缺点,满足对电压和电流相关电能质量问题同时治理的多任务要求,而受到国内外学术界及工业界的广泛关注.但在以工频变压器进行电压补偿的UPQC中,工频变压器存在质量重和体积大的缺点,不利于装置模块化生产,降低了系统的灵活性,更重要的是,变压器可能出现的磁饱和问题将会影响系统安全稳定运行[12 ] . ...
Three-phase UPQC topology based on quadruple-active-bridge
2
2020
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
Optimal design and decoupling control of series DC-link voltages for quadruple-active-bridge based UPQC
2
2022
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
Analysis and validations of operation behaviors for dual active bridge-based unified power quality conditioner under different working conditions
2
2023
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
Three-phase unified power quality conditioner based on high-frequency link
2
2022
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
一种新型的单相统一电能质量调节器
2
2004
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
A novel single phase unified power quality conditioner
2
2004
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
基于直流隔离单元的新型统一电能质量调节器
2
2007
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
Implementing of the unified power quality conditioner based on the DCI unit
2
2007
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
Control strategy for single-phase transformerless three-leg unified power quality conditioner based on space vector modulation
2
2016
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
Transformer-less single-phase unified power quality conditioner of no circulating current
2
2020
... 为解决UPQC中工频变压器所引发的问题,文献[13 ⇓ -15 ]中提出一种基于双有源桥(DAB)变换器的UPQC,通过将DAB连接至UPQC的直流母线的方式来消除工频变压器的不利影响,但同时增加了系统拓扑的复杂度和控制策略的设计难度;Felinto等[16 ] 提出一种基于多绕组高频变压器的直流拓扑,以实现对UPQC直流母线的隔离与控制,但二极管器件的使用导致该直流拓扑只具备单相运行能力,因此该直流拓扑必须额外加入电阻和开关以消耗电网电压升高时系统的多余能量,这将影响UPQC的整体运行效率;文献[17 -18 ]中摒弃DAB思路,在串联和并联变换器的直流侧各加入一对开关器件,从而大大降低系统的复杂程度,但该结构中直流母线电压波动较大;文献[19 -20 ]中提出一种三桥臂型UPQC,由于串联与并联变换器共用一个桥臂,将导致两变换器之间存在耦合问题,增加了控制策略的设计难度. ...
... 以单相拓扑所需的高频变压器、电力电子开关器件数量和功率二极管数量为例,文献[13 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -20 ]与所提无工频变压器型UPQC进行对比,如表1 所示.由表可知,所提TLTT-UPQC不含高频变压器且所 需开关器件最少,因此其具备轻量化和高灵活性的特征. ...
Generalized coupling resonance modeling, analysis, and active damping of multi-parallel inverters in microgrid operating in grid-connected mode
1
2016
... 根据式(21)可得到G scpiqr (s )的伯德图,如图11 所示.由图可知,在调节过程中PI控制器起主要作用,而准谐振控制器在特定谐振点位置具有较大增益.因此,电压环中主要考虑对PI控制器的设计,而对准谐振控制器的k r 和ω c 参数设计可参考文献[21 ]. ...
A critical examination of frequency-fixed second-order generalized integrator-based phase-locked loops
1
2017
... 阻尼系数k 与SOGI的滤波性能和动态响应有关,即k 越小SOGI滤波性能越好,但动态响应越慢,反之亦然.因此考虑SOGI的滤波性能和动态响应,选取k = 2 . 基于文献[22 ],SOGI-PLL的等效控制框图如图20 所示,其中利用一阶惯性环节 1/(τ p s +1) 等效SOGI环节和派克(dq )变换. ...