基于用户信用指数的园区电动汽车充放电调度机制

doi:10.16183/j.cnki.jsjtu.2023.196

基于用户信用指数的园区电动汽车充放电调度机制

孙欣^,^a, 江海林^a, 谢敬东^b, 王思敏^a, 王森^a

上海电力大学 a. 电气工程学院; b. 能源电力科创中心,上海 200090

Charging and Discharging Scheduling Mechanism of Electric Vehicles in Park Based on User Credit Index

SUN Xin^,^a, JIANG Hailin^a, XIE Jingdong^b, WANG Simin^a, WANG Sen^a

a. College of Electrical Engineering; b. Energy and Power Innovation Center, Shanghai University of Electric Power, Shanghai 200090, China

收稿日期: 2023-05-16 修回日期: 2023-05-29 接受日期: 2023-05-31

基金资助:

国家自然科学基金(U2066214)

Received: 2023-05-16 Revised: 2023-05-29 Accepted: 2023-05-31

作者简介 About authors

孙欣(1980—),副教授,从事电力系统优化,电力市场、综合能源研究;E-mail:sunxin@shiep.edu.cn.

摘要

电动汽车用户人为提前结束充电的违约行为易对负荷聚集商及用户自身造成违约损失.因此,考虑违约行为的充放电调度机制至关重要.基于吴氏三维信用理论量化电动汽车用户信用,并从放电深度和充电优先级两个维度修正电动汽车充放电计划;同时,建立考虑区域配电网负荷波动和用户成本的多目标优化模型.以园区为例进行仿真计算,对比分析多种场景下仿真结果及不同违约规模和电动汽车渗透率对所提充放电调度机制的影响.结果表明:基于用户信用指数的充放电调度机制在平抑园区配电网负荷波动和提高用户充电体验上都具有优势,相比未考虑用户执行情况的有序充放电策略,该机制能够更好地适应电动汽车渗透率升高及违约规模扩大的场景.

关键词： 电动汽车; 有序放充电; 用户信用指数; 充电优先级; 三维信用理论

Abstract

The default behavior of electric vehicle (EV) users to end charging in advance is easy to cause default losses to load aggregators and users themselves. Therefore,it is crucial to dispatch charging behavior rationally considering default behavior. This paper quantifies EV user credit based on Wu’s three-dimensional credit theory, and revises EV charging and discharging plan in the dimensions of discharge depth and charging priority. In addition, it establishes a multi-objective optimization model considering the load fluctuation of regional distribution network and the user cost. Using a park as an example for simulation, it compares and analyzes the effects of different user default rates and EV permeability on the proposed multi-dimensional modified charging and discharging strategy. The results show that the charging and discharging scheduling mechanism based on the user credit index has advantages in calming the load fluctuation of the distribution network in the park and improving the charging experience of users. Compared with the orderly charging and discharging strategy which does not consider the charging and discharging execution of users, the proposed mechanism can better adapt to the scenario of increasing penetration rate of EV and expanding default scale.

Keywords： electric vehicle (EV); orderly charging and discharging; user credit index; charging priority; three dimensional credit theory

PDF (1363KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙欣, 江海林, 谢敬东, 王思敏, 王森. 基于用户信用指数的园区电动汽车充放电调度机制[J]. 上海交通大学学报, 2025, 59(2): 200-207 doi:10.16183/j.cnki.jsjtu.2023.196

SUN Xin, JIANG Hailin, XIE Jingdong, WANG Simin, WANG Sen. Charging and Discharging Scheduling Mechanism of Electric Vehicles in Park Based on User Credit Index[J]. Journal of Shanghai Jiaotong University, 2025, 59(2): 200-207 doi:10.16183/j.cnki.jsjtu.2023.196

当今全球传统资源短缺和环境污染问题日益严重,人们愈加重视低碳能源的使用和碳排放量的减少^[1⇓-3].使用电动汽车(electric vehicle,EV)出行是缓解资源短缺、减小环境污染问题的有效方式.然而,大规模电动汽车并入电网会给电网的安全稳定运行带来不可忽视的影响^[4].因此,设计有效的电动汽车充放电调度策略,对于平抑配电网负荷波动、降低用户充电成本、减小电动汽车负荷对电网的冲击都有很大意义^[5-6].

现阶段国内外对于电动汽车充放电策略一般以负荷波动情况和用户利益为目标进行研究.田文奇等^[7]提出优化策略,解决了单目标优化中调度策略填充“最低谷”效果差的问题,有效降低电网峰谷差.李海斌等^[8]根据居民小区电动私家车的特点,基于配电网负荷波动最小和用户充电费用最低建立多目标优化模型,完成对各辆车的优化调度.魏大钧等^[9]基于车网互动模式和分时电价制度,求解考虑用户侧和电网侧利益多目标模型,证明分时电价制度相较于固定电价具有更大优势.

此外,部分研究着眼于车辆自身或外界相关性因素对电动汽车调度策略的影响.雷敏等^[10]设计考虑电池寿命的电价奖惩机制,既保障了车主利益,又减小了负荷波动.檀勤良等^[11]探究碳配额和需求响应的协同作用对电动汽车调度策略的影响,证实赋予电动汽车碳配额有利于加强充电响应程度和提升能源消纳水平.

目前,针对电动汽车调度的研究大多假设所设计调度计划能够完美执行,未考虑用户充放电的执行情况,部分用户会因自身原因出现提前结束充电的违约行为.因此,提出一种考虑用户信用指数的园区电动汽车充放电调度机制.首先,基于吴氏三维信用理论建立三维指标评估用户信用指数,并从“放电深度”和“充电优先级”两个维度修正用户充放电计划;其次,构建计及配电网负荷波动和用户充放电成本的多目标优化模型,通过算例仿真验证了该机制平抑配电网负荷波动及提高用户收益的有效性.

1 电动汽车用户信用指数

在园区充放电场景中,电动汽车充放电服务一般由园区内负荷聚集商提供.如果电动汽车用户选择经济性的“有序充电”模式,在向聚集商提供预计离开时间、期望电量等充电信息后,聚集商会根据用户所提供的信息需求进行充放电调度^[12].但部分用户会出现提前结束充电的违约行为,该行为不仅会降低区域资源优化水平,造成区域配电网负荷波动异常,还会对用户自身造成影响,因此需要计算用户信用指数用以量化用户违约行为.

1.1 指标建立

将吴氏三维信用理论^[13-14]应用于电动汽车用户的信用评价体系中,为电动汽车用户的信用评价指标建立提供理论支撑,该理论将用户信用分为诚信度、合规度和践约度3个维度,是目前较为成熟的信用理论体系.基于3个维度分别建立指标用于评估用户信用指数,各指标定义如下.

(1) 用户违约时长占比.违约时长是直接影响用户信用的主要因素,利用用户违约时长占比可以较为直观地从诚信维度定量评估用户信用,指标计算如下:

(1)$P_{i, \mathrm{~d}}=t_{i, \mathrm{~d}} / t_{i, \mathrm{p}}$

(2)$t_{i, \mathrm{~d}}=T_{i, \mathrm{p}}-T_{i, \mathrm{e}}$

式中:P_i_,d为电动汽车用户i违约时长占比;t_i_,d为EV_i的违约时长;t_i_,p为EV_i的预计充电时长;T_i_,p为用户的预计充电结束时刻;T_i_,e为用户发生违约行为后EV_i实际结束充电的时刻.

(2) 荷电状态比.用户充电电量未达到期望值不仅会使聚集商营业收入受损,甚至会影响其品牌承诺.因此,建立荷电状态比指标从合规维度进行评估:

(3)E_i_,d=

\frac{S_{o c, i}^{p} - S_{o c, i}^{l}}{S_{o c, i}^{p} - S_{o c, i}^{o}}

式中:E_i_,d为电动汽车用户i发生违约行为的荷电状态比; $S_{o c, i}^{p}$ 为调度计划中EV_i结束充电时的预计荷电状态; $S_{o c, i}^{l}$ 为EV_i实际离开时的荷电状态; $S_{o c, i}^{o}$ 为EV_i接入充电桩时的荷电状态.

(3) 历史违约水平.从履约能力角度建立用户历史违约水平指标,从践约维度评估用户信用,指标计算式如下:

(4)$H_{i, \mathrm{~d}}=n_{i, \mathrm{~d}} / n_{i}$

式中:H_i_,d为用户历史违约水平;n_i_,d为用户历史违约次数;n_i为用户充电次数.

以上3个指标取值在0%~100%之间,值越大,用户违约情况越严重.

1.2 用户信用指数计算

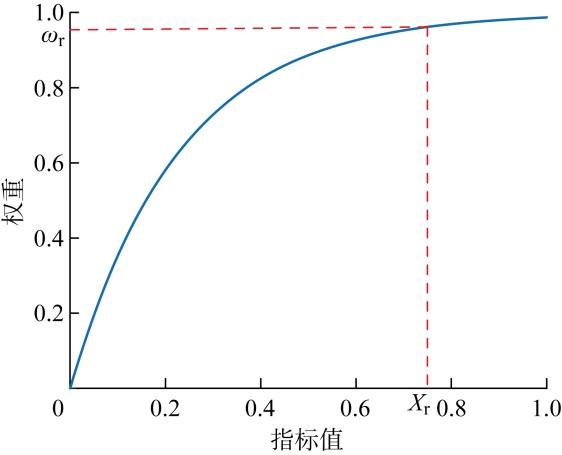
考虑到单一维度指标中违约情况较严重的用户所造成的影响会远超轻度违约用户,为避免加权平均而忽略某个指标中较高指标值用户的影响,采用动态加权法加大每项指标中较高值的权重.图1为动态加权法权重示意图,高于X_r的指标值,权重都会被放大到ω_r以上.基于动态加权法,用户信用指数计算公式如下:

(5)$I_{i, \mathrm{c}}=\omega_{1} P_{i, \mathrm{~d}}+\omega_{2} E_{i, \mathrm{~d}}+\omega_{3} H_{i, \mathrm{~d}}$

(6)ω_i=1-exp

[- {(\frac{X_{i}}{σ_{i}})}^{2}]

,1≤i≤3

式中:I_i_,c为用户信用指数;ω_i为P_i_,d、E_i_,d、H_i_,d指标值的权重;X_i为指标i预先设置的指标值,由调度人员根据实际情况确定;σ_i为计算系数.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 动态加权法权重示意图

Fig.1 Weight of dynamic weighting method

2 充放电调度机制

电动汽车用户信用指数不仅反映了用户的违约严重性,同时也表征着其发生违约行为的可能性.为最大化降低用户的违约损失,提出基于用户信用指数的充放电调度机制,从“放电深度”和“充电优先级”两个维度修正电动汽车用户的充放电调度计划.

2.1 放电深度修正

基于电动汽车用户信用指数设置不同的允许放电临界值,通过适当降低用户放电所获收益,提高用户在突发违约情况下的汽车剩余电量,规定低于该值无法进行放电行为,即

(7)

S_{o c, i}^{m i n}

S_{o c, i, c}^{m i n}

+ϕ_d(

S_{o c, i}^{e}

S_{o c, i, c}^{m i n}

)

(8)

S_{o c, i, c}^{m i n}

\frac{1}{B_{i}} (\frac{L_{i} W_{i}}{100} - t_{i, p} P_{i, c})

式中: $S_{o c, i}^{m i n}$ 为考虑用户信用修正后的允许放电临界值; $S_{o c, i, c}^{m i n}$ 为未考虑信用下该值的计算方法^[15]; $S_{o c, i}^{e}$ 为EV_i期望离开时的荷电状态;ϕ_d为放电修正系数;L_i为EV_i的预计日行驶里程;W_i为EV_i百公里所消耗电量;P_i_,c为EV_i的充电功率;B_i为EV_i的电池总电量; t_i_,p为EV_i的预计充电时长.

其中放电修正系数ϕ_d是影响允许放电临界值的关键参数,计算公式如下:

(9)$\phi_{\mathrm{d}, i}=\phi_{\mathrm{d}, \min }+I_{i, \mathrm{c}}\left(1-\phi_{\mathrm{d}, \min }\right)$

式中:ϕ_d,_i为EV_i的放电修正系数;ϕ_d,min为放电修正系数的最小值.

2.2 充电优先级修正

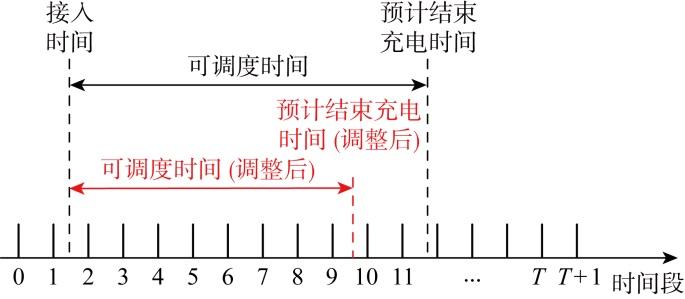
为保证用户充电体验,避免部分违约用户离开时充电量过低,对后续出行造成影响,基于信用指数对其充电优先级进行调整.充电优先级的修正有多种方式,采用缩短用户可调度时间的方式达到提高其充电优先级的目的.依据用户信用指数,计算修正时长t_i,_r对可调度时间进行修正,使用户达到提前充电的目的.修正原理如图2所示.其中,修正时长受多方面因素的影响,包括用户信用情况、用户可调度时间等,结合相关因素设计计算公式如下:

(10)$t_{i, \mathrm{r}}=\phi_{\mathrm{c}}\left(T_{i, 1}-T_{i, \mathrm{a}}\right)$

式中:T_i,_l为EV_i预计离开充电桩的时刻;T_i,_a为EV_i接入充电桩的时刻;ϕ_c为充电修正系数,取值方法与ϕ_d同理.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 可调度时间修正示意图

Fig.2 Correction of schedulable time

3 电动汽车充放电优化模型

负荷聚集商为商业运营者,其运行目标之一为平抑聚集商向电网购买电能的负荷波动,另一目标为保证用户充放电收益以吸引用户参与.因此,同时考虑电网侧和用户侧利益建立双层优化模型:上层从电网层面出发,对区域配电网负荷波动率进行优化,实现配电网负荷曲线波动平稳,并向下层下发充电负荷指导曲线;下层从用户层面出发,实现用户整体充电费用最低的同时,保证实际充电负荷曲线与指导曲线的相关系数较高.

3.1 上层模型

(1) 目标函数.上层优化考虑区域配电网整体负荷波动平稳,并利用负荷均方差作为目标函数来表示配电网的负荷波动情况,具体表达式如下:

(11)F₁=

\frac{1}{N} \overset{N}{\sum_{a = 1}}

(P_b,_a+

P_{E V, a}^{1}

-P_av)²

(12)P_av=

\frac{1}{N} \overset{N}{\sum_{a = 1}}

(P_b,_a+

P_{E V, a}^{1}

)

式中:P_b,_a为一天中第a时间段园区的基本负荷; $P_{E V, a}^{1}$ 为充电负荷指导曲线中的对应第a时间段的充电指导负荷;P_av为平均负荷;N为将一天划分的时间段数.

(2) 约束条件.园区变压器负载约束,园区的整体负荷不能超过变压器负载的最大允许值,即

(13)$P_{\mathrm{b}, a}+P_{\mathrm{EV}, a} \leqslant P_{\max }, \quad a \in 1,2, \cdots, N$

式中:P_max为变压器负载的最大允许值.

3.2 下层模型

(1) 目标函数.下层以最小化用户充电成本为优化目标的同时跟踪上层优化所下发的充电负荷指导曲线,用相关系数表示两曲线的相似程度,具体表达式如下:

(14)F₂=α₁

\overset{m}{\sum_{i = 1}} \overset{24}{\sum_{j = 1}}

|D_ij|S_j+α₂ρ(

P_{E V, a}^{1}

P_{E V, a}^{2}

)

式中:m为参与充电的电动汽车数量;S_j为电动汽车在j时间段与电网的交互电价,充电为正,放电为负;D_ij为电动汽车i在j时段与电网的交互电量; $P_{E V, a}^{2}$ 为实际充电负荷曲线中的对应第a时间段的充电负荷;ρ为两变量间的相关系数;α₁、α₂为权重系数.

(2) 约束条件.以园区为研究场景,假设电动汽车采用恒功率充放电.故只考虑充放电时间和电池容量对电动汽车充放电的影响.

可调度时间约束:

(15)$T_{i, \mathrm{a}} \leqslant T_{i} \leqslant T_{i, 1}$

式中:T_i为用户i的充放电时间.

电池放电荷电状态约束^[9]:为保证电动汽车放电安全,电池放电荷电状态必须有上下限限制,即

(16)$S_{\mathrm{oc}, \min } \leqslant S_{\mathrm{oc}, \mathrm{ij}^{2}} \leqslant S_{\mathrm{oc}, \max }$

式中:S_oc,_ij为EV_i在j时刻的荷电状态;S_oc,max和S_oc,min分别为电池放电时荷电状态的上下限.

用户期望荷电状态约束:电动汽车结束充电时,其荷电状态不应低于用户期望荷电状态,且不高于1,其中用户期望荷电状态取0.9.公式如下:

(17)0.9≤

S_{o c, i}^{p}

≤1

式中: $S_{o c, i}^{p}$ 为调度计划中EV_i结束充电时的预计荷电状态.

4 算例分析

4.1 仿真参数设置

选取某园区典型日负荷曲线^[16]为基础负荷曲线,负荷峰值为877 kW,峰谷差为355 kW.其中配电变压器最大可用有功功率为900 kW,充电桩最大充放电功率为7.2 kW,效率为0.9^[8];电动汽车采用锂电池,额定能量为32 kW·h,每百km耗电量15 kW·h;电动汽车用户的期望充电量假设都为90%;园区汽车总量为300辆.研究样本采用美国交通部对全美私家车出行情况的调查结果^[17],并利用蒙特卡罗法模拟电动汽车用户的接入充电桩时间、离开时间以及基本违约信息^[18].采用峰谷电价^[19],峰时段为6:00—20:00,电价为1.23元/(kW·h),其余时段为谷时段,电价为0.37元/(kW·h),且放电电价为0.6元/(kW·h);ϕ_{d, min}和ϕ_{c, min}取值均为0;时间段数N取24;S_oc,max为1,S_oc,min取0.5^[20]和计算所得允许放电临界值中的较大值;采用仿真平台MATLAB求解.

为说明所提充放电机制的有效性,设置3种场景进行对比分析.场景1为无序充电,电动汽车用户接入充电桩立即充电,无放电过程;场景2为未考虑用户执行情况有序充放电,可进行放电操作,但不基于用户的信用情况对其充放电计划做出调整;场景3为基于用户信用指数的充放电调度机制,基于用户信用指数从两个维度修正充放电计划后,再按照充放电模型进行优化.

4.2 仿真结果分析

(1) 三场景下负荷曲线及机制有效性分析.经调研园区内电动汽车的渗透率大约在50%,一次充电周期大约20%的用户会出现违约情况,即用户违约率为20%.因此,设置50%电动汽车渗透率、20%用户违约率为标准情况,在标准情况下对3种场景进行仿真分析.

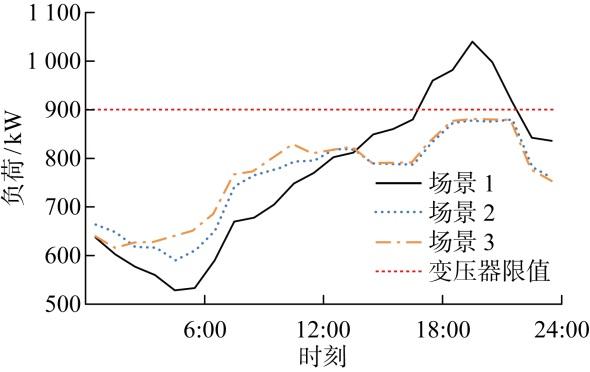
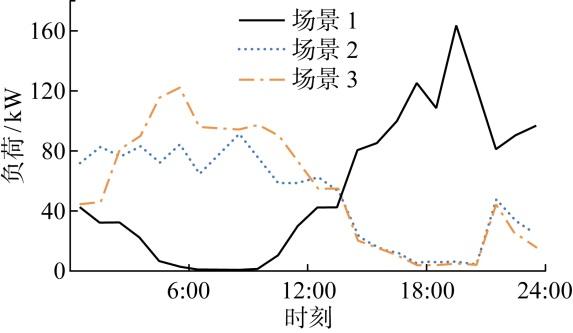
图3为标准情况下园区总负荷曲线三场景对比图.图4为标准情况下园区电动汽车充电负荷曲线三场景对比图.无序充电下的电动汽车充电负荷曲线在晚上19:00—21:00达到充电峰阶段,在早上6:00—9:00为充电谷阶段,这与园区用户的生活习惯有关.同时,在峰时段若采用无序充电模式,则会出现“峰上加峰”的情况.由图3可见,无序充电模式下,园区总负荷出现越限情况,影响变压器的安全运行;若采用未考虑用户执行情况的有序充放电或者是基于用户信用指数的充放电调度机制时,则会将负荷高峰期的充电负荷转移至负荷低谷期,从而避免变压器过限的问题出现.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 标准情况下园区总负荷

Fig.3 Total residential load under standard conditions

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 标准情况下电动汽车充电负荷

Fig.4 EV charging load under standard conditions

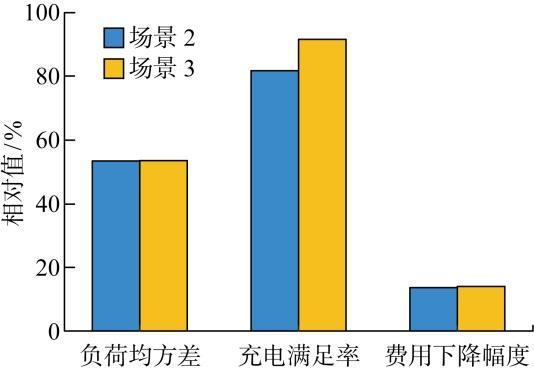
表1为3种场景下仿真结果对比,图5为场景2、3相对场景1的数据相对值对比.从负荷波动和用户收益角度进行分析:与无序充电场景相比,两者的负荷均方差相对值几乎相同,这是由于未考虑用户执行情况的有序充放电和基于用户信用指数的充放电调度机制都将部分充电负荷由峰时段转移至谷时段,从而降低了充电费用.同时,在不考虑违约行为对充电费用的影响下,有序充放电场景的充电费用略低于基于用户信用指数的充放电调度机制,这是由于“充电优先级”调整的影响,电动汽车用户因为缩短了充电时间,所以无法更好地将充电负荷转移至电价低谷时间段;而有序充放电场景的放电收益略高于后者,这是由于“放电深度”调整的影响,电动汽车用户的放电深度受到限制,并不能够进行更深度的放电行为;但图5中显示,两者总费用相差不大,说明基于用户信用指数的充放电调度机制可以较好地保障用户的充放电利益.

表1 标准情况下三场景仿真结果

Tab.1 Simulation results in three scenarios under standard conditions

参数	场景1	场景2	场景3
负荷均方差/kW	155.78	83.22	83.41
充电费用/元	1170.20	1047.79	1064.91
放电收入/元	0	37.25	35.15
总费用/元	1170.20	1010.54	1029.76
应充电量/(kW·h)	1332.20	1332.20	1332.20
未充电量/(kW·h)	0	243.04	111.53

新窗口打开| 下载CSV

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 场景2、3相对场景1的数据相对值

Fig.5 Data values of Scenarios 2 and 3 relative to Scenario 1

从用户充电满足率角度进行分析,充电满足率定义为所有电动汽车实际充电量与计划充电量的比值.图5中场景2和场景3关于充电满足率的差别相对于其他两方面较为明显,在应充电量相同的情况下,场景3的充电满足率比场景2高出9.87百分点,未充电量只有场景2的45.9%,说明基于用户信用指数的充放电调度机制能够在平抑区域配电网负荷波动和降低充电费用的同时,大幅度地减小用户因违约行为造成的损失.

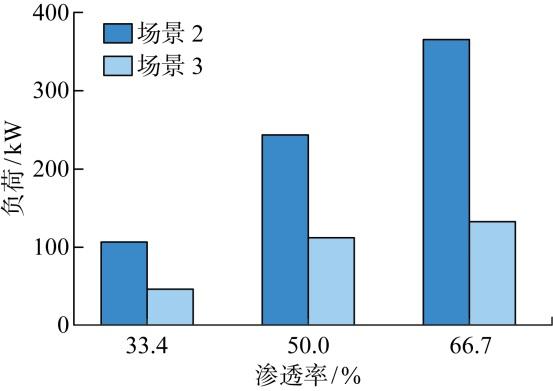
(2) 双场景下电动汽车渗透率及违约规模分析.本节着重分析后两种场景下不同汽车渗透率及违约规模对充电满足率的影响.图6为20%违约率时场景2和场景3不同电动汽车渗透率未充电量的对比.随着电动汽车渗透率的增加,场景2中未充电量的上升幅度远高于场景3,这是由于电动汽车数量较少时,违约行为对未充电量的影响不明显.随着电动汽车数量的进一步上升,影响会逐渐增大.上述结果能够充分说明基于用户信用指数的充放电调度机制在高渗透率场景中更能有效保障用户利益.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 20%违约率下不同渗透率电动汽车未充电量双场景对比

Fig.6 Double scenario comparison of uncharged amount of electric vehicles with different penetration rates at a default rate of 20%

表2为50%渗透率下不同违约率电动汽车充电满足率双场景对比.随着用户违约率升高,未考虑用户执行情况的有序充放电场景的用户满足率下降幅度较快,由违约率5%时的96.33%突降至违约率30%时的75.11%.相比之下,基于用户信用指数的充放电调度机制下降幅度较为缓慢,违约率由20%上升至30%时,用户满足率仅仅下降1.95百分点.说明随着违约规模扩大,该机制也能够保障用户的充放电体验.

表2 50%渗透率下不同违约率电动汽车充电满足率双场景对比

Tab.2 Double scenario comparison of charging satisfaction rate of electric vehicles with different default rates at a penetration rate of 50%

违约率/%	充电满足率/%
违约率/%	场景2	场景3
5	96.33	97.41
20	81.76	91.63
30	75.11	89.68

新窗口打开| 下载CSV

(3) 场景3设计原理及机制优越性分析.表3为标准情况下场景3中违约用户与未违约用户的计算结果分析.其中,相比未违约用户的零损失,违约用户的充电满足率和放电收入都受到违约行为的影响,基于用户信用指数的充放电调度机制能够减小但并不能完全消除该影响,违约用户仍会受到损失.因此,只有用户自身提高信用水平,才能进一步减小违约损失.

表3 标准情况下不同用户类型结果对比

Tab.3 Comparison of results of different user types under standard conditions

用户	充电满足率/%	预计放电收入/元	实际放电收入/元
违约	40.84	11.18	4.37
未违约	100	30.78	30.78

新窗口打开| 下载CSV

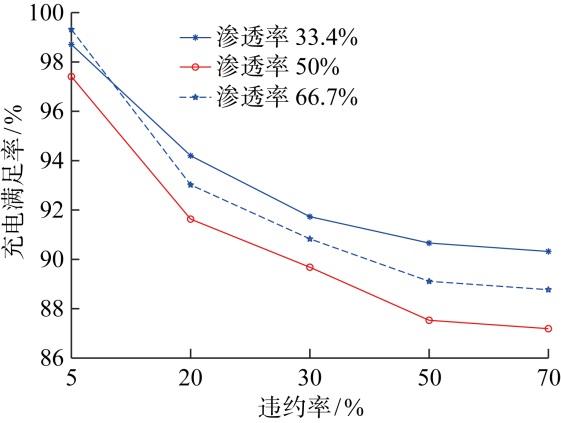
设置场景3下电动汽车渗透率为33.4%、50%、66.7%时5种用户违约率情况进行分析,如图7所示.无论电动汽车渗透率如何,随着用户违约率升高,充电满足率都呈下降趋势;但是在用户违约率高于50%之后,下降幅度逐渐减小,趋于水平.说明基于用户信用指数的充放电调度机制不仅在低违约率时能够起到作用,同样也能够较好地应对高违约率的场景.造成此种现象的原因是:在渗透率不变的情况下,违约率升高,违约用户的未充电量也会随之增加,但总充电量不变,导致充电满足率呈下降趋势.然而,随着违约率升高,用户整体信用情况下降,基于用户信用指数的充放电调度机制对用户充放电计划的修正也会更加严格,从而造成充电满足率下降幅度逐渐变缓.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 场景3违约率灵敏度分析

Fig.7 Sensitivity analysis of default rate in Scenario 3

算例结果表明:当固定园区电动汽车渗透率和用户违约规模时,该调度机制相比无序充电,能够满足负荷集成商平抑负荷波动、提高用户收益的目标;相比未考虑用户执行情况的有序充放电,则能在保证充放电利益的同时,提高用户充电满足率,也能够适应电动汽车渗透率升高和违约规模扩大的情况,整体上优于其他两种充放电场景.

5 结论

提出一种考虑用户违约行为的电动汽车充放电调度机制,将用户信用与电动汽车充放电计划相结合,基于用户信用指数修正充放电计划,并观察园区汽车充放电结果受该调度机制的影响,主要结论如下:

(1) 基于用户信用指数的充放电调度机制能够提高双方利益.从提供充放电服务的负荷聚集商的角度分析,该机制能够平抑配电网负荷波动,提高区域资源优化水平,为用户提供良好的充放电体验以吸引用户;从用户角度分析,该机制能够减小用户违约行为对自身后续出行里程的影响.

(2) 电动汽车的高速发展会使市场上电动汽车的占比逐年升高,而基于用户信用指数的充放电调度机制在高电动汽车渗透率的场景中能够呈现出更好的优化效果,具有良好的应用前景.

(3) 目前所提机制适用于园区场景,后续研究需进一步考虑市场机制间的相互配合,设计多元化的用户信用指标,以适用于电动汽车充电站等其他场景.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

JOO

J Y

, RAGHAVAN

, SUN

Z Y

Integration of sustainable manufacturing systems into smart grids with high penetration of renewable energy resources

[C]// 2016 IEEE Green Technologies Conference. Kansas City, USA: IEEE, 2016: 12-17.