含高比例风电低碳园区灵活性资源鲁棒协调运行

doi:10.16183/j.cnki.jsjtu.2023.262

含高比例风电低碳园区灵活性资源鲁棒协调运行

孟毓¹, 郭瑞¹, 石子川^,², 薛俊逸¹, 吕嘉文¹, 樊飞龙²

1.上海电力设计院有限公司科技信息部;数字化创新研究院,上海 200025

2.上海交通大学电子信息与电气工程学院;国家电投智慧能源创新学院,上海 200240

Robustly Coordinated Operation for Flexible Resources in Low-Carbon Park with High Penetration of Wind Power

MENG Yu¹, GUO Rui¹, SHI Zichuan^,², XUE Junyi¹, LÜ Jiawen¹, FAN Feilong²

1. Department of Science and Technology Information; Digital Innovation Research Institute, Shanghai Electric Power Design Institute Co., Ltd., Shanghai 200025, China

2. School of Electronic Information and Electrical Engineering; College of Smart Energy, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 石子川,博士生;E-mail:shizichuan@sjtu.edu.cn.

收稿日期: 2023-06-25 修回日期: 2023-08-6 接受日期: 2023-09-18

基金资助:

风光数字孪生一体化关键技术研究(KJ-2021-106)

Received: 2023-06-25 Revised: 2023-08-6 Accepted: 2023-09-18

作者简介 About authors

孟毓(1974—),高级工程师,研究方向为新能源发电系统设计与运行.

摘要

为应对风电出力不确定性给低碳园区运行可靠性与经济性带来的挑战,提出一种以最小化低碳园区电-碳综合运行成本为目标的多时间尺度鲁棒协调运行方案,充分发挥低碳园区中氢储能、天然气储能与电化学储能等灵活性资源的多样化调节能力.运行方案包含两个阶段:第1阶段为日前决策阶段,通过考虑风电出力与负荷需求的多时间尺度波动特点,制定氢储能、天然气储能与电化学储能的鲁棒调度指令;第2阶段为日内决策阶段,通过结合风电出力和负荷需求的短期预测结果,动态调整风力发电机组功率调度指令.日前决策为自适应鲁棒优化问题,通过列约束生成算法进行求解;日内决策为确定性优化问题,通过线性规划算法求解.最后,结合某实际低碳园区风电出力和负荷需求的小时级功率数据与运行天级电量数据,构建仿真模型,验证运行方案的有效性.仿真结果表明,本方法能够有效提升含高比例风电低碳园区运行经济性与可靠性.

关键词： 高比例风电; 低碳园区; 灵活性资源; 电-碳综合成本; 协调运行

Abstract

In order to meet the challenges of operational reliability and economy in the low-carbon park caused by the uncertainty of wind power output, a multi-timescale robustly coordinated operation scheme is proposed to minimize the integrated electricity-carbon operation cost in the low-carbon park, where the diverse regulation capabilities of the flexible resources, such as hydrogen, natural gas, and electrochemical energy storages are fully utilized. The first stage of the proposed operation scheme is the day-ahead decision stage, which considers the multi-timescale fluctuation of wind power output and load demand, and formulates the robust scheduling commands for hydrogen, natural gas, and electrochemical energy storage. The second stage is the intra-day decision stage, which combines the short-term forecast results of wind power output and load demand to dynamically adjust the wind turbine power scheduling commands. The day-ahead decision is an adaptive robust optimization problem, which is solved by the column-and-constraint generation (C&CG) algorithm, while the intra-day decision is a deterministic optimization problem, which is solved by the linear programming algorithm. Finally, this paper proposes an operation simulation model to validate the effectiveness of the operation scheme by combining the hourly and daily operation data of wind power and the load demand in a practical low-carbon park. The simulation results show that the proposed method can effectively improve the operational economy and reliability of the low carbon park with a high penetration of wind power.

Keywords： high penetration of wind power; low-carbon park; flexible resources; integrated electricity-carbon operation cost; coordinated operation

PDF (2164KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孟毓, 郭瑞, 石子川, 薛俊逸, 吕嘉文, 樊飞龙. 含高比例风电低碳园区灵活性资源鲁棒协调运行[J]. 上海交通大学学报, 2025, 59(2): 165-174 doi:10.16183/j.cnki.jsjtu.2023.262

MENG Yu, GUO Rui, SHI Zichuan, XUE Junyi, LÜ Jiawen, FAN Feilong. Robustly Coordinated Operation for Flexible Resources in Low-Carbon Park with High Penetration of Wind Power[J]. Journal of Shanghai Jiaotong University, 2025, 59(2): 165-174 doi:10.16183/j.cnki.jsjtu.2023.262

随着“碳达峰”与“碳中和”目标的提出,以风力发电(简称风电)为代表的清洁能源发电技术快速发展,成为降低园区能源系统碳排放^[1-2]的重要手段.风电的间歇性与波动性严重影响了低碳园区风力资源的高效利用^[3],弃风率高、经济效益低等问题逐步凸显^[4-5],低碳园区对灵活性资源的需求进一步增大.储能系统作为重要的灵活性资源,可以有效平抑风电出力波动,降低低碳园区的整体运行成本^[6].现有储能系统主要包含氢储能^[7]、天然气储能^[8]与电化学储能^[9]等多种类型,其中,氢储能存储容量大,爬坡能力弱;电化学储能响应迅速,但存储容量有限;天然气储能的存储容量与响应能力处于两者之间.通过氢储能、天然气储能与电化学储能的相互配合,充分利用不同类型储能之间的互补特性,可有效提升低碳园区灵活性资源的调节能力.

提升氢储能、天然气储能和电化学储能应用效果的关键是制定合理的调度方案.在氢储能方面,徐桂芝等^[10]考虑峰谷电价规则与氢储能响应特性,以经济性最优为目标建立了综合能源系统日前调度模型;Ma等^[11]建立了基于氢储能的含高比例风电电力系统经济调度模型,以应对高渗透率风电的消纳难题;郭成威等^[12]利用氢储能系统和火电机组配合来平滑可再生能源出力,以系统最小运行成本为目标,建立了发电系统日前调度模型,从而提升可再生能源的利用率;顾慧杰等^[13]构建一种基于新能源与电制氢技术为主体的电力系统短期生产模型,增加系统综合效益.在天然气储能方面,主要依托电转气(power to gas, P2G)技术^[14].樊国旗等^[15]提出一种以燃气轮机和P2G设备为基础的能源系统日前优化调度方法,以解决供电缺口和弃风问题;孟冰冰等^[16]建立了一种考虑电力与天然气耦合的多能源系统架构,研究了P2G设备消纳风电的原理与启停策略,分析了P2G配置容量与天然气管网储气能力的关系;朱海南等^[17]构建了以最低经济成本和碳排放量的电-气优化模型,分析了在不同目标函数的情况下各设备间的耦合关系.在电化学储能方面,时瑞廷等^[18]分析了影响电化学储能运行特性的关键因素,提出了综合考虑需求响应与削峰填谷的联合优化策略;梁剑等^[19]提出一种基于电化学储能的风储联合系统调峰优化调度模型,利用电化学储能系统参与风电机组调峰,提升系统的经济性和稳定性;易林等^[20]从低碳经济角度建立了含大规模风电系统的风储联合电力系统优化调度模型.以上研究主要以有效利用单一类型或者多类型储能调节能力为目标,对不同类型储能之间的能量转换过程及其碳减排效应缺乏细致研究.

上述灵活性资源调节效果也受所在系统源荷随机特性的影响,现有研究结合源荷随机性,重点对高比例风电接入系统的协调调度方案展开研究.韩子娇等^[21]基于高比例新能源渗透综合能源系统,提出一种含电转氢的鲁棒优化调度方法.顾雪平等^[22]针对风电接入电力系统比例不断提高的情况建立了考虑风电不确定性的两阶段鲁棒模型.岑有奎等^[23]以降低弃风和提高系统经济性为目标,考虑风电不确定性,提出了含大规模风电的电力系统鲁棒调度模型.陆秋瑜等^[24]提出考虑源荷不确定性的海上风电调度方法,以最大化其日运行收益.上述研究主要考虑每一调度时段的源荷随机性,缺乏对完整调度周期所有调度时段源荷整体波动特征的分析,以此构建的鲁棒运行方案较为保守,为保障运行可靠性所需付出的经济代价较高.

基于上述研究现状,本文考虑风电出力与负荷需求的多时间尺度组合不确定性,提出含高比例风电低碳园区灵活性资源鲁棒协调运行方法.在多时间尺度组合不确定性建模方面,构建风电出力与负荷需求的单一调度时段(30 min)功率不确定集与完整日运行周期(24 h)电量不确定集.在灵活性资源建模方面,综合考虑电解制氢、氢甲烷化制备天然气、氢燃料电池发电与燃气轮机发电等多个过程的耦合关系、动态响应能力与成本以及对应的碳减排效应,构建了包含氢储能、天然气储能和电化学储能的多类型灵活性资源一体化模型.在运行方案制定方面,在日前阶段,通过自适应鲁棒优化调度与列约束生成(column-and-constraint generation, C&CG)算法,制定氢储能、天然气储能与电化学储能的功率调度指令;在日内阶段,根据风电出力与负荷需求的短期预测结果,通过求解确定性凸优化问题,制定风电机组的功率调度指令,以此降低含高比例风电低碳园区电-碳综合运行成本.创新点包括:考虑风电出力与负荷需求的多时间尺度组合不确定性,建立了两阶段鲁棒优化模型,在保证协调运行可行性的基础上降低了总体运行成本;构建了包含氢气、天然气、电化学储能的多类型灵活性资源一体化模型,充分利用转化可再生能源,进一步降低含高比例风电低碳园区电-碳综合运行成本.

1 含高比例风电低碳园区协调运行架构

1.1 能源系统基本结构

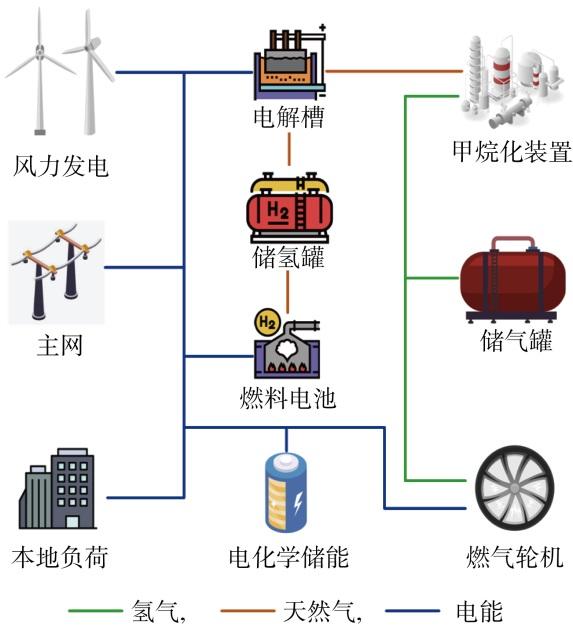
含高比例风电低碳园区能源系统基本结构如图1所示.含高比例风电低碳园区能源系统主要包含风电机组、氢储能、天然气储能与电化学储能等多种能源设备.在现有的以风电与电化学储能配合运行的基础上,进一步考虑氢储能、天然气储能设备的协调运行,以提升其灵活性,降低运行成本.电能通过电解制氢装置转换成氢气;氢气存储在储氢罐中,或通过甲烷化装置转换成天然气存储在储气罐中;氢气通过燃料电池转换成电能,天然气通过燃气轮机转换成电能,多余的电能则可存储在电化学储能中.氢储能(储氢罐、电解槽、燃料电池)、天然气储能(甲烷化装置、储气罐、燃气轮机)与电化学储能是上述能源系统的主要灵活性资源.氢储能主要承担大容量小波动的功率调节需求;电化学储能主要承担小容量大波动的功率调节需求;天然气储能与氢储、电储过程相互耦合,用于提升混合储能系统的短期快速响应能力,平抑不确定性风电出力和本地负荷的功率波动,在保证源荷供需平衡的情况下增加风能的利用率,降低含高比例风电低碳园区电-碳综合运行成本.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 含高比例风电低碳园区能源系统基本结构

Fig.1 Structure of low-carbon park energy system with high penetration of wind power

1.2 灵活性资源多时间尺度协调运行方案

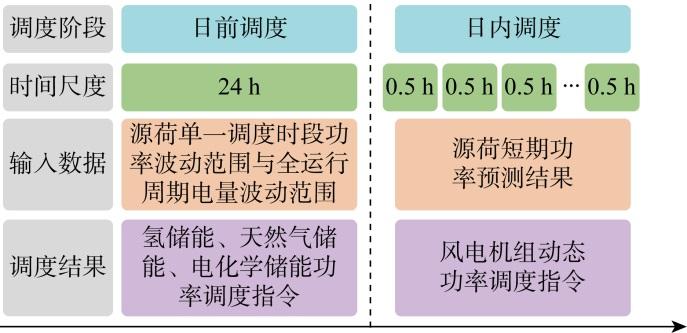
考虑风电机组出力与本地负荷需求的多时间尺度不确定性,提出一种面向氢储能、天然气储能、电化学储能等多种灵活性资源的低碳协调运行方法,充分发掘不同灵活性资源的调节能力,最小化含高比例风电低碳园区电-碳综合运行成本.具体运行方案如图2所示,包含日前与日内调度两个阶段.在日前调度阶段,考虑多时间尺度不确定性作用下所有潜在运行场景,制定氢储能、天然气储能与电化学储能的鲁棒调度指令;在日内调度阶段,基于风电机组最大出力与本地负荷需求的短期预测结果,制定风电机组的动态功率指令.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 多时间尺度决策流程

Fig.2 Multi-timescale coordinated decision

2 含高比例风电低碳园区灵活性资源建模

2.1 氢储能模型构建

氢储能由储氢罐、电解制氢装置和氢气燃料电池等组成.储氢罐储存氢气,电解制氢装置消耗电能制取氢气,燃料电池通过燃烧氢气提供电能.储氢罐中所存储氢能的计算过程如下:

(1)$E_{\mathrm{HT}_{-} t+1}=E_{\mathrm{HT}_{-} t}+\eta_{\mathrm{ED}} P_{\mathrm{HT}_{-} t} \Delta t-\frac{P_{\mathrm{FC}_{-} t}}{\eta_{\mathrm{FC}}} \Delta t$

(2)$P_{\mathrm{ED}_{-} t}=P_{\mathrm{HT}_{-} t}+P_{\mathrm{HG}_{-} t}$

式中:E_HT_{_t}表示t调度时段的氢储能所储能量;η_ED和η_FC分别表示电解制氢装置(ED)和氢气燃料电池(FC)的能量转化效率;P_ED_{_t}和P_FC_{_t}分别表示电解制氢装置和氢气燃料电池的电功率;Δt表示调度时段的时间跨度;P_HT_{_t}表示氢储能充氢功率;P_HG_{_t}表示甲烷化装置的电功率.

氢储能功率波动对应的寿命衰减成本如下:

(3)$\begin{aligned}C_{\lambda_{-} \mathrm{FL}}= & { }_{t=2}^{\mathrm{T}} \kappa_{\lambda_{-} \mathrm{FL}}\left|P_{\lambda_{-} t}-P_{\lambda_{-} t-1}\right| r_{\lambda_{-} t} r_{\lambda_{-} t-1}, \\& \forall \lambda \in\{\mathrm{ED}, \mathrm{FC}\}\end{aligned}$

式中:κ_{λ_}_FL表示电解制氢装置和氢气燃料电池的单位功率波动对应的寿命衰减成本;P_{λ_t}表示电解制氢装置和氢气燃料电池的电功率;r_{λ_t}表示电解制氢装置和氢气燃料电池的启停状态.

电解制氢装置和氢气燃料电池的启停成本为

(4)$C_{\lambda_{-} \mathrm{SU}}={ }_{t=1}^{\mathrm{T}} \kappa_{\lambda_{-} \mathrm{SU}} r_{\lambda_{-} \mathrm{SU}-t}, \quad \forall \lambda \in\{\mathrm{ED}, \mathrm{FC}\}$

(5)$C_{\lambda_{-} \mathrm{SD}}={ }_{t=1}^{T} \kappa_{\lambda_{-} \mathrm{SD}} r_{\lambda_{-} \mathrm{SD}-t}, \quad \lambda \quad\{\mathrm{ED}, \mathrm{FC}\}$

式中:κ_{λ_}_SU和κ_{λ_}_SD分别表示电解制氢装置与氢气燃料电池的单位启停成本;r_{λ_}_SU_{_t}和r_{λ_}_SD_{_t}分别表示电解制氢装置和氢气燃料电池的启停状态.

电解制氢装置和氢气燃料电池的维护成本为

(6)C_{λ_}_OM=

\overset{T}{\sum_{t = 1}}

κ_{λ_}_OMΔt, ∀λ∈

\{E D, F C\}

式中:κ_λ_{_OM}表示电解制氢装置和氢气燃料电池的单位时间维护成本.

电解制氢装置和氢气燃料电池的历史运行时间对应的寿命衰减成本如下:

(7)C_{λ_}_AGE=

\overset{T}{\sum_{t = 1}}

κ_{λ_}_AGE

\frac{Δ t}{T_{λ_L T}}

, ∀λ∈

\{E D, F C\}

式中:κ_λ_{_AGE}表示电解制氢装置/氢气燃料电池单位运行时间对应的寿命衰减成本;T_λ_{_LT}表示电解制氢装置/氢气燃料电池的预期寿命.

氢储能的总运行成本如下:

(8)$\begin{array}{c}C_{\mathrm{HS}}=+C_{\lambda-\mathrm{FL}}+C_{\lambda_{\lambda} \mathrm{SU}}+C_{\lambda \_\mathrm{SD}}+C_{\lambda \_\mathrm{OM}}+C_{\lambda_{-\mathrm{AGE}}}, \\\forall \lambda \in\{\mathrm{ED}, \mathrm{FC}\}\end{array}$

2.2 天然气储能模型构建

天然气储能包含P2G系统、燃气轮机和储气罐等关键设备.P2G系统在风电资源过剩时,甲烷化装置将电解制氢装置产生的部分氢气转化为天然气;在风电资源不足时,燃气轮机发电,快速支撑低碳园区的用能需求,降低低碳园区的用能成本.天然气储气罐中所含能量如下:

(9)E_GT_{_t}₊₁=E_GT_{_t}+η_EDη_HGP_HG_{_t}Δt-

\frac{P_{G T G_t}}{η_{G T G}}

Δt

式中:E_{GT_}_t表示天然气储气罐中所含能量;η_HG表示甲烷化装置的能量转化效率;η_GTG表示燃气轮机的能量转化效率;P_{GTG_}_t表示燃气轮机的电功率.

2.3 电化学储能模型构建

相较于氢储能与天然气储能,电化学储能的动态响应速度更快,主要用于满足快速功率调节需求.电化学储能存储的能量与充放电功率的关系如下:

(10)E_BS_{_t}₊₁=E_BS_{_t}+η_BSCP_BSC_{_t}Δt-

\frac{P_{B S D_t}}{η_{B S D}}

Δt

式中:E_BS_{_t}表示电化学储能所存储的能量;η_BSC和η_BSD分别表示电化学储能充电和放电过程中的能量转换效率;P_BSC_{_t}和P_BSD_{_t}分别表示充电和放电过程中的电功率.

电化学储能充放电循环对应的衰减成本如下:

(11)C_{BS_CL}=

\overset{T}{\sum_{t = 1}}

μ_{BS_CL}

(η_{B S C} P_{B S C_t} Δ t + \frac{1}{η_{B S D}} P_{B S D_t} Δ t)

式中:μ_{BS_CL}表示单位循环成本.

电化学储能历史运行时间对应的寿命衰减成本如下:

(12)C_{BS_AGE}=

\overset{T}{\sum_{t = 1}}

κ_{BS_AGE}Δt

式中:κ_{BS_AGE}表示单位时间老化折旧成本.

电化学储能的维护成本如下:

(13)C_{BS_OM}=

\overset{T}{\sum_{t = 1}}

κ_{BS_OM}Δt

式中:κ_{BS_OM}表示单位时间维护成本.

电化学储能的总运行成本如下:

(14)$C_{\mathrm{BS}}=C_{\mathrm{BS} \_\mathrm{CL}}+C_{\mathrm{BS} \mathrm{~A}_{\mathrm{AGE}}}+C_{\mathrm{BS} \_\mathrm{OM}}$

3 低碳园区能源系统优化调度模型

3.1 目标函数

优化目标为最小化含高比例风电低碳园区的日运行成本,其计算过程如下所示:

(15)$\min C_{\mathrm{TO}}=C_{\mathrm{TL}}+C_{\mathrm{HS}}+C_{\mathrm{BS}}+C_{\mathrm{WT}}+C_{\mathrm{CP}}$

式中:C_TL表示园区从主网购电成本;C_WT表示风电装置的运行成本;C_CP表示碳交易成本.其中,园区从主网购电成本、碳交易成本分别为

(16)C_TL=

\overset{T}{\sum_{t = 1}}

μ_TL_{_t}P_TL_{_t}

(17)$\begin{aligned}C_{\mathrm{CP}}= & \mu_{\mathrm{CP}} \sum_{t=1}^{T}\left[\left(E_{\mathrm{TL}_{-} \mathrm{C}}-E_{\mathrm{A}^{}}\right) P_{\mathrm{TL}_{-} t}+\right. \\& \left(E_{\mathrm{WT}_{-} C}-E_{\mathrm{A}}\right) P_{\mathrm{WT}_{-} t}+ \\& \left(E_{\mathrm{HG}_{-} \mathrm{C}}-E_{\mathrm{A}}\right) P_{\mathrm{HG}_{-} t}+ \\& \left.\left(E_{\mathrm{GTG}_{-} \mathrm{C}}-E_{\mathrm{A}^{}}\right) P_{\mathrm{GTG}_{-} t}\right]\end{aligned}$

式中:μ_TL_{_t}表示主网分时电价;P_TL_{_t}表示联络线功率;μ_CP表示碳交易价格;E_A表示单位发电量的碳排放分配额;E_{TL_C}表示主电网单位发电量碳排放量;E_{WT_C}表示风电装置单位发电量碳排放量;E_{HG_C}表示甲烷化装置单位发电量碳排放量;E_{GTG_C}表示燃气轮机单位发电量碳排放量.

3.2 约束条件

3.2.1 氢储能约束条件

氢储能约束条件如下所示:

(18)$E_{\mathrm{HT}_{-} \min } \leqslant E_{\mathrm{HT}_{-} t} \leqslant E_{\mathrm{HT}_{-} \max }$

(19)$P_{\text {ED_min }} \leqslant P_{\text {ED_t }^{2} t} \leqslant r_{\text {ED_t }^{2}} P_{\mathrm{ED}_{-} \max }$

(20)$P_{\mathrm{FC}_{-} \min } \leqslant P_{\mathrm{FC}_{-} t} \leqslant r_{\mathrm{FC}_{-} t} P_{\mathrm{FC}_{-} \max }$

(21)$r_{\mathrm{ED}_{-} t}+r_{\mathrm{FC}_{-} t} \leqslant 1$

(22)$\Delta t_{\lambda_{-} \mathrm{ON}} \geqslant \Delta T_{\lambda_{-} \mathrm{ON}}, \quad \lambda \in\{\mathrm{ED}, \mathrm{FC}\}$

(23)$\Delta t_{\lambda_{-} \text {OFF }} \geqslant \Delta T_{\lambda_{-} \text {OFF }}, \quad \lambda \in\{\mathrm{ED}, \mathrm{FC}\}$

式中:E_{HT_max}和E_{HT_min}分别表示储氢罐中所含能量上限和下限;P_{ED_max}和P_{ED_min}分别表示电解装置电功率的上限和下限;P_{FC_max}和P_{FC_min}分别表示氢气燃料电池功率的上限和下限;r_ED_{_t}和r_FC_{_t}分别表示电解装置和氢气燃料电池的启停状态;Δt_λ_{_ON}和Δt_λ_{_OFF}表示电解装置和燃料电池的实际启停时间;ΔT_λ_{_ON}和ΔT_λ_{_OFF}表示电解装置和燃料电池的最小启停时间.式(18)表示储氢罐中所储能量的范围约束;式(19)表示电解装置的电功率约束;式(20)表示氢气燃料电池的电功率约束;式(21)确保电解装置和氢气燃料电池不能同时工作;式(22)和(23)分别表示电解装置和氢气燃料电池的启停时间约束.

3.2.2 天然气储能约束条件

天然气储能约束条件如下所示:

(24)$E_{\text {GT_min }} \leqslant E_{\text {GT }_{-} t} \leqslant E_{\text {GT_max }}$

(25)$P_{\mathrm{HG}_{-\min }} \leqslant P_{\text {HG_t }} \leqslant r_{\mathrm{HG}_{-} t} P_{\mathrm{HG}_{-} \max }$

(26)$P_{\text {GTG }_{-} \min } \leqslant P_{\text {GTG }_{-} t} \leqslant r_{\text {GTG }_{-} t} P_{\text {GTG_max }^{\max }}$

(27)$r_{\mathrm{HG}_{-} t}+r_{\mathrm{GTG}_{-} t} \leqslant 1$

式中:E_{GT_min}和E_{GT_max}分别表示天然气储气罐中所含能量的上限和下限;P_{HG_max}和P_{HG_min}分别表示甲烷化装置电功率的上限和下限;P_{GTG_max}和P_{GTG_min}分别表示燃气轮机的电功率上下限;r_HG_{_t}和r_GTG_{_t}分别表示甲烷化装置和燃气轮机的启停状态.式(24)表示天然气储气罐中所储能量范围的约束;式(25)表示甲烷化装置的电功率约束;式(26)表示燃气轮机的电功率约束;式(27)规定天然气储气罐不能同时充放.

3.2.3 电化学储能约束条件

电化学储能约束条件如下所示:

(28)$E_{\mathrm{BS}_{-\min }} \leqslant E_{\mathrm{BS}_{-} t} \leqslant E_{\mathrm{BS}_{-} \text {max }}$

(29)$P_{\mathrm{BSC}_{-} \min } \leqslant P_{\mathrm{BSC}_{-} t} \leqslant r_{\mathrm{BSC}_{-} t} P_{\mathrm{BSC}_{-} \max }$

(30)$P_{\text {BSD_min }^{\min }} \leqslant P_{\text {BSD_ }^{2} t} \leqslant r_{\mathrm{BSD}_{-} t} P_{\mathrm{BSD}_{\_} \max }$

(31)$r_{\mathrm{BSC}_{-} t}+r_{\mathrm{BSD}_{-} t} \leqslant 1$

式中:E_{BS_max}和E_{BS_min}分别表示电化学储能所含能量的上限和下限;P_{BSC_max}和P_{BSC_min}分别表示电化学储能充电功率的上限和下限;P_{BSD_max}和P_{BSD_min}分别表示电化学储能放电功率的上限和下限;r_BSC_{_t}和r_BSD_{_t}分别表示电化学储能的启停状态.式(28)表示电化学储能所含能量范围的约束;式(29)表示电化学储能的充电功率约束;式(30)表示电化学储能的放电功率约束;式(31)表示电化学储能充电和放电不能同时进行.

3.2.4 功率平衡约束条件

低碳园区功率平衡约束条件如下所示:

(32)$P_{\mathrm{WT}_{\mathrm{T}_{\text {min }}} t} \leqslant P_{\mathrm{WT}_{-} t} \leqslant P_{\left.\mathrm{WT}_{-} \max \right]_{-} t}$

(33)$P_{\mathrm{TL}_{-} \min } \leqslant P_{\mathrm{TL}_{-} t} \leqslant P_{\mathrm{TL}_{2} \max }$

(34)$\begin{array}{c}P_{\mathrm{TL}_{-} t}+P_{\mathrm{FC}_{-} t}+P_{\mathrm{BSD}_{-} t}+P_{\mathrm{GTG}_{-} t}+P_{\mathrm{WT}_{-} t}- \\P_{\mathrm{ED}_{-} t}-P_{\mathrm{BSC}_{-} t}-P_{\mathrm{HG}_{-} t}-P_{\mathrm{LL}_{-} t}=0\end{array}$

式中,P_{WT_max}_{_t}和P_{WT_min}_{_t}分别表示风电装置功率的上限和下限;P_{TL_max}和P_{TL_min}分别表示联络线电功率的上限和下限;P_LL_{_t}表示低碳园区的负荷需求.式(32)表示风电装置电功率约束;式(33)表示联络线电功率约束;式(34)表示低碳园区能源系统的功率平衡约束.

3.3 两阶段鲁棒优化模型

相比未考虑源荷不确定性的日前调度模型,两阶段鲁棒优化模型在日前调度阶段根据日前预测不确定数据的波动范围确定日前变量,在日内调度阶段根据短期实时预测精确数据确定日内变量;在保证优化结果全局可行的基础上取得最优解,并充分发挥不同类型灵活性资源的调节能力.考虑风电机组与本地负荷需求的不确定性,建立两阶段鲁棒优化调度模型:

(35)

\underset{x}{m i n}

[

a_{1}^{T}

a_{2}^{T}

I+a₃+

\underset{u \in W}{m a x} \underset{y \in f (x, u)}{m i n}

(

{b^{T}}_{1}

y)]

(36)$\text { s. t. } \boldsymbol{A}_{1} \boldsymbol{x}+\boldsymbol{B}_{1} \boldsymbol{I} \leqslant \boldsymbol{V}_{1}$

(37)$\boldsymbol{C}_{1} \boldsymbol{x}+\boldsymbol{D}_{1} \boldsymbol{I}=\boldsymbol{W}_{1}$

(38)$\boldsymbol{A}_{2} \boldsymbol{x}+\boldsymbol{B}_{2} \boldsymbol{y}+\boldsymbol{C}_{2} \boldsymbol{u} \leqslant \boldsymbol{V}_{2}$

(39)$\boldsymbol{D}_{2} \boldsymbol{x}+\boldsymbol{E}_{2} \boldsymbol{y}+\boldsymbol{F}_{2} \boldsymbol{u}=\boldsymbol{W}_{2}$

式中:x表示第1阶段决策变量,包括所有储能的充放功率;I表示第1阶段决定所有储能启停状态的二进制变量;y表示第2阶段决策变量,包括风电出力功率和输入主电网的功率;u表示不确定性变量,包括风力和本地负荷情况;A、B、C、D、E、F、V、W均为常数矩阵,表示两阶段鲁棒中的相关约束系数.其中,约束式(35)和(36)表示约束式(18)~(31)、约束式(37)表示约束式(1)~(14)、约束式(38)表示约束式(32)和(33)、约束式(39)表示约束式(34)的两阶段模型.

第1阶段目标函数具体表达式:

(40)

a_{1}^{T}

x=C_{λ_}_FL+C_{BS_CL}

(41)$\boldsymbol{a}_{2}^{\mathrm{T}} \boldsymbol{I}=C_{\lambda_{-} \mathrm{SU}}+C_{\lambda_{-} \mathrm{SD}}$

(42)$a_{3}=C_{\lambda_{-} \mathrm{OM}}+C_{\lambda_{-} \mathrm{AGE}}+C_{\mathrm{BS} \mathrm{~A}_{-}}+C_{\mathrm{BS} S_{-} \mathrm{OM}}$

式中: $a_{1}^{T}$ x由电解装置和氢气燃料电池的功率波动成本、电化学储能的循环充放成本组成; $a_{2}^{T}$ I表示电解装置和氢气燃料电池的启停成本;a₃表示氢储能和电化学储能的维护成本.

第2阶段目标函数具体表达式:

(43)

b_{1}^{T}

y=C_TL+C_WT+C_CP

$b_{1}^{T}$ y由园区从主网购电成本、风电成本以及碳交易成本构成.

4 优化模型求解方法

4.1 源荷多时间尺度不确定性建模

考虑风电机组最大出力与本地负荷需求等源荷变量的多时间尺度不确定性,不确定性变量的约束包括单位调度间隔的功率上下限约束和日运行周期的总体电量约束.不确定变量建模如下:

(44)Ω=

\{\begin{array}{l} {\underline{ψ}}_{t} \leq ψ_{t} \leq {\bar{ψ}}_{t}, \forall t = 1, 2, \dots, T \\ {\underline{Q}}_{ψ} \leq \overset{T}{\sum_{t = 1}} ψ_{t} Δ t \leq {\bar{Q}}_{ψ} \end{array}

式中:ψ_t表示每一调度时段的不确定性变量,可以是最大风电出力和负荷需求功率; ${\underline{ψ}}_{t}$ 和 ${\bar{ψ}}_{t}$ 分别表示每一调度时段内功率波动的下界和上界; ${\underline{Q}}_{ψ}$ 和 ${\bar{Q}}_{ψ}$ 表示日运行周期风电机组输出或者本地负荷消纳总电量的下界和上界.

4.2 列约束生成算法

本文两阶段鲁棒优化模型通过基于多时间尺度不确定性的列约束生成算法进行求解.原鲁棒模型被分解为主问题和子问题:主问题根据列约束生成算法得到的潜在场景求解最小运营成本对应的决策方案;子问题在主问题已固定的决策变量x^*下,寻找最极端的潜在运行场景.而后主问题再根据子问题返回的潜在运行场景集,调整主问题的决策变量,以此循环,直至主问题与子问题目标函数的差值满足停止条件要求,则输出鲁棒调度指令.

主问题如下所示:

(45)P_M=

\underset{x}{m i n}

(

a_{1}^{T}

a_{2}^{T}

I+a₃+η)

(46)$\text { s. t. } \boldsymbol{A}_{1} \boldsymbol{x}+\boldsymbol{B}_{1} \boldsymbol{I} \leqslant \boldsymbol{V}_{1}$

(47)$\boldsymbol{C}_{1} \boldsymbol{x}+\boldsymbol{D}_{1} \boldsymbol{I}=\boldsymbol{W}_{1}$

(48)η≥

b_{1}^{T}

y_l

(49)A₂x+B₂y_l+C₂

u_{l}^{*}

≤V₂

(50)D₂x+E₂y_l+F₂

u_{l}^{*}

=W₂

式中:y_l和 $u_{l}^{*}$ 为子问题返回的不确定变量.在主问题中,由子问题返回不确定参数 $u_{l}^{*}$ 被固定,从而将主问题转化为一个混合整数线性规划模型,确定当前最优解;当前最优参数确定后,主问题已固定的决策变量x^*将被传给子问题.

子问题如下所示:

(51)P_S=

\underset{u \in Ω}{m a x} \underset{y \in f (x, u)}{m i n}

(

a_{1}^{T}

x^*+

a_{2}^{T}

I^*+a₃+

b_{1}^{T}

(52)$\text { s. t. } \boldsymbol{A}_{2} \boldsymbol{x}^{*}+\boldsymbol{B}_{2} \boldsymbol{y}+\boldsymbol{C}_{2} \boldsymbol{u} \leqslant \boldsymbol{V}_{2}$

(53)$\boldsymbol{D}_{2} \boldsymbol{x}^{*}+\boldsymbol{E}_{2} \boldsymbol{y}+\boldsymbol{F}_{2} \boldsymbol{u}=\boldsymbol{W}_{2}$

子问题利用Karush-Kuhn-Tucker (KKT)条件将max-min优化问题转化为一个混合整数线性规划问题.

5 算例分析

5.1 仿真参数

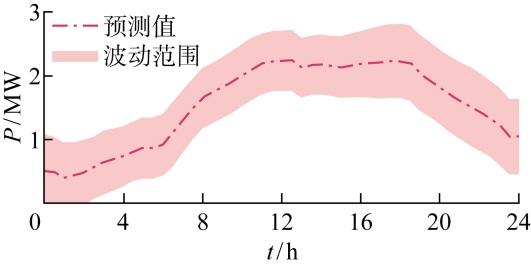
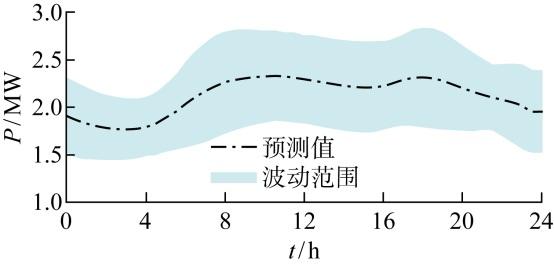
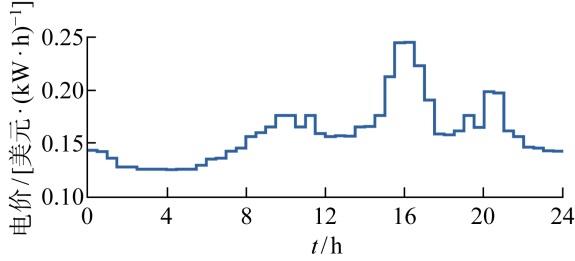
以某低碳园区的历史运行数据为基础,依托MATLAB仿真平台与Gurobi求解器,构建仿真模型对所提方法进行验证.仿真模型的调度周期为24 h,单位调度时段为30 min;风电和本地负荷波动参数参考文献[25].风电出力波动范围如图3所示,其日运行周期总输出电量波动在 32 252.025~41 981.345 kW·h之间.负荷需求波动范围如图4所示,其日运行周期总负荷需求电量波动在 44 676.34~57 114.02 kW·h之间.主电网分时电价如图5所示;算例中设备参数如表1所示.氢储能相关参数参考文献[26],电化学储能相关参数参考文献[27],天然气储能相关参数参考文献[28 ⇓-30].

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 风电设备最大出力范围

Fig.3 Range of maximum power of wind turbines

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 本地负荷需求范围

Fig.4 Range of local load demand

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 主网分时电价

Fig.5 Time-of-use electricity price of main grid

表1 储能参数

Tab.1 Key parameters of energy storages

参数	取值	参数	取值
氢储能最大容量/(MW·h)	3	电池充放最大功率	240
氢储能最小容量/(kW·h)	600	电池充放效率	0.92
电解装置最大功率/MW	1	天然气储能最小容量/(kW·h)	0
燃料电池最大功率/kW	400	天然气储能最大容量/(MW·h)	1.2
电解装置效率	0.74	甲烷化装置最大功率/kW	600
燃料电池效率	0.5	燃气轮机最大功率/kW	600
电化学储能最小容量/(kW·h)	320	甲烷化装置效率	0.75
电化学储能最大容量/(kW·h)	80	燃气轮机效率	0.34

新窗口打开| 下载CSV

5.2 仿真结果

5.2.1 日前调度结果

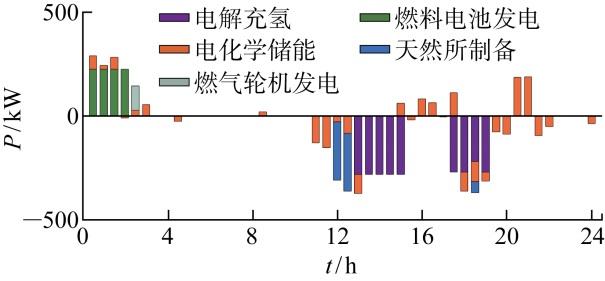
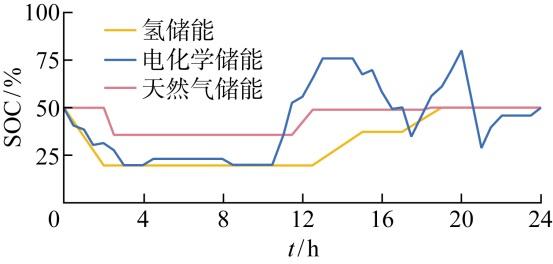
利用氢储能、电化学储能和天然气储能进行协同调度,以运营成本最小为目标进行仿真计算.日前调度结果主要包含各储能设备的功率、荷电状态(state of charge, SOC)等,如图6和7所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 储能关键装置调度功率

Fig.6 Dispatch power of key devices in energy storages

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 储能关键装置荷电状态

Fig.7 SOC of key devices in energy storages

由日前调度结果可以看出,为了避免造成功率波动导致的额外成本,电解装置和燃料电池的输出功率保持定值.由于能量转换效率相对较低,天然气储能的能量变化相对较少,主要取辅助调节、减少成本的作用.与氢储能、天然气储能相比,电化学储能相对灵活,功率变化频繁,因此被用来平抑本地负荷与风电出力波动.混合储能装置主要被用于保持低碳园区的功率平衡,并依靠其主动调节能力灵活控制与主网的能量流动,降低运营成本.当本地负荷小而风电出力大时,混合储能装置储存冗余的能量;当风能不足、本地负荷或电价过高时,混合储能装置释放能量,在满足需求的同时降低成本.

5.2.2 日内调度结果

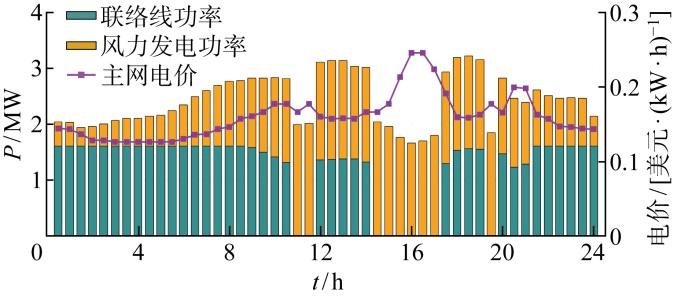
日内调度结果主要包含联络线和风电机组的短期调度功率,如图8所示.当主网电价较高或风电出力足够时,联络线功率相对较低;当电价相对较低时,联络线功率较高.低碳园区会在低电价时尽可能购电,多余的电能将会被存储在混合储能装置中,在高负荷、高电价时段释放,以降低在高电价区间的用能成本.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 联络线和风电功率

Fig.8 Power of tie line and wind turbines

5.3 储能系统在低碳园区中的应用效益

为验证储能系统在低碳园区中的应用效果,比较不同储能系统组合方式对应的运行结果,如表2所示.可知,储能设备可有效提升运行方案在不同运行场景下的可行率.其中,由于氢储能的容量最大,氢储能提升可行率的效果最明显.而与单一储能相比,混合储能可以充分发掘不同储能系统的响应能力与容量特性,可行率提升的效果最佳.

表2 不同储能系统组合方式下的运行效果

Tab.2 Operation effectiveness of different energy storage system combination modes

调度方法	日前成本/ 美元	日内平均成本/美元	总平均运行成本/美元	可行率/%
不含储能	0	1472.60	1472.60	4.8
只含氢储能	0.38	1528.74	1529.12	11.2
只含天然气储能	-47.51	1057.07	1009.56	8.4
只含电化学储能	0.43	1477.08	1477.51	6.7
氢-气-电混合储能	-11.79	1603.17	1591.38	100.0

新窗口打开| 下载CSV

5.4 不同运行方案在低碳园区中的应用效果

为了体现碳交易政策、多时间尺度协调运行方案在调度指令制定中起到的作用,将确定性运行方案(方法1)、未考虑碳交易的鲁棒运行方案(方法2)、考虑碳交易的鲁棒运行方案(方法3)与本文多时间尺度鲁棒协调运行方案(方法4)进行对比,结果如表3所示.

表3 不同运行方案对比

Tab.3 Comparison of different operation schemes

调度方法	日前成本/ 美元	日内平均成本/美元	总平均运行成本/美元	可行率/%
方法1	0.30	111.39	111.69	7.5
方法2	0.99	2614.63	2615.62	100.0
方法3	-11.42	1655.26	1666.68	100.0
方法4	-11.79	1603.17	1591.38	100.0

新窗口打开| 下载CSV

由表3可知,与确定性运行方案相比,所提运行方案将可行率从7.5%提升至100.0%;与不考虑碳交易的鲁棒运行方案相比,所提运行方案可降低总平均运行成本39.16%;与考虑碳交易的鲁棒运行方案相比,所提运行方案可降低总平均运行成本4.52%.综上所述,所提方法可以最低成本保障运行方案适用于不确定集内的所有潜在运行场景.

6 结语

提出一种面向含高比例风电低碳园区的鲁棒协调运行方法.所提运行方法包含两个部分,即考虑多时间尺度不确定性的日前自适应鲁棒调度方案与基于短期预测的日内调度方案.与现有方法相比,所提方法可充分利用氢储能、天然气储能与电化学储能的动态响应能力与能量存储水平,并充分考虑源荷单位调度时段与运行日完整周期的组合不确定性,以最小的经济成本保障运行方案的可靠性.下一步研究工作将对模型场景进行细化建模,考虑多能流耦合运行;同时在多时间尺度两阶段鲁棒优化方法的基础上,研究多阶段鲁棒优化方法,进一步完善含高比例风电低碳园区的鲁棒协调运行方法.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

QIU

H F

, GU

, XU

Y L

et al.

Tri-level mixed-integer optimization for two-stage microgrid dispatch with multi-uncertainties

[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3636-3647.