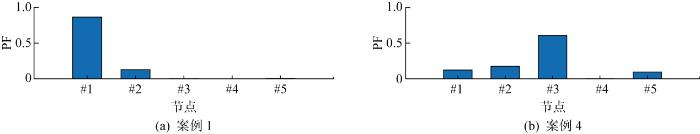i g dq dq 电流,包含d 轴电流i g d q 轴电流i g q
mdq —控制器输出的dq 调制比,包含d 轴调制比md 和q 轴调制比mq
u c dq dq 电压,包含d 轴电压u c d q 轴电压u c q
u g dq dq 电压,包含d 轴电压u g d q 轴电压u g q
U c d 0 , U c q 0 —上述变换器侧交流dq 电压的稳态值
U g d 0 , U g q 0 —上述变换器交流dq 电压的稳态值
为推进实现“双碳”目标,我国能源电力正向以新能源为主体的新型电力系统转型[1 ] ,其对新能源电源的频率、电压支撑能力提出了迫切需求[2 ] .目前用于风、光等新能源电源的并网控制方式主要包括跟网型(GFL)和构网型(GFM)控制,其中跟网型控制具有快速功率响应的能力,而构网型控制在主动频率/电压支撑和自组网运行等方面更具优势[3 ] .这使得控制优势互补的跟网型与构网型异构多变换器系统受到重视,其内部的跟网、构网同步特性和交互稳定问题是近几年国内外关注的热点.
相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论.
上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准.
由上述现状分析可知,受限于当前同步稳定分析方法在机理直观性以及判稳准确性之间难以平衡的问题,跟网型与构网型变换器的同步交互稳定机理仍需进一步探索.为此,本文开展了如下工作:采用节点导纳网络矩阵和频域模态分析法,构建计及各变换器和传输网络动态的同步视角频域模型,揭示锁相环、虚拟同步环在变换器多带宽控制耦合作用下的交互失稳机理,避免聚合反馈回路引入的开环右半平面极点问题,通过典型两机异构系统的时域仿真验证了上述所提方法和分析结论的正确性.
1 异构多变换器系统的频域网络建模
异构多变换器系统的小扰动同步稳定性受各变换器控制动态以及传输网络动态的影响,需要建立能够详细计及上述各类动态的多机小扰动模型.基于阻抗建模理论,首先建立涵盖跟网/构网同步控制、内/外环控制等多带宽控制环节的变换器三端口阻抗,进而构建含各变换器及无源元件的频域节点导纳矩阵,为后续同步稳定分析方法的提出奠定基础.
1.1 跟网型与构网型变换器的三端口阻抗建模
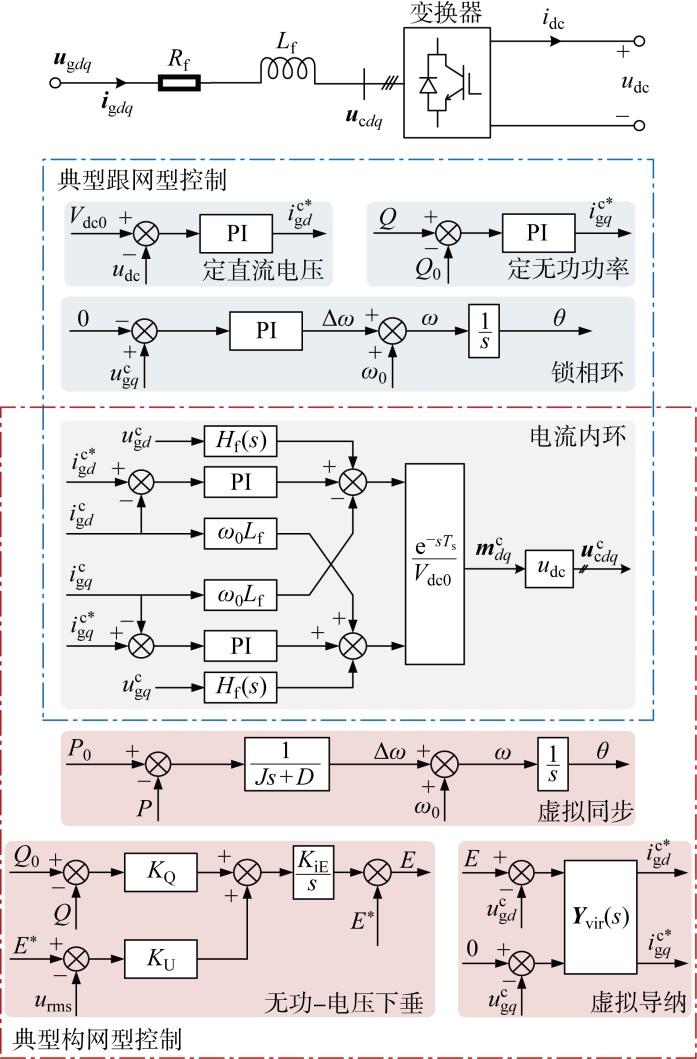
以图1 所示典型跟网型和构网型控制为例,包括锁相环/虚拟同步环、电流内环、定直流电压环、定无功功率环、无功-电压下垂环、虚拟导纳控制等,建立两类变换器的交直流三端口阻抗.该模型同时保留了交直流电气端口,便于后续系统建模将各台变换器与交/直流传输网络进行电路互联.
图1
图1
典型跟网型和构网型变换器主电路及控制结构
Fig.1
Main circuit and control scheme of typical grid-following and grid-forming converter
1.1.1 跟网型变换器三端口阻抗
(1) Δu c dq Z f d q g dq +Δug dq
式中:Z f d q ( s )代表交流滤波器dq 阻抗. 本文中的dq 变量均以向量形式表征,如Δu c dq Δ u c d Δ u c q T . 变换器交直流侧耦合动态的小扰动模型可表示为
(2) $\Delta \boldsymbol{u}_{\mathrm{c} d q}=\Delta \boldsymbol{m}_{d q} V_{\mathrm{dc} 0}+\boldsymbol{m}_{d q 0} \Delta u_{\mathrm{dc}}$
(3) Δi dc = 3 2 V d c 0 U T c d q 0 g dq + I g d q 0 T c dq )- I d c 0 V d c 0 dc
式中:mdq 0 =m d 0 m q 0 U c dq 0 =U c d 0 U c q 0 I g dq 0 =I g d 0 I g q 0 .
(4) Δθ = H P I ( s ) s + U g d 0 H P I ( s ) g q =Tpll (s)Δug q
式中:T pll (s )代表并网点处q 轴电压Δu g q θ 的传递函数.受锁相环影响,变换器小信号动态将存在控制与系统两种参考系,二者关系为
(5) Δ i g d q c = Δ i g d q + I g d q 0 Δ θ Δ u g d q c = Δ u g d q + U g d q 0 Δ θ Δ m c d q = Δ m d q + M d q 0 Δ θ
I g dq 0 =I g q 0 - I g d 0 Mdq 0 =m q 0 - m d 0 U g dq 0 =U g q 0 - U g d 0
(6) $\begin{aligned}\Delta \boldsymbol{m}_{d q}^{\mathrm{c}}= & -\frac{\mathrm{e}^{-s T_{\mathrm{s}}}}{V_{\mathrm{dc} 0}}\left[\boldsymbol{H}_{\mathrm{cc}}\left(\Delta \boldsymbol{i}_{\mathrm{g} d q}^{\mathrm{c} \stackrel{*}{c}}-\Delta \boldsymbol{i}_{\mathrm{g} d q}^{\mathrm{c}}\right)-\right. \\& \left.\boldsymbol{K}_{\mathrm{d}} \Delta \boldsymbol{i}_{\mathrm{g} d q}^{\mathrm{c}}-\boldsymbol{H}_{\mathrm{f}} \Delta \boldsymbol{u}_{\mathrm{g} d q}^{\mathrm{c}}\right]\end{aligned}$
外环由定直流电压(d 轴)和定无功功率(q 轴)控制组成,其小扰动模型为
(7) Δ i g d q c * PQ U g d q 0 p q g dq +HPQ I g d q 0 p q g dq -Hdc Δudc
U g d q 0 p q 3 2 U g d 0 U g q 0 U g q 0 - U g d 0
I g d q 0 p q 3 2 I g d 0 I g q 0 - I g q 0 I g d 0
将式(7)中的Δi g d q c * u c dq
(8) $\Delta \boldsymbol{i}_{\mathrm{g} d q}=\boldsymbol{Y}_{d q}(s) \Delta \boldsymbol{u}_{\mathrm{g} d q}+\boldsymbol{a}_{2 \times 1}(s) \Delta u_{\mathrm{dc}}$
(9) $\Delta i_{\mathrm{dc}}=\boldsymbol{b}_{1 \times 2}(s) \Delta \boldsymbol{u}_{\mathrm{g} d q}+Y_{\mathrm{dc}}(s) \Delta u_{\mathrm{dc}}$
式中:Ydq (s )代表交流端口自身导纳;Y dc (s )代表直流端口自身导纳;a 2×1 (s )代表直流侧对交流侧的耦合影响项;b 1×2 (s )代表直流侧对交流侧的耦合影响项.
将式(8)和式(9)改写为矩阵形式,即可获得跟网型变换器的三端口导纳模型:
(10) $\begin{array}{l}\begin{array}{l}d q \text { 两端口 } \\d c \text { 单端口 }\end{array} \quad\left[\begin{array}{c}\Delta \boldsymbol{i}_{\mathrm{g} d q} \\\Delta i_{\mathrm{dc}}\end{array}\right]=\\\left[\begin{array}{cc}\boldsymbol{Y}_{d q}(s) & \boldsymbol{a}_{2 \times 1}(s) \\\boldsymbol{b}_{1 \times 2}(s) & \boldsymbol{Y}_{\mathrm{dc}}(s)\end{array}\right]\left[\begin{array}{c}\Delta \boldsymbol{u}_{\mathrm{g} d q} \\\Delta u_{\mathrm{dc}}\end{array}\right]\end{array}$
1.1.2 构网型变换器交流阻抗
构网型变换器主电路及电流内环的小扰动建模与上述跟网型变换器一致,故主要给出虚拟同步环、无功-电压下垂环、虚拟导纳控制的小扰动建模过程.虚拟同步控制主要根据有功功率的变化进行频率跟踪调节,有功功率的dq 小扰动模型为
(11) Δp = 3 2 g dq 0 Δig dq + 3 2 g dq 0 Δug dq
式中:U g dq 0 =U g d 0 U g q 0 I g dq 0 =I g d 0 I g q 0 . 虚拟同步环的小扰动模型可表示为
(12) Δθ =- 1 s 1 J s + D vsg (s)Δp
式中:T vsg (s )代表有功功率Δp 与同步相角Δθ 的传递函数.受虚拟同步环影响,构网型变换器同样存在控制和系统参考系,二者关系与式(5)所示一致.根据图1 ,虚拟导纳控制的小扰动模型可表示为
(13) Δ i g d q c * vir (s) Δ E 0 T - Δ u g d q c
式中:Y vir (s )=R v i r + s L v i r - ω L v i r ω L v i r R v i r + s L v i r - 1 R vir 为虚拟电阻,L vir 为虚拟电感.
(14) ΔE = K i E s Q Δq-KU Δurms )
式中:交流电压有效值Δu rms =U g d 0 U r m s 0 U g q 0 U r m s 0 u g d q c U rms0 为电压有效值的稳态值;
Δq =3 2 U' g dq 0 Δi g dq 3 2 I' g dq 0 Δu g dq
将式(11)~ (14)代入式(5)和(6)可获得系统参考系下输出调制比Δmdq ,进而代入式(1)和(2)并消去中间变量可得交流侧导纳模型,该交流导纳模型代入式(3)可得直流侧导纳模型,从而建立式(10)所示的三端口导纳模型.
1.2 频域节点导纳网络矩阵建模
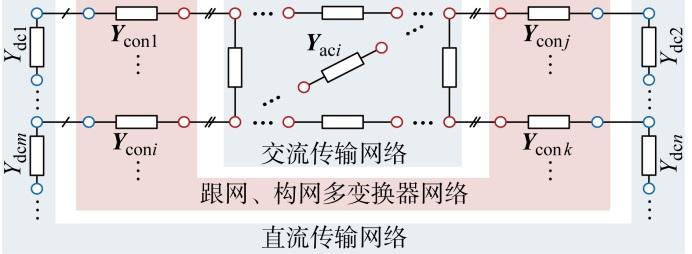
异构多变换器系统主要由跟网型变换器、构网型变换器以及交/直流传输网络组成,将上述各元件以阻抗/导纳形式表征,可获得图2 所示保留系统完整拓扑信息的节点导纳网络.如1.1节所述,跟网/构网变换器可采用三端口导纳Y c o n i ( s ) 3 × 3 dq 导纳Y a c i ( s ) 2 × 2 Y dc i s )刻画.
图2
图2
多变换器系统的节点导纳网络
Fig.2
Node admittance of multi-converter system
借鉴传统电力系统中对节点/回路矩阵的构建方式,建立图2 所示节点导纳网络的频域矩阵模型.首先,将各个支路的导纳按对角元素形式排列,列写支路导纳矩阵:
(15) $\boldsymbol{Y}_{\mathrm{br}}(s)=\operatorname{blk} \operatorname{diag}\left[\begin{array}{llllll}\boldsymbol{Y}_{\mathrm{acl}} & \cdots & \boldsymbol{Y}_{\mathrm{ac} i} & \cdots & \boldsymbol{Y}_{\mathrm{dcl}} & \cdots\end{array}\right.\begin{array}{llllll}\boldsymbol{Y}_{\mathrm{dc} i} & \cdots & \boldsymbol{Y}_{\mathrm{con} 1} & \cdots & \boldsymbol{Y}_{\text {con } i} & \cdots]\end{array}$
式中:Y ac i Y dc i Y con i
根据各元件的电路连接关系,可建立相应的支路-节点关联矩阵A ,构建原则[17 ] 如下:
(16) 0 / 0 , 节 点 < k > 不 是 支 路 < l > 的 端 点 I / 1 , 节 点 < k > 是 支 路 < l > 的 发 点 - I / - 1 , 节 点 < k > 是 支 路 < l > 的 收 点
式中:alk 为A 的矩阵元素;0=diag(0, 0);I =diag(1, 1);0/ 0、I/ 1和-I/ -1分别表示交流节点和直流节点所采用的矩阵元素.
系统的节点导纳矩阵Y node (s )可由下式计算获得:
(17) $\boldsymbol{Y}_{\text {node }}(s)=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{Y}_{\mathrm{br}}(s) \boldsymbol{A}$
2 考虑振荡源分布的同步主导回路稳
定分析方法 同步主导回路法通过提取同步控制环节作为前向通路,而将剩余控制动态、主电路以及外电网等效表示为反馈通路,形成以同步动态变量为输入输出的“控制-反馈”模型,从而直观分析系统的同步失稳.但该方法主要用于简单的单变换器并网系统,在复杂多变换器系统的应用上存在两个难点:①如何对多机系统进行前向-反馈子系统划分,从而避免开环右半平面极点的引入;②如何建立涵盖多变换器动态及传输网络的反馈通路模型.为此,提出一种考虑振荡源分布的多变换器同步主导回路稳定分析方法.
2.1 基于频域模态法的振荡源定位
通过对系统的振荡分布进行预分析,选取振荡源位置作为前向-反馈子系统的分割点,能够有效防止聚合反馈子系统含有失稳谐振点,从而避免引入开环右半平面极点.参与因子是刻画系统主导特性的有效工具,由于本文主要基于频域模型开展,故采用频域模态法[19 -20 ] 计算失稳参与因子.首先,基于节点导纳Y node (s )的行列式零点可获取系统的振荡模式:
(18) $\operatorname{det}\left(\boldsymbol{Y}_{\text {node }}(s)\right)=0 \quad \lambda_{m}, \quad m \in[1, N]$
式中:N 代表系统振荡模式的数量;λm 和时域状态矩阵A 的特征值一致. 选取关心的失稳模式λm (多选实部大于0的不稳定模式)作为分析对象,将其代入Y node (s )并进行特征值分解,
(19) $\boldsymbol{Y}_{\text {node }}\left(\lambda_{m}\right)=\boldsymbol{R}\left(\lambda_{m}\right) \boldsymbol{\Lambda}\left(\lambda_{m}\right) \boldsymbol{T}\left(\lambda_{m}\right)$
式中:R (λm )=r 1 ( λ m ) … r n ( λ m ) T (λm )=t T 1 ( λ m ) … t T n ( λ m ) T R (λm )T (λm )=I ;特征矩阵 Λ (λm )=diag(Λ 1 (λm ), …, Λn (λm ))定义为模态导纳,其中某一特征值为0,如Λk (λm )=0,这是因为行列式det(Y node (λm ))=0,该特征值也称为最弱模态导纳. 下文为简化符号表示,将括号内的λm 隐去,如Λk (λm )→Λk . 提取最弱模态导纳对应的左右特征向量,可得:
(20) t k Y n o d e = Λ k t k Y n o d e r k = Λ k r k t k r k = 1
考虑任意参数α ,对式(20)中的第一项进行偏导求解,可得:
(21) ∂ t k ∂ α node +tk ∂ Y n o d e ∂ α ∂ Λ k ∂ α k +Λk ∂ t k ∂ α
对上式左右两边同乘rk ,同时根据式(20)中Y node rk =Λk rk 和tk rk =1,可得:
(22) ∂ Λ k ∂ α k ∂ Y n o d e ∂ α k
若考虑参数α =Y node, ii
(23) $\begin{array}{c}\frac{\Lambda_{k}}{\boldsymbol{Y}_{\text {node }, i i}}=\boldsymbol{t}_{k} \frac{\boldsymbol{Y}_{\text {node }}}{\boldsymbol{Y}_{\text {node }, i i}} \boldsymbol{r}_{k}=\left[\boldsymbol{r}_{k} \boldsymbol{t}_{k}\right]_{i i}=\xi_{i}^{\mathrm{PF}}, \\i \in[1, n]\end{array}$
式中:ξ i P F i 的振荡参与因子;n 为系统节点的数量. ξ i P F i 的振荡主导地位越强,由此可量化评估系统的振荡源位置.
2.2 同步主导回路构建与机理分析方法
根据上述节点参与因子的分析结果,可确定引起系统失稳的主导变换器.保留该变换器的交直流节点,采用Kron消元法消去系统的剩余非主导节点,获得相应的降维模型:
(24) $\left[\boldsymbol{Y}_{\text {node }}(s)\right]_{n \times n} \quad \text { Kron 消元 } \quad\left[\boldsymbol{Y}_{\text {node }}^{\text {Redu }}(s)\right]_{3 \times 3}$
n 维节点导纳模型降阶至3维等效模型.从该等效模型中减去主导变换器的三端口导纳,如 Y con i
(25) Y n o d e e q Y n o d e R e d u con i (s)
对于本文所考虑的异构多变换器系统,其直流网络主要为变换器自身的直流电容、滤波器等,不存在互联,因此所得外部系统等效导纳可进一步分解为交流、直流两个子系统:
(26) $\boldsymbol{Y}_{\text {node }}^{\mathrm{eq}}(s)=\operatorname{blk} \operatorname{diag}\left(\boldsymbol{Y}_{\text {node }}^{\text {eq-ac }}(s), Y_{\text {node }}^{\text {eq-dc }}(s)\right)$
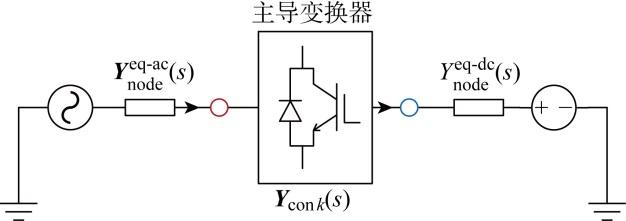
图3 直观给出了上述所获得等效系统的示意.图中,Y n o d e e q - a c ( s )主要为剩余非主导变换器及其交直流互联网络的等效导纳,而Y n o d e e q - d c ( s )为主导变换器自身的直流侧无源元件导纳.
图3
图3
多变换器系统的节点导纳网络
Fig.3
Node admittance of multi-converter system
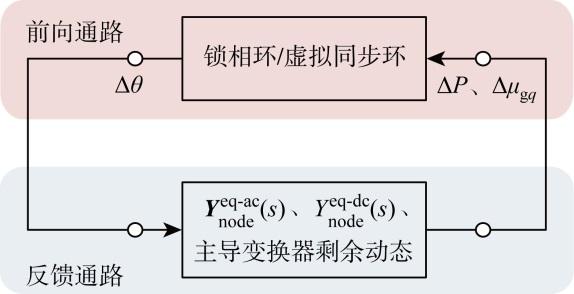
基于上述等效单机并网系统,可建立考虑多机动态的同步主导回路模型.如图4 所示,将锁相环或虚拟同步环作为前向通路G sync (s ),联立变换器剩余动态(主要为内/ 外环控制环节以及交流滤波器)与等效外电网(Y n o d e e q - a c ( s )和Y n o d e e q - d c ( s ))方程,消去除同步控制输入输出Δθ 和ΔP/ Δu g q H sync (s ).
图4
图4
多机同步主导回路模型示意
Fig.4
Diagram of multi-converter synchronization-dominated loop
具体地,若跟网型变换器主导振荡,其前向通路模型即锁相环控制为
(27) Δθ =H PI (s )Δ u g q c pll (s)Δ u g q c
式中:G pll (s )代表锁相环的控制传递函数.此时,交直流侧等效电网模型可表示为
(28) $\left.\begin{array}{l}\Delta \boldsymbol{i}_{g d q}=-\boldsymbol{Y}_{\text {node }}^{\text {eqac }}(s) \Delta \boldsymbol{u}_{\mathrm{gdq}} \\\Delta i_{\mathrm{dc}}=Y_{\text {node }}^{\text {ende }}(s) \Delta u_{\mathrm{dc}}\end{array}\right\}$
联立式(1)~(3)、式(5)~(7)和式(28),共计9个方程10个变量Δθ 、Δu g d q c u g dq i g d q c i g dq m c d q mdq 、Δu dc 、Δi dc 、Δu c dq θ 为参量可联立求解剩余变量关于Δθ 的传递函数,如下式所示:
(29) $\Delta \boldsymbol{u}_{\mathrm{g} d q}^{\mathrm{c}}=\left[\begin{array}{cc}H_{\mathrm{pll}}^{d}(s) & H_{\mathrm{pll}}^{q}(s)\end{array}\right] \Delta \theta$
式中:H p l l q ( s )对应Δu g q c θ 的传递函数关系,即为聚合反馈通路模型.
类似地,若构网型变换器主导振荡,其前向通路模型即虚拟同步控制为
(30) $\Delta \theta=T_{\text {vsg }}(s) \Delta p=G_{\text {vsg }}(s) \Delta p$
式中:G vsg (s )代表虚拟同步环的控制传递函数. 此时,交直流侧等效电网模型可由式(28)表示.
联立式(1)~ (3)、(5)、(6)、(11)、(13)、(14),总共10个方程11个变量Δθ 、Δp 、Δu g d q c u g dq i g d q c i g dq m c d q mdq 、Δu dc 、Δi dc 、Δu c dq θ 为参量可联立求解剩余变量关于的Δθ 传递函数,如下式所示:
(31) $\Delta p=H_{\mathrm{vsg}}(s) \Delta \theta$
基于上述所得到的前馈、反馈通路传函,可获得系统的开环增益:
(32) L (s )=G pll (s ) H p l l q vsg (s)Hvsg (s)
基于L (s ),采用伯德判据、奈氏判据等可对闭环系统的稳定性进行分析.
需要注意的是,上述反馈通路H p l l q ( s )或H vsg (s )为剩余变换器和传输网络的聚合等效模型,可能引入开环右半平面极点,即H p l l q ( s )、H vsg (s )开环不稳定,易导致判稳分析的失准.
3 案例研究与仿真分析
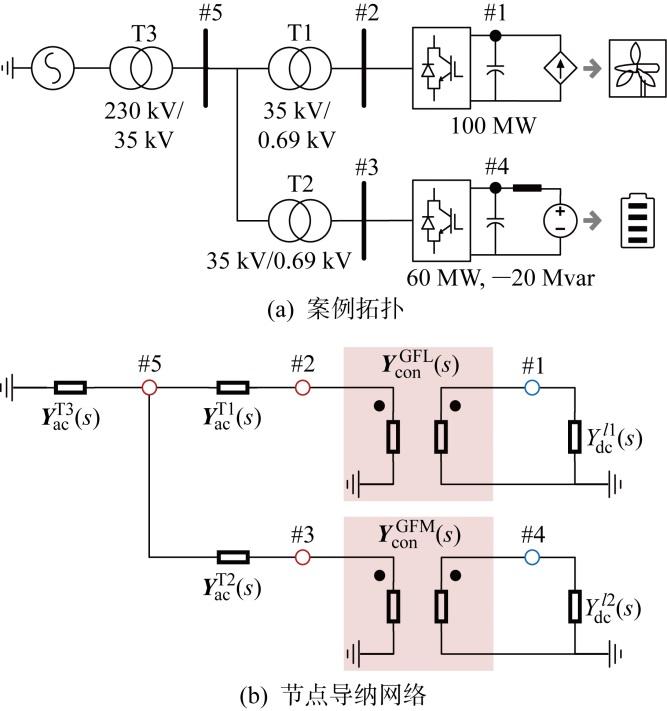
考虑图5 所示测试系统,其主要从实际风电场抽象简化得来,采用1台聚合跟网型变换器表征各台风电机组、1台构网型变换器来表征储能电站,各变换器以及传输网络的主要参数如表1 所示.
图5
图5
测试案例拓扑
Fig.5
Topology of test system
图5 测试系统共含有5个节点, 包括2个直流节点和3个交流节点(含有d 、q 轴两个通道).节点导纳网络如图5(b) 所示,Y a c T 1 ( s )等代表各变压器的dq 导纳,Y d c l 1 ( s )等代表各变换器直流侧的等效导纳,Y c o n G F L ( s )、Y c o n G F M ( s )分别为跟网型和构网型变换器的三端口导纳.基于该案例系统,首先对单变换器及多变换器网络建模的准确性进行验证,继而分析子系统划分对开环右半平面极点的影响,最后采用所提同步回路分析法分析异构多变换器系统的同步失稳机理与参数影响.
3.1 单变换器及多变换器网络建模验证
3.1.1 跟网型与构网型变换器的三端口阻抗模型验证
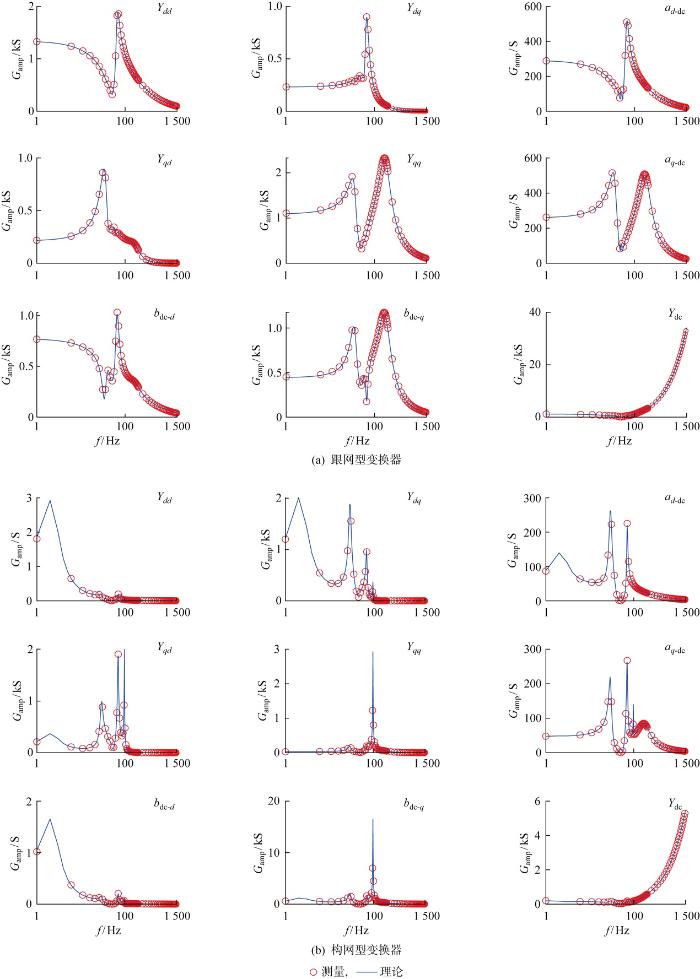
将上述跟网型变换器的交直流侧分别接入理想电压源和电流源(恒功率特性),通过串联电压扰动源对其进行3次扫频(d 、q 轴和直流通道各1次),可获得测量三端口阻抗;类似地,将构网型变换器交直流侧均接入理想电压源,通过3次扫频获得测量三端口阻抗.如图6 所示,红色测量曲线与蓝色理论曲线符合较好,验证了所建立单变换器模型的准确性.图中,ad- dc 和aq- dc 分别为直流通道对交流d 、q 轴通道的耦合项,b dc- d b dc- q d 、q 轴通道对直流通道的耦合项,f 为频率,G amp 为幅值.
图6
图6
三端口阻抗验证
Fig.6
Validation of three-port impedance
3.1.2 多变换器系统的节点导纳矩阵模型验证
基于图5(b) 所示节点导纳网络,列写测试系统的支路导纳矩阵:
(33) $\begin{aligned}\boldsymbol{Y}_{\mathrm{br}}(s)= & \operatorname{blk} \operatorname{diag}\left[\boldsymbol{Y}_{\mathrm{con}}^{\mathrm{GFL}} \quad Y_{\mathrm{dc}}^{l 1} \quad \boldsymbol{Y}_{\mathrm{ac}}^{\mathrm{T} 1} \quad \boldsymbol{Y}_{\mathrm{con}}^{\mathrm{GFM}}\right. \\& \left.Y_{\mathrm{dc}}^{l 2} \boldsymbol{Y}_{\mathrm{ac}}^{\mathrm{T} 2} \quad \boldsymbol{Y}_{\mathrm{ac}}^{\mathrm{T3}}\right]_{14 \times 14}\end{aligned}$
基于图5(b) 所示支路与节点的连接关系,列写测试系统的支路-节点关联矩阵:
(34) A = I 1 1 I - I I 1 1 I - I I 14 × 8
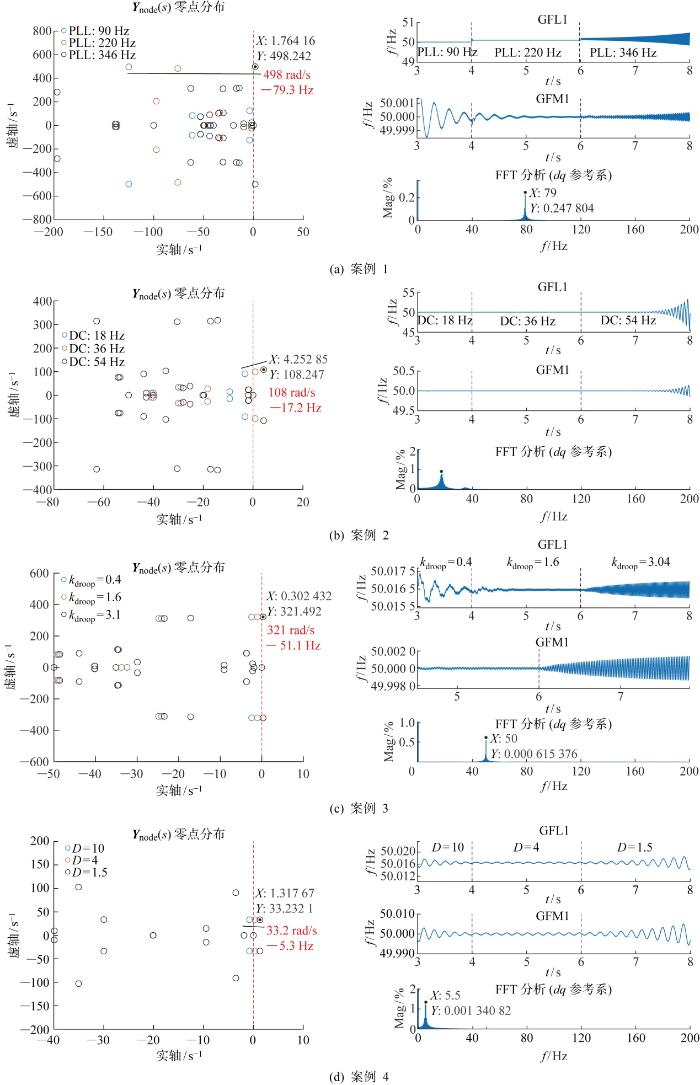
将式(33)、(34)代入式(17)可获得测试系统的节点导纳矩阵Y node (s ),基于该模型对图7 所示4种临界失稳工况进行分析,计算零点分布,其中k droop 为下垂系数.如图7(a) 所示,案例1理论分析失稳频率为79.3 Hz,而同样参数条件下时域仿真给出失稳频率为79 Hz,二者较为符合.图7(b)~7(d) 中理论分析结果与时域仿真结果也较为符合,由此验证了所建立Y node (s )的准确性.图中:GFL1为跟网型变换器1;GFM1为构网型变换器1;FFT为快速傅里叶变换; Mag代表幅值,以直流分量的百分比为度量;以DC简化示意直流电压环带宽,18、36、54 Hz代表采用的不同带宽,下同.
图7
图7
节点导纳矩阵准确性验证
Fig.7
Accuracy validation of node admittance matrix
3.1.3 同步主导回路模型验证
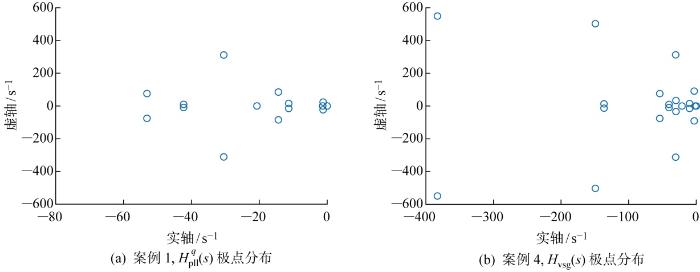
针对上述案例1和案例4,选取失稳模式作为分析对象,案例1为1.76±j498.2、案例4为1.32±j33.2,基于2.1节计算相应的节点参与因子(PF).如图8 所示,案例1中节点#1占主导,而案例4中节点#3占主导,与之相连的分别为跟网型和构网型变换器.基于参与因子分析,案例1应选取跟网型变换器的同步端口来划分子系统,分别为G pll (s )和H p l l q ( s );而案例4应选取构网型变换器的同步端口,分别为G vsg (s )和H vsg (s ).
图8
图8
节点参与因子计算结果
Fig.8
Calculation results of node PF
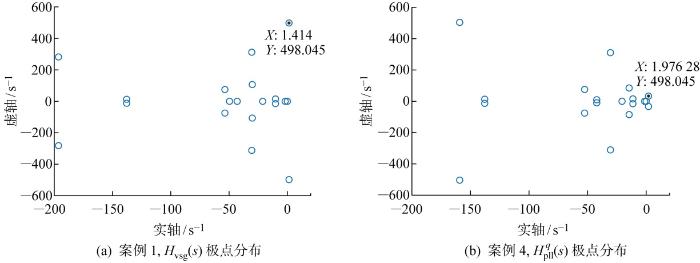
图9 对案例1中H p l l q ( s )和案例4中H vsg (s )的极点分布进行分析,可以看到二者均为开环稳定,即不含有右半平面极点,可直接采用伯德判据对L (s )进行分析.
图9
图9
开环右半极点评估(主导变换器划分同步回路)
Fig.9
Evaluation of open-loop right-half-plane pole (sync loop divided by dominated converter)
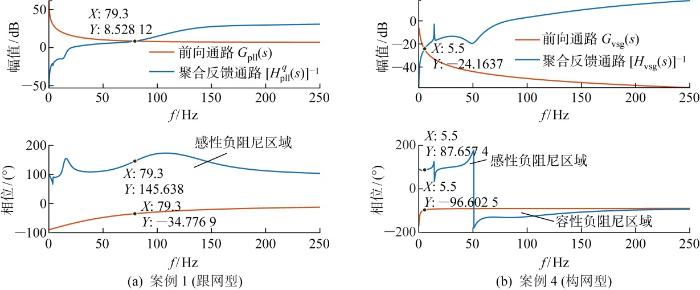
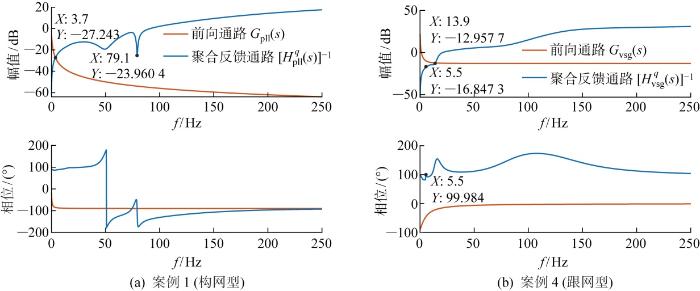
图10 为伯德判稳分析结果.如图10(a) 所示,案例1中聚合反馈通路的感性负阻尼区域,即相位大于+90°,幅相平面上的实轴投影体现为负电阻特性,而虚轴投影体现为电感特性的区域是诱发锁相环同步失稳的主要诱因,若锁相环参数选取不当将会使得幅值交点的相位裕度超过-180°.如图10(b) 所示,案例4中聚合反馈通路则存在较大的感性、容性负阻尼,即相位小于-90°,幅相平面上的实轴投影体现为负电阻特性,而虚轴投影体现为电容特性,在幅值交点5.5 Hz处,相位裕度超过-180°.上述分析结果与图7(a)、7(d) 时域仿真符合,由此验证了所建同步主导回路模型的准确性.
图10
图10
伯德判稳分析(主导变换器划分同步回路)
Fig.10
Bode criterion-based stability analysis (sync loop divided by dominated converter)
3.2 跟网与构网同步交互稳定的参数影响
由图10(a) 分析可知,聚合反馈通路的感性/容性负阻尼区域是诱发跟网、构网变换器同步失稳的主要原因,而聚合反馈通路受剩余变换器多带宽控制以及交直流传输网络的共同影响.针对聚合反馈通路的相位裕度,在跟网型主导和构网型主导两种同步回路视角下,分析主要控制参数及线路参数对感性/容性负阻尼的作用规律.
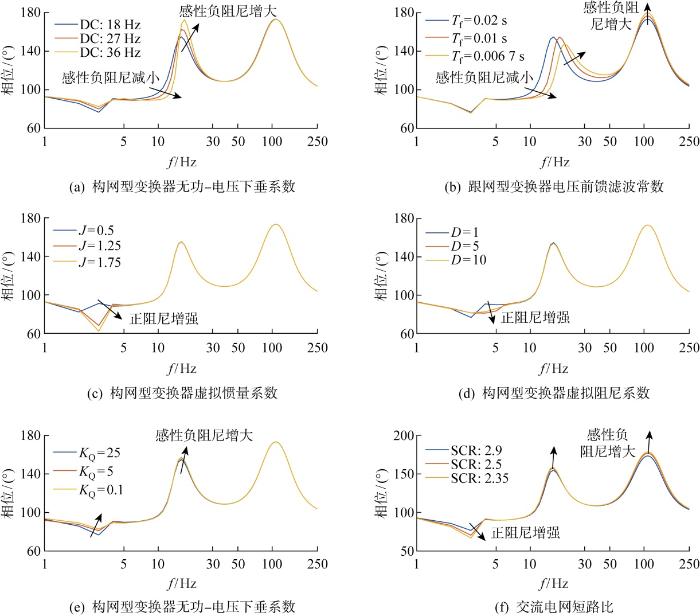
如图11 所示,以跟网型同步回路为分析视角.升高跟网型变换器直流电压带宽,将减小10 Hz附近的感性负阻尼、增大20 Hz附近的感性负阻尼;降低跟网型变换器的电压前馈滤波常数,将减小10 Hz 处的感性负阻尼,增大20~50、100 Hz附近的感性负阻尼;构网型变换器的虚拟惯量/阻尼主要影响低频处阻尼,二者增大会使得2~5 Hz附近的感性正阻尼加强,无功-电压下垂系数也主要作用于低频段,其减小会削弱感性正阻尼;降低系统短路比(short circuit ratio,SCR),将增大15、100 Hz附近的感性负阻尼,同时增强2~5 Hz附近的感性正阻尼.综上,减小跟网型变换器直流电压带宽、增大电压前馈滤波常数,增大构网型变换器虚拟惯量、阻尼系数,或者提高电网短路比,有助于减小跟网型变换器锁相环主导的同步失稳风险.
图11
图11
跟网型变换器主导的同步聚合反馈回路稳定性分析
Fig.11
Stability analysis of aggregated sync feedback path dominated by grid-following converter
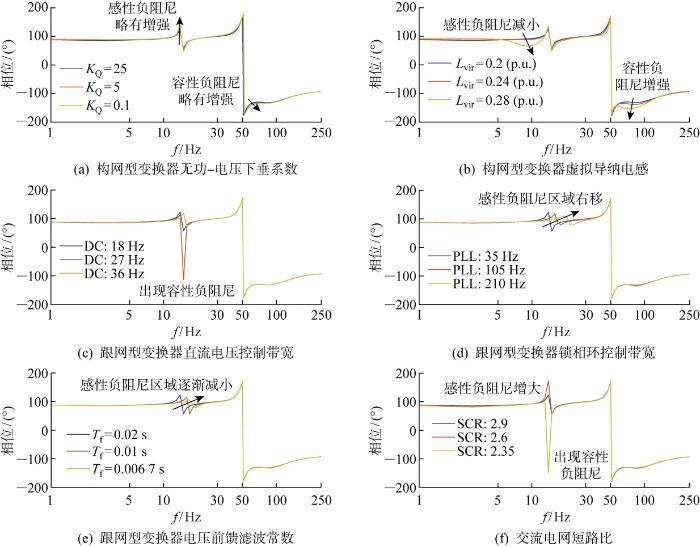
如图12 所示,以构网型同步回路为分析视角.构网型变换器无功-电压下垂系数增大后,使得10、50~100 Hz附近的感性/容性负阻尼略有增强,而虚拟导纳电感的增大能够减小5~10 Hz附近的感性负阻尼,但也会使得50~100 Hz处的容性负阻尼增强;跟网型变换器的直流电压带宽升高,可能导致感性负阻尼变为容性负阻尼,而锁相环带宽(图例中以PLL简化示意锁相环控制带宽,35、105、210 Hz代表采用的不同带宽)的升高或电压前馈滤波常数的减小,将会导致感性负阻尼的作用频段有所抬升(15 Hz→30 Hz);降低交流电网的短路比,会使得15 Hz左右的感性负阻尼增强,并逐渐转变为容性负阻尼,而前馈通路主要体现容性特性(见图10(b) ),故失稳风险较小.综上,增大构网型变换器的虚拟导纳电感,增大跟网型变换器锁相环带宽、减小直流电压带宽、电压前馈滤波常数,或者降低电网短路比,有助于减小构网型变换器虚拟同步环主导的同步失稳风险.
图12
图12
构网型变换器主导的同步聚合反馈回路稳定性分析
Fig.12
Stability analysis of aggregated sync feedback path dominated by grid-forming converter
从上述分析中可以看出,某个参数变化对跟网同步端口或构网同步端口的稳定性影响不同甚至相反,这主要是因为跟网(79 Hz)、构网(5 Hz)同步动态的主导失稳模式不同,一般情况下某参数对不同失稳模式的作用方向不同.因此,对于含多类型同步控制变流器系统的同步失稳抑制,不能仅考虑单类型同步控制的稳定,还需计及不同类型同步动态间的耦合.
3.3 主导回路选取与开环右半平面极点引入
聚合反馈通路可能存在的右半平面极点会极大影响L (s )判稳的准确性,而本文方法由于考虑了振荡源的分布可有效避免该问题,图9 对H p l l q ( s )和H vsg (s )的极点评估后并未发现开环右半平面极点.相反,若案例1选取构网型变换器(非主导)进行同步端口划分,而案例4选取跟网型变换器(非主导)进行同步端口划分,则聚合反馈通道将出现开环不稳定现象,即存在右半平面开环极点,如图13 所示.
图13
图13
开环右半极点影响(非主导变换器划分同步回路)
Fig.13
Influence of open-loop right-half-plane pole (sync loop divided by non-dominated converter)
若采用上述非主导变换器划分所得同步回路,则无法准确给出判稳结果.如图14 所示,案例1和4的理论分析交点频率分别为3.7和 13.9 Hz,与图7 时域仿真不符.
图14
图14
伯德判稳分析(非主导变换器划分同步回路)
Fig.14
Bode criterion-based stability analysis (sync loop divided by non-dominated converter)
观察图14 发现,反馈回路曲线中存在明显的谐振峰,案例1为79.1 Hz、案例4为5.5 Hz,频率与系统失稳频率近似,也从侧面反映出聚合反馈回路中存在主导谐振点.该案例表明,本文方法基于振荡源分布来划分同步回路,能够避免反馈回路在聚合其他变换器和传输网络时导致的判稳失效问题,从而保障同步交互机理分析的可靠性.
4 结论
提出一种面向包含跟网和构网控制的多变换器同步主导回路分析法,有如下发现:
(1) 同步聚合反馈回路包含主导谐振点是引入开环右半平面极点的主要原因,通过参与因子定位振荡源位置并指导同步回路的构建,能够有效避免这一问题.
(2) 异构多变换器系统的同步失稳主要是由于跟网/构网同步控制参数设置不当,与反馈回路的感、容性负阻尼产生交互所致,而反馈回路受到宽频控制动态及传输网络的共同作用.
若系统规模持续扩大,本文方法在构建高维系统的单入单出同步回路时存在困难,且无法同时分析多个同步回路间的交互作用.同时,由于失稳模态在变流器的多控制环路中分布较广,可能出现主导模式不位于同步环路的情况,需考虑以其他控制环路为主视角进行划分.上述问题将在下一步工作中深入探讨.
参考文献
View Option
[1]
黄远明 , 张玉欣 , 夏赞阳 , 等 . 考虑需求响应资源和储能容量价值的新型电力系统电源规划方法
[J]. 上海交通大学学报 2023 , 57 (4 ): 432 -441 .
DOI:10.16183/j.cnki.jsjtu.2021.477
[本文引用: 1]
高比例可再生能源的接入对电力系统容量充裕性带来了新的挑战,系统必须具备充足的置信容量应对可再生能源的出力波动性和随机性.由于储能置信容量与电源规划结果的非线性关系,传统电源规划方法难以准确计算储能置信容量并建立系统置信容量充裕度约束.通过综合考虑火电、可再生能源、储能以及需求侧响应建立了电源规划模型,内嵌全年8 760时段生产运行模拟以确保系统具有充足灵活性,同时改进容量充裕性约束以考虑需求响应资源和储能的容量价值.针对储能置信容量的非线性问题,设计了迭代算法进行求解,并用某区域电力系统验证了模型的有效性.结果表明,高比例可再生能源系统中,影响系统成本的主要因素是灵活性约束,引入少量需求侧响应资源可大幅降低系统成本,为未来高比例可再生资源电力系统规划问题提供了新的思路.
HUANG Yuanming ZHANG Yuxin XIA Zanyang et al Power system planning considering demand response resources and capacity value of energy storage
[J]. Journal of Shanghai Jiao Tong University 2023 , 57 (4 ): 432 -441 .
[本文引用: 1]
[2]
邓小宇 , 刘牧阳 , 常喜强 , 等 . 新型电力系统点对网惯性支撑能力在线监测方法
[J]. 上海交通大学学报 2024 , 58 (9 ): 1390 -1399 .
DOI:10.16183/j.cnki.jsjtu.2023.029
[本文引用: 2]
准确及时地监测低惯量新型电力系统中聚合电源汇集点对电网的惯性支撑能力,对于提升系统安全、稳定、经济化运行具有重要意义.为阐明点对网的惯性支撑能力在线监测方法的基本原理,首先对以摇摆方程为基础的电力系统等效惯性常数定义及现有在线监测方法进行回顾;然后,为弥补现有在线监测方法在准确性上的欠缺,创新性地提出基于回归法的等效惯性常数辨识方法,并与在线惯量监测方法结合,构建基于同步相量测量单元的新型电力系统点对网惯性支撑能力在线监测的系统性方法;最后,利用改进的新英格兰10机39节点系统仿真分析,论证了该惯性支撑能力在线监测方法的实时性、准确性及其对新型电力系统的适用性.
DENG Xiaoyu LIU Muyang CHANG Xiqiang et al On-line estimation method of the inertial support capacity of point-to-grid in power system
[J]. Journal of Shanghai Jiao Tong University 2024 , 58 (9 ): 1390 -1399 .
[本文引用: 2]
[3]
詹长江 , 吴恒 , 王雄飞 , 等 . 构网型变流器稳定性研究综述
[J]. 中国电机工程学报 2023 , 43 (6 ): 2339 -2359 .
[本文引用: 1]
ZHAN Changjiang WU Heng WANG Xiongfei et al An overview of stability studies of grid-forming voltage source converters
[J]. Proceedings of the CSEE 2023 , 43 (6 ): 2339 -2359 .
[本文引用: 1]
[4]
刘新宇 , 逯芯妍 , 曾龙 , 等 . 双馈风电场并网抑制频率振荡控制策略
[J]. 上海交通大学学报 2022 , 56 (3 ): 303 -311 .
[本文引用: 1]
LIU Xinyu LU Xinyan ZENG Long et al Control strategies for suppressing frequency oscillation of doubly-fed wind farms connected to grid
[J]. Journal of Shanghai Jiao Tong University 2022 , 56 (3 ): 303 -311 .
[本文引用: 1]
[5]
徐政 . 电力系统广义同步稳定性的物理机理与研究途径
[J]. 电力自动化设备 2020 , 40 (9 ): 3 -9 .
[本文引用: 1]
XU Zheng Physical mechanism and research approach of generalized synchronous stability for power systems
[J]. Electric Power Automation Equipment 2020 , 40 (9 ): 3 -9 .
[本文引用: 1]
[6]
黄林彬 , 辛焕海 , 鞠平 , 等 . 电力电子并网装备的同步稳定分析与统一同步控制结构
[J]. 电力自动化设备 2020 , 40 (9 ): 10 -25 .
[本文引用: 1]
HUANG Linbin XIN Huanhai JU Ping et al Synchronization stability analysis and unified synchronization control structure of grid-connected power electronic devices
[J]. Electric Power Automation Equipment 2020 , 40 (9 ): 10 -25 .
[本文引用: 1]
[7]
张琛 , 蔡旭 , 李征 . 电压源型并网变流器的机-网电气振荡机理及稳定判据研究
[J]. 中国电机工程学报 2017 , 37 (11 ): 3174 -3183 .
[本文引用: 1]
ZHANG Chen CAI Xu LI Zheng Stability criterion and mechanisms analysis of electrical oscillations in the grid-tied VSC system
[J]. Proceedings of the CSEE 2017 , 37 (11 ): 3174 -3183 .
[本文引用: 1]
[8]
胡祺 , 付立军 , 马凡 , 等 . 弱电网下基于锁相控制并网变换器小扰动同步稳定分析
[J]. 中国电机工程学报 2021 , 41 (1 ): 98 -108 .
[本文引用: 1]
HU Qi FU Lijun MA Fan et al Small signal synchronizing stability analysis of PLL-based VSC connected to weak AC grid
[J]. Proceedings of the CSEE 2021 , 41 (1 ): 98 -108 .
[本文引用: 1]
[9]
罗魁 , 郭剑波 , 王伟胜 , 等 . 跟网型新能源附加频率控制对频率稳定及小扰动同步稳定影响分析综述
[J]. 中国电机工程学报 2023 , 43 (4 ): 1262 -1281 .
[本文引用: 1]
LUO Kui GUO Jianbo WANG Weisheng et al Analysis and summary of the influence of additional frequency control of grid-following new energy on frequency stability and small disturbance synchronous stability
[J]. Proceedings of the CSEE 2023 , 43 (4 ): 1262 -1281 .
[本文引用: 1]
[10]
李霞林 , 李佳鑫 , 朱琳 , 等 . 弱连接VSC在“外环-锁相环”时间尺度下的一类小扰动稳定性提升方法及等效性分析
[J]. 电网技术 2023 , 47 (4 ): 1632 -1642 .
[本文引用: 1]
LI Xialin LI Jiaxin ZHU Lin et al Equivalence analysis of a class of small-signal stability enhancement for weak grid connected VSCs in “outer-loop & PLL” time-scale
[J]. Power System Technology 2023 , 47 (4 ): 1632 -1642 .
[本文引用: 1]
[11]
LI Y T GU Y J GREEN T C Revisiting grid-forming and grid-following inverters: A duality theory
[J]. IEEE Transactions on Power Systems 2022 , 37 (6 ): 4541 -4554 .
[本文引用: 1]
[12]
李翼翔 , 田震 , 唐英杰 , 等 . 考虑构网型与跟网型逆变器交互的孤岛微电网小信号稳定性分析
[J]. 电力自动化设备 2022 , 42 (8 ): 11 -18 .
[本文引用: 1]
LI Yixiang TIAN Zhen TANG Yingjie et al Small-signal stability analysis of island microgrid considering interaction between grid-forming converter and grid-following converter
[J]. Electric Power Automation Equipment 2022 , 42 (8 ): 11 -18 .
[本文引用: 1]
[13]
张志强 , 李秋彤 , 余浩 , 等 . 海上直驱风电经柔直并网系统的次/超同步振荡特性分析
[J]. 上海交通大学学报 2022 , 56 (12 ): 1572 -1583 .
DOI:10.16183/j.cnki.jsjtu.2021.434
[本文引用: 1]
海上直驱风电经柔性直流输电并网系统由多变流器构成,具有不同时间尺度的控制回路和复杂的动态特性.基于双风电场经柔性直流并网系统算例,采用状态空间分析法研究系统次/超同步振荡模态与电流控制回路的关联关系.研究表明,系统存在3种与变流器电流环相关的主导振荡模态,分别对应于风场-柔直模态、风场间模态以及柔直-交流系统模态,风场侧的模态与柔直-交流系统模态是解耦的,相关变流器控制参数、系统的运行工况对3种模态稳定性具有重要影响;单个主导模态失稳引起的振荡会波及到柔直的另一端,需要甄别引起振荡的根本原因,以利于针对性设计抑制策略.研究结果对于认识海上风电经柔直并网系统动态特性、参数设计以及振荡抑制具有指导作用.
ZHANG Zhiqiang LI Qiutong YU Hao et al Analysis of sub/super-synchronous oscillation of direct-drive offshore wind power grid-connected system via VSC-HVDC
[J]. Journal of Shanghai Jiao Tong University 2022 , 56 (12 ): 1572 -1583 .
[本文引用: 1]
[14]
胡宇飞 , 田震 , 查晓明 , 等 . 构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略
[J]. 电力系统自动化 2022 , 46 (24 ): 121 -131 .
[本文引用: 1]
HU Yufei TIAN Zhen ZHA Xiaoming et al Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid-following converters
[J]. Automation of Electric Power Systems 2022 , 46 (24 ): 121 -131 .
[本文引用: 1]
[15]
ZOU Z X TANG J WANG X F et al Modeling and control of a two-bus system with grid-forming and grid-following converters
[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics 2022 , 10 (6 ): 7133 -7149 .
[本文引用: 1]
[16]
YANG C R HUANG L B XIN H H et al Placing grid-forming converters to enhance small signal stability of PLL-integrated power systems
[J]. IEEE Transactions on Power Systems 2021 , 36 (4 ): 3563 -3573 .
[本文引用: 1]
[17]
HUANG L B XIN H H LI Z Y et al Grid-synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control
[J]. IEEE Transactions on Smart Grid 2020 , 11 (1 ): 501 -516 .
[本文引用: 2]
[18]
ZHANG C MOLINAS M RYGG A et al Impedance-based analysis of interconnected power electronics systems: Impedance network modeling and comparative studies of stability criteria
[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics 2020 , 8 (3 ): 2520 -2533 .
[本文引用: 1]
[19]
宗皓翔 , 张琛 , 蔡旭 . 电力电子主导的交直流混联电网振荡分析与评估
[J]. 中国电机工程学报 2023 , 43 (10 ): 3844 -3856 .
[本文引用: 1]
ZONG Haoxiang ZHANG Chen CAI Xu Oscillation analysis and evaluation of the power electronics-dominated hybrid AC/DC grid
[J]. Proceedings of the CSEE 2023 , 43 (10 ): 3844 -3856 .
[本文引用: 1]
[20]
ZHANG C ZONG H X CAI X et al On the relation of nodal admittance-and loop gain-model based frequency-domain modal methods for converters-dominated systems
[J]. IEEE Transactions on Power Systems 2023 , 38 (2 ): 1779 -1782 .
[本文引用: 1]
考虑需求响应资源和储能容量价值的新型电力系统电源规划方法
1
2023
... 为推进实现“双碳”目标,我国能源电力正向以新能源为主体的新型电力系统转型[1 ] ,其对新能源电源的频率、电压支撑能力提出了迫切需求[2 ] .目前用于风、光等新能源电源的并网控制方式主要包括跟网型(GFL)和构网型(GFM)控制,其中跟网型控制具有快速功率响应的能力,而构网型控制在主动频率/电压支撑和自组网运行等方面更具优势[3 ] .这使得控制优势互补的跟网型与构网型异构多变换器系统受到重视,其内部的跟网、构网同步特性和交互稳定问题是近几年国内外关注的热点. ...
Power system planning considering demand response resources and capacity value of energy storage
1
2023
... 为推进实现“双碳”目标,我国能源电力正向以新能源为主体的新型电力系统转型[1 ] ,其对新能源电源的频率、电压支撑能力提出了迫切需求[2 ] .目前用于风、光等新能源电源的并网控制方式主要包括跟网型(GFL)和构网型(GFM)控制,其中跟网型控制具有快速功率响应的能力,而构网型控制在主动频率/电压支撑和自组网运行等方面更具优势[3 ] .这使得控制优势互补的跟网型与构网型异构多变换器系统受到重视,其内部的跟网、构网同步特性和交互稳定问题是近几年国内外关注的热点. ...
新型电力系统点对网惯性支撑能力在线监测方法
2
2024
... 为推进实现“双碳”目标,我国能源电力正向以新能源为主体的新型电力系统转型[1 ] ,其对新能源电源的频率、电压支撑能力提出了迫切需求[2 ] .目前用于风、光等新能源电源的并网控制方式主要包括跟网型(GFL)和构网型(GFM)控制,其中跟网型控制具有快速功率响应的能力,而构网型控制在主动频率/电压支撑和自组网运行等方面更具优势[3 ] .这使得控制优势互补的跟网型与构网型异构多变换器系统受到重视,其内部的跟网、构网同步特性和交互稳定问题是近几年国内外关注的热点. ...
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
On-line estimation method of the inertial support capacity of point-to-grid in power system
2
2024
... 为推进实现“双碳”目标,我国能源电力正向以新能源为主体的新型电力系统转型[1 ] ,其对新能源电源的频率、电压支撑能力提出了迫切需求[2 ] .目前用于风、光等新能源电源的并网控制方式主要包括跟网型(GFL)和构网型(GFM)控制,其中跟网型控制具有快速功率响应的能力,而构网型控制在主动频率/电压支撑和自组网运行等方面更具优势[3 ] .这使得控制优势互补的跟网型与构网型异构多变换器系统受到重视,其内部的跟网、构网同步特性和交互稳定问题是近几年国内外关注的热点. ...
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
构网型变流器稳定性研究综述
1
2023
... 为推进实现“双碳”目标,我国能源电力正向以新能源为主体的新型电力系统转型[1 ] ,其对新能源电源的频率、电压支撑能力提出了迫切需求[2 ] .目前用于风、光等新能源电源的并网控制方式主要包括跟网型(GFL)和构网型(GFM)控制,其中跟网型控制具有快速功率响应的能力,而构网型控制在主动频率/电压支撑和自组网运行等方面更具优势[3 ] .这使得控制优势互补的跟网型与构网型异构多变换器系统受到重视,其内部的跟网、构网同步特性和交互稳定问题是近几年国内外关注的热点. ...
An overview of stability studies of grid-forming voltage source converters
1
2023
... 为推进实现“双碳”目标,我国能源电力正向以新能源为主体的新型电力系统转型[1 ] ,其对新能源电源的频率、电压支撑能力提出了迫切需求[2 ] .目前用于风、光等新能源电源的并网控制方式主要包括跟网型(GFL)和构网型(GFM)控制,其中跟网型控制具有快速功率响应的能力,而构网型控制在主动频率/电压支撑和自组网运行等方面更具优势[3 ] .这使得控制优势互补的跟网型与构网型异构多变换器系统受到重视,其内部的跟网、构网同步特性和交互稳定问题是近几年国内外关注的热点. ...
双馈风电场并网抑制频率振荡控制策略
1
2022
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
Control strategies for suppressing frequency oscillation of doubly-fed wind farms connected to grid
1
2022
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
电力系统广义同步稳定性的物理机理与研究途径
1
2020
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
Physical mechanism and research approach of generalized synchronous stability for power systems
1
2020
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
电力电子并网装备的同步稳定分析与统一同步控制结构
1
2020
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
Synchronization stability analysis and unified synchronization control structure of grid-connected power electronic devices
1
2020
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
电压源型并网变流器的机-网电气振荡机理及稳定判据研究
1
2017
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
Stability criterion and mechanisms analysis of electrical oscillations in the grid-tied VSC system
1
2017
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
弱电网下基于锁相控制并网变换器小扰动同步稳定分析
1
2021
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
Small signal synchronizing stability analysis of PLL-based VSC connected to weak AC grid
1
2021
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
跟网型新能源附加频率控制对频率稳定及小扰动同步稳定影响分析综述
1
2023
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
Analysis and summary of the influence of additional frequency control of grid-following new energy on frequency stability and small disturbance synchronous stability
1
2023
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
弱连接VSC在“外环-锁相环”时间尺度下的一类小扰动稳定性提升方法及等效性分析
1
2023
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
Equivalence analysis of a class of small-signal stability enhancement for weak grid connected VSCs in “outer-loop & PLL” time-scale
1
2023
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
Revisiting grid-forming and grid-following inverters: A duality theory
1
2022
... 相较于同步机由于阻尼转矩不足导致的同步功角失稳[4 ] ,电力电子变换器主导系统的同步稳定性主要受宽频控制动态影响,体现为跟网型如锁相环(PLL)或构网型控制(如虚拟同步环)输出的同步相角失稳,也有学者将其称为“虚拟功角”动态同步失稳[5 -6 ] .其中,跟网型主导系统的同步失稳机理主要为锁相环在弱电网下体现为负阻尼特性并抵消剩余控制动态提供的正阻尼[7 -8 ] ,罗魁等[9 ] 分析了跟网型附加调频、附加惯量控制对系统小干扰稳定的影响,李霞林等[10 ] 提出一种考虑外环与锁相环交互作用的同步稳定性提升控制策略.而构网型主导系统在弱电网下的稳定性较好,但受电压源控制特性影响易在强电网下发生失稳[11 ] ,邓小宇等[2 ] 对构网型同步控制虚拟惯量与阻尼系数的稳定性影响进行了讨论. ...
考虑构网型与跟网型逆变器交互的孤岛微电网小信号稳定性分析
1
2022
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
Small-signal stability analysis of island microgrid considering interaction between grid-forming converter and grid-following converter
1
2022
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
海上直驱风电经柔直并网系统的次/超同步振荡特性分析
1
2022
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
Analysis of sub/super-synchronous oscillation of direct-drive offshore wind power grid-connected system via VSC-HVDC
1
2022
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略
1
2022
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid-following converters
1
2022
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
Modeling and control of a two-bus system with grid-forming and grid-following converters
1
2022
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
Placing grid-forming converters to enhance small signal stability of PLL-integrated power systems
1
2021
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
Grid-synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control
2
2020
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
... 根据各元件的电路连接关系,可建立相应的支路-节点关联矩阵A ,构建原则[17 ] 如下: ...
Impedance-based analysis of interconnected power electronics systems: Impedance network modeling and comparative studies of stability criteria
1
2020
... 上述关于同步稳定的研究主要针对单类型同步控制变换器,对于同时含跟网和构网控制的异构型多变换器互联系统,目前多采用时域状态空间法或频域阻抗法进行稳定性分析.李翼翔等[12 ] 采用状态空间法[13 ] 分析跟网和构网型变换器主导微电网的稳定裕度及参数影响;文献[14 -15 ]中采用阻抗网络聚合法研究跟网、构网变换器并联系统的小扰动稳定性;Yang等[16 ] 从“广义短路比”的角度出发,量化评估构网型变换器接入后系统的短路比变化并提供最优接入点参考.相比于状态空间法和阻抗法,Huang等[17 ] 提出的同步主导回路法适于揭示变换器同步失稳机理,其主要原理为将同步控制环作为前馈回路而将剩余系统动态聚合为反馈回路,通过相角阻尼直观分析同步环的失稳机理.然而该方法目前主要面向单变换器并网系统,如何计及多变换器系统的复杂控制及传输网络动态尚不清楚,并且同步反馈回路由于进行了聚合运算极易引入开环右半平面极点[18 ] ,可能导致稳定性判据失准. ...
电力电子主导的交直流混联电网振荡分析与评估
1
2023
... 通过对系统的振荡分布进行预分析,选取振荡源位置作为前向-反馈子系统的分割点,能够有效防止聚合反馈子系统含有失稳谐振点,从而避免引入开环右半平面极点.参与因子是刻画系统主导特性的有效工具,由于本文主要基于频域模型开展,故采用频域模态法[19 -20 ] 计算失稳参与因子.首先,基于节点导纳Y node (s )的行列式零点可获取系统的振荡模式: ...
Oscillation analysis and evaluation of the power electronics-dominated hybrid AC/DC grid
1
2023
... 通过对系统的振荡分布进行预分析,选取振荡源位置作为前向-反馈子系统的分割点,能够有效防止聚合反馈子系统含有失稳谐振点,从而避免引入开环右半平面极点.参与因子是刻画系统主导特性的有效工具,由于本文主要基于频域模型开展,故采用频域模态法[19 -20 ] 计算失稳参与因子.首先,基于节点导纳Y node (s )的行列式零点可获取系统的振荡模式: ...
On the relation of nodal admittance-and loop gain-model based frequency-domain modal methods for converters-dominated systems
1
2023
... 通过对系统的振荡分布进行预分析,选取振荡源位置作为前向-反馈子系统的分割点,能够有效防止聚合反馈子系统含有失稳谐振点,从而避免引入开环右半平面极点.参与因子是刻画系统主导特性的有效工具,由于本文主要基于频域模型开展,故采用频域模态法[19 -20 ] 计算失稳参与因子.首先,基于节点导纳Y node (s )的行列式零点可获取系统的振荡模式: ...