风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义.
目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题.
针对上述问题,本文综合考虑风电不确定性,首先基于历史数据,采用拉丁超立方抽样技术生成风电场景,并通过欧氏距离法削减相似场景,提取典型场景中的数据作为风电基础数据;其次,利用正余弦算法优化的变分模态分解方法,对风电数据进行分解及高低频重构,遴择出符合并网波动量限值的直接并网分量与混合储能功率平抑值;最后,将混合储能系统的荷电状态进行分区划分,并基于多模糊控制对混合储能系统的功率进行再次分配,从而实现混合储能系统功率的合理分配.
1 风电与混合储能系统模型搭建
1.1 系统结构示意图
风电混储系统结构图如图1 所示.为应对风电的随机性、波动性与“弃风”现象[1 ] ,在交流母线处集中配置混合储能系统, 并经电力电子器件与风电机组组合为风电混储系统.图中:${P}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\left(t\right)$ t 时刻风电输出功率;${P}_{\mathrm{H}\mathrm{e}\mathrm{s}\mathrm{s}}\left(t\right)$ t 时刻混合储能系统的充电或者放电功率;PG (t) 为t 时刻风电并网功率;${P}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻蓄电池的充电或者放电功率;${P}_{\mathrm{s}\mathrm{c}}\left(t\right)$ t 时刻超级电容的充电或者放电功率;$P{\text{'}}_{\mathrm{s}\mathrm{c}}\left(t\right)$ t 时刻功率修正后的超级电容的功率;$P{\text{'}}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻功率修正后蓄电池的功率;AC、DC分别表示交流、直流电.规定充电时功率为正,放电时功率为负.根据图1 中的功率关系,建立如下表达式:
(1) $\begin{array}{c}\left.\begin{array}{l}{P}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\left(t\right)={P}_{\mathrm{H}\mathrm{e}\mathrm{s}\mathrm{s}}\left(t\right)+{P}_{\mathrm{G}}\left(t\right)\\ {P}_{\mathrm{H}\mathrm{e}\mathrm{s}\mathrm{s}}\left(t\right)={P}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)+{P}_{\mathrm{s}\mathrm{c}}\left(t\right)\end{array}\right\}\end{array}$
图1
图1
风电混储系统拓扑结构
Fig.1
Topology of wind hybrid storage system
1.2 数学模型
1.2.1 风电功率模型
(2) $\begin{array}{c}{P}_{m}\left(t\right)=\left\{\begin{array}{l}0,{v}_{\mathrm{m}\mathrm{i}\mathrm{n}}>v,v>{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}\\ 0.5\rho A{v}^{3},{v}_{\mathrm{m}\mathrm{i}\mathrm{n}}<v<{v}_{\mathrm{n}}\\ {P}_{\mathrm{N}},{v}_{\mathrm{n}}<v<{v}_{\mathrm{m}\mathrm{a}\mathrm{x}}\end{array}\right.\end{array}$
式中: Pm (t) 为第m 个涡轮机在t 时刻的功率;v 为涡轮机轮毂高度实际风速;${v}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ ${v}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ vn 为额定风速;$\mathrm{\rho }$ A 为涡轮机叶片转一周所围成的面积;PN 为涡轮机额定功率.
1.2.2 蓄电池设备模型
蓄电池装置的主要作用是削减功率峰值,从而承担混合储能系统功率任务的中低频分量[6 ] ,而电池模型参数会随着电池的蓄电池荷电状态、循环次数、容量衰减而不断发生变化.基于上述因素,可将电池数学模型表示为
(3) ${S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{B}\mathrm{a}\mathrm{t}}(t+\mathrm{\Delta }t)=\mathrm{ }{S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)-\frac{1}{{Q}_{\mathrm{n}}}{\int }_{0}^{\mathrm{\Delta }t}I\left(\tau \right)({\eta }_{\mathrm{B}\mathrm{a}\mathrm{t}}^{-1},{\eta }_{\mathrm{B}\mathrm{a}\mathrm{t}})d\tau $
(4) $\begin{array}{c}\begin{array}{c}{E}_{\mathrm{B}\mathrm{a}\mathrm{t}}(t+\mathrm{\Delta }t)={E}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)-\\ \mathrm{e}\mathrm{x}\mathrm{p}\left[{C}_{\mathrm{t}}\right({T}_{\mathrm{B}\mathrm{a}\mathrm{t}}-25)-{b}_{\mathrm{c}}{\int }_{0}^{\mathrm{\Delta }t}I(\tau \left)\mathrm{d}\tau \right]{a}_{\mathrm{u}}+\end{array}\\ {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{B}\mathrm{a}\mathrm{t}}(t+\mathrm{\Delta }t)\left[{S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{B}\mathrm{a}\mathrm{t}}\right(t+\mathrm{\Delta }t)-\\ {\int }_{0}^{\mathrm{\Delta }t}I{\left(\tau \right)\mathrm{d}\tau ]}^{-1}K\end{array}$
(5) ${Q}_{\mathrm{B}\mathrm{a}\mathrm{t}}(t+\mathrm{\Delta }t)={Q}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)-{\int }_{0}^{\mathrm{\Delta }t}I\left(\tau \right)({\eta }_{\mathrm{B}\mathrm{a}\mathrm{t}}^{-1},{\eta }_{\mathrm{B}\mathrm{a}\mathrm{t}})d\tau $
(6) ${Q}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=0.3{\mathrm{e}}^{-1400/{T}_{\mathrm{B}\mathrm{a}\mathrm{t}}}{l}_{\mathrm{h}}^{0.6}$
(7) ${S}_{\mathrm{S}\mathrm{O}\mathrm{H},\mathrm{B}\mathrm{a}\mathrm{t}}=1-{Q}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}/{Q}_{\mathrm{n}}$
式中:${S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻荷电状态;Qn 为电池额定容量;${\eta }_{\mathrm{B}\mathrm{a}\mathrm{t}}$ ${\eta }_{\mathrm{B}\mathrm{a}\mathrm{t}}^{-1}$ ${E}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻电池电动势;${T}_{\mathrm{B}\mathrm{a}\mathrm{t}}$ au 为电压变化系数;bc 为容量变化系数;K 为极化电压系数;Ct 为极化效应系数;${Q}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻容量;$I\left(\tau \right)$ ${Q}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$ lh 为$\Delta t$ ${S}_{\mathrm{S}\mathrm{O}\mathrm{H},\mathrm{B}\mathrm{a}\mathrm{t}}$
1.2.3 超级电容器模型
超级电容器在储能系统中具有响应速度快、能够进行频率调节和峰值削减、循环次数和响应速率远大于蓄电池等优点[7 ] .综合上述优点,可以利用其承担混储系统功率任务的高频分量.本文更关注超级电容在系统中的电气特性,其数学模型表达式如下:
(8) $ {Q}_{\mathrm{s}\mathrm{c}}(t+\mathrm{\Delta }t)={Q}_{\mathrm{s}\mathrm{c}}\left(t\right)-{\int }_{0}^{\mathrm{\Delta }t}{I}_{\mathrm{s}\mathrm{c}}\left(\tau \right)({\eta }_{\mathrm{s}\mathrm{c}}^{-1},{\eta }_{\mathrm{s}\mathrm{c}})d\tau $
式中:${Q}_{\mathrm{s}\mathrm{c}}\left(t\right)$ t 时刻超级电容容量;${I}_{\mathrm{s}\mathrm{c}}\left(\tau \right)$ ${\eta }_{\mathrm{s}\mathrm{c}}$ ${\eta }_{\mathrm{s}\mathrm{c}}^{-1}$
(9) $\begin{array}{l} {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{s}\mathrm{c}}(t+\mathrm{\Delta }t)=\\ {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{s}\mathrm{c}}\left(t\right)-\frac{1}{{Q}_{\mathrm{s}\mathrm{c},\mathrm{n}}}{\int }_{0}^{\mathrm{\Delta }t}{I}_{\mathrm{s}\mathrm{c}}\left(\tau \right)({\eta }_{\mathrm{s}\mathrm{c}}^{-1},{\eta }_{\mathrm{s}\mathrm{c}})d\tau \end{array}$
式中:${S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{s}\mathrm{c}}\left(t\right)$ t 时刻荷电状态;${Q}_{\mathrm{s}\mathrm{c},\mathrm{n}}$
1.3 约束条件
为了保证风电混储系统安全工作,蓄电池和超级电容在运行过程中需满足以下约束,具体公式如下所示:
(10) $\mathrm{s}.\mathrm{t}\left\{\begin{array}{l}0\le \left|{P}_{\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)\right|\le {U}_{\mathrm{s}}\left(t\right){P}_{\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{m}\mathrm{a}\mathrm{x}}\\ 0\le \left|{P}_{\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{c}\mathrm{h}}\left(t\right)\right|\le (1-{U}_{\mathrm{s}}(t\left)\right){P}_{\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{m}\mathrm{a}\mathrm{x}}\\ {Q}_{\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{m}\mathrm{i}\mathrm{n}}\le {Q}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)\le {Q}_{\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{m}\mathrm{a}\mathrm{x}}\\ {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{m}\mathrm{i}\mathrm{n}}\le {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)\le {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{m}\mathrm{a}\mathrm{x}}\end{array}\right.$
(11) $\mathrm{s}.\mathrm{t}\left\{\begin{array}{l}0\le \left|{P}_{\mathrm{s}\mathrm{c},\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)\right|\le {U}_{\mathrm{s}}\left(t\right){P}_{\mathrm{s}\mathrm{c},\mathrm{m}\mathrm{a}\mathrm{x}}\\ 0\le \left|{P}_{\mathrm{s}\mathrm{c},\mathrm{c}\mathrm{h}}\left(t\right)\right|\le (1-{U}_{\mathrm{s}}(t\left)\right){P}_{\mathrm{s}\mathrm{c},\mathrm{m}\mathrm{a}\mathrm{x}}\\ {Q}_{\mathrm{s}\mathrm{c},\mathrm{m}\mathrm{i}\mathrm{n}}\le {Q}_{\mathrm{s}\mathrm{c}}\left(t\right)\le {Q}_{\mathrm{s}\mathrm{c},\mathrm{m}\mathrm{a}\mathrm{x}}\\ {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{s}\mathrm{c},\mathrm{m}\mathrm{i}\mathrm{n}}\le {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{s}\mathrm{c}}\left(t\right)\le {S}_{\mathrm{S}\mathrm{O}\mathrm{C},\mathrm{s}\mathrm{c},\mathrm{m}\mathrm{a}\mathrm{x}}\end{array}\right.$
式中:P Bat,max 、P sc,max 分别为蓄电池和超级电容充放电功率限值;${P}_{\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{c}\mathrm{h}}\left(t\right)$ ${P}_{\mathrm{B}\mathrm{a}\mathrm{t},\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)$ t 时刻充放电功率;${P}_{\mathrm{s}\mathrm{c},\mathrm{c}\mathrm{h}}\left(t\right)$ ${P}_{\mathrm{s}\mathrm{c},\mathrm{d}\mathrm{i}\mathrm{s}}\left(t\right)$ t 时刻充放电功率;Us (t) 为充放电状态,放电时其值为1,反之为0;S SOC,min 、S SOC,max 为对应储能单元荷电状态的下限和上限;Q min 、Q max 为对应储能单元容量的下限和上限.
针对混合储能系统中各储能元件的工作特性,为了保证风电能够在合理的条件下并网又要保证混合储能系统的功率能够得到合理的分配,避免过充过放,提出基于变分模态分解-多模糊控制的风电混储系统功率分配策略.
2 基于变分模态分解-多模糊控制的风电混储系统功率分配策略
2.1 基于正余弦算法优化的VMD初次功率分配策略
2.1.1 变分模态分解
针对风电出力的波动性与不稳定性,引入变分模态分解法分解原始风电信号,来获得符合条件的并网分量和初次混合储能功率任务,具体计算过程如下.
(1) 构建约束变分模型.将原始信号Y(t) 分解为S 个模态函数us (t) ,每个模态都对应一个独立的中心频率${\omega }_{s}$ us (t) 之和等于原始信号为约束,以us (t) 估计带宽和最小为目标,构建约束变分模型如下:
(12) $\left.\begin{array}{l}\underset{\left\{{u}_{s}\right\},\left\{{\omega }_{s}\right\}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left\{\stackrel{S}{\sum _{s=1}}{\left({\partial }_{t}\left[\left(\delta \left(t\right)+\frac{\mathrm{j}}{\mathrm{\pi }t}\right)\mathrm{*}{u}_{s}\left(t\right)\right]{\mathrm{e}}^{-\mathrm{j}{\omega }_{s}t}\right)}_{2}^{2}\right\}\\ \mathrm{s}.\mathrm{t}\stackrel{S}{\sum _{s=1}}{u}_{s}\left(t\right)=Y\left(t\right)\end{array}\right\}$
式中:${\partial }_{t}$ $\delta \left(t\right)$ $\left\{{u}_{s}\right\}$ $\left\{{\omega }_{s}\right\}$
(2) 求解模型.通过引入二次惩罚因子$\alpha $ $\lambda \left(t\right)$
(13) ${\hat{u}}_{s,n+1}\left(\omega \right)=\frac{\hat{Y}\left(\omega \right)-\sum _{i\ne s}{\hat{u}}_{i}\left(\omega \right)+\hat{\lambda }\left(\omega \right)\mathrm{*}0.5}{2\alpha (\omega -{\omega }_{s}{)}^{2}+1}$
(14) ${\omega }_{s,n+1}={\int }_{0}^{\infty }\omega |{\hat{u}}_{s}(\omega ){|}^{2}\mathrm{d}\omega \mathrm{*}({\int }_{0}^{\infty }|{\hat{u}}_{s}\left(\omega \right){|}^{2}\mathrm{d}\omega ){}^{-1}$
式中:n 为迭代次数;$\mathrm{ }{\hat{u}}_{s,n+1}$ s 个模态分量更新后频域,$\omega $ ${\omega }_{s,n+1}$ s 个模态分量的更新频率;$\mathrm{ }\hat{Y}\left(\omega \right)$ ${\hat{u}}_{i}\left(\omega \right)$ $\hat{\lambda }\left(\omega \right)$ i 个模态分量、拉格朗日乘子对应的频域.
(15) $\begin{array}{c}\stackrel{S}{\sum _{s=1}}\frac{\left({\hat{u}}_{s,n+1}-{\hat{u}}_{s,n}\right)}{\left({\hat{u}}_{s,n}\right)}<q\end{array}$
式中:q 为判断精度,q >0.若满足判别精度式(15)之后停止迭代,最后得到原始功率分解后的S 个窄带模态分量.
2.1.2 正余弦算法优化的变分模态分解
针对VMD存在过分解、欠分解、波段信息丢失的问题,提出用正余弦算法( sine cosine algorithm,SCA)优化VMD的模态分解数S 和二次惩罚因子α .
SCA算法以正弦和余弦函数为基础,其迭代过程分为全局探索和局部开发,通过正弦和余弦函数相互协作搜索,以寻找全局最佳解,其中决策变量$X={\left[S\alpha \right]}^{\mathrm{T}}$
(16) $\begin{array}{l}{X}_{j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}+1}=\\ \left\{\begin{array}{l}{X}_{j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}+{\omega }_{1}\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_{2}\right)\left|{\omega }_{3}{X}_{\mathrm{p}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t},j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}-{X}_{j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}\right|,\\ {\omega }_{4}\ge 0.5\\ {X}_{j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}+{\omega }_{1}\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{2}\right)\left|{\omega }_{3}{X}_{\mathrm{p}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t},j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}-{X}_{j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}\right|,\\ {\omega }_{4}<0.5\end{array}\right.\end{array}$
式中:ω 1 为幅度参数,当值较大时,SCA偏向于全局搜索,反之则倾向于局部开发;ω 2 为周期参数,用来调整粒子的搜索方向和距离,ω 2 ∈[0,2π];${\omega }_{3}$ ${\omega }_{3}>1$ ${\omega }_{3}\in \left[-\mathrm{2,2}\right]$ ${\omega }_{4}$ ${\omega }_{4}\in \left[\mathrm{0,1}\right]$ ${I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}$ j 为种群第j 个体;${X}_{\mathrm{p}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t},j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}}$ ${I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}$ j 最佳位置;${X}_{j,{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}+1}$ j 在第${I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}+1$
(17) $\begin{array}{c}{\omega }_{1}=\theta -\frac{\theta }{{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r},\mathrm{m}\mathrm{a}\mathrm{x}}}{I}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}\end{array}$
其中,风电功率初次分配策略流程图如图2 所示.具体步骤对应如下:首先,依据最优S ,α 对原始信号进行变分模态分解,得到IMF分量和残差信号(residual,res);将分量进行重构,令k 从1取到S ,分别求出对应k 时的高频重构(fine to coarse,f2c)分量和低频重构分量(coarse to fine,c2f)[8 -9 ] ;当k=1 ,计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k 值,判断k 是否为最低阶分量,若是则无并网功率,全部需要储能系统进行平抑,循环结束;若不是,令k=k+1 并计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k=1 ,则直接结束;若$k\ne 1$ k 值,计算对应k 值的并网分量和混合储能系统所需要的功率,其中功率分配表达式如下:
(18) $ \left.\begin{array}{l}{P}_{\mathrm{G}}=\mathrm{c}2\mathrm{f}\left(\mathrm{k}\right), {P}_{\mathrm{H}\mathrm{e}\mathrm{s}\mathrm{s}}=\mathrm{f}2\mathrm{c}(\mathrm{S}-\mathrm{k}+1)\\ {P}_{\mathrm{s}\mathrm{c}}=\stackrel{h}{\sum _{v=1}}{u}_{v}\left(t\right), {P}_{\mathrm{B}\mathrm{a}\mathrm{t}}=\stackrel{v-1}{\sum _{v=h+1}}{u}_{v}\left(t\right)\end{array}\right\}$
式中:P G 为系统的直接并网分量;P Hess 为混合储能系统的功率分量;uv (t )为P Hess 在SCA-VMD分解后的功率分量,按式(18)对其进行高低频重构,其中h 为功率分量的高频与中低频分界点,经重构得到式中P sc 和P Bat .
图2
图2
风电功率初次分配策略流程图
Fig.2
Flow chart of initial wind power allocation strategy
风电并网波动量定义为:规定时间间隔内最大功率与最小功率之差满足10 min并网波动量限值,该值通常为风电装机容量的5%~7.5%[8 ] .
2.2 计及混合储能系统特性的多模糊功率再分配策略
风电初次分配策略仅从频率特性角度出发,未考虑超级电容和蓄电池的荷电状态和荷电状态变化量对功率分配的影响[10 -11 ] .因此,将上述影响考虑在内,利用多模糊控制修正混合储能系统的功率.
单模糊控制策略没有对超级电容和蓄电池的荷电状态进行分区考虑,且单模糊控制器具有精度不高、难以调参、鲁棒性差等问题.因此,对混合储能系统的荷电状态进行动态分区并考虑混合储能特性,针对不同区间采用不同模糊控制器修正超级电容和蓄电池的功率.控制原理图如图3 所示.其中,功率二次分配中的多模糊控制器中均包含3个双输入单输出的单模糊控制器.输入为S SOC 和ΔS SOC ,其中S SOC 的基本论域为[0,1],模糊控制集为{VS、S、MS、M、MB、B、VB},分别代表很小、小、中等偏小、中等、中等偏大、大、很大;ΔS soc 的基本论域为[-1,1];模糊集为{NB、NM、NS、PS、PM、PB},分别代表负大、负中、负小、正小、正中、正大.输出为功率修正系数k 1 、k 2 ,基本论域为[0,1],模糊集为{VS、S、MS、M、MB、B、VB}.图中P 为功率.每个控制器均服从相同的模糊控制规则,其中规则如表1 所示.
图3
图3
功率二次分配策略图
Fig.3
Power secondary allocation strategy
以优化超级电容的多模糊控制为例来展示其中的3个模糊控制器的输入隶属函数以及输入与输出之间关系的三维曲面图,如图4 所示.
图4
图4
各模糊控制器输入相对应的隶属函数及其对应输出3D图
Fig.4
Relative affiliation function of each fuzzy controller input and corresponding output 3D plot
设计多模糊控制器时,针对S SOC 的分区情况,对各区间选择合适的模糊控制器,实现对混合储能系统S SOC 的动态分区控制.当设置模糊控制器中隶属函数斜率较高时,系统会针对输入量的微小变化而做出调节;当设置模糊控制器中隶属函数斜率较为平缓时,系统会针对输入量的较大变化范围而做出调节.
根据荷电状态的动态分区修正混合储能系统的功率.具体修正原则如下:当超级电容的S SOC 维持在合理范围内时,可维持初次分配策略.当S SOC,sc 低于超级电容S SOC 下限且ΔS SOC 小于0时,或者S SOC,sc 超过超级电容S SOC 上限时且ΔS SOC,sc 大于0时,需要对混合储能系统进行修正;另外,超级电容修正前后的功率变化量由蓄电池进行辅助补充或吸收,在此过程中利用多模糊控制器对蓄电池进行控制,以保证蓄电池的荷电状态维持在合理变化范围内.修正后的功率分别为P 'sc 和P 'Bat .
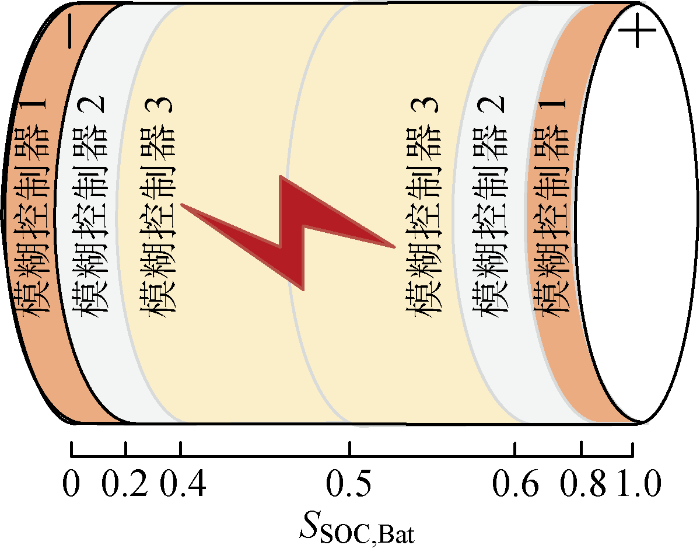
基于上述思想,首先对超级电容和蓄电池的S SOC 进行动态分区,然后根据S SOC 分区选择合适的模糊控制器.其中,超级电容、蓄电池荷电状态的允许波动范围分别应为[0.1,0.9]、[0.2,0.8],且超级电容与蓄电池荷电状态的动态分区规则如图5 和图6 所示.
图5
图5
S SOC,sc 的动态分区规则
Fig.5
Dynamic partitioning rules for S SOC,sc
图6
图6
S SOC,Bat 的动态分区规则
Fig.6
Dynamic partitioning rules for S SOC,Bat
对混合储能系统来说,当S SOC,sc 处于[0,0.1],[0.9,1]与S SOC,Bat 处于[0,0.2],[0.8,1]时,二者采用控制器1进行调节,以实现对功率的快速调节,使其恢复到合理范围以内;当S SOC,sc 与S SOC,Bat 均处于[0.4,0.6]时,二者采用控制器3进行调节,使其继续保持在最佳工作范围;当S SOC,sc 处于[0.1,0.4],[0.6,0.9]与S SOC,Bat 处于[0.2,0.4],[0.6,0.8]时,二者采用控制器2进行调节,其目的是既要避免荷电状态越界现象,又要动态调整荷电状态使其维持在合理范围内.
3 算例分析
3.1 基础数据
以我国西部某风电场2023年每天中的每5 min 实际风速${v}_{r,d}\left(r=\mathrm{1,2}\dots,M;d=\mathrm{1,2},\dots,288\right)$ M ,其中M=365 .由于Weibull分布对风速概率分布的拟合最为精确[18 ] ,所以以测得的历史数据为基础,结合Weibull分布得到每一观测时刻的风速概率密度函数、概率分布函数以及每一时刻概率分布反函数.
在此基础上,首先采用拉丁超立方抽样算法生成风电场景,具体步骤是:利用分层抽样思想,将每一观测时刻概率分布函数的取值范围分布成M 个等概率子区域;在每个概率子区域内随机选取一个采样值;然后根据反函数计算每一采样值下所对应的风速,最后根据式(2)得到对应的风电出力情况,其生成场景如图7(a) 所示,规定图中每个时刻为5 min,后续同理.依据该地风电场实际情况设置式(2)中v min =3 m/s、 v n =10.5 m/s、 v max =20 m/s.由于生成场景中并非每一组风电数据都符合实际需求[19 ] ,所以采用欧氏距离法削减相似场景,最终得到10个风电典型出力场景,其典型场景情况如图7(b) 所示,典型场景对应概率和天数情况如表2 所示.
图7
图7
场景分析结果
Fig.7
Scenario analysis results
3.2 功率初次分配
选取场景6数据作为风电数据,如图8(a) 所示,其中风电装机容量为706.3 kW.根据装机容量应选取10 min风电并网波动量限值为50 kW.设置SCA优化变分模态分解时的迭代次数为200,种群大小为100,根据优化后的$S、\alpha $ 图8(b) 所示,因此选择c2f(5)作直接并网分量,即res+IMF(6)+IMF(5)+IMF(4)+IMF(3);f2c(2)作为初次混储系统的功率任务.最后,对比改进前后VMD所得并网分量以验证策略有效性,结果如图8(c) 所示.
图8
图8
风电数据与其低频分量重构结果
Fig.8
Reconstruction results of wind power data with its low frequency components
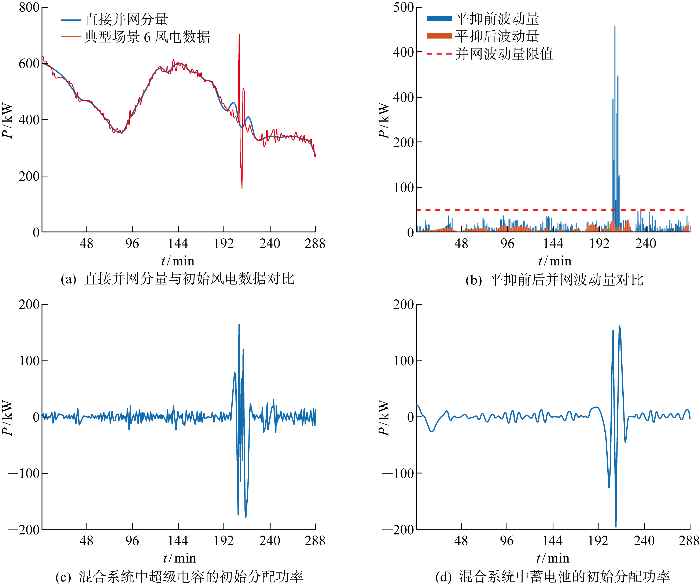
根据初次分配结果,可得混合储能系统的参数配置情况,如表3 所示.图9(a)~9(d) 分别为直接并网分量与初始风电数据对比、平抑后与平抑前并网波动量对比、混合储能系统中超级电容的初次分配功率以及蓄电池的初次分配功率.
图9
图9
功率初次分配结果图
Fig.9
Results of initial distribution of power
分析表明,采用SCA-VMD方法处理原始风电信号,能够有效平抑风电波动,提升并网质量;同时,蓄电池主要承担波动较为平滑的低频功率部分,而超级电容则负责应对充放电波动频繁、瞬时幅值较大的高频功率部分,该分配结果符合混合储能元件的特性.
3.3 功率二次分配
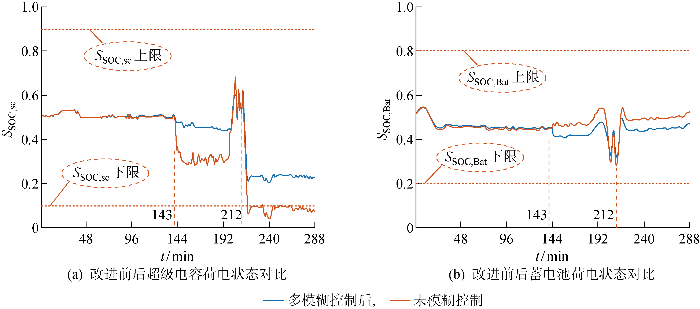
初次分配后,可以得到超级电容和蓄电池的S SOC 变化曲线如图10 所示.为了弥补功率初次分配后混合储能系统容易出现S SOC 越限的问题,采用多模糊控制策略修正初次分配功率.
图10
图10
修正前后混合储能系统荷电状态变化对比
Fig.10
Comparison of change in S SOC of hybrid energy storage system before and after correction
由图10 可知,基于动态分区下的修正规则下,在[1,142]时刻,储能系统的S SOC 均维持在[0.4,0.6]内,此时采用隶属函数斜率最缓的控制器3调节系统,以保证系统的功率分配情况维持初次分配结果.在[143,212]时刻,超级电容的S SOC,sc 处于限值内的最佳工作范围外,为了避免S SOC,sc 越限且尽可能让其恢复到最佳工作范围内,需要选取调节力度适中的控制器2对其进行调节,此过程的调节功率需蓄电池承担.在[212,288]时刻,当超级电容S SOC,sc 出现越限情况且ΔS SOC,sc 发生急剧变化时,需要控制器能做出迅速调节以使系统恢复到合理工作范围内,因此该状况下应采用隶属函数斜率最高的控制器1对其进行控制,在此过程中超级电容的调节功率也由蓄电池进行出力或消纳;同时,蓄电池工作时刻均采用多模糊控制器对蓄电池功率进行不断修正,以此实现二者之间的互补.
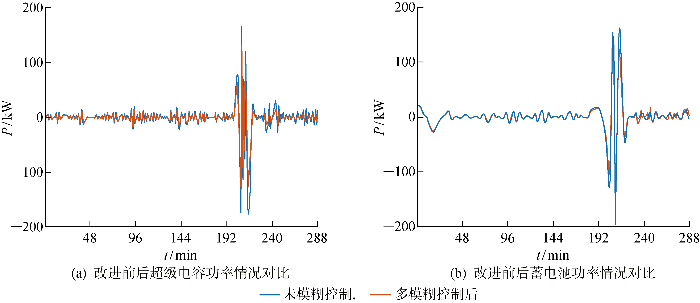
图11 是修正前后的超级电容和蓄电池的功率情况对比.由图可见,在基于多模糊策略的控制下,在[1,142]时刻,储能系统的S SOC 处于最佳工作范围,此时系统的出力维持初次分配结果;在[143,288] 时刻,对混合储能系统的功率进行了修正,有效减小了混合储能系统的功率波动范围并使系统工作在安全范围内.
图11
图11
修正前后混合储能系统功率情况对比
Fig.11
Comparison of power cases of hybrid energy storage systems before and after correction
功率二次分配后,超级电容的S SOC,sc 能够维持在较好的工作范围内,蓄电池在进行辅助任务时S SOC,Bat 也能保持稳定,混合储能S SOC 越限问题得到了很好的修正;其次,混合储能系统的功率波动范围有效减小,保证了混合储能系统能够安全稳定运行.
4 结论
考虑风电的随机性与波动性对混合储能系统特性与并网电能质量的影响,提出基于变分模态分解-多模糊控制的风电混储系统功率分配策略.经过实例分析,该策略不仅可以更好地平抑风电,而且也能保证混合储能系统安全可靠工作,结论如下:
(1) 考虑到风电的不确定性,利用基于拉丁超立方抽样和欧氏距离的场景分析法,能够得到不受极端因素影响的典型目标场景.
(2) 利用正余弦算法优化的变分模态分解能够避免变分模态分解的过分解、欠分解问题,完成对风电功率的初次分配,并根据并网波动量限值得到直接并网分量和混合储能的初次功率任务,能更好地平抑风电.
(3) 综合考虑混合储能出力特性,采用多模糊控制策略和荷电状态的动态分区规则修正混合储能系统容易出现过充过放的缺点,该过程中蓄电池起到辅助任务.该种策略下实现了功率型储能元件和能量型储能元件互补调节,使其修正后的混合储能系统功率波动范围有效减小,并保证了混合储能系统的SOC均在合理范围内变化.
参考文献
View Option
[1]
李建林 , 张则栋 , 梁策 , 等 . 计及源-荷不确定性的综合能源系统多目标鲁棒优化调度
[J/OL]. 上海交通大学学报 https://doi.org/10.16183/j.cnki.jsjtu.2023.238 .
URL
[本文引用: 2]
LI Jianlin ZHANG Zedong LIANG Ce et al . Multi-objective robust optimal scheduling of integrated energy systems taking into account source-load uncertainty
[J/OL]. Journal of Shanghai Jiao Tong University https://doi.org/10.16183/j.cnki.jsjtu.2023.238 .
URL
[本文引用: 2]
[2]
袁小明 , 程时杰 , 文劲宇 . 储能技术在解决大规模风电并网问题中的应用前景分析
[J]. 电力系统自动化 2013 , 37 (1 ): 14 -18 .
[本文引用: 1]
YUAN Xiaoming CHENG Shijie WEN Jinyu . Prospects analysis of energy storage application in grid integration of large-scale wind power
[J]. Automation of Electric Power Systems 2013 , 37 (1 ): 14 -18 .
[本文引用: 1]
[3]
林森 , 文书礼 , 朱淼 , 等 . 考虑碳交易机制的海港综合能源系统电-热混合储能优化配置
[J]. 上海交通大学学报 2024 , 58 (9 ): 1344 -1356 .
DOI:10.16183/j.cnki.jsjtu.2022.428
[本文引用: 1]
随着港口电气化进程逐渐加速,单一的港口供能方式正在向多种能源深度融合演变.为响应我国“碳达峰、碳中和”战略目标,进一步提升海港综合能源系统的经济与环境双重效益,提出一种考虑碳交易机制的电-热混合式储能优化配置方案.首先,建立海港综合能源系统模型,并给出计及碳交易市场的交易方案;其次,构建双层优化配置框架,上层优化配置混合式储能容量,下层引入碳交易机制,满足港口综合能源系统低碳经济运行需求;最后,结合网格自适应直接搜索法与自适应混沌粒子群算法优势,利用混合式优化算法对双层优化模型进行求解.以天津港的实际运行数据为例,验证该方法的有效性.算例结果表明,所提方法不仅可以降低系统的投入成本,还能显著减少港区碳排放,从而进一步提升港口经济和环境效益.
LIN Sen WEN Wenli ZHU Miao et al . Optimal allocation of hybrid electric-thermal energy storage for harbour integrated energy system considering carbon trading mechanism
[J]. Journal of Shanghai Jiao Tong University 2024 , 58 (9 ): 1344 -1356 .
[本文引用: 1]
[4]
赵永熹 , 高鹏超 , 范宏 . 基于虚拟阻抗-模糊算法的交直流微电网混合储能功率协调策略
[J/OL]. 上海交通大学学报 https://doi.org/10.16183/j.cnki.jsjtu.2023.308 .
URL
ZHAO Yongxi GAO Pengchao FAN Hong . Hybrid energy storage power coordination strategy for AC/DC microgrid based on virtual impedance-fuzzy algorithm
[J/OL]. Journal of Shanghai Jiao Tong University https://doi.org/10.16183/j.cnki.jsjtu.2023.308 .
URL
[5]
李建林 , 李雅欣 , 刘海涛 , 等 . 计及储能电站安全性的功率分配策略研究
[J]. 电工技术学报 2022 , 37 (23 ): 5976 -5986 .
LI Jianlin LI Yaxin LIU Haitao et al . Research on power distribution strategy considering the safety of energy storage power station
[J]. Transactions of China Electrotechnical Society 2022 , 37 (23 ): 5976 -5986 .
[6]
乔亮波 , 张晓虎 , 孙现众 , 等 . 电池-超级电容器混合储能系统研究进展
[J]. 储能科学与技术 2022 , 11 (1 ): 98 -106 .
DOI:10.19799/j.cnki.2095-4239.2021.0229
[本文引用: 2]
储能是解决可再生能源大规模发电并网、推动新能源汽车发展、实现“碳达峰”“碳中和”中长期目标的关键支撑技术。能量型储能器件与功率型储能器件组成的混合储能系统是能量管理和功率管理的高效系统,充分发挥了能量型储能的持久性和功率型储能的快速性,大幅提升了储能系统的综合性能和经济性。本文概述了能量型和功率型电化学储能技术及特点,总结了各类电池-超级电容器混合储能系统,分析了混合储能系统在电网储能、新能源汽车、轨道交通等领域的应用。详细分析了电池-超级电容器混合储能系统关键技术,包括混合储能系统控制和能量管理,总结了近期较为常见的混合储能系统使用的控制方法;混合储能系统的参数匹配和技术经济性进行分析;介绍了混合储能系统拓扑结构分类,并讨论各种拓扑结构的优缺点。此外,还对电池-超级电容器混合储能系统和单一储能系统进行了仿真对比,验证了混合储能系统相较于单一储能系统的优越性。最后,对电池-超级电容器混合储能系统进行了总结和展望。
QIAO Liangbo ZHANG Xiaohu SUN Xianzhong et al . Advances in battery-supercapacitor hybrid energy storage system
[J]. Energy Storage Science & Technology 2022 , 11 (1 ): 98 -106 .
[本文引用: 2]
[7]
蒋新科 , 刘春 , 张雪松 , 等 . 基于双储能的风电功率波动平抑策略研究
[J/OL]. 电测与仪表
URL
[本文引用: 2]
JIANG Xinke LIU Chun ZHANG Xuesong et al . Research on wind power fluctuation smoothing strategy based on dual energy storage
[J/OL]. Electrical Measurement & Instrumentation
URL
[本文引用: 2]
[8]
韩晓娟 , 田春光 , 程成 , 等 . 基于经验模态分解的混合储能系统功率分配方法
[J]. 太阳能学报 2014 , 35 (10 ): 1889 -1896 .
[本文引用: 3]
HAN Xiaojuan TIAN Chunguang CHENG Cheng et al . Power allocation method of hybrid energy storage system based on empirical mode decomposition
[J]. Acta Energiae Solaris Sinica 2014 , 35 (10 ): 1889 -1896 .
[本文引用: 3]
[9]
付菊霞 , 陈洁 , 邓浩 , 等 . 平抑风电波动的混合储能系统控制策略
[J]. 电测与仪表 2020 , 57 (5 ): 94 -100 .
[本文引用: 2]
FU Juxia CHEN Jie DENG Hao et al . Control strategy of hybrid energy storage system for mitigating wind power fluctuations
[J]. Electrical Measurement & Instrumentation 2020 , 57 (5 ): 94 -100 .
[本文引用: 2]
[10]
杨锡运 , 曹超 , 李相俊 , 等 . 基于模糊经验模态分解的电池储能系统平滑风电出力控制策略
[J]. 电力建设 2016 , 37 (8 ): 134 -140 .
DOI:10.3969/j.issn.1000-7229.2016.08.021
[本文引用: 2]
为减少风电波动率,提高并网可靠性,提出一种基于模糊经验模态分解(empirical mode decomposition,EMD)的储能系统平滑风电功率波动的控制策略。采用经验模态分解对风电功率进行滤波,低频分量并网,高频分量并入电池储能系统(battery energy storage system,BESS)。使用平滑后风电波动率和储能电池荷电状态(state of charge,SOC)作为约束条件,利用模糊控制算法,自适应在线调整EMD滤波阶数,通过模糊自适应控制器,能够更好地平滑风电波动。对比其他平抑风电功率储能控制策略,仿真实例表明,该方法可以有效地平抑风电功率波动,避免储能电池过充过放,稳定储能荷电状态。
YANG Xiyun CAO Chao LI Xiangjun et al . Control strategy of smoothing wind power output using battery energy storage system based on fuzzy empirical mode decomposition
[J]. Electric Power Construction 2016 , 37 (8 ): 134 -140 .
DOI:10.3969/j.issn.1000-7229.2016.08.021
[本文引用: 2]
To reduce the fluctuation rate of wind power and improve the reliability of grid, this paper proposes a control method of smoothing wind power output with battery energy storage system based on fuzzy empirical mode decomposition (EMD). Wind power is decomposed by EMD into two parts, the low-frequency part is used as wind power grid-connected value and the high-frequency part is stored by battery energy storage system (BESS). Taking the fluctuation rate of wind power output after smoothing and the state of charge (SOC) as constraints, the orders of EMD filter can be adaptively adjusted on-line based on fuzzy control method, which can smooth wind power fluctuation better through fuzzy adaptive controller. Compared with another energy storage system control strategies for smoothing wind power, the simulation results show that the proposed method can effectively smooth the fluctuation of winds power output and avoid the over-charging and over-discharging of energy storage system so as to keep SOC stable.
[11]
郭志彬 . 基于模糊控制的光储联合系统控制策略研究 [D]. 沈阳 : 沈阳农业大学 , 2023 .
[本文引用: 2]
GUO Zhibin . Research on control strategy of optical storage joint system based on fuzzy control [D]. Shenyang : Shenyang Agricultural University , 2023 .
[本文引用: 2]
[12]
陈洪磊 , 孙泽贤 . 模糊控制下混合储能平抑风电波动控制策略
[J]. 低温与超导 2023 , 51 (7 ): 82 -89 .
[本文引用: 1]
CHEN Honglei SUN Zexian . Hybrid energy-storage control strategy based on fuzzy control to stabilize wind power fluctuation
[J]. Cryogenics & Superconductivity 2023 , 51 (7 ): 82 -89 .
[本文引用: 1]
[13]
程龙 , 张方华 . 用于混合储能系统平抑功率波动的小波变换方法
[J]. 电力自动化设备 2021 , 41 (3 ): 100 -104 .
[本文引用: 1]
CHENG Long ZHANG Fanghua . Wavelet transform method for hybrid energy storage system smoothing power fluctuation
[J]. Electric Power Automation Equipment 2021 , 41 (3 ): 100 -104 .
[本文引用: 1]
[14]
陈景文 , 周婧 , 张文倩 . 基于小波包-模糊算法的混合储能功率分配策略
[J]. 智慧电力 2023 , 51 (1 ): 61 -68 .
CHEN Jingwen ZHOU Jing ZHANG Wenqian . Hybrid energy storage power allocation strategy based on wavelet packet-fuzzy algorithm
[J]. Smart Power 2023 , 51 (1 ): 61 -68 .
[15]
毛志宇 , 李培强 , 郭思源 . 基于自适应时间尺度小波包和模糊控制的复合储能控制策略
[J]. 电力系统自动化 2023 , 47 (9 ): 158 -165 .
[本文引用: 1]
MAO Zhiyu LI Peiqiang GUO Siyuan . Control strategy of composite energy storage based on wavelet packet with adaptive time scale and fuzzy control
[J]. Automation of Electric Power Systems 2023 , 47 (9 ): 158 -165 .
[本文引用: 1]
[16]
LI Y M DING Z M YU Y H et al . Hybrid energy storage power allocation strategy based on parameter-optimized VMD algorithm for marine micro gas turbine power system
[J]. Journal of Energy Storage 2023 , 73 : 109189 .
[本文引用: 1]
[17]
李亚楠 , 王倩 , 宋文峰 , 等 . 混合储能系统平滑风电出力的变分模态分解-模糊控制策略
[J]. 电力系统保护与控制 2019 , 47 (7 ): 58 -65 .
[本文引用: 1]
LI Yanan WANG Qian SONG Wenfeng et al . Variational mode decomposition and fuzzy control strategy of hybrid energy storage for smoothing wind power outputs
[J]. Power System Protection & Control 2019 , 47 (7 ): 58 -65 .
[本文引用: 1]
[18]
车兵 , 李轩 , 郑建勇 , 等 . 基于LHS与BR的风电出力场景分析研究
[J]. 电力工程技术 2020 , 39 (6 ): 213 -219 .
[本文引用: 2]
CHE Bing LI Xuan ZHENG Jianyong et al . Scenario analysis of wind power output based on LHS and BR
[J]. Electric Power Engineering Technology 2020 , 39 (6 ): 213 -219 .
[本文引用: 2]
[19]
鲍俊文 , 胡欣宇 , 邢明源 , 等 . 可靠度分析中拉丁超立方和传统舍选抽样法对比研究
[J]. 华北科技学院学报 2021 , 18 (3 ): 81 -84 .
[本文引用: 2]
BAO Junwen HU Xinyu XING Mingyuan et al . Comparing LHS with traditional rejection sampling methods in the analysis of reliability
[J]. Journal of North China Institute of Science & Technology 2021 , 18 (3 ): 81 -84 .
[本文引用: 2]
计及源-荷不确定性的综合能源系统多目标鲁棒优化调度
2
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
... 风电混储系统结构图如图1 所示.为应对风电的随机性、波动性与“弃风”现象[1 ] ,在交流母线处集中配置混合储能系统, 并经电力电子器件与风电机组组合为风电混储系统.图中:${P}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\left(t\right)$ t 时刻风电输出功率;${P}_{\mathrm{H}\mathrm{e}\mathrm{s}\mathrm{s}}\left(t\right)$ t 时刻混合储能系统的充电或者放电功率;PG (t) 为t 时刻风电并网功率;${P}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻蓄电池的充电或者放电功率;${P}_{\mathrm{s}\mathrm{c}}\left(t\right)$ t 时刻超级电容的充电或者放电功率;$P{\text{'}}_{\mathrm{s}\mathrm{c}}\left(t\right)$ t 时刻功率修正后的超级电容的功率;$P{\text{'}}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻功率修正后蓄电池的功率;AC、DC分别表示交流、直流电.规定充电时功率为正,放电时功率为负.根据图1 中的功率关系,建立如下表达式: ...
Multi-objective robust optimal scheduling of integrated energy systems taking into account source-load uncertainty
2
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
... 风电混储系统结构图如图1 所示.为应对风电的随机性、波动性与“弃风”现象[1 ] ,在交流母线处集中配置混合储能系统, 并经电力电子器件与风电机组组合为风电混储系统.图中:${P}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\left(t\right)$ t 时刻风电输出功率;${P}_{\mathrm{H}\mathrm{e}\mathrm{s}\mathrm{s}}\left(t\right)$ t 时刻混合储能系统的充电或者放电功率;PG (t) 为t 时刻风电并网功率;${P}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻蓄电池的充电或者放电功率;${P}_{\mathrm{s}\mathrm{c}}\left(t\right)$ t 时刻超级电容的充电或者放电功率;$P{\text{'}}_{\mathrm{s}\mathrm{c}}\left(t\right)$ t 时刻功率修正后的超级电容的功率;$P{\text{'}}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(t\right)$ t 时刻功率修正后蓄电池的功率;AC、DC分别表示交流、直流电.规定充电时功率为正,放电时功率为负.根据图1 中的功率关系,建立如下表达式: ...
储能技术在解决大规模风电并网问题中的应用前景分析
1
2013
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
Prospects analysis of energy storage application in grid integration of large-scale wind power
1
2013
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
考虑碳交易机制的海港综合能源系统电-热混合储能优化配置
1
2024
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
Optimal allocation of hybrid electric-thermal energy storage for harbour integrated energy system considering carbon trading mechanism
1
2024
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
基于虚拟阻抗-模糊算法的交直流微电网混合储能功率协调策略
0
Hybrid energy storage power coordination strategy for AC/DC microgrid based on virtual impedance-fuzzy algorithm
0
计及储能电站安全性的功率分配策略研究
0
2022
Research on power distribution strategy considering the safety of energy storage power station
0
2022
电池-超级电容器混合储能系统研究进展
2
2022
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
... 蓄电池装置的主要作用是削减功率峰值,从而承担混合储能系统功率任务的中低频分量[6 ] ,而电池模型参数会随着电池的蓄电池荷电状态、循环次数、容量衰减而不断发生变化.基于上述因素,可将电池数学模型表示为 ...
Advances in battery-supercapacitor hybrid energy storage system
2
2022
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
... 蓄电池装置的主要作用是削减功率峰值,从而承担混合储能系统功率任务的中低频分量[6 ] ,而电池模型参数会随着电池的蓄电池荷电状态、循环次数、容量衰减而不断发生变化.基于上述因素,可将电池数学模型表示为 ...
基于双储能的风电功率波动平抑策略研究
2
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
... 超级电容器在储能系统中具有响应速度快、能够进行频率调节和峰值削减、循环次数和响应速率远大于蓄电池等优点[7 ] .综合上述优点,可以利用其承担混储系统功率任务的高频分量.本文更关注超级电容在系统中的电气特性,其数学模型表达式如下: ...
Research on wind power fluctuation smoothing strategy based on dual energy storage
2
... 风电作为清洁的可再生能源,在新型电力系统中应用广泛.但风电出力的随机性与波动性会对风电的并网质量、电力调峰以及系统安全稳定运行造成一定影响[1 -2 ] .混合储能系统中的功率型储能具有高功率密度、响应速度快的优点,而能量型储能具有高能量密度的优点,二者结合在一起使用能弥补单一储能的不足.因此,混合储能系统的接入能有效解决上述问题[3 6 ] .但若对混合储能系统的功率分配不佳,则难以发挥出两类储能元件的互补特性,从而影响混合储能系统寿命和安全运行[7 ] .因此,如何在最大限度平抑风电波动性的情况下实现混合储能功率合理分配具有重要意义. ...
... 超级电容器在储能系统中具有响应速度快、能够进行频率调节和峰值削减、循环次数和响应速率远大于蓄电池等优点[7 ] .综合上述优点,可以利用其承担混储系统功率任务的高频分量.本文更关注超级电容在系统中的电气特性,其数学模型表达式如下: ...
基于经验模态分解的混合储能系统功率分配方法
3
2014
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 其中,风电功率初次分配策略流程图如图2 所示.具体步骤对应如下:首先,依据最优S ,α 对原始信号进行变分模态分解,得到IMF分量和残差信号(residual,res);将分量进行重构,令k 从1取到S ,分别求出对应k 时的高频重构(fine to coarse,f2c)分量和低频重构分量(coarse to fine,c2f)[8 -9 ] ;当k=1 ,计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k 值,判断k 是否为最低阶分量,若是则无并网功率,全部需要储能系统进行平抑,循环结束;若不是,令k=k+1 并计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k=1 ,则直接结束;若$k\ne 1$ k 值,计算对应k 值的并网分量和混合储能系统所需要的功率,其中功率分配表达式如下: ...
... 风电并网波动量定义为:规定时间间隔内最大功率与最小功率之差满足10 min并网波动量限值,该值通常为风电装机容量的5%~7.5%[8 ] . ...
Power allocation method of hybrid energy storage system based on empirical mode decomposition
3
2014
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 其中,风电功率初次分配策略流程图如图2 所示.具体步骤对应如下:首先,依据最优S ,α 对原始信号进行变分模态分解,得到IMF分量和残差信号(residual,res);将分量进行重构,令k 从1取到S ,分别求出对应k 时的高频重构(fine to coarse,f2c)分量和低频重构分量(coarse to fine,c2f)[8 -9 ] ;当k=1 ,计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k 值,判断k 是否为最低阶分量,若是则无并网功率,全部需要储能系统进行平抑,循环结束;若不是,令k=k+1 并计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k=1 ,则直接结束;若$k\ne 1$ k 值,计算对应k 值的并网分量和混合储能系统所需要的功率,其中功率分配表达式如下: ...
... 风电并网波动量定义为:规定时间间隔内最大功率与最小功率之差满足10 min并网波动量限值,该值通常为风电装机容量的5%~7.5%[8 ] . ...
平抑风电波动的混合储能系统控制策略
2
2020
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 其中,风电功率初次分配策略流程图如图2 所示.具体步骤对应如下:首先,依据最优S ,α 对原始信号进行变分模态分解,得到IMF分量和残差信号(residual,res);将分量进行重构,令k 从1取到S ,分别求出对应k 时的高频重构(fine to coarse,f2c)分量和低频重构分量(coarse to fine,c2f)[8 -9 ] ;当k=1 ,计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k 值,判断k 是否为最低阶分量,若是则无并网功率,全部需要储能系统进行平抑,循环结束;若不是,令k=k+1 并计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k=1 ,则直接结束;若$k\ne 1$ k 值,计算对应k 值的并网分量和混合储能系统所需要的功率,其中功率分配表达式如下: ...
Control strategy of hybrid energy storage system for mitigating wind power fluctuations
2
2020
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 其中,风电功率初次分配策略流程图如图2 所示.具体步骤对应如下:首先,依据最优S ,α 对原始信号进行变分模态分解,得到IMF分量和残差信号(residual,res);将分量进行重构,令k 从1取到S ,分别求出对应k 时的高频重构(fine to coarse,f2c)分量和低频重构分量(coarse to fine,c2f)[8 -9 ] ;当k=1 ,计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k 值,判断k 是否为最低阶分量,若是则无并网功率,全部需要储能系统进行平抑,循环结束;若不是,令k=k+1 并计算$\mathrm{c}2\mathrm{f}\left(k\right)$ k=1 ,则直接结束;若$k\ne 1$ k 值,计算对应k 值的并网分量和混合储能系统所需要的功率,其中功率分配表达式如下: ...
基于模糊经验模态分解的电池储能系统平滑风电出力控制策略
2
2016
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 风电初次分配策略仅从频率特性角度出发,未考虑超级电容和蓄电池的荷电状态和荷电状态变化量对功率分配的影响[10 -11 ] .因此,将上述影响考虑在内,利用多模糊控制修正混合储能系统的功率. ...
Control strategy of smoothing wind power output using battery energy storage system based on fuzzy empirical mode decomposition
2
2016
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 风电初次分配策略仅从频率特性角度出发,未考虑超级电容和蓄电池的荷电状态和荷电状态变化量对功率分配的影响[10 -11 ] .因此,将上述影响考虑在内,利用多模糊控制修正混合储能系统的功率. ...
2
2023
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 风电初次分配策略仅从频率特性角度出发,未考虑超级电容和蓄电池的荷电状态和荷电状态变化量对功率分配的影响[10 -11 ] .因此,将上述影响考虑在内,利用多模糊控制修正混合储能系统的功率. ...
2
2023
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 风电初次分配策略仅从频率特性角度出发,未考虑超级电容和蓄电池的荷电状态和荷电状态变化量对功率分配的影响[10 -11 ] .因此,将上述影响考虑在内,利用多模糊控制修正混合储能系统的功率. ...
模糊控制下混合储能平抑风电波动控制策略
1
2023
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
Hybrid energy-storage control strategy based on fuzzy control to stabilize wind power fluctuation
1
2023
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
用于混合储能系统平抑功率波动的小波变换方法
1
2021
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
Wavelet transform method for hybrid energy storage system smoothing power fluctuation
1
2021
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
基于小波包-模糊算法的混合储能功率分配策略
0
2023
Hybrid energy storage power allocation strategy based on wavelet packet-fuzzy algorithm
0
2023
基于自适应时间尺度小波包和模糊控制的复合储能控制策略
1
2023
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
Control strategy of composite energy storage based on wavelet packet with adaptive time scale and fuzzy control
1
2023
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
Hybrid energy storage power allocation strategy based on parameter-optimized VMD algorithm for marine micro gas turbine power system
1
2023
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
混合储能系统平滑风电出力的变分模态分解-模糊控制策略
1
2019
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
Variational mode decomposition and fuzzy control strategy of hybrid energy storage for smoothing wind power outputs
1
2019
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
基于LHS与BR的风电出力场景分析研究
2
2020
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 以我国西部某风电场2023年每天中的每5 min 实际风速${v}_{r,d}\left(r=\mathrm{1,2}\dots,M;d=\mathrm{1,2},\dots,288\right)$ M ,其中M=365 .由于Weibull分布对风速概率分布的拟合最为精确[18 ] ,所以以测得的历史数据为基础,结合Weibull分布得到每一观测时刻的风速概率密度函数、概率分布函数以及每一时刻概率分布反函数. ...
Scenario analysis of wind power output based on LHS and BR
2
2020
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 以我国西部某风电场2023年每天中的每5 min 实际风速${v}_{r,d}\left(r=\mathrm{1,2}\dots,M;d=\mathrm{1,2},\dots,288\right)$ M ,其中M=365 .由于Weibull分布对风速概率分布的拟合最为精确[18 ] ,所以以测得的历史数据为基础,结合Weibull分布得到每一观测时刻的风速概率密度函数、概率分布函数以及每一时刻概率分布反函数. ...
可靠度分析中拉丁超立方和传统舍选抽样法对比研究
2
2021
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 在此基础上,首先采用拉丁超立方抽样算法生成风电场景,具体步骤是:利用分层抽样思想,将每一观测时刻概率分布函数的取值范围分布成M 个等概率子区域;在每个概率子区域内随机选取一个采样值;然后根据反函数计算每一采样值下所对应的风速,最后根据式(2)得到对应的风电出力情况,其生成场景如图7(a) 所示,规定图中每个时刻为5 min,后续同理.依据该地风电场实际情况设置式(2)中v min =3 m/s、 v n =10.5 m/s、 v max =20 m/s.由于生成场景中并非每一组风电数据都符合实际需求[19 ] ,所以采用欧氏距离法削减相似场景,最终得到10个风电典型出力场景,其典型场景情况如图7(b) 所示,典型场景对应概率和天数情况如表2 所示. ...
Comparing LHS with traditional rejection sampling methods in the analysis of reliability
2
2021
... 目前,针对混合储能系统的功率分配策略研究已取得一定进展.文献[8 -9 ]中针对风电出力随机性与波动性对并网电能质量造成的影响,使用经验模态分解法,在充分考虑频率特性的基础上分解原始风电功率,之后结合并网波动量限值对分解信号进行高低频重构,再选取出符合条件的并网分量和储能系统的任务功率.文献[10 ]中将经验模态分解法与自适应控制相结合,在考虑混合储能系统荷电状态的基础上,对功率进行合理分配.文献[11 -12 ]中针对混合储能系统容易出现过充过放的问题,提出利用模糊控制的方法修正混合储能系统的功率.文献[13 15 ]中将小波包算法与模糊控制相结合,并将混合储能系统的荷电状态以及蓄电池温度作为模糊控制输入量,对功率修正系数进行控制.文献[16 -17 ]中针对小波包与经验模态分解容易出现混叠现象与混合储能系统容易出现过充过放的问题,提出变分模态分解(variational modal decomposition,VMD)与模糊控制相结合的控制策略.该种控制策略下以超级电容的荷电状态和其变化量作为模糊控制的输入,通过计算的修正系数来调整混合储能系统的功率分配情况.文献[18 -19 ]中充分考虑到风电具有较强的随机性和波动性,利用拉丁超立方抽样算法和欧氏距离法来生成典型场景,结果表明,利用典型场景数据进行相关策略研究说服力更强.目前仅有少量文献结合变分模态分解与模糊控制平抑风电波动,其中考虑对变分模态分解进行优化的相对较少;其次,大多数研究中采用单一模糊控制器,但单一模糊控制器并不适合每个时段混合储能系统的功率修正,从而导致混合储能系统功率分配不佳,出现过充过放的问题. ...
... 在此基础上,首先采用拉丁超立方抽样算法生成风电场景,具体步骤是:利用分层抽样思想,将每一观测时刻概率分布函数的取值范围分布成M 个等概率子区域;在每个概率子区域内随机选取一个采样值;然后根据反函数计算每一采样值下所对应的风速,最后根据式(2)得到对应的风电出力情况,其生成场景如图7(a) 所示,规定图中每个时刻为5 min,后续同理.依据该地风电场实际情况设置式(2)中v min =3 m/s、 v n =10.5 m/s、 v max =20 m/s.由于生成场景中并非每一组风电数据都符合实际需求[19 ] ,所以采用欧氏距离法削减相似场景,最终得到10个风电典型出力场景,其典型场景情况如图7(b) 所示,典型场景对应概率和天数情况如表2 所示. ...