在全球气候变暖、能源和环境危机日益加剧的大背景下,我国将加速推进向含高渗透率可再生能源的新型电力系统建设.由于可再生能源出力的波动性与不确定性,电网需要提前预留灵活性资源,以提供充足的爬坡容量,确保系统功率实时平衡,从而促进风光消纳[1 ] 并降低切负荷概率[2 ] .风力发电、光伏与储能的联合发电系统,作为提升供电可靠性和促进风光消纳的主要方式之一,将成为新能源场站建设的主流趋势.
为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台.
目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求.
在此基础上,多时间尺度下灵活爬坡建模成为研究重点,文献[23 ]中考虑日前市场与日内灵活性爬坡需求结合,有效缓解了实时爬坡容量短缺的问题;文献[24 ]中改进了现有日前市场灵活需求模型,并通过实时模拟来反映灵活性价值;文献[25 ]中基于预测净负荷误差概率分布对灵活性资源需求进行最优确定,提出了虚拟竞标曲线的两阶段实时市场出清模型,能对机组产生的机会成本设置合理补偿;文献[26 -27 ]则采用鲁棒优化处理净负荷波动,确保系统获取足够爬坡能力来面对最差调度场景,并提出两阶段分布式鲁棒优化的灵活爬坡备用调度方案,有助于降低灵活调节成本.但是以上研究在处理多时间尺度灵活性资源调度问题时,通常基于相同出清间隔进行市场出清,未充分考虑出清间隔缩短带来的影响,在日前每1 h FRPs决策时预留容量并不一定能够应对实时市场更精细的15 min净负荷变化.
为联合风光储场站等灵活性资源参与电能量与灵活爬坡市场,本文首先分析了灵活爬坡需求的构成,特别是不同时间尺度出清间隔下爬坡需求调整.其次针对风光储场站日前市场和实时市场的特点来进行电能量与灵活爬坡市场建模.然后提出了基于随机规划模型的两阶段联合出清机制,利用风光储场站在日前市场减小净负荷波动,在实时市场风光不确定环境下配合燃气机组提供时间尺度更精细的FRPs,来提高系统实时灵活性.该机制能够消除更新的灵活性需求与日前市场预留容量不匹配带来的误差,平缓因灵活性不足惩罚带来的尖峰电价.最后,将所提出的风光储场站参与的两阶段市场联合出清模型同现有FRPs设计的市场模型对比,验证本文两阶段联合出清模型的有效性和优势.
1 灵活爬坡需求
随着新能源接入比例的提高,系统净负荷波动性与不确定性将更为显著.为保证实时调度时段内足够的灵活性爬坡能力跟随净负荷变化,系统需要将可以实时调度并预留容量的资源以市场化方式作为FRPs引入系统,获取灵活性爬坡能力,通过市场手段调动可调节机组为抵御净负荷不确定性.
1.1 灵活爬坡需求构成
FRPs的需求由系统爬坡需求变化量确定,一是系统下一个时段净负荷相较当前时段的变化量,为预测净负荷波动;二是为满足系统风光与负荷预测误差在一定置信区间内的偏差而额外产生的需求量,为不确定性需求.考虑调节能力的灵活爬坡更新需求如图1 所示.
图1
图1
考虑调节能力的更新爬坡需求
Fig.1
Rolling update ramping demand considering adjustment ability
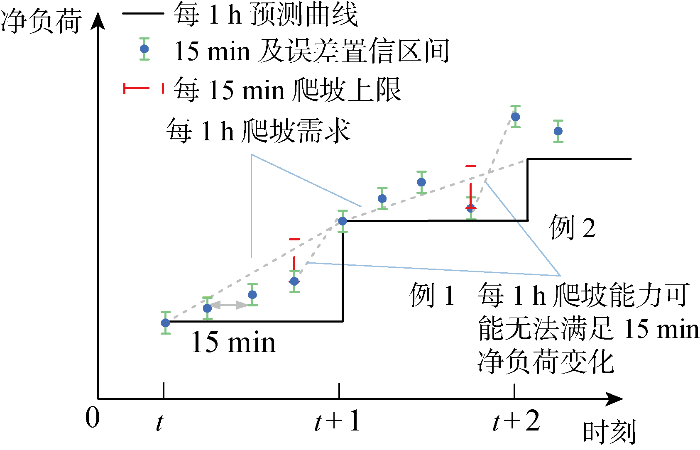
假设各个时刻系统均有预留相同的灵活爬坡和滑坡容量,当下一时刻没有足够向上灵活调节能力时,即红色调节需求超过蓝色的调节能力极限,会导致系统切除部分负荷.当系统没有足够向下调节能力时,会导致系统强制弃风光.因此需要在提前确定FRPs的采购量,来满足系统实时功率平衡.
1.2 不同时间尺度下灵活爬坡调整
以每1 h出清间隔的日前市场和每15 min出清间隔的实时市场举例,图2 反映了每1 h和每15 min FRPs需求对比.在日前阶段,系统为应对净负荷波动,可以提前预留足够的灵活性.但随着出清间隔的缩小,例如图中的例1和例2,每15 min的爬坡能力并不足以应对每15 min更新下的净负荷变化,在部分时段将会带来缺额增加.在此基础上,当净负荷波动存在误差时,可能会加剧爬坡缺额,随着不确定性的增加,该现象将尤为明显.此时系统需要利用调节速度更快,调节能力更强的资源参与灵活性调整,从而减少灵活性缺失概率以及减少实时运行成本.
图2
图2
每1 h与每15 min FRPs需求对比
Fig.2
Comparison of hourly and 15 min FRPs demand
日前市场采购的FRPs可以用确定爬坡需求式来计算:
(1) $\begin{array}{c}\left.\begin{array}{l}{R}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{P}_{\mathrm{d}\mathrm{a},t+1}^{\mathrm{n}\mathrm{e}\mathrm{t}}-{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{n}\mathrm{e}\mathrm{t}},0\right\}\\ {R}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}-{P}_{\mathrm{d}\mathrm{a},t+1}^{\mathrm{n}\mathrm{e}\mathrm{t}},0\right\}\end{array}\right\}\end{array}$
式中:${R}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}$ ${R}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}$ ${P}_{\mathrm{d}\mathrm{a},t+1}^{\mathrm{n}\mathrm{e}\mathrm{t}}$ ${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}$ t+1 和t 时刻的系统净负荷预测值.
在实时市场中,为应对更严峻的爬坡需求,需要对灵活爬坡需求进行更精确的量化,通过引入风光储场站共同提供FRPs,调整风光储场站和机组电能量市场与灵活爬坡市场出力分配,从而为系统实时爬坡能力提供保障.
(2) $\begin{array}{c}\left.\begin{array}{l}{R}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{P}_{\mathrm{r}\mathrm{t},t+1}^{\mathrm{n}\mathrm{e}\mathrm{t}}-{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}+{\xi }_{\mathrm{u}\mathrm{p},t},0\right\}\\ {R}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}-{P}_{\mathrm{r}\mathrm{t},t+1}^{\mathrm{n}\mathrm{e}\mathrm{t}}+{\xi }_{\mathrm{d}\mathrm{n},t},0\right\}\end{array}\right\}\end{array}$
式中:${P}_{\mathrm{r}\mathrm{t},t+1}^{\mathrm{n}\mathrm{e}\mathrm{t}}$ ${P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}$ t+1 和t 时刻系统净负荷预测值,为实时市场负荷预测与新能源出力预测之差;${R}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}$ ${R}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}$ ${\xi }_{\mathrm{u}\mathrm{p},t}$ ${\xi }_{\mathrm{d}\mathrm{n},t}$ t 时刻考虑净负荷预测误差预留向上和向下误差量,若假设净负荷预测误差服从高斯分布,及$\xi ~N\left(0,{\sigma }^{2}\right)$
(3) $\begin{array}{c}\left.\begin{array}{l}{R}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{P}_{\mathrm{r}\mathrm{t},t+1}^{\mathrm{n}\mathrm{e}\mathrm{t}}-{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}+1.96\sigma,0\right\}\\ {R}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}=\mathrm{m}\mathrm{a}\mathrm{x}\left\{{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}-{P}_{\mathrm{r}\mathrm{t},t+1}^{\mathrm{n}\mathrm{e}\mathrm{t}}+1.96\sigma,0\right\}\end{array}\right\}\end{array}$
2 风光储场站建模
由于风力发电、光伏出力的波动性与随机性,风光储场站的内部协同调控主要通过储能来实现.本文主要通过以下3点来丰富储能的调控方法:① 场站可以利用部分风光来给储能充电,提高场站可用容量,利用储能削峰填谷,减少净负荷波动;② 当风力发电、光伏的实时市场与日前市场出力偏差较大时,储能需要配合新能源出力来达到实时市场输出功率的稳定性;③ 风光储场站可以利用储能提供FRPs,并实时市场配合燃气机组进行灵活性调整,提升系统整体灵活性,减少期望弃风光与切负荷惩罚.
2.1 风光储场站参与电能量市场
考虑到风光储场站的储能可以受场站控制并且容量较大,假设参与日前市场前,风光储场站以日前市场净负荷方差最小为目标进行削峰填谷,此时风光储场站按预计输出的功率向日前市场申报.在日前市场中,可以看成风光储场站按预计风光全部消纳,以输出功率${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{E}\mathrm{d}}$
(4) $\begin{array}{c}\left.\begin{array}{l}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}={P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{D}}-{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{E}\mathrm{d}}\\ {P}_{\mathrm{d}\mathrm{a},\mathrm{a}\mathrm{v}\mathrm{e}}^{\mathrm{n}\mathrm{e}\mathrm{t}}=\frac{1}{T}\stackrel{T}{\sum _{t}}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}\\ \mathrm{m}\mathrm{i}\mathrm{n}f=\frac{1}{T}\stackrel{T}{\sum _{t=1}}\sqrt{({P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{n}\mathrm{e}\mathrm{t}}-{P}_{\mathrm{d}\mathrm{a},\mathrm{a}\mathrm{v}\mathrm{e}}^{\mathrm{n}\mathrm{e}\mathrm{t}}{)}^{2}}\end{array}\right\}\end{array}$
式中:${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{D}}$ ${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{E}\mathrm{d}}$ t 时刻输出功率;${P}_{\mathrm{d}\mathrm{a},\mathrm{a}\mathrm{v}\mathrm{e}}^{\mathrm{n}\mathrm{e}\mathrm{t}}$ T 表示日前市场的时段总数.
日前市场中,风光储场站需要满足储能充放电约束、电量约束和风光出力约束.
(5) $\begin{array}{c}\left.\begin{array}{l}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{E}\mathrm{d}}={P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{w}1}+{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{p}\mathrm{v}1}+{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{d}}\\ {P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{c}}={P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{w}2}+{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{p}\mathrm{v}2}\end{array}\right\}\end{array}$
式中:${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{w}1}$ ${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{p}\mathrm{v}1}$ t 时刻风光储场站中风光对外出力;${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{w}2}$ ${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{p}\mathrm{v}2}$ t 时刻风光对储能充电量;${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{c}}$ ${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{d}}$ t 时刻总的充电/放电的功率,其大小需要满足充放电功率上下限约束:
(6) $\begin{array}{c}\left.\begin{array}{l}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{d}}\le {x}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{d}}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{e}\mathrm{d}}\\ {P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{c}}\le {x}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{c}}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{e}\mathrm{c}}\end{array}\right\}\end{array}$
${x}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{c}}$ ${\mathrm{x}}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{d}}$ ${P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{e}\mathrm{c}}$ ${P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{e}\mathrm{d}}$
(7) $\begin{array}{c}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{c}}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{d}}=0\end{array}$
(8) $\left.\begin{array}{l}{S}_{\mathrm{d}\mathrm{a},0}^{\mathrm{E}}={S}_{\mathrm{d}\mathrm{a},T}^{\mathrm{E}}\\ {S}_{\mathrm{d}\mathrm{a},\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{E}}\le {S}_{\mathrm{d}\mathrm{a},t}^{\mathrm{E}}\le {S}_{\mathrm{d}\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{E}}\\ {S}_{\mathrm{d}\mathrm{a},t}^{\mathrm{E}}=\left(1-{\eta }^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right){S}_{\mathrm{d}\mathrm{a},t-1}^{\mathrm{E}}+\frac{{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{c}}{\eta }^{\mathrm{c}}}{{W}^{\mathrm{E}}}-\frac{{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{d}}}{{\eta }^{\mathrm{d}}{W}^{\mathrm{E}}}\end{array}\right\}$
式中:W E 表示风光储场站中储能的容量;${S}_{\mathrm{d}\mathrm{a},\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{E}}$ ${S}_{\mathrm{d}\mathrm{a},\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{E}}$ ${S}_{\mathrm{d}\mathrm{a},t}^{\mathrm{E}}$ t 时刻的荷电状态;η loss 表示储能损耗系数;η c 和η d 表示储能的充/放电效率.
(9) $\begin{array}{c}\left.\begin{array}{l}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{w}1}+{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{w}2}={P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{w}}\\ {P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{p}\mathrm{v}1}+{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{p}\mathrm{v}2}={P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{p}\mathrm{v}}\end{array}\right\}\end{array}$
式中:${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{w}}$ ${P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{p}\mathrm{v}}$ t 时刻风光储场站中风光的出力预测.
实时市场与日前市场风光储场站充放电约束与电量约束类似.在实时市场中,考虑风光的不确定性,风光对外出力与对风光对储能充电功率之和应该小于实时市场风光预测与不确定性误差之和.此时风光出力约束更改如下:
(10) $\begin{array}{c}\left.\begin{array}{l}{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{w}1}+{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{w}2}\le {P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{w}}+\mathrm{\Delta }{{P}^{\mathrm{w}}}_{t}\\ {P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{p}\mathrm{v}1}+{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{p}\mathrm{v}2}\le {P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{p}\mathrm{v}}+\mathrm{\Delta }{P}_{t}^{\mathrm{p}\mathrm{v}}\end{array}\right\}\end{array}$
式中:$\mathrm{\Delta }{{P}^{\mathrm{w}}}_{t}$ $\mathrm{\Delta }{P}_{t}^{\mathrm{p}\mathrm{v}}$
当风光储系统实际出力与申报存在偏差时,可以设置实时市场偏差成本系数,提高风光储场站可调度性.
2.2 风光储场站参与灵活爬坡市场
在实时市场中,考虑风光的不确定性,构建风光场景,风光储场站可以利用储能联合风光提供向上灵活爬坡产品(FRU)与向下灵活爬坡产品(FRD).此时风光储场站可以提供的向上和向下爬坡容量受当前时段储能充放电容量以及荷电状态约束共同影响,其能提供的爬坡容量大小约束为
(11) $\begin{array}{c}\left.\begin{array}{l}0\le {P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t}^{\mathrm{E}\mathrm{d}}\le \left({S}_{\mathrm{r}\mathrm{t},t}^{\mathrm{E}}-{S}_{\mathrm{r}\mathrm{t},\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{E}}\right){W}^{E}{\eta }^{\mathrm{d}}/\Delta t\\ {P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t}^{\mathrm{E}\mathrm{d}}+{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{e}\mathrm{d}}\le {x}_{\mathrm{r}\mathrm{t},t}^{\mathrm{e}\mathrm{d}}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{e}\mathrm{d}}\\ 0\le {P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t}^{\mathrm{E}\mathrm{c}}\le \left({S}_{\mathrm{r}\mathrm{t},\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{E}}-{S}_{\mathrm{r}\mathrm{t},t}^{\mathrm{E}}\right){W}^{E}{\eta }^{\mathrm{c}}/\Delta t\\ {P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t}^{\mathrm{E}\mathrm{c}}+{P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{e}\mathrm{c}}\le {x}_{\mathrm{r}\mathrm{t},t}^{\mathrm{e}\mathrm{c}}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{e}\mathrm{c}}\end{array}\right\}\end{array}$
式中:${P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{e}\mathrm{c}}$ ${P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{e}\mathrm{d}}$ t 时刻充电/放电的功率;${P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t}^{\mathrm{E}\mathrm{d}}$ ${P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t}^{\mathrm{E}\mathrm{c}}$ t 时刻风光储场站可以提供的上调和下调灵活爬坡产品;$\mathrm{\Delta }t$
3 含风光储场站的电能量与灵活爬坡市场两阶段联合出清
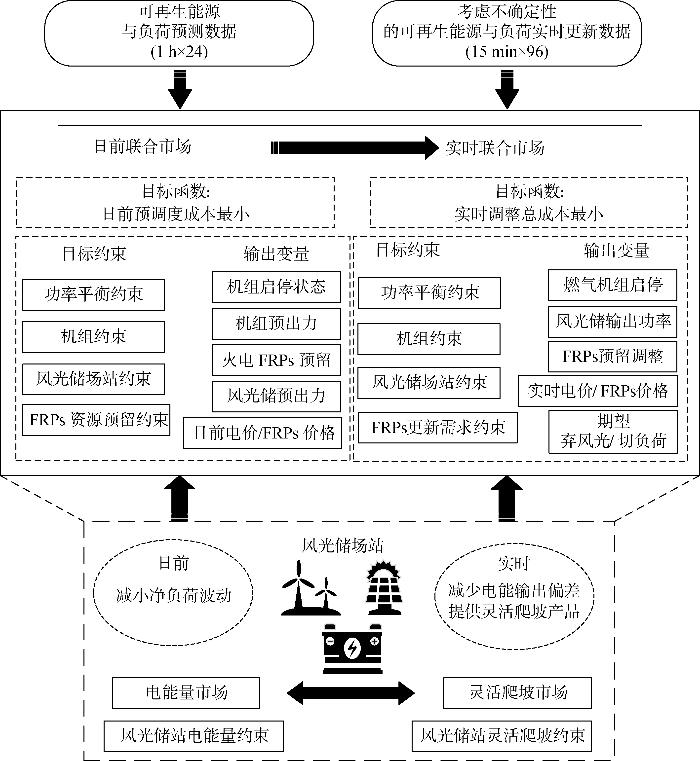
含风光储场站的电能量市场与灵活爬坡市场联合出清主要可以分为日前市场和实时市场两阶段出清,在日前市场上,风光储场站需要提前以电能量市场净负荷最小方差为目标,以1 h为精度向电力交易中心提交其日前市场发电量,机组为其能源供应提交电能量报价与报量;实时市场在日前市场基础上考虑不确定性,负荷与风光则需要重新以15 min为精度向电力交易中心提交其发电与用电预测量,并通过风光预测误差场景生成与削减,以最小化实际运行成本为目标,为每个场景寻找最优发电策略,重新确定燃气机组状态,进行FRPs的二次调整,并确定机组和风光储场站电能量市场和灵活爬坡市场的出力分配.本文两阶段出清模型框架如图3 所示.
图3
图3
考虑风光储场站参与的两阶段联合市场出清模型
Fig.3
Two stage joint market clearing model considering wind/photovoltaic/energy storage power station
(1) 本文重点是在精细FRPs预留,文章重点并不在于实际中的收益结算问题;
(2) 仅实时市场考虑风光不确定性,日前市场风光储场站出力按风光预测值全部消纳;
(3) 为了便于系统电价对比,假设机组采用单段报价;且未考虑潮流对系统的影响.
3.1 日前市场联合出清
3.1.1 目标函数
日前联合市场的目标是最小化系统总预调度成本,即预留满足预测净负荷下爬坡需求的FRPs,使得日前能量市场总成本最小,目标函数表示为
(12) $\begin{array}{l}min\mathrm{f}=\stackrel{T}{\sum _{t=1}}\stackrel{I}{\sum _{i=1}}({u}_{i,t}{{C}^{\mathrm{G}}}_{i,t}+{c}_{i,t}{{U}^{\mathrm{G}}}_{i,t}+{v}_{i,t}{{D}^{\mathrm{G}}}_{i,t})+\\ \stackrel{T}{\sum _{t=1}}\stackrel{I}{\sum _{i=1}}{{F}^{\mathrm{G}}}_{i,t}\left({P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}\right)+\stackrel{T}{\sum _{t=1}}F\left({{P}^{\mathrm{E}}}_{t}\right)\end{array}$
式中:上标G表示机组;I 表示包含日前联合市场机组的集合;ui,t 、ci,t 、vi,t 分别表示机组i 在t 时刻的开关(1为开机,0为关机)、启动(1为启动,0为不启动)和停机(1为停机,0为不停机)的二元变量;CG i,t 、UG i,t 、DG i,t 表示日前市场中第i台机组t 时刻空载、开机、停机成本系数.${P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}$ i 台机组在日前市场t 时刻的输出功率;${{F}^{\mathrm{G}}}_{i,t}\left({P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}\right)$ $F\left({{P}^{\mathrm{E}}}_{t}\right)$ $F\left({{P}^{\mathrm{E}}}_{t}\right)={\lambda }_{t}^{\mathrm{e}\mathrm{d}}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{d}}+{\lambda }_{t}^{\mathrm{e}\mathrm{c}}{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}\mathrm{c}}$ ${\lambda }_{t}^{\mathrm{e}\mathrm{d}}$ ${\lambda }_{t}^{\mathrm{e}\mathrm{c}}$
机组最小启停时间约束与开关状态的逻辑关系约束如下:
(13) $\begin{array}{c}\left.\begin{array}{l}{{T}^{\mathrm{U}}}_{i,t}-\left({u}_{i,t-1}-{u}_{i,t}\right){{T}^{\mathrm{U}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}\ge 0\\ {{T}^{\mathrm{D}}}_{i,t}-\left({u}_{i,t}-{u}_{i,t-1}\right){{T}^{\mathrm{D}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}\ge 0\\ {{T}^{\mathrm{U}}}_{i,t}=\stackrel{t-1}{\sum _{\tau =t-{{T}^{\mathrm{U}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}}}{u}_{i,\tau }\\ {{T}^{\mathrm{D}}}_{i,t}=\stackrel{t-1}{\sum _{\tau =t-{{T}^{\mathrm{D}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}}}(1-{u}_{i,\tau })\\ {u}_{i,t-1}-{u}_{i,t}-{c}_{i,t}\le 0\\ -{u}_{i,t-1}+{u}_{i,t}-{v}_{i,t}\le 0\end{array}\right\}\end{array}$
式中:TU i,t 和TD i,t 分别表示机组i 在t 时刻开、停机时间;${{T}^{\mathrm{U}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}$ ${{T}^{\mathrm{D}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}$ i 最小开、停机时间要求;$\tau $ t 和${{T}^{\mathrm{U}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}$ ${{T}^{\mathrm{D}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}$
3.1.2 约束条件
(14) $\begin{array}{c}\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}+{P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{E}\mathrm{d}}={P}_{\mathrm{d}\mathrm{a},t}^{\mathrm{D}}, t\in T:{\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}}\end{array}$
式中:${\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}}$
(2) 机组和风光储场站电能量约束.日前市场机组约束主要包括机组出力上下限约束、爬坡约束、备用大小与需求约束以及FRPs资源预留约束以及考虑灵活爬坡备用的容量约束.
(15) $\begin{array}{c}{u}_{i,t}{{P}^{\mathrm{G}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}\le {P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}\le {u}_{i,t}{{P}^{\mathrm{G}}}_{i,\mathrm{m}\mathrm{a}\mathrm{x}}\end{array}$
(16) $\begin{array}{c}\left.\begin{array}{l}-{R}_{\mathrm{u}\mathrm{p},i}^{\mathrm{G}}\mathrm{\Delta }t\le {P}_{\mathrm{d}\mathrm{a},i,t+1}^{\mathrm{G}}-{P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}\le {R}_{\mathrm{u}\mathrm{p},i}^{\mathrm{G}}\mathrm{\Delta }t\\ -{R}_{\mathrm{d}\mathrm{n},i}^{\mathrm{G}}\mathrm{\Delta }t\le {P}_{\mathrm{d}\mathrm{a},i,t+1}^{\mathrm{G}}-{P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}\le {R}_{\mathrm{d}\mathrm{n},i}^{\mathrm{G}}\mathrm{\Delta }t\end{array}\right\}\end{array}$
(17) $\begin{array}{c}\left.\begin{array}{l}0\le {P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}\mathrm{r}}\le {R}_{\mathrm{u}\mathrm{p},i}^{\mathrm{G}}\mathrm{\Delta }t\\ 0\le {P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}\mathrm{r}}\le {R}_{\mathrm{d}\mathrm{n},i}^{\mathrm{G}}\mathrm{\Delta }t\end{array}\right\}\end{array}$
(18) $\begin{array}{c}\left.\begin{array}{l}0\le {P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}\le {R}_{\mathrm{u}\mathrm{p},i}^{\mathrm{G}}\mathrm{\Delta }t\\ 0\le {P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}\le {R}_{\mathrm{d}\mathrm{n},i}^{\mathrm{G}}\mathrm{\Delta }t\end{array}\right\}\end{array}$
(19) $\begin{array}{c}\left.\begin{array}{l}{P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}+{P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}+{P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}\mathrm{r}}\le {u}_{i,t}{{P}^{\mathrm{G}}}_{i,\mathrm{m}\mathrm{a}\mathrm{x}}\\ {u}_{i,t}{{P}^{\mathrm{G}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}\le {P}_{\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}-{P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}-{P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}\mathrm{r}}\end{array}\right\}\end{array}$
式中:${R}_{\mathrm{u}\mathrm{p},i}^{\mathrm{G}}$ ${R}_{\mathrm{d}\mathrm{n},i}^{\mathrm{G}}$ i 台机组的正爬坡与负爬坡限制;${P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}\mathrm{r}}$ ${P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}\mathrm{r}}$ i 台机组在日前市场t 时刻向上和向下备用容量;${P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}$ ${P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}$ i 台机组在日前市场t 时刻参与的FRU 和FRD 容量;${{P}^{\mathrm{G}}}_{i,\mathrm{m}\mathrm{a}\mathrm{x}}$ ${{P}^{\mathrm{G}}}_{i,\mathrm{m}\mathrm{i}\mathrm{n}}$ i 台机组在t 时刻的输出功率最大值和最小值.
风光储场站日前仅参与电能量市场,具体约束见式(4)~(9).
(20) $\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}-{R}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}\ge 0, t\in T:{\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{u}\mathrm{p}}$
(21) $\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}-{R}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}\ge 0, t\in T:{\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{d}\mathrm{n}}$
式中:${R}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}$ ${R}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}$ t 时刻所需上行爬坡功率与下行滑坡功率,由式(1)计算所得,${\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{u}\mathrm{p}}$ ${\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{d}\mathrm{n}}$
3.2 实时市场联合出清
3.2.1 目标函数
实时市场的目标是考虑风光不确定性基础上,重新调整风光储场站出力,通过风光储场站内部协同优化来缓解实时市场更精确时间段的不确定性,使得系统期望的运行成本最小.该成本包括机组出力调整成本;风光储场站出力调整成本,以及未满足灵活性需求时期望的切负荷和弃风光惩罚成本,具体目标函数如下:
(22) $\begin{array}{l}min\mathrm{f}=\stackrel{S}{\sum _{s=1}}\stackrel{{T}_{\mathrm{r}\mathrm{t}}}{\sum _{t=1}}F\left(\mathrm{\Delta }{P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}\right)\mathrm{\Delta }t+\\ \stackrel{S}{\sum _{s=1}}\stackrel{{T}_{\mathrm{r}\mathrm{t}}}{\sum _{t=1}}\stackrel{I}{\sum _{i=1}}{\pi }_{s}{{F}^{\mathrm{G}}}_{i,t}\left(\mathrm{\Delta }{P}_{\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}\right)\mathrm{\Delta }t+\\ \stackrel{S}{\sum _{s=1}}\stackrel{{T}_{\mathrm{r}\mathrm{t}}}{\sum _{t=1}}{\pi }_{s}\left({C}_{\mathrm{q}\mathrm{i}}E\left({P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{q}\mathrm{i}}\right)+{C}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}E\left({P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right)\right)\mathrm{\Delta }t\end{array}$
式中:第1、2项表示实时市场机组和风光储场站调整费用;第3项表示期望的弃风光与切负荷费用;${\pi }_{s}$ s 出现的概率;Trt 表示实时市场出清时段;$\mathrm{\Delta }{P}_{\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}$ s 场景下第i 台机组在实时市场t 时刻调整的电能量市场偏差出力;${{F}^{\mathrm{G}}}_{i,t}\left(\mathrm{\Delta }{P}_{\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}\right)$ s 场景下实时市场机组偏差成本;$\mathrm{\Delta }{P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}$ s 场景下风光储场站实时市场输出功率偏差量;$F\left(\mathrm{\Delta }{P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}\right)$ s 场景下实时市场风光储场站出力偏差成本;$E\left({P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{q}\mathrm{i}}\right)$ $E\left({P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right)$ s 场景下实时市场期望弃风光与切负荷量,其大小反映该场景下上调与下调灵活性的缺失;Cqi 和${C}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$
3.2.2 约束条件
(23) $\begin{array}{l}\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}+{P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}={P}_{\mathrm{r}\mathrm{t},t}^{\mathrm{D}}+E\left({P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right),\\ \begin{array}{c}t\in {T}_{\mathrm{r}\mathrm{t}}:{\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{e}}\end{array}\end{array}$
式中:${P}_{\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}$ i 台机组在场景s 中t 时刻的中标功率;${P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}$ s 场景下风光储场站实时市场输出功率实际中标量;${\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{e}}$ s 中实时市场功率平衡对应的拉格朗日乘子.
(2) 机组和风光储场站约束.实时市场中,机组与风光储场站将参与电能量市场与灵活爬坡市场功率分配调整,其参与电能量约束与日前市场类似,具体分别见式(15)~(19)和式(5)~(10).仅需将下标日前市场标志da改为在实时市场场景s 中的标志rt.风光储场站在实时市场可以向系统提供实时调整的灵活爬坡产品,风光储场站参与灵活爬坡市场约束见式(11).
(3) 灵活爬坡调整约束.在实时市场,系统需要根据每15 min的预测负荷和新能源出力重新进行出力分配,尤其在爬坡缺额时段,为了保障系统灵活性,需进行灵活爬坡容量二次调整,确保系统有足够的爬坡能力,减少弃风光和切负荷的高额成本.此时,灵活爬坡调整约束的公式如下:
(24) $\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}+{P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}+E\left({P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}\right)\ge {R}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}, t\in {T}_{\mathrm{r}\mathrm{t}}:{\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{u}\mathrm{p}}$
(25) $\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}+{P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}+E\left({P}_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{q}\mathrm{i}}\right)\ge {R}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}, t\in {T}_{\mathrm{r}\mathrm{t}}:{\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{d}\mathrm{n}}$
式中:${R}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}$ ${R}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t}^{\mathrm{r}\mathrm{e}\mathrm{q}}$ ${P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}$ ${P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}$ s 中t 时刻机组灵活爬坡产品上调与下调中标容量;${P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}$ ${P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}$ s 中t 时刻风光储场站上灵活爬坡产品上调下调中标容量;${\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{u}\mathrm{p}}$ ${\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{d}\mathrm{n}}$
3.3 出清流程与电价分析
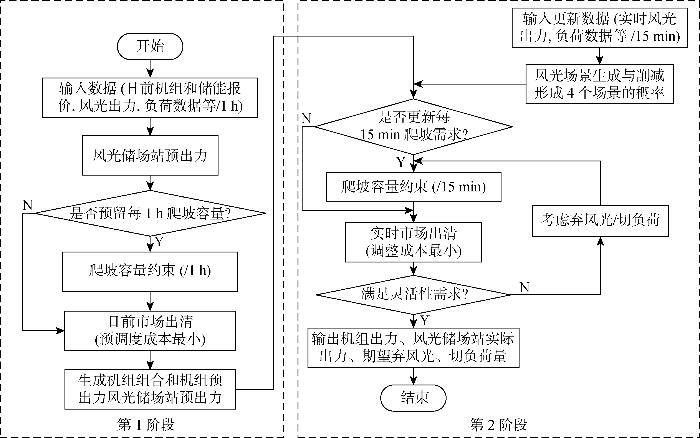
考虑风光储场站参与灵活爬坡的两阶段出清模型为混合整数线性规划模型(mixed integer linear programming,MILP),针对该问题,在MATLAB R2021a中基于YALMIP调用Gurobi 10.0.1求解器进行求解.该模型的市场出清流程如图4 所示.
图4
图4
两阶段市场出清流程图
Fig.4
Flow chart of two-stage market clearing
该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0.
图4 第1阶段得到日前电价${\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{e}},$ 图4 第2阶段生成实时市场系统边际电价${\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{e}}$ s 中功率平衡约束式(23)对应的拉格朗日乘子,表示较日前预调度负荷单位偏移变动引起的目标函数成本变化.
3.4 FRPs费用计算
该两阶段出清模型中,FRPs费用主要由日前市场FRPs成本以及实时市场FRPs调整成本构成.其中日前出清费用按日前出清数量与价格结算;实时市场出清按与日前市场的出清数偏差量与实时市场FRPs出清价格结算.其中,${\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{u}\mathrm{p}}$ ${\lambda }_{\mathrm{d}\mathrm{a},t}^{\mathrm{d}\mathrm{n}}$ t 时刻的出清价格,对应约束式 (20)~(21)的拉格朗日乘子,反映的是增加单位爬坡需求带来的电能量成本市场变化.${\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{u}\mathrm{p}}$ ${\lambda }_{\mathrm{r}\mathrm{t},t,s}^{\mathrm{d}\mathrm{n}}$ s 中t 时刻的出清价格,对应约束式(24)~(25)的拉格朗日乘子,其数值大小表示在场景s中增加单位爬坡需求带来的电能量成本市场变化.
(26) ${P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},t}^{\mathrm{F}\mathrm{R}\mathrm{P}}=\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}$
(27) ${P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},t}^{\mathrm{F}\mathrm{R}\mathrm{P}}=\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}$
(28) $\mathrm{\Delta }{P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t,s}^{\mathrm{F}\mathrm{R}\mathrm{P}}=\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}-\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{u}\mathrm{p},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}+{P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}$
(29) $\mathrm{\Delta }{P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t,s}^{\mathrm{F}\mathrm{R}\mathrm{P}}=\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},i,t,s}^{\mathrm{G}}-\stackrel{I}{\sum _{i=1}}{P}_{\mathrm{d}\mathrm{n},\mathrm{d}\mathrm{a},i,t}^{\mathrm{G}}+{P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t,s}^{\mathrm{E}\mathrm{d}}$
式中:$\mathrm{\Delta }{P}_{\mathrm{u}\mathrm{p},\mathrm{r}\mathrm{t},t,s}^{\mathrm{F}\mathrm{R}\mathrm{P}}$ $\mathrm{\Delta }{P}_{\mathrm{d}\mathrm{n},\mathrm{r}\mathrm{t},t,s}^{\mathrm{F}\mathrm{R}\mathrm{P}}$ s 中t 时刻FRPs上调与下调中标容量变化量.
4 算例分析
4.1 算例说明
为验证所建立模型的有效性,本文参考文献[29 ]中机组和负荷数据,并加入风光储场站进行测试,该风光储场站中,风光装机容量分别是100 MW与75 MW,储能容量15 MW/60 MW·h;机组和风光储场站具体参数见附录A中的表A1和表A2,其中G1~G4为火电机组,G5~G6为燃气机组,均自愿参加灵活爬坡市场且无需对FRPs进行报价,FRPs价格由机会成本确定.假设风光储场站内仅储能参与电能量市场充放电报价,且实时市场电能量市场输出功率正偏差和负偏差的惩罚系数[31 ] 分别为0.95和1.05.弃风光和弃负荷惩罚假设分别设为708 元/(MW·h)和4 963元/(MW·h)[25 ,29 ] .
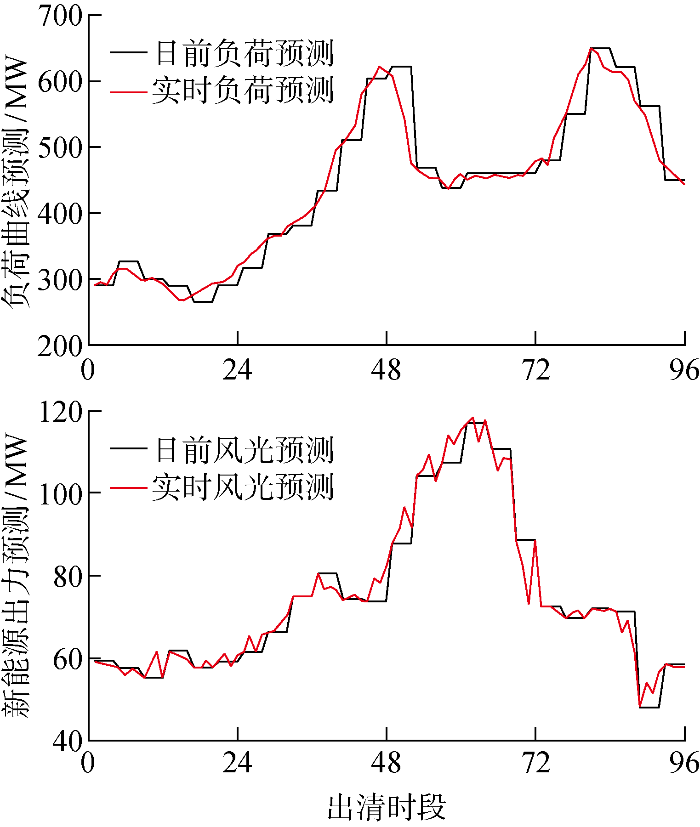
日前与实时市场的新能源预测曲线及系统负荷需求预测曲线见图5 ,假设实时市场新能源预测误差服从正态分布,利用拉丁超立方抽样和同步削减进行风光场景生成与削减,分别给出削减后服从σ 2 =5%的正态分布风光预测曲线记为场景a1~a4,σ 2 =10%的正态分布风光预测曲线记为场景b1~b4,具体实时市场中风光削减后场景见附录图A1.
图5
图5
风光和负荷预测曲线
Fig.5
Wind photovoltaic and load forecasting curves
4.2 两阶段市场联合出清的影响分析
为研究机组和风光储场站参与灵活爬坡服务对系统灵活性的影响,现设置了3种方案:Case1是未考虑灵活性资源参与灵活爬坡市场;Case2仅考虑机组参与日前爬坡预留,未考虑灵活性资源参与实时灵活爬坡市场;Case3是本文考虑两阶段灵活爬坡市场出清模型.
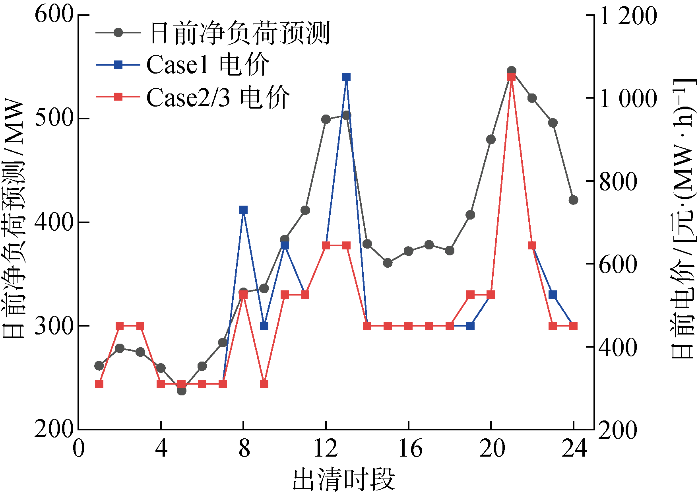
(1) 两阶段出清对实时灵活性的影响.在日前市场出清中,大部分时段,系统自身灵活性足够支撑下一时刻爬坡需求,各方案系统边际电价相同且与市场净负荷预测基本呈正相关.Case1并未考虑爬坡容量预留,而Case2和Case3考虑了下一时刻的灵活性预留,因此在时段7提前开启G3机组,为系统在净负荷增加阶段提供足够的向上灵活性,此时系统新增负荷由新增机组与原机组共同承担,边际电价更低,但部分时段调用昂贵的机组参与电能量市场提供上调与下调灵活性,使得日前市场预调度费用上升.此时图6 反映了各场景日前市场的发电边际机组与净负荷的关系,一定程度上能反映灵活性稀缺情况.
图6
图6
日前出清电价对比
Fig.6
Comparison of day-ahead electricity prices
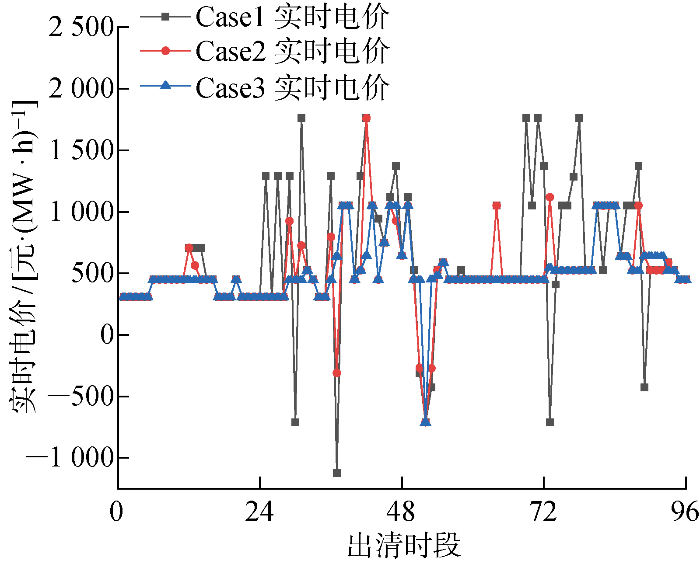
图7 展示了实时市场的实时电价,大部份时段,Case1、Case2和Case3的实时电价相等.但是在时段36和时段72附近,系统先后面临严峻的爬坡和滑坡挑战,Case1在实时调节时并没有足够的灵活性,实时电价将会在多个时段表现为尖峰电价与负电价.Case3与Case2中,FRPs的介入减少系统弃风光和切负荷的现象,能减少实时电价波动.实时市场电价与日前市场曲线类似,均能一定程度上反映市场能源供需情况,并且其尖峰电价能够准确的反映灵活调节能力缺失的时段.
图7
图7
实时出清电价对比图
Fig.7
Comparison of real-time clearing electricity prices
附录B中介绍了系统灵活调节能力的计算过程,以风光场景a1为例,图8 展示了通过计算后系统各方案当前时段灵活调节能力与爬坡需求对比.Case1未考虑灵活性资源参与预留FRPs,面对实时市场的爬坡需求,在多个时段出现灵活性调节能力不足的情况,于时段24~40和时段60~69附近上调能力明显不足,于时段48~60和时段90~96附近下调能力明显不足,只能被迫改变机组出力,甚至切负荷和弃风光.Case2和Case3在日前市场预留的爬坡容量提高了系统的上调下调能力,在大部分时段都可以满足实时爬坡需求.与Case2比,风光储场站提供FRPs,能够重新分配机组出力,在爬坡需求严峻的时段能够保障系统拥有足够的上调与下调能力,也能更好地应对风光不确定性,从而减少弃风光与切负荷量.
图8
图8
3种方案下系统灵活调节能力对比
Fig.8
Comparison of real-time market flexible adjustment capabilities in three cases
(2) 两阶段出清对总运行成本的影响.考虑风光不确定性,系统在应对实时市场每15 min的出清时段和更高的爬坡能力需求时仍可能会有缺额,此时Case1在实时市场被迫开启燃气机组来提供上调和下调灵活性,而Case2和Case3因为提前开启机组系统将优先调用日前市场预留的灵活资源,当爬坡滑坡仍产生缺额时,Case3风光储场站可以通过提供FRPs,从而弥补部分滑坡爬坡缺额.针对场景a1的3种方案,其日前市场预购成本、实时市场调整成本、FRPs成本、总成本以及情况如表1 所示.
Case2/3尽管在日前市场中提前预留机组灵活性,增加了日前市场的调用成本,但是可以很大程度上减少实时市场资源调整成本以及灵活不足带来的期望切负荷和弃风光惩罚成本.针对该算例,两阶段出清方式仅仅提供FRPs在总成本的0.5%左右的基础上,增加的实时调节能力可以大幅减少期望切负荷量以及弃风光量,消纳率由90%提高到98.9%.因此其总成本要小于Case1.
4.3 风光储场站作用分析
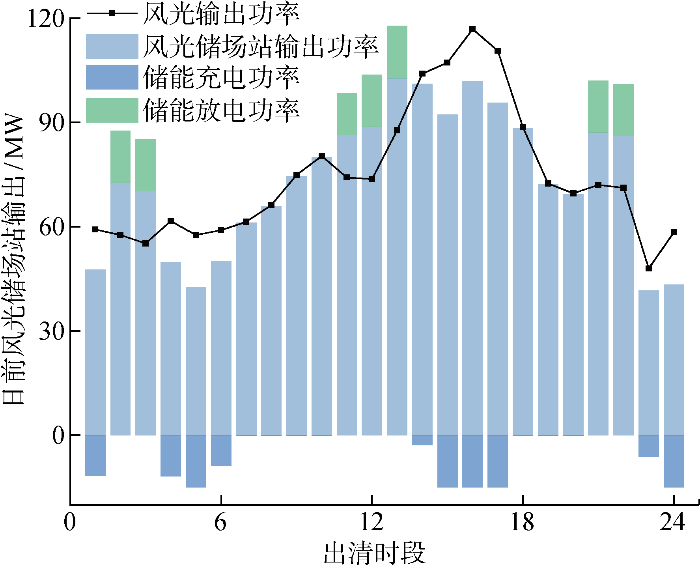
同样以场景a1为例日前市场中,风光储场站以满足市场净负荷方差最小为目标,提前申报场站对外输出功率.此时风光储场站在净负荷较大时利用储能充电,净负荷较小时利用储能放电,可以实现削峰填谷,平抑净负荷波动.具体风光储场站输出功率与各时段储能如图9 所示.
图9
图9
日前市场风光储场站出力情况
Fig.9
Output of WPS in day ahead market
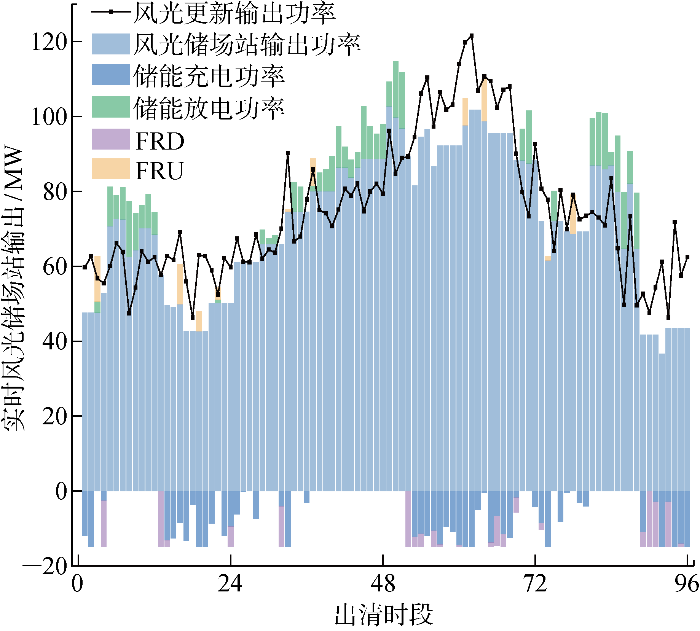
实时市场中,风光的预测精度较日前有较大提高.一方面,风光储场站可以利用储能调节风光与日前市场出力偏差,减少实时市场风光储场站输出偏差;另一方面,风光储场站在部分时段预留FRPs,可以更好应对灵活性的不足.实时市场风光储场站功率输出如图10 所示,风光储场站的储能充/放电时段与日前市场储能充/放电时段较为一致,但在20和60等时段机组上调灵活性缺失时刻风光储场站预留FRU,可以避免Case2中切负荷情况,在48和90等时段附近,随着负荷突然减少,此时场站趋向于预留FRD,减少机组燃气机组G5和G6的启动频率,降低成本.
图10
图10
实时市场风光储场站出力情况
Fig.10
Output of WPS in real time market
4.4 风光预测误差对出清结果的影响分析
为验证风光不确定性误差对出清结果的影响,在实时市场设置了不同误差系数的风光场景a与b,表2 对比场景a与b,各方案成本以及面临灵活性不足时,系统期望弃风光和切负荷情况.
随着风光误差系数的增加,所需的FRPs需求量与成本越高,同时引入FRPs将减少的系统总成本减少越明显.这是由于Case1午夜和早晨时分附近随着火电机组数量减少且部分机组被安排出力至最低技术要求附近,系统更容易出现下调灵活性缺额.场景b中随着风光误差增加,实时市场爬坡面临的极端场景更加频繁,参与灵活爬坡市场能够使弃风光量从原有242.84 MW减少到27.12 MW.
5 结论
本文在考虑可再生能源和出力不确定的前提下,建立了基于随机规划模型的两阶段电能量和灵活爬坡市场联合出清模型,并在实时市场利用风光储场站提供FRPs来减少期望切负荷和弃风光量.通过研究得出以下结论:
(1) 基于考虑灵活爬坡约束的出清模型,尽管日前市场运行成本提升,但可以大幅减少系统在实时市场的弃风光与切负荷带来的惩罚成本,其实时市场出清价格能反映市场供需比的同时反映灵活调节能力的稀缺程度.
(2) 考虑实时市场爬坡更新的两阶段市场出清模型可以有效避免日前每1 h FRPs与实际灵活性需求不匹配带来的误差,能更好调整灵活性资源,应对实时市场的风光不确定性.
(3) 利用风光储场站联合风光协同调控,能丰富储能的调控手段,既可以减小净负荷波动,又能够提供FRPs,解决了日前市场每1 h FRPs在实时市场中爬坡容量不匹配的问题,增加系统实时灵活性.
但是本文并未站在风光储场站角度提供合适的储能充放电以及灵活爬坡市场报价策略,市场各主体提供灵活爬坡产品的收益问题和结算方式将成为下一步研究的重点.
附录见本刊网络版(xuebao.sjtu.edu.cn/CN/10.16183/j.cnki.jsjtu.2023.570)
参考文献
View Option
[1]
黄远明 , 张玉欣 , 夏赞阳 , 等 . 考虑需求响应资源和储能容量价值的新型电力系统电源规划方法
[J]. 上海交通大学学报 2023 , 57 (4 ): 432 -441 .
DOI:10.16183/j.cnki.jsjtu.2021.477
[本文引用: 1]
高比例可再生能源的接入对电力系统容量充裕性带来了新的挑战,系统必须具备充足的置信容量应对可再生能源的出力波动性和随机性.由于储能置信容量与电源规划结果的非线性关系,传统电源规划方法难以准确计算储能置信容量并建立系统置信容量充裕度约束.通过综合考虑火电、可再生能源、储能以及需求侧响应建立了电源规划模型,内嵌全年8 760时段生产运行模拟以确保系统具有充足灵活性,同时改进容量充裕性约束以考虑需求响应资源和储能的容量价值.针对储能置信容量的非线性问题,设计了迭代算法进行求解,并用某区域电力系统验证了模型的有效性.结果表明,高比例可再生能源系统中,影响系统成本的主要因素是灵活性约束,引入少量需求侧响应资源可大幅降低系统成本,为未来高比例可再生资源电力系统规划问题提供了新的思路.
HUANG Yuanming ZHANG Yuxin XIA Zanyang et al . Power system planning considering demand response resources and capacity value of energy storage
[J]. Journal of Shanghai Jiao Tong University 2023 , 57 (4 ): 432 -441 .
[本文引用: 1]
[2]
亢丽君 , 王蓓蓓 , 薛必克 , 等 . 计及爬坡场景覆盖的高比例新能源电网平衡策略研究
[J]. 电工技术学报 2022 , 37 (13 ): 3275 -3288 .
[本文引用: 1]
KANG Lijun WANG Beibei XUE Bike et al . Research on the balance strategy for power grid with high proportion renewable energy considering the ramping scenario coverage
[J]. Transactions of China Electrotechnical Society 2022 , 37 (13 ): 3275 -3288 .
[本文引用: 1]
[3]
李江 , 马吴天 , 宋田宇 . 风储联合系统爬坡事件的日前能量最优平抑方法
[J]. 中国电机工程学报 2021 , 41 (12 ): 4153 -4164 .
[本文引用: 1]
LI Jiang MA Wutian SONG Tianyu . An event-based day-ahead energy optimization method to smooth ramp events of combined wind storage systems
[J]. Proceedings of the CSEE 2021 , 41 (12 ): 4153 -4164 .
[本文引用: 1]
[4]
夏芹芹 , 罗永捷 , 王荣茂 , 等 . 考虑新能源爬坡的风光火耦合系统源荷匹配性分析及容量优化配置
[J]. 上海交通大学学报 2024 , 58 (1 ): 69 -81 .
DOI:10.16183/j.cnki.jsjtu.2022.260
[本文引用: 1]
风力发电、光伏发电与火力发电经同一点并网形成耦合系统,是我国北方地区发电侧灵活性调节电源与新能源间高效、低碳协同的一种形式.考虑区域新能源爬坡特性,结合源荷匹配分析,发掘和利用其规律,研究风光火耦合系统的容量优化配置方法,为耦合系统规划提供参考.首先,简述耦合系统运行模式和不确定性处理方法;其次,考虑耦合系统风光互补、爬坡事件和关键负荷特性,选取并提出相关指标用于源荷匹配评价;再次,考虑源荷特性、匹配、成本和收益等约束,建立耦合系统容量优化配置模型;最后,基于辽宁地区实际数据进行算例仿真,得到该地区耦合系统风、光的最优安装容量,并分析上述源荷相关因素与容量优化配置结果之间的相互影响,为新能源最优容量配置提供了参考与建议.
XIA Qinqin LUO Yongjie WANG Rongmao et al . Source-load matching analysis and optimal planning of wind-solar-thermal coupled system considering renewable energy ramps
[J]. Journal of Shanghai Jiao Tong University 2024 , 58 (1 ): 69 -81 .
[本文引用: 1]
[5]
李军徽 , 安晨宇 , 李翠萍 , 等 . 计及调峰市场交易的储能-新能源-火电多目标优化调度
[J]. 电工技术学报 2023 , 38 (23 ): 6391 -6406 .
LI Junhui AN Chenyu LI Cuiping et al . Multi-objective optimization scheduling method considering peak regulating market transactions for energy storage-new energy-thermal power
[J]. Transactions of China Electrotechnical Society 2023 , 38 (23 ): 6391 -6406 .
[6]
郭怿 , 明波 , 黄强 , 等 . 考虑输电功率平稳性的水-风-光-储多能互补日前鲁棒优化调度
[J]. 电工技术学报 2023 , 38 (9 ): 2350 -2363 .
[本文引用: 1]
GUO Yi MING Bo HUANG Qiang et al . Robust optimal scheduling of water wind light storage multi energy complementary day ahead considering the stability of transmission power
[J]. Transactions of China Electrotechnical Society 2023 , 38 (9 ): 2350 -2363 .
[本文引用: 1]
[7]
王凯 , 延肖何 , 蒋凯 , 等 . 考虑碳交易的风光储场站参与电力现货市场报价策略与调控方法
[J]. 中国电机工程学报 2023 , 43 (18 ): 7091 -7103 .
[本文引用: 1]
WANG Kai YAN Xiaohe JIANG Kai et al . The bidding strategy and regulation method for the unified wind/photovoltaic/energy storage power stations in electricity spot market considering carbon trading
[J]. Proceedings of the CSEE 2023 , 43 (18 ): 7091 -7103 .
[本文引用: 1]
[8]
ARABI-NOWDEH S NASRI S SAFTJANI P B et al . Multi-criteria optimal design of hybrid clean energy system with battery storage considering off-and on-grid application
[J]. Journal of Cleaner Production 2021 , 290 : 125808 .
[本文引用: 1]
[9]
YAMUJALA S JAIN A SREEKUMAR S et al . Enhancing power systems operational flexibility with ramp products from flexible resources
[J]. Electric Power Systems Research 2022 , 202 : 107599 .
[本文引用: 1]
[10]
SHOFERPOUR A KARIMI A . Improving the flexibility of power systems using transportable battery, transmission switching, demand response, and flexible ramping product market in the presence of high wind power
[J]. IET Renewable Power Generation 2023 , 17 (6 ): 1413 -1435 .
[本文引用: 1]
[11]
吴珊 , 边晓燕 , 张菁娴 , 等 . 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述
[J]. 电工技术学报 2023 , 38 (6 ): 1662 -1677 .
[本文引用: 1]
WU Shan BIAN Xiaoyan ZHANG Jingxian et al . A review of domestic and foreign ancillary services market for improving flexibility of new power system
[J]. Transactions of China Electrotechnical Society 2023 , 38 (6 ): 1662 -1677 .
[本文引用: 1]
[12]
SABERI L ALIZADEH M I MOGHADDAM M P . Optimal scheduling of flexible ramp product and emerging flexible resources considering short-term variability impacts in power system with high RESs penetration: A novel robust UC approach
[J]. International Journal of Electrical Power & Energy Systems 2022 , 142 : 108279 .
[本文引用: 1]
[13]
CHEN K CHEN W LIN C et al . Integrated energy system day-ahead dispatch considering supply-side and demand-side flexibility
[C]// 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2) Taiyuan, China : IEEE , 2021 : 1662 -1667 .
[14]
KHOSHJAHAN M FOTUHI-FIRUZABAD M MOEINI-AGHTAIE M et al . Enhancing electricity market flexibility by deploying ancillary services for flexible ramping product procurement
[J]. Electric Power Systems Research 2021 , 191 : 106878 .
[本文引用: 1]
[15]
HU J SARKER M R WANG J et al . Provision of flexible ramping product by battery energy storage in day-ahead energy and reserve markets
[J]. IET Generation , Transmission & Distribution 2018 , 12 (10 ): 2256 -2264 .
[本文引用: 1]
[16]
ZHANG X HU J WANG H et al . Electric vehicle participated electricity market model considering flexible ramping product provisions
[J]. IEEE Transactions on Industry Applications 2020 , 56 (5 ): 5868 -5879 .
[本文引用: 1]
[17]
TAN W S SHAABAN M . Dual-timescale generation scheduling with nondeterministic flexiramp including demand response and energy storage
[J]. Electric Power Systems Research 2020 , 189 : 106821 .
[本文引用: 1]
[18]
彭超逸 , 陈文哲 , 徐苏越 , 等 . 支持虚拟电厂提供灵活爬坡服务的云边协同市场模型
[J]. 上海交通大学学报 2025 , 59 (2 ): 186 -199 .
DOI:10.16183/j.cnki.jsjtu.2023.240
[本文引用: 2]
虚拟电厂(VPP)拥有一定的负荷时移能力和功率调节能力,具备参与电力市场并提供灵活性爬坡服务(FRPs)的潜能,但受系统需求不确定影响,VPP难以进行准确的市场申报.因此,提出支持VPP参与电力市场并提供FRPs的云边协同市场架构,建立了对应的分布式优化交易模型.市场出清过程由系统运营商和VPP协同交互完成,能够准确引导VPP优化用电曲线并提供灵活爬坡服务.分布式优化模型采用目标级联分析方法迭代求解,并引入启发式约束条件来提升算法的收敛性.最后,在“鸭形曲线”典型场景中验证了所提市场交易模型的有效性,算例结果表明所提模型能有效降低系统运营费用,同时提升可再生能源消纳.
PENG Chaoyi CHEN Wenzhe XU Suyue et al . Modeling of cloud-edge collaborated electricity market considering flexible ramping products provided by VPPs
[J]. Journal of Shanghai Jiao Tong University 2025 , 59 (2 ): 186 -199 .
[本文引用: 2]
[19]
HUANG C MA H YAN Z et al . Portfolio management for a wind-storage system based on distributionally robust optimisation considering a flexible ramping product
[J]. IET Renewable Power Generation 2020 , 14 (16 ): 3192 -3199 .
[本文引用: 1]
[20]
张景淳 , 陈胜 , 彭琰 , 等 . 计及灵活爬坡的气, 电耦合综合能源系统低碳经济调度研究
[J]. 电网技术 2022 , 46 (9 ): 3315 -3325 .
[本文引用: 1]
ZHANG Jingchun CHEN Sheng PENG Yan et al . Low carbon economic scheduling of gas-electric coupling integrated energy system considering flexible ramping products
[J]. Power System Technology 2022 , 46 (9 ): 3315 -3325 .
[本文引用: 1]
[21]
KRAD I GAO D W WU H Y . An assessment of flexibility reserves in stochastic modeling at multiple timescales
[J]. CSEE Journal of Power and Energy Systems 2017 , 3 (1 ): 84 -92 .
[本文引用: 1]
[22]
MIRZAEI M A NAZARI-HERIS M MOHAMMADI-IVATLOO B et al . Network-constrained joint energy and flexible ramping reserve market clearing of power-and heat-based energy systems: A two-stage hybrid IGDT-stochastic framework
[J]. IEEE Systems Journal 2020 , 15 (2 ): 1547 -1556 .
[本文引用: 1]
[23]
PARK H HUANG B BALDICK R . Enhanced flexible ramping product formulation for alleviating capacity shortage in look-ahead commitment
[J]. Journal of Modern Power Systems and Clean Energy 2022 , 10 (4 ): 850 -860 .
[本文引用: 1]
[24]
GHALJEHEI M KHORSAND M . Day-ahead operational scheduling with enhanced flexible ramping product: Design and analysis
[J]. IEEE Transactions on Power Systems 2021 , 37 (3 ): 1842 -1856 .
[本文引用: 1]
[25]
钟佳宇 , 陈皓勇 , 陈武涛 , 等 . 含灵活性资源交易的电力市场实时出清
[J]. 电网技术 2021 , 45 (3 ): 1032 -1041 .
[本文引用: 2]
ZHONG Jiayu CHEN Haoyong CHEN Wutao et al . Real-time clearing of electricity markets with flexible resource transactions
[J]. Power System Technology 2021 , 45 (3 ): 1032 -1041 .
[本文引用: 2]
[26]
JIANG T WU C ZHANG R et al . Flexibility clearing in joint energy and flexibility markets considering TSO-DSO coordination
[J]. IEEE Transactions on Smart Grid 2022 , 14 (2 ): 1376 -1387 .
[本文引用: 1]
[27]
马洪艳 , 贠靖洋 , 严正 . 基于分布鲁棒优化的灵活爬坡备用调度方法
[J]. 中国电机工程学报 2020 , 40 (19 ): 6121 -6132 .
[本文引用: 1]
MA Hongyan YUN Jingyang YAN Zheng . Distributionally robust optimization based dispatch methodology of flexible ramping products
[J]. Proceedings of the CSEE 2020 , 40 (19 ): 6121 -6132 .
[本文引用: 1]
[28]
江婷 , 邓晖 , 陆承宇 , 等 . 电能量和旋转备用市场下电-热综合能源系统低碳优化运行
[J]. 上海交通大学学报 2021 , 55 (12 ): 1650 -1662 .
DOI:10.16183/j.cnki.jsjtu.2021.297
[本文引用: 1]
建立电-热综合能源系统,同时参与电能量市场和旋转备用市场的日前优化决策模型,并将阶梯式碳交易引入该模型中.模型采用条件风险价值方法对新能源和电负荷不确定性风险进行管理,以电-热综合能源系统运营方案成本和碳排放成本最低为目标函数,制定运行计划和安排备用资源.算例分析表明,该模型通过发挥综合能源系统多能互补优势和合理安排备用资源应对不确定性因素引发的风险,提高了能源供应的可靠性、经济性和低碳性.
JIANG Ting DENG Hui LU Chengyu et al . Low-carbon optimal operation of an integrated electricity-heat energy system in electric energy and spinning reserve market
[J]. Journal of Shanghai Jiao Tong University 2021 , 55 (12 ): 1650 -1662 .
[本文引用: 1]
[29]
王蓓蓓 , 仇知 , 丛小涵 , 等 . 基于两阶段随机优化建模的新能源电网灵活性资源边际成本构成的机理分析
[J]. 中国电机工程学报 2021 , 41 (4 ): 1348 -1359 .
[本文引用: 2]
WANG Beibei QIU Zhi CONG Xiaohan et al . Mechanism analysis of flexible resources’ marginal price in new energy grid based on two-stage stochastic optimization modeling
[J]. Proceedings of the CSEE 2021 , 41 (4 ): 1348 -1359 .
[本文引用: 2]
[30]
赵越 , 蔡秋娜 , 王龙 , 等 . 考虑不同需求弹性的爬坡辅助服务市场出清模型
[J]. 电力系统自动化 2024 , 48 (5 ): 48 -57 .
[本文引用: 1]
ZHAO Yue CAI Qiuna WANG Long et al . Clearing model for ramping auxiliary service market considering different demand elasticity
[J]. Automation of Electric Power Systems 2024 , 48 (5 ): 48 -57 .
[本文引用: 1]
[31]
肖云鹏 , 张兰 , 张轩 , 等 . 包含独立储能的现货电能量与调频辅助服务市场出清协调机制
[J]. 中国电机工程学报 2020 , 40 (Sup.1 ): 167 -180 .
[本文引用: 2]
XIAO Yunpeng ZHANG Lan ZHANG Xuan et al . The coordinated market clearing mechanism for spot electric energy and regulating ancillary service incorporating independent energy storage resources
[J]. Proceedings of the CSEE 2020 , 40 (Sup.1 ): 167 -180 .
[本文引用: 2]
考虑需求响应资源和储能容量价值的新型电力系统电源规划方法
1
2023
... 在全球气候变暖、能源和环境危机日益加剧的大背景下,我国将加速推进向含高渗透率可再生能源的新型电力系统建设.由于可再生能源出力的波动性与不确定性,电网需要提前预留灵活性资源,以提供充足的爬坡容量,确保系统功率实时平衡,从而促进风光消纳[1 ] 并降低切负荷概率[2 ] .风力发电、光伏与储能的联合发电系统,作为提升供电可靠性和促进风光消纳的主要方式之一,将成为新能源场站建设的主流趋势. ...
Power system planning considering demand response resources and capacity value of energy storage
1
2023
... 在全球气候变暖、能源和环境危机日益加剧的大背景下,我国将加速推进向含高渗透率可再生能源的新型电力系统建设.由于可再生能源出力的波动性与不确定性,电网需要提前预留灵活性资源,以提供充足的爬坡容量,确保系统功率实时平衡,从而促进风光消纳[1 ] 并降低切负荷概率[2 ] .风力发电、光伏与储能的联合发电系统,作为提升供电可靠性和促进风光消纳的主要方式之一,将成为新能源场站建设的主流趋势. ...
计及爬坡场景覆盖的高比例新能源电网平衡策略研究
1
2022
... 在全球气候变暖、能源和环境危机日益加剧的大背景下,我国将加速推进向含高渗透率可再生能源的新型电力系统建设.由于可再生能源出力的波动性与不确定性,电网需要提前预留灵活性资源,以提供充足的爬坡容量,确保系统功率实时平衡,从而促进风光消纳[1 ] 并降低切负荷概率[2 ] .风力发电、光伏与储能的联合发电系统,作为提升供电可靠性和促进风光消纳的主要方式之一,将成为新能源场站建设的主流趋势. ...
Research on the balance strategy for power grid with high proportion renewable energy considering the ramping scenario coverage
1
2022
... 在全球气候变暖、能源和环境危机日益加剧的大背景下,我国将加速推进向含高渗透率可再生能源的新型电力系统建设.由于可再生能源出力的波动性与不确定性,电网需要提前预留灵活性资源,以提供充足的爬坡容量,确保系统功率实时平衡,从而促进风光消纳[1 ] 并降低切负荷概率[2 ] .风力发电、光伏与储能的联合发电系统,作为提升供电可靠性和促进风光消纳的主要方式之一,将成为新能源场站建设的主流趋势. ...
风储联合系统爬坡事件的日前能量最优平抑方法
1
2021
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
An event-based day-ahead energy optimization method to smooth ramp events of combined wind storage systems
1
2021
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
考虑新能源爬坡的风光火耦合系统源荷匹配性分析及容量优化配置
1
2024
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
Source-load matching analysis and optimal planning of wind-solar-thermal coupled system considering renewable energy ramps
1
2024
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
计及调峰市场交易的储能-新能源-火电多目标优化调度
0
2023
Multi-objective optimization scheduling method considering peak regulating market transactions for energy storage-new energy-thermal power
0
2023
考虑输电功率平稳性的水-风-光-储多能互补日前鲁棒优化调度
1
2023
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
Robust optimal scheduling of water wind light storage multi energy complementary day ahead considering the stability of transmission power
1
2023
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
考虑碳交易的风光储场站参与电力现货市场报价策略与调控方法
1
2023
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
The bidding strategy and regulation method for the unified wind/photovoltaic/energy storage power stations in electricity spot market considering carbon trading
1
2023
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
Multi-criteria optimal design of hybrid clean energy system with battery storage considering off-and on-grid application
1
2021
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
Enhancing power systems operational flexibility with ramp products from flexible resources
1
2022
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
Improving the flexibility of power systems using transportable battery, transmission switching, demand response, and flexible ramping product market in the presence of high wind power
1
2023
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
面向新型电力系统灵活性提升的国内外辅助服务市场研究综述
1
2023
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
A review of domestic and foreign ancillary services market for improving flexibility of new power system
1
2023
... 为了最大限度地提升系统灵活性,文献[3 ]中通过建立风储联合系统来减轻风力发电出力随机性与波动性对电网安全稳定运行的影响,提高系统接纳风力发电的能力;文献[4 6 ]中凭借储能提高风光输出容量,同时利用快速充放电能力平抑爬坡事件稳定输出功率,降低系统净负荷偏差.在参与市场竞标时,风光储场站可以通过调节日前和实时市场出力份额实现跨期套利[7 ] .文献[8 ]中通过改善新能源模型与算法,提高其预测精度,来提高系统整体灵活性.然而,仅将风光储场站整合到系统中,可能仍无法确保它们在实时提供足够爬坡容量.美国加州电力市场(CAISO)和美国中西部电力市场(MISO)均提出基于新型灵活性市场的灵活爬坡产品(flexible ramping products,FRPs)[9 -10 ] ,通过提前调度灵活性资源,来为下一时段内快速变化的净负荷预留容量.FRPs相较备用来说价格更低,部署频率更高,能缓解系统维持实时有功平衡的压力,降低系统运营成本[11 ] .灵活爬坡市场的出现能够充分激发风光储场站等资源灵活性,为其参与市场交易提供平台. ...
Optimal scheduling of flexible ramp product and emerging flexible resources considering short-term variability impacts in power system with high RESs penetration: A novel robust UC approach
1
2022
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
Integrated energy system day-ahead dispatch considering supply-side and demand-side flexibility
0
2021
Enhancing electricity market flexibility by deploying ancillary services for flexible ramping product procurement
1
2021
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
Provision of flexible ramping product by battery energy storage in day-ahead energy and reserve markets
1
2018
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
Electric vehicle participated electricity market model considering flexible ramping product provisions
1
2020
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
Dual-timescale generation scheduling with nondeterministic flexiramp including demand response and energy storage
1
2020
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
支持虚拟电厂提供灵活爬坡服务的云边协同市场模型
2
2025
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
... 该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31 ] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0. ...
Modeling of cloud-edge collaborated electricity market considering flexible ramping products provided by VPPs
2
2025
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
... 该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31 ] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0. ...
Portfolio management for a wind-storage system based on distributionally robust optimisation considering a flexible ramping product
1
2020
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
计及灵活爬坡的气, 电耦合综合能源系统低碳经济调度研究
1
2022
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
Low carbon economic scheduling of gas-electric coupling integrated energy system considering flexible ramping products
1
2022
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
An assessment of flexibility reserves in stochastic modeling at multiple timescales
1
2017
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
Network-constrained joint energy and flexible ramping reserve market clearing of power-and heat-based energy systems: A two-stage hybrid IGDT-stochastic framework
1
2020
... 目前针对FRPs的研究主要集中在系统日前的灵活爬坡调用方法和提供FRPs可行性分析及建模方面[12 14 ] .现有研究表明,任何可实时调度的资源均可提供FRPs,如传统火电机组、储能[15 ] 、电动汽车[16 ] 、需求响应[17 ] 、虚拟电厂[18 ] 、风力发电[19 ] 和电-气耦合系统[20 ] 等.但大部分研究基于单时段传统确定性爬坡问题,未处理风光和负荷误差带来的爬坡需求不确定性.文献[21 ]中利用随机规划方法将不确定性考虑进含灵活爬坡的调度问题,解决了灵活爬坡备用评估与经济调度问题.文献[22 ]中采用信息决策理论处理负荷和风力发电不确定性,同时考虑规避风险和寻求风险策略下的实时调度.上述模型对FRPs建模的基本目标均是增加系统实时的爬坡能力,随着时间颗粒度的细分,日前市场FRPs出清模型在爬坡精度上并不能满足实际需求. ...
Enhanced flexible ramping product formulation for alleviating capacity shortage in look-ahead commitment
1
2022
... 在此基础上,多时间尺度下灵活爬坡建模成为研究重点,文献[23 ]中考虑日前市场与日内灵活性爬坡需求结合,有效缓解了实时爬坡容量短缺的问题;文献[24 ]中改进了现有日前市场灵活需求模型,并通过实时模拟来反映灵活性价值;文献[25 ]中基于预测净负荷误差概率分布对灵活性资源需求进行最优确定,提出了虚拟竞标曲线的两阶段实时市场出清模型,能对机组产生的机会成本设置合理补偿;文献[26 -27 ]则采用鲁棒优化处理净负荷波动,确保系统获取足够爬坡能力来面对最差调度场景,并提出两阶段分布式鲁棒优化的灵活爬坡备用调度方案,有助于降低灵活调节成本.但是以上研究在处理多时间尺度灵活性资源调度问题时,通常基于相同出清间隔进行市场出清,未充分考虑出清间隔缩短带来的影响,在日前每1 h FRPs决策时预留容量并不一定能够应对实时市场更精细的15 min净负荷变化. ...
Day-ahead operational scheduling with enhanced flexible ramping product: Design and analysis
1
2021
... 在此基础上,多时间尺度下灵活爬坡建模成为研究重点,文献[23 ]中考虑日前市场与日内灵活性爬坡需求结合,有效缓解了实时爬坡容量短缺的问题;文献[24 ]中改进了现有日前市场灵活需求模型,并通过实时模拟来反映灵活性价值;文献[25 ]中基于预测净负荷误差概率分布对灵活性资源需求进行最优确定,提出了虚拟竞标曲线的两阶段实时市场出清模型,能对机组产生的机会成本设置合理补偿;文献[26 -27 ]则采用鲁棒优化处理净负荷波动,确保系统获取足够爬坡能力来面对最差调度场景,并提出两阶段分布式鲁棒优化的灵活爬坡备用调度方案,有助于降低灵活调节成本.但是以上研究在处理多时间尺度灵活性资源调度问题时,通常基于相同出清间隔进行市场出清,未充分考虑出清间隔缩短带来的影响,在日前每1 h FRPs决策时预留容量并不一定能够应对实时市场更精细的15 min净负荷变化. ...
含灵活性资源交易的电力市场实时出清
2
2021
... 在此基础上,多时间尺度下灵活爬坡建模成为研究重点,文献[23 ]中考虑日前市场与日内灵活性爬坡需求结合,有效缓解了实时爬坡容量短缺的问题;文献[24 ]中改进了现有日前市场灵活需求模型,并通过实时模拟来反映灵活性价值;文献[25 ]中基于预测净负荷误差概率分布对灵活性资源需求进行最优确定,提出了虚拟竞标曲线的两阶段实时市场出清模型,能对机组产生的机会成本设置合理补偿;文献[26 -27 ]则采用鲁棒优化处理净负荷波动,确保系统获取足够爬坡能力来面对最差调度场景,并提出两阶段分布式鲁棒优化的灵活爬坡备用调度方案,有助于降低灵活调节成本.但是以上研究在处理多时间尺度灵活性资源调度问题时,通常基于相同出清间隔进行市场出清,未充分考虑出清间隔缩短带来的影响,在日前每1 h FRPs决策时预留容量并不一定能够应对实时市场更精细的15 min净负荷变化. ...
... 为验证所建立模型的有效性,本文参考文献[29 ]中机组和负荷数据,并加入风光储场站进行测试,该风光储场站中,风光装机容量分别是100 MW与75 MW,储能容量15 MW/60 MW·h;机组和风光储场站具体参数见附录A中的表A1和表A2,其中G1~G4为火电机组,G5~G6为燃气机组,均自愿参加灵活爬坡市场且无需对FRPs进行报价,FRPs价格由机会成本确定.假设风光储场站内仅储能参与电能量市场充放电报价,且实时市场电能量市场输出功率正偏差和负偏差的惩罚系数[31 ] 分别为0.95和1.05.弃风光和弃负荷惩罚假设分别设为708 元/(MW·h)和4 963元/(MW·h)[25 ,29 ] . ...
Real-time clearing of electricity markets with flexible resource transactions
2
2021
... 在此基础上,多时间尺度下灵活爬坡建模成为研究重点,文献[23 ]中考虑日前市场与日内灵活性爬坡需求结合,有效缓解了实时爬坡容量短缺的问题;文献[24 ]中改进了现有日前市场灵活需求模型,并通过实时模拟来反映灵活性价值;文献[25 ]中基于预测净负荷误差概率分布对灵活性资源需求进行最优确定,提出了虚拟竞标曲线的两阶段实时市场出清模型,能对机组产生的机会成本设置合理补偿;文献[26 -27 ]则采用鲁棒优化处理净负荷波动,确保系统获取足够爬坡能力来面对最差调度场景,并提出两阶段分布式鲁棒优化的灵活爬坡备用调度方案,有助于降低灵活调节成本.但是以上研究在处理多时间尺度灵活性资源调度问题时,通常基于相同出清间隔进行市场出清,未充分考虑出清间隔缩短带来的影响,在日前每1 h FRPs决策时预留容量并不一定能够应对实时市场更精细的15 min净负荷变化. ...
... 为验证所建立模型的有效性,本文参考文献[29 ]中机组和负荷数据,并加入风光储场站进行测试,该风光储场站中,风光装机容量分别是100 MW与75 MW,储能容量15 MW/60 MW·h;机组和风光储场站具体参数见附录A中的表A1和表A2,其中G1~G4为火电机组,G5~G6为燃气机组,均自愿参加灵活爬坡市场且无需对FRPs进行报价,FRPs价格由机会成本确定.假设风光储场站内仅储能参与电能量市场充放电报价,且实时市场电能量市场输出功率正偏差和负偏差的惩罚系数[31 ] 分别为0.95和1.05.弃风光和弃负荷惩罚假设分别设为708 元/(MW·h)和4 963元/(MW·h)[25 ,29 ] . ...
Flexibility clearing in joint energy and flexibility markets considering TSO-DSO coordination
1
2022
... 在此基础上,多时间尺度下灵活爬坡建模成为研究重点,文献[23 ]中考虑日前市场与日内灵活性爬坡需求结合,有效缓解了实时爬坡容量短缺的问题;文献[24 ]中改进了现有日前市场灵活需求模型,并通过实时模拟来反映灵活性价值;文献[25 ]中基于预测净负荷误差概率分布对灵活性资源需求进行最优确定,提出了虚拟竞标曲线的两阶段实时市场出清模型,能对机组产生的机会成本设置合理补偿;文献[26 -27 ]则采用鲁棒优化处理净负荷波动,确保系统获取足够爬坡能力来面对最差调度场景,并提出两阶段分布式鲁棒优化的灵活爬坡备用调度方案,有助于降低灵活调节成本.但是以上研究在处理多时间尺度灵活性资源调度问题时,通常基于相同出清间隔进行市场出清,未充分考虑出清间隔缩短带来的影响,在日前每1 h FRPs决策时预留容量并不一定能够应对实时市场更精细的15 min净负荷变化. ...
基于分布鲁棒优化的灵活爬坡备用调度方法
1
2020
... 在此基础上,多时间尺度下灵活爬坡建模成为研究重点,文献[23 ]中考虑日前市场与日内灵活性爬坡需求结合,有效缓解了实时爬坡容量短缺的问题;文献[24 ]中改进了现有日前市场灵活需求模型,并通过实时模拟来反映灵活性价值;文献[25 ]中基于预测净负荷误差概率分布对灵活性资源需求进行最优确定,提出了虚拟竞标曲线的两阶段实时市场出清模型,能对机组产生的机会成本设置合理补偿;文献[26 -27 ]则采用鲁棒优化处理净负荷波动,确保系统获取足够爬坡能力来面对最差调度场景,并提出两阶段分布式鲁棒优化的灵活爬坡备用调度方案,有助于降低灵活调节成本.但是以上研究在处理多时间尺度灵活性资源调度问题时,通常基于相同出清间隔进行市场出清,未充分考虑出清间隔缩短带来的影响,在日前每1 h FRPs决策时预留容量并不一定能够应对实时市场更精细的15 min净负荷变化. ...
Distributionally robust optimization based dispatch methodology of flexible ramping products
1
2020
... 在此基础上,多时间尺度下灵活爬坡建模成为研究重点,文献[23 ]中考虑日前市场与日内灵活性爬坡需求结合,有效缓解了实时爬坡容量短缺的问题;文献[24 ]中改进了现有日前市场灵活需求模型,并通过实时模拟来反映灵活性价值;文献[25 ]中基于预测净负荷误差概率分布对灵活性资源需求进行最优确定,提出了虚拟竞标曲线的两阶段实时市场出清模型,能对机组产生的机会成本设置合理补偿;文献[26 -27 ]则采用鲁棒优化处理净负荷波动,确保系统获取足够爬坡能力来面对最差调度场景,并提出两阶段分布式鲁棒优化的灵活爬坡备用调度方案,有助于降低灵活调节成本.但是以上研究在处理多时间尺度灵活性资源调度问题时,通常基于相同出清间隔进行市场出清,未充分考虑出清间隔缩短带来的影响,在日前每1 h FRPs决策时预留容量并不一定能够应对实时市场更精细的15 min净负荷变化. ...
电能量和旋转备用市场下电-热综合能源系统低碳优化运行
1
2021
... 该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31 ] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0. ...
Low-carbon optimal operation of an integrated electricity-heat energy system in electric energy and spinning reserve market
1
2021
... 该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31 ] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0. ...
基于两阶段随机优化建模的新能源电网灵活性资源边际成本构成的机理分析
2
2021
... 为验证所建立模型的有效性,本文参考文献[29 ]中机组和负荷数据,并加入风光储场站进行测试,该风光储场站中,风光装机容量分别是100 MW与75 MW,储能容量15 MW/60 MW·h;机组和风光储场站具体参数见附录A中的表A1和表A2,其中G1~G4为火电机组,G5~G6为燃气机组,均自愿参加灵活爬坡市场且无需对FRPs进行报价,FRPs价格由机会成本确定.假设风光储场站内仅储能参与电能量市场充放电报价,且实时市场电能量市场输出功率正偏差和负偏差的惩罚系数[31 ] 分别为0.95和1.05.弃风光和弃负荷惩罚假设分别设为708 元/(MW·h)和4 963元/(MW·h)[25 ,29 ] . ...
... ,29 ]. ...
Mechanism analysis of flexible resources’ marginal price in new energy grid based on two-stage stochastic optimization modeling
2
2021
... 为验证所建立模型的有效性,本文参考文献[29 ]中机组和负荷数据,并加入风光储场站进行测试,该风光储场站中,风光装机容量分别是100 MW与75 MW,储能容量15 MW/60 MW·h;机组和风光储场站具体参数见附录A中的表A1和表A2,其中G1~G4为火电机组,G5~G6为燃气机组,均自愿参加灵活爬坡市场且无需对FRPs进行报价,FRPs价格由机会成本确定.假设风光储场站内仅储能参与电能量市场充放电报价,且实时市场电能量市场输出功率正偏差和负偏差的惩罚系数[31 ] 分别为0.95和1.05.弃风光和弃负荷惩罚假设分别设为708 元/(MW·h)和4 963元/(MW·h)[25 ,29 ] . ...
... ,29 ]. ...
考虑不同需求弹性的爬坡辅助服务市场出清模型
1
2024
... 该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31 ] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0. ...
Clearing model for ramping auxiliary service market considering different demand elasticity
1
2024
... 该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31 ] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0. ...
包含独立储能的现货电能量与调频辅助服务市场出清协调机制
2
2020
... 该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31 ] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0. ...
... 为验证所建立模型的有效性,本文参考文献[29 ]中机组和负荷数据,并加入风光储场站进行测试,该风光储场站中,风光装机容量分别是100 MW与75 MW,储能容量15 MW/60 MW·h;机组和风光储场站具体参数见附录A中的表A1和表A2,其中G1~G4为火电机组,G5~G6为燃气机组,均自愿参加灵活爬坡市场且无需对FRPs进行报价,FRPs价格由机会成本确定.假设风光储场站内仅储能参与电能量市场充放电报价,且实时市场电能量市场输出功率正偏差和负偏差的惩罚系数[31 ] 分别为0.95和1.05.弃风光和弃负荷惩罚假设分别设为708 元/(MW·h)和4 963元/(MW·h)[25 ,29 ] . ...
The coordinated market clearing mechanism for spot electric energy and regulating ancillary service incorporating independent energy storage resources
2
2020
... 该市场中不需要针对FRPs服务单独报价,根据电力市场边际成本理论[28 31 ] 可知,电能量市场的清算价格由边际成本决定,FRPs的出清价格代表其提供最少FRPs对应的影子价格[18 ,30 ] ,在系统爬坡能力充足时,对应爬坡产品价格为0. ...
... 为验证所建立模型的有效性,本文参考文献[29 ]中机组和负荷数据,并加入风光储场站进行测试,该风光储场站中,风光装机容量分别是100 MW与75 MW,储能容量15 MW/60 MW·h;机组和风光储场站具体参数见附录A中的表A1和表A2,其中G1~G4为火电机组,G5~G6为燃气机组,均自愿参加灵活爬坡市场且无需对FRPs进行报价,FRPs价格由机会成本确定.假设风光储场站内仅储能参与电能量市场充放电报价,且实时市场电能量市场输出功率正偏差和负偏差的惩罚系数[31 ] 分别为0.95和1.05.弃风光和弃负荷惩罚假设分别设为708 元/(MW·h)和4 963元/(MW·h)[25 ,29 ] . ...