水下管口附近脉动气泡溃灭及射流特性实验和数值研究

doi:10.16183/j.cnki.jsjtu.2023.118

水下管口附近脉动气泡溃灭及射流特性实验和数值研究

张越尧^a, 乔峰^a, 吕详^a, 张天源^b, 韩蕊^,^a, 李帅^b

哈尔滨工程大学 a. 核科学与技术学院; b. 船舶工程学院,哈尔滨 150001

Pulsating Bubble Collapse and Jet Characteristics Near the Nozzle of Underwater Tube

ZHANG Yueyao^a, QIAO Feng^a, LÜ Xiang^a, ZHANG Tianyuan^b, HAN Rui^,^a, LI Shuai^b

a. College of Nuclear Science and Technology; b. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China

通讯作者: 韩蕊,副教授; E-mail:hanrui@hrbeu.edu.cn.

责任编辑: 李博文

收稿日期: 2023-04-3 修回日期: 2023-05-18 接受日期: 2023-06-29

基金资助:

国家自然科学基金(12072087)
黑龙江省自然科学基金(YQ2022E017)
国家级大学生创新创业训练计划(202210217185)

Received: 2023-04-3 Revised: 2023-05-18 Accepted: 2023-06-29

作者简介 About authors

张越尧(2002—),本科生,从事气泡动力学研究.

摘要

通过实验和数值方法研究水下管口附近脉动气泡溃灭及射流特性.在实验方面,采用电火花放电技术产生厘米级脉动气泡,并利用高速摄影捕捉气泡的瞬态动力学行为;在数值方面,采用基于势流理论的边界积分方法模拟气泡与管壁的耦合作用.实验发现,脉动气泡在管口附近溃灭过程中会产生指向管内的射流,进而威胁水中管道设备的结构安全,数值模拟结果和实验现象吻合良好.通过对气泡距管口距离与管口半径之比γ和气泡的最大半径与管口半径之比λ两个无量纲参数进行系统研究发现:当γ≤1.5时,气泡溃灭阶段只会产生指向管内的射流,当γ>1.5时,气泡产生指向管内射流的趋势随λ的增加而增加;总体而言,气泡产生向下射流的速度随λ的增加而增加,随γ的增大先增大后减小.当γ<0时,射流速度随λ和γ的变化很小,但射流宽度随两者的增加而增加;当γ>0时,射流速度随γ的增大先增大后减小.研究结论为水下管口附近气泡溃灭的动力学行为提供了重要参考.

关键词： 气泡动力学; 近管口气泡; 边界积分法; 高速摄影

Abstract

In this paper, the characteristics of a pulsating bubble collapse near the nozzle of an underwater tube were investigated both experimentally and numerically. The experiments involved generating pulsating bubbles using the electric spark discharge technology and capturing their transient behavior by high-speed photography. A boundary integral method based on potential flow theory was used to simulate the coupling between the bubble and the tube in the numerical simulation. The results show that the collapsing bubble can produce a jet directed towards the tube, which poses a safety threat to the pipeline equipment. The numerical simulation results and experimental phenomena are in good agreement. In addition, a systematic study was conducted of two dimensionless parameters, i.e., the ratio of bubble distance from the tube nozzle and the tube nozzle radius γ and the ratio of the maximum radius of the bubble and the tube nozzle radius λ. The findings indicate that when γ≤1.5, bubbles will only produce jets pointing into the tube during the collapse phase, and when γ>1.5, the tendency for bubbles to produce jets pointing into the tube increases as λ increases. Moreover, the maximum velocity of the downward jet increases with the increase of λ, and increases and then decreases with the increase of γ. Additionally, the maximum velocity of the downward jet generally increases with the increase of λ and increases and then decreases with the increase of γ. This study provides valuable insights into the dynamic behavior of bubble collapse near the nozzle of a submerged tube, which can provide safety measures for pipeline equipment.

Keywords： bubble dynamics; bubbles near the nozzle of the tube; boundary integral method; high-speed photography

PDF (22230KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张越尧, 乔峰, 吕详, 张天源, 韩蕊, 李帅. 水下管口附近脉动气泡溃灭及射流特性实验和数值研究[J]. 上海交通大学学报, 2025, 59(1): 99-110 doi:10.16183/j.cnki.jsjtu.2023.118

ZHANG Yueyao, QIAO Feng, LÜ Xiang, ZHANG Tianyuan, HAN Rui, LI Shuai. Pulsating Bubble Collapse and Jet Characteristics Near the Nozzle of Underwater Tube[J]. Journal of Shanghai Jiaotong University, 2025, 59(1): 99-110 doi:10.16183/j.cnki.jsjtu.2023.118

空化现象一直是工程界的热点问题,通常是由于局部压力降至蒸汽压力以下而引起的,该现象广泛发生在水力机械^[1]、血管^[2]、超声波清洗^[3]等流动的流体中.空化气泡溃灭时产生的局部高压和高速射流会对螺旋桨、水轮机、进水阀等水力机械造成严重损害^[4⇓⇓-7],对实际机械维护十分不利.这一过程在核电、石油、化工等领域十分常见^[8].此外,当直接接触冷凝换热现象发生时,也会产生大量空化气泡混入蒸汽射流中^[9],并随着喷管不断喷出.这些气泡的不断产生与溃灭导致过高的压力载荷,不仅会改变冷凝换热的热量传递过程,还会导致水中机械系统运行异常,产生噪声与振动,甚至会剥蚀结构表面.因此,为延长不同领域水中仪器设备的使用寿命,需尽量减少空化气泡对其的影响.在工程领域内,空化气泡往往出现在导流管、文丘里管等各种输送液体的管道中^[10].与在自由液面等无界界面中产生的空化气泡不同,在管道附近产生的气泡具有非对称式膨胀、收缩^[11]、产生极高速度射流^[12]等特征.为深入理解这一复杂过程及气泡溃灭时产生射流对水力机械的影响,研究管口附近的气泡动力学特性十分必要.

喷墨打印机的发明催生了有关管内气泡动力学的研究.在喷墨打印机中,喷嘴出口狭窄流道中,液滴喷出时掺杂大量气泡,Yuan等^[13]对气泡射流式喷墨打印机中气泡的动力学特性进行了研究;Ory等^[14]利用数值模拟方法探究存有黏性液体的窄管中,气泡增长和溃灭的具体过程,并控制雷诺数Re、斯坦顿数St、韦伯数We等无量纲参数,以探究表面张力、初始气泡压力及温度等对该过程的影响.近年来,对管内气泡动力学的研究更加深入,马兆伟等^[15]研究了气泡在文丘里气泡发生器喉部和扩张段处的运动和碎化特性,将气泡在管内的运动分为了4个阶段;徐明等^[16]和Ni等^[17]结合电火花气泡实验和边界积分法探究了圆管内气泡的脉动过程,记录了气泡的膨胀、溃灭及第一周期结束后环状气泡的产生;Zhang等^[18]研究了圆管中电火花放电产生气泡的动力学行为,并讨论了气泡脉动末期产生的自由液面射流的特性;Li等^[19]研究了管内激光诱导气泡在不同初始条件下的动力学行为,将气泡收缩过程中产生的指向管前端的轴向射流按照崩塌模式分为一维、过渡和三维3种类型;Wang等^[20]使用高速摄影技术研究了电火花放电产生气泡在浸没于水中的水平刚性管内的动力学特性,进一步研究了当气泡偏离管道中心时其动力学特性的变化;Xu等^[21]和Wang等^[22]通过使用管阻法研究了在瞬态过程中,圆管和具有截头圆锥形状封闭端的管中产生的空化气泡的动力学行为;Ren等^[10]对刚性变截面管的对称轴上单个空化气泡的动力学特征进行了研究,提出气泡射流速度的标度定律, 通过研究气泡整个周期中周围的流场变化,得到维护液压管道结构安全的相应措施,同时有助于对更加复杂几何形状的管状管道中的气泡动力学特性进行研究.综上所述,现有的研究多关注管内气泡的动力学特性,鲜有对管口附近气泡动力学特性的相关研究.

利用水下放电生成脉动气泡的技术及高速摄影的实验方法,研究气泡在近管口处的膨胀、坍塌、高速射流的形成等动力学行为,建立基于势流理论的边界积分模型,通过网格与时间步的收敛性分析验证数值模型的正确性和可行性.将该数值模型与实验工况进行对比研究,获取气泡周围流场的速度与压力,以揭示气泡行为背后的力学机理.最后,探讨距离与尺度比两个重要的无量纲参数对气泡射流的影响,以期指导工程应用,减少管口附近气泡对仪器设备的损害.

1 实验设置

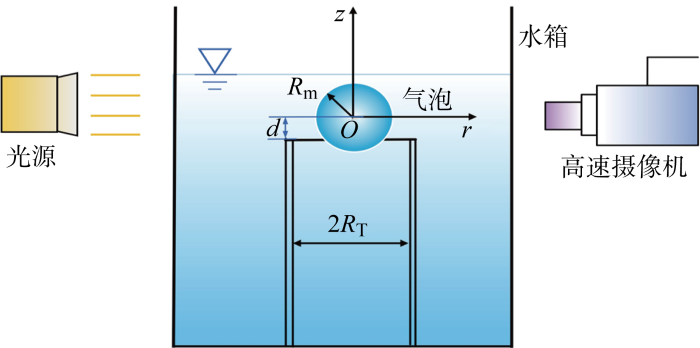
本实验在200 mm×200 mm×400 mm的水箱中进行,环境温度处于约20 ℃的室温下,水深约为150 mm.在水箱中放置一个外径、内径、壁厚与高度分别为20、17、1.5、100 mm的刚性管,将其下端密封,经简化后的实验工况如图1所示.图中,R_m为气泡的初始直径;d为气泡球心与管口之间的距离;R_T为圆柱形管口的半径.后续开展数值模拟时采用柱坐标系,初始气泡中心为原点O,r轴水平向右,z轴铅直向上.实验采用水下放电方法生成脉动气泡^[23].利用两根直径约为0.23 mm的铜合金导线相交并接触在一点上,该点即为原点O.铜丝搭接后紧贴刚性管外壁与电源相连.电容器对外界放电时,交叉点铜丝燃烧,该点处温度急剧升高,产生的大量热量使周围流体汽化,从而产生厘米尺度的气泡.由于细铜线直径远小于气泡与管口直径,所以其对气泡的脉动过程的影响可忽略不计.展示3个典型的实验工况,即气泡初始中心分别位于刚性管管口上方、管口平面与管口下方.水箱两侧分别放置连续光源与 18 000 帧/s的高速摄像机,可清晰地捕捉到较长时间尺度上的瞬态气泡行为,便于实验的图像分析.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 实验装置示意图

Fig.1 Schematic diagram of experimental setup

2 基本理论与数值模型

2.1 基本控制方程

根据格林公式与Laplace方程可进一步获得边界积分方程^[24],即流域内任意一点的函数值可采用边界上的值及法向导数表示

$\begin{array}{l} α (p, t) ϕ (p, t) = \underset{S}{\int \int} [\frac{\partial ϕ (q, t)}{\partial n} G (p, q) - \\ ϕ (q, t) \frac{\partial G (p, q)}{\partial n}] d S \end{array}$

(1)

式中:p为流场控制点的位置矢量;q为边界积分点的位置矢量;S为边界面;α为p点观察流场的立体角;ϕ为流场上节点的速度势;t为时间;n为边界上的法向量,以指向流场外部为正;G为格林函数,G(p, q)= ${|p - q|}^{- 1}$ .

气泡表面上需要满足的动力学和运动学边界条件^[25]分别为

$\begin{matrix} \frac{d ϕ}{d t} = \frac{{|\nabla ϕ|}^{2}}{2} + \frac{p_{\infty}}{ρ} - \frac{p_{b}}{ρ} - g z \end{matrix}$

(2)

$\frac{d p}{d t} = \nabla ϕ$

(3)

式中:ρ为流体的密度;z为柱坐标系下位置矢量p在重力方向上的分量;p_∞表示z=0时,所在平面无穷远处的流场静压;p_b为气泡内部的气体压力;g为重力加速度.

假设气泡内部的不可冷凝气体满足理想气体绝热方程,在忽略液体表面张力的情况下,p_b可按照下述公式^[26]计算

$\begin{matrix} p_{b} = p_{v} + p_{0} {(\frac{V_{0}}{V})}^{κ} \end{matrix}$

(4)

式中:p_v为可冷凝气体的饱和蒸汽压,取值为 2 337 Pa;p₀与V₀分别为气泡初始时刻的内部压力与体积;V为某一时刻的气泡体积;κ为不可冷凝气体的绝热指数,κ=1.4.

管壁上满足不可穿透边界条件,即

$\begin{matrix} \frac{\partial ϕ}{\partial n} = 0 \end{matrix}$

(5)

使用边界积分法对气泡运动过程的求解步骤如下.首先,结合已知的瞬时气泡和管口液面处的速度势分布,利用Laplace方程与式(1)计算得到气泡表面法向速度ϕ_n;其次,利用差分方程代替偏微分方程解得气泡表面切向速度ϕ_τ, 将其与法向速度合成计算,得到气泡表面实际速度∇ϕ;最后,应用式(3)计算出新的节点位置,同时利用式(2)不断计算新的速度势.

为更深入地探究圆管对气泡脉动的影响,引入开尔文冲量I,便于更全面地分析管外气泡的动力学特性.其表达示为

$\begin{matrix} I = \underset{V}{\int \int \int} \nabla ϕ d V = \underset{S}{\int \int} ϕ n d S \end{matrix}$

(6)

2.2 无量纲化

为使研究工作具有普遍意义,将所有研究特征变量无量纲化.即以R_T、Δp、R_T(ρ/Δp)¹^/²、R_T(Δp/ρ)¹^/²及(Δp/ρ)¹^/²分别作为长度、压力、时间、速度势及速度的特征量,将相应的变量无量纲化.Δp为压力差,使用Δp=p_∞-p_v计算.设置管口内圆半径R_T=8.5 mm,水密度ρ=1 000 kg/m³.

分别定义强度参数ε、距离参数γ、尺度比参数λ、半径参数R₀等重要无量纲参数如下:

$\begin{array}{l} ε = p_{0} / Δ p, γ = z / R_{T}, \\ λ = R_{m} / R_{T}, R_{0} = R / R_{T} \end{array}$

(7)

式中:R为某一瞬时时刻的气泡半径.通过调节ε得到不同半径的气泡.

数值模型中所用的时间步长计算公式^[27]如下:

$Δ t = \frac{Δ ϕ}{m a x |1 + 0.5 \nabla {|ϕ|}^{2} - ε {(\frac{V_{0}}{V})}^{κ} - δ^{2} z|}$

(8)

式中:Δϕ为单步最大的速度势改变量;δ=(ρgR_T/Δp)^1/2.

3 实验结果分析与讨论

3.1 收敛性分析

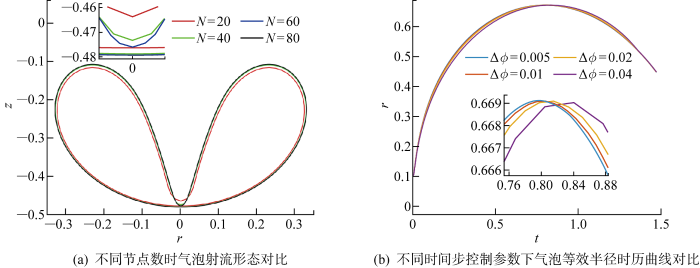
为确保数值模型正确可行,从网格与时间步两方面对所提数值模型进行收敛性分析.选用ε为100,γ为0时的工况分析网格的收敛性.选用4种不同的初始气泡网格节点数,即N=20, 40, 60, 80时,分析网格的收敛性.不同节点数下射流即将穿透气泡下表面时的气泡形态如图2(a)所示.由图可知,当节点数N≥40时,气泡轮廓基本重合,当N分别为20、40、60、80时,气泡的最大等效半径分别为 0.667 890、0.668 900、0.669 110、0.669 180,最大半径与最小半径的误差不足0.2%,可得到收敛的结果,计算模型具有较好的网格收敛性.采用龙格-库塔(Runge-Kutta)显式算法模拟近管口处的气泡与圆管相互作用的过程,可通过修改时间步控制参数,对该算法进行时间步的收敛性分析.取时间步控制参数分别为0.005、0.01、0.02、0.04进行计算.气泡的无量纲等效半径随着时间步的变化曲线如图2(b)所示,当时间步控制参数Δϕ≥0.01时,两条曲线基本重合,气泡的最大半径分别为 0.669 110、0.669 108、0.669 101、0.669 051,半径的变化量随Δϕ的减小而逐渐减小.当0.005≤Δϕ≤0.01时,差别仅在 0.000 3% 左右,证明了所建数值模型的可行性.由此,节点数与时间步的收敛性得到证明.为保证程序的计算精度和节省计算成本,选取N=40,Δϕ=0.01作为数值模拟的对应参数.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 节点数与时间步的收敛性验证

Fig.2 Verification of convergence in number of nodes and time step

3.2 典型工况分析

选定3个典型γ下的气泡脉动过程,结合数值模拟对实验过程中产生的物理现象进行力学机理分析.

3.2.1 气泡初始中心位于管口上方

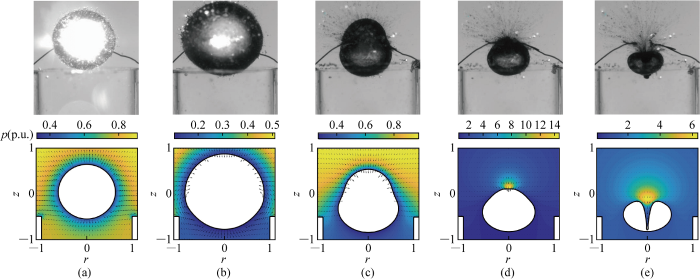
实验中气泡初始中心位于管口上方4.17 mm处,其最大半径R_m=7.26 mm,对应无量纲参数γ=0.49,λ=0.85,ε=55,气泡初始无量纲半径R₀=0.16.气泡运动典型形态实验图与相应的数值结果对比如图3所示,在数值结果图中,不同颜色的区域代表流场内的不同压力,见对应的无量纲压力云图.其中,每张实验图片的宽度对应的长度为18 mm.实验时刻按编号顺序分别为 0.4、1.1、1.7、1.8、1.9.数值模拟时刻按编号顺序分别为0.4、1.1、1.6、1.7、1.8,时间单位为ms.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 管口上方处产生气泡的实验现象与数值模拟对比

Fig.3 Comparison of experimental phenomena and numerical simulations of bubbles generated at the top of the nozzle

初始时刻,铜丝燃烧使得周围液体被汽化,产生一个高温高压的气核,并在内部高压驱动下迅速膨胀,气泡内部压力随之迅速减小.如图3(a)所示,气泡发生过度膨胀^[28],其内部压力低于周围静水压力,此时,气泡将由于惯性继续膨胀直至体积达到最大值,如图3(b)所示.在此过程中,由于管内液体的阻碍,气泡下方流体无法排开,气泡底部膨胀受限,而气泡上半部分近似球形膨胀,使气泡呈现出明显的椭球形.气泡坍塌并产生射流的过程见图3(c)~3(e).在达到最大体积后,气泡在内外压力差作用下开始收缩.在坍塌阶段,气泡下方流体受到圆管的阻碍而无法自由地流向气泡,从而抑制其底部收缩,而上方流体向下的运动几乎不受影响.因此,气泡上半部分收缩较快,导致气泡在坍塌前期呈现出“梨”形,如图3(c)所示.Li等^[29]提到,气泡表面运动速度快的部分对周围环境造成扰动更大,更易形成局部高压区.在坍塌阶段后期,气泡上半部分快速收缩,其周围流体快速流向气泡,在气泡上方逐渐形成局部高压区,如图3(d)所示.在此高压区作用下,气泡顶部坍塌速度进一步增大,最终形成向下射流,在此“正反馈”作用下,射流速度最高可达131 m/s.

3.2.2 气泡初始中心位于管口平面

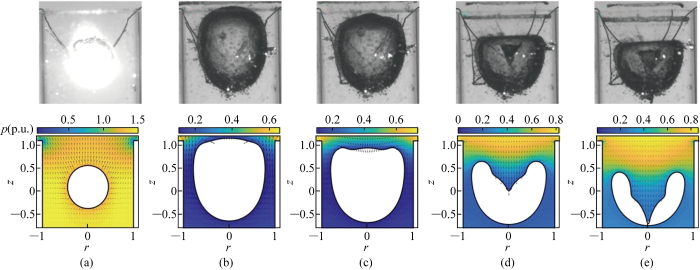
在此实验中,气泡初始中心位于管口平面处,其最大半径R_m=7.41 mm,对应无量纲参数γ=0,λ=0.87,ε=57,R₀=0.16.气泡运动典型形态实验与数值结果对比与对应的无量纲压力云图,如图4所示.每张实验图片的宽度对应的长度为18 mm.实验时刻按编号顺序分别为0.6、1.0、1.7、1.8、2.1.数值模拟时刻按编号顺序分别为0.6、1.0、1.6、1.7、1.8,单位为ms.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 在管口平面产生气泡的实验现象与数值模拟对比

Fig.4 Comparison of experimental phenomena and numerical simulations of bubbles generated at the plane of the nozzle

起始阶段,气泡在内部高压推动下迅速膨胀.值得注意的是,气泡下方在径向上的膨胀受到管壁的限制,气泡的整体形状明显偏离球形(见图4(b)).这种形态与初始中心位于管口上方的气泡形态形成了直观的对比.同时,由于气泡上下部分处于不同的流场环境,其曲率在管口平面附近产生剧烈变化.在气泡坍塌过程中,管口平面以下的流体在管壁和气泡的限制下无法汇入气泡中心,导致气泡下半部分在坍塌阶段几乎保持静止,气泡的收缩几乎全部由上半部分气泡完成(见如图4(c)).气泡上方在收缩过程中逐渐形成高压区,最终导致气泡产生指向管内的高速射流.

3.2.3 气泡初始中心位于管口下方

在此实验中,气泡初始中心位于管口下方8.7 mm处,其R_m=6.95 mm,对应无量纲参数γ=-1.02,λ=0.82,ε=50,R₀=0.16.气泡运动典型形态实验与数值结果对比与对应的无量纲压力云图如图5所示.实验时刻按编号顺序分别为0.5、1.5、1.8、2.2、2.4.数值模拟时刻按编号顺序分别为0.5、1.6、1.8、2.3、2.6,时间单位为ms.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 在管口下方产生气泡的实验现象与数值模拟对比

Fig.5 Comparison of experimental phenomena and numerical simulations of bubbles generated below the nozzle

起始阶段,由于整个气泡完全浸没在管内液体中,受到圆管两侧边界的限制作用,呈现出明显的“横窄竖宽”的椭球形形态(见图5(b)).在气泡坍塌过程中,气泡上方更接近管口平面位置,受到圆管的限制作用更小,因而气泡顶部率先收缩,形态逐渐变得扁平(图5(c)).在气泡坍塌过程中,管口流体径向流动受到圆管的限制,其速度远小于流体轴向的流动速度,故气泡上方逐渐形成均匀的高压区(见图5(d)).气泡受到此均匀高压的作用最终形成比前两种工况更宽的射流.

3.3 尺度比参数和距离参数的影响

影响水下管口附近气泡运动特性的主要因素包括γ与λ,本文主要讨论无量纲参数对气泡射流方向和速度的影响.

3.3.1 气泡射流方向

在ε=250的条件下,不同距离参数气泡顶部和底部节点位置随时间的变化曲线如图6所示,其中虚线表示气泡顶部节点位置随着时间的变化,实线表示气泡的底部节点位置随着时间的变化.由图可知,气泡脉动周期随距离参数的减小而增大.当γ≤0时,气泡脉动周期随时间的变化程度较大;当γ>0时,气泡脉动周期随时间的变化程度很小.这是由于当γ很小时,气泡下方区域一直受到圆管的限制作用,在塌缩阶段不会向上收缩.因此,在这些实验工况下,气泡的收缩全靠其上方区域完成,最终产生指向管内的射流.该种限制作用在γ>1后显著减弱.在3.2节中,研究的3种典型实验工况都处于该γ范围内,因此气泡射流方向也全部指向管口.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同距离参数时气泡顶部及底部节点位置随时间的变化曲线

Fig.6 Top and tail nodes of the bubble over time at different distances

不同γ与λ时射流方向的变化情况如图7所示.倒三角标记表示第一周期内穿透气泡表面的射流,即强射流,射流方向沿着管口向下;菱形标记表示第一周期内存在向下射流的趋势,但射流未能穿透气泡表面,即弱射流.在数值模拟中,由于当前的数值模型未考虑流体的可压缩性及气泡溃灭后的能量损失,因此将第一周期结束后未产生射流的情况记为无射流状态,使用圆形标记进行表示.由于当气泡的产生位置位于管内时,即γ<0时,气泡最终均会产生向下的射流,故相应数据不计入相图之中.设置的相应参数分别为0≤γ≤4,0.65≤λ≤1,R₀=0.1.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 距离参数-尺度比参数-射流方向散点图

Fig.7 Distance parameter-scale ratio parameter-jet direction scatter plot

由图7可知,在本文计及的工况中,当γ≤1.5时,λ的改变不影响气泡最终的射流方向,气泡总产生向下的强射流;当 2≤γ≤2.5时,较大的λ会使得气泡在第一周期最终产生向下的强射流,较小的λ会使气泡在第一周期内产生弱射流或甚至只有产生射流的趋势.随着γ继续增大,气泡射流达到临界状态,即无射流状态,所需的γ越大;当γ=3时,气泡在第一周期内无强射流产生,在较大的λ下会产生弱射流;当3.5≤γ≤4时,在所研究的λ范围内,气泡在第一周期均不会产生明显的射流.此特性可应用于工程实际应用中,以减小气泡溃灭产生的高压对工程器械的损伤.

3.3.2 气泡射流速度

在本小节设置的数值模拟初始条件之下,气泡于第一周期内所产生的射流均为指向管内的方向,即向下的射流.因此,本节着重研究射流速度v_jet随无量纲参数的变化关系,包括强射流与弱射流.本节设置的实验参数为-1≤γ≤2.5,0.65≤λ≤1,R₀=0.1.

由图6可知,当气泡距离管口较近时,气泡受到管口的限制较大,其半径变化随着λ变化相对明显,变化范围在0.01~0.02,其相应的λ难以统一,因此使用ε代替尺度比参数更便于统一所固定的变量.但对于整体的物理现象阐述上,为使读者对气泡尺度有更直观的认识,选取尺度比参数作为研究对象.ε分别为100、125、150、175、200、225、250、275、300时,分别对应的λ约为0.67、0.73、0.78、0.82、0.86、0.90、0.93、0.96、0.99.

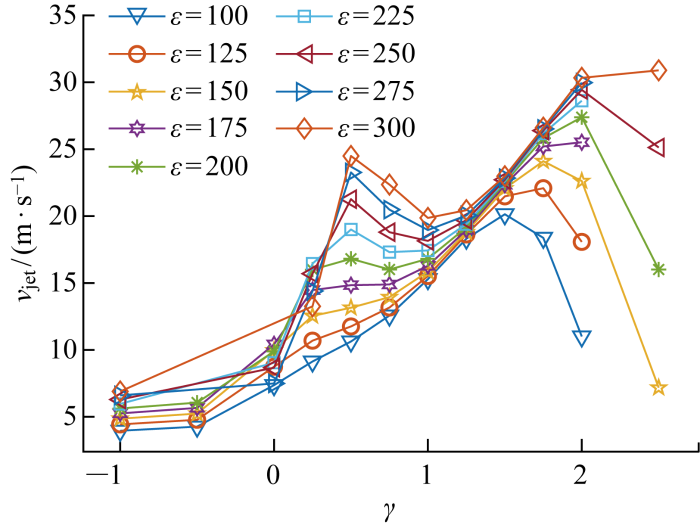
保持γ相同时,气泡射流速度v_jet随着λ变化的关系如图8所示.整体而言,除了处于管口处及产生位置位于管外,但离管口较近的气泡,即0≤γ≤0.25,其他位置的v_jet随气泡最大半径的增大而增大.当气泡的产生位置处于管内,即 -1≤γ≤-0.5 时,气泡射流速度增长的趋势不明显.当气泡的产生位置位于管口处及产生位置位于管外,但离管口较近时,即0≤γ≤0.25,气泡v_jet先增大再减小,但总体上变化平稳,趋势并不明显.当气泡产生位置位于管外,距离管口较远时,即1≤γ≤1.75,气泡v_jet增长趋势随γ的增加而趋于平缓.0.5≤γ≤0.75及 2≤γ≤2.5处的气泡v_jet随尺度比参数的增加而明显增加,可见,距离参数之间存在交叉.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同距离参数时尺度比参数-射流速度关系

Fig.8 Scale-ratio parameter-jet velocity magnitude at different distances

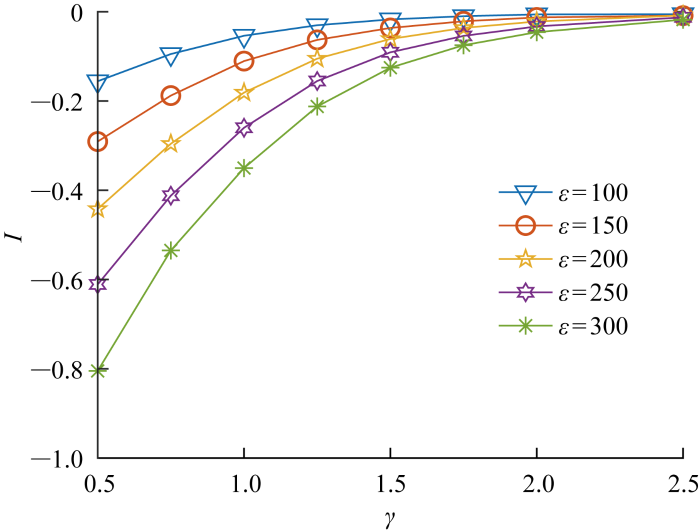
在设置的实验工况下,圆管起到壁面的作用,会使得气泡产生向下射流的趋势,即气泡在溃灭时开尔文冲量I为负.当ε保持不变时,I随着γ增大而增大,气泡产生向下射流的趋势不断减小;当γ保持不变时,I随着ε增大而减小,气泡产生向下射流的趋势不断增大,如图9所示.这表明,γ较小与ε较大的气泡更易产生向下射流的趋势.此外,I随ε的变化趋势展现出良好的一致性和单调性.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同距离参数时强度参数-开尔文冲量关系

Fig.9 Intensity parameter-Kelvin impulse at different distances

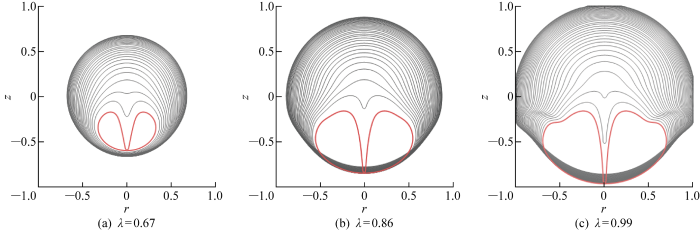
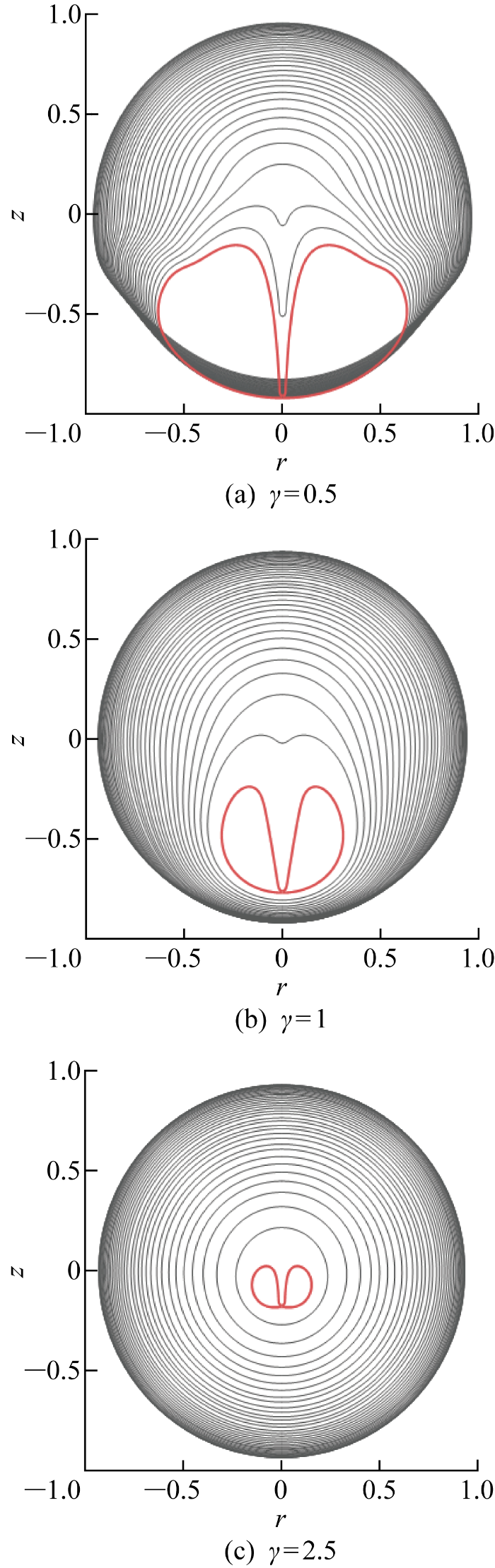
以γ=0.5为例,分别选取λ=0.67,0.86,0.99这3个工况展开分析,气泡在第一周期收缩阶段的形态演变图如图10所示,相邻两条轮廓曲线间的时间间隔均为Δt=0.025,红色轮廓线表示射流抵达气泡下边界时刻.对于λ较小的气泡,其膨胀受圆管的限制较小,气泡膨胀至最大半径时仍保持近似的球形.而对于λ较大的气泡,其膨胀至最大半径时,上下两部分呈现出不同大小的半球状.由于气泡上半球半径大于相同λ下自由场中的气泡,所以气泡溃灭也较为剧烈.此外,λ较大的气泡收缩时,上部具有较大的曲率,这使得气泡产生更加细长的射流,气泡射流速度进一步增加.因此,γ=0.5时,气泡射流速度随λ的增加而明显增加.γ=1.5时,气泡在第一周期收缩阶段的形态演变如图11所示.对于该工况下的气泡而言,随着λ增大,气泡射流的形态依旧保持一致,射流速度逐渐上升.γ=2时,气泡在第一周期收缩阶段的形态演变如图12所示.对于该工况下的气泡而言,λ=0.67时,气泡产生第一周期无法穿透气泡的弱射流,略微增大λ后气泡即处于强射流区间,因此射流速度也相应显著增大(见图12(a)),这一趋势对于γ=2.5处的气泡仍然成立.综上,距离参数存在交叉的问题得到了解决.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 固定距离参数γ=0.5时不同尺度比参数气泡收缩阶段形态演变图

Fig.10 Morphometric evolution of bubble shrinkage stage at different scale ratios and a fixed distance parameter γ of 0.5

图11

新窗口打开| 下载原图ZIP| 生成PPT

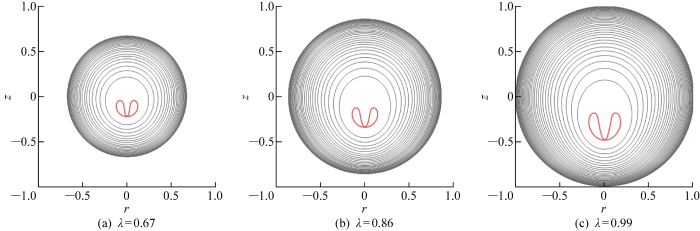
图11 固定距离参数γ=1.5时不同尺度比参数气泡收缩阶段形态演变图

Fig.11 Morphometric evolution of bubble shrinkage stage at different scale ratios and a fixed distance parameter γ of 1.5

图12

新窗口打开| 下载原图ZIP| 生成PPT

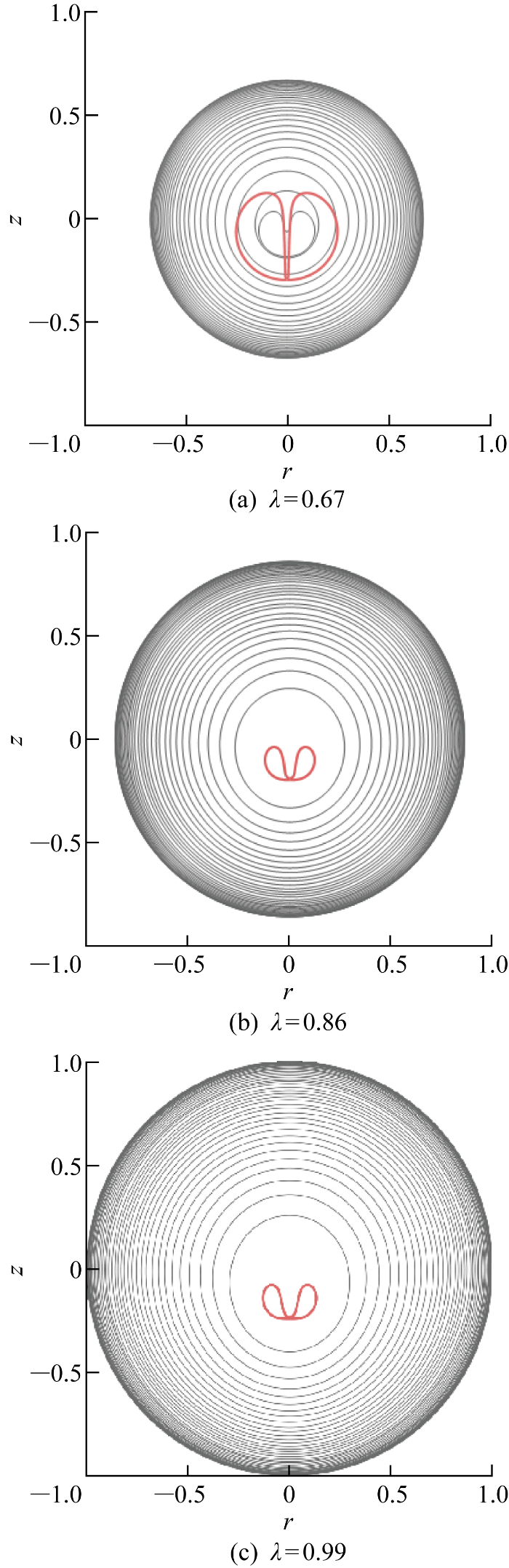
图12 固定距离参数γ=2时不同尺度比参数气泡收缩阶段形态演变图

Fig.12 Morphometric evolution of bubble shrinkage stage at different scale ratios and a fixed distance parameter γ of 2

保持ε相同的情况下,v_jet与γ之间存在着非线性关系如图13所示.对于气泡在管口及管口上方产生的情况,当100≤ε≤300,即0.66≤λ≤0.93时,随着气泡的产生位置远离管口平面,射流速度变化存在多种模式.当100≤ε≤150时,气泡较小,v_jet随γ的增大先增大后减小.当175≤ε≤275时,气泡较大,v_jet随γ的增大会出现两处速度的峰值.当ε=300时,气泡很大,v_jet随γ的增大先增大后减小,随后在γ>1处再次增大.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同尺度比参数(强度参数)时的距离参数-射流速度关系

Fig.13 Distance parameter-jet velocity magnitude at different scale ratios (intensity parameter)

综上所述,保持气泡λ不变,当0.66≤λ<0.73,即100≤ε<150时,v_jet随γ的增大呈现出先增大后减小的趋势,这是由于气泡的产生位置位于管口及管内时,气泡收缩过程中其上方流体的运动仍然受到圆管侧壁的影响,流体无法从四周不受阻碍地流向气泡中心,造成v_jet较小.随着γ的增大,这种限制逐渐减小,因此v_jet逐渐增大.随着γ继续增大,气泡受到圆管及其内部流体的限制作用逐渐减小,产生向下射流的趋势随之减弱,因此气泡向下的v_jet逐渐减小.受限于本文研究的工况参数范围,当λ ≈ 0.99,即ε=300时,无法界定该工况下的射流速度峰值.当0.73≤λ<0.99,即150≤ε<300时,会出现v_jet的峰值.对该现象的解释如下.

当γ保持不变时,I随着λ增大而减小,如图14所示.这种单调变化的趋势表明,气泡射流速度随距离参数的非单调变化主要由射流形态的区别导致.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 不同强度参数时的距离参数-开尔文冲量关系

Fig.14 Distance parameters-Kelvin impulse curves at different strengths

以ε=250为例,射流速度的两个峰值分别出现在γ=0.5和γ=2.5处,谷值出现在γ=1处,与不同距离参数下射流速度变化的交叉区间相吻合.因此,取ε=300下的3个典型工况,即γ=0.5,1,2.5时,展开说明.相邻两条轮廓曲线间的时间间隔均为Δt=0.025,如图15所示,红色轮廓线表示射流抵达气泡下边界时刻.当γ=0.5时,气泡在最大时刻明显偏离球形,其上下两部分呈现出不同大小的半球状.气泡在收缩时顶部出现明显较高的曲率,在此情况下,气泡将产生指向管口的细长型高速射流.由于气泡上半球半径大于同样强度参数下自由场中的气泡,所以气泡溃灭也较为剧烈,射流速度随即出现第一个峰值.当γ=2.5时,射流穿透时刻气泡已收缩至很小,射流已被充分加速,因此出现第二个峰值.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 固定强度参数ε=250时不同距离参数气泡收缩阶段形态演变图

Fig.15 Morphology evolution of bubble shrinkage stage at different distances and a constant strength parameter ε of 250

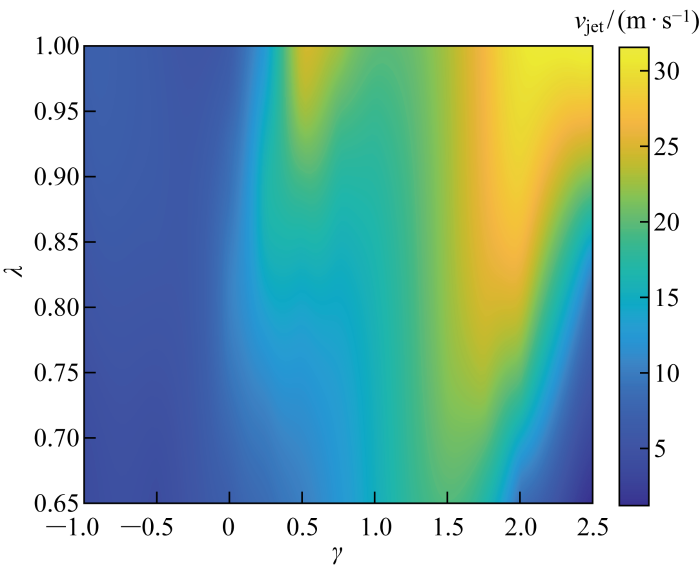
射流速度v_jet随γ与λ变化而变化的云图如图16所示.图中,黄色代表高速,蓝色代表低速.由图可知,产生于圆管内部的气泡,即γ<0,射流速度均较低且变化不明显;产生于圆管管口平面及外部的气泡,即γ≥0,射流速度变化明显;较大的射流速度集中在较高的距离参数与尺度比参数以及低尺度比参数下对应峰值的距离参数下,在本文中分别为1.5≤γ≤2.5,0.85≤λ≤1与γ=0.5,λ=0.99.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 距离参数-尺度比参数-射流速度云图

Fig.16 Cloud plot of distance parameter-scale-ratio parameter-jet velocity magnitude

4 结论

针对水下管口附近气泡动力学行为和流场特征开展实验和数值研究.在实验中,采用水下瞬时放电生成脉动气泡,并利用高速摄像机捕捉气泡膨胀、坍塌、高速射流形成等脉动过程.在数值计算部分,采用基于势流理论的边界积分模型模拟气泡动力学行为.结合实验中观察到的物理现象和数值计算得到的流场信息,探究管口附近脉动气泡的动力学特性,分析气泡射流方向和速度在不同参数条件下的变化及成因,得到主要结论如下:

(1) 由于管内边界的阻碍作用,气泡下半部分靠近管口一侧的运动受到抑制,其膨胀和收缩速度均比气泡上半部分慢,气泡上半部分率先收缩,从而形成指向管内的射流.

(2) 在气泡坍塌阶段,其顶部附近的流场会逐渐形成局部高压区.该高压区和气泡高速射流形成“正反馈”效应,使指向管内的射流速度可达数百米每秒.对于管内生成的气泡,其射流宽度明显大于管外生成的气泡.

(3) γ与λ是影响气泡射流方向和速度的两个重要因素.当0.65≤λ≤1且γ≤1.5时,气泡最终只产生指向管内的射流,且方向变化与λ无关;当γ>1.5时,只在较大λ下产生指向管内的射流;当γ≥3.5时,气泡不产生射流.

(4) 当0.65≤λ≤1且1≤γ≤1.75时,λ对气泡射流速度的影响较小;当0≤γ≤0.25时,气泡的射流速度随λ先增大后减小;当0.5≤γ≤0.75及 2≤γ≤2.5时,气泡射流速度随λ增大而增大.

(5) 当-1≤γ≤2.5且0.66≤λ<0.86时,γ增大,射流速度先增大后减小;当0.86≤λ<0.99时,射流速度随γ的增大会出现两个峰值.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LUO

X W

, JI

, TSUJIMOTO

A review of cavitation in hydraulic machinery

[J]. Journal of Hydrodynamics, Ser B, 2016, 28(3): 335-358.