在建、构筑物密集的地区开挖基坑将不可避免对邻近既有结构产生扰动,如房屋的沉降和不均匀沉降、隧道和地下管线的位移,严重时甚至会造成结构的破坏[1 ⇓ -3 ] .因此,准确预测基坑开挖诱发的地表沉降具有重要的现实意义.
当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法.
基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法.
综上所述,本文利用PLAXIS 3D软件和软土蠕变模型,建立杭州某超深基坑的三维数值模型,与实测数据的对比验证了模型的合理性;基于参考算例展开参数讨论,深入分析了时空因素对围护墙侧移、地表沉降及二者关系的影响;引入互补误差函数和三折线模型,利用数值分析结果对既有互补误差函数进行修正,提出了考虑时空效应的地表沉降快速分析方法,并应用于其他超深基坑工程验证该方法的适用性.
1 模型建立与验证
1.1 工程概况
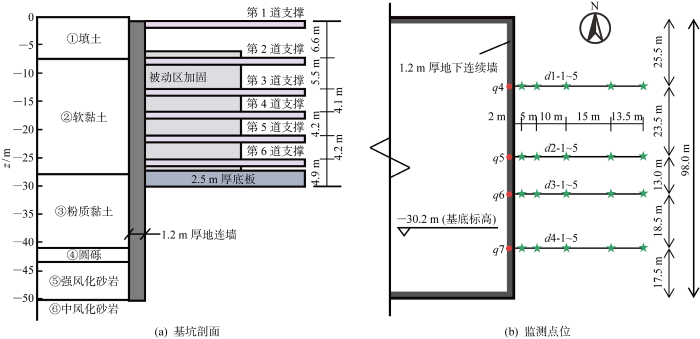
杭州中心项目超深顺作基坑采用分坑施工方法,Cheng等[16 ] 分析了B2分坑开挖的变形性状,平剖面如图1 所示.图中:z 为纵坐标;q 为地连墙测斜孔;d 为地表沉降观测点.如图1(a) 所示,主要地层自上而下分别为:①填土、②软黏土、③粉质黏土、④圆砾、⑤强风化、⑥中风化砂岩;基坑开挖深度为30.2 m,平面尺寸约98 m×92 m;围护结构采用厚1.2 m、深50 m的地连墙结合6道混凝土满堂对撑和被动区裙边加抽条加固.如图1(b) 所示为地连墙测斜以及坑外地表沉降监测点,自2019年4月1日第1道支撑形成开始,至2019年11月16日地下室基础底板形成强度,基坑开挖施工可分为如表1 所示的6个主要工况.
图1
图1
基坑示意图
Fig.1
Schematic diagram of excavation
1.2 三维数值计算
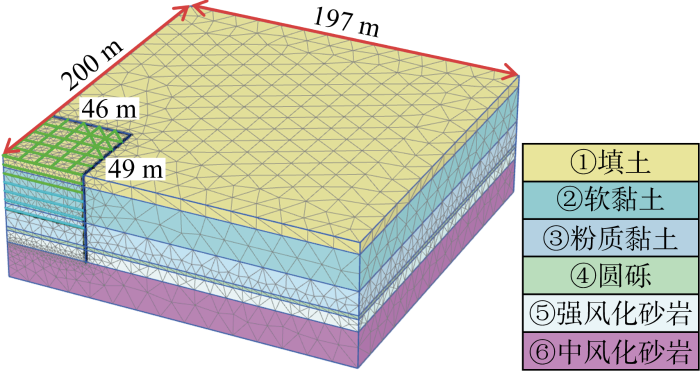
采用PLAXIS 3D有限元软件,考虑对称性,将前述B2分坑的1/4作为三维数值分析对象.为降低模型边界对计算精确性的影响,地连墙至水平边界的距离取5倍开挖深度,竖向边界取至地连墙墙底以下约20 m,模型尺寸为200 m×197 m×70 m.至于计算模型的边界条件则为:下边界位移约束,上边界位移自由,水平边界水平方向位移约束,竖直方向位移自由;设置每个开挖步中临空面为孔压为0的边界面.
计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数;E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点.
图2
图2
网格划分
Fig.2
Mesh subdivision
1.3 模型验证
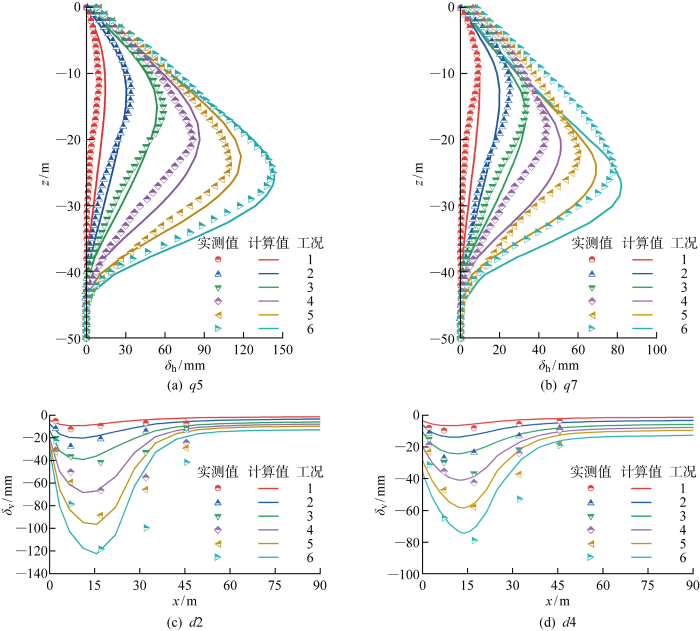
图3 给出了不同工况下计算值与实测值的基坑变形对比.图中:δ h 为围护墙侧移;δ v 为地表竖向位移.由图3(a) 、3(b) 可知,围护墙侧移的计算值与实测值较为相符.观察图3(c) 、3(d) 可知,不同监测剖面地表沉降的计算值都与实测值较为吻合;围护墙后方32.0 m的地表沉降计算值相比于实测值偏小,可能是由于该实测点位于城市道路上,受车辆交通荷载影响大.总体而言,基坑水平位移和地表沉降的计算值与实测值吻合较好,可以认为建立的三维数值模型比较合理.
图3
图3
基坑变形计算值与实测值对比
Fig.3
Comparison of excavation deformations between calculated and measured value
2 参数分析
将所建数值模型作为参考算例,以工况6作为对比工况,进一步探讨不同时空因素对基坑变形,尤其是坑外地表沉降的影响.值得说明的是,墙体、支撑刚度对超深基坑来说一般都足够大,且杭州主城区典型软黏土的刚度也基本相同,因此本文不对以上参数展开分析,仅聚焦影响软黏土超深基坑坑外地表沉降的5个关键因素.本文利用修正系数对参考算例中δ vm 和δ vm /δhm 进行修正,使方法具有普适性,而非仅给出定性的结论.
2.1 开挖速率
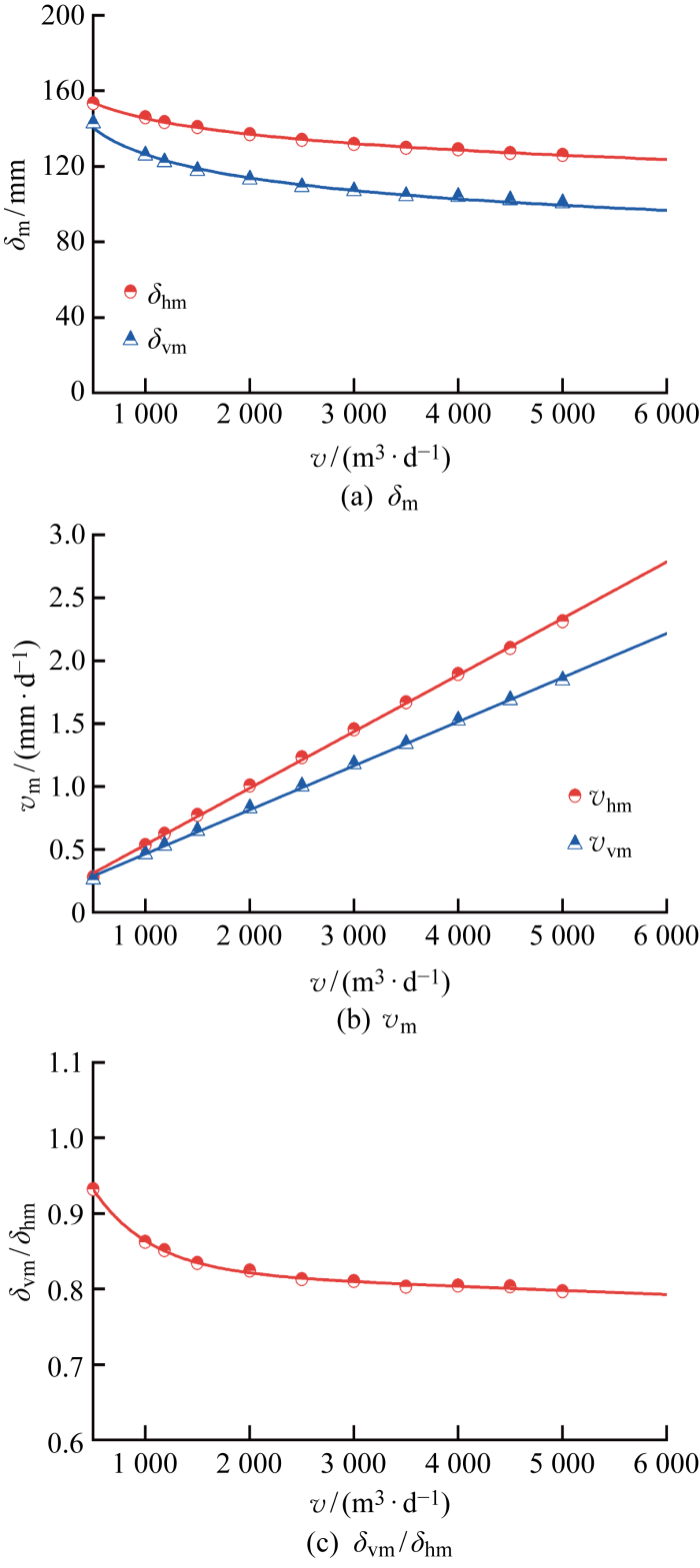
软黏土基坑的蠕变变形受开挖时间t 的影响,通过改变表1 中不同工况的时长,图4 给出了基坑开挖速率v =V s /t 对基坑变形的影响,V s 为基坑需开挖的土方体积. 图中:δ m 为基坑最大变形量;v m =δ m /t ,为最大变形的平均变化速率;v hm 和v vm 分别为围护墙最大侧移和地表最大沉降的平均变化速率.由图4(a) 可知,地表沉降受开挖速率的影响与围护墙侧移相当,考虑到地表最大沉降增量一般小于围护墙最大侧移增量,可以说明软土蠕变诱发坑外土体产生了不依赖于围护墙侧移的沉降;由图4(b) 可知,随着开挖速率的提高,基坑变形减小,而最大变形的平均变化速率却有所提高.工程实践中,过大的变形和变形速率都是不被允许的,因此设计施工人员应选择合理的开挖速率;由图4(c) 可知,随着开挖速率的提高,δ vm /δ hm 逐渐下降但下降速率趋缓,这是因为开挖速率的提高意味着时效变形的减小,而非时效地表沉降仅与非时效墙体侧移的形态和大小有关,所以δ vm /δ hm 存在极限小值.
图4
图4
开挖速率对基坑变形的影响
Fig.4
Influence of excavation rate on excavation deformations
从图4 可得土方开挖速率对参考算例(v =1 184 m3 /d)的δ vm 和δ vm /δ hm 的修正系数:
(1) ξv =1. 033 7[v/ (1 000v 0 )]-0 . 149 , R 2 =0. 99
(2) ηv =1. 020 8[v/ (1 000v 0 )]-0 . 061 , R 2 =0. 92
式中:ξv 、ηv 分别为土方开挖速率对参考算例的δ vm 和δ vm /δ hm 的修正系数;v 0 为单位开挖速率;R 为Pearson相关系数.
2.2 软土层厚度
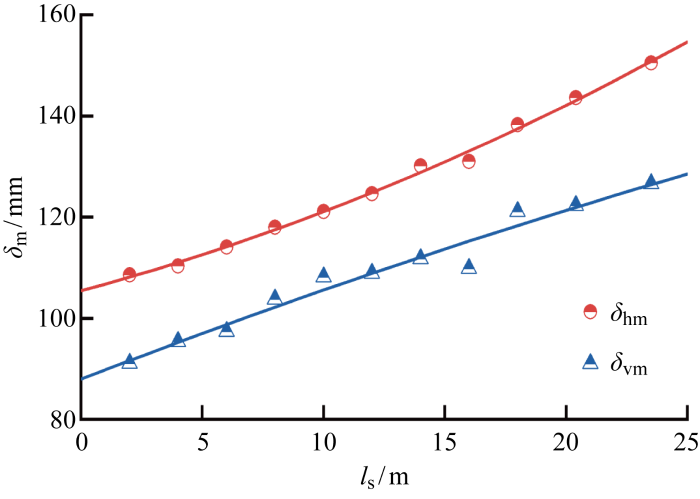
由于岩土工程的复杂性,杭州城区不同方位软土层的厚度有一定的差异性,有必要针对软土层厚度进行分析.图5 给出了软土层厚度l s 对基坑变形的影响,其中软土层厚度指①填土层底至②软黏土层底的距离.由图5 可见,软土层厚度与基坑变形大致呈线性增长关系.参数分析表明软土层厚度对δ vm /δ hm 的影响不十分显著,因此下文的修正系数近似取1.
图5
图5
软土层厚度对基坑变形的影响
Fig.5
Influence of soft soil thickness on excavation deformations
可得软土层厚度对参考算例(l s =20.4 m)的δ vm 和δ vm /δ hm 的修正系数:
(3) ξ l s s /ls0 )+0.727 9, R2 =0.96
(4) η l s
式中:ξ l s η l s δ vm 和δ vm /δ hm 的修正系数;l s0 为单位软土层厚度.
2.3 软土修正蠕变指数
PLAXIS 3D软件中软土蠕变模型的修正蠕变指数的计算公式[20 ] 如下:
(5) μ* ≈ C α 2.3 ( 1 + e 0 )
式中:Cα 为蠕变指数,可由室内试验得到,若无试验数据时可利用经验公式C c /Cα ≈15~ 25来确定[20 ] ,C c 为压缩指数;e 0 为土体的初始孔隙比.
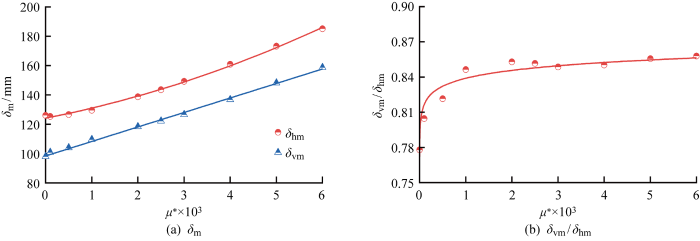
图6 给出了软土修正蠕变指数μ * 对基坑变形的影响.由图6(a) 可知,随着软土修正蠕变指数的增大,基坑变形接近线性增大;可以发现,软黏土蠕变诱发了围护墙的附加侧移,地表沉降受蠕变的影响与围护墙侧移相当,然而围护墙的附加侧移一般不引起相同增量的地表沉降,这说明软土蠕变诱发坑外土体产生了不依赖于围护墙侧移的沉降.由图6(b) 可知, δ vm /δ hm 随着软土蠕变性的增强而增大但逐渐趋缓.
图6
图6
软土修正蠕变指数对基坑变形的影响
Fig.6
Influence of modified creep index of soft soil on excavation deformations
从图6 可得到软土修正蠕变指数对参考算例(μ * =0.002 5)的δ vm 和δ vm /δ hm 的修正系数:
(6) ξ μ * * +0.808, R2 =0.99
(7) η μ * * 0 . 011 9 , R2 =0.94
式中:ξ μ * η μ * δ vm 和δ vm /δ hm 的修正系数.
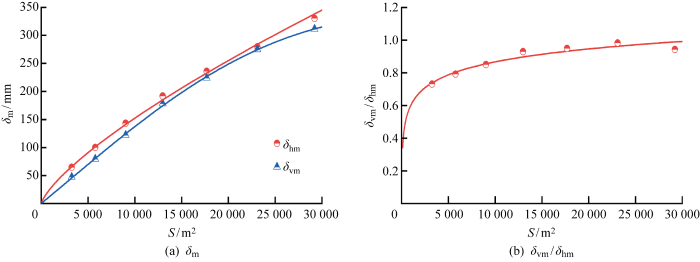
2.4 开挖面积
在不改变开挖速率和基坑长宽比的条件下,图7 给出了开挖面积S (基坑平面面积)对基坑变形的影响.可见,开挖面积对基坑变形的影响较大,这可以从两个方面进行解释.从平面上看,规模越大,基坑变形受开挖尺寸的影响也越大;从时间上看,相同开挖速率下平面尺寸大的基坑开挖历时也相应增加,受软黏土蠕变的影响也更大.随着开挖面积的增加,δ vm /δ hm 逐渐增长但增长速率趋缓.如图7 所示,当基坑开挖面积为 17 000 m2 时,坑外地表沉降最大值已超过了200 mm,显然在工程实践中是不被允许的,设计上一般会采用分仓施工方法减小基坑变形,这也间接证明了深大基坑分仓施工的有效性.
图7
图7
开挖面积对基坑变形的影响
Fig.7
Influence of excavation area on excavation deformations
由图7 可得开挖面积对参考算例(S =9 016 m2 )的δ vm 和δ vm /δ hm 的修正系数:
(8) ξS =-0. 001 6[S/ (1 000S 0 )]2 +0. 135 4[S/ (1 000S 0 )]-0. 059 5, R 2 =0. 99
(9) ηS =0. 134 3ln[S/ (1 000S 0 )]+0. 711 5, R 2 =0. 92
式中:ξS 、ηS 分别为基坑开挖面积对参考算例的δ vm 和δ vm /δ hm 的修正系数;S 0 为单位开挖面积.
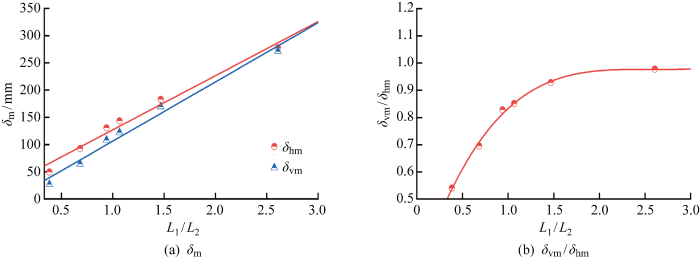
2.5 基坑长宽比
在不改变基坑开挖面积的条件下,图8 给出了不同长宽比L 1 /L 2 对基坑变形的影响,δ hm 、δ vm 取自边长为L 1 的围护墙及其坑外地表. 这里仅考虑 1/ 3<L 1 /L 2 <3的情况,是因为实际工程中一般会利用基坑空间效应分块或分仓开挖,避免基坑施工接近平面应变状态. 可以看出,随着L 1 /L 2 的提高,基坑变形基本呈线性提高,显然这是因为随着L 1 /L 2 逐渐增大,矩形基坑边长为L 1 中部的空间效应减弱,逐渐接近平面应变状态;同时也可发现 δ vm /δ hm 随着L 1 /L 2 的提高逐渐增长但增长速率趋缓.
图8
图8
长宽比对基坑变形的影响
Fig.8
Influence of length-width ratio on excavation deformations
由图8 可得基坑长宽比对参考算例(L 1 /L 2 =1.065)的δ vm 和δ vm /δ hm 的修正系数:
(10) ξ L 1 / L 2 1 /L2 )2 +1.403 8(L1 /L2 )- 0.310 6, R2 =0.99
(11) η L 1 / L 2 1 /L2 )+0.943 7, R2 =0.94
式中:ξ L 1 / L 2 η L 1 / L 2 δ vm 和δ vm /δ hm 的修正系数.
2.6 δ vm 和δ vm /δ hm 拟合公式的建立
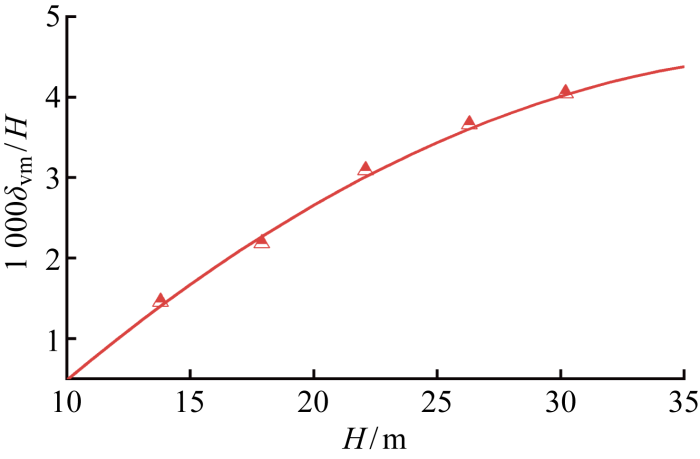
基于数值模型的参考算例中不同开挖深度H 下的坑外地表沉降最大值,图9 给出了基坑开挖深度与坑外地表沉降最大值的关系.
图9
图9
开挖深度与地表沉降最大值的关系
Fig.9
Excavation depth versus maximum ground settlement
(12) 1 000δ vm /H =-0. 004 1(H/H 0 )2 +0. 340 4(H/H 0 )-2. 509 3, R 2 =0. 99
式中:H 0 为单位开挖深度.结合前文考虑时空因素的各项修正系数即可得到杭州软黏土地区任意超深基坑地表沉降的最大值:
(13) 1 000δvm /H=ξv ξ l s ξ μ * S ξ L 1 / L 2 0 )2 + 0.340 4(H/H0 )-2.509 3]
如果已有确定墙体最大水平位移δ hm 的经验关系,也可按下式确定坑外地表最大沉降δ vm :
(14) δvm /δhm =ηv η l s η μ * S η L 1 / L 2 0 )+0.007 9]
3 地表沉降的快速分析方法
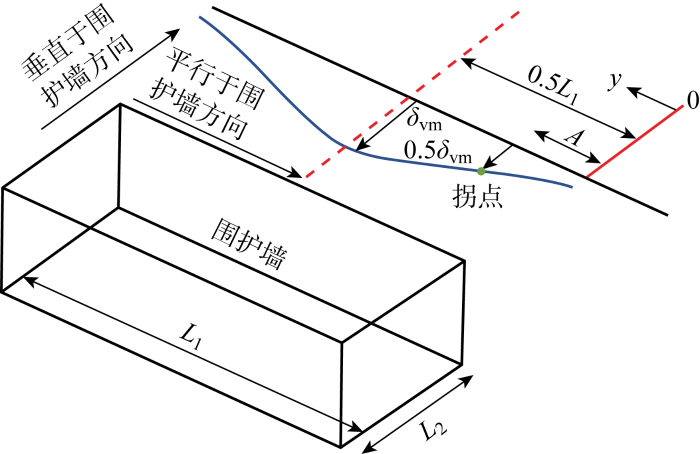
3.1 平行于围护墙方向
图10 所示为平行于围护墙方向的坑外地表沉降示意图,Roboski等[22 ] 使用互补误差函数来描述该方向的地表沉降:
(15) δv = 1 - 1 2 e r f c 2.8 ( y - A ) 0.5 L 1 - A vm
(16) 2A/L 1 =-0. 069ln(H/L 1 )-0. 03
式中:A 为原点至拐点的距离,拐点指平行于围护墙剖面上地表沉降为沉降最大值1/2的点.
图10
图10
平行于围护墙方向的地表沉降示意图
Fig.10
Schematic diagram of ground settlements parallel to retaining wall
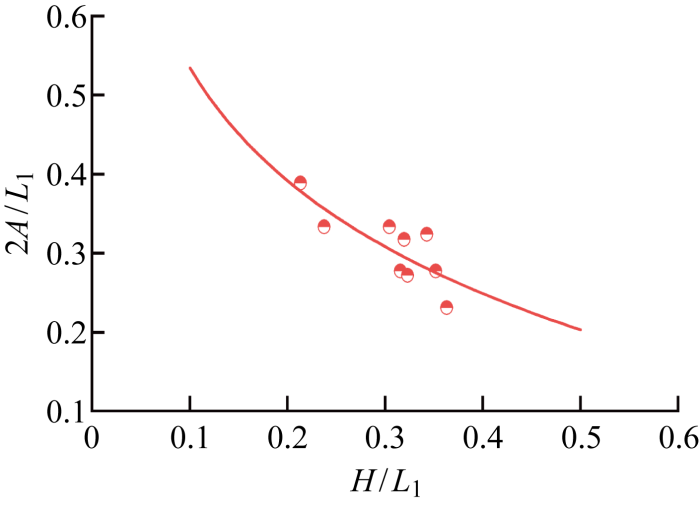
然而,参数A 为由实测数据拟合得到的经验值,并不适用于时间效应显著的杭州软黏土地区,需要利用本文数值结果对A 重新拟合,如图11 所示.拟合公式如下:
(17) 2A/L 1 =-0. 21ln(H/L 1 )+0. 06
图11
图11
拐点坐标拟合曲线
Fig.11
Fitting curve of inflection point coordinate
利用式(15)、(17),结合y =49.0 m的实测沉降,图12 给出了平行于围护墙方向的计算值与本文参考算例的实测数据对比.可见计算值与实测值较为吻合,验证了拟合参数的合理性.
图12
图12
地表沉降计算值与实测值对比(平行于围护墙方向)
Fig.12
Comparison of ground settlements between calculated and measured value (parallel to retaining wall)
3.2 垂直于围护墙方向
引入《基坑工程技术规范》[23 ] 中的三折线模型对垂直于围护墙方向的地表沉降进行描述,三折线模型定义了坑外4点的沉降与沉降最大值的关系,4点分别为(0, 0.2δ vm )、(H/ 2, δ vm )、(2H , 0.1δ vm )、(4H , 0).
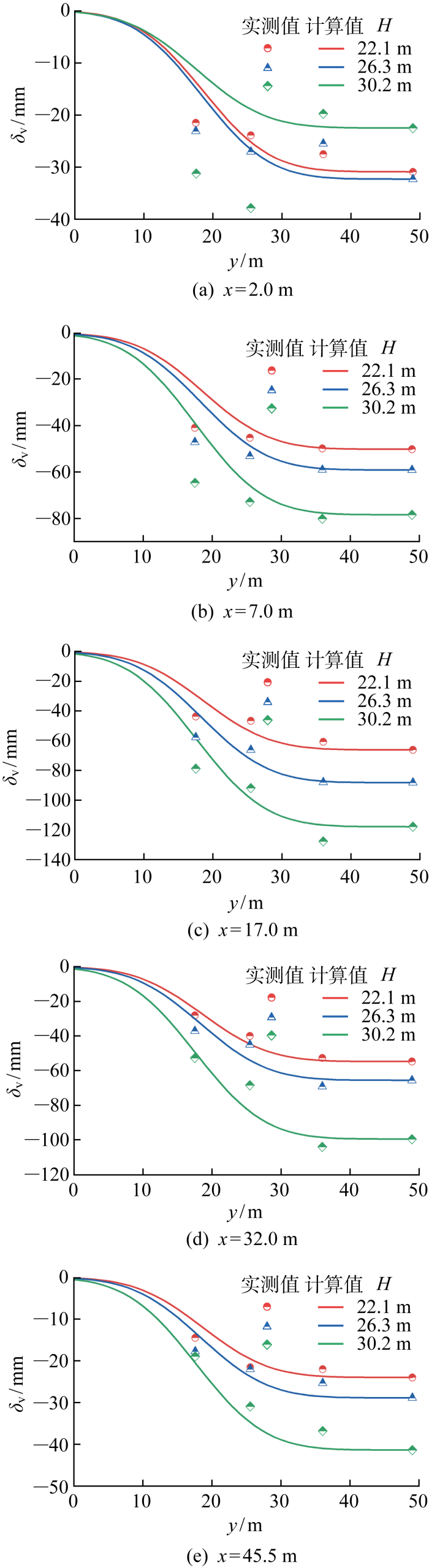
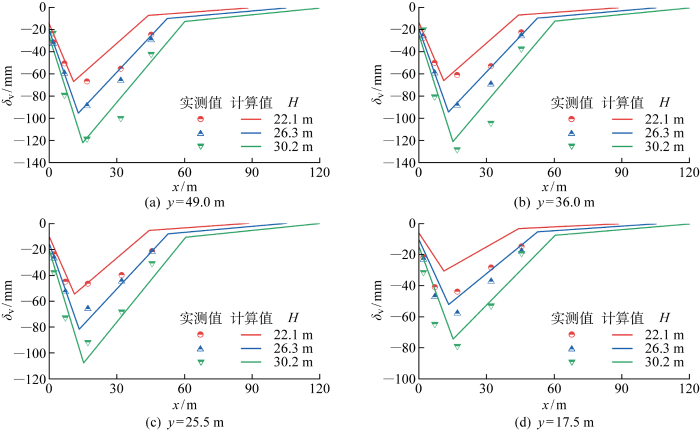
利用式(12)、(15)和(17),图13 给出了垂直于围护墙方向计算值与参考算例的实测值对比.可见,除距围护墙32.0 m处受道路交通荷载扰动的监测点以外,其他各点计算值与实测值吻合较好.
图13
图13
地表沉降计算值与实测值对比(垂直于围护墙方向)
Fig.13
Comparison of ground settlements between calculated and measured value (perpendicular to retaining wall)
4 应用与验证
上述超深基坑地表沉降快速分析方法是基于杭州中心项目超深基坑群中最早施工的B2基坑实测数据和三维数值分析建立的,为检验其适用性,将该方法应用于该超深基坑群中第2期施工的B1基坑.
4.1 工程概况
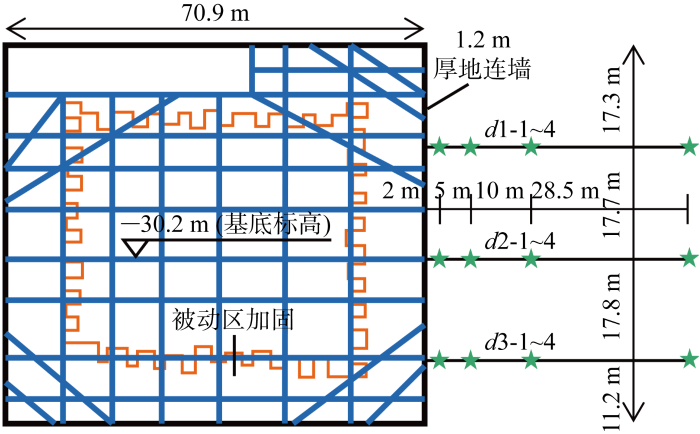
杭州中心B1基坑深度为30.2 m,开挖面积为 5 219 m2 ,平面非严格矩形,尺寸约70.9 m×64.0 m,分析对象位于临近市政道路的短边,L 1 /L 2 =0.903;如图14 所示,坑外埋设了3×4个地表沉降监测点,垂直于围护墙方向的监测点由近及远分别距围护墙2.0、7.0、17.0、45.5 m,平行于围护墙方向上,d 1~d 3沉降观测断面分别距较近的角部17.3、29.0、11.2 m;自2020年4月3日第1道支撑形成开始,至2020年8月17日地下室基础底板形成强度,基坑开挖施工总计约137 d,开挖速率约 1 150 m3 /d;在土层条件和围护结构设计参数等方面,B1与B2基坑一致.从平面上看,B1基坑规模明显比B2小,同样开挖深度下坑外地表沉降受开挖尺寸的影响更大;从时间因素考虑,二者开挖速率大抵相当,故B1基坑开挖施工的历时明显小于B2基坑,受软黏土蠕变的影响相对更小.
图14
图14
B1基坑平面示意图
Fig.14
Schematic plan of excavation B1
4.2 计算流程
(1) 将v 、l s 、μ* 、S 、L 1 /L 2 代入式(1)、(3)、(6)、(8)、(10),求得ξv =1. 01、ξ l s . 00、ξ μ * . 00、ξS =0. 60、ξ L 1 / L 2 . 82.
(2) 将ξv 、ξ l s ξ μ * ξS 、ξ L 1 / L 2 H 代入式(13),分别求得H =22.1,26.3,30.2 m时的δ vm =33.4,47.6,61.1 mm.
(3) 将H 和L 1 =64.0 m代入式(17)求得H =22.1,26.3,30.2 m时的A =9.1,7.9,7.0 m.
(4) 将δ vm 、L 1 和A 代入式(15)可求得不同开挖深度下y =29.0,17.3,11.2 m剖面的δ vm .
(5) 将不同深度下y =29.0,17.3,11.2 m剖面的δ vm 代入三折线模型即可求得不同深度下相应剖面任意点处的δ v .
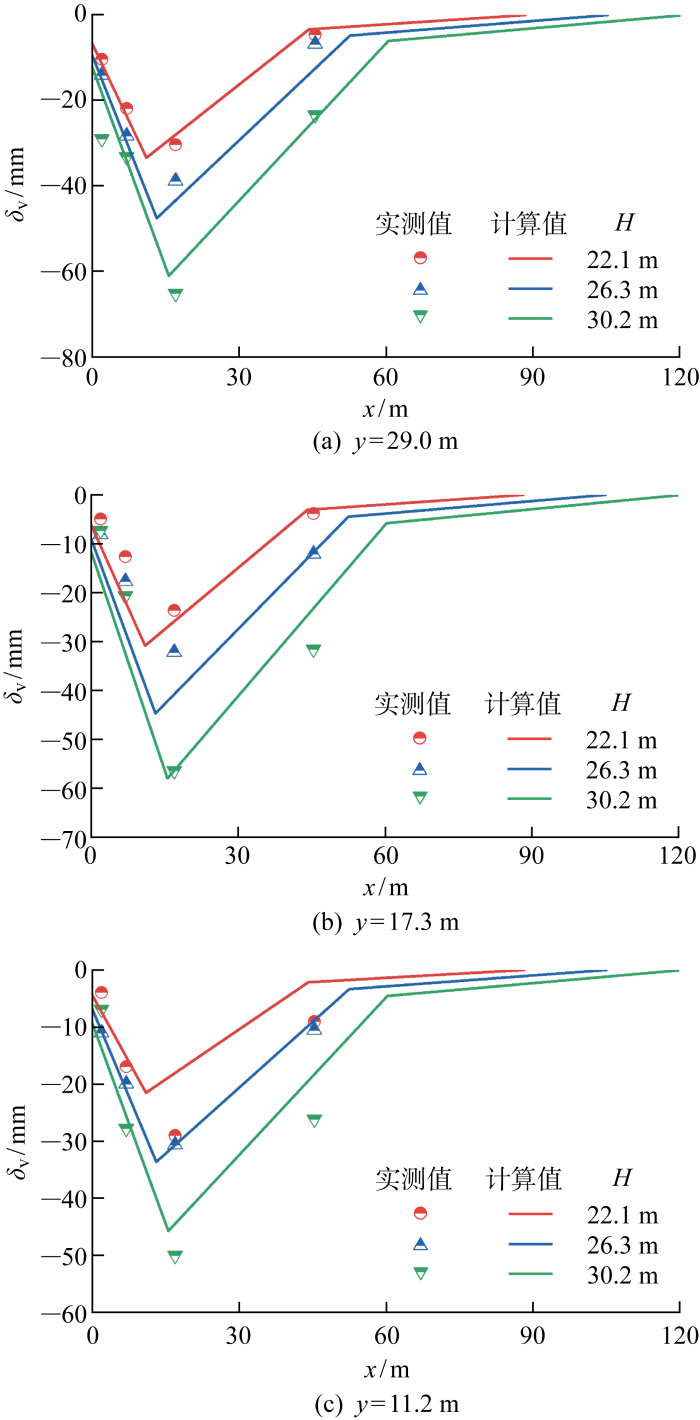
4.3 结果对比
图15 给出了本文方法与实测数据的地表沉降对比.可见,计算值与实测值较为相符,可以认为本文方法可以较为准确地预测杭州软黏土地区超深基坑坑外地表沉降.同时还可发现,B1基坑的坑外地表沉降计算值和实测值均明显小于B2基坑,与B1基坑平面尺寸更小、施工历时更短、时空效应更为有利的客观分析是吻合的.
图15
图15
B1基坑地表沉降计算值与实测值对比
Fig.15
Comparison of ground settlements of excavation B1 between calculated and measured value
5 结论
采用软土蠕变模型,建立杭州中心项目超深基坑群B2基坑的三维数值模型;基于参考算例展开参数讨论,深入分析了坑外地表沉降的时空效应,获得了考虑时空因素的坑外地表最大沉降的修正系数;引入互补误差函数和三折线模型,利用数值结果对既有互补误差函数进行修正,提出了考虑时空效应的地表沉降快速分析方法.结果表明:
(1) 软黏土蠕变既诱发围护墙的附加侧移从而引起土体沉降,又诱发坑外土体产生不依赖于围护墙侧移的沉降;忽略软土蠕变对预测超深基坑坑外地表沉降的影响不弱于其对墙体侧移的影响.
(2) 基坑深度和开挖速率相同时,开挖面积直接决定施工时间的长短,从而影响软黏土蠕变诱发的地表沉降.
(3) 本文方法可以较为准确地预测杭州深厚软黏土超深基坑的坑外地表沉降,也为建立其他软黏土地区超深基坑开挖环境影响的快速评估方法提供了思路.
需要说明的是,本文研究的是城市中心区软黏土超深基坑工程的环境影响预测方法,由于此类工程的重要性,其围护墙刚度、插入深度以及支撑刚度一般都足够大,所以提出的预测方法未考虑这些常规因素的影响.
参考文献
View Option
[1]
张抗寒 , 陈锦剑 , 王建华 , 等 . 紧邻基坑同步施工下坑间隧道的变形特性
[J]. 上海交通大学学报 2013 , 47 (10 ): 1537 -1541 .
DOI:10.16183/j.cnki.jsjtu.2013.10.009
[本文引用: 1]
采用非线性平面有限元方法研究紧邻基坑同步施工下坑间土体与隧道的变形特性.将该方法运用到上海某基坑工程中的隧道位移预测,实测数据与有限元结果比较吻合,验证了其可行性.通过参数分析,讨论了基坑之间的距离、开挖宽度对坑间土体竖向位移的影响,并由此推算出了使得坑间地表土体平均竖向位移接近零的最优基坑间距与开挖宽度的关系.同时讨论了盾构隧道、明挖暗埋隧道与基坑的距离对于隧道竖向位移、支护结构侧移的影响.研究表明,开挖完成后,坑间盾构隧道的沉降比周围土体的沉降略小,而有围护结构的明挖暗埋隧道则表现为上抬,距离基坑越远,上抬量越小.
ZHANG Kanghan CHEN Jinjian WANG Jianhua , et al Movement of tunnel between two adjacent concurrent excavations
[J]. Journal of Shanghai Jiao Tong University 2013 , 47 (10 ): 1537 -1541 .
[本文引用: 1]
[2]
肖潇 , 李明广 , 夏小和 , 等 . 基坑开挖对临近明挖暗埋隧道竖向变形的影响机理
[J]. 上海交通大学学报 2018 , 52 (11 ): 1437 -1443 .
DOI:10.16183/j.cnki.jsjtu.2018.11.004
[本文引用: 1]
结合上海地区某邻近明挖暗埋隧道基坑工程案例,采用数值方法模拟了深基坑开挖的过程,并通过与实测数据进行对比验证了模型的合理性.针对隧道与基坑之间的连接墙进行对比分析,揭示了连接墙所起的作用.通过分析相邻地连墙竖向位移以及其两侧土体位移,得出地连墙与隧道之间以及墙土之间的相互影响规律.根据地连墙墙体轴力分布,研究墙体在开挖过程中的受力形态,揭示临近基坑开挖对地下结构(明挖暗埋隧道)的影响机理.结果表明,对于明挖隧道与基坑共墙的情况,隧道的隆起主要由地连墙以及连接墙的共同影响所致.明挖隧道受到基坑地连墙变形的影响明显大于受周围土体位移的影响.地连墙发生竖向隆起的原因为坑内土体提供的摩擦力大于坑外土体提供的摩擦力.
XIAO Xiao LI Mingguang XIA Xiaohe , et al Mechanism analysis of influence of deep excavation on deformation of nearby cut-and-cover tunnel
[J]. Journal of Shanghai Jiao Tong University 2018 , 52 (11 ): 1437 -1443 .
[本文引用: 1]
[3]
刘俊城 , 谭勇 , 张生杰 . 地铁车站深基坑开挖变形智能多步预测方法
[J]. 上海交通大学学报 2024 , 58 (7 ): 1108 -1117 .
DOI:10.16183/j.cnki.jsjtu.2022.419
[本文引用: 1]
为更好预测深基坑开挖期间地下连续墙的侧向位移变形,基于长短期记忆神经网络(LSTM)智能算法理论构建了LSTM多步预测模型.首先对多步预测模型的多输出策略进行论述,其次详细介绍了LSTM多步预测模型的构建方法,并对模型输入集空间维度和时间维度两项超参数进行探究,以提高模型的预测准确度.最后依托某富水砂土深基坑工程实例,分析了模型预测值与实际监测值的差异.3个典型监测点的数据分析结果表明LSTM多步预测模型具有较强的泛化能力,相关算法对深基坑开挖变形预测方法的改进优化具有参考价值.
LIU Juncheng TAN Yong ZHANG Shengjie . Multi-step prediction of excavation deformation of subway station based on intelligent algorithm
[J]. Journal of Shanghai Jiao Tong University 2024 , 58 (7 ): 1108 -1117 .
[本文引用: 1]
[4]
王卫东 , 徐中华 , 王建华 . 上海地区深基坑周边地表变形性状实测统计分析
[J]. 岩土工程学报 2011 , 33 (11 ): 1659 -1666 .
[本文引用: 2]
WANG Weidong XU Zhonghua WANG Jianhua . Statistical analysis of characteristics of ground surface settlement caused by deep excavations in Shanghai soft soils
[J]. Chinese Journal of Geotechnical Engineering 2011 , 33 (11 ): 1659 -1666 .
[本文引用: 2]
[5]
江晓峰 , 刘国彬 , 张伟立 , 等 . 基于实测数据的上海地区超深基坑变形特性研究
[J]. 岩土工程学报 2010 , 32 (Sup.2 ): 570 -573 .
[本文引用: 2]
JIANG Xiaofeng LIU Guobin ZHANG Weili , et al Deformation characteristics of ultra-deep foundation pit in Shanghai based on measured data
[J]. Chinese Journal of Geotechnical Engineering 2010 , 32 (Sup.2 ): 570 -573 .
[本文引用: 2]
[6]
应宏伟 , 杨永文 . 杭州深厚软黏土中某深大基坑的性状研究
[J]. 岩土工程学报 2011 , 33 (12 ): 1838 -1846 .
[本文引用: 2]
YING Hongwei YANG Yongwen . Characteristics of a large and deep soft clay excavation in Hangzhou
[J]. Chinese Journal of Geotechnical Engineering 2011 , 33 (12 ): 1838 -1846 .
[本文引用: 2]
[7]
GONZÁLEZ C SAGASETA C . Patterns of soil deformations around tunnels. Application to the extension of Madrid Metro
[J]. Computers and Geotechnics 2001 , 28 (6/7 ): 445 -468 .
[本文引用: 2]
[8]
ZHENG C FRANZA A JIMENEZ R . Analytical prediction for ground movements due to deep excavations in soils
[J]. Tunnelling and Underground Space Technology 2023 , 141 : 105316 .
[本文引用: 1]
[9]
QIAN J TONG Y MU L , et al A displacement controlled method for evaluating ground settlement induced by excavation in clay
[J]. Geomechanics and Engineering 2020 , 20 (4 ): 275.
[本文引用: 1]
[10]
胡之锋 , 陈健 , 邱岳峰 , 等 . 挡墙水平变位诱发地表沉降的显式解析解
[J]. 岩土力学 2018 , 39 (11 ): 4165 -4175 .
[本文引用: 1]
HU Zhifeng CHEN Jian QIU Yuefeng , et al Analytical formula for ground settlement induced by horizontal movement of retaining wall
[J]. Rock and Soil Mechanics 2018 , 39 (11 ): 4165 -4175 .
[本文引用: 1]
[11]
FAN X PHOON K K XU C , et al Closed-form solution for excavation-induced ground settlement profile in clay
[J]. Computers and Geotechnics 2021 , 137 : 104266 .
[本文引用: 1]
[12]
CHEN H LI J YANG C , et al A theoretical study on ground surface settlement induced by a braced deep excavation
[J]. European Journal of Environmental and Civil Engineering 2022 , 26 (5 ): 1897 -1916 .
[本文引用: 1]
[13]
MU L HUANG M . Small strain based method for predicting three-dimensional soil displacements induced by braced excavation
[J]. Tunnelling and Underground Space Technology 2016 , 52 : 12 -22 .
[本文引用: 3]
[14]
GOH A T C ZHANG R H WANG W , et al Numerical study of the effects of groundwater drawdown on ground settlement for excavation in residual soils
[J]. Acta Geotechnica 2020 , 15 : 1259 -1272 .
[本文引用: 2]
[15]
YING H CHENG K LIU S , et al An efficient method for evaluating the ground surface settlement of Hangzhou metro deep basement considering the excavation process
[J]. Acta Geotechnica 2022 , 17 : 5759 -5771 .
[本文引用: 3]
[16]
CHENG K XU R YING H , et al Observed performance of a 30.2 m deep-large basement excavation in Hangzhou soft clay
[J]. Tunnelling and Underground Space Technology 2021 , 111 : 103872 .
[本文引用: 2]
[17]
上海市住房和城乡建设管理委员会 . 基坑工程技术标准: DG/TJ 08-61-2018 [S]. 上海 : 同济大学出版社 , 2018 .
[本文引用: 1]
Shanghai Housing and Urban-Rural Construction Management Committee . Foundation pit engineering technical standards: DG/TJ 08-61-2018 [S]. Shanghai : Tongji University Press , 2018 .
[本文引用: 1]
[18]
顾晓强 , 吴瑞拓 , 梁发云 , 等 . 上海土体小应变硬化模型整套参数取值方法及工程验证
[J]. 岩土力学 2021 , 42 (3 ): 833 -845 .
[本文引用: 1]
GU Xiaoqiang WU Ruituo LIANG Fayun , et al On HSS model parameters for Shanghai soils with engineering verification
[J]. Rock and Soil Mechanics 2021 , 42 (3 ): 833 -845 .
[本文引用: 1]
[19]
应宏伟 , 孙威 , 吕蒙军 , 等 . 复杂环境下某深厚软土基坑的实测性状研究
[J]. 岩土工程学报 2014 , 36 (Sup.2) : 424 -430 .
[本文引用: 1]
YING Hongwei SUN Wei LÜ Mengjun , et al Measured characteristics of a deep soft soil excavation in complex environment
[J]. Chinese Journal of Geotechnical Engineering 2014 , 36 (Sup.2) : 424 -430 .
[本文引用: 1]
[20]
杜金龙 , 魏祥 , 杨敏 . 软土基坑逆作开挖的时效分析
[J]. 岩土工程学报 2008 , 30 (Sup.1): 395 -399 .
[本文引用: 3]
DU Jinlong WEI Xiang YANG Min . Time effect analysis of top-down excavation of foundation pits in soft clay
[J]. Chinese Journal of Geotechnical Engineering 2008 , 30 (Sup.1): 395 -399 .
[本文引用: 3]
[21]
北京金土木软件技术有限公司 . PLAXIS岩土工程软件使用指南 [M]. 北京 : 人民交通出版社 , 2010 .
[本文引用: 2]
Beijing Jintumu Software Technology Co., Ltd. . PLAXIS geotechnical engineering software usage guide [M]. Beijing : China Communications Press , 2010 .
[本文引用: 2]
[22]
ROBOSKI J FINNO R J . Distributions of ground movements parallel to deep excavations in clay
[J]. Canadian Geotechnical Journal 2006 , 43 (1 ): 43 -58 .
[本文引用: 1]
[23]
上海市勘察设计行业协会 , 上海市现代建筑设计(集团)有限公司 , 上海市建工(集团)总公司 . 基坑工程技术规范: DG/TJ 08-61-2010 [S]. 上海 : [出版者不详] , 2010 .
[本文引用: 1]
Shanghai Survey and Design Industry Association , Shanghai Modern Architectural Design (Group) Co., Ltd. , Shanghai Construction Engineering (Group) Corporation . Foundation pit engineering technical specification: DG/TJ 08-61-2010 [S]. Shanghai : [s. n.] , 2010 .
[本文引用: 1]
紧邻基坑同步施工下坑间隧道的变形特性
1
2013
... 在建、构筑物密集的地区开挖基坑将不可避免对邻近既有结构产生扰动,如房屋的沉降和不均匀沉降、隧道和地下管线的位移,严重时甚至会造成结构的破坏[1 ⇓ -3 ] .因此,准确预测基坑开挖诱发的地表沉降具有重要的现实意义. ...
Movement of tunnel between two adjacent concurrent excavations
1
2013
... 在建、构筑物密集的地区开挖基坑将不可避免对邻近既有结构产生扰动,如房屋的沉降和不均匀沉降、隧道和地下管线的位移,严重时甚至会造成结构的破坏[1 ⇓ -3 ] .因此,准确预测基坑开挖诱发的地表沉降具有重要的现实意义. ...
基坑开挖对临近明挖暗埋隧道竖向变形的影响机理
1
2018
... 在建、构筑物密集的地区开挖基坑将不可避免对邻近既有结构产生扰动,如房屋的沉降和不均匀沉降、隧道和地下管线的位移,严重时甚至会造成结构的破坏[1 ⇓ -3 ] .因此,准确预测基坑开挖诱发的地表沉降具有重要的现实意义. ...
Mechanism analysis of influence of deep excavation on deformation of nearby cut-and-cover tunnel
1
2018
... 在建、构筑物密集的地区开挖基坑将不可避免对邻近既有结构产生扰动,如房屋的沉降和不均匀沉降、隧道和地下管线的位移,严重时甚至会造成结构的破坏[1 ⇓ -3 ] .因此,准确预测基坑开挖诱发的地表沉降具有重要的现实意义. ...
地铁车站深基坑开挖变形智能多步预测方法
1
2024
... 在建、构筑物密集的地区开挖基坑将不可避免对邻近既有结构产生扰动,如房屋的沉降和不均匀沉降、隧道和地下管线的位移,严重时甚至会造成结构的破坏[1 ⇓ -3 ] .因此,准确预测基坑开挖诱发的地表沉降具有重要的现实意义. ...
Multi-step prediction of excavation deformation of subway station based on intelligent algorithm
1
2024
... 在建、构筑物密集的地区开挖基坑将不可避免对邻近既有结构产生扰动,如房屋的沉降和不均匀沉降、隧道和地下管线的位移,严重时甚至会造成结构的破坏[1 ⇓ -3 ] .因此,准确预测基坑开挖诱发的地表沉降具有重要的现实意义. ...
上海地区深基坑周边地表变形性状实测统计分析
2
2011
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
Statistical analysis of characteristics of ground surface settlement caused by deep excavations in Shanghai soft soils
2
2011
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
基于实测数据的上海地区超深基坑变形特性研究
2
2010
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
Deformation characteristics of ultra-deep foundation pit in Shanghai based on measured data
2
2010
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
杭州深厚软黏土中某深大基坑的性状研究
2
2011
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
Characteristics of a large and deep soft clay excavation in Hangzhou
2
2011
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
Patterns of soil deformations around tunnels. Application to the extension of Madrid Metro
2
2001
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... [7 ]所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
Analytical prediction for ground movements due to deep excavations in soils
1
2023
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
A displacement controlled method for evaluating ground settlement induced by excavation in clay
1
2020
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
挡墙水平变位诱发地表沉降的显式解析解
1
2018
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
Analytical formula for ground settlement induced by horizontal movement of retaining wall
1
2018
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
Closed-form solution for excavation-induced ground settlement profile in clay
1
2021
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
A theoretical study on ground surface settlement induced by a braced deep excavation
1
2022
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
Small strain based method for predicting three-dimensional soil displacements induced by braced excavation
3
2016
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
... [13 ,15 ]由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
Numerical study of the effects of groundwater drawdown on ground settlement for excavation in residual soils
2
2020
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
An efficient method for evaluating the ground surface settlement of Hangzhou metro deep basement considering the excavation process
3
2022
... 当前,研究基坑开挖诱发坑外地表沉降的方法大多分为以下几种.一是现场实测法.王卫东等[4 ] 整理统计了35个工程的实测数据,给出了上海软土地区深基坑地表最大沉降δ vm 与围护墙最大侧移δ hm 比值的平均值为0.84,该数值与江晓峰等[5 ] 归纳总结的平均值0.83极为接近.应宏伟等[6 ] 基于杭州某深厚软黏土基坑的实测数据进行分析,发现时空特性是影响坑外地表沉降的重要因素,且δ vm ≈0.6δ hm .二是理论解析法.González等[7 ] 利用虚拟镜像技术和弹性力学理论推导了圆孔收缩诱发土体位移的解析公式;Zheng等[8 ] 利用González等[7 ] 所推公式和面积等效原理,进一步推导了围护墙变位诱发坑外地表沉降的公式.Qian等[9 ] 基于平面应变下的位移-位移弹性边值问题,推导了刚性围护墙水平变位诱发坑外地表沉降的显式解;以此为基础,许多学者进一步推导了柔性围护墙变位下坑外地表沉降的理论解答[10 ⇓ -12 ] .当围护墙的变位模式为抛物线时,所有理论解答给出的关系均为δ vm /δ hm ≈0.4.三是数值模拟法.Mu等[13 ] 利用实测数据对某基坑进行反分析建模,总结数值模型中土体位移的衰减规律,提出了考虑小应变特性的土体三维位移场经验公式.Goh等[14 ] 通过大量有限元分析确定了影响地表沉降的关键参数,并开发了人工神经网络模型来估计地表最大沉降.Ying等[15 ] 利用既有工程资料建立了杭州地铁基坑的标准化模型,基于标准化模型进行三维数值模拟,提出了一种针对杭州地区地铁基坑坑外地表沉降的估算方法. ...
... 基坑开挖下坑外软土的变形和强度会随时间发生明显变化,实测研究成果[4 ⇓ -6 ] 虽能在一定程度上反映软土的蠕变特性,却无法详尽考虑不同时效或非时效因素对坑外地表沉降的影响;解析方面,既有理论方法没有考虑软土的蠕变效应,且大多基于平面应变假定,无法考虑坑外地表的空间效应;利用数值模拟方法的研究成果[13 ⇓ -15 ] 中,HS-Small模型[13 ,15 ] 由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
... ,15 ]由于能够考虑土体的小应变特性常为学者们所使用,然而其无法考虑与时间相关的软黏土蠕变.另一方面,坑外地表沉降的性状受到地层条件、基坑尺寸和围护结构型式等不同因素的影响,一般很难对坑外地表沉降进行准确的评估.然而,周边环境复杂的软土顺作法超深基坑一般在围护结构体系设计、土方开挖及施工上存在很多相似性,对某地区特定地层条件下典型的超深基坑案例进行建模,以期给出该地区超深基坑开挖引发地表沉降的可行分析方法. ...
Observed performance of a 30.2 m deep-large basement excavation in Hangzhou soft clay
2
2021
... 杭州中心项目超深顺作基坑采用分坑施工方法,Cheng等[16 ] 分析了B2分坑开挖的变形性状,平剖面如图1 所示.图中:z 为纵坐标;q 为地连墙测斜孔;d 为地表沉降观测点.如图1(a) 所示,主要地层自上而下分别为:①填土、②软黏土、③粉质黏土、④圆砾、⑤强风化、⑥中风化砂岩;基坑开挖深度为30.2 m,平面尺寸约98 m×92 m;围护结构采用厚1.2 m、深50 m的地连墙结合6道混凝土满堂对撑和被动区裙边加抽条加固.如图1(b) 所示为地连墙测斜以及坑外地表沉降监测点,自2019年4月1日第1道支撑形成开始,至2019年11月16日地下室基础底板形成强度,基坑开挖施工可分为如表1 所示的6个主要工况. ...
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
1
2018
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
1
2018
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
上海土体小应变硬化模型整套参数取值方法及工程验证
1
2021
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
On HSS model parameters for Shanghai soils with engineering verification
1
2021
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
复杂环境下某深厚软土基坑的实测性状研究
1
2014
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
Measured characteristics of a deep soft soil excavation in complex environment
1
2014
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
软土基坑逆作开挖的时效分析
3
2008
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
... PLAXIS 3D软件中软土蠕变模型的修正蠕变指数的计算公式[20 ] 如下: ...
... 式中:Cα 为蠕变指数,可由室内试验得到,若无试验数据时可利用经验公式C c /Cα ≈15~ 25来确定[20 ] ,C c 为压缩指数;e 0 为土体的初始孔隙比. ...
Time effect analysis of top-down excavation of foundation pits in soft clay
3
2008
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
... PLAXIS 3D软件中软土蠕变模型的修正蠕变指数的计算公式[20 ] 如下: ...
... 式中:Cα 为蠕变指数,可由室内试验得到,若无试验数据时可利用经验公式C c /Cα ≈15~ 25来确定[20 ] ,C c 为压缩指数;e 0 为土体的初始孔隙比. ...
2
2010
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
... ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
2
2010
... 计算分析时采用的土体模型及其参数如表2 所示.表中:l 为层厚;γ 为土体重度;c' 为土体有效黏聚力;φ' 为土体有效内摩擦角;λ* 为修正压缩指数;κ* 为修正膨胀指数;μ* 为修正蠕变指数; E 50 r e f E o e d r e f E u r r e f G 0 r e f γ 0 . 7 为割线模量减小到初始值的70%时的切应变;m 为模量应力水平相关幂指数;E 为弹性模量;υ 为泊松比.采用在基坑工程中广为使用的HS-Small土体模型考虑①填土、③粉质黏土和加固土,参数的选取参照《基坑工程技术标准》[17 ] 和顾晓强等[18 ] 的研究;然而,HS-Small土体模型无法模拟土体的蠕变和应力松弛等流变现象.尽管传统的观点认为,基坑工程属于临时性工程,在如此短的时间之内,主固结尚且没有结束,次固结更是无从谈起.然而,众多工程实践[16 ,19 ] 表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形会明显增长,表现出很强的蠕变行为,这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应,选取软土蠕变(SSC)模型作为②软黏土的本构,参数的选取参照文献[20 -21 ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
... ];④圆砾和⑤强风化、⑥中风化砂岩则采用传统的摩尔库伦MC本构,参数的选取参照文献[21 ].依据表1 定义模拟工况,网格划分如图2 所示,生成了 27 188 个单元、42 252 个节点. ...
Distributions of ground movements parallel to deep excavations in clay
1
2006
... 图10 所示为平行于围护墙方向的坑外地表沉降示意图,Roboski等[22 ] 使用互补误差函数来描述该方向的地表沉降: ...
1
2010
... 引入《基坑工程技术规范》[23 ] 中的三折线模型对垂直于围护墙方向的地表沉降进行描述,三折线模型定义了坑外4点的沉降与沉降最大值的关系,4点分别为(0, 0.2δ vm )、(H/ 2, δ vm )、(2H , 0.1δ vm )、(4H , 0). ...
1
2010
... 引入《基坑工程技术规范》[23 ] 中的三折线模型对垂直于围护墙方向的地表沉降进行描述,三折线模型定义了坑外4点的沉降与沉降最大值的关系,4点分别为(0, 0.2δ vm )、(H/ 2, δ vm )、(2H , 0.1δ vm )、(4H , 0). ...