不同灌浆效果下黏土海床导管架桩基础的竖向承载特性离心试验

doi:10.16183/j.cnki.jsjtu.2023.110

不同灌浆效果下黏土海床导管架桩基础的竖向承载特性离心试验

宋俊霖¹, 刘博²^,³, 唐立恒¹, 廖晨聪^,¹

1.上海交通大学海洋工程国家重点实验室,上海 200240

2.中电海洋能源工程技术研究院,广州 510663

3.中国能源建设集团广东省电力设计研究院有限公司,广州 510663

Centrifuge Tests on Vertical Bearing Capacity of Jacket Pile Foundation in Clay Seabed Under Different Grouting Effects

SONG Junlin¹, LIU Bo²^,³, TANG Liheng¹, LIAO Chencong^,¹

1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. China Electric Ocean Energy Engineering Technology Research Institute, Guangzhou 510663, China

3. China Energy Engineering Group Guangdong Electric Power Design Institute Co., Ltd., Guangzhou 510663, China

通讯作者: 廖晨聪,副研究员,博士生导师;E-mail:billaday@sjtu.edu.cn.

责任编辑: 李博文

收稿日期: 2023-03-28 修回日期: 2023-05-16 接受日期: 2023-07-3

基金资助:

国家自然科学基金(52279106)
上海市晨光计划(20CG15)
上海市教委科研创新计划(2021-01-07-00-02-E00089)

Received: 2023-03-28 Revised: 2023-05-16 Accepted: 2023-07-3

作者简介 About authors

宋俊霖(1998—),硕士生,现主要从事海洋桩基相关的研究工作.

摘要

在40~60 m水深海域,海上风力发电机多使用导管架基础作为主要支撑结构.导管架通过水下高强灌浆与桩基础顶部连接,形成顶端密封段,共同承载竖向荷载.针对桩基顶部灌浆正常、灌浆不足、灌浆不良存在通孔3种不同灌浆效果开展离心模型试验,分析极限状态下基础的竖向承载力及灌浆段与桩身段的承载力分担比,并与现有理论计算方法进行对比.结果表明,灌浆密封顶盖的承载力取决于密封效果.对于灌浆密封顶盖灌浆正常和灌浆不足的基础,灌浆密封顶盖的承载力约占基础总承载力的25%~30%;灌浆不良存在通孔时,基础灌浆段承载力发挥较早且很快达到极限,其分担比远低于其他两者承载力.试验结果可为导管架桩基础设计中的灌浆段承载力计算提供参考依据.

关键词： 离心模型试验; 顶部灌浆桩基; 不排水抗剪强度; 竖向承载力; 分担比

Abstract

Jacket foundations are often used as the main support structure for offshore wind turbines in waters with a depth of 40—60 meters. The jacket foundation is connected to the top of the pile foundation through underwater high-strength grouting to form a top sealing section, which together bears the vertical load. In this paper, centrifugal model tests are conducted for three different grouting effects: normal grouting at the top of a pile foundation, insufficient grouting, and poor grouting with through-holes. The vertical bearing capacity of the foundation and the bearing capacity sharing ratio between the grouting section and the pile body section under the limit state are analyzed, and compared with existing theoretical calculation methods. The results show that the bearing capacity of the grouting sealing cap depends on the sealing effect. For foundations with normal grouting and insufficient grouting of grouting sealing caps, the bearing capacity of grouting sealing caps accounts for approximately 25%—30% of the total bearing capacity of the foundation. When there are through-holes in poor grouting, the bearing capacity of the foundation grouting section develops early and quickly reaches its limit, whose sharing ratio is far lower than the other two bearing capacities. The test results in this paper can provide a reference for the calculation of bearing capacity in foundation design.

Keywords： centrifugal model test; top grouting pile foundation; undrained shear strength; vertical bearing capacity; share ratio

PDF (15124KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

宋俊霖, 刘博, 唐立恒, 廖晨聪. 不同灌浆效果下黏土海床导管架桩基础的竖向承载特性离心试验[J]. 上海交通大学学报, 2025, 59(1): 38-47 doi:10.16183/j.cnki.jsjtu.2023.110

SONG Junlin, LIU Bo, TANG Liheng, LIAO Chencong. Centrifuge Tests on Vertical Bearing Capacity of Jacket Pile Foundation in Clay Seabed Under Different Grouting Effects[J]. Journal of Shanghai Jiaotong University, 2025, 59(1): 38-47 doi:10.16183/j.cnki.jsjtu.2023.110

我国海上风电建设逐渐从浅水过渡至深远海域.风电机组受台风、海啸、风暴潮等复杂海域荷载作用的影响,对下部支撑结构的设计提出了更高的要求^[1].我国海域海床普遍覆盖一层深厚软黏土^[2],随着水深加大,受海床条件和机组质量影响,若仍使用单桩基础会给设计和施工带来很大挑战^[3].导管架基础对黏土海床适应性好,具有结构强度大、承载能力高、便于安装和拆卸等优点,适合由浅水至深水的过渡海域使用.在欧洲,海上风电场已得到广泛应用且有望成为今后海上风电机组主要基础型式之一.

导管架与桩基进行连接时,常使用顶部灌浆方法^[3-4],在此类工法下形成一种介于管桩基础和吸力桶基础之间的顶部灌浆桩基型式,其灌浆段与桩体协同承载着竖向荷载.现有软黏土海床中,大直径桩基础承载力研究主要以理论公式结合数值模拟进行验证的方法为主.Kikuchi等^[5]对东京沿海公路大桥桥墩基础的大直径钢管桩进行大量现场荷载试验,获得有关桥梁基桩承载机理的相关研究成果,结果表明相对较小的位移即可达到桩体所能承受的最大承载力;Park等^[6]通过数值模拟得到在砂土中土体的水平应力显著增加且桩身摩阻力会随土体应力增加而相应增加的结论,提出砂土中的吸力桶基础桩身摩阻力的预测方程及桩基础土压力的影响因子等;吴荣辉等^[7]对江苏海岸辐射沙洲地层中大直径钢管桩基础承载性能进行轴向抗压现场试验,结果表明大直径钢管桩为典型摩擦桩,其极限承载力高于美国石油学会(API)规范^[8]计算值,且桩内土体对管壁的侧摩阻力作用很小,主要是桩外土对管壁的侧摩阻力发挥作用.

综上所述,现场试验不仅耗时、费力,而且不便于操作.现有研究大多采用理论公式结合数值模拟的方法确定海上风电大直径桩基的竖向承载力,对于顶部灌浆桩基在饱和软黏土海床上的竖向承载特性缺少研究.顶部灌浆桩基的灌浆段施工大多采用先桩法^[8],即安装时先将钢管桩打入海床,再吊起风电导管架并将其桩腿插入已打入海床的钢管桩中,最后在两管之间的环形空间内灌浆进行连接,使灌浆体与原先的桩基础、导管架腿、海床连接在一起.尽管型式上与空心管桩基础及吸力桶基础相似,但由于制造及施工方式的不同,此类基础受力机制兼具两者的特点又有所不同.目前,对于此类基础尚未有较明确的承载力计算理论和规范,且缺少对于灌浆段承载力的考虑依据,而海上作业时又难以保证灌浆段的施工质量,故无法推测灌浆不良对承载力可能造成的影响.

顶部灌浆桩基础的桩身段在插入海床时,海床土体涌入桩体内形成一定高度的土柱,由于灌浆过程的不确定性,一方面可能导致灌浆体深度不足,与桩内土体表面夹有海水层等;另一方面由于灌浆过程中操作不规范等造成的灌浆不均可能导致灌浆体各处渗透性差别较大,故考虑不同灌浆质量下,其竖向承载特性对支撑上部风电机组的重要作用.针对桩基顶部灌浆正常、灌浆不足、灌浆不良存在通孔3种不同灌浆效果开展离心模型试验,分析极限状态下桩基础的竖向承载力发展趋势及承载力分担比等特性,同时与现有理论计算方法进行对比,对顶部灌浆桩基的设计及应用提供一定参考.

1 离心模型试验

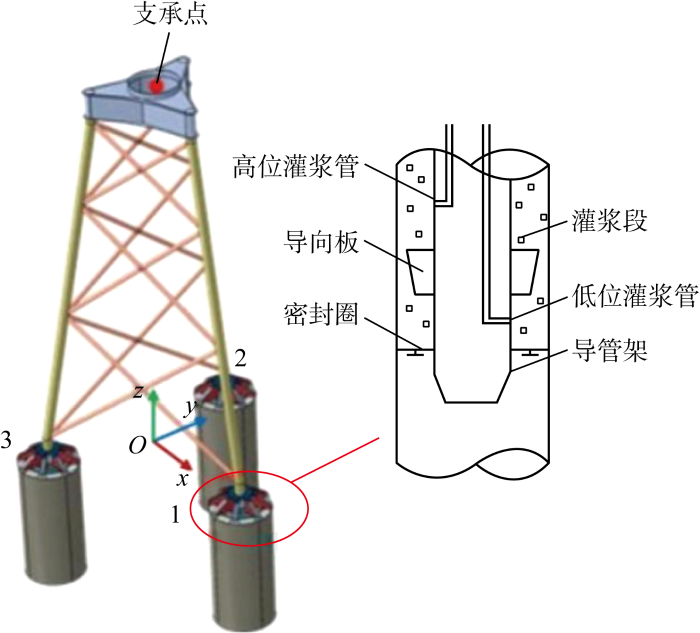
土工离心模型试验的基本原理是按相似准则将原型的几何形状按比例缩小,再通过离心机高速旋转在模型上产生ng倍离心加速度,使其在离心力场中的应力状态与原型重力场中一致,从而模拟出和原型相同的受力情况^[9-10].此外,通过离心机营造的超重力加速度环境还能充分缩短土体固结所需的时间,同时减小试验模型尺寸进而规避现场试验所需的昂贵成本.目前,海上风电平台工程项目所采用的顶部灌浆大直径桩基通常如图1所示.传统物理模型试验对相关工程模拟有许多限制,而离心模型试验利用定义明确的人造重力场模拟应力在模型内的分布情形,在实验室内以物理模拟探究原型结构的力学行为能适用于现行多数工程项目,其结果也可为数值分析提供验证.不排水抗剪强度随深度线性增加的饱和软黏土在海洋环境中较为常见,结合试验测得的土体强度随深度变化关系,对长径比 L/D=5的顶部灌浆桩基开展离心模型试验.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 海上风电平台导管架基础

Fig.1 Jacket foundation of offshore wind power platform

1.1 试验设备

离心试验采用上海交通大学DC2200鼓式离心机,如图2所示.鼓槽直径R为2.2 m,径向深度L_s为0.4 m,高度H为0.7 m,总容重达600g t,最大离心加速度为200g.试验拟采用的离心加速度为125g.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 上海交通大学鼓式离心机

Fig.2 DC2200 drum centrifuge of Shanghai Jiao Tong University

1.2 试验工况设置

为研究不同的顶部灌浆型式对桩基础承载力的影响,通过对试验中桩基模型的顶部灌浆段(下文简称顶盖)进行调整,共设置3种不同顶部型式工况.桩基模型采用铝合金材料,桩体外径为4 cm,桩长为20 cm,壁厚为0.8 mm,顶盖厚为8 mm,外径与桩体保持一致.顶盖与桩体间采用螺栓连接,制作顶盖时将下半部分的半径内缩0.8 mm以保证顶盖能塞入桩体内,同时在桩体外壁及顶盖相应位置对称开设4个螺纹孔,将两者连接为一体,螺栓强度对试验结果不产生影响.

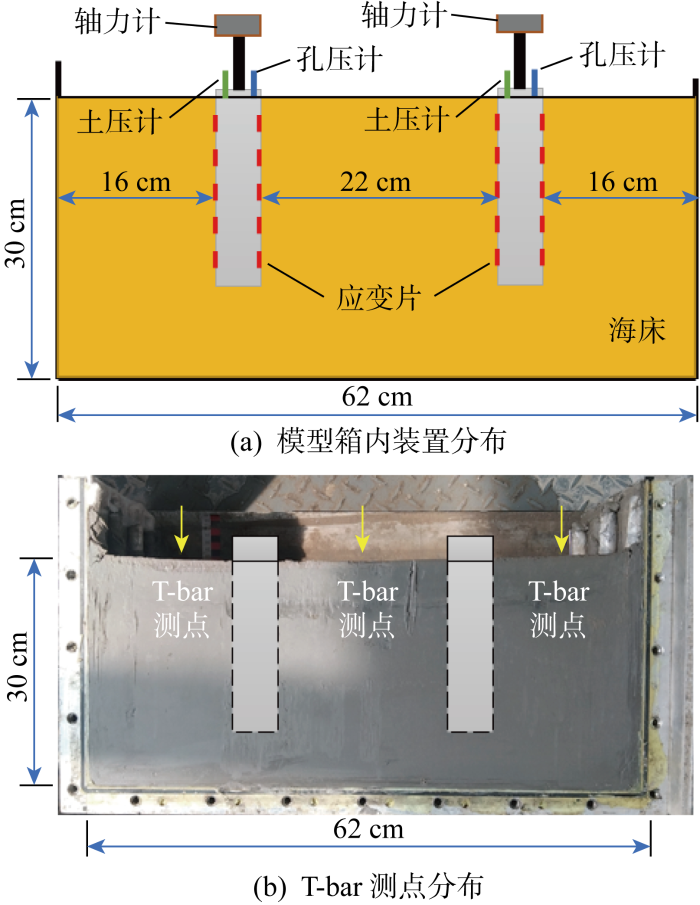
对应的实际原型桩体外径为5 m,桩长为25 m,桩体壁厚为0.1 m,顶盖厚为1 m.顶盖上设有用于安装传感器的孔位,桩身按一定间距贴有2列5排共10片应变片,使用环氧树脂对其进行保护.模型桩体与顶盖实物图如图3所示,在桩基模型顶盖底部安装孔压计和土压计分别测量顶盖底部超孔隙水压力和顶盖承载力,顶盖通过顶杆连接轴力计以测量其竖向总承载力,桩身按一定距离分布,粘贴2列共10片应变片,以测量沿桩身分布的桩侧摩阻力.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 模型桩体与顶盖实物图

Fig.3 Pile body and top cap of model

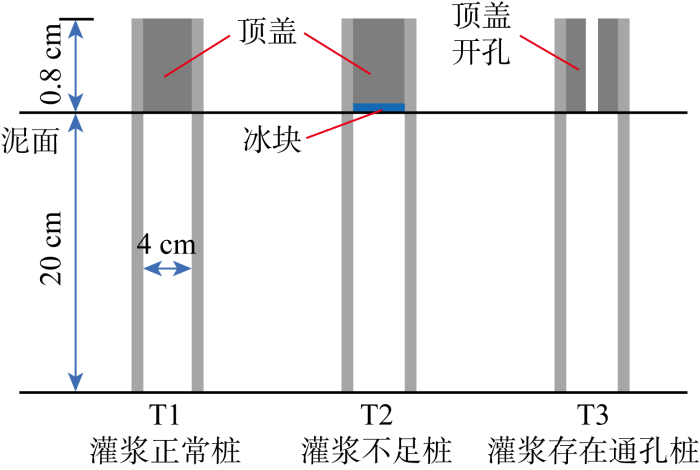
利用3种桩基型式分别模拟不同的灌浆效果,T1为灌浆正常桩、T2为灌浆不足桩、T3为灌浆存在通孔桩,如图4所示.T2通过在顶盖底部塞入同样直径为0.5 cm的厚圆形冰块实现,待冰块融化后模拟灌浆段与海床间夹有水层的工况.经测试,在夏季离心机工作温度下,放置于鼓内的冰块在15 min内可全部融化.模拟T3时,在顶盖开设直径为2 mm 的贯通小孔,以此模拟灌浆不良导致渗透率过大存在通孔缺陷的情况.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同灌浆效果的桩基模型示意图

Fig.4 Schematic diagram of three types of pile foundation model

1.3 模型布置

试验模型箱内长宽高尺寸为62 cm×20 cm×35 cm,如图5所示.箱内固结土体高度为30 cm,为避免模型箱边界对测量结果的影响,顶部灌浆桩基距离侧面边界不小于2倍桩径^[9].通过轴力计示数、桩顶下第一排应变片示数平均值和土压计示数分别得到总承载力、摩阻力和顶盖承载力结果.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 试验模型布置图示意图

Fig.5 Schematic graphic of model layout

2 模型试验流程

离心模型试验流程主要包括土体固结、土体不排水抗剪强度测试和顶部灌浆桩基竖向承载力试验3部分.为更加直观反映原型情况,在后续数据处理时将试验结果按离心机缩放比1∶125的相似关系换算成原型尺寸下的结果.

2.1 土体固结

试验用土为重塑土,土体固结前需布置模型箱,主要包括铺设土工布、固定排水管和粘贴刻度尺等,以便后期观察模型箱底部土体在固结过程中的排水过程及箱内泥面和水面高度变化.固结土体前,先采用人工方式将土体晾干、粉碎;然后,借助工具将粉碎后的土体颗粒置于孔眼直径为1 mm的筛砂网上进行过筛,再将其置于搅拌机内,其间加水至饱和状态,充分搅拌均匀;同时,在模型箱内壁涂抹硅油并粘贴塑料薄膜,以降低土体与模型箱侧壁的摩擦力,减小边界效应;最后,在125g离心加速度下通过注浆管,将泥浆注入模型箱内,4 d后完成土体固结.试验用土的部分基本物理力学指标参数如表1所示.

表1 土体基本物理力学指标参数

Tab.1 Basic physical and mechanical index parameters of soil

土体类别	有效重度/ (kN·m^-3)	相对体积质量,G_s	饱和度, S_r/%	固结系数, C_v/(cm²·s^-1)
黏土	7.2	2.74	98	2.04×10^-3

新窗口打开| 下载CSV

2.2 土体不排水抗剪强度测试

土体不排水抗剪强度是影响桩基竖向承载力的重要因素.由于T-bar全流贯入仪具有受土体应力历史及土体刚度等因素影响小的特点,通过测定T-bar贯入阻力大小可获取试验土体不排水抗剪强度沿深度的分布规律^[11],因此该技术被广泛运用于离心模型试验中软黏土地基不排水强度的测定.Chung等^[12]和House等^[13]提出排水条件和T-bar加载速度间的关系,通常可用无量纲速度 ${v_{m}}^{*}$ 确定T-bar所处排水状态:

${v_{m}}^{*}$ =vd/C_v

(1)

式中:v为T-bar贯入速度;d为T-bar探头直径.当 ${v_{m}}^{*}$ <0.2时,T-bar贯入过程处于排水状态; ${v_{m}}^{*}$ >20时,T-bar贯入过程处于不排水状态.本次试验中 d=5 mm,C_v=2.04×10^-3 cm²/s,经计算在125g离心加速度下,为使T-bar贯入过程处于不排水状态,贯入速度需满足v>0.82 mm/s.当v取值过大时将导致读取数据量过少,故试验时T-bar以v=1 mm/s 的贯入速度进行测定.T-bar贯入阻力与土体不排水抗剪强度关系^[11]为

P=N_b(s_ud)

(2)

式中:P为T-bar单位长度受力大小;s_u为土体不排水抗剪强度;N_b取决于T-bar表面的粗糙度,文献[11]中建议取10.5.T-bar测点布置见图5(b).

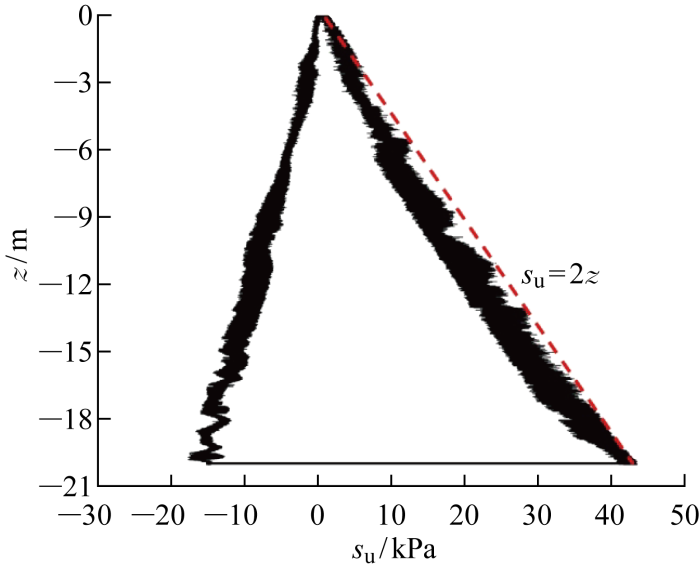
T-bar测得的土体强度曲线如图6所示.土体不排水抗剪强度随深度的增大而增大,两者关系近似于线性分布.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 土体强度分布曲线

Fig.6 Strength distribution curve of soil model

对饱和黏土海床土体的不排水抗剪强度进行线性拟合,得到其沿深度的变化规律为

s_u=2z

(3)

根据对试验用土的基本物理参数指标,测定可得土体的有效重度γ'=7.2 kN/m³,进而得到土体不排水抗剪强度与竖向有效应力的关系为

s_u=2(σ'_v0/γ')=0.28σ'_v0

(4)

2.3 顶部灌浆桩基竖向承载力试验

桩基模型与轴力计一同连接于离心机作动机械手上,通过控制机械手的运动模拟桩基贯入过程,桩基的加载速度与排水状态关系可用无量纲速度 $v_{n}^{*}$ 计算^[14]:

$v_{n}^{*}$ =v_nD_n/C_v

(5)

式中:v_n为桩基模型贯入速度;D_n为桩基排水路径长度.在本次试验中,D_n取桩基模型直径为4 cm.当 $v_{n}^{*}$ >30时,桩基处于不排水状态;当 $v_{n}^{*}$ <0.01时,桩基处于排水状态.经计算,v_n>0.18 mm/s时,桩基处于不排水状态,当v_n取值过大时除了将导致读取数据量过少外,还会带来应变速率效应,因此试验时取v_n=0.5 mm/s.

调整好机械手点位后,在离心机静止即1g作用下时,以v_n=0.5 mm/s将模型桩插入模型箱内土体,通过传感器与监控显示屏判断桩顶与泥面接触后停止作动,后提速至125g下旋转30 min.为模拟桩基在海床中的真实加载环境,桩基加载前需先向模型箱内注入约2 cm高度的水位,以确保桩基模型顶盖底部接触海床表面时桩顶整体已没入水中.随后在125g离心加速度下控制机械手以v_n=0.5 mm/s进行加载贯入试验.根据API规范^[8],黏土中桩基贯入约0.1倍桩径后即视为达到极限承载状态,故控制桩基模型持续贯入2 cm(0.5倍桩径),以确保达到承载极限并获得足够多的数据,从而记录试验过程中各传感器及应变片示数的变化.

3 试验结果与分析

试验取顶部灌浆桩基荷载-位移曲线拐点^[15]处的荷载为顶部灌浆桩基极限状态下的竖向承载力,顶部灌浆桩实际桩径D为 5 m.

3.1 桩基竖向承载力分析

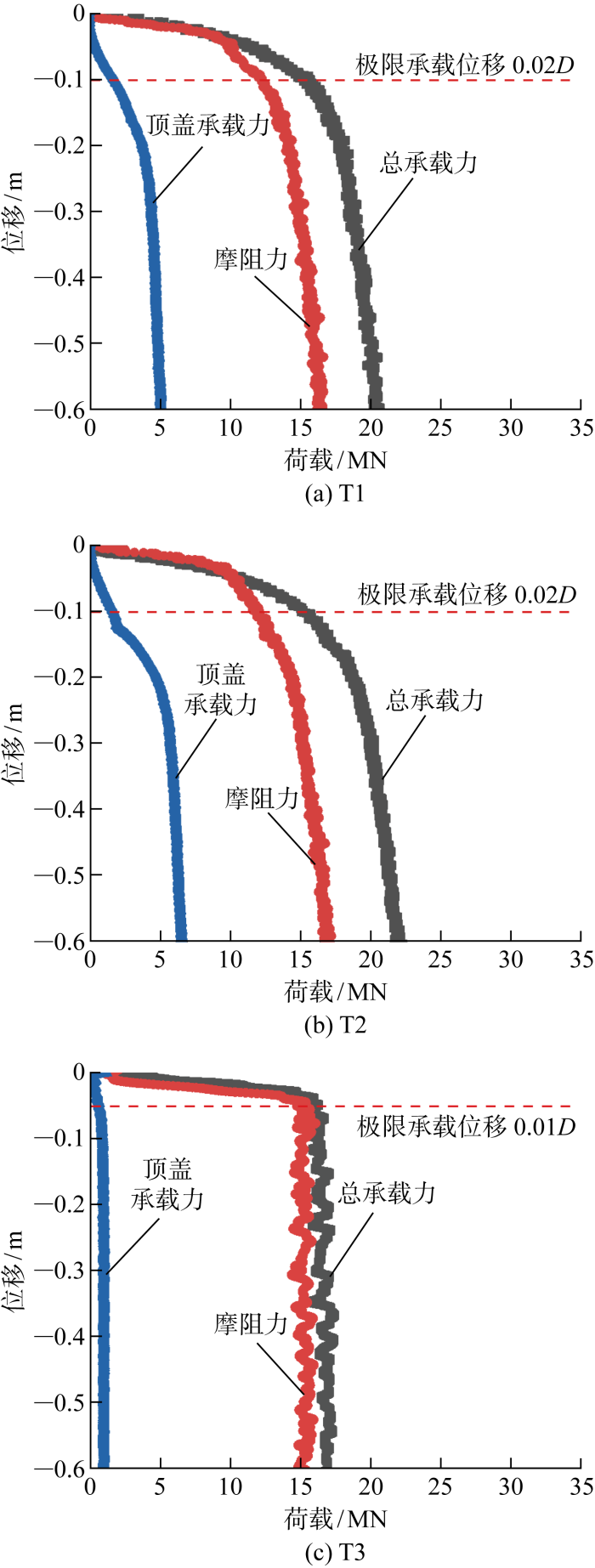
3种不同灌浆效果的桩基贯入饱和黏土地层的荷载-位移变化曲线如图7所示.由图可知,在桩基的贯入过程中,竖向荷载随贯入深度的增加而不断增大,在加载初期荷载增长较快且荷载-位移曲线均出现明显拐点,到达拐点后,荷载增长速率逐渐减小.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 3种型式桩基荷载-位移曲线

Fig.7 Q-s curves of three types of pile foundations

由图7(a)所示的荷载-位移曲线可知,T1所对应极限状态下总承载力为16.5 MN,摩阻力为12.0 MN,拐点位置均在0.02D(0.1 m)左右,是以摩阻力为主要承载力的典型摩擦桩.由于离心机提速至125g的过程中,地层压缩变形导致顶盖与土体脱离,故在位移0.05 m后,顶盖才开始逐渐发挥承载作用.取顶部灌浆桩基荷载-位移曲线拐点处的荷载为顶部灌浆桩基极限状态下的竖向承载力,位移至0.2 m后到达拐点,增长速率随之放缓,对应极限状态约为4.5 MN.如图7(b)所示,T2荷载-位移曲线变化趋势与T1相似,反映的承载规律也是在桩体贯入前期,总承载力基本由桩侧摩阻力提供,到达一定深度后顶盖开始承担一定承载力,其达到极限状态所对应的拐点位置也低于摩阻力和总承载力的拐点位置,说明当桩侧摩阻力到达极限状态后,顶盖承载力仍有一定的承载力发挥空间.

取荷载-位移曲线拐点处的荷载作为极限状态下的竖向承载力.轴力计测得的总承载力应等于桩侧摩阻力与顶盖承载力及桩端阻力之和,由图7(a)所示,T1的顶盖承载力为4.4 MN,即顶盖部分所承担的承载力占比约为27.3%,基本满足顶盖承载力与摩阻力之和近似等于总承载力,符合实际规律.总承载力多出部分即为桩端阻力,约为0.1 MN,因桩身壁厚仅为0.8 mm,其所对应的桩端环形截面的面积也较小,其承载力占比仅约0.4%,对总承载力分布影响不大.T2总承载力为16.2 MN,摩阻力约为11.8 MN,顶盖承载力为4.3 MN,即顶盖部分所承担的承载力占比约为27.2%,与T1差距不大.

T3由于顶盖存在一定大小的通孔,在贯入过程中可明显看到土体从小孔内逐渐涌出直至顶盖被完全覆盖,如图8所示.由图7(c)可知,T3顶盖承载力变化也不同于其他两者,自贯入之初即开始变化,短时间内到达拐点,之后稳定在1.0 MN左右.拐点位置约在0.01D(0.05 m)处.T3与T1、T2的不同之处在于,前两者的桩顶均为密闭环境,而T3近似于开口桩情况,总承载力基本由桩侧摩阻力提供,土体从小孔内涌出致使土体提供的反力减小,故顶盖所承担的承载力占比远小于其他两者.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 T3加载前后对比图

Fig.8 T3-comparison before and after loading

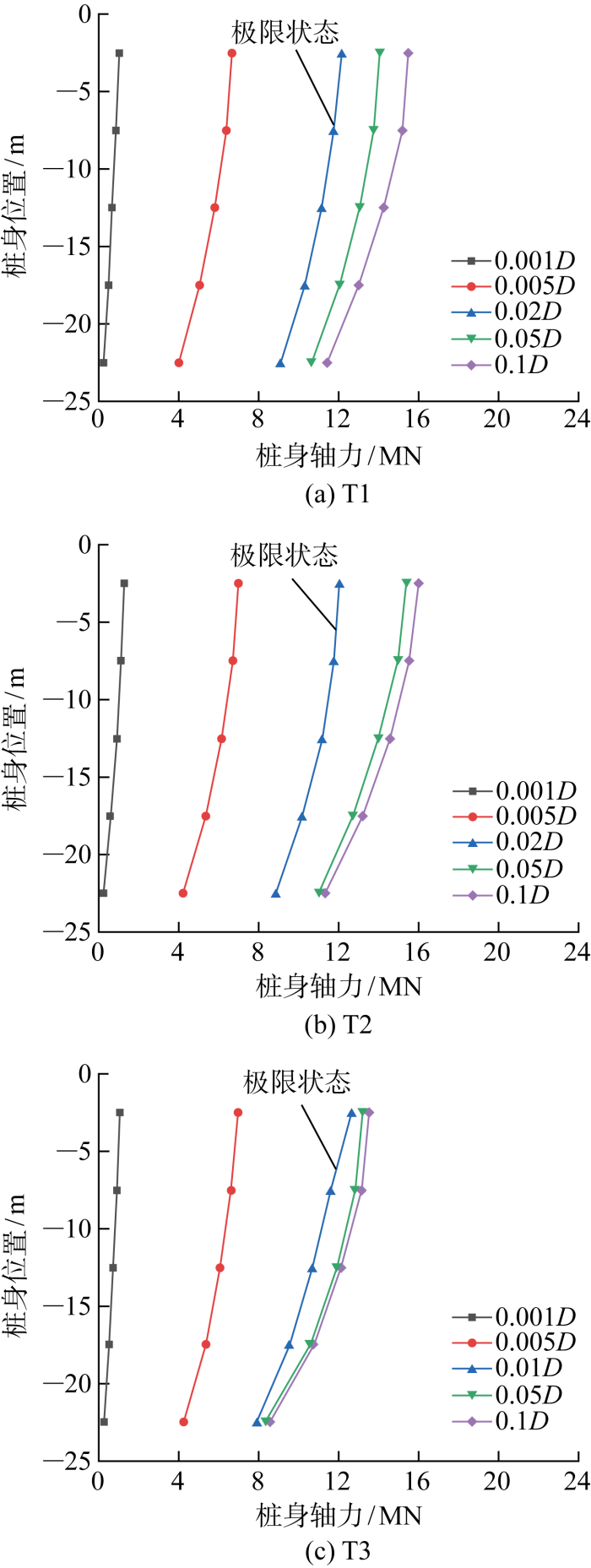
3.2 桩身轴力与桩侧摩阻力分析

桩体竖向加载时,桩身受力产生向下的位移,相应带动桩周土体下沉,而桩周土体的沉降量小于桩身的位移量从而产生相对位移,而土体自身的黏聚力阻止相对运动进行,因此产生桩侧摩阻力.通过上下两个截面间的桩身轴力差可得到土层中的摩擦阻力:

$\begin{array}{l} {\bar{f}}_{i} = α s_{u i}, α \leq 1.0 \\ f_{i} = \frac{F_{i}}{U h_{i}} = \frac{Q_{i} - Q_{i - 1}}{U h_{i}} \end{array}\}$

(6)

式中:f_i为试验测得桩身任意一点i处的侧摩阻力; ${\bar{f}}_{i}$ 为API规范^[8]中建议黏土中桩身任意一点i处的侧摩阻力;s_u_i为桩身任意一点i处的土体抗剪强度;α为修正系数;Q_i为桩身任意一点i处的桩身轴力;U为桩身周长;h_i为点i至点i-1截面间的桩身段长度;F_i为h_i对应桩身段内的摩阻力.桩身受力示意图如图9所示,图中Q_s为桩端阻力.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 桩身受力示意图

Fig.9 Schematic diagram of pile body stress

由图10(a)可知,到达极限状态前,桩身各点处轴力随位移变化迅速增长,到达极限状态后增速放缓.此外,越接近桩端的相邻截面间摩阻力越大,故同样呈现随深度线性变化规律.随着加载过程中法向应力的增加,到达极限状态后,桩身轴力随桩身位置曲线的斜率不再改变,表明此时桩身上部侧摩阻力已经达到极限状态不再改变.而桩身下部的侧摩阻力桩身轴力随桩身位置曲线的斜率仍在改变,尚未达到极限,但其增大的幅值对于总承载力的贡献有限,工程设计时不再考虑其对承载力的影响.如图10(b)和10(c)所示,T2、T3的桩身轴力随桩身应变片位置的分布规律与T1基本一致,其桩身侧摩阻力也大小相近且呈现相同的变化趋势.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 3种型式桩基桩身轴力分布曲线

Fig.10 Axial force of three types of pile foundations

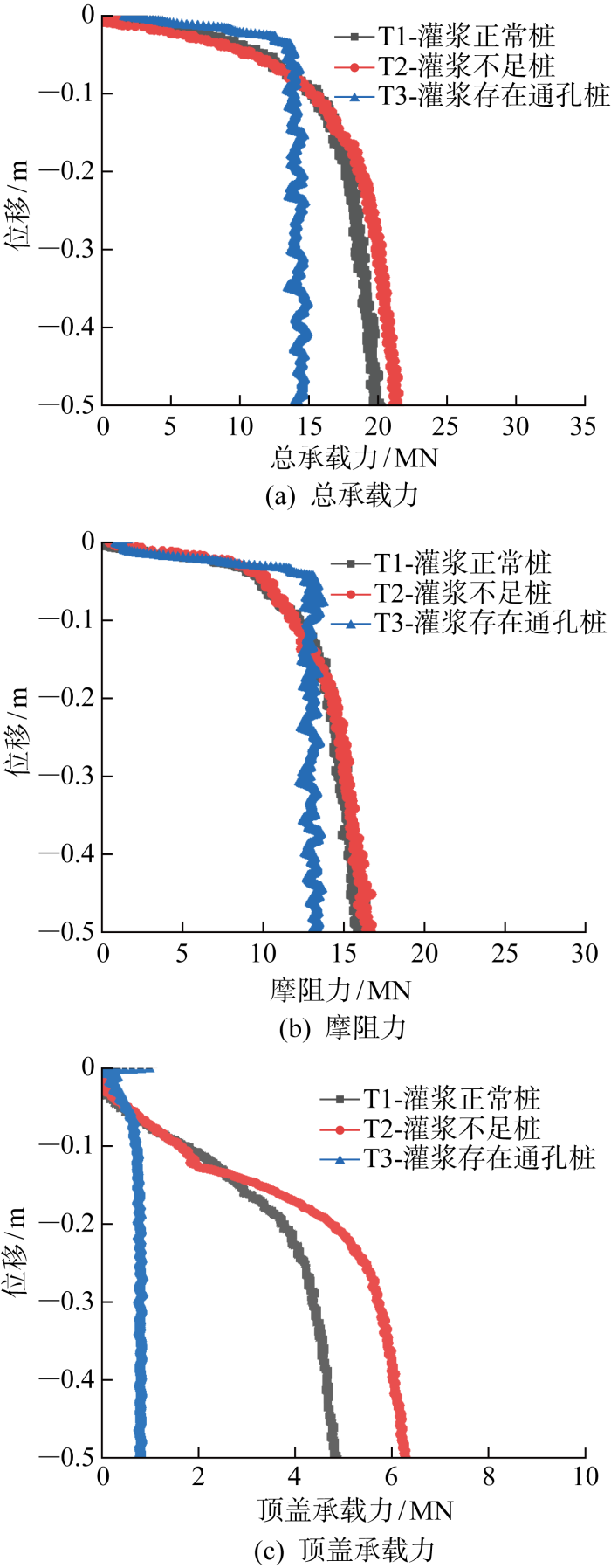
3.3 不同型式桩基竖向承载特性对比

不同顶部型式灌浆桩基总承载力、摩阻力及顶盖承载力的对比如图11所示.由图11(a)可知,横向对比T1、T2、T3共3种型式总承载力曲线,对于顶部灌浆段密闭性较好的T1、T2两种型式桩基础,两者总承载力相差不大,且顶盖承载力在总承载力中占比达到25%~30%,能得到充分发挥进而提升桩基础的总承载力上限.由图11(b)可知,3种型式桩基摩阻力大小差别不大,因此,图11(a)中总承载力差异主要由图11(c)所示的顶盖承载力所造成.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同顶部型式灌浆桩基各曲线对比

Fig.11 Comparison of different types of top grouting pile foundations

顶盖承载力对比如图10(c)所示,T1、T2两者拐点位置相近且均出现位置滞后于总承载力拐点,故在到达总承载力曲线拐点后,顶盖承载力仍在持续增长.而顶部灌浆质量较差存在贯通孔的T3,尽管顶盖承载力发挥较早,但很快到达极限不再增长,因此其承载力能力发挥远小于其他两者.

3.4 顶部灌浆桩基的承载力确定方法

对于海上风电桩基础,目前主要根据API规范^[8]及挪威船级社(DNV)规范^[16]将其作为长径比较大的单桩基础考虑,即桩的竖向极限承载力等于桩侧摩阻力和桩端端阻力之和减去桩体自重,API规范的计算公式具体如下:

$\begin{array}{l} V_{u l t} = Q_{s f} + Q_{b f} - W'_{p i l e} \\ Q_{s f} = π D \int_{0}^{L} f (z) h_{i} = π D \int_{0}^{L} α s_{u i} h_{i} \\ Q_{b f} = A_{p i l e} q_{b f} = 9 A_{p i l e} s_{u} \end{array}\}$

(7)

式中:V_ult为竖向极限承载力;Q_sf为桩侧极限摩阻力;Q_bf为桩端极限端阻力;W'_pile为桩基扣除浮力后的有效自重;A_pile为桩底截面面积;q_bf为单位桩端有效承载力;f(z)为黏土中沿吸力桩桩身任意一点的侧摩阻力.

式(7)对实际海床环境及桩体的自身条件进行了一定简化,且未考虑桩内土体刚度有限、存在压缩等情况,直接将桩体作为长径比L/D>10的大直径单桩基础进行计算,而本文所研究的中尺度顶部灌浆导管架桩基础长径比L/D大于0.5而小于10,因此无法确定其是否可适用.

Kay等^[17]将0.5<L/D<10的桩基类型定义为中尺度基础,具有介于浅基础和深基础之间的几何形状和承载力分布情况.因此,竖向受压的导管架基础最大轴向承载力的设计方式与海上竖向受荷管桩类似,但又有所不同,故文献[17]中提出一种新的基于中尺度基础受力特点的竖向承载力计算模式,即中尺度基础公式:

V_ult=F_o+N_cs_uA_base-W'_steel

N_c=min{6.2(1+0.34arctan(L/D)), 9}

(8)

式中:F_o为外壁摩阻力;N_c为基础竖向荷载承载力系数;A_base为基础顶面面积;W'_steel为基础扣除浮力后的有效自重.

式(8)创新性地提出了N_c承载力系数,从而将中尺度基础的承载力计算得更为精确,目前在工程中广泛应用于长径比L/D≤4.5的情况,而对于长径比L/D>4.5的情况仍以单桩基础进行设计.但由于式(8)并未考虑灌浆效果可能造成的影响,故不能完全适用于存在灌浆缺陷的工况.

通过前文对T3竖向承载力试验的分析可知,T3因类似于开口桩,土体在加载过程中从孔内涌出,桩内形成的土塞强度减小进而导致提供至顶盖的反力减小.因此,若直接采用桩端土体抗剪强度进行承载力计算将不符合实际情况.

将T-bar测得的土体实际不排水强度代入式(8)计算,得到计算理论值和实际试验值的对比图如图12所示.由图12可知,API规范公式和中尺度基础公式对于L/D=5的灌浆桩基在极限状态下的承载力计算结果一致,T1、T2在极限状态下的承载力大小与公式结果均较为接近,说明灌浆正常和灌浆不足的工况均可适用API规范公式和中尺度基础公式.T1结果略小于API规范公式和中尺度基础公式,从公式构成角度分析,式(7)和式(8)考虑的土体抗剪强度s_u均为桩端所在标高处的土体抗剪强度,而表层土体的强度要远小于桩端处的土体抗剪强度,因此相比于实际结果会略有偏大.T3结果与式(7)和式(8)结果差距较大,进一步说明灌浆效果的优劣对桩基础的承载力具有一定的影响,在实际工程中应保证灌浆质量,本文结果可为存在灌浆缺陷的桩基设计提供参考.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 桩基承载力试验值与理论值对比

Fig.12 Comparison of theoretical and experiment values of foundation bearing capacity

4 结论

通过离心机模型试验结合理论公式计算的方法研究了不同顶部灌浆效果下长径比L/D=5的桩基在饱和黏土海床上的竖向承载力特性,主要结论如下:

(1) 在饱和软黏土地层中,顶部灌浆桩基呈典型摩擦桩性质,竖向承载力主要由桩侧摩阻力承担.灌浆顶盖能够提升桩基础的总承载力,对于T1-灌浆正常桩和T2-灌浆不足桩,顶盖承载力在总承载力中占比达到25%~30%,灌浆段在桩基贯入过程中能较好地发挥承载作用,灌浆不足情况下的总承载力与灌浆正常情况相差不大.T3-灌浆存在通孔桩,土体在加载过程中从孔内涌出,因此在设计时必须确保桩顶灌浆段的灌浆质量以保证其具有足够的承载能力.

(2) 到达极限状态前,桩身各点处轴力随位移变化迅速增长.到达极限状态后增速放缓,此时桩身上部侧摩阻力已经达到极限状态不再改变,而桩身下部的侧摩阻力仍尚未达到极限,其增大的幅值对于总承载力的贡献不大,工程设计时通常不考虑其对承载力的影响.

(3) 对于长径比L/D=5的顶部密闭性良好的灌浆桩基,API规范公式和文献[17]中尺度基础公式的计算结果仍可适用.而对于灌浆不良存在通孔的情况则与公式结果相差较大,考虑原因为表层土体的强度远小于桩端处的土体抗剪强度,且土体不断从通孔处流出,致使无法对顶盖提供充足的反力,所以相比于实际结果会略有偏大.

致谢

本文的离心机试验工作由上海交通大学叶冠林教授指导开展,朱文轩博士在论文写作过程中提供了重要帮助,特此感谢.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

K Y

, NAM

, RYU

M S

, et al.

A review of foundations of offshore wind energy convertors: Current status and future perspectives

[J]. Renewable and Sustainable Energy Reviews, 2018, 88: 16-36.