内压作用下耐磨胶带层对非黏结柔管扭转特性的影响

doi:10.16183/j.cnki.jsjtu.2023.163

内压作用下耐磨胶带层对非黏结柔管扭转特性的影响

罗春苗¹^,², 付世晓^,¹^,², 张萌萌¹^,², 陈鲲鹏¹^,², 崔晓轩³

1.上海交通大学海洋工程国家重点实验室,上海 200240

2.上海交通大学海洋装备研究院,上海 200240

3.浙江恒安泰石油工程有限责任公司,浙江舟山 316000

Effect of Wear-Resistant Tape Layers on Torsional Characteristics of Unbonded Flexible Pipes Under Internal Pressure

LUO Chunmiao¹^,², FU Shixiao^,¹^,², ZHANG Mengmeng¹^,², CHEN Kunpeng¹^,², CUI Xiaoxuan³

1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Institute of Marine Equipment, Shanghai Jiao Tong University, Shanghai 200240, China

3. Heng’antai Petroleum Engineering Co., Ltd., Zhoushan 316000, Zhejiang, China

通讯作者: 付世晓,教授,博士生导师,电话(Tel.):021-34207053-2052;E-mail:shixiao.fu@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-04-28 修回日期: 2023-05-17 接受日期: 2023-05-22

基金资助:

上海市晨光计划(21CGA15)
国家自然科学基金基础科学中心项目(52088102)
中央高校基本科研业务费专项资金(22X010201787)

Received: 2023-04-28 Revised: 2023-05-17 Accepted: 2023-05-22

作者简介 About authors

罗春苗(1998—),硕士生,从事非黏结软管截面力学性能研究.

摘要

非黏结柔管在海洋油气田的开发中得到广泛应用,其扭转平衡是保证作业期间结构安全的重要原则,然而现有分析理论简化假设较多,导致仍有非黏结柔管设计出现扭转不平衡现象.为了提高扭转模拟的准确性,不影响管道实际使用,本文聚焦现有设计分析中所忽视的螺旋铠装内外侧耐磨胶带,基于理论推导,建立耐磨胶带层扭转刚度及弹性模量修正算法,结合有限元模型,探究胶带层叠压对于非黏结柔管整体扭转的影响.结果显示,采用经过修正的胶带层弹性模量所得管道扭转结果更接近实测结果,对实际工程应用具有一定的指导意义.进一步研究发现,非黏结软管的整体扭转角与耐磨胶带的宽度正相关,与耐磨胶带的铺设角负相关,而随着叠压率增加,管道扭转角减小.

关键词： 非黏结柔性管; 耐磨胶带; 扭转平衡; 修正弹性模量; 敏感性分析

Abstract

Unbonded flexible pipe has been widely used in the offshore oil and gas industry and its torsional balance plays an important role in safety insurance during the whole service life. However, there are still torsional imbalances due to simplifying assumptions in the current analytical theory. To improve the accuracy of torsion simulation and reduce the impacts on the practical applications of the pipelines, this paper focuses on the wear-resistant layer neglected in previous studies. Based on theoretical derivation, in combination with the finite element method, a correction algorithm for the torsional stiffness and elastic modulus of the tape layer is developed to investigate the effect of tape layer stacking on the overall torsion of the unbonded flexible pipe. The results show that overall torsion results obtained by using the corrected elastic modulus of the tape layer are closer to the test results, which have guiding significance for practical applications. Further sensitivity research shows that the width of the tape layer is positively correlated with the flexible pipe torsion angle, while the tape laying angle is negatively correlated with the overall torsion angle. With an increase in the stacking ratio of the tape, the pipeline torsion angle decreases.

Keywords： unbonded flexible pipe; wear-resistant tape; torsional balance; corrected elastic modulus; sensitivity research

PDF (9450KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

罗春苗, 付世晓, 张萌萌, 陈鲲鹏, 崔晓轩. 内压作用下耐磨胶带层对非黏结柔管扭转特性的影响[J]. 上海交通大学学报, 2025, 59(1): 121-130 doi:10.16183/j.cnki.jsjtu.2023.163

LUO Chunmiao, FU Shixiao, ZHANG Mengmeng, CHEN Kunpeng, CUI Xiaoxuan. Effect of Wear-Resistant Tape Layers on Torsional Characteristics of Unbonded Flexible Pipes Under Internal Pressure[J]. Journal of Shanghai Jiaotong University, 2025, 59(1): 121-130 doi:10.16183/j.cnki.jsjtu.2023.163

相比于传统钢管,海洋非黏结柔性管在保证轴向强度的同时,可承载较大的动态弯曲载荷,已在海洋油气资源开发中得到广泛应用^[1].海洋非黏结柔性管的常见截面组成结构有:内骨架层、内护套层、抗压螺旋层、抗拉螺旋层、耐磨胶带层、外护套等.在常态化内压、外压和张力等轴对称载荷作用下,非黏结柔性管中的螺旋层(抗拉层、耐磨层等)将发生扭转.各螺旋层的缠绕方向不同,将产生不同方向的扭矩;通常情况下,非黏结软管设计中要求不同方向的扭矩可以相互抵消,使得整体管道处于扭转平衡的状态.然而,设计不足、生产制造缺陷或安装操作不当等,仍会导致软管出现扭转失效的现象.

已有诸多学者开展了轴对称载荷下非黏结软管的扭转特性及失效机理研究,主要分为数值模拟和模型实验研究.Witz等^[2]建立了非黏结软管螺旋层和圆柱层的载荷与位移关系,并推导了考虑了层间接触压力及层间间隙时,非黏结管在不同方向的扭转刚度的理论解.Skallerud^[3] 选取一根实际管道开展了轴对称载荷作用下的力学实验,实验发现管道扭矩和扭转角度近乎线性关系,即管道扭转刚度为定值.Zhou等^[4]开展了不同压力下的扭转实验,发现压力载荷作用下的扭转存在阻尼效应, 即测得的扭转刚度随内压增大而增大.Ramos等^[5-6]研究了软管在轴对称压力载荷作用下的拉伸性能和扭转性能,推导得到非黏结柔性管道各层的应力和应变的线性解析解,并通过了有限元验证.为了更精确地考虑管道扭转性能,吴尚华等^[7⇓-9]将轴向力以及层间的相互作用纳入考虑,确定了铠装钢丝的几种潜在的扭转失效模式,并给出每种失效模式下的单位长度扭转角的保守预测方法.Liu等^[10]将材料及边界条件非线性等都纳入考虑,建立了考虑层间摩擦效应的管道有限元模型;结果显示非线性因素和摩擦效应均对扭转下的非黏结管的应力-应变关系存在影响.Kim等^[11]使用了多梁有限元对螺旋钢丝进行建模,考虑了线对线接触和材料的弹塑性,分析了螺旋绞合系统在轴向和横向载荷下的力学行为.牛学超等^[12]研究了拉伸载荷作用下脐带缆的有限元模型,并采用控制变量法进行了扭转平衡设计.

总体来说,以往针对非黏结柔管的力学分析通常集中于金属层,而位于金属层之间以抗磨为主要目的的耐磨螺旋胶带层(以下简称耐磨层)在分析中常常被省略^[13].Ye等^[14]通过实验方法和数值分析方法,分析了耐磨胶带对弯曲的影响.而近期实验研究发现,耐磨层对非黏结软管整体扭转也存在不可忽视的影响.

本文针对这一问题,基于螺旋层和圆柱层在轴对称载荷下的扭转刚度等效原则,推导了考虑胶带叠压影响的耐磨层扭转修正算法,并结合实验结果及有限元模型,验证了扭转修正算法的必要性和准确性.最后基于所提出的扭转修正算法,系统研究了螺旋胶带叠压率、铺设角和宽度对管道整体扭转性能的影响.

1 基本理论

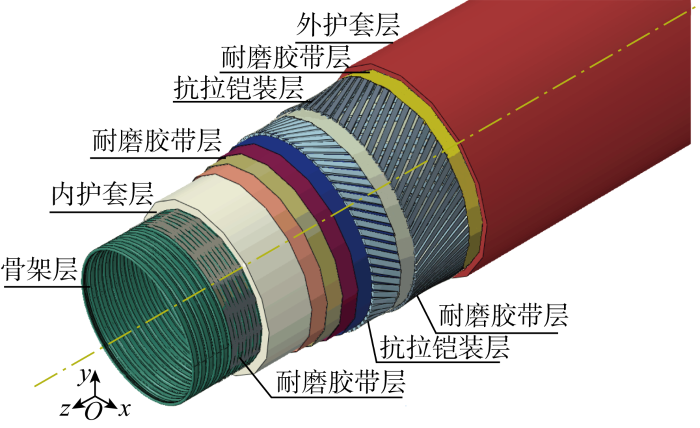
典型的非黏结柔性管道的结构如图1所示.非黏结柔管在作业状态下,会持续承受内部流体带来的内压载荷,从而产生轴向应变与扭转,而过度扭转可能会导致管道结构损坏,因此设计时要求管道整体截面的扭转处于平衡状态^[15].如图2所示,螺旋钢带按照一定角度铺设,为管道提供抗扭强度.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 典型非黏结软管截面示意图

Fig.1 Cross-section of a typical unbonded pipe

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 螺旋层与耐磨层

Fig.2 Spiral layer and wear-resistant layer

耐磨层通常设置于金属螺旋层内外部,在金属层之间和金属层与其他层之间起固定和耐磨作用.在现阶段的工业生产上,耐磨层的实际情况是叠压缠绕的,并不对缠绕角度和方向做要求,仅需完全包覆住螺旋层即可. 因此耐磨层的性能一般都被简化或者忽略,即被当成圆柱层或者忽略处理.在本文中,重新将耐磨层纳入考虑,研究在内压载荷下,耐磨层对非黏结软管扭转性能的影响.

1.1 轴对称载荷作用下螺旋层和圆柱层扭转刚度

1.1.1 螺旋层扭转刚度

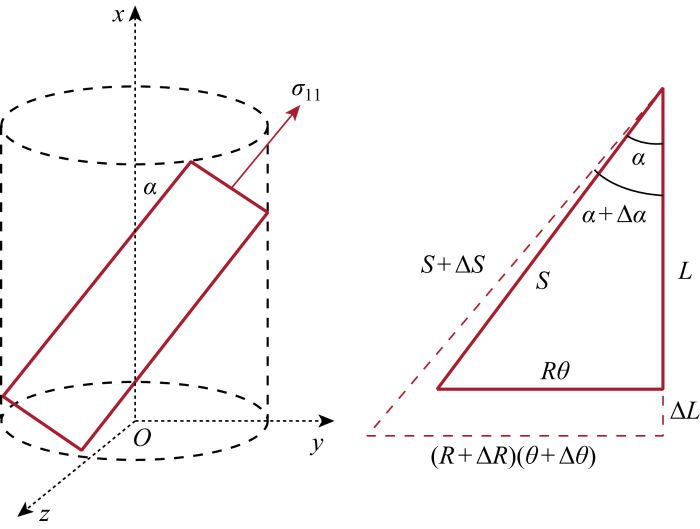
金属螺旋层的几何形状为空间螺旋曲线.一根螺旋带在轴对称载荷的作用下会产生如图3所示的变形,主要为轴向伸长ΔL、半径增大ΔR、环向扭转Δθ、螺旋角变化Δα.图中:σ₁₁为轴向应力;α为螺旋层的铺设角;L为螺旋层的轴向长度;S为沿铺设角的长度;R为螺旋层的半径;θ为螺旋对应的螺旋角.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 金属螺旋带在轴对称载荷作用下的变形

Fig.3 Deformation of metal spiral tendons under axisymmetric loading

将该螺旋带沿铺设角α展开沿铺设角的长度变化为ΔS,则螺旋带的轴向应变ε₁₁可以写为

(1)

\begin{array}{l} ε_{11} = \frac{Δ S}{S} = \\ \frac{\sqrt{[(R + Δ R) {(θ + Δ θ)]}^{2} + {(L + Δ L)}^{2}} - L / c o s α}{L / c o s α} \end{array}

根据小变形假定,螺旋带的轴向伸长、半径增大、环向扭转角度变化和螺旋角变化的二阶及其高阶项可以忽略,可以线性化为

(2)

ε_{11} \approx \frac{Δ L}{L} c o s^{2} α + \frac{Δ R}{R} s i n^{2} α + \frac{R Δ θ}{L} s i n α c o s α

引入螺旋层的轴向伸长率 $ε_{x x} = \frac{Δ L}{L}$ ,径向应变ε_zz= $\frac{Δ R}{R}$ 和环向应变 $ε_{z x} = \frac{R Δ θ}{L}$ 定义,每根螺旋带的轴向应变可简化为

(3)

\begin{matrix} ε_{11} \approx ε_{x x} c o s^{2} α + ε_{z z} s i n^{2} α + ε_{x z} s i n α c o s α \end{matrix}

一个螺旋层由n根螺旋带构成,并假设每根螺旋带沿管道的周向均匀分布,则截面张力F为

(4)

\begin{matrix} F = n E A ε_{11} \end{matrix}

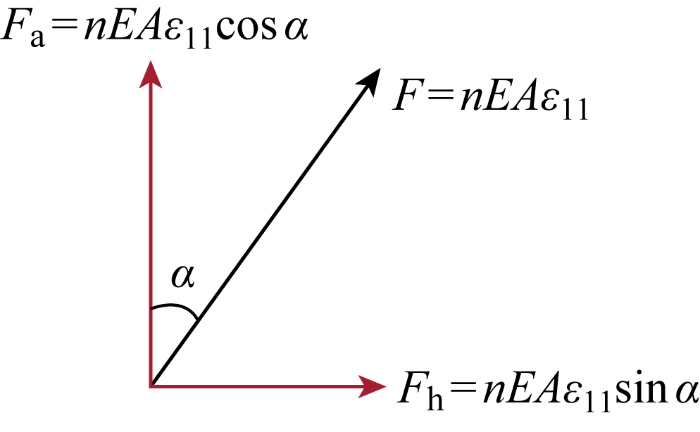
式中:E为材料的弹性模量;A为每根螺旋带的横截面面积.再将截面张力沿管的轴向和径向进行分解,如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 螺旋带轴向张力分解

Fig.4 Decomposition of spiral tendon tension

在轴向忽略螺旋层的环向应变,径向忽略螺旋层的轴向伸长率和径向应变,假设螺旋层的平均半径为R,可以得到环向张力和扭矩为

(5)

\begin{matrix} \begin{array}{l} F_{h} = n E A (ε_{z x} s i n α c o s α) s i n α = \\ n E A s i n^{2} α c o s α ε_{z x} \\ M_{t} = F_{h} R \approx n E A R s i n^{2} α c o s α ε_{z x} \end{array}\} \end{matrix}

进而可以得到该螺旋层的扭转刚度为

(6)

\begin{matrix} (G_{h} J_{h}) = \frac{M_{t}}{Δ θ / L} = n E A R^{2} s i n^{2} α c o s α \end{matrix}

式中:G_h为螺旋层材料的切变模量;J_h为螺旋钢带截面的极惯性矩.

1.1.2 圆柱层的扭转刚度

采用厚壁圆筒理论^[16]可得第i层圆柱壳的扭转刚度为

(7)

\begin{matrix} (G_{s} J_{s})_{i} = \frac{π}{32} E_{i} [(D_{i} + 2 d_{i})^{4} - D_{i}] \end{matrix}

式中:G_s为圆柱壳层材料的切变模量;J_s为螺旋钢带截面的极惯性矩;G_sJ_s为该层螺旋的扭转刚度;E_i为圆柱层材料的弹性模量;D_i为第i层的内径;d_i为第i层的厚度.

1.2 耐磨层的扭转修正

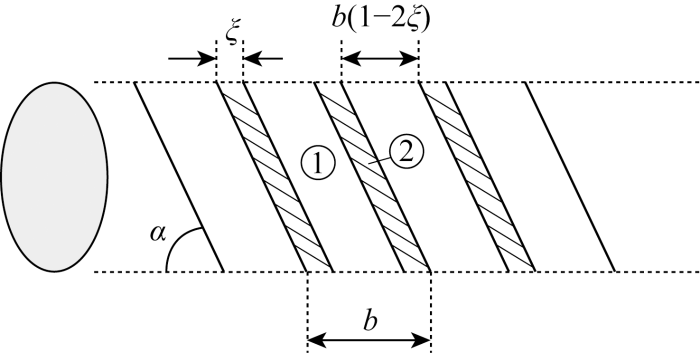
对于耐磨层,在以往的分析中,通常都将其简化为厚壁圆柱壳.然而实际情况下的耐磨带是层层交叠且厚度不均匀的结构,其简化结构如图5所示.图中:ξ为相邻胶带的叠压率;b为胶带的宽度.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 实际的耐磨层形态

Fig.5 Actual layer pattern of wear-resistant

为了考虑叠压的影响,本文提出了一种改进的耐磨层等效建模方式,其遵循以下等效原则:

(1) 为了不影响其他层,等效前后的耐磨层厚度不改变.

(2) 等效后的耐磨层仍为均匀圆柱层.

(3) 等效前后的扭转刚度相等.根据上述原则,等效前后的耐磨层应当满足以下公式:

(8)

\begin{matrix} \begin{array}{l} (d_{a c})_{m a x} = d_{e q} \\ d_{a c} = v a r, d_{e q} = c o n s t \\ {(G J)}_{a c} = {(G J)}_{e q} \end{array}\} \end{matrix}

式中:d_ac为耐磨层的实际厚度;d_eq为耐磨层的等效厚度;(GJ)_ac 为实际扭转刚度;(GJ)_eq为等效后的薄壁圆柱层的扭转刚度;var代表变量;const代表常量.

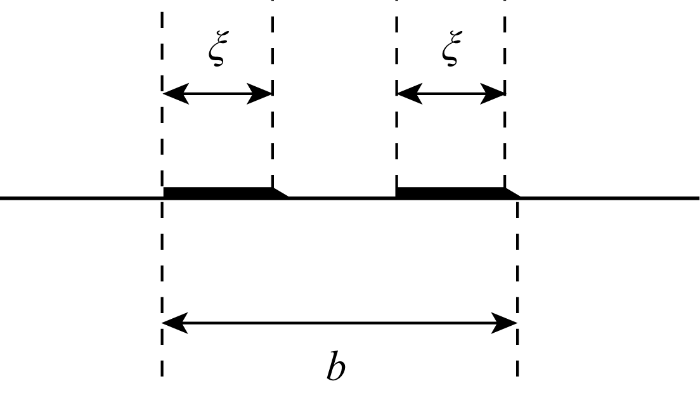
图6为耐磨层的简化模型.一根耐磨带可以看作是若干根宽厚不同的胶带叠压形成,其中阴影处为重叠部分,叠压率ξ定义为一根耐磨带重叠部分的比例,一般为0.1~0.3.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 耐磨层的简化模型

Fig.6 Simplified model of wear-resistant layer

假设铺设的根数为N,两层胶带叠压产生的总厚度为t_i.当ξ=0时,耐磨带不发生叠压,可以看作一根宽度为b,厚度为t_i/2的螺旋带;ξ=0.5时,耐磨层完全叠压,耐磨层可以看作两根宽度为b/2,厚度为t_i的螺旋带.为了表示胶带重叠与不重叠部分覆盖的面积对比,假设不重叠部分的胶带根数为n₁,重叠部分的胶带根数为n₂,且设n₁,n₂与ξ满足线性关系,则有:

(9)

\begin{matrix} \begin{array}{l} n_{1} = (1 - 2 ξ) N \\ n_{2} = 4 ξ N \end{array}\} \end{matrix}

式中:等效螺旋带①厚度为t_i/2,宽度为b(1-2ξ);等效螺旋带②的厚度为t_i,宽度为bξ.结合扭转等效原则(1)和(2),根据扭转刚度计算理论,螺旋带①和②的扭转刚度分别为

(10)

\begin{matrix} \begin{array}{l} {(G J)}_{1} = \frac{n_{1} R_{1}^{2} b (1 - 2 ξ) t_{i} s i n^{2} α c o s α}{2} E_{a c} \\ {(G J)}_{2} = n_{2} R_{2}^{2} b ξ t_{i} s i n^{2} α c o s α E_{a c} \end{array}\} \end{matrix}

式中:螺旋带①和②的平均半径分别为(2D_i+t_i)/4和(D_i+t_i)/2;第i层耐磨层的实际的扭转刚度(GJ)_ac为螺旋带①和②的扭转刚度之和:

(11)

\begin{array}{l} {(G J)}_{a c} = [(\frac{2 D_{i} + t_{i}}{4})^{2} \frac{n_{1} b (1 - 2 ξ)}{2} + \\ (\frac{D_{i} + t_{i}}{2})^{2} n_{2} b ξ] t_{i} s i n^{2} α c o s α E_{a c} \end{array}

等效后圆柱层的扭转刚度(GJ)_eq为

(12)

\begin{matrix} {(G J)}_{e q} = \frac{π}{32} [(D_{i} + 2 d_{i})^{4} - D_{i}^{4}] E_{e q} \end{matrix}

由等效原则(3),等效弹性模量为

(13)

\begin{matrix} E_{e q} = \frac{[{(\frac{2 D_{i} + t_{i}}{4})}^{2} \frac{n_{1} b (1 - 2 ξ)}{2} + {(\frac{D_{i} + t_{i}}{2})}^{2} n_{2} b ξ] t_{i} s i n^{2} α c o s α}{\frac{π}{32} [(D_{i} + 2 d_{i})^{4} - D_{i}^{4}]} E_{a c} \end{matrix}

可以简化为

(14)

\begin{matrix} \begin{array}{l} E_{e q} = ζ E_{a c} \\ ζ = \frac{[{(\frac{2 D_{i} + t_{i}}{4})}^{2} \frac{n_{1} b (1 - 2 ξ)}{2} + {(\frac{D_{i} + t_{i}}{2})}^{2} n_{2} b ξ] t_{i} s i n^{2} α c o s α}{\frac{π}{32} [(D_{i} + 2 d_{i})^{4} - D_{i}^{4}]} \end{array}\} \end{matrix}

式中:ζ记为耐磨层弹性模量的扭转修正系数.

对于一根已知截面参数和材料参数的非黏结软管,可以计算各耐磨层弹性模量的扭转修正系数,并在有限元模拟中使用等效弹性模量代替实际弹性模量,得到非黏结柔管在轴对称载荷下的修正后扭转响应.

2 内压作用下的管道扭转试验

为了验证耐磨胶带层扭转等效的必要性和模型精度,本文对一根内径为23.65 cm、长度为31.45 m的非黏结软管开展了内压作用下的扭转实验.管道的扭转正方向规定如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 扭转实验示意图

Fig.7 Diagram of torsion test

试验的管截面参数如表1所示,材料参数如表2所示.表中: MOPP为玻璃纤维单面胶带; HDPE为高密度聚乙烯.

表1 试验管截面参数

Tab.1 Parameters of pipe section for both experiments

层号	层名	材料	内径/mm	螺旋铺设角/(°)	铺设根数
1	骨架层	不锈钢	236.5	88	1
2	胶带层1	MOPP	247.5		1
3	内护套层	HDPE	249.1
	抗压层4层	高强度碳钢		72~77	1
	胶带层4层	MOPP		75~88	1
12	抗拉层1	高强度碳钢	308.5	33.0	66
13	胶带层6	MOPP	316.5		1
14	抗拉层2	高强度碳钢	318.9	-32.0	68
15	胶带层7	MOPP	326.9		1
16	外护套层	HDPE	328.1

注: 耐磨带的铺设角为75°~88°,抗压层的铺设角为72°~77°,间隔分布;“空白”代表无此项.

新窗口打开| 下载CSV

表2 各层材料属性

Tab.2 Material properties for each layer

材料名称	弹性模量/GPa	泊松比
不锈钢	205	0.30
高强度碳钢	210	0.30
HDPE	0.348	0.49
MOPP	9.94	—

新窗口打开| 下载CSV

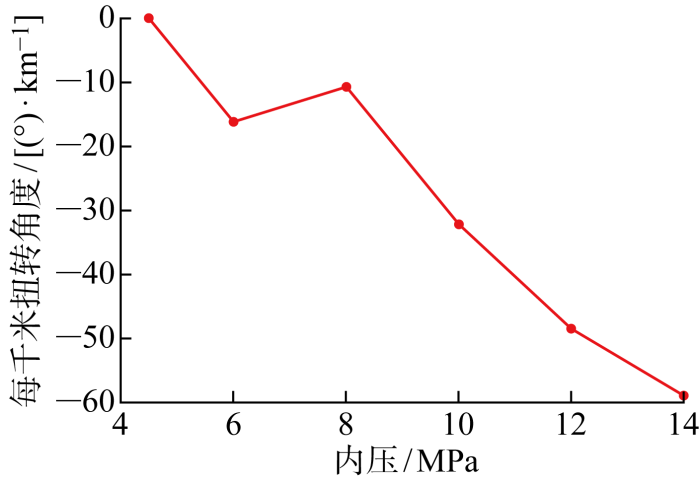
试验中从管道的一头打压,测量两端管体的扭转,计算两端扭转差值.在内压为0 MPa时在管体上作标记,然后加压到4.5 MPa,标记此时管体的位移记录.在继续加压到6 MPa后,每次升压2 MPa,打压的时间间隔不少于20 min,最终升压到14 MPa后结束加压.在升压过程中,待管体变形稳定后再测量扭转距离.正对测试端方向观察,升压过程中管体先顺时针旋转后又逆时针旋转.实验管体和测量装置如图8所示.管道的扭转测量结果如表3所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 扭转实验及测量装置记录图

Fig.8 Torsion test and measuring device record

表3 试验管扭转实验结果

Tab.3 Torsion angle of test of pipe

内压/MPa	总扭转角/(°)
4.5	1.18
6	0.67
8	0.84
10	0.17
12	-0.34
14	-0.67

新窗口打开| 下载CSV

首先对试验结果进行后处理.在初始加压时,管体发生顺时针扭转,随后连续向逆时针扭转.该短暂的反向扭转现象可能与管道制造时引入了初始扭转、管道与地板之间的摩擦力、接头设置、测量误差等原因有关.因此将最大的顺时针扭转值作为开始零点,去除初始条件影响,将处理后的扭转结果绘制如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 内压扭转实验结果

Fig.9 Test results of internal pressure torsion

从非黏结软管的内压扭转试验结果可以看出,在4.5~14 MPa的内压范围内,管体首先逆时针扭转16.21°,然后短暂顺时针扭转5.4° 后,一直保持逆时针的扭转方向,最终增大至58.82 (°)/km,扭转方向与外层抗拉铠装带的方向保持一致.内压加载至8 MPa后,柔管的总体扭转角与内压基本呈线性关系,随着内压增大,总体扭转角线性增大.

3 内压作用下管道扭转的有限元模拟

采用有限元数值分析法对非黏结柔性立管在轴对称载荷下的扭转响应进行模拟分析计算,分别采用管道分析专业软件BFLEX^[10]和有限元分析软件Abaqus/Explict对非黏结柔管在内压下的整体扭转进行建模计算.管道的建模参数基于实验管道,耐磨带的建模选择厚度均匀的圆柱层进行模拟,用扭转修正弹性模量表现其厚度不均匀的影响.耐磨带的宽度为80 mm,铺设角约为85°,叠压率约为0.2,根据式(14),计算出耐磨层的修正弹性模量,如表4所示.分别采用修正前后的耐磨层弹性模量进行内压作用下非黏结软管整体扭转的模拟计算.

表4 耐磨层的修正弹性模量

Tab.4 Corrected elastic modulus of wear-resistant tape

耐磨层编号	E_eq /MPa
1	6.89
2~5	11.10
6	15.51
7	31.02

新窗口打开| 下载CSV

3.1 BFLEX模型

在BFLEX中对该管进行建模,采用螺旋单元HSHEAR353模拟抗拉螺旋层,采用圆柱壳单元HSHEAR363模拟其他层,管长设置为3 m,一端固定,一端自由,选取静态分析模式以确保内压增大时的数值稳定性.BFLEX中的软管各层模型如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 BFLEX模型

Fig.10 BFLEX model

3.2 Abaqus模型

在Abaqus中对该管进行建模,长度选择两个抗拉层螺距长度,为3.136 m,一端完全固定,另一端自由.

采用C3D8I线性非协调六面体单元对管体进行建模,层间接触选择通用硬接触.由于接触数量庞大,分析模式选择非线性动力显式分析.内压载荷的加载幅值选择平滑曲线模式,内压载荷从0增加到4 MPa后,再缓慢增加到14 MPa.此外,为了和实验管加载情况一致,采用在模型端部施加等效张力的形式模拟实验管端帽效应所引起的轴对称载荷,具体等效公式为

(15)

\begin{matrix} T_{e f f} = p_{i n} π R_{i n}^{2} - p_{o u} π R_{o u}^{2} \end{matrix}

式中:T_eff为等效张力;p_in为内层的压强;R_in为内层的半径;p_ou为外层的压强;R_ou为外层的半径.

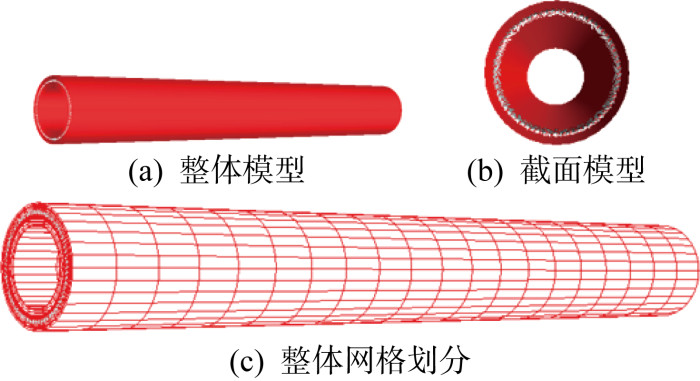
有限元模型及各层结构如图11所示.为清晰显示胶带层,抗压层不予显示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 Abaqus柔管模型

Fig.11 Pipe model in Abaqus

3.3 实验与模型结果对比分析

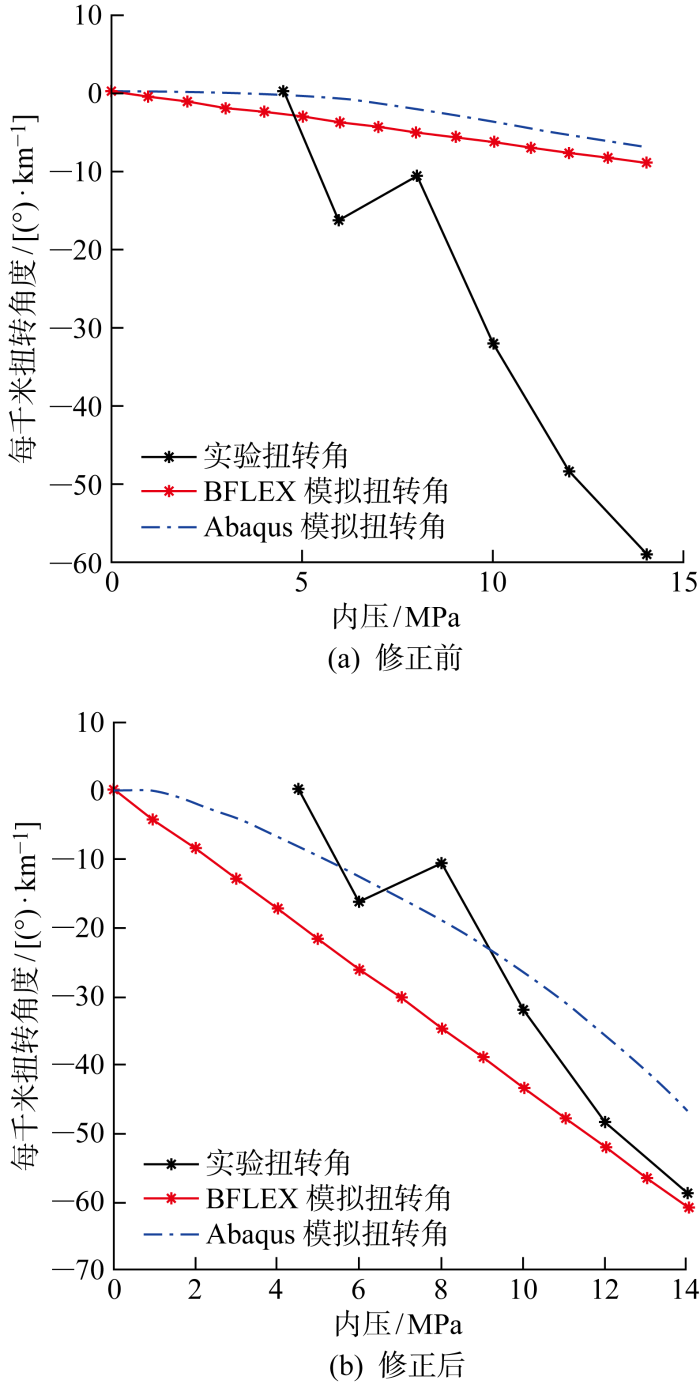
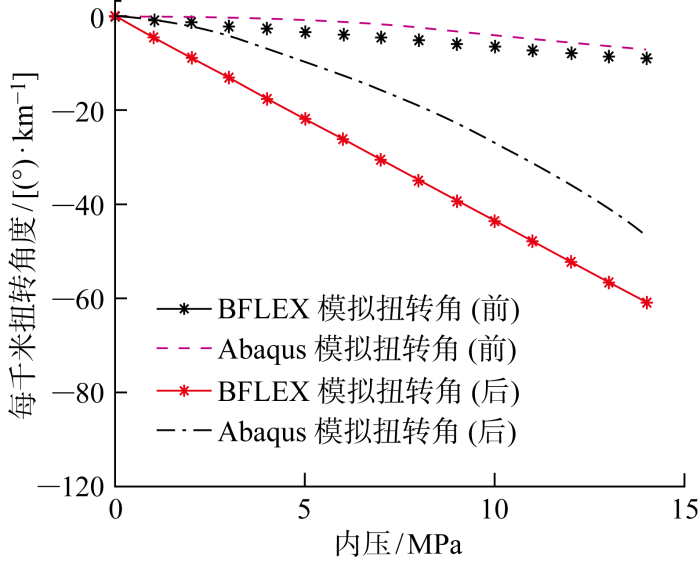
图12为不考虑耐磨层扭转修正和考虑之后的管体扭转实验结果与数值结果的对比.从图中可以看出,若不考虑耐磨层扭转修正,如图12(a)所示,实验的扭转角度远大于数值模拟结果:在 14 MPa 内压作用下,BFLEX建立的非黏结柔管模型的扭转角为8.91 (°)/km,Abaqus中建立的非黏结柔管模型的扭转角为6.94 (°)/km,与实验结果的相对误差分别达到了84.5%和88.2%.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 实验结果与模拟结果对比

Fig.12 Comparison of test results with simulation results

当考虑了耐磨层扭转修正后,如图12(b)所示,BFLEX和Abaqus的数值模拟结果均更为接近实验结果:在14 MPa内压作用下,BFLEX模拟所得扭转角为60.85 (°)/km,略大于实验结果,Abaqus所得扭转角为46.64 (°)/km,略小于实验结果;两者与实验结果的相对误差分别减少至3.5%和20.7%.该结果说明,耐磨层对于非黏结柔管在内压下的扭转性能存在重要影响,对耐磨层进行扭转修正可以显著改善数值模拟的准确性.耐磨层对于管道整体扭转的影响,可能是由于厚度不均匀的耐磨胶带通过弹性模量的改变,对层间压力的分布产生影响,也可能是不同弹性模量的耐磨带对螺旋层的扭转抑制程度不同.

从图12(b)中可以看出,对耐磨层的弹性模量进行扭转修正后,非黏结柔管的有限元模拟结果与实验结果更为接近.将两种有限元模拟结果绘制如图13所示.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 内压下的扭转修正前后有限元结果对比

Fig.13 Comparison of FE results before and after torsion correction under internal pressure

除此之外,需要说明的是,BFLEX模拟结果与Abaqus模拟结果的主要差别是由于Abaqus模型假设各层初始状态下保持无接触.随着内压增加,Abaqus模型的层间接触逐步发生,而BFLEX模型假定初始状态下层间保持完全接触无间隙.这种初始接触差异导致管道内部层间压力分布不同,进而影响管体初始的扭转特性.在实际生产中,管体内部初始状态为近乎全接触状态,更接近BFLEX模拟结果,因而BFLEX的最终扭转结果更接近实验结果.

同时,相比于Abaqus有限元动力显式模拟,BFLEX模拟可以较好地计算非黏结柔性管在内压下的整体扭转.因为动力显示模拟对于计算资源要求较高,而BFLEX不仅模拟的扭转结果与实验结果更接近,且计算速度较快,计算成本低,适合工程估算.

4 耐磨层参数敏感性分析

为了研究耐磨胶带结构参数和铺设参数对非黏结软管整体扭转性能的影响,本文重点考察耐磨胶带层叠压率、铺设角及厚度对软管扭转性能的影响规律.采用3.1节建立的BFLEX模型,分析内压作用下,不同耐磨带参数对非黏结软管整体扭转性能的影响.

4.1 叠压率

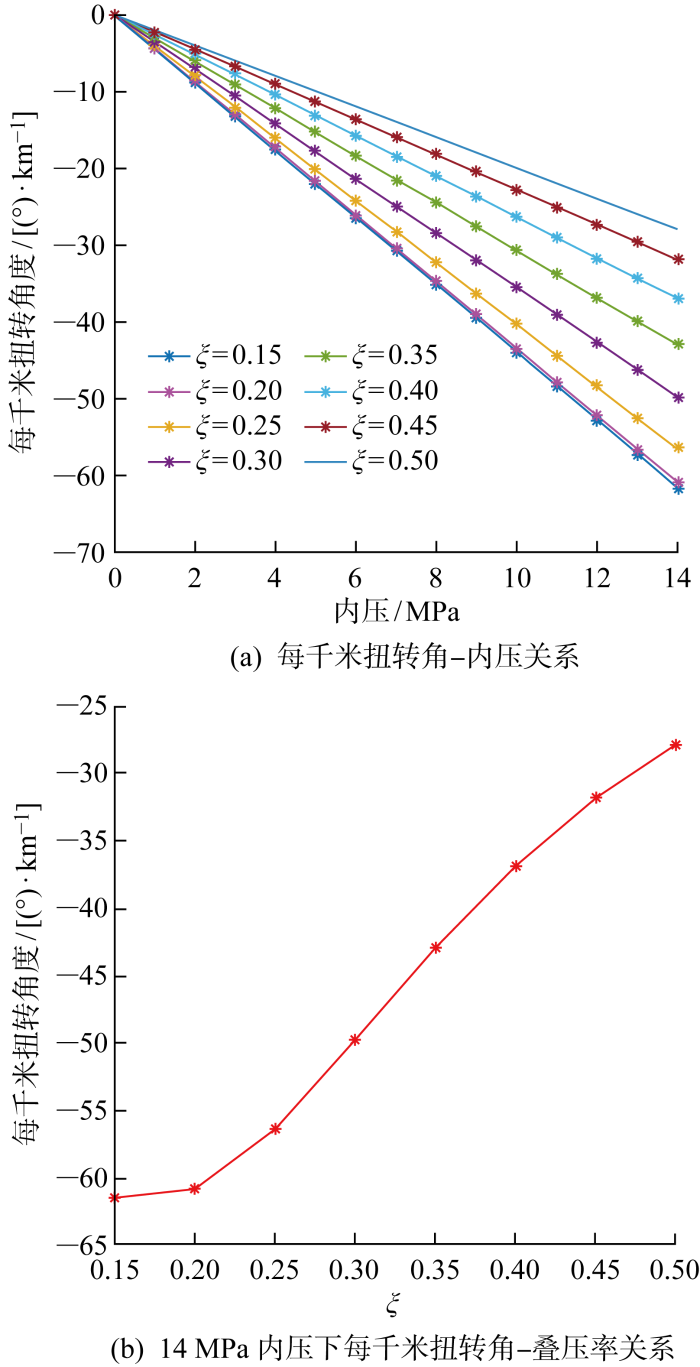
在耐磨胶带层的叠压率敏感性分析中,耐磨胶带的叠压率从0.15增至0.50(间隔为0.05),并同时保证耐磨带宽度为80 mm,铺设角为85°.模拟所得管道扭转结果如图14所示,图14(a)为不同耐磨带叠压率下,非黏结软管的整体扭转随内压的变化曲线,图14(b)为14 MPa内压下,耐磨带采用不同叠压率的情况下的软管整体扭转角.从图中可知,相同的内压下,随着耐磨胶带叠压率的增加,管道的整体扭转角不断减小,当叠压率为0.5时,耐磨胶带彼此之间完全重叠,单位面积的耐磨层体积密度最大,此时对金属螺旋层的扭转抑制效果最好.因此在进行非黏结柔性管结构设计时,为了使单位长度管体的整体扭转角更小,保证结构的扭转安全性,应当尽量选择较大的耐磨层叠压率.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 耐磨带叠压率对扭转的影响

Fig.14 Influence of lamination ratio on torsion

4.2 铺设角

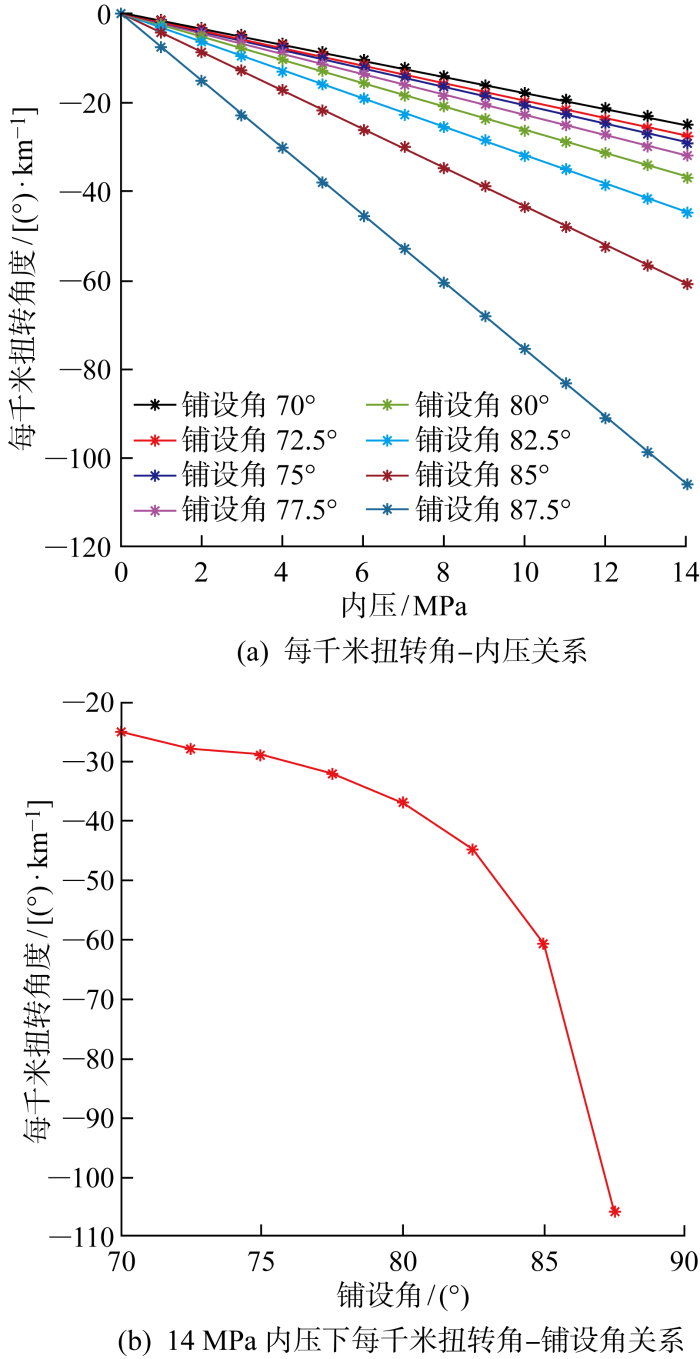
在非黏结软管耐磨胶带的铺设角敏感性分析中,耐磨胶带的铺设角从70°增至87.5°(间隔为2.5°),并同时保证耐磨带宽度为80 mm,叠压率为0.2.模拟所得管道扭转计算结果如图15所示,图15(a)为不同耐磨带铺设角下,非黏结软管的整体扭转随内压的变化曲线,图15(b)为14 MPa内压下,耐磨带采用不同铺设角的情况下的软管整体扭转角.由图可知,相同的内压下,当铺设角从70°增加到87.5°时,软管的总体扭转角逐渐增大,且增大趋势呈现非线性特征,铺设角越大,扭转角增加速率越快.这种非线性规律可能是由于非黏结软管的在内压增大过程中结构变形引起的.因此在进行非黏结柔性管结构设计时,为了使单位长度管体的整体扭转角更小,保证结构的扭转安全性,应当尽量保持其铺设角在85° 以下,以改善其扭转性能.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 耐磨带铺设角对扭转的影响

Fig.15 Influence of lay angle on torsion

4.3 宽度

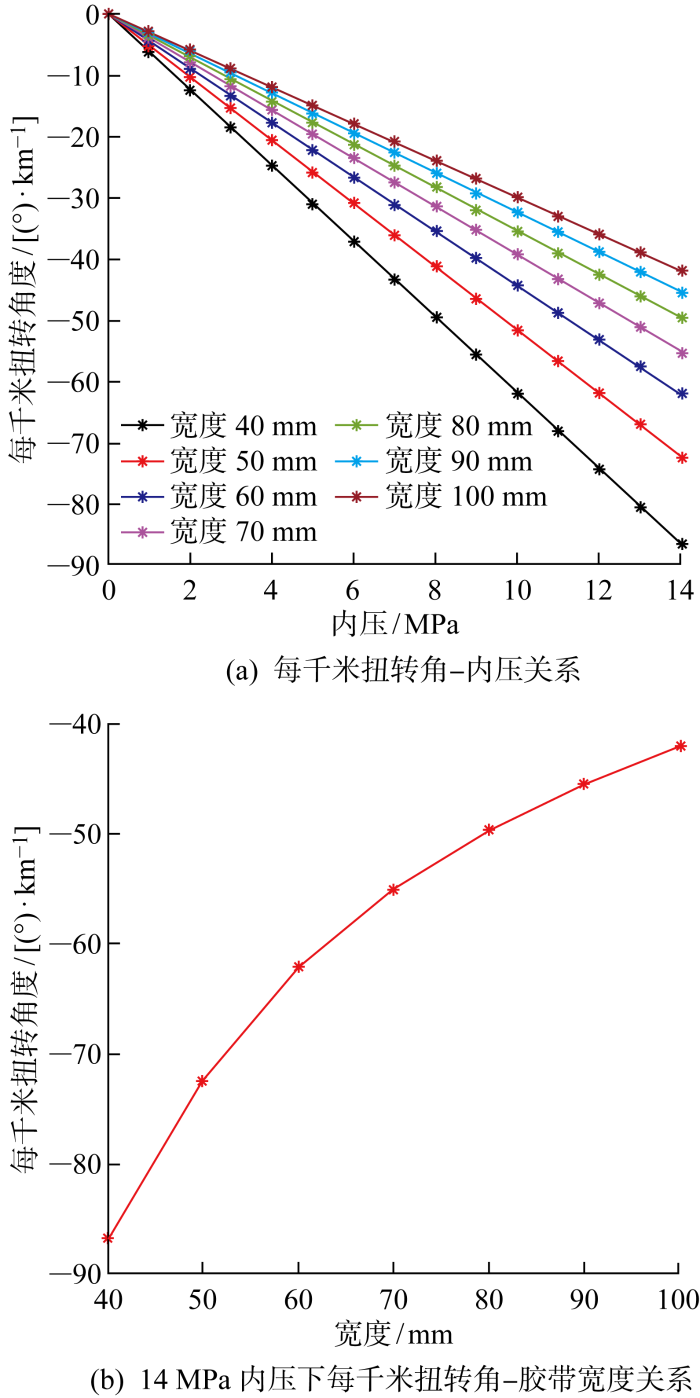
在非黏结软管耐磨胶带的宽度敏感性分析中,耐磨胶带的裁剪宽度从40 mm增至100 mm(间隔为5 mm),并同时保持耐磨带的叠压率为0.3,铺设角为85°.模拟所得管道扭转计算结果如图16所示,图16(a)为不同耐磨带宽度下,非黏结软管的整体扭转随内压的变化曲线,图16(b)为14 MPa内压下,耐磨带采用不同宽度胶带的情况下的软管整体扭转角.从图中可以看出,在相同的内压下,非黏结软管的整体扭转角随耐磨带的宽度增加而逐渐减小,且减小趋势同样呈现出非线性的变化关系.当耐磨带的宽度越大时,扭转角的减小趋势越小.当耐磨带宽度较小时,可以适当裁剪更宽的耐磨带以改善软管的扭转平衡性能;当耐磨带宽度已经较大时,则不宜再增加耐磨带的宽度,否则可能会对耐磨带的铺设安装造成不利影响.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 耐磨带宽度对扭转的影响

Fig.16 Influence of width on torsion

5 结论

本文以轴对称载荷作用下的非黏结柔管耐磨胶带层扭转修正为研究对象,基于螺旋层和圆柱层扭转理论及等效原则,发展耐磨胶带层扭转刚度及弹性模量修正算法;分别开展了内压下非黏结软管扭转实验和有限元仿真计算,验证了耐磨层扭转修正的必要性,并开展了耐磨层关键参数敏感性分析,主要结论如下.

(1) 采用耐磨层扭转修正的数值模型所得模拟结果较修正前更接近实验结果,这说明耐磨层扭转修正对于管道扭转平衡设计不可或缺.

(2) 耐磨胶带层的叠压率、铺设角和宽度均会对非黏结柔管的整体扭转性能存在影响.在内压作用下,耐磨带的铺设角越大,管道整体扭转角越大,而耐磨带的宽度越大,管道的整体扭转角越小,其改变趋势均为非线性;随着叠压率增加,管道扭转角不断减小.

(3) 在今后的工作中,可对耐磨胶带层进行更详细的有限元建模计算与分析,同步开展多载荷联合作用下的非黏结柔性管扭转实验,进一步探究耐磨层应力分布及其对非黏结软管的扭转性能影响的深层机理.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

余荣华, 袁鹏斌, 秦林肖.

海洋非粘结型柔性软管制造装备现状分析

[J]. 机械设计与制造, 2018(2): 97-103.