为克服转动惯量不足的问题,使新能源电源为电网提供类似于同步机的主动惯性支撑,基于电压源型电力电子变流器的虚拟同步机(Virtual Synchronous Generator, VSG)技术[8]获得了长足发展,并已在国内外部分地区示范应用[9⇓-11],可能成为新型电力系统建设的关键组成部分.该技术利用电力电子控制及功率型储能的配合模拟转动惯量为系统提供紧急频率救助.此类在惯量响应时间尺度内的、由电力电子接口设备快速响应频率变化而释放的有用功统称为虚拟惯量[12-13].在新能源发电机逐步取代传统能源发电机的过程中,由电力电子接口电压源提供的虚拟惯量可在一定程度上替代系统对转动惯量的需求.VSG的惯性支撑能力受控制手段、控制参数、储能设备等条件的制约,表现出较强的时变性[14-15].因此,针对包括转动惯量与虚拟惯量在内的电力系统综合惯量的监测对保证系统安全稳定和提升电网的经济化运行水平具有重要意义.
广域测量系统(Wide Area Measurement System, WAMS)与同步相量测量单元(Phasor Measurement Unit,PMU)的广泛应用为电力系统的动态监测及综合惯量评估奠定了技术基础[16].文献[17⇓⇓⇓⇓⇓-23]中提出可利用数据采集与监视控制(Supervisory Control and Data Acquisition, SCADA)系统和WAMS记录系统意外发生的扰动事件,根据系统响应过程估测系统惯量水平.文献[17-18]中提出可根据系统低频机电暂态振荡时联络线功率变化估测不同区域电网惯量.此方法准确性高,但仅适用于长距离区域互联电网,难以准确监控节点级惯量变化,无法准确反映惯量的空间分布特性.文献[19-20]中则基于系统有功大扰动后频率演化过程进行惯量估测.此方法为事件驱动法,难以对正常运行系统的惯量水平进行实时监测.同时,考虑到虚拟惯量可根据系统运行状态进行自适应变化[24-25],文献[21]中基于电力系统频差原理,提出能够实时追踪虚拟惯量自适应变化的基于大扰动事件的惯量评估方法.电力系统频差原理[26]主要用于刻画电力系统动态频率时空分布特性,为追踪系统中各节点频率与惯量的实时变化提供了理论基础.
本文首先针对等效惯性常数理论及现有在线惯量监测理论进行回顾与讨论;在此基础上,创新性地提出基于数据回归的等效惯性常数辨识方法,弥补现有实时惯量监测法收敛后准确性不足的问题,并将非实时性的等效惯性常数辨识方法与实时惯量监测技术结合,构建兼顾实时性与准确性的基于PMU测量的新型电力系统点对网惯性支撑能力系统性在线监测方法;最后,采用改进的10机39节点系统验证所提方法的效果.
1 等效惯性常数及其实时监测方法
1.1 等效惯性常数概念
狭义的电力系统惯量仅仅指同步发电机的转动惯量.等效惯性常数是用于表征同步发电机惯量水平的物理量,利用摇摆方程对其进行定义.标幺值形式下,同步发电机的摇摆方程可写为
式中:M为同步发电机的机械启动时间;ω为同步机的角频率;pm、pe分别为机械功率和电磁功率;pD为由阻尼效应引起的有功功率变化,具体为
式中:D为阻尼系数,用于描述同步发电机阻止转矩突变的能力;t为时间;H为等效惯性常数.
随着电力电子接口电源主动支撑电网相关技术的发展,电力电子控制可模拟同步发电机惯量响应为电网提供虚拟惯量,此类虚拟惯量对电网的惯性支撑能力也可由等效惯性常数进行量化[21].
1.2 等效惯性常数辨识
在式(1)中,pm无法直接测量.因此,若要根据式(1)估测H,需对pm的变化规律做进一步探讨.可将pm分解为3个部分:
式中:pUC为当前优化调度结果给予的功率参考点;pPFC为由一次频率控制调节的有功功率;pSFC为由二次频率控制调节的有功功率.将式(4)代入式(1)并求等号两侧关于时间的微分得:
在分析对象为接入电网的同步机组聚合电源时,
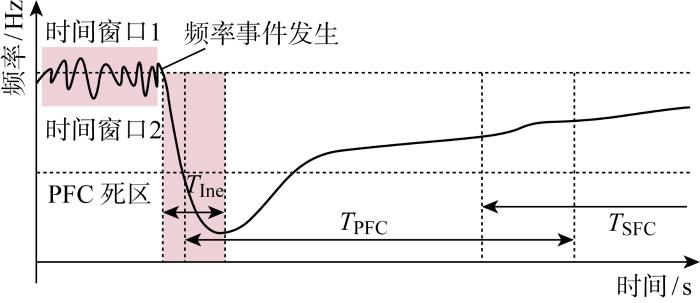
图1
图1
高新能源渗透电力系统频率响应
Fig.1
Frequency response of power system with a high penetration of new energies
在图1所示的两个时间窗口中均可认为
因此,在惯性主导阶段可由式(5)推导出:
1.3 惯量实时监测技术
在实际应用中,基于式(6)的等效惯性常数计算需改写为
式中:上标“*”表示估计值;ηp、ηω分别为功率和角频率的测量误差.式(7)存在严重的数值稳定性问题,即当分子
文献[21]中通过规避分式结构,提出在线惯量监测方法,有效提升了数值稳定性,表示为
式中:时间常数TM和TD可决定惯量监测的收敛速度,
式中:ζx为一个接近于0的正阈值,用于剔除导数过零时的数值问题.式(10)为惯量监测创造了一个死区,即(-ζx, ζx),选择合适的ζx可以有效减少频率波动和噪声的影响,但若ζx取值过大,则可能因丢失过多暂态过程信息降低惯量监测的准确性.
2 基于频差原理的新型电力系统惯量监测系统性方法
2.1 基于数据回归的等效惯性常数辨识
2.1.1 电源内部角频率测量
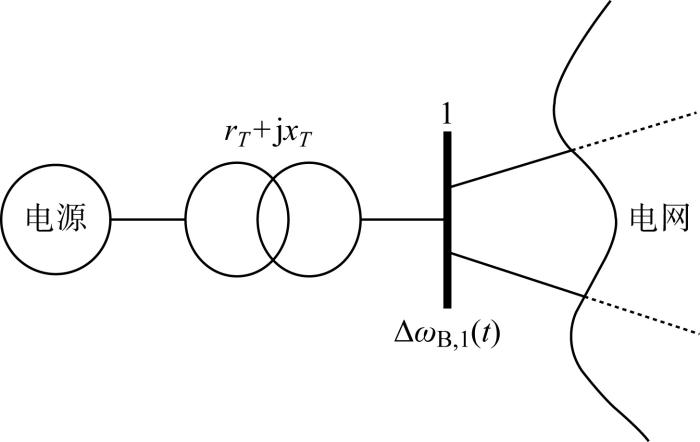
在已知系统拓扑的情况下,可测量电源汇集点(Point of Interconnection, POI)[29]处母线的动态频率测量同步机组的等效角频率.
如图2所示,若可测得机组的输出RoCoP,则可仅通过电源汇集点处的母线角频率ΔωB,1,对机组等效角频率进行测量,如下:
式中:xk为同步机电抗,xk=1/b,b为电纳.图中:rT、xT分别为变压器参数电阻和电抗.
图2
2.1.2 RoCoP测量
根据电力系统潮流计算直流法[27]作时间的微分可得如下关系:
需注意的是,直流法是一种较为粗略的计算方法,忽略了电压暂态变化的影响.因此,基于式(12)的电源RoCoP测量可能难以准确刻画电压暂态带来的影响,但电压暂态相较于有功频率衍化过程而言时间尺度较短,影响相对有限.后文实验部分将对该影响作直观展示.
2.1.3 基于数据回归的等效惯性常数辨识
1.3节所展示的在线惯量监测方法[21]难以兼顾实时性与准确性,虽能有效监测电源接入点惯量的变化趋势,但其对等效惯性常数H*监测的准确性有限.对此提出一种基于数据回归的等效惯性常数辨识方法,牺牲惯量监测的部分实时性以保障其准确性.
据式(6),基于ti时刻测得的RoCoP与机组角频率存在如下关系:
式中:
对于一组采样时间序列t1,t2,…,tN,可以定义以下向量:
式中:每个矩阵的维度为N×1,N由时间窗的长度τ=tN-t1以及PMU的采样率决定.
根据式(14)可将等效惯性常数辨识问题转化为针对式(15)矩阵中数据的回归问题,采用最小平方差的方法,可将此回归问题表述为
线性方程(16)的解即
表达式(17)可以用来有效辨识等效惯性常数.为了避免出现奇异的XTX矩阵,可采用下式针对X进行修正,
式中:ζ=diag(ε, ε, …, ε),即维度为N×N的矩阵,其对角元素均为一极小的非零元素ε.在后文案例分析中,使用ε=10-6来避免XTX的奇异问题.
相比1.3节的实时惯量监测方法[21],基于数据回归的等效惯性常数辨识方法具有更强数值稳定性,对测量窗口的选择相对要求更加宽泛.
2.2 新型电力系统惯性支撑能力在线监测系统性方法
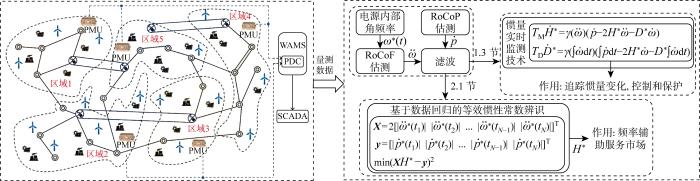
1.3节所提方法可用于在线监测电源的实时惯量变化,并将该信息用于辅助新型电力系统的先进保护与控制策略,但其收敛后的等效惯性常数通常存在一定误差,且其准确性对参数ζx的敏感度极高;2.1节提出基于数据回归的等效惯性常数辨识,可在惯性支撑效果未发生显著变化的时间段内辨识该时段此电源的等效惯性常数,为电力系统运营及频率辅助服务市场提供参考信息[30],但该方法不具有1.3节惯量监测方法的实时性.结合上述两种惯量监测方法,提出如图3所示的兼顾实时性与准确性的新型电力系统点对电网惯性支撑能力在线监测的系统性方法,监测针对的是安装有PMU/WAMS设备的关键POI,惯性支撑能力由等效惯性常数进行量化表征.如图3所示,该系统性方法需要利用PMU测量估测两个关键变量:聚合电源内部角频率和聚合点输入电网的RoCoP,2.1节介绍了相关估测方法.
图3
图3
新型电力系统点对电网惯性支撑能力在线监测系统性方法
Fig.3
Systematic method of online monitoring of inertia support capacity of point-to-grid in new power system
3 案例分析
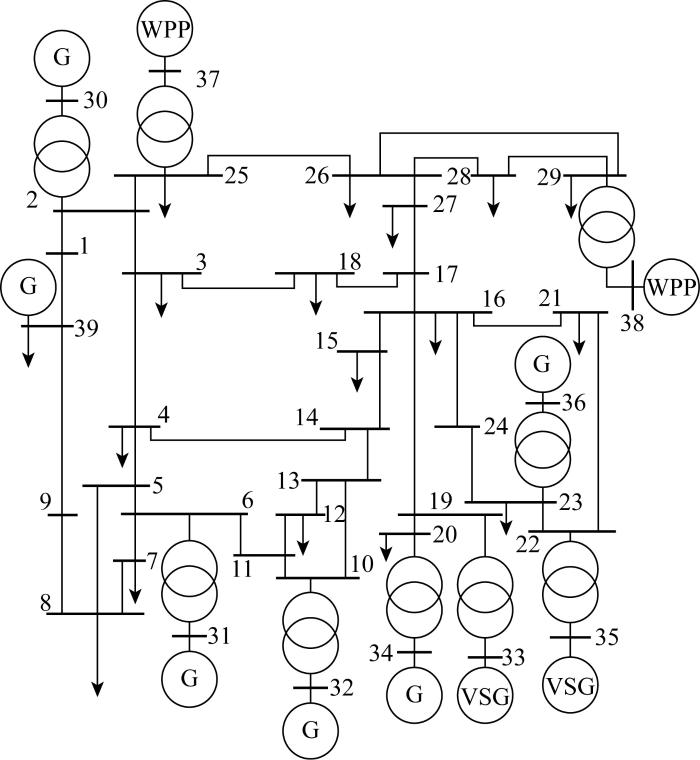
图4
表1 改进后10机39节点系统的新能源电源
Tab.1
| 母线序号 | 发电机编号 | 装机量/MW | 有功出力/MW |
|---|---|---|---|
| 33 | 4号VSG | 1000 | 632 |
| 35 | 6号VSG | 1000 | 650 |
| 37 | 1号WPP | 606 | 540 |
| 38 | 2号WPP | 900 | 830 |
所进行的大干扰仿真中,大干扰事件为母线30连接的同步发电机解列;小干扰仿真中,小干扰事件为风速的连续变化,风速模型为基于Weibull分布的连续变换的时序随机数列,其跳变步长为 0.1 s[31].
表2 各聚合电源实际惯量信息
Tab.2
| 编号 | 母线 | 发电机编号 | 等效惯性常数/ [MW·s·(MV·A)-1] |
|---|---|---|---|
| 1 | 39 | 1号G | 100 |
| 2 | 31 | 2号G | 60.6 |
| 3 | 32 | 3号G | 71.6 |
| 4 | 34 | 5号G | 52 |
| 5 | 36 | 7号G | 52.8 |
| 6 | 33 | 4号VSG | 120 |
| 7 | 35 | 6号VSG | 100 |
3.1 基于 PMU 测量的大扰动下的实时惯量监测效果
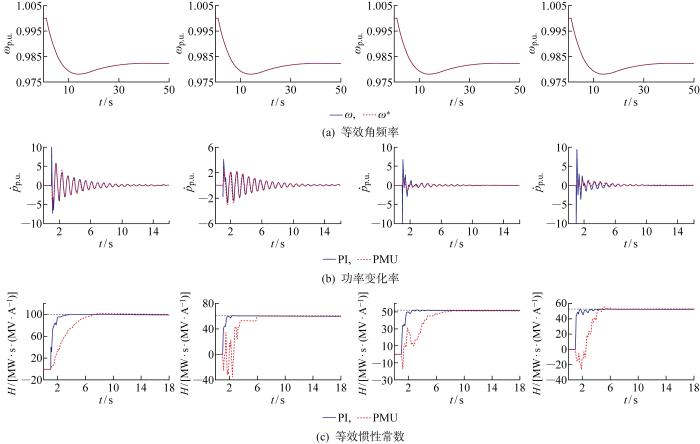
探讨在系统遭受大扰动时,基于PMU测量数据和频差原理的电源等效角频率和RoCoP估测方法追踪动态变化的准确性;对比分析基于PMU测量数据的式(8)和(9)的惯量实时监测效果,并与文献[21]中的方法进行对比,从而论证基于PMU测量的惯量实时监测的可行性.为了直观展示实时惯量监测方法的数值特性,未引入其他小干扰,即采用常风速模型.
将同步发电机组在大扰动下的等效角频率、RoCoP和等效惯性常数的估计值分别记作ω*、
图5
图5
1号、2号、5号和7号同步发电机组大扰动下的动态演化过程及其监测结果
Fig.5
Dynamic evolution and monitoring results of the synchronous generators No.1, No.2, No.5 and No.7
图5(a)对比了机组等效角频率准确值ω和基于PMU测量的估测值ω*,论证了文中式(11)所示方法的准确性,仿真发现两者在动态过程中的相对误差绝对值保持在0.1 %以内,估测准确性极高.图5(b)展示了由准确的机组出力通过PI滤波器测量所得RoCoP以及基于PMU测量估测所得RoCoP的结果对比,PI滤波器获得的RoCoP相比PMU测量结果在动态过程中展现出更剧烈的波动性,但总体而言两者捕获的RoCoP动态演化特性基本一致.图5(c)对比了基于PI滤波器及准确的机组等效角频率与RoCoP的同步发电机组惯量监测结果和完全基于PMU测量的惯量结果,可见两种情况下基于式(8)和(9)的惯量监测方法均可收敛到较为准确的等效惯性常数,然而基于PMU测量时其收敛速度更慢,约需要5~10 s.上述实验结果证明,基于PMU的RoCoP测量中,直流潮流法中假设条件造成不可避免的误差,因为在有功功率变化剧烈时忽略了电压暂态带来的影响,所以在故障后2 s内的追踪效果存在一定误差,进而影响惯量监测的收敛速度.但将采用测量的RoCoP用于在线惯量监测仍能确保收敛至较为准确的等效惯性常数,故总体而言不影响实时惯量监测方法的可行性.
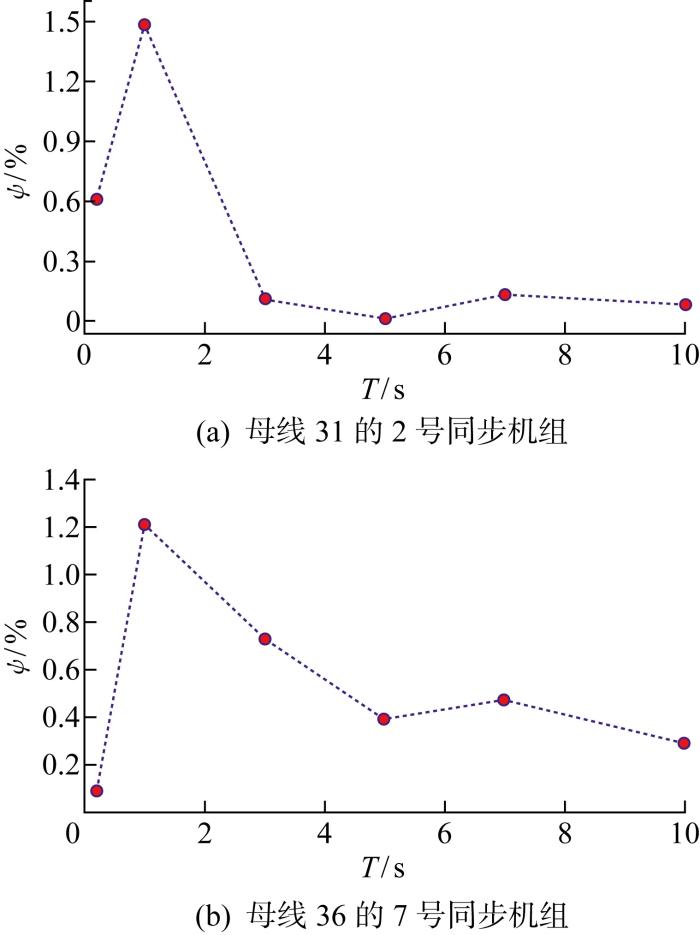
3.2 基于PMU测量的等效惯性常数识别效果
对2.1节所提等效惯性常数识别方法的准确性进行论证,并探讨所需时间窗口长度.实验对象选取经由母线31和36接入电网的同步机组进行验证.主要考虑受风速随机波动影响的小干扰仿真,并假设每个PMU均具有测量噪声.测量噪声利用奥恩斯坦-乌伦贝克随机函数[33]进行模拟,该噪声的主要分布范围标幺值为±0.001,符合实际PMU要求.考虑在电力系统正常运行状态下即无大干扰事件发生的情况下,采用蒙特卡罗实验法,重复300次实验以充分考虑新能源出力不确定性的影响,并对结果求取平均值.相对误差计算方法如下:
图6
图6
不同时间窗口下同步机的等效惯性常数识别
Fig.6
Identification results of equivalent inertia constant of synchronous generator via different time windows
由图6可知,当时间窗口长度在2 s以上时,等效惯性常数识别相对误差收敛至0.5%以内,具有极高的准确性.因此,在高比例新能源电力系统正常运行状态下,选取长度为2 s及以上的时间窗口可保证获得较为准确的同步机等效惯性常数.
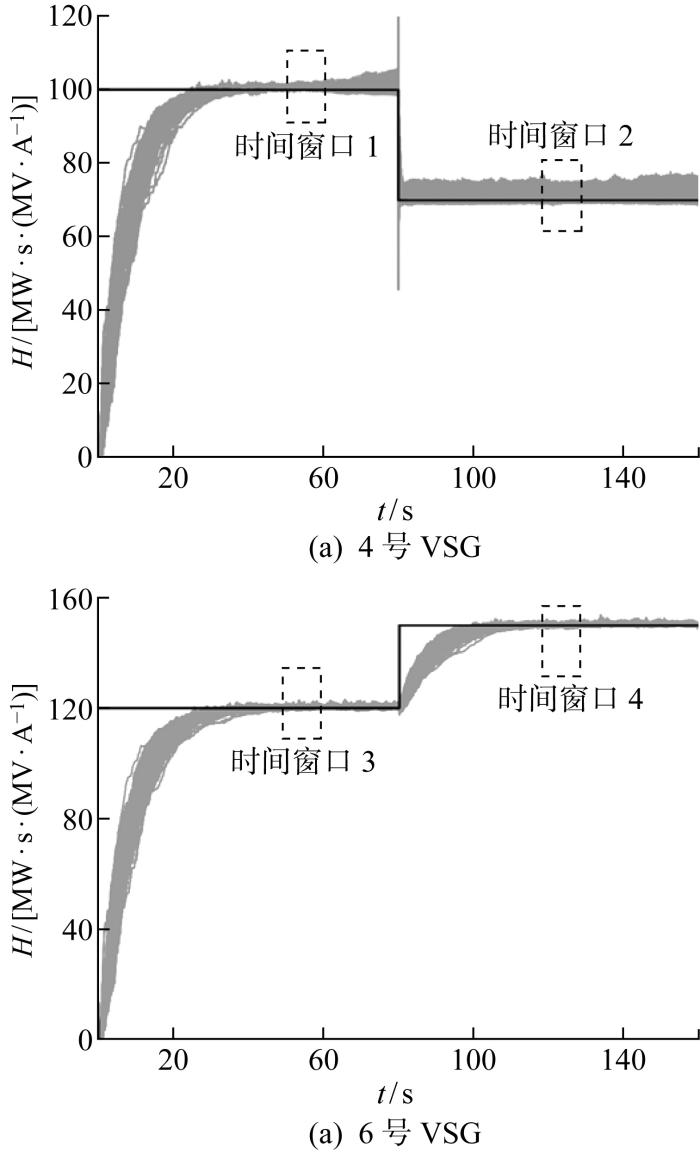
3.3 虚拟惯量在线监测效果
讨论2.2节所提点对网惯性支撑能力在线监测系统性方法对提供虚拟惯量的POI的监测作用.相较于同步发电机组,VSG为系统提供的虚拟惯性支撑效果可能因储能及(或)新能源电源运行情况、运营商对控制参数整定等因素发生改变,故等效惯性常数在不同时间段可能发生变化.2.2节所提惯量在线监测系统性方法将式(8)和(9)与式(17)相结合,在监测虚拟惯性支撑效果变化的同时,准确辨识不同时段下VSG的等效惯性常数.
现考虑两种不同情况:
(1) 在仿真时间为80 s时,母线33上4号VSG的等效惯性常数由100 MW·s/(MV·A),下降为70 MW·s/(MV·A).
(2) 在仿真时间为80 s时,母线35上6号VSG的等效惯性常数由120 MW·s/(MV·A),上升为150 MW·s/(MV·A).
图7展示了上述两种情况下,300组蒙特卡罗模拟实验所获得的VSG虚拟惯量在线监测结果及用于等效惯性常数辨识的时间窗口.由图可见,基于式(8)和(9)的在线惯量监测在不输入初始估值的情况下收敛至VSG准确的等效惯性常数附近大约需要30 s,且存在一定误差.如图7(a)所示,4号VSG的虚拟惯性支撑效果削弱后,2.2节所提方法能立刻对此变化进行监测.图7(b)则展示了6号VSG虚拟惯性支撑效果增强后,另需约30 s时间才能收敛到新的等效惯性常数附近.具有这个差异性的原因是虚拟惯性支撑效果削弱后,小扰动造成的频率及RoCoP变化更为剧烈,所以基于频差原理的惯量监测方法反应迅速;而虚拟惯性支撑效果增强后,小扰动影响被抑制,故需要一定时间才能对该变化进行准确监测.
图7
采用实时监测与数据回归结合的系统性方法,以确保避开汇集点对电网惯性支撑能力调整时段;选用10 s的时间窗口用于等效惯性常数辨识,以保证其监测结果的准确性.具体实验结果如表3所示.由表可见,4个不同时间窗口所测得的等效惯性常数平均相对误差范围均保持在0.5 %以内,准确性极高.综上所述,所提在线监测系统性方法能够准确监测虚拟机接入点的惯量变化情况.
表3 不同时间窗口下等效惯性常数的识别结果
Tab.3
| VSG | 时间 窗口 | H*/[MW·s· (MV·A)-1] | H/[MW·s· (MV·A-1)] | ψ/% |
|---|---|---|---|---|
| 4号 | 1 | 100.20 | 100.00 | 0.20 |
| 2 | 70.33 | 70.00 | 0.48 | |
| 6号 | 1 | 120.39 | 120.00 | 0.33 |
| 2 | 150.63 | 150.00 | 0.42 |
4 结论
在梳理已有惯量在线监测技术的基础上,提出基于数据回归的等效惯性常数识别,构建适用于新型电力系统的点对网惯性支撑能力在线监测系统性方法.利用改进的新英格兰10机39节点系统对所提惯量监测方法的准确性及可行性进行探讨,可得到结论如下:
(1) 电网控制调度中心可通过汇集点PMU的测量数据准确监测系统中各关键聚合电源内部角频率及其对网输出的RoCoP.
(2) 基于式(8)和(9)的在线惯量监测在大干扰及小干扰下均可准确监测惯量变化,为新型电力系统的控制与保护提供相关信息.
(3) 基于式(17)的等效惯性常数识别方法可通过较短的时间窗口准确监测转动惯量及虚拟惯量的等效惯性常数,为新型电力系统运营及频率辅助服务市场提供参考信息.
(4) 结合在线惯量监测与等效惯性常数辨识的汇集点惯量监测方法可实现对传统同步机组及其他电力电子电源的惯性支撑效果的全面监测,适应新型电力系统精确运行监测与控制需求.
基于上述结论可知,所提电力系统点对网惯性支撑能力在线监测系统性方法具有准确性、普适性和及时性3个突出特征.未来将进一步探究区域级电网等效惯量的监测方法,利用尽可能少的测量设备对区域级电网惯量水平进行准确监测.
参考文献
计及风速分布与机组惯量转化不确定性的风电场可用惯量估计
[J].
Estimation of wind farm available inertia considering uncertainty of wind speed distribution and unit Inertia transformation
[J].
高比例电力电子电力系统频率响应的惯量体系研究
[J].
Research on inertia system of frequency response for power system with high penetration electronics
[J].
构建100%可再生能源电力系统述评与展望
[J].
Review and prospect of toward 100% renewable energy power systems
[J].
高比例新能源电力系统的惯量控制技术与惯量需求评估综述
[J].
Review of inertia control technology and requirement evaluation in renewable-dominant power system
[J].
高比例可再生能源电力系统的快速频率响应市场发展与建议
[J].
Development and recommendation of fast frequency response market for power system with high proportion of renewable energy
[J].
大型风电机组惯量控制研究现状与展望
[J].
DOI:10.16183/j.cnki.jsjtu.2018.10.004
[本文引用: 1]

随着风能利用规模的发展,风电渗透率不断提高,局部地区已达到50%以上.由于风电变流器的隔离作用,风电机组的转子运动和系统频率解耦,使得风电机组对于电力系统的惯量几乎没有贡献,降低了系统等效惯量,严重影响系统的频率稳定性.大型风电机组的惯量控制技术旨在利用机组转子动能赋予风电机组主动惯量响应和抑制电网频率跌落的能力,本文综述目前大型风电机组实现惯量控制的主要技术路线,从稳定性分析、控制系统优化、性能分析与评估等方面,介绍惯量控制在双馈风电机组以及全功率风电机组的研究与工程现状,并展望亟待解决的问题与技术需求.
Research status and prospect of inertia control for large scale wind turbines
[J].
计及频率约束的风电最大接入比例研究
[J].
Study on the maximum access ratio of wind power considering frequency constraint
[J].
虚拟同步机技术在电力系统中的应用与挑战
[J].
Application and challenge of virtual synchronous machine technology in power system
[J].
100% Converter-interfaced generation using virtual synchronous generator control: A case study based on the Irish system
[J].
基于频率响应区间划分的风电机组虚拟惯量模糊自适应控制
[J].
Fuzzy adaptive virtual inertia control strategy of wind turbines based on system frequency response interval division
[J].
虚拟同步机与自主电力系统
[J].
Virtual synchronous machines and autonomous power systems
[J].
低惯量电力系统频率稳定分析与控制研究综述及展望
[J].
Review and prospect of frequency stability analysis and control of low-inertia power systems
[J].
高风电渗透率系统的模糊自适应虚拟惯量控制
[J].
Fuzzy adaptive virtual inertia control for high wind power penetration system
[J].
基于新能源出力比例的大规模系统惯量估计
[J].
Large-scale system inertia estimation based on new energy output ratio
[J].
频率扰动下虚拟同步电机控制型分布式电源自适应惯性控制策略
[J].
Adaptive inertial control strategy for inverter interfaced distributed generator based on virtual synchronous generator under frequency disturbances
[J].
电力系统惯量评估研究框架与展望
[J].
Research framework and prospect on power system inertia estimation
[J].
Inertia estimation based on observed electromechanical oscillation response for power systems
[J].
Non-invasive identification of inertia distribution change in high renewable systems using distribution level PMU
[J].
基于差值计算法的系统分区惯量评估方法
[J].
Assessment method of system partition inertia based on differential calculation method
[J].
Online estimation of power system inertia using dynamic regressor extension and mixing
[J].
On-line inertia estimation for synchronous and non-synchronous devices
[J].
A method for evaluating frequency regulation in an electrical grid-part I: Theory
[J].
A method for evaluating frequency regulation in an electrical grid-part II: Applications to non-synchronous devices
[J].
Adaptive virtual synchronous generator considering converter and storage capacity limits
[J].
基于参数自适应调节的虚拟同步发电机暂态响应优化控制
[J].
Optimal control of transient response of virtual synchronous generator based on adaptive parameter adjustment
[J].
Frequency divider
[J].
Online estimation of POI-level aggregated inertia considering frequency spatial correlation
[J].
A systematic method to model power systems as stochastic differential algebraic equations
[J].