目前,国内外学者以运行经济性、可再生能源消纳能力以及降低碳排放等为目标,对微能源网优化调度进行深入研究[4⇓-6].然而,这部分研究中未考虑可再生能源出力及负荷的不确定性对微能源网运行的影响.在当前可再生能源渗透率不断提高的背景下,不确定性因素对系统安全运行的不利影响将越发突出.因此,在针对微能源网优化调度的研究中,有必要考虑不确定性因素的影响.当前针对不确定性因素的优化方法包括场景分析法、随机优化和鲁棒优化等[7⇓-9].其中,场景分析法和随机优化方法均依赖不确定变量的概率分布信息,需要大量的样本数据,增大问题的复杂性,同时可能忽略部分极端场景.鲁棒优化不依赖不确定变量的概率分布,以不确定集的形式表示变量的不确定性,能够求解出极端场景下系统最优的调度方案,因此在微网优化调度中得到了广泛应用[10-11].文献[12]中针对可再生能源出力的不确定性,建立微能源网两阶段鲁棒优化调度模型.文献[13]中针对热电联供型微网中风电的不确定性,建立双层鲁棒模型以得到最恶劣场景下的微网最优调度方案.然而以上研究均基于单区间不确定集,所得到最恶劣场景均取在区间边界,在实际情况中这种极端场景几乎不会出现,因此得到的结果往往过于保守.
综合需求响应能够有效提升系统运行的经济性,促进新能源的消纳并平抑新能源的波动[14].文献[15]中构建计及电能需求响应的微网鲁棒经济多目标优化调度模型,兼顾了调度方案的经济性和保守性.文献[16]中考虑冷热负荷的柔性,通过鲁棒线性优化理论将随机优化模型转化为确定性模型,兼顾微能源网运行的经济性和鲁棒性.文献[17]中提出一种自适应鲁棒优化方法,解决微电网在风力发电(简称风电)、光伏出力以及负荷存在不确定性时的调度问题.文献[18]中考虑直接负荷控制,建立了微能源网鲁棒随机优化调度模型.以上研究虽然考虑了需求响应参与系统调度,但是对需求响应的类型考虑较为单一,并且对需求响应的不确定性考虑较少.
基于以上研究,针对单区间不确定集保守性强的问题,引入多区间不确定集描述微能源网内风光及负荷不确定性,以降低模型的保守性.为了充分挖掘用户侧调度潜力,平抑不确定性因素波动,提高调度方案的经济性,设计包含可削减电负荷、可转移电负荷、柔性冷、热负荷及可替代负荷的综合需求响应模型,并在此基础上考虑综合需求响应的不确定性.最后,建立微能源网两阶段鲁棒优化调度模型,并通过算例验证了所提模型能够兼顾微能源网调度方案鲁棒性和经济性.
1 微能源网结构
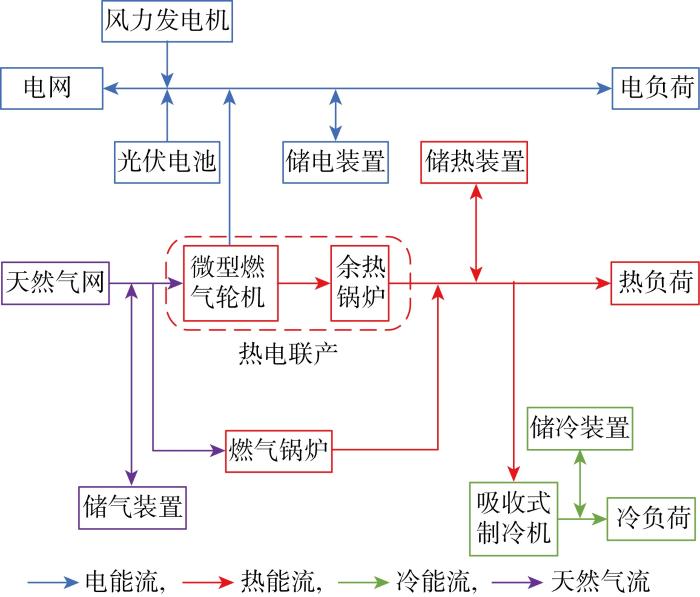
微能源网系统结构如图1所示.系统包含风力发电机(WT)、光伏(PV)组成的可再生能源发电机组,微型燃气轮机(MT)和余热锅炉(HG)组成的热电联产机组(CHP),吸收式制冷机(AC),燃气锅炉(GB),电储能(ES)、热储能(HS)、冷储能(CS)、气储能(GS)构成的储能系统.系统通过电力线路和传输管道与上级能源网络连接,包含电、热、冷多种负荷,通过引导用户参与综合需求响应(IDR),能够提高运行的经济性.
图1
2 源荷多区间不确定集
目前,微能源网鲁棒优化调度多采用单区间不确定集描述参数的不确定性,优化得出的最恶劣场景通常取在区间的边界处,然而实际上取到这种情况的概率极小,使得使用单区间不确定集得到的优化调度方案往往过于保守.因此,为了改善单区间不确定集过于保守的缺点,引入多区间不确定集[19],将传统的单区间不确定集划分为多个区间,并根据不确定参数的分布分配各个区间的不确定预算参数,使得所定义的多区间不确定集更加符合实际情况,有效降低调度方案的保守性.虽然多区间不确定集已有相关文献研究,但并未应用于微能源网调度中,针对微能源网内源荷不确定性构建的多区间不确定集如图2所示.图中,j∈{wt, pv, e, c, h},各元素分别表示风电、光伏、电储能、冷负荷、热负荷(下同),每个源荷不确定区间被划分为n个区间,
图2
根据所构建的源荷多区间不确定集,微能源网内风光及负荷不确定性可表示为
式中:u为不确定变量集合;Pj,t为源荷不确定变量;
3 综合需求响应模型
微能源网内包含电、冷、热多种类型的负荷,根据是否能够参与IDR将各类负荷分为基本负荷和柔性负荷,为了充分挖掘需求侧可调度资源,平抑不确定因素波动,提高系统调度的经济性,根据需求侧各类柔性负荷的响应特性建立IDR模型.IDR模型中的柔性负荷包括可削减电负荷、可转移电负荷、柔性冷、热负荷以及可替代负荷.
3.1 可削减电负荷
微能源网通过对可削减电负荷参与需求响应给予经济补偿的方式,引导用户主动削减用电高峰时段部分不必要的电负荷.可削减电负荷数学模型可表示为
式中:Pint,t为t时刻可削减电负荷功率;δint,t为布尔变量,表示t时刻是否进行可削减电负荷需求响应;Pint,t,max为t时刻可削减负荷的最大功率;Lint,max 为可削减电负荷参与响应的次数上限.
3.2 可转移电负荷
微能源网可通过给予用户补偿的方式,引导用户将具有可转移性质的电负荷,从电负荷高峰时段转移到电负荷低谷时段.可转移电负荷数学模型可表示为
式中:
3.3 柔性冷、热负荷
用户对于冷、热负荷的感知具有模糊性,对用户而言存在一个舒适区间,在舒适区间内调节冷、热负荷对用户舒适度影响较小,因此可以作为柔性负荷参与需求响应[20].柔性冷、热负荷数学模型可表示为
式中:i∈{c, h},下同;
3.4 可替代负荷
微能源网内电、冷、热3种负荷之间具有替代作用.微能源网可以运行经济性最优为目标,向用户提供同等用能质量的能源替代方案.可替代负荷数学模型可表示为
式中:
3.5 考虑IDR的负荷模型
式中:Pe,IDR,t和Pi,IDR,t分别为IDR后电和冷(热)负荷.
3.6 综合需求响应不确定性
微能源网在实际运行过程中,除了受到可再生能源出力及负荷不确定性的影响,综合需求响应的不确定性也是影响调度方案可靠性的因素之一.因此,在所建立的综合需求响应模型基础上,进一步考虑其不确定性,建立不确定性模型如下.
(1) 可削减电负荷不确定性:
式中:
(2) 可转移电负荷不确定性.可转移电负荷转入和转出功率需要维持平衡,因此仅考虑转入负荷的不确定性,然后根据转入负荷的实际响应量安排转出负荷的响应计划.表示为
式中:
(3) 柔性冷、热负荷不确定性:
式中:
(4) 可替代负荷不确定性:
式中:
4 两阶段鲁棒优化调度模型
4.1 目标函数
微能源网的调度目标为最小化日运行运行成本,不考虑源荷不确定性时,确定性优化调度模型目标函数为
式中: l∈{ES, HS, CS, GS};Ceg,t、Com,t、CIDR,t分别为t时刻系统与电网及气网交互成本、设备运维成本、IDR成本;
微能源网在实际运行过程中,受到源荷多重不确定性的影响,目前已有的预测方法得到的预测值与实际值仍存在较大偏差,因此确定性优化模型得到的优化方案往往过于乐观.因此,综合考虑风光、负荷及综合需求响应不确定性建立两阶段鲁棒模型,目标函数为
式中:
4.2 约束条件
(1) 功率平衡约束:
式中:
(2) 机组约束:
式中:m表示机组类型,m∈{CHP, GB, AC},下同;
(3) 储能运行约束:
式中:
(4) 与电网、气网交互约束:
式中:
(5) IDR约束.IDR约束见式(2)~(6).
(6) 不确定变量约束.不确定变量约束见式(1)和式(7)~(10).
4.3 求解方法
为了方便表示,将所提两阶段鲁棒模型写为紧凑形式如下:
式中:d为目标函数式(11)对应的系数列变量;A、B、D、K、J为对应约束下变量的系数矩阵;f为常数列向量;x和y为优化变量,具体含义如下:
式(21)中第一行和第二行约束对应前文不等式约束,第三行约束对应前文等式约束,第四行约束表示可再生能源出力及负荷取值为各时刻不确定变量取值.
两阶段鲁棒问题无法直接求解,目前,Benders分解算法和行列生成(C&CG)算法是解决此类问题的两种主要算法.C&CG算法相比于Benders分解算法能够更快收敛到最优解,有效降低迭代次数,因此本文选用C&CG算法[21],将原式(21)分解为主问题和子问题交互迭代求解.
分解后的主问题形式为
式中:a为当前迭代次数;yz为第z-1次迭代后子问题返回变量;uz为第z-1次迭代后求出的u;εIDR, z为第z-1次迭代后求出的εIDR.
子问题可表示为
为了便于求解,通过强对偶理论进一步将子问题转化为一个单层优化问题,如下式所示.
式中:α1、α2、α3、α4为对偶变量.由于式中存在双线性项α4u和α3εIDR,zK,所以子问题是NP-hard问题[22],难以直接求解.同时因为K中包含正数和负数,不能直接通过大M法线性化,所以首先将矩阵K中正数和负数分离,分解为矩阵K+、K-,然后通过大M法线性化可得:
式中:Δuk+=[Δ
经过上述推导转换,所提两阶段鲁棒模型已转化为混合整数线性规划问题的形式,可以通过C&CG算法求解,求解流程如下:
(1) 给定一组不确定变量的取值u1和εIDR,1作为初始最恶劣场景, 上界Ub=+∞,下界Lb=-∞,迭代次数a=1,收敛间隙设为λ=0.01.
(2) 将uz和εIDR, z代入主问题,得到问题的最优解(xa, yz),更新Lb=θa.
(3) 将求得的xa代入子问题,得到子问题的最优解(ua+1, εIDR, a+1),更新子问题目标函数值作为新的上界.
(4) 如果Ub-Lb≤λ,停止迭代,返回最优解;否则,增加变量ya+1及以下约束:
令a=a+1,返回步骤(2).
5 算例分析
5.1 算例参数设置
图3
表1 微能源网参数
Tab.1
| 设备名称 | 效率 | 容量 | 运维费用/ [元·( kW·h)-1] |
|---|---|---|---|
| 热电联产机组 | 0.25(电), 0.48(热) | 500 kW | 0.0045 |
| 燃气锅炉 | 0.8 | 400 kW | 0.0043 |
| 吸收式制冷机 | 1.1 | 200 kW | 0.003 |
| 电储能设备 | 0.95 | 200 kW·h | 0.1 |
| 热储能设备 | 0.9 | 150 kW·h | 0.05 |
| 气储能设备 | 0.95 | 200 kW·h | 0.05 |
| 冷储能设备 | 0.88 | 100 kW·h | 0.05 |
表2 能源分时价格
Tab.2
| 时间 | 购/售电价格 | 购气价格 |
|---|---|---|
| 1:00—7:00 | 0.41/0.246 | 0.21 |
| 8:00—10:00, 23:00—24:00 | 0.74/0.444 | 0.33 |
| 11:00—22:00 | 1.10/0.660 | 0.41 |
所建立的两阶段鲁棒模型采用MATLAB R2021b结合yalmip插件调用Gurobi求解器进行求解,系统以24 h为调度周期,1 h为间隔进行仿真.
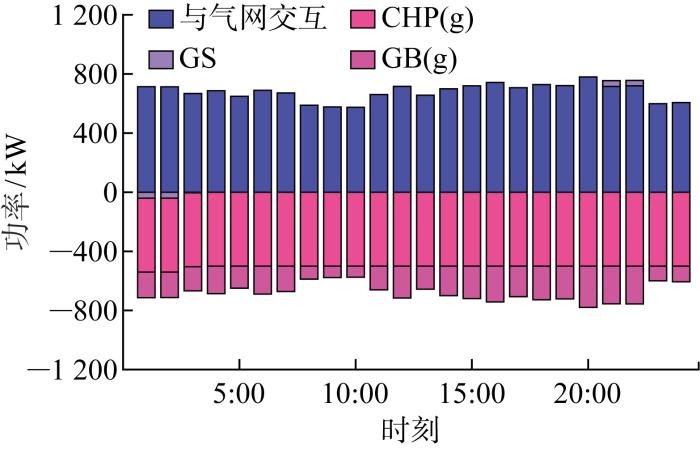
5.2 鲁棒模型优化结果
可再生能源出力在预测值的±10%范围内波动,分为3个不确定区间,对应的偏差上下界为分别±2%、±5%、±10%;电、冷、热负荷功率在预测值的±5%范围内波动,分为两个不确定区间,波动偏差上下界为预测值的±2%、±5%.假设可再生能源及负荷功率服从平均值为
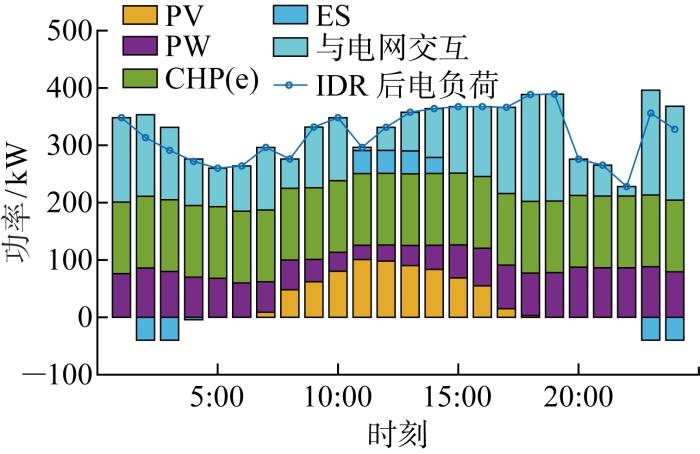
图4
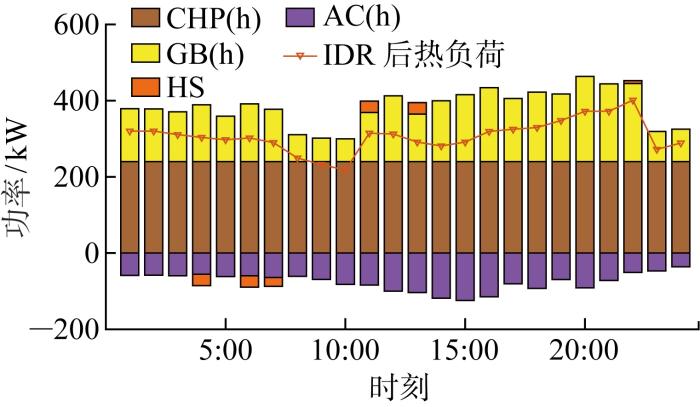
图5
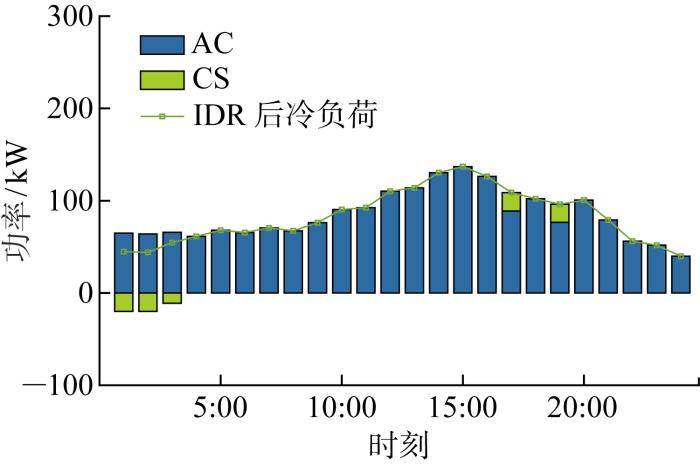
图6
图7
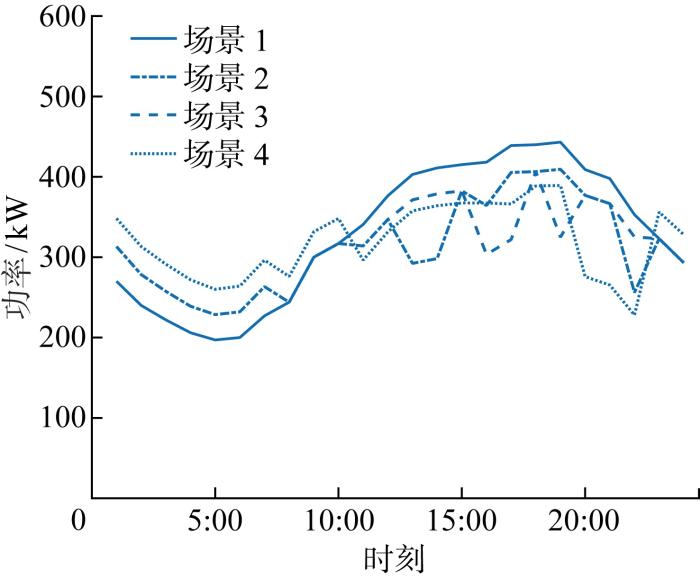
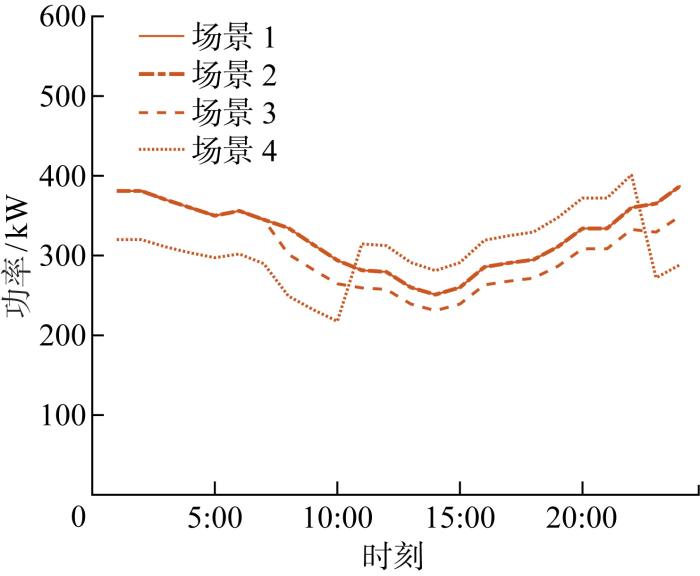
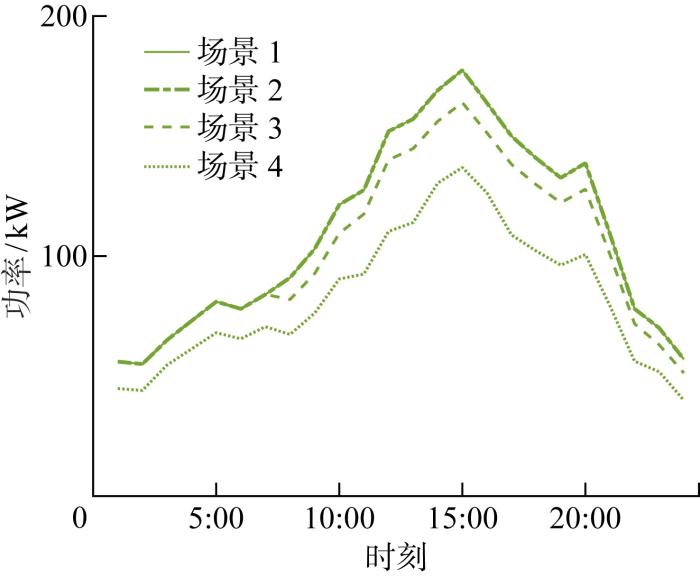
5.3 综合需求响应效果分析
为了研究所提IDR模型对微能源网调度的影响,验证IDR模型的有效性,构建4种不同场景进行对比.场景1为不考虑IDR的场景;场景2为仅考虑可削减电负荷和可转移电负荷参与IDR的场景;场景3为仅考虑可削减电负荷、可转移电负荷和柔性冷、热负荷参与IDR的场景;场景4为综合考虑可削减电负荷、可转移电负荷、柔性冷、热负荷和可替代负荷参与IDR的场景.
表3 各场景下调度成本
Tab.3
| 场景 | 总成本 | 购能成本 | 设备维护成本 | IDR成本 |
|---|---|---|---|---|
| 1 | 8528.4 | 8410.8 | 117.6 | 0 |
| 2 | 8279.7 | 7823.5 | 117.6 | 338.5 |
| 3 | 8173.7 | 7534.6 | 114.5 | 524.5 |
| 4 | 8090.3 | 7454.3 | 111.4 | 524.5 |
综上,场景2~4相比于场景1系统调度总成本分别降低了2.92%、4.16%、5.14%,说明IDR策略能够有效平抑最恶劣场景下风光及负荷波动,降低系统调度成本,具有较好的经济性.
图8
图9
图10
5.4 不确定性因素对调度结果影响
为了分析所考虑的源荷多重不确定性因素对系统调度的影响,以场景4为基础,设置4种不同的优化模型进行对比,优化结果如表4所示.其中,模型1为确定性优化模型,不考虑不确定性因素;模型2为考虑风光及负荷不确定性,通过单区间不确定集描述,不考虑综合需求响应不确定性;模型3为考虑风光及负荷不确定性,通过多区间不确定集描述,不考虑综合需求响应不确定性;模型4为考虑风光及负荷不确定性,通过多区间不确定集描述,并考虑综合需求响应不确定性.
表4 不同模型优化结果
Tab.4
| 模型 | 总成本 | 购能成本 | 设备维护成本 | IDR成本 |
|---|---|---|---|---|
| 1 | 7695.7 | 6946.9 | 109.0 | 639.8 |
| 2 | 8236.7 | 7486.5 | 110.4 | 639.8 |
| 3 | 7994.9 | 7245.3 | 109.8 | 639.8 |
| 4 | 8090.3 | 7454.3 | 111.4 | 524.5 |
从表4可以看出,模型1因为未考虑不确定因素的影响,所以调度成本最低,但是由于系统实际运行时存在不确定因素的影响,所以得到的调度结果鲁棒性较差.相比于模型2,模型3系统调度总成本降低了241.8元,这是因为多区间不确定集相比于单区间不确定集进一步考虑了不确定参数的分布特性,更加符合实际情况,在保证调度结果鲁棒性的同时,降低了模型的保守性.相比于模型3,模型4由于考虑了综合需求响应不确定性,减少了综合需求响应量,提高了购能成本,所以总成本上升了95.4元,通过牺牲一定的经济效益提高了模型的鲁棒性.
为了分析不确定预算参数对微能源网运行成本的影响,不同不确定预算参数下的系统调度成本如表5所示.
表5 不同预算参数优化结果
Tab.5
| Γpv,k | Γwt,k | Γe,k | Γc,k | Γh,k | ΓIDR | 总成本/元 |
|---|---|---|---|---|---|---|
| (0, 0, 0) | (0, 0, 0) | (0, 0) | (0, 0) | (0, 0) | 0 | 7695.7 |
| (0, 2, 1) | (2, 3, 1) | (4, 2) | (4, 2) | (4, 2) | 6 | 7926.4 |
| (2, 3, 1) | (5, 5, 2) | (9, 3) | (9, 3) | (9, 3) | 12 | 8090.3 |
| (5, 5, 2) | (10, 10, 4) | (18, 6) | (18, 6) | (18, 6) | 24 | 8271.3 |
从表5可以看出,不确定预算参数均取0时,鲁棒优化模型转化为确定性优化模型,得到的系统调度总成本最低.随着不确定预算参数不断增大,系统的调度总成本也不断提高,调度方案逐渐趋于保守.因此,实际制定调度方案的过程中,可以根据需要设定合适的不确定预算参数,灵活调节调度方案的经济性和鲁棒性.
6 结论
针对电、热、冷联供型微能源网,考虑源荷多区间不确定集和综合需求响应,建立微能源网两阶段鲁棒优化调度模型,通过算例分析得出结论如下:
(1) 综合考虑可削减电负荷、可转移电负荷、柔性冷、热负荷和可替代负荷参与IDR,能够充分挖掘用户侧调度潜力,有效平抑最恶劣场景下风光及负荷波动,降低系统运行成本.
(2) 利用多区间不确定集描述风光及负荷不确定性,由于考虑了不确定参数的分布特性,更加符合实际情况,所以能够降低微能源网调度方案的保守性,降低系统调度总成本.
(3) 考虑综合需求响应不确定性后,综合需求响应量减少,系统购能成本升高,牺牲了一定经济性,提高了调度方案的鲁棒性.
(4) 当不确定预算参数设置较小时,系统的调度成本较低,但鲁棒性较弱;不确定参数设置较大时,系统调度结果的鲁棒性较强,但调度成本较高.因此,在实际制定调度的方案的过程中可以根据需要选择合适的不确定预算参数,灵活调节调度方案的鲁棒性和经济性.
参考文献
微能源网多能源耦合枢纽的模型搭建与优化
[J].
Modelling and optimization of multi-energy coupling hub for micro-energy network
[J].
Energy flow modeling and optimal operation analysis of the micro energy grid based on energy hub
[J].
计及多类型需求响应的孤岛型微能源网经济运行
[J].
Optimal operation of islanded micro energy grid with multi-type demand responses
[J].
含热泵和相变储能的多能互补微能源网运行优化方法研究
[J].
Research on an operational optimization method of multi-energy complementary micro energy grid with heat pump and phase change energy storage
[J].
Optimal economic operation of isolated community microgrid incorporating temperature controlling devices
[J].
考虑碳排放成本的多能互补微能源网储能装置优化运行
[J].
Optimized operation of energy storage in a multi-energy complementary micro-energy network considering carbon emission cost
[J].
Stochastic-based scheduling of the microgrid operation including wind turbines, photovoltaic cells, energy storages and responsive loads
[J].
Optimal operation of electrical and thermal resources in microgrids with energy hubs considering uncertainties
[J].
基于改进两阶段鲁棒优化的主动配电网经济调度
[J].
Economic dispatch of active distribution network based on improved two-stage robust optimization
[J].
含电动汽车的微网鲁棒经济调度
[J].
Robust economic dispatch of microgrid with electric vehicle
[J].
含高渗透率风电的微网系统鲁棒经济调度方法
[J].
Robust economic dispatch method of microgrid containing high propotion of wind power
[J].
基于鲁棒优化的微能源网综合需求响应协同调度策略
[J].
Robust optimization based coordinated scheduling strategy for integrated demand response in micro energy grid
[J].
考虑风电消纳的热电联供型微网日前鲁棒经济调度
[J].
Robust day-ahead economic dispatch of microgrid with combined heat and power system considering wind power accommodation
[J].
考虑综合需求响应的综合能源系统多能协同优化调度
[J].
Multi-energy collaborative optimization scheduling of integrated energy system considering integrated demand response
[J].
基于机会约束高斯混合模型的含光热电站热电联供型微网鲁棒经济调度
[J].
Robust economic dispatch of CSP-CHPMG based on chance constrained Gaussian mixture model
[J].
冷热电气多能互补的微能源网鲁棒优化调度
[J].
Robust optimal dispatch of micro-energy grid with multi-energy complementation of cooling heating power and natural gas
[J].
Adaptive robust optimization framework for day-ahead microgrid scheduling
[J].
考虑直接负荷控制不确定性的微能源网鲁棒优化运行
[J].
Robust optimal operation for micro-energy grid considering uncertainties of direct load control
[J].
Interval-partitioned uncertainty constrained robust dispatch for AC/DC hybrid microgrids with uncontrollable renewable generators
[J].
基于综合需求响应和主从博弈的多微网综合能源系统优化调度策略
[J].
Optimal dispatch of multi-microgrids integrated energy system based on integrated demand response and stackelberg game
[J].
Solving two-stage robust optimization problems using a column-and-constraint generation method
[J].
Adaptive robust optimization for the security constrained unit commitment problem
[J].