综合能源系统电气热多能量流建模及优化

doi:10.16183/j.cnki.jsjtu.2022.494

综合能源系统电气热多能量流建模及优化

李冰洁¹, 袁晓昀¹, 史静¹, 徐华池^,², 罗子萱²

1.国网江苏省电力有限公司经济技术研究院,南京 210000

2.清华四川能源互联网研究院,成都 610042

Multi-Energy Flow Modeling and Optimization of Electric-Gas-Thermal Integrated Energy System

LI Bingjie¹, YUAN Xiaoyun¹, SHI Jing¹, XU Huachi^,², LUO Zixuan²

1. Economic Research Institute, State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210000, China

2. Sichuan Energy Internet Research Institute, Tsinghua University, Chengdu 610042, China

通讯作者: 徐华池,博士,助理研究员,电话(Tel.):028-61956712;E-mail:xuhuachi0307@163.com.

责任编辑: 孙伟

收稿日期: 2022-12-2 修回日期: 2023-04-24 接受日期: 2023-05-8

基金资助:

国网江苏省电力有限公司科技项目(J2021079)

Received: 2022-12-2 Revised: 2023-04-24 Accepted: 2023-05-8

作者简介 About authors

李冰洁(1990—),硕士,从事能源经济研究.

摘要

针对区域综合能源系统中电、气、热多种能源形式的转换严重影响系统运行的经济性,建立区域综合能源系统(RIES)能量流数学模型和优化模型,以提升系统的经济性和对可再生能源的消纳.建立系统中各类能源转换设备数学模型,确定电力、燃气、热能3种能源传输网络约束条件;以经济性运行为首要目标,兼顾低碳排放和提高可再生能源消纳率的目标函数,构建RIES多能流优化模型.在大型综合能源系统基础上,引入负荷侧需求响应,建立仿真模型.仿真结果表明,需求响应的引入提高了系统调度灵活性,减少了系统对储能设备的依赖,有效降低了用户的用能成本.

关键词： 区域综合能源系统; 多能流; 线性化; 需求响应

Abstract

In view of the fact that the conversion of various energy forms such as electricity, gas, and heat in the regional integrated energy system (RIES) seriously affects the economy of the system operation, a mathematical model and an optimization model of RIES energy flow are established to improve the economy of the system and the absorption of renewable energy. First, the mathematical models of all kinds of energy conversion equipment in the system are established to determine the constraints of three kinds of energy transmission networks, namely electricity, natural gas, and heat. Then, taking economic operation as the primary objective, and taking into account the objective function of low carbon emissions and increasing the uptake rate of renewable energy, the RIES multi-energy flow optimization model is constructed. Finally, based on the large-scale integrated energy system, the load side demand response is introduced and the simulation model is established. The simulation results show that the introduction of demand response improves the flexibility of system scheduling, reduces the dependence of the system on energy storage equipment, and effectively reduces the energy consumption cost of users.

Keywords： regional integrated energy system (RIES); multi-energy flow; linearization; demand response

PDF (8902KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李冰洁, 袁晓昀, 史静, 徐华池, 罗子萱. 综合能源系统电气热多能量流建模及优化[J]. 上海交通大学学报, 2024, 58(9): 1297-1308 doi:10.16183/j.cnki.jsjtu.2022.494

LI Bingjie, YUAN Xiaoyun, SHI Jing, XU Huachi, LUO Zixuan. Multi-Energy Flow Modeling and Optimization of Electric-Gas-Thermal Integrated Energy System[J]. Journal of Shanghai Jiaotong University, 2024, 58(9): 1297-1308 doi:10.16183/j.cnki.jsjtu.2022.494

21世纪以来,全球经济发展迅速,世界各国对能源的需求逐年上升,在传统供能体系中,存在严重依赖化石能源、能源利用效率低等问题^[1⇓-3].在此背景下,能源互联网(Energy Internet, EI)以其低碳环保、清洁高效等特点为未来能源系统的研究提供了全新思路,综合能源系统实现了电、热、气、冷、氢能源的梯级利用,最大限度提高了可再生能源消纳量与能源利用率^[4⇓-6].

综合能源系统由于包含能源形式众多,在数学模型、时间尺度等方面具有显著差异^{[7⇓⇓⇓-11]},相较于电力系统潮流计算,多能流计算问题中包含的决策变量和方程个数更多,呈现典型非线性特征,求解难度较大.

文献[12]中搭建了基本电-气区域综合能源系统网络解耦,以综合系统运行费用最低为优化目标,引入二阶锥松弛技术对电网潮流约束凸化松弛,将原优化问题转变为混合整数规划问题求解.文献[13]中建立了能源集线器模型,统一综合能源系统中的电、热、气、冷多能流模型,构建了效率最大化、排放指标最小化的多目标优化调度模型,通过原对偶内点法将优化问题转换为非线性规划问题求解.文献[14]中基于能源集线器理论和热电联产设备,考虑电-热-气网络约束,提出了针对微型能源系统的最优潮流模型,采用粒子群算法求解优化问题.文献[15]中针对含能源集线器的大规模非线性电-气网络,采用多智能体遗传算法将多能流最优潮流问题分解为独立的最优潮流问题,通过算例验证了该算法的通用性和鲁棒性.文献[16]中建立以能源集线器为核心的电-热-气双向耦合的能源系统模型,采用改进后的基于教学的优化算法求解多能流系统的多时段最优潮流问题,相较于其他启发式算法具有更快的收敛速度.文献[17]中构建了针对区域综合电-热-气能源系统的多目标最优潮流模型,同时考虑最低经济运行和污染气体排放最小,采用改进的非劣排序遗传算法求解得到多目标优化帕累托前沿,求解得到最优混合潮流.

为实现包含电力、天然气、热力多种能源类型的区域综合能源系统的多能协调互补与集成优化,充分发挥区域综合能源系统供能潜力,面向包含多种供能设备、能量转换设备以及供能网络的多能流优化调度展开研究.首先,基于常规火力发电机组、热电联产机组、可再生能源发电机组、电转气等供能设备,考虑网络运行约束条件,建立包含电力、天然气和供热网络的综合能源系统多能流数学模型.其次,对综合能源系统多能流模型中电力潮流、热网潮流、天然气管道流量、机组启停约束等非线性约束进行线性化处理,在保证求解精度的同时,降低模型的求解难度.最后,在负荷侧引入负荷需求响应,通过大规模系统对所提的综合系统多能流模型进行仿真验证.

1 区域综合能源系统数学模型

1.1 区域综合能源系统

区域综合能源系统是综合能源系统的一种典型形态^[18],旨在一定区域空间范围内,通过对不同种类的能源,如电力、热力、天然气、氢气等的统一设计规划和运行,满足全体用能负荷的安全、经济、高效供给.选取包含电力、天然气、热力3种能源形式的区域综合能源系统进行分析,系统结构如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 区域综合能源系统结构

Fig.1 Structure of regional integrated energy system

1.2 电力网络

1.2.1 电力系统数学模型

根据文献[19],可得电力系统支路传输有功功率的表达式为

(1)P_ij=Re[

{\overset{\cdot}{U}}_{i} I_{i j}^{*}

]=Re[

{\overset{\cdot}{U}}_{i} y_{i j}^{*}

(

U_{i}^{*}

U_{j}^{*}

)]=

U_{i}^{2}

g_ij-U_iU_j(g_ijcos δ _ij+b_ijsin δ _ij)

式中:U为电压相量;I为电流相量;y为导纳;g为电导;δ为电压相角;b为电纳;下标i、j表示电力系统不同的网络节点;上标*表示取共轭.在实际电力系统中,相邻两节点的电压标幺值近似相等,之间的相角差一般在10°以内,因此可假设sin δ_ij≈δ_ij=δ_i-δ_j,cos δ_ij≈1,U_i≈U_j≈1.此外,由于只考虑有功功率的传输,所以在等效电路中不考虑变压器和架空线路的对地电容,认为其对有功功率的分布无影响,即g_ij≈0,b_ij≈-1/x_ij,x_ij为节点i、j之间的支路阻抗,由此可将式(1)进一步变形为

(2)P_ij=

U_{i}^{2}

g_ij-U_iU_j(g_ijcos δ _ij+b_ijsin δ _ij)≈ g_ij-(g_ij+b_ijδ_ij)=-b_ijδ_ij

电力网络注入节点的有功功率为

(3)P_i=

\sum_{j \neq i}

P_ij=

\sum_{j \in i}

B_ij(δ_i-δ_j)= -

(- \sum_{j \in i} B_{i j} δ_{i} + \sum_{j \in i} B_{i j} δ_{j})

式中:B_ij为节点电纳矩阵B的第i行、第j列元素.电纳矩阵的对角线元素可定义为

(4)-

\sum_{j \in i}

B_ij=B_ii

将式(4)代入式(3)可得节点注入有功功率的表达式:

(5)P_i=-

(B_{i i} δ_{i} + \sum_{j \in i} B_{i j} δ_{j})

\overset{n}{\sum_{j = 1}}

(-B_ijδ_j)

1.2.2 电力系统模型约束主要包括以下3种约束.

(1) 电力网络节点注入有功功率平衡约束:

(6)P_i_,_t=

P_{i, t}^{T P P}

P_{i, t}^{C H P}

P_{i, t}^{W P}

P_{i, t}^{P V}

P_{i, t}^{P 2 G}

P_{i, t}^{l o a d}

式中: $P_{i, t}^{T P P}$ 为t时刻常规火力发电机组在节点i发出的有功功率; $P_{i, t}^{C H P}$ 为t时刻热电联产机组在节点i发出的有功功率; $P_{i, t}^{W P}$ 为t时刻风力发电机组在节点i发出的有功功率; $P_{i, t}^{P V}$ 为t时刻光伏发电机组在节点i发出的有功功率; $P_{i, t}^{P 2 G}$ 为t时刻电转气机组在节点i消耗的有功功率; $P_{i, t}^{l o a d}$ 为t时刻负荷在节点i消耗的有功功率.

(2) 电力网络节点相角约束:

(7)θ_min≤θ_i_,_t≤θ_max

式中:θ_min和θ_max为节点允许的电压相角θ_i_,_t的最小值和最大值.

(3) 电力网络支路潮流约束:

(8)P_ij_,min≤P_ij_,_t≤P_ij_,max

式中:P_ij_,min和P_ij_,max为节点i、j之间的支路ij允许流过功率P_ij_,_t的最小值和最大值.

1.3 燃气网络数学模型

(1) 天然气气源约束:

(9)

f_{i_{1}, m i n}^{s_{1}}

≤

f_{i_{1}}^{s_{1}}

≤

f_{i_{1}, m a x}^{s_{1}}

式中:上标s₁表示气源; $f_{i_{1}}^{s_{1}}$ 为气源节点i₁在单位时间内的出气量; $f_{i_{1}, m i n}^{s_{1}}$ 和 $f_{i_{1}, m a x}^{s_{1}}$ 分别为出气量的最小值和最大值.

(2) 天然气网络节点压力约束:

(10)

π_{i_{1}, m i n}

≤

π_{i_{1}}

≤

π_{i_{1}, m a x}

式中: $π_{i_{1}}$ 为节点i₁气压值; $π_{i_{1}, m i n}$ 和 $π_{i_{1}, m a x}$ 分别为节点压力的下限和上限.

(3) 管道流量与节点压力数学模型.假设天然气在管道中为恒温稳定流动,在流动中与管道摩擦系数不计,即忽略流动过程中的动能变化,采用Weymouth模型描述天然气在管道中流量与管道两端节点气压的关系,如下式所示:

(11)

f_{b_{1}}

f_{i_{1} j_{1}}

K_{i_{1} j_{1}} S_{i_{1} j_{1}} \sqrt{S_{i_{1} j_{1}} (π_{i_{1}}^{2} - π_{j_{1}}^{2})}

(12)

K_{i_{1} j_{1}}

=ε

\frac{3 848 T_{0} D_{b_{1}}^{5 / 2}}{π_{0} \sqrt{G L_{b_{1}} T_{b_{1} a_{1}} Z_{a_{1}}}}

(13)

S_{i_{1} j_{1}}

\{\begin{array}{l} + 1, & π_{i_{1}} - π_{j_{1}} \geq 0 \\ - 1, & π_{i_{1}} - π_{j_{1}} < 0 \end{array}

式中: $f_{b_{1}}$ 和 $f_{i_{1} j_{1}}$ 为位于天然气网络节点i₁和节点j₁之间的管道b₁的流量; $K_{i_{1} j_{1}}$ 为天然气节点压力平方差与气流量关系的系数; $S_{i_{1} j_{1}}$ 为管道内气体流动的方向,当节点i₁的气压大于节点j₁的气压时规定为正方向,反之规定为反方向;ε为天然气管道的效率参数,其与管道的摩擦系数相关;T₀为标准测试温度; $D_{b_{1}}$ 为管道直径;π₀为标准压力;G为天然气典型相对密度,一般空气取1.0,天然气取0.6; $L_{b_{1}}$ 为管道b₁的长度; $T_{b_{1} a_{1}}$ 为管道运行情况下的平均温度; $Z_{a_{1}}$ 为气体平均压缩系数.

(4) 节点气流量平衡约束:

(14)∑

A_{i_{1} j_{1}} f_{i_{1} j_{1}}

+∑

C_{s_{1}} f_{s_{1}}

- ∑D

f_{l o a d_{1}}

式中: $A_{i_{1} j_{1}}$ 为不含管道-节点关联矩阵; $C_{s_{1}}$ 为气源-节点关联矩阵;D为负荷-节点关联矩阵; $f_{s_{1}}$ 、 $f_{l o a d_{1}}$ 分别为气源和负荷气流量.

1.4 热力网络

1.4.1 供热网络

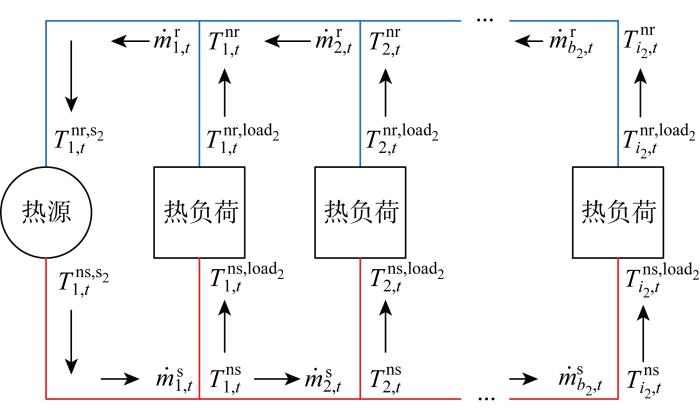
供热系统一般由热源、热负荷以及供热网络3部分组成,其中供热网络用于连接热源与热负荷.供热网络中的节点主要分为中间节点和热负荷节点两类,中间节点由于不发生热量交换,所以在该节点处供水网络与回水网络相互独立;热负荷节点则通过等效负荷将供水网络与回水网络连接在一起,区域供热网络结构示意图如图2所示.图中, ${\overset{\cdot}{m}}^{s}_{b_{2}, t}$ 为t时刻上游供水管道b₂流入节点i₂的水流量; ${\overset{\cdot}{m}}^{r}_{b_{2}, t}$ 为t时刻上游回水管道b₂流入节点i₂的水流量; $T_{i_{2}, t}^{n s}$ 和 $T_{i_{2}, t}^{n r}$ 分别为热源节点或热负荷节点处t时刻的供水温度与回水温度;上标s₂和load₂分别表示热源和热负荷.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 区域供热网络结构

Fig.2 Structure of district heating network

对供热网络的建模一般将其拆分为水力和热力两个模型描述^[20-21].水力模型用于求解节点压力、管道流量;热力模型的决策变量则为节点供水温度和回水温度以及满足热功率约束.

1.4.2 水力模型

热水在管道中流动可类比电流在导线中流动,管道流量的连续性描述可类比基尔霍夫电流定律得到,即流入任意节点i的水流量等于流出该节点的水流量与消耗水流量之和,同时注意到水流量的有向性,该连续性方程为矢量方程,如下式所示:

(15)

\sum_{b_{2} \in {P^{u}}_{i_{2}}} {\overset{\cdot}{m}}^{s}_{b_{2}, t}

\sum_{b_{2} \in {P^{d}}_{i_{2}}} {\overset{\cdot}{m}}^{s}_{b_{2}, t}

{\overset{\cdot}{m}}_{i_{2}, t}^{n s}

, ∀i ₂∈N^s

(16)

\sum_{b_{2} \in {P^{u}}_{i_{2}}} {\overset{\cdot}{m}}^{r}_{b_{2}, t}

\sum_{b_{2} \in {P^{d}}_{i_{2}}} {\overset{\cdot}{m}}^{r}_{b_{2}, t}

{\overset{\cdot}{m}}_{i_{2}, t}^{n r}

, ∀i ₂∈N^r

式中: ${\overset{\cdot}{m}}_{i_{2}, t}^{n s}$ 和 ${\overset{\cdot}{m}}_{i_{2}, t}^{n r}$ 分别为t时刻流入供水网络节点i₂和回水网络节点i₂的水流量; ${P^{u}}_{i_{2}}$ 和 ${P^{d}}_{i_{2}}$ 分别为上游管道与下游管道的集合;N^s和N^r分别为供水网络全部节点与回水网络全部节点的集合.

水力模型不仅需要求解节点和支路的流量,还需要求解管道中的压力分布.热水与天然气均为典型流体,热水在管道中流动时也会受到管壁的摩擦力做功,与气体类似产生压力损失,在流体力学中称为水头损失,表现为下游节点压力下降,水头损失可由下式计算:

(17)Δ

{p^{s}}_{b_{2}, t}

{R^{s}}_{b_{2}}

(

{\overset{\cdot}{m}}^{s}_{b_{2}, t}

)², ∀b ₂∈P^s

(18)Δ

{p^{r}}_{b_{2}, t}

{R^{r}}_{b_{2}}

(

{\overset{\cdot}{m}}^{r}_{b_{2}, t}

)², ∀b ₂∈P^r

式中:Δ ${p^{s}}_{b_{2}, t}$ 为t时刻供水网络中供水管道b₂带来的水头损失;Δ ${p^{r}}_{b_{2}, t}$ 为t时刻回水网络中回水管道b₂带来的水头损失,水头损失由长度单位表示; ${R^{s}}_{b_{2}}$ 和 ${R^{r}}_{b_{2}}$ 分别为供水网络与回水网络的管道阻尼系数;P^s和P^r分别为全体供水及回水网络节点集合.

水头损失类似于电路中的电压下降,因此类比电路中的回路电压定理可知,对于供热网络中的一个封闭回路,沿该回路l一圈的水头压力之和为0,可用下式表示:

(19)

\sum_{b_{2} \in l}

{p^{s}}_{b_{2}, t}

(20)

\sum_{b_{2} \in l}

{p^{r}}_{b_{2}, t}

引入关联矩阵简化网络表达式,可将上式改写成矢量矩阵形式为

(21)

\begin{array}{l} A_{h} m = m_{q} \\ B_{h} h_{f} = 0 \end{array}\}

(22)h_f=K_hm

|m|

式中:A_h为网络的节点-支路关联矩阵;B_h为网络的回路-支路关联矩阵;m为表示管道流量大小和方向的矢量矩阵;m_q为节点流量的矢量矩阵;h_f为节点水头损失矩阵;K_h为管道阻力系数矩阵.

1.4.3 热力模型

不考虑热力网络的动态过程,将其简化为静态模型,将管道中热量连续损耗的过程等效为类似热负荷的直接热量交换.

(1) 热功率约束.热功率约束存在于热源和热负荷节点,表示为热功率与供水和回水温度的约束条件,热功率计算公式如下:

(23)

Q_{i_{2}, t}

=c_p

{\overset{\cdot}{m}}_{i_{2}, t}

(

T_{i_{2}, t}^{n s}

T_{i_{2}, t}^{n r}

)×10^-3

式中: $Q_{i_{2}, t}$ 为t时刻热源节点i₂输出的热功率或热负荷节点i₂消耗的热功率; ${\overset{\cdot}{m}}_{i_{2}, t}$ 为t时刻流经热源或热负荷节点i₂的水流量;c_p为热水的比热容.

无论是热源节点还是热负荷节点,为了保证提高热量利用效率以及提高用户用能舒适度,对于供水温度和回水温度均有约束,如下式所示:

(24)

T_{i_{2}, m i n}^{n s, s_{2}}

≤

T_{i_{2}, t}^{n s, s_{2}}

≤

T_{i_{2}, m a x}^{n s, s_{2}}

(25)

T_{i_{2}, m i n}^{n r, s_{2}}

≤

T_{i_{2}, t}^{n r, s_{2}}

≤

T_{i_{2}, m a x}^{n r, s_{2}}

(26)

T_{i_{2}, m i n}^{n s, l o a d_{2}}

≤

T_{i_{2}, t}^{n s, l o a d_{2}}

≤

T_{i_{2}, m a x}^{n s, l o a d_{2}}

(27)

T_{i_{2}, m i n}^{n r, l o a d_{2}}

≤

T_{i_{2}, t}^{n r, l o a d_{2}}

≤

T_{i_{2}, m a x}^{n r, l o a d_{2}}

式中: $T_{i_{2}, m i n}^{n s, s_{2}}$ 和 $T_{i_{2}, m a x}^{n s, s_{2}}$ 分别为热源最小和最大时的供水温度; $T_{i_{2}, m i n}^{n r, s_{2}}$ 和 $T_{i_{2}, m a x}^{n r, s_{2}}$ 分别为热源最小和最大时的回水温度; $T_{i_{2}, m i n}^{n s, l o a d_{2}}$ 和 $T_{i_{2}, m a x}^{n s, l o a d_{2}}$ 分别为热负荷最小和最大时的供水温度; $T_{i_{2}, m i n}^{n r, l o a d_{2}}$ 和 $T_{i_{2}, m a x}^{n r, l o a d_{2}}$ 分别为热负荷最小和最大时的回水温度.

(2) 温度损耗约束.热力网络管道在t时刻的出口温度如下式所示:

(28)

T_{b_{2}, t}^{e n d}

(T_{b_{2}, t}^{s t a r t} - T_{a_{2}}) e^{- \frac{λ L}{c_{p} m}}

T_{a_{2}}

式中: $T_{b_{2}, t}^{s t a r t}$ 为t时刻管道b₂的始端温度; $T_{b_{2}, t}^{e n d}$ 为t时刻管道b₂的末端温度; $T_{a_{2}}$ 为管道所处环境温度;λ为管道的热传导系数;L为管道长度;m为流经管道的水流量.

(3) 节点温度混合约束.在节点温度混合约束中,包含3个描述不同位置的温度,一是上游管道末端温度,二是节点温度,三是下游管道始端温度.3个温度的混合关系由下式所示:

(29)

\sum_{b_{2} \in {P^{u}}_{i_{2}}}

(

{\overset{\cdot}{m}}_{b_{2}} T_{b_{2}, t}^{e n d}

(\sum_{b_{2} \in {P^{d}}_{i_{2}}} {\overset{\cdot}{m}}_{b_{2}}) T_{i_{2}, t}

式中: ${\overset{\cdot}{m}}_{b_{2}}$ 为上游管道b₂的流量; $\sum_{b_{2} \in {P^{d}}_{i_{2}}} {\overset{\cdot}{m}}_{b_{2}}$ 为注入节点i₂的水流量; $T_{i_{2}, t}$ 为t时刻节点i₂的混合温度.

而热水从混合节点流入下游管道时,全体下游管道始端温度等于该混合节点温度,数学表达式为

(30)

T_{b_{2}, t}^{s t a r t}

T_{i_{2}, t}

式中: $T_{b, t}^{s t a r t}$ 为下游管道始端温度.

2 区域综合能源多能流优化模型

2.1 目标函数

区域综合能源系统运行目标函数如下:

(31)F=min

\overset{N_{t}}{\sum_{t = 1}}

(

F_{t}^{i n}

F_{t}^{u n i t}

F_{t}^{e q}

F_{t}^{l o s s}

{F^{w}}_{t}

)

(32)

F_{t}^{i n}

F_{t}^{i n, g a s}

F_{t}^{i n, T P P}

(33)

F_{t}^{u n i t}

F_{t}^{u n i t, s t a r t}

F_{t}^{u n i t, d o w n}

(34)

F_{t}^{e q}

F_{t}^{e q, C H P}

F_{t}^{e q, P V}

F_{t}^{e q, W P}

F_{t}^{e q, G B}

F_{t}^{e q, P 2 G}

F_{t}^{e q, S O C}

F_{t}^{e q, H S S}

(35)

F_{t}^{l o s s}

F_{t}^{l o s s, P V}

F_{t}^{l o s s, W P}

(36)

{F^{w}}_{t}

F_{t}^{w, T P P}

F_{t}^{w, C H P}

F_{t}^{w, G B}

F_{t}^{w, P 2 G}

式中:F为总目标函数,为系统总运行成本; $F_{t}^{i n}$ 为系统购能成本; $F_{t}^{u n i t}$ 为机组启停成本; $F_{t}^{e q}$ 为机组运行成本; $F_{t}^{l o s s}$ 为弃风弃光惩罚成本; ${F^{w}}_{t}$ 为碳排放惩罚成本;N_t为系统调度时间; $F_{t}^{i n, g a s}$ 为气源向气井或上级气网购气成本; $F_{t}^{i n, T P P}$ 为常规火力发电机组购买的燃料成本; $F_{t}^{u n i t, s t a r t}$ 和 $F_{t}^{u n i t, d o w n}$ 分别为常规火力发电机开机与停机成本; $F_{t}^{e q, C H P}$ 、 $F_{t}^{e q, P V}$ 、 $F_{t}^{e q, W P}$ 、 $F_{t}^{e q, G B}$ 、 $F_{t}^{e q, P 2 G}$ 、 $F_{t}^{e q, S O C}$ 、 $F_{t}^{e q, H S S}$ 分别为t时刻热电联产、光伏发电、风力发电、燃气锅炉、电转气、电储能、热储能机组的运行成本; $F_{t}^{l o s s, P V}$ 为t时刻弃光惩罚费用; $F_{t}^{l o s s, W P}$ 为t时刻弃风惩罚费用; $F_{t}^{w, T P P}$ 为常规火力发电机组碳排放惩罚费用; $F_{t}^{w, C H P}$ 为热电联产机组碳排放惩罚费用; $F_{t}^{w, G B}$ 为燃气锅炉机组碳排放惩罚费用.电转气机组工业生产天然气中的甲烷化过程会消耗二氧化碳,因此用 $F_{t}^{w, P 2 G}$ 表示电转气机组削减碳排放的奖励费用.

2.2 非线性约束线性化

对能量流优化调度问题中的其他非线性约束进行线性化,将该问题调整为混合整数线性规划(Mixed Integer Linear Programming,MILP)问题,便于调用求解器得到全局最优解.

2.2.1 天然气管道流量约束线性化

在天然气网络约束中,描述管道流量与节点压力的Weymouth方程式(10)呈现典型的非线性和非凸性,目前对气体流量方程线性化的方法主要有两种,一种方法为二维近似法^[22-23],但该方法的计算较为复杂.因此采用气体流量方程一维近似线性化方法,引入变量 $φ_{i_{1}}$ = $π_{i_{1}}^{2}$ 和 $φ_{j_{1}}$ = $π_{j_{2}}^{2}$ ,且记 $φ_{i_{1} j_{1}}$ = $φ_{i_{1}}$ - $φ_{j_{1}}$ ,将等式(11)变形为

(37)

f_{i_{1} j_{1}}

K_{i_{1} j_{1}} S_{i_{1} j_{1}} \sqrt{S_{i_{1} j_{1}} φ_{i_{1} j_{1}}}

$φ_{i_{1} j_{1}}$ 的约束可以写为

(38)

φ_{i_{1} j_{1}, m i n}

≤

φ_{i_{1} j_{1}}

≤

φ_{i_{1} j_{1}, m a x}

将 $φ_{i_{1} j_{1}}$ 的取值范围划分为N段,将非线性方程式(37)平方后转化为如下表达式:

(39)

f_{i_{1} j_{1}}^{2}

K_{i_{1} j_{1}}^{2} φ_{i_{1} j_{1}}

K_{i_{1} j_{1}}^{2}

(

φ_{i_{1}}

φ_{j_{1}}

\overset{N}{\sum_{l_{1} = 1}}

(

A_{i_{1} j_{1}}^{l_{1}}

d_{i_{1} j_{1}}^{l_{1} - 1} k_{i_{1} j_{1}}^{l_{1}}

b_{i_{1} j_{1}}^{l_{1}} δ_{i_{1} j_{1}}^{l_{1}}

)

式中: $A_{i_{1} j_{1}}^{l_{1}}$ 为第l₁段目标函数的取值; $k_{i_{1} j_{1}}^{l_{1}}$ 为第l₁段的斜率; $δ_{i_{1} j_{1}}^{l_{1}}$ 用于判断 $A_{i_{1} j_{1}}^{l_{1}}$ 位于哪一段; $d_{i_{1} j_{1}}^{l_{1} - 1}$ 为第l₁-1段区间右端点函数值; $b_{i_{1} j_{1}}^{l_{1}} δ_{i_{1} j_{1}}^{l_{1}}$ 表示分段后每段的离散量,即直线方程中的截距. $A_{i_{1} j_{1}}^{l_{1}}$ 和 $δ_{i_{1} j_{1}}^{l_{1}}$ 的约束分别为

(40)

\begin{array}{l} 0 \leq A_{i_{1} j_{1}}^{l_{1}} \leq δ_{i_{1} j_{1}}^{l_{1}} d_{i_{1} j_{1}}^{l_{1}}, & l_{1} = 1 \\ δ_{i_{1} j_{1}}^{l_{1}} d_{i_{1} j_{1}}^{l_{1} - 1} \leq A_{i_{1} j_{1}}^{l_{1}} \leq δ_{i_{1} j_{1}}^{l_{1}} d_{i_{1} j_{1}}^{l_{1}}, & l_{1} \geq 2 \end{array}\}

(41)

\overset{N}{\sum_{l_{1} = 1}} δ_{i_{1} j_{1}}^{l_{1}}

=1;

δ_{i_{1} j_{1}}^{l_{1}}

=0,1

第l₁段区间右端点函数值表示为

(42)

d_{i_{1} j_{1}}^{l_{1}}

\frac{A_{i_{1} j_{1}, m a x} l_{1}}{N}

$b_{i_{1} j_{1}}^{l_{1}} δ_{i_{1} j_{1}}^{l_{1}}$ 数学表达式为

(43)

b_{i_{1} j_{1}}^{l_{1}}

=0, l₁=1

(44)

b_{i_{1} j_{1}}^{l_{1}}

d_{i_{1} j_{1}}^{l_{1} - 1}

)², l₁≥2

根据上述表达式,定义压力分段间隔将非线性问题线性化求解,对于分段线性化带来的分段直线与实际函数之间的最大插值误差,可以通过增加分段数的方式减小^[24].

2.2.2 机组二次函数成本线性化

机组的出力或运行成本与该机组的出力成二次函数关系,该非线性条件存在于目标函数中,前文已将约束条件中的非线性约束线性化,再将目标函数中的非线性条件去除后,整个问题不包含任何非线性条件,能够显著降低求解难度,提升求解速率.成本函数如下式所示:

(45)f(P_e,t)=A_e

P_{e, t}^{2}

+B_eP_e,t+C_eU_e,t

式中:A_e、B_e、C_e分别为机组供能成本的二次项、一次项和常数项系数;U_e,t为0-1型变量,表示机组e在t时段的运行成本.

由式(45)可知,成本函数横坐标为机组出力,纵坐标为成本,假设对横坐标分N₁段,记每段长度为L₁,表达式为

(46)L₁=

\frac{P_{e, m a x} - P_{e, m i n}}{N_{1}}

式中:P_e,_max和P_e,_min分别为机组出力最大值和最小值.引入 $p_{e, t, l_{2}}$ 表示机组e在t时段第l₂个分段中的实际出力值,因此将式(45)改写为

(47)f(P_e,t)=

\overset{N_{1}}{\sum_{l_{2} = 1}} k_{l_{2}} p_{e, t, l_{2}}

+U_e,tP_e,0

式中: $k_{l_{2}}$ 为各分段的斜率;P_e,0为机组在最低出力情况下的成本,可由下式计算,

(48)

k_{l_{2}}

=[(A_e

P_{e, t, l_{2} + 1}^{2}

+B_e

p_{e, t, l_{2} + 1}

+C_e)-(A_e

P_{e, t, l_{2}}^{2}

+B_e

p_{e, t, l_{2}}

+C_e)]/(

p_{e, t, l_{2} + 1}

p_{e, t, l_{2}}

)

(49)P_e,0=A_e

P_{e, m i n}^{2}

+B_eP_e,_min+C_e

3 算例分析

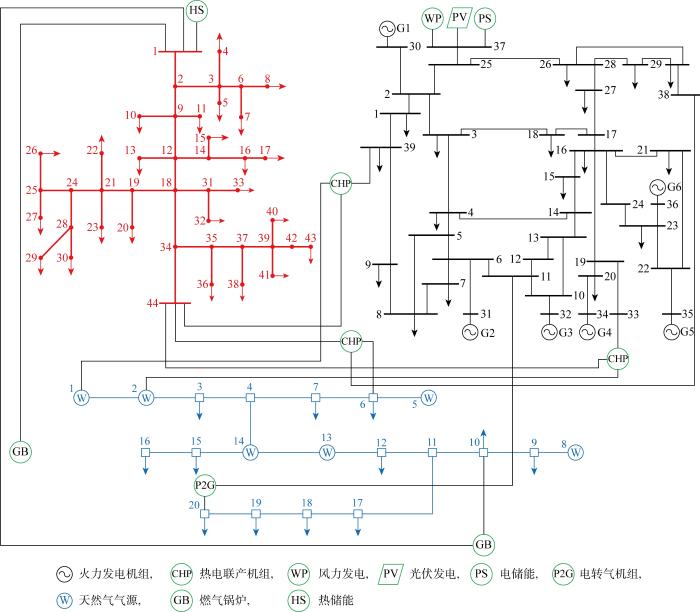
本算例为MW级,由IEEE 39节点电力网络、比利时20节点天然气网络、改进后的44节点供热网络组成.39节点电力网络系统中包含6台常规火力发电机组、3台可变热电比热电联产机组、接入MW级的风力、光伏发电厂且在接入节点增加电储能装置;20节点天然气网络系统中包含6个天然气气源,用于满足系统对天然气需求;44节点供热网络为双端供热网络,系统中的1号和44号节点通过热网母线分别与燃气锅炉、热电联产机组相连,将机组输出的热功率汇集后再通过供热管道供给系统中各热负荷节点.系统结构如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 系统结构

Fig.3 Structure of system

3.1 算例求解

区域综合能源系统通过常规火力、风力、光伏发电机组对综合能源系统进行供电,通过热电联产机组实现天然气网络向电力和热力网络的能量转换、电转气机组实现电力网络向天然气网络的能量转换,以及通过燃气锅炉实现天然气网络向热力网络的能量转换.将多余的能量储存到电储能和热储能设备中,及时对储能设备进行储存与释放能量,保证综合能源系统的能量供需平衡,从而对风力、光伏发电进行消纳.

(1) 热电联产机组通过燃气轮机燃烧的天然气产生具有一定比例的热能和电能,以实现天然气网络向电力网络和热力网络的能量转换.

(2) 电转气机组通过电解水装置和甲烷化过程将输入机组的电能以天然气的形式输出,以实现电力网络向天然气网络的能量转换.

(3) 燃气锅炉机组通过燃烧天然气产生热能,以实现天然气网络向热力网络的能量转换.

对模型线性化后将原问题转化为混合整数线性规划问题求解,采用CPLEX大型求解器求解.在日前调度中,设置求解时长为24 h,最小时段为1 h,求解得到机组调度安排与系统的潮流情况.

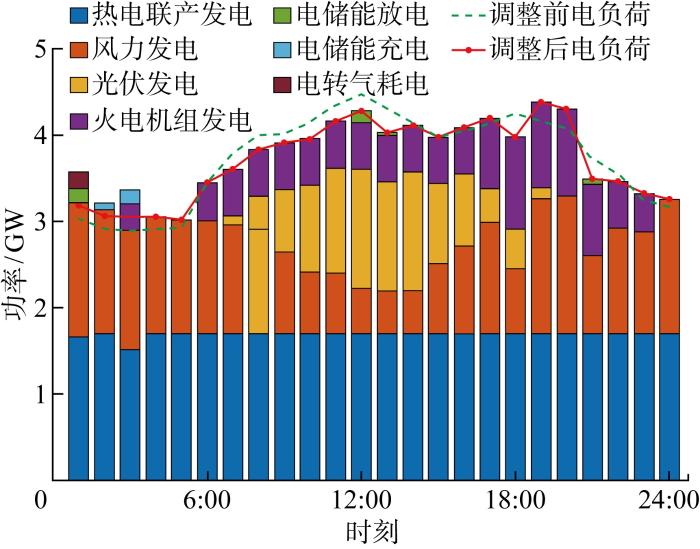
(1) 电力网络.图4为电力网络中各输出电功率机组与消耗电功率机组的调度安排.在0:00—5:00电负荷较为稳定的时段,区域综合能源系统优先使用电储能装置释放电能,当电储能装置释放完电能后,再充分消纳可再生能源发电中的风力发电,最后再调度热电联产机组输出电功率满足系统电功率平衡,具体情况如下.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 电功率平衡情况

Fig.4 Electrical power balance

在1:00—2:00时段,电储能装置进行充电用于消纳多余的可再生能源发电量.在2:00—3:00时段,电储能装置已对风力发电的剩余电量进行充分消纳,因此电储能装置不再进行充电,为实现系统电功率平衡,热电联产机组输出的电功率下降.在3:00—5:00时段,电储能装置再次充电,热电联产机组输出的电功率有所提升以保证系统电功率平衡,电储能装置电量充满时,热电联产机组输出的电功率又再次下降.在5:00—12:00时段,电负荷持续上涨达到当日第一个用电峰值,同时随着白天到来,光伏发电开始出力,系统优先保证消纳风力光伏等可再生能源的发电量,之后的缺额首先由热电联产机组电出力满足,在该时间段热电联产机组始终保持着最大电功率输出,仍存在缺额时即启动常规火力发电机组实现系统电功率的平衡.在12:00—20:00用电高峰时段,系统优先保证对可再生能源发电的利用,同时常规火力发电机组存在爬坡约束,无法快速调节自身出力,因此电储能装置在该时段频繁充放电,用于弥补常规火力发电机组由于上爬坡约束无法及时出力的电功率缺额,或用于吸纳常规火力发电机组由于下爬坡约束无法及时削减的富裕电功率.在20:00—24:00当日调度时段末尾,系统电负荷下降,常规火力发电机组逐步减少出力直至停机,随着系统电负荷需求持续下降,调度保证可再生能源发电始终保持最大值.

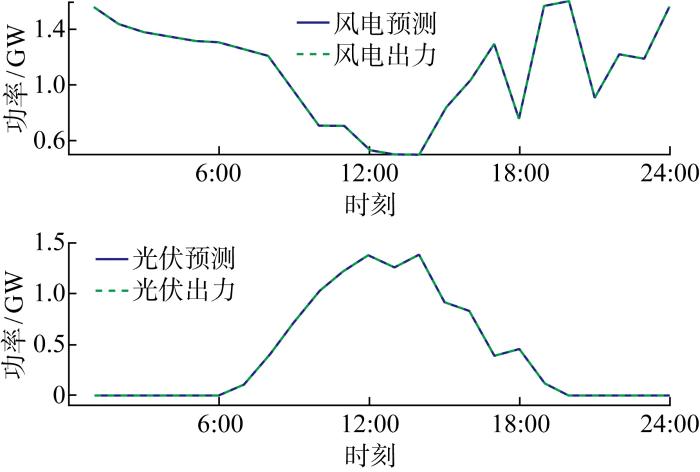
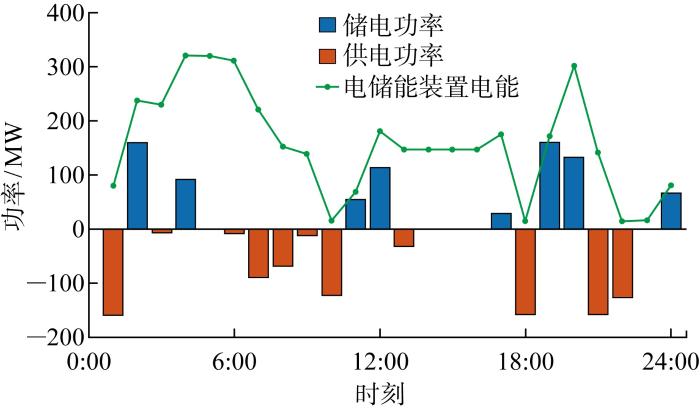
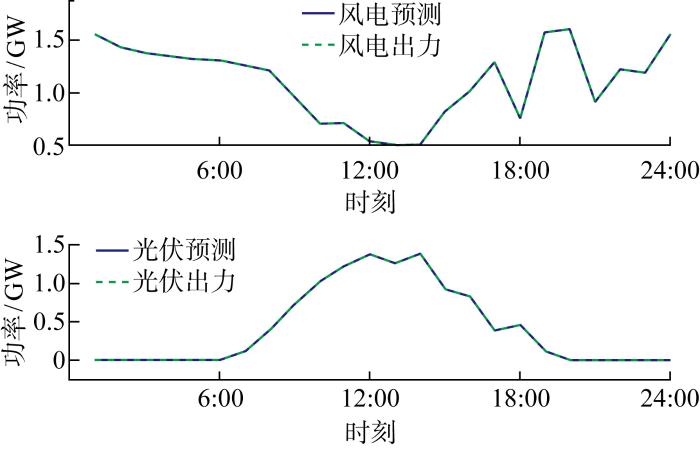
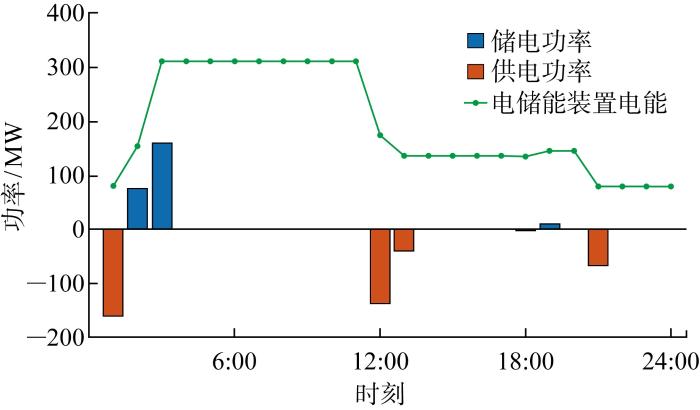
图5为风力与光伏发电的消纳情况,蓝色实线为预测的当日风力光伏出力情况,绿色虚线为在调度安排中实际消纳的风力光伏输出功率,可知在调度安排下,对可再生能源的消纳率基本达100%.图6为系统中与风力光伏发电接在同一节点的电储能设备运行工况.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 可再生能源消纳情况

Fig.5 Consumption of renewable

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 电储能设备运行情况

Fig.6 Operation of electric energy storage equipment

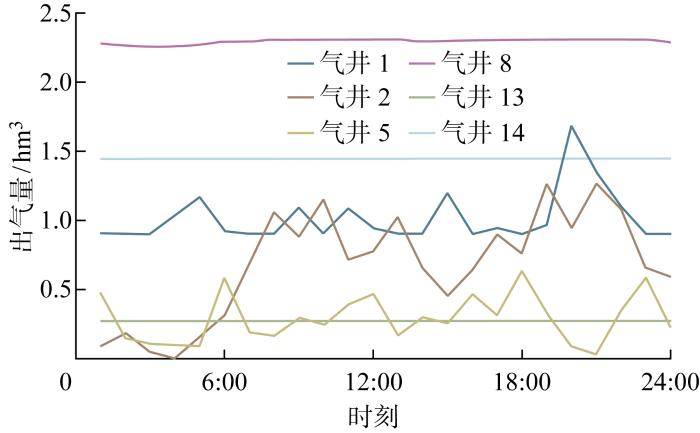
(2) 天然气网络.天然气网络气流量平衡由气源产气量进行实时平衡,网络中6个气源产气量随时间的关系如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 天然气气源产气量

Fig.7 Gas production of natural gas source

由图7以及天然气网络拓扑结构可知,天然气负荷节点9、10、11、17、18、19、20均需要来自编号为8的气源供应,且节点10与燃气锅炉相连,因此编号为8的气源出力在全调度过程中始终保持最大产气量,且该值相较于其余气源最大.天然气负荷节点3、4、5、6、7、15、16均需要来自编号为14的气源供应,且节点16与燃气锅炉相连,因此编号为14的气源出力在全调度过程中始终保持最大产气量,且该值较大.编号为8和14的气源为整个系统提供了最基础的天然气供应,满足天然气系统自身耗气需求.而在当日调度过程中,编号为1、2和5的气源产气量发生波动较明显,该类气源的产气量受到天然气系统负荷波动情况、耗气机组工作状况的影响,其产气量均在约束范围内变化,用于平衡系统中的实时波动.编号为13的气源在调度日内始终保持较低的产气量,该气源主要用于平衡系统节点压力约束.

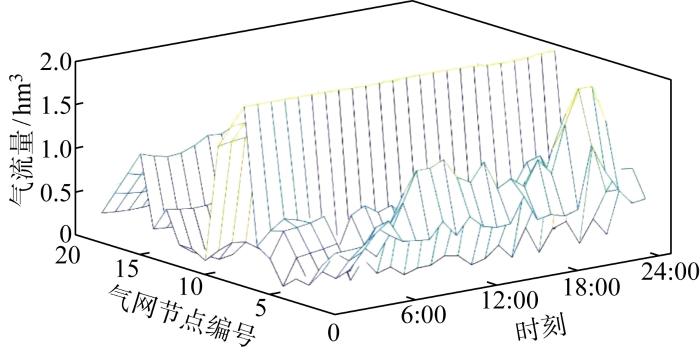
天然气网络中潮流由管道气流量分布情况和气网节点气压情况表示,分别如图8和9所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 天然气管道气流量

Fig.8 Gas flow of natural gas pipeline

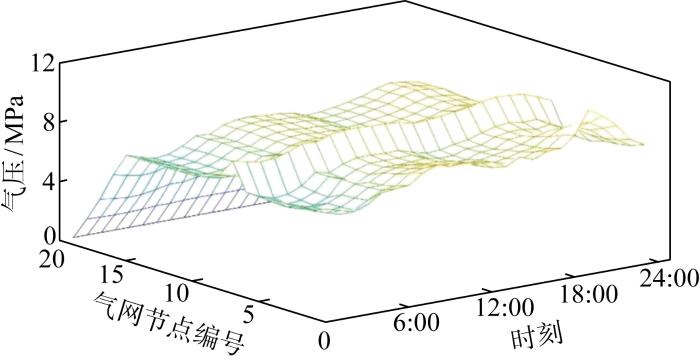
图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 天然气节点气压

Fig.9 Pressure of natural gas node

图8中,天然气管道1的两端节点1和2均为气源节点,因此相对于管道3和4,管道1和2的气流量较大.但由于管道1两端节点均与热电联产机组相连,且气源1和2的出气量相对于气源8较小,所以相对于管道10,管道1的气流量较小.此外,由于气源2出气量随时间的变化出现大幅波动,所以管道2和3的气流量随着时间变化出现一定幅度的波动.天然气气源2需要一直为热电联产机组提供天然气供应,因此流经管道3的天然气流量相对于其余管道均较小.管道4与气源5相连,因此流经管道4的气流量有一定幅度的增加;但气源5随时间变化具有出气波动性,因此管道4的气流量也有一定程度的波动.气源14的出气量较大,因此管道5、6、7的流量值逐渐增加.

由于仅有天然气管道8与气源8相连以及气源8具有较高的出气量,所以天然气管8的气流量基本保持稳定,并且流量值比其他管道的流量值大.之后受管道因素影响,天然气管道9的气流量开始下降,气体流经天然气节点10时,由于天然气节点10与燃气锅炉相连,来自气源8的部分天然气通过燃气锅炉进行燃烧,所以管道10和11的气流量出现大幅下降.管道12和13两端与气源相连,因此管道流量有一定的增加;管道14通过管道15与燃气锅炉相连,随着燃气锅炉运行,管道14和15的气流量开始减少.管道16~19没有气源出气的补充,因此管道的流量值逐步减少,并且流量值趋于稳定.

图9中,节点1~15之间与多个气源相连,有大量的气源供应,因此节点1~15的节点气压相对于节点16~19较高.气源8的出气量最大,因此节点8的气压达到最高.节点16~19由于没有直接与气源相连,所以节点气压逐渐下降.整个天然气网络由于具有4个较为稳定的气源,所以天然气网络的节点电压随着时间变化无大幅度波动,随着调度过程中热电联产机组、燃气锅炉和电转气机组的运行,天然气网络的节点电压产生小幅度波动.

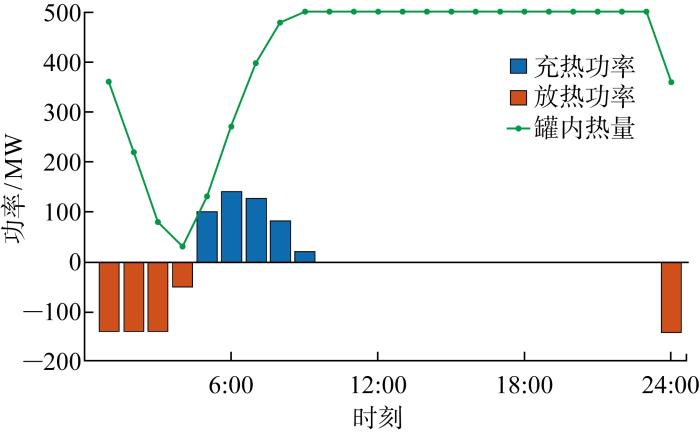
(3) 供热网络.图10为供热网络输出热功率与热负荷的平衡关系,可知,在该供热网络中由燃气锅炉作为主要出力设备,热电联产机组热出力为第二热出力源,用于平衡系统中的全部热负荷.热储能设备可在系统中存在少量不平衡时,吸收多余热量或释放热量以增加系统调度灵活性.图11为系统中储能设备运行工况,储能设备有一定容量限制,不可越过总容量无限制充能,此外在调度最后时段释放部分热量,满足储能设备在一个调度日的开始和结束时储存热量相同.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 热功率平衡情况

Fig.10 Thermal power balance

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 热储能装置运行情况

Fig.11 Operation of thermal energy storage device

3.2 负荷侧需求响应作用分析

对供电网络负荷侧采用需求响应的方式进行用户侧管理,在负荷电价高峰时通过转移负荷或削减负荷,降低区域综合能源系统设备出力,缓解高峰时供能压力.采用三级式负荷电价分别表示峰、谷、平3种用电特征,电价如表1所示.

表1 负荷侧分时电价

Tab.1 Time-of-use price of load side

时段	负荷电价/[元/(kW·h)^-1]
0:00—7:00,22:00—24:00	0.25
7:00—8:00,12:00—18:00	0.38
8:00—12:00,18:00—22:00	0.65

新窗口打开| 下载CSV

为分析负荷侧需求响应对调度成本以及设备调度安排的影响,需设置参与需求响应调度的负荷比例.本文电力网络中20号和39号节点作为与外部电网连接进行负荷削减、平移的节点,设置可削减负荷量不超过3%,可转移负荷量不超过10%.加入需求响应后,系统仿真结果如图12所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 加入需求响应后电功率平衡情况

Fig.12 Electrical power balance after adding demand response

在该调度日内,共削减负荷496.33 MW,在单位调度时段内最大削减电负荷为24.11 MW,占该时段总负荷的0.55%.在调度时段内转移负荷量最大的时段为12:00—13:00,转移了259.92 MW,占该时段总负荷的5.8%,均满足约束条件.

图12中,在0:00—7:00和22:00—24:00低电价时段,实际电负荷功率均高于原电负荷功率,主要通过电负荷转移将外部电网负荷引入,充分利用低电价时段区域综合能源系统供能潜力.而在7:00—22:00中高电价时段,普遍呈现调度后的电负荷功率低于原电负荷功率趋势,在该时段内主要通过负荷削减与向外部电网转移电负荷两种方式调整系统负荷情况,降低供电高峰时供电压力,改变电负荷曲线使其趋于平稳.在原有10:00—14:00的用电高峰时段,通过增加需求响应调度手段,平滑系统的峰值负荷;而在17:00—19:00等夜间用电高峰时段则通过需求响应调度推迟用电高峰,使用电高峰在低电价时段出现.

引入负荷侧需求响应前后系统供能成本如表2所示.引入需求响应前后,系统运行成本变化不大,略有下降,原因是系统削减了少量负荷,降低了部分机组出力,从而减少了系统的供能成本.系统转移负荷对系统供能成本无影响,因为根据转移负荷约束,系统转移出的电负荷与转移进入的电负荷一致,并不改变系统总出力情况.

表2 供能成本比较

Tab.2 Comparison of energy cost 万元

场景	火电机组成本	天然气费用	设备费用	弃风弃光惩罚成本	碳排放惩罚成本	总成本
无需求响应	3.7494	696.93	1.9233	0.000006	0.2522	702.8549
有需求响应	3.4414	689.93	1.9232	0.000003	0.2548	695.5494

新窗口打开| 下载CSV

图13为对可再生能源消纳情况,与图5相比,在引入需求响应前后,设备对风力发电和光伏发电的消纳率均为100%,因此需求响应调度方案不会对原有系统的消纳能力产生冲击.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 加入需求响应后可再生能源发电消纳情况

Fig.13 Consumption of renewable energy generation after adding demand response

图14为电储能设备运行情况,与图6相比,可以发现设备对电储能的调度明显减少且每次调度中储存和释放能量值也较少,电储能装置在大部分时间段中保持满容量,与电网交换能量频率减小.引入需求响应调度有利于缓解系统供能压力,转移和削减电负荷的运行方式类似于电储能装置的储存和释放能量过程,减少了系统对储能装置的依赖.在采用负荷侧需求管理的系统中,系统负荷波幅度较为稳定,可采用小容量的储能装置.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 加入需求响应后电储能设备运行情况

Fig.14 Operation of electric energy storage equipment after adding demand response

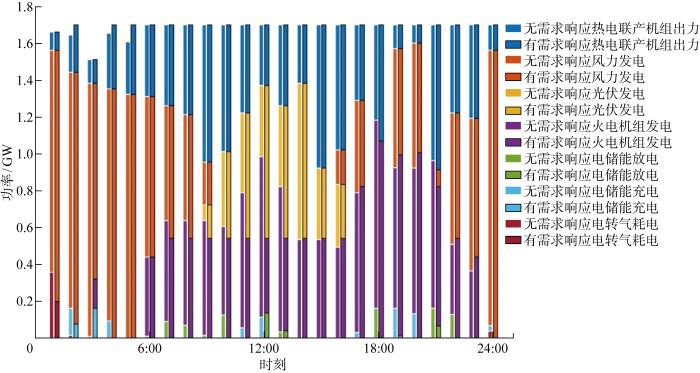
图15中,同一时间节点时无框线的条形图表示未引入需求响应的设备出力情况,黑色框线的条形数据表示引入需求响应的设备出力情况,不同颜色的条形图最高点表示对应设备的电功率值,该图表示了引入需求响应前后热电联产机组、风力发电、光伏发电、电储能等各设备在0:00—24:00的出力情况对比.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 加入需求响应前后各设备的电功率对比

Fig.15 Comparison of electrical power of each device before and after adding demand response

4 结论

对区域综合能源系统的研究,主要从供能设备工作特性仿真和网络传输过程建模两方面入手,结合具体算例,完成了如下工作:

(1) 为分析区域综合能源系统多能流的流通路径,进一步探究多能流耦合情况,对不同能源形式的供能网络进行建模.考虑系统中以有功功率交换为主且方便后续求解,采用直流潮流模型分析;利用Weymouth方程以节点气压和管道气流量描述天然气网络中的潮流分布情况.

(2) 结合供能设备与供能网络约束条件,设置以经济性运行为主要目标,其次兼顾低碳运行与提高风力光伏消纳,得到系统电、气、热综合能量流运行优化模型.为保证模型收敛,提高求解速度,在保证精度的前提下对优化模型中非线性条件进行线性化处理.

(3) 通过算例验证了模型和算法的正确性,并进一步研究了区域综合能源系统多能协同的特点.在算例中引入电网负荷侧需求响应调度方案与原方案进行对比,分析发现需求响应的引入提高了系统调度的灵活性,减少了系统对储能设备的依赖;同时需求响应的引入可以使部分在高电价高负荷时转移出去,在低电价低负荷时转移进来,有效削弱了负荷的波动情况.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

邱雨微, 郑徐跃, 詹翔燕, 等.

耦合可再生能源的分布式联供系统设计及运行策略优化

[J]. 厦门大学学报(自然科学版), 2019, 58(1): 103-110.