核反应堆堆芯吊篮压紧弹簧松弛特性

doi:10.16183/j.cnki.jsjtu.2023.024

核反应堆堆芯吊篮压紧弹簧松弛特性

杨泰波¹^,², 刘佳鑫², 彭志科^,³, 罗能², 刘才学²

1.上海交通大学机械与动力工程学院,上海 200240

2.中国核动力研究设计院,成都 610213

3.宁夏大学前沿交叉学院,银川 750021

Relaxation Characteristics of Hold-Down Spring of Core Support Barrel in Nuclear Reactor

YANG Taibo¹^,², LIU Jiaxin², PENG Zhike^,³, LUO Neng², LIU Caixue²

1. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Nuclear Power Institute of China, Chengdu 610213, China

3. School of Advanced Interdisciplinary Studies, Ningxia University, Yinchuan 750021, China

通讯作者: 彭志科,教授;E-mail:z.peng@sjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2023-01-19 修回日期: 2023-04-23 接受日期: 2023-04-24

Received: 2023-01-19 Revised: 2023-04-23 Accepted: 2023-04-24

作者简介 About authors

杨泰波(1986-),副研究员,从事反应堆故障诊断与健康管理技术研究.

摘要

核反应堆中堆芯吊篮的稳定性是反应堆正常运行的保障和前提.压紧弹簧作为堆芯吊篮的约束与支撑直接影响堆芯吊篮的振动特性.在高温、辐射等恶劣工况下,压紧弹簧力学性能会发生如应力松弛的退化,影响堆芯吊篮振动以及反应堆运行安全,因此需要对堆芯吊篮压紧弹簧松弛特性展开研究.首先,建立堆芯吊篮及压紧弹簧在内的装配体有限元模型,利用湿模态法分析并获得压紧弹簧松弛情况下的堆芯吊篮梁式模态振动频率的变化.然后,开展堆芯吊篮压紧弹簧松弛试验,试验结果验证了模型的有效性.进一步利用仿真模型生成更多压紧弹簧松弛影响下的堆芯吊篮梁式模态频率数据,结合试验数据建立堆芯吊篮压紧弹簧松弛程度识别的数学模型,为反应堆堆芯吊篮压紧弹簧松弛劣化监测奠定了技术基础.

关键词： 堆芯吊篮; 压紧弹簧; 松弛特性; 模态分析; 松弛试验

Abstract

The stability of the core support barrel (CSB) in a nuclear reactor is the guarantee and premise for the normal operation of the reactor core. As the constraint and support of the CSB, the hold-down spring (HDS) directly affects the vibration characteristics of the CSB. Under harsh conditions such as high temperature and radiation, degradation such as stress relaxation may occur in terms of the performance of the HDS, which will affect the vibration of the CSB and the operation security of the reactor. Therefore, it is necessary to study the relaxation characteristics of the HDS of the CSB. First, a finite element model including the CSB and the HDS is established. The wet modal method is adapted to analyze and obtain the change of the beam mode frequency of the CSB with the relaxation degradation of the HDS. Then, a relaxation test of the HDS of the CSB is conducted to verify the simulation results. The simulation model is further used to generate more beam mode frequency data of the CSB under the impact of different relaxation degrees of the HDS. Finally, combined with simulation and test data, a mathematical model for identifying the relaxation degree of the HDS of the CSB is established, which lays a technical foundation for monitoring the relaxation and degradation of the HDS of the CSB in nuclear reactor.

Keywords： core support barrel (CSB); hold-down spring (HDS); relaxation characteristics; modal analysis; relaxation test

PDF (5304KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨泰波, 刘佳鑫, 彭志科, 罗能, 刘才学. 核反应堆堆芯吊篮压紧弹簧松弛特性[J]. 上海交通大学学报, 2024, 58(8): 1290-1296 doi:10.16183/j.cnki.jsjtu.2023.024

YANG Taibo, LIU Jiaxin, PENG Zhike, LUO Neng, LIU Caixue. Relaxation Characteristics of Hold-Down Spring of Core Support Barrel in Nuclear Reactor[J]. Journal of Shanghai Jiaotong University, 2024, 58(8): 1290-1296 doi:10.16183/j.cnki.jsjtu.2023.024

堆芯吊篮作为核反应堆的核心部件,通过吊篮法兰将整个堆芯的质量传递给压力容器,是堆芯的容器与支撑.压紧弹簧作为堆芯吊篮的预紧件为堆芯吊篮法兰提供足够的预紧力,防止吊篮产生滑移等异常运动,是堆芯吊篮以及堆芯安全稳定运行的保障.然而在反应堆运行过程中,堆芯核裂变会持续释放大量辐射和热量^[1],造成极其恶劣的工况.研究表明,辐射高温会影响金属材料的微观结构和力学性能^[2-3],导致具有内应力的金属构件产生蠕变(应力恒定、应变随时间增加)、应力松弛(应变恒定、应力随时间减少)等劣化行为^[4⇓⇓-7].而压紧弹簧在为吊篮法兰提供预紧力的同时,自身会产生恒定形变量的压应力,因此在高温和辐射影响下压紧弹簧的弹性形变会逐渐转化为塑性形变,产生应力松弛现象,导致吊篮结构预紧力下降,影响堆芯吊篮及堆芯安全.Kang等^[8]采用有限元分析研究堆芯吊篮法兰处约束退化对结构振动的影响,将压紧弹簧对吊篮法兰的约束建模为多个约束集进行法兰松弛劣化模拟,结果表明法兰约束退化会造成堆芯吊篮振动频率下降,其中梁式振动频率下降幅度最大.赖姜等^[9]基于有限元法进一步研究堆芯吊篮在空气和静水中时法兰约束劣化对结构振动的影响,将压紧弹簧对吊篮法兰的约束建模为多个轴向弹簧单元,结果表明法兰约束退化在空气和静水中均会造成堆芯吊篮振动频率降低,且主要影响梁式振动频率.由此可见,压紧弹簧的预紧性能会影响堆芯吊篮的振动特性.反应堆回路中高压湍流的冷却剂会激发堆芯吊篮产生相应振动,长时间或异常的振动会导致反应堆内部结构疲劳、磨损、松动,甚至导致设备损坏^[10-11].上世纪俄罗斯新沃罗涅日压水堆核电站就发生一起由冷却剂诱导振动引起的吊篮热屏松动和脱落事件,导致反应堆关闭超过1.5年,造成严重经济损失^[12].因此,压紧弹簧的预紧性能关系着堆芯核反应的运行安全,需要通过理论结合试验的方式对其进行深入研究.然而,现有针对压紧弹簧松弛特性的研究较少,而已有研究对于压紧弹簧与堆芯吊篮法兰间相互作用的简化建模也只考虑法向的位移约束而忽略切向的摩擦力约束,理论建模方法尚不够完善.

因此,以数值仿真结合松弛试验的方法对核反应堆堆芯吊篮压紧弹簧松弛特性开展研究.利用有限元法直接建立包含压紧弹簧和堆芯吊篮等在内的装配体模态分析模型,采用湿模态法,考虑流体环境对结构模态的影响,获得压紧弹簧松弛程度与堆芯吊篮梁式振动频率之间的关系.搭建包含压紧弹簧、堆芯吊篮等在内的1∶1试验装置,开展压紧弹簧松弛试验,得到弹簧不同松弛程度下堆芯吊篮的真实振动频率,以验证仿真模型的有效性.最后,利用仿真结果和试验结果建立压紧弹簧松弛评价模型,为反应堆堆芯吊篮振动和支撑状态监测技术的应用奠定技术基础.

1 压紧弹簧劣化下的堆芯吊篮模态分析

1.1 模态分析理论

结构的运动方程为

(1)

\ddot{M x}

\overset{\cdot}{C x}

+Kx=F

式中:M、C、K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;x、F分别为系统位移向量和外载荷向量.模态分析求解的是系统固有振动频率,因此外载荷向量F为0,阻尼忽略不计,式(1)简化为

(2)

\ddot{M x}

+Kx=0

(3)x=x'sin(ωt)

式中:ω为系统固有振动频率;t为时间.

式(2)代入式(3)可得:

(4)(K-ω²M)x'=0

结构自由振动时,节点振幅x'为非零向量,因此式(4)转换为

(5)det(K-ω²M)=0

求解式(5)行列式得到系统的各阶模态.

1.2 几何模型及网格划分

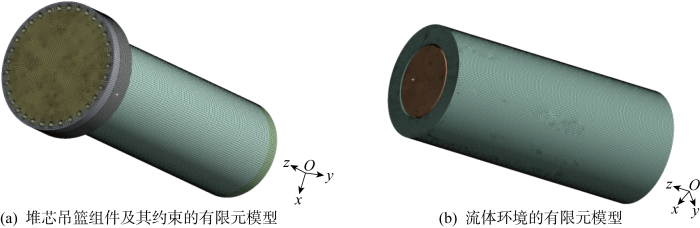
堆芯吊篮组件:堆芯吊篮组件结构复杂,由吊篮法兰、吊篮筒体、下堆芯支撑板、围板、成形板、二次支撑等部件组成.因此,利用Design Modeler软件建立堆芯吊篮组件三维模型,包括吊篮法兰、吊篮筒体和吊篮底部等主体结构.针对固定在堆芯吊篮上的下堆芯支撑板、围板、成形板、二次支撑等部件,利用质量附加法^[13]将其质量附加至对应的堆芯吊篮主体结构中,以考虑其对堆芯吊篮模态的影响.针对堆芯吊篮底部的多个冷却剂流通孔,为了有效缩短计算时间,减小耦合面数量,将其简化为具有相同通量的一个冷却剂流通孔.此外,在建模过程中忽略对堆芯吊篮模态几乎没有影响的圆角、倒角、销孔等细微结构,便于网格划分.

堆芯吊篮法兰约束:堆芯吊篮组件整体重力通过吊篮法兰下表面传递给反应堆压力容器筒体的内部下凸缘,吊篮法兰上表面受到压紧弹簧的预紧作用,压紧弹簧由压力容器顶盖提供约束,压力容器顶盖由预紧螺栓紧固在压力容器筒体上.堆芯吊篮法兰处的约束情况较为复杂,因此在堆芯吊篮法兰约束建模时不作简化,直接将压紧弹簧与堆芯吊篮、压力容器顶盖等结构直接建模为装配体模型,其中压紧弹簧的预紧力由压力容器顶盖向下挤压压紧弹簧产生压缩形变所获得,直接作用在吊篮的法兰上表面对堆芯吊篮法兰进行预紧.利用Design Modeler直接建立压力容器筒体内部下凸缘、压力容器顶盖和压紧弹簧的三维模型,以充分考虑堆芯吊篮法兰处约束对其模态的影响.

堆芯吊篮流体环境:由于堆芯吊篮处于冷却剂流体中,结构与流体之间存在耦合,流体会在结构表面产生附加压力,所以需要考虑流体环境对堆芯吊篮模态的影响.利用Design Modeler建立堆芯吊篮内部及外部的流体三维模型,保证堆芯吊篮始终浸没在流体环境中.

将三维模型导入ANSYS Meshing组件进行模型网格的划分.针对堆芯吊篮组件结构,吊篮筒体和底部采用六面体网格划分,吊篮法兰采用四面体网格划分,单元大小设为40 mm.针对压紧弹簧结构,采用四面体网格划分,单元大小设为20 mm.针对压力容器顶盖结构,采用六面体网格划分,单元大小设为40 mm.针对压力容器筒体内部下凸缘结构、流体模型,分割为多个区域以便实现均匀的网格划分,采用六面体网格,单元大小设为40 mm.结构与流体之间的耦合面网格大小设为40 mm.此外,结构之间的接触面网格大小会影响接触力的求解精度,因此在保证计算效率的前提下适当减小接触面网格尺寸,面网格大小设为10 mm.计算域有限元模型如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 计算域有限元模型

Fig.1 Finite element model of computational domain

为了计算在流体作用下的结构模态,采用湿模态分析法,将流体视为一种声学介质,忽略流体的黏性力,只考虑流体的体积变化及其带来的压力^[14-15].采用ANSYS WORKBENCH的Acoustic Modal模块进行结构的湿模态分析,将所建立的堆芯吊篮等结构的模型设为Physics Region,将所建立的流体模型设为Acoustic Region,定义两者之间的耦合面.将压力容器筒体内部下凸缘设为Fixed Support,压力容器顶盖下表面与压力容器筒体内部下凸缘上表面设为bonded.各结构接触面设置为摩擦接触,系数为0.2.在ANSYS中,具有摩擦、预应力等非线性问题下的系统模态分析一般采用近似的分析方法其将非线性问题进行求解后以附加刚度的形式对结构的整体刚度矩阵进行修正,然后进行模态分析求解.最后定义材料参数,堆芯吊篮等结构材料为不锈钢,冷却剂流体材料为水.

1.3 压紧弹簧劣化下的模态分析结果

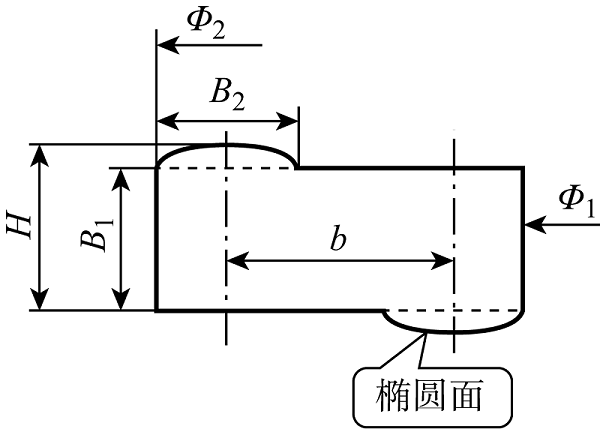
压紧弹簧为Z形截面结构,如图2所示.图中:H为弹簧总厚度;Φ₁为弹簧内径;Φ₂为弹簧外径;B₁为弹簧主体厚度;B₂为弹簧接触面宽度;b为上下表面受力点横向距离.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 原始压紧弹簧截面示意图

Fig.2 Schematic diagram of original section of HDS

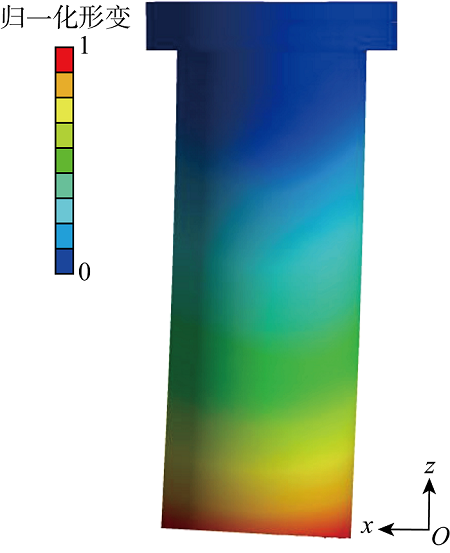
为了分析压紧弹簧松弛对堆芯吊篮固有频率的影响,需要计算压紧弹簧预紧力减少情况下的堆芯吊篮一阶梁式模态频率变化,而模型中针对预紧力的设置通过改变压紧弹簧的刚度获得,压紧弹簧的刚度^[16]可表示为

(6)K=

\frac{4 π E I_{x}}{b^{2} Φ}

(7)I_x=

\frac{1}{12}

B_{1}^{3}

+B₂H³)

(8)Φ=

\frac{Φ_{1} + Φ_{2}}{2}

式中:K为压紧弹簧刚度;E为弹性模量;I_x为压紧弹簧断面对中性轴的惯性矩;Φ为压紧弹簧平均直径.通过在模型中调整压紧弹簧的高度B₁,可获得不同的预紧力.计算压紧弹簧预紧力减少0%、15%、30%、50%时堆芯吊篮一阶梁式模态频率,图3所示为频率10.619 Hz下压紧弹簧预紧力正常时堆芯吊篮组件模态振型,图4所示为压紧弹簧松弛程度与堆芯吊篮一阶梁式固有频率之间的变化关系.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 压紧弹簧预紧力正常时堆芯吊篮组件模态振型

Fig.3 Vibration mode of CSB with normal preload

图4

新窗口打开| 下载原图ZIP| 生成PPT

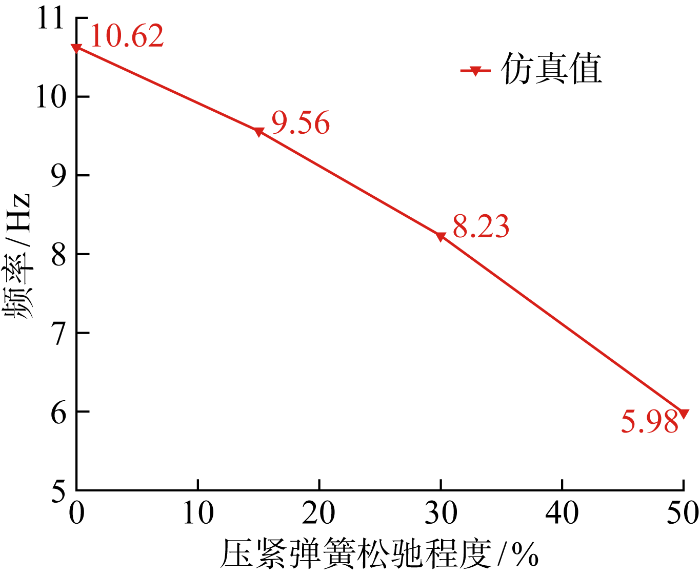
图4 压紧弹簧松弛对堆芯吊篮一阶梁式固有频率的影响

Fig.4 Impact of relaxation of HDS on first-order beam mode frequency of CSB

根据计算结果可知,堆芯吊篮压紧弹簧松弛会对堆芯吊篮一阶梁式模态产生明显影响,当压紧弹簧松弛50%时,堆芯吊篮一阶梁式模态频率下降 4.64 Hz,且随着松弛程度增加,堆芯吊篮一阶梁式模态频率下降幅度也增大.

2 压紧弹簧松弛试验

为了验证仿真结果,并建立压紧弹簧松弛评价模型,在某综合试验台架上开展压紧弹簧松弛试验,以获得压紧弹簧不同松弛程度下的堆芯吊篮振动频率变化趋势.

2.1 试验装置及信号采集系统

所采用的综合试验台由多个回路系统协同工作,包括主系统、压力安全系统、过滤系统、补水系统、设备冷却水系统.主系统采用相同的4台泵对称布置在压力容器的主泵接管上,压力容器体内包括堆芯吊篮、压紧弹簧等组件.

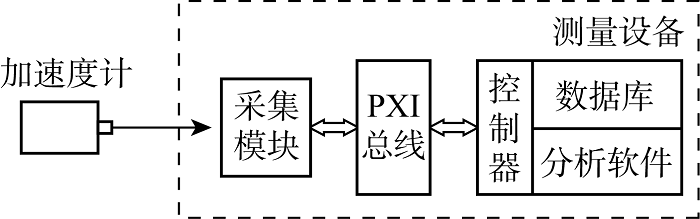
信号采集系统主要包括传感器和测量设备两部分,如图5所示.图中:PXI为面向仪器系统的外围组件互联扩展.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 信号采集系统示意图

Fig.5 Schematic diagram of signal acquisition system

利用5个振动加速度计测量堆芯吊篮4个方向的振动响应,主要参数为如下:型号Kistler 8640;传感器类型为IEPE型;灵敏度(100±5) mV/g;测量范围±50 g;频率响应(1±0.05)~(1±0.05) kHz;防护等级IP68.

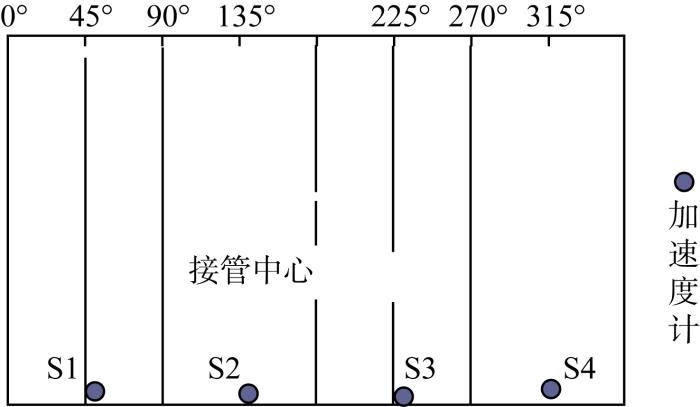
传感器的布置方案如图6所示,在堆芯吊篮外壁面距底部100 mm处,沿径向布置4个防水加速度计S1~S4,环向角度分别为45°(S1)、135°(S2)、225°(S3)、315°(S4),电缆从容器下部的引线孔密封引出.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 传感器布置方案示意图

Fig.6 Schematic diagram of sensor layout

2.2 压紧弹簧试验件

基于图2和式(6)~(8),通过调整高度B₁,获得松弛程度分别为15%、30%和50%的压紧弹簧松弛试验件.如图7所示,为压紧弹簧松弛试验件实物图.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 压紧弹簧松弛试验件实物图

Fig.7 Relaxation test piece of HDS

2.3 试验内容

本试验包括压紧弹簧正常状态试验和压紧弹簧松弛试验.堆芯吊篮压紧弹簧松弛试验内容和顺序如表1所示.

表1 堆芯吊篮压紧弹簧松弛试验内容及顺序

Tab.1 Contents and sequence of HDS relaxation test

试验顺序	试验内容	试验模拟方法
1	压紧弹簧正常状态下堆芯吊篮振动特性试验	正常刚度弹簧
2	不同刚度压紧弹簧堆芯吊篮振动特性试验	压紧弹簧减小15%刚度
3	不同刚度压紧弹簧堆芯吊篮振动特性试验	压紧弹簧减小30%刚度
4	不同刚度压紧弹簧堆芯吊篮振动特性试验	压紧弹簧减小50%刚度

新窗口打开| 下载CSV

2.4 试验结果分析及讨论

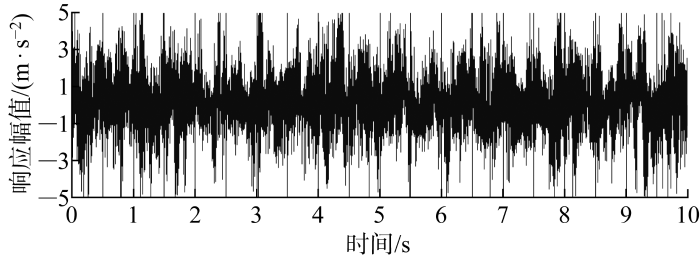
图8所示为S2通道加速度计所测得的压紧弹簧正常状态下堆芯吊篮振动加速度时域响应.由图可见,堆芯吊篮的振动加速度信号存在一定的周期分量,代表信号中包含结构的有效振动信息,但是信号中还夹杂大量由环境干扰造成的毛刺,无法直接从时域波形中分析得到所包含的堆芯吊篮振动信息.因此,基于S1~S4这4个不同方位传感器获得堆芯吊篮振动加速度时域信号,进一步采用谱分析法分别计算S1和S3、S2和S4的互功率谱、相干性和相位差.其中互功率谱能够得到不同传感器信号间相同的特征频率;相干性能够进一步抑制噪声干扰,得到堆芯吊篮的振动频率;相位差能够确定堆芯吊篮的振动形式,以此可分析堆芯吊篮的振动.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 压紧弹簧正常状态下的堆芯吊篮振动加速度时域响应波形

Fig.8 Time domain waveform of vibration acceleration response of CSB under normal condition of HDS

基于此分析方式分别对压紧弹簧不同松弛程度下的堆芯吊篮加速度振动响应进行分析,得到压紧弹簧不同松弛程度下的堆芯吊篮一阶频率变化,并与仿真数据进行对比,如表2和图9所示.

表2 压紧弹簧松弛与堆芯吊篮一阶梁式频率关系

Tab.2 Relaxation degrees of HDS versus first-order beam mode frequencies of CSB

序号	松弛程度/%	堆芯吊篮一阶梁式频率
序号	松弛程度/%	试验值/Hz	仿真值/Hz	误差/%
1	0	10.4	10.62	2.12
2	15	9.4	9.56	1.70
3	30	8.1	8.23	1.60
4	50	6.1	5.98	-1.97

新窗口打开| 下载CSV

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 压紧弹簧松弛与堆芯吊篮一阶梁式频率关系(试验值和仿真值)

Fig.9 HDS relaxation degrees versus beam mode frequency of CSB (test values and simulation values)

由表2和图9可见,试验数据显示随着压紧弹簧松弛程度增加, 堆芯吊篮一阶梁式模态频率明显下降,当压紧弹簧松弛程度达到50%时,模态频率下降4.3 Hz.试验得到的模态频率变化趋势与仿真得到的趋势一致,且仿真结果和试验数据之间的误差最大为2.12%,最小为1.60%,证明了仿真模型的有效性.

3 压紧弹簧劣化评价模型

所建立的压紧弹簧劣化下堆芯吊篮模态分析模型的有效性已经过试验验证.利用仿真模型计算得到压紧弹簧更多松弛程度下的堆芯吊篮一阶梁式模态频率,结合已有的试验数据得到相应拟合值,如表3所示.表中:空白表示不适用.

表3 压紧弹簧松弛时的堆芯吊篮一阶梁式模态频率拟合值

Tab.3 Fitting values of first-order beam mode frequency of CSB with relaxation of HDS

序号	压紧弹簧松弛程度/%	堆芯吊篮一阶梁式频率
序号	压紧弹簧松弛程度/%	仿真值/Hz	试验值/Hz	拟合值/Hz
1	0	10.62	10.4	10.400
2	5	10.31		10.110
3	10	9.95		9.770
4	15	9.56	9.4	9.400
5	20	9.17		9.020
6	30	8.23	8.1	8.100
7	40	7.16		7.115
8	50	5.98	6.1	6.100
9	60	4.76		5.005
10	70	3.39		3.760

新窗口打开| 下载CSV

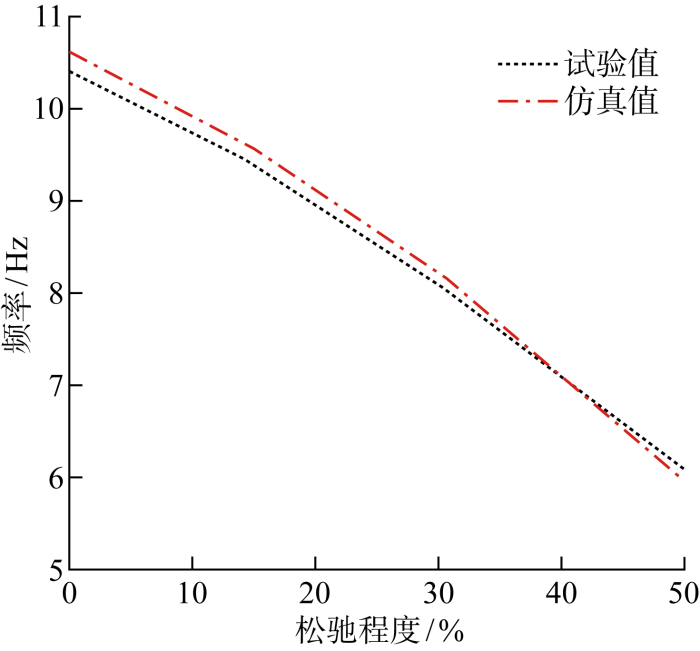
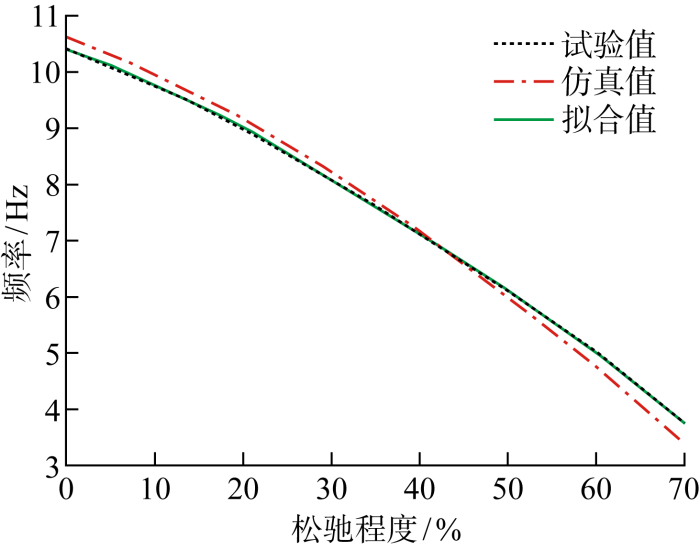
利用试验数据、仿真数据及二者拟合得到的拟合数据绘制曲线图,如图10所示,可见所获得的拟合值与试验值十分吻合.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 压紧弹簧松弛与堆芯吊篮一阶梁式频率关系(试验值、仿真值和拟合值)

Fig.10 HDS relaxation degrees versus beam mode frequencies of CSB (test values, simulation values, and fitted values)

基于所获得的拟合值,利用MATLAB拟合成二次函数式,建立堆芯吊篮一阶模态频率与压紧弹簧松弛程度的定量关系式,作为堆芯吊篮压紧弹簧松弛程度识别的数学模型:

(9)F=a₁D²+a₂D+a₃

式中:a₁~a₃为常系数,其中a₁=-4.497×10^-4,a₂=-6.395×10^-2,a₃=10.437;F为堆芯吊篮一阶模态频率;D为松弛程度.

4 结论

以数值分析与模拟试验相结合的方式开展核反应堆堆芯吊篮压紧弹簧松弛特性研究,主要结论如下:

(1) 采用湿模态法研究反应堆堆芯吊篮组件在压紧弹簧松弛情况下的模态特性变化.有限元计算结果表明,压紧弹簧松弛会造成堆芯吊篮一阶梁式模态下降,且随着松弛程度增加,堆芯吊篮一阶梁式模态频率的下降幅度也增大.当压紧弹簧松弛50%时,堆芯吊篮一阶梁式模态频率下降4.64 Hz.

(2) 开展堆芯吊篮压紧弹簧松弛试验,以验证有限元计算结果的有效性.试验结果表明,随着压紧弹簧松弛程度增加,堆芯吊篮一阶梁式模态频率明显下降,当压紧弹簧松弛程度达到50%时,模态频率下降4.3 Hz,试验得到的模态频率变化趋势与仿真得到的趋势一致,且仿真结果和试验数据之间的误差最大为2.12%,最小为1.60%,证明了仿真模型的有效性.

(3) 基于仿真数据和试验数据建立堆芯吊篮压紧弹簧松弛程度识别的数学模型.利用仿真模型计算得到更多不同压紧弹簧松弛程度下的堆芯吊篮一阶梁式模态频率,结合有限的试验数据获得相应压紧弹簧松弛程度处的拟合值,并进一步拟合得到堆芯吊篮模态频率漂移量与压紧弹簧松弛程度的函数关系式,作为堆芯吊篮压紧弹簧松弛程度的识别模型.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

MALAPLATE

, GAVOILLE

, PAGEOT

, et al.

Assessment of potential swelling of pressurized water reactor internals the Gondole experiment in Osiris reactor

[C]// Fontevraud 9-Contribution of Materials Investigations and Operating Experience to Light Water NPPs’ Safety, Performance and Reliability. Avignon, France: CEA, 2018: cea-02338721.