基于组合边界条件的固体材料热扩散系数测试方法

doi:10.16183/j.cnki.jsjtu.2023.018

基于组合边界条件的固体材料热扩散系数测试方法

陈清华^,¹^,²^,³, 吴佳乐¹, 陆育¹, 季家东¹^,²^,³, 刘萍¹^,²^,³

1.安徽理工大学机械工程学院,安徽淮南 232001

2.安徽理工大学环境友好材料与职业健康研究院, 安徽芜湖 241003

3.安徽理工大学矿山智能装备与技术省重点实验室,安徽淮南 232001

Testing Method for Thermal Diffusivity of Solid Materials Based on Combined Boundary Conditions

CHEN Qinghua^,¹^,²^,³, WU Jiale¹, LU Yu¹, JI Jiadong¹^,²^,³, LIU Ping¹^,²^,³

1. School of Mechanical Engineering, Anhui University of Science and Technology, Huainan 232001, Anhui, China

2. Environmental Friendly Materials and Occupational Health Research Institute, Anhui University of Science and Technology, Wuhu 241003, Anhui, China

3. Key Laboratory of Mine Intelligent Equipment and Technology, Anhui University of Science and Technology, Huainan 232001, Anhui, China

责任编辑: 王一凡

收稿日期: 2023-01-16 修回日期: 2023-04-12 接受日期: 2023-05-22

基金资助:

国家自然科学基金(52175070)
安徽理工大学环境友好材料与职业健康研究院研发专项基金(ALW2021YF12)

Received: 2023-01-16 Revised: 2023-04-12 Accepted: 2023-05-22

作者简介 About authors

陈清华(1978-),教授,从事材料热物性、传热传质学等领域的研究;E-mail:ahhnds@163.com.

摘要

提出了一种组合边界条件下结合传热反问题思想测算固体材料热扩散系数的方法.建立了正问题理论模型,基于有限体积法和交替方向隐式方法的思想利用MATLAB软件对正问题温度场进行数值求解,利用共轭梯度法结合软件编程求解反问题,反演得到材料的热扩散系数.设计了实验方案并搭建了完整的测试系统,利用测试装置对亚克力板(PMMA)、硼硅玻璃(Pyrex7740)、大理石3种材料进行了综合实验,结果表明导热系数测试结果与文献值的最大相对偏差为3.45%,小于5%,验证了测试方法和装置的可行性与准确性.进一步对PMMA热扩散系数实验的不确定度进行了分析,得到扩展不确定度为4.86%,处于较低水平,说明实验数据可靠,测试方法科学.

关键词： 固体材料; 对流边界; 组合边界; 热扩散系数; 传热反问题

Abstract

A method for measuring the thermal diffusivity of solid materials under combined boundary conditions in combination with the idea of inverse heat transfer problem is proposed. Based on the idea of the finite volume method and the alternating direction implicit method, MATLAB software is used to numerically solve the temperature field of the forward problem. The conjugate gradient method in combination with software programming is used to solve the inverse problem, and the thermal diffusion coefficient of the material is obtained by inversion. Based on the test principle, an experimental scheme is designed and a complete test system is built. The structure design, selection, and machining of the device equipment for constructing three types of boundary conditions and collecting temperature data are performed. The main program of each functional module of the software part is programmed and debugged in LabVIEW software. The comprehensive experiments of acrylic plate (PMMA), borosilicate glass (Pyrex7740) and marble are conducted by using the test device. The results show that the maximum relative deviation between the thermal conductivity test results and the literature values is 3.45%, less than 5%, which verifies the feasibility and accuracy of the test method and device. The uncertainty of PMMA thermal diffusion coefficient experiment is further analyzed, and the expanded uncertainty is 4.86%, which is at a low level, indicating that the experimental data are reliable and the test method is scientific.

Keywords： solid materials; convection boundary; combined boundary; thermal diffusion coefficient; inverse heat transfer problem

PDF (5652KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈清华, 吴佳乐, 陆育, 季家东, 刘萍. 基于组合边界条件的固体材料热扩散系数测试方法[J]. 上海交通大学学报, 2024, 58(8): 1201-1210 doi:10.16183/j.cnki.jsjtu.2023.018

CHEN Qinghua, WU Jiale, LU Yu, JI Jiadong, LIU Ping. Testing Method for Thermal Diffusivity of Solid Materials Based on Combined Boundary Conditions[J]. Journal of Shanghai Jiaotong University, 2024, 58(8): 1201-1210 doi:10.16183/j.cnki.jsjtu.2023.018

近年来,随着人们对舒适性要求的提高和材料加工工艺的不断进步,材料性质愈加多样化,对材料热物性测试技术提出更高要求.材料热物性参数为衡量材料能否适应特定传热过程环境需求提供依据,是对特定热传过程进行基础研究、分析计算和工程设计的关键参数^[1],对其进行研究在新材料的研发、能源的有效利用等方面具有重要科学意义^[2].其中热扩散系数作为材料重要的热物性参数之一,其测试方法也一直是研究热点之一.材料热扩散系数的准确测量对非稳态过程的分析研究非常重要,结合比热容和密度可以计算材料的导热系数,进而了解材料的导热特性.目前,材料热扩散系数的测试方法分为稳态法和非稳态法两大类,稳态法因测量周期较长、精度不高、难度较大等局限性,阻碍测量技术的发展.非稳态法在测量上存在较大优势,其中具有代表性的主要有闪光法^[3]、周期热流法^[4]和瞬态平面热源法^[5]等.闪光法自1961年由Parker和Jenkins等提出以来,各国学者和专家都对其进行了深入研究,Hu等^[6]创新了一种双波长闪光拉曼(DFR)映射方法,实现了对悬浮纳米线热扩散率的测量,进一步提高热扩散系数的测量灵敏度;虽然闪光法已被公认为标准方法,但测量条件苛刻、装置复杂、对被测试样预处理要求高,因此更多新的测试方法被提出和研究.于帆等^[7]基于脉冲式平面热源法系统分析和测量了材料导热系数和热扩散系数;平面热源法存在面热源热流密度难以准确给定、侧边绝热条件难以完全实现等问题;Cernuschi等^[8]提出空间解析法,利用红外相机观测试样背面温度的扩散情况,在柱坐标系下推导出热扩散系数的解析解;Dong等^[9]在Cernuschi测量模型的基础上把角度可调的高斯光束作为热源,可以在任何入射角度下根据增长速率求得材料热扩散系数.这些方法对实验设备的精度要求较高,存在局限性.且在实际生产生活中,由于测试环境较复杂,测试结构不稳定等因素,传统测试方法的准确性会大大降低.传热反问题为这类问题提供新的求解方法,并在短时间内被大量学者深入研究和完善,在热物性参数反演领域得到了快速发展和应用.韩雯雯等^[10]在有限元法基础上建立温度场数学模型,利用圆管外壁面可测的有限温度信息同时反演出内壁面温度、近内壁流体温度以及表面传热系数;杨秋足^[11]从傅里叶和热力学基本定律出发,得到2D-FGM板在上边界为对流换热、左右边界为恒温、下边界为绝热或恒温组合作用时平面稳态温度场的分布情况;Mattia等^[12]将共轭梯度法和伴随问题方法相结合对边界热流进行了反演求解,测试系统抗干扰性好;Dai等^[13]将粒子群优化算法应用到传热反问题中,研究发现粒子群优化后的深度神经网络模型可以提高求解复合材料导热系数的精度.现有的热物性参数测试方法基本都需使用价格较为昂贵的专业设备,对测试条件、试样预处理、实验设备精度等均有严格要求,从而限制了其推广和应用.

针对这些问题,本文提出一种实验室内在三类边界条件组合作用下对固体材料热扩散系数进行准确测试的方法,由于组合边界条件较为复杂难以直接求解,所以引入传热反问题相关理论,同时搭建出测试系统实物装置.利用恒温水浴箱在试样下表面构建恒温边界.利用气泵产生的稳定气流在试样上表面构建对流边界.在试样侧壁面包裹绝热材料构建绝热边界.通过MATLAB软件联合仿真求解正问题温度场,基于共轭梯度法进行反问题分析,代入实测温升数据准确反演出亚克力板(PMMA)、大理石和硼硅酸玻璃3种材料的热扩散系数.将反演结果与文献参考值对比验证了测试结果的准确性,通过不确定度分析进一步验证了该方法的可行性和科学性.测试结果满足精度要求,装置结构简单,成本大大降低.

1 热传导正问题数值求解

材料热物性参数的反演需要基于传热学原理,构建理论传热数学模型,推导理论传热公式.从传热的发生方向出发,利用完整的数学模型、定解条件和材料部分已知的热物性参数等,结合分析解析或数值求解方法,对导热微分方程进行求解,从而得到材料内部或表面温度场的分布情况,这种问题称为热传导正问题^[14].

1.1 物理模型

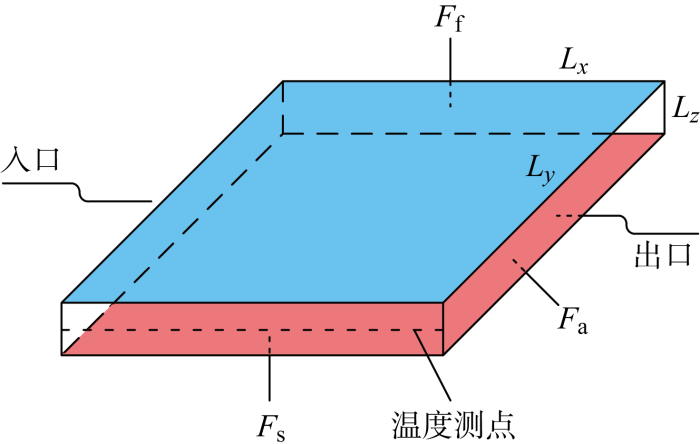
建立的传热三维物理模型如图1所示.假设待测平板的长、宽、高分别L_x、L_y和L_z,其中蓝色面F_f为空气对流边界,红色面F_s为恒温边界,其余4个外壁面F_a为绝热边界.流体以均匀速度和初始温度从试样左侧进入流场域,从右侧流出.在试样侧壁中线位置均匀布置温度测点.为简化求解方程提高求解精度,假设试样内部热物性参数在一定的温度范围内为一个定值,且试样外表面平整光滑,层间接触良好,流场域空气速度和温度分布均匀.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 测试方法的传热物理模型

Fig.1 Physical model of heat transfer for test method

1.2 数学模型

基于上述物理模型,假设试样初始温度为T₀,试样下表面为恒温热源,加热时间为t.根据热力学第一定律和傅里叶定律建立的常物性、无内热源的三维非稳态导热微分方程^[15]为

(1)

\frac{\partial T}{\partial t}

\frac{\partial}{\partial x} (α \frac{\partial T}{\partial x})

\frac{\partial}{\partial y} (α \frac{\partial T}{\partial y})

\frac{\partial}{\partial z} (α \frac{\partial T}{\partial z})

式中:α为试样热扩散系数,为一个常数.

初始条件:

(2)T=T₀, t=0

边界条件:

(3)

\begin{array}{l} {T|}_{z = 0} = T (a) \\ {- λ (\frac{\partial T}{\partial x})|}_{x = 0, L_{x}} = 0 \\ {- λ (\frac{\partial T}{\partial y})|}_{y = 0, L_{y}} = 0 \\ {- λ (\frac{\partial T}{\partial z})|}_{z = L_{z}} = h (T_{w} - T_{f}) \end{array}\}

式中:T(a)为恒温水浴温度;T_f为空气流体温度;T_w为试样上表面温度;h为试样上表面与流体间的对流换热系数,为常数;λ为材料导热系数.

根据上述传热数学模型,由于边界条件较为复杂,难以直接进行求解,所以选择数值解法结合计算机编程计算得到试样内及测点位置任意时刻t的温度分布情况.数值求解过程中,采用在流体与换热问题中广泛运用的有限体积法对计算域均匀划分网格,选择中心差分格式对空间微分项进行离散,选择全隐式计算时间积分,得到离散方程为

(4)a_PT_P=a_ET_E+a_WT_W+a_NT_N+a_ST_S+a_FT_F+a_BT_B+b

a_E=

\frac{Δ y Δ z}{{(δ x)}_{e} / k_{e}}

, a_W=

\frac{Δ y Δ z}{{(δ x)}_{w} / k_{w}}

a_N=

\frac{Δ x Δ z}{{(δ y)}_{n} / k_{n}}

, a_S=

\frac{Δ x Δ z}{{(δ y)}_{s} / k_{s}}

a_F=

\frac{Δ x Δ y}{{(δ z)}_{f} / k_{f}}

, a_B=

\frac{Δ x Δ y}{{(δ z)}_{b} / k_{b}}

a_P=a_E+a_W+a_N+a_S+a_F+a_B+

a_{P}^{0}

a_{P}^{0}

\frac{{(ρ c)}_{P} Δ x Δ y Δ z}{Δ t}

, b=

a_{P}^{0} T_{P}^{0}

式中:P表示内点法中心节点;E、W、N、S、F、B分别为节点P的6个邻近节点;e、w、n、s、f、b表示两个控制体间的界面位置;Δx、Δy、Δz代表控制容积沿x、y、z方向的边界长度;(δx)_e、(δx)_w、(δy)_n、(δy)_s、(δz)_f、(δz)_b 分别表示节点P与6个邻近节点间距离;k表示每个单元网格的导热系数.通过上述数值离散化将计算域内各节点的导热微分方程转化成线性方程组.针对三维非稳态导热问题,为了节省内存同时进行高效求解,选择交替方向隐式(ADI)方法^[16],其求解思路为:先在某一方向例如x方向用隐式格式求解,此时将y和z方向按照显式格式处理,然后在y和z方向上分别利用隐式方法再进行求解,将三维问题转换为3个一维的隐式格式问题,通过三对角矩阵算法(TDMA)对所有一维隐式问题直接求解.本文选择ADI方法中的Brian ADI格式求解离散方程,该格式是一种无条件收敛的稳定格式,其在各方向上用隐式格式求解时的时间间隔为Δt/2,可以表示为

(5)

\begin{array}{l} \frac{U_{i, j, k} - T_{i, j, k}^{n}}{Δ t / 2} = \\ α (δ_{x}^{2} U_{i, j, k} + δ_{y}^{2} T_{i, j, k}^{n} + δ_{z}^{2} T_{i, j, k}^{n}) \\ \frac{V_{i, j, k} - T_{i, j, k}^{n}}{Δ t / 2} = \\ α (δ_{x}^{2} U_{i, j, k} + δ_{y}^{2} V_{i, j, k}^{n} + δ_{z}^{2} T_{i, j, k}^{n}) \\ \frac{T_{i, j, k}^{n + 1} - V_{i, j, k}}{Δ t / 2} = \\ α (δ_{x}^{2} U_{i, j, k} + δ_{y}^{2} V_{i, j, k}^{n} + δ_{z}^{2} T_{i, j, k}^{n + 1}) \end{array}\}

式中:U_i_,_j_,_k和V_i_,_j_,_k表示Δt/2时刻两个中间温度值; $δ_{x}^{2}$ , $δ_{y}^{2}$ , $δ_{z}^{2}$ 分别表示x、 y、 z方向上的温度值;U_i_,_j_,_k用来计算三步中的 $δ_{x}^{2}$ ;V_i_,_j_,_k用来计算后两步中的 $δ_{y}^{2}$ ; $T_{i, j, k}^{n}$ 表示上一时刻整体温度; $T_{i, j, k}^{n + 1}$ 表示下一时刻整体温度.针对测试方法数学模型,根据有限体积法和ADI方法的基本理论,通过 MATLAB 软件获取试样温度分布情况.

2 热传导反问题模型构建

在组合边界条件下固体材料热物性参数反演问题中,以图1中温度测点的实测温度变化为观测量,来反演固体材料的热扩散系数数值,是一个最优化问题.为了保证较好的抗干扰性和精确度,本文使用共轭梯度算法^[17]求解传热反问题,建立目标函数如下:

(6)J(X)=

\sum_{i = 1}^{N} {(T_{i} (X) - T_{i}^{*})}^{2}

式中:T_i(X)为进行正问题求解得到的第i个温度测点的仿真温度值; $T_{i}^{*}$ 为第i个测点的实测温度值;N为测点数量;X为待反演参数.

共轭梯度法的迭代公式可表示为

(7)Xⁿ⁺¹=Xⁿ+αⁿdⁿ

式中:Xⁿ为第n次待反演参数的估计值;αⁿ为迭代步长;dⁿ为搜索方向,

(8)dⁿ=-ΔJ(Xⁿ)+βⁿ^-1dⁿ^-1

βⁿ为共轭系数,

(9)βⁿ^-1=

\frac{Δ J (X^{n}) Δ J^{T} (X^{n})}{Δ J (X^{n - 1}) Δ J^{T} (X^{n - 1})}

, β ⁰=0

设X_i为待反演的未知参数,则目标函数的梯度向量ΔJ可表示为

(10)ΔJ=

[\frac{\partial J}{\partial X_{1}} \frac{\partial J}{\partial X_{2}} \dots \frac{\partial J}{\partial X_{M}}]

式中: $\frac{\partial J}{\partial X_{N}}$ =2 $\sum_{i = 1}^{N}$ [(T_i(X)-T_i) $\frac{\partial T_{i} (X)}{\partial X_{n}}$ ](n=1, 2, …, M).

对目标函数J(Xⁿ+αⁿdⁿ)进行优化,得到迭代步长αⁿ:

(11)αⁿ=

\frac{\sum_{i = 1}^{N} (T_{i} (X) - T_{i}^{*}) Δ T_{i} d^{n}}{\sum_{i = 1}^{N} {(Δ T_{i} d^{n})}^{2}}

式中:ΔT_i为计算温度函数的梯度向量,可利用差分法近似计算得到,

(12)ΔT_i=

[\frac{\partial T_{i}}{\partial X_{1}} \frac{\partial T_{i}}{\partial X_{2}} \dots \frac{\partial T_{i}}{\partial X_{M}}]

实际测量中由于传感器放置、人工测量不准确等因素会产生误差.因此在算法程序的迭代计算过程中,通过在实测的温度数据上添加一个随机的测量误差的方式提高反演准确度,则实测温度 $T_{i}^{*}$ 可表示为

(13)

T_{i}^{*}

=T_e_i+σω

式中:T_e_i为第i个测点的准确测量温度;ω为一个在-1和1之间均匀变化的随机变量;σ为测量误差.得到迭代收敛条件为

(14)J(X)=

\sum_{i = 1}^{N} {(T_{i} (X) - T_{i}^{*})}^{2}

<Nσ²

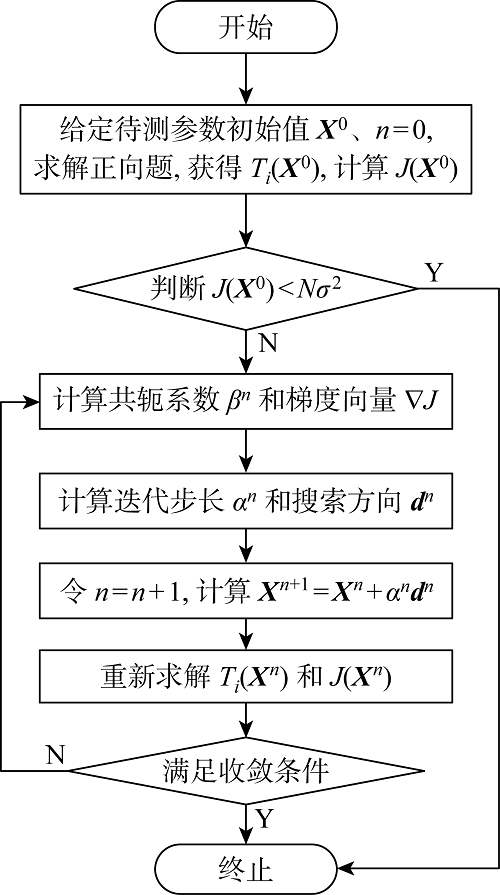
采用共轭梯度法求解传热反问题的反演流程如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 共轭梯度法求解流程图

Fig.2 Flow chart of conjugate gradient method

借助计算机编程求解传热反问题反演得到待测材料的热扩散系数α,再根据公式λ=αρc可计算材料的导热系数.其中:ρ为材料的密度;c为材料的比热容.

3 实验装置设计

测试系统如图3所示,主要由恒温水浴单元、试样固定单元和数据采集单元3个部分构成.实验选用型号为HH-601A的恒温水浴箱提供恒温热源,其加热功率为 2 kW,控温精度为±0.05 ℃,显示精度为0.01 ℃,利用其内循环功能对试样底部恒温加热,能够有效保证恒温边界条件,为测试提供稳定的恒温环境.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 测试实验平台

Fig.3 Test experiment platform

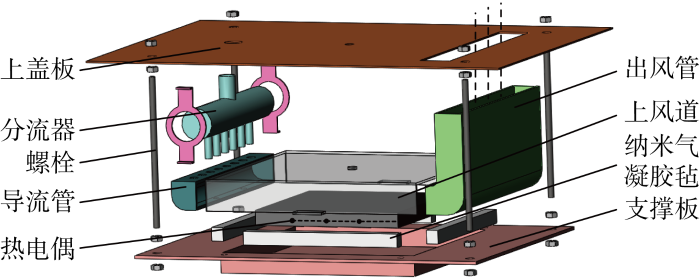
为解决试样固定承载、上表面对流边界建立以及传感器定位等关键性问题,设计了一种试样固定单元,其结构示意图如图4所示,主要由上盖板、导流管、出风管、上风道和支撑板等组成.支撑板底部镂空焊接厚度1 mm的紫铜板加工成试样承载容器.待测试样导热系数远小于紫铜导热系数,因此试样与紫铜板之间的接触热阻忽略不计.实验选用型号ACO-001A的气泵提供气源,其功率为25 W,实际排气量为16 L/min.气体经过分流器和导流管均匀流至测试区域,从左向右掠过试样上表面以建立对流边界,之后从出风管道流出,构造一个稳定的对流传热环境.测试区域外部均包裹有绝热材料,避免气体在传输过程中与外界环境发生热交换造成热量损失.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 试样固定单元示意图

Fig.4 Schematic diagram of sample fixing unit

数据采集单元如图5所示,包括硬件和软件两个部分,二者相辅相成,共同发挥作用,其中硬件部分主要由温度传感器、数据采集模块以及计算机装置等组成.为避免探头和导线对流场域的影响,选择型号为cwx-2的超细K型热电偶进行测温,其探头直径为0.2 mm,测温范围为-20~200 ℃,测温精度为0.1 ℃.数据采集模块选用泓格公司生产的I-7000系列中的i-7018,该模块为16位10 Hz、8路差动热电偶输入模块.运行时,使用稳压开关电源对其供电,采集的温度信号经转换后通过UT-890a双向USB转RS-485接口转换器传输至上位机中由LabVIEW软件^[18]开发的数据采集界面.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 数据采集单元示意图

Fig.5 Schematic diagram of data acquisition unit

4 实验及结果分析

4.1 正问题数值模拟结果及分析

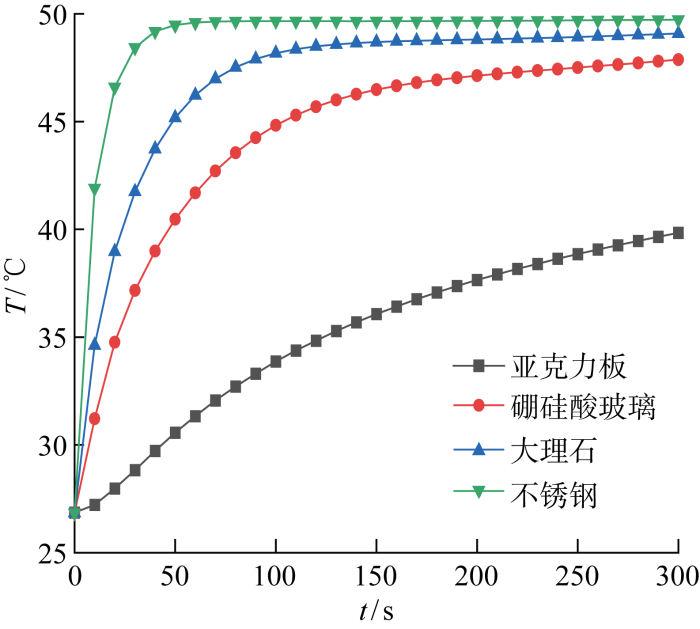
热传导正问题计算过程较为复杂且计算量较大,需要结合计算机编程进行求解.针对三维热传导正问题以式(1)为基础通过 MATLAB求解代数方程组,获取材料温度场分布情况.为了反映正问题模型对不同材料的普适性,分别选用导热系数为0.193 W/(m·K)的亚克力板、1.1 W/(m·K)的硼硅酸玻璃、2.8 W/(m·K)的大理石以及16 W/(m·K) 的304不锈钢^[18-19] 4种导热性能差异较大的材料进行正问题数值求解.试样尺寸为100 mm×100 mm×10 mm,初始温度设置为24 ℃,恒温水浴温度为50 ℃,时间步长为1 s,空气温度为26 ℃,试样上表面对流换热系数为32.4 W/(m·K).在试样侧壁与绝热材料接触面沿长度方向均匀布置5个测点,取5个监测点温度的算术平均值为测点最终仿真计算温升,得到4种材料温升曲线如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 温升曲线对比

Fig.6 Comparison of temperature rise curves

观察图6发现,材料温升速度随导热系数的增大逐渐增大,其中导热系数最大的304不锈钢测点温升最快,在50 s左右基本达到一个稳定的状态,同时温升过快,导致温度传感器采集的有效数据较少,不能完全保证计算精度;大理石和硼硅酸玻璃测点温升速度适宜,能够获得多组具有较大温度梯度的较为理想的温升数值;亚克力板测点温升最慢,需要较长时间温度才能稳定,导致温升数据与时间的关联性降低,为避免影响计算精度,需选取有效测试时间内的温升数据进行反演计算.

不同材料的测点温升整体都呈现随时间先上升后逐渐趋于稳定的趋势,但上升速度则存在较大差异,因此可根据测点温度随时间的变化反演计算材料的热扩散系数.

4.2 标准试样实验验证

本文选择PMMA材料为标准试样进行实验验证.试样尺寸为100 mm×100 mm×10 mm,通过称重法计算得到密度为1 170 kg/m³,通过混合水浴法得到比热容为 1 380 J/(kg·K).初始温度为环境温度24 ℃,空气温度为26 ℃,对流换热系数为32.364 W/(m²·K),水浴温度为50 ℃.测试系统采集速率为1次/s,采集精度为0.1 ℃.在试样侧壁均匀布置5个温度测点,记为测点1、测点2、测点3、测点4和测点5,取5个测点的平均温升作为最终实测温升数据作为传热反问题的输入条件,由反问题程序反演出试样热扩散系数,再通过公式λ=αρc计算得到材料的导热系数.为了判别实验过程中温度这个因素对测试结果的影响效果,进一步计算导热系数的相对偏差.

PMMA材料实验和热物性参数计算结果如表1所示.可以看出,由于测点1和测点5离边界位置较近,容易受到空气流场、位置误差以及边界热交换的影响,导致其温升数据存在误差,所以取5个测点温度的平均值为最终实测温度,减小温度不均匀性对反演精度的影响.在有效测试时间内PMMA热物性参数的反演结果受温度的影响作用基本可以忽略不计,即可近似将其热物性参数视为一个稳定的常数.其中导热系数的最大相对误差为120 s时刻的3.66%,在测试标准允许的偏差范围5%以内,说明实验测量的温升数据是有效的.取多组热扩散系数反演结果的平均值为最终测试结果,即标准试样在测试时间内的热扩散系数为1.186×10^-7m²/s,导热系数为 0.191 6 W/(m·K),与文献[19-20]中参考值的相对误差为1.34%,说明该测试方法和装置具有可行性和较高的准确性.

表1 PMMA热扩散系数计算结果

Tab.1 Calculation results of thermal diffusion coefficient of PMMA

t/s	T/℃					α×10⁷/ (m²·s^-1)	λ/ [W·(m·K)^-1]	Δλ/%
t/s	测点1	测点2	测点3	测点4	测点5	α×10⁷/ (m²·s^-1)	λ/ [W·(m·K)^-1]	Δλ/%
100	29.0	29.4	29.8	30.3	30.9	1.168	0.188 6	1.46
120	30.0	30.6	30.9	31.5	32.3	1.229	0.198 4	3.66
140	31.1	31.8	32.1	32.7	33.5	1.214	0.196 0	2.40
160	32.1	32.8	33.2	33.7	34.5	1.206	0.194 7	1.72
180	33.1	33.7	34.2	34.7	35.4	1.192	0.192 5	0.57
200	33.9	34.6	35.1	35.5	36.2	1.163	0.187 8	1.88
220	34.6	35.4	35.8	36.3	37.1	1.166	0.188 3	1.62
240	35.3	36.1	36.5	37.0	37.7	1.155	0.186 5	2.56
平均值						1.186	0.191 6

新窗口打开| 下载CSV

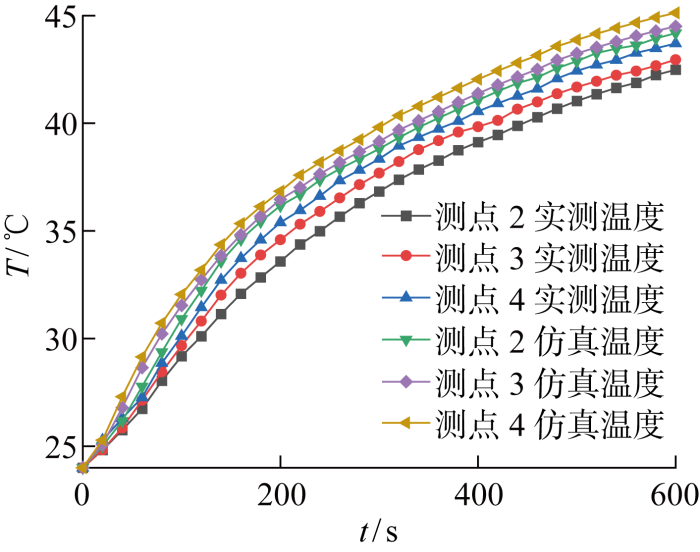
为验证正问题模型的可靠性,仿真求解传热正问题得到标准试样3个监测点2、3、4的温度变化情况,并与实际测量得到的3个监测点温度变化情况进行对比,结果如图7所示.由图可见,PMMA材料的仿真计算温升与实测温升曲线上升趋势基本吻合,计算得到两者之间最大相对误差为5.10%,且在100~250 s内仿真与实测温升最大相对误差不超过4.74%,吻合度较高,证明本测试方法的正问题数学模型是可靠的.由于本装置使用纳米气凝胶毡对试样侧壁面进行绝热处理,随着试样内部热量增加,有一小部分热量会传递到绝热材料中,且空气流场域难以完全实现表面绝热和底部密封,造成一定热损失,所以实测温度稍低于仿真计算温度.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 亚克力板实测温升与仿真温升曲线对比

Fig.7 Comparison of the measured and simulated temperature rise curves of acrylic plate

4.3 综合实验分析

为探究本测试方法对不同材料的检测精度,分别选择大理石和硼硅酸玻璃(Pyrex7740)材料作为对比试样在相同条件下进行实验.其中大理石的尺寸为100 mm×100 mm×17 mm,密度为2 634.2 kg/m³,比热容为816.9 J/(kg·K);Pyrex7740的尺寸为100 mm×100 mm×10 mm,密度为2 250 kg/m³,比热容为740.2 J/(kg·K).在试样侧壁面均匀布置3个温度测点,测试结果分别如表2和表3所示.

表2 大理石材料测试结果

Tab.2 Test results of marble material

t/s	T/℃			α×10⁷/ (m²·s^-1)	λ/[W· (m·K)^-1]	Δλ/ %
t/s	测点1	测点2	测点3	α×10⁷/ (m²·s^-1)	λ/[W· (m·K)^-1]	Δλ/ %
24	29.9	30.4	31.1	13.830	2.976	4.53
32	32.0	32.6	33.2	13.595	2.925	2.74
40	33.6	34.2	34.7	13.386	2.881	1.19
48	35.0	35.6	36.1	13.289	2.860	0.46
56	36.1	36.7	37.2	13.135	2.826	0.74
64	37.1	37.7	38.2	13.036	2.805	1.48
68	37.6	38.2	38.6	12.661	2.724	4.32
76	38.4	39.9	39.5	12.934	2.783	2.25
平均值				13.228	2.847

新窗口打开| 下载CSV

表3 Pyrex7740材料测试结果

Tab.3 Test results of Pyrex7740 material

t/s	T/℃			α×10⁷/ (m²·s^-1)	λ/[W· (m·K)^-1]	Δλ/ %
t/s	测点1	测点2	测点3	α×10⁷/ (m²·s^-1)	λ/[W· (m·K)^-1]	Δλ/ %
26	28.6	28.7	28.9	6.943	1.181	3.87
30	30.1	30.3	30.5	6.765	1.151	1.23
34	31.3	31.5	31.9	6.646	1.158	1.85
38	32.4	32.7	33.1	6.710	1.147	0.88
42	33.5	33.8	34.2	6.649	1.131	0.53
46	34.4	34.7	35.2	6.624	1.127	0.88
50	35.3	35.6	36.1	6.639	1.114	2.02
54	36.2	36.4	36.8	6.545	1.111	2.29
平均值				6.679	1.137

新窗口打开| 下载CSV

由表2和表3可知,开始时刻测点温升较慢且容易受到初始温度场不均匀的影响,造成计算结果有较大的随机性.当有效温升较小或较大时,热扩散系数反演结果会在参考值附近区间范围内出现上下波动.大理石材料导热系数的最大相对误差为 24 s 时的4.53%,硼硅酸玻璃材料导热系数的最大相对误差为26 s时的3.87%,均小于5%,符合测试标准,说明实测数据较为可靠,该测试方法和装置在测量导热性能有差异的材料时仍有较高的准确性.

为进一步检验测试结果的可重复性和稳定性,分别对3种材料在相同条件下进行3次实验,利用实验数据反演热扩散系数,对比3次实验的测试结果分别如图8所示.由图8可以看出,PMMA相较于大理石和Pyrex7740材料来说,各时刻的测试结果变化趋势更稳定.大理石的测试结果变化幅度更明显,出现异常点的个数也最多.实际实验中各种不确定因素的影响,因此在有效测试时间内3次实验的测试结果均出现在文献参考值^[19-20]附近上下波动的情况,但整体偏离幅度都不大,基本保持稳定,整体计算准确.为保证测试结果的精确性,舍去异常点的计算值,取3次实验反演的热扩散系数的平均值作为最终实验测试结果,计算材料的导热系数以及与文献参考值之间的相对误差,结果如表4所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 3种材料热扩散系数重复性测试结果

Fig.8 Repeatability test of thermal diffusion coefficients of three materials

表4 3种材料对比结果

Tab.4 Comparison of three materials

材料	ρ/(kg·m^-3)	c/[J·(kg·℃)^-1]	α×10⁷/(m²·s^-1)	λ/[W· (m·K) ^-1]		Δλ/%
材料	ρ/(kg·m^-3)	c/[J·(kg·℃)^-1]	α×10⁷/(m²·s^-1)	计算值	文献值^[19-20]	Δλ/%
PMMA	1 170	1 380	1.193	0.193	0.194	0.72
Pyrex7740	2 250	740.2	6.833	1.138	1.1	3.45
大理石	2 634.2	816.9	13.205	2.842	2.8	1.50

新窗口打开| 下载CSV

由表4可以看出,3种材料中Pyrex7740的导热系数与文献参考值的相对误差最大,为3.45%,PMMA的相对误差最小,为0.72%,均在允许的误差范围5%以内,符合测试标准,说明本测试方法和实验装置具有较高的可靠性,且在测量导热系数较小的固体材料时精度更高.

4.4 系统热物性测试不确定度分析

不确定度用来描述被测量值的分散程度,在一定程度上可以直接表明试验结果的可信赖程度.以PMMA材料为研究对象,对其热扩散系数的测试进行不确定度分析.

4.4.1 标准不确定度A类评定

针对PMMA材料,在相同实验条件下对同一试样重复进行10次实验,数据代入MATLAB程序中反演10组热扩散系数的数值,计算得到热扩散系数的A类标准不确定度,结果如表5所示.

表5 重复性实验测试结果

Tab.5 Results of repeatability test

实验次数	A类标准不确定度	α×10⁷/ (m²·s^-1)	残差	残差平方
1	4.825×10^-3	1.203	0.001 4	1.96×10^-6
2		1.231	0.029 4	8.64×10^-4
3		1.217	0.015 4	2.37×10^-4
4		1.184	-0.017 6	3.1×10^-4
5		1.190	-0.011 6	1.35×10^-4
6		1.205	0.003 4	1.16×10^-5
7		1.212	0.010 4	1.08×10^-4
8		1.198	-0.003 6	1.3×10^-5
9		1.184	-0.017 6	3.1×10^-4
10		1.192	-0.009 6	9.22×10^-5

新窗口打开| 下载CSV

4.4.2 标准不确定度B类评定

考虑本测试方法的数学模型可知,测点温度、测试时间、试样尺寸、测点布置位置、热源温度、初始温度、空气流量和空气温度等都会影响试样热扩散系数的测定,因此分别从这些影响因素出发进行不确定度分析.

(1) 时间引入的不确定度.试验中,由于时间的延迟或提前,造成数据的记载出现一定的误差.本测试装置要求满足时间精度在2%以内的需求,包含因子μ=2,所以由时间引入的标准不确定度为

u(t)=0.01 s

(2) 温度引入的不确定度.本测试装置选用的HH-601A恒温水浴箱实现精度等级为0.01,控温精度为±0.03 ℃,即半宽度γ=0.03,均匀分布的包含因子μ= $\sqrt{3}$ ,得到标准不确定度为

u(T₁)=

\frac{γ}{μ}

=0.017 ℃

测试装置中选择K型细丝热电偶传感器进行测温,根据产品说明书显示其引入的扩展不确定度U(T₂)=0.02 ℃,包含因子μ=2,计算得到标准不确定度为

u(T₂)=

\frac{U (T_{2})}{μ}

=0.01 ℃

两个不确定度分量相互独立,因此由温度测定引入的标准不确定度为

u(T)=

\sqrt{u (T_{1})^{2} + u (T_{2})^{2}}

=0.019 723 ℃

(3) 数据采集模块引入的不确定度.本测试系统使用的i-7018数据采集模块精度为0.1%,由产品手册可知测量电压上限为20 V,服从均匀分布,包含因子μ= $\sqrt{3}$ ,计算得到标准不确定度为

u(c)=

\frac{U (c)}{μ}

=0.012 V

(4) 试样尺寸和测点位置引入的不确定度.试样尺寸以及测点位置的确定选择测量范围为0~150 mm,分度值为0.02 mm的游标卡尺通过人工测量确定,由文献[21]可知所用的游标卡尺的不确定度为0.02 mm,服从两点分布原则,即包含因子k'=1,则u(δ₁)=0.02 mm,游标卡尺的扩展不确定度 U(δ₂) 为3×10^-4 mm,包含因子μ=3,计算得到标准不确定度为

u(δ₂)=

\frac{U (δ_{2})}{μ}

=1×10^-4 mm

因此计算得到试样厚度引入的标准不确定度为

u(δ)=

\sqrt{u^{2} (δ_{1}) + u^{2} (δ_{2})}

=0.02 mm

(5) 空气流量引入的不确定度.根据产品说明书可知实验选用的气泵稳压精度为0.003 MPa,包含因子μ=2,引入的标准不确定度为

u(f)=1.5×10^-3 MPa

4.4.3 合成不确定度和扩展不确定度评定

待测量的求解受到若干个其他输入量的影响时,可将各不确定分量按照A类评定和B类评定两种方法评估的不确定度进行合成获得合成不确定度u_c(y)来表征对测试结果的影响^[22],可表示为

u_{c}^{2}

(y)=

\sum_{q = 1}^{M}

u²(x_i)+

\sum_{q = 1}^{N} {(\frac{\partial f}{\partial x_{i}})}^{2}

u²(x_q)

其中: $\frac{\partial f}{\partial x_{q}}$ 表示各不确定分量的敏感系数;q表示不确定来源的序号.通过MATLAB软件拟合计算得到材料热扩散系数的合成不确定度为

u_{c}^{2}

(α)=

u_{α}^{2}

\sum_{m = 1}^{3} c_{m}^{2} u_{m}^{2}

=5.887×10^-4

u_c(α)=

\sqrt{u_{c} (α)}

=0.024 3

将合成不确定度u_c(y)与包含因子k相乘得到扩展不确定度U,本文取包含因子μ=2,则得到扩展不确定度为

U₉₅=μu_c(α)=4.86%

计算得到亚克力板热扩散系数的合成不确定度为2.43%,扩展不确定度为4.86%.表明不确定度处于较低的水平,实验数据比较可靠,测试系统与测试方法科学.从A类不确定度评定可以看出,实验重复次数越多,测试结果准确性更高.从B类不确定度评定中可以发现,主要影响因素为试样尺寸和温度引入的不确定度,其次是时间引入的不确定度.因此实验中应多次测量试样的尺寸以及测点位置,尽量避免人为误差,同时应严格控制环境温度,提高测试精度.

5 结论

(1) 组合边界条件下结合传热反问题算法估计固体材料的热扩散系数在原理和技术上具有可行性.对比分析标准试样仿真温升与实际测量温升,发现两者之间最大相对误差为5.1%,证明本测试方法的正问题数学模型是可靠的.

(2) 利用测试系统分别对PMMA、大理石和Pyrex7740这3种材料进行了综合实验,结果表明:反演结果最大相对误差为3.45%,小于5%,进一步说明了本测试方法和装置的准确性,且在测量导热系数较小的固体材料时精度更高.

(3) 对PMMA热扩散系数反演实验进行了不确定度分析,得到扩展不确定度为4.86%,处于较低水平,说明实验数据比较可靠,测试系统与方法科学.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

姚彧敏, 李红, 刘正启, 等.

高导热碳/碳复合材料微观结构及导热性能

[J]. 材料工程, 2020, 48(11): 155-161.

DOI:10.11868/j.issn.1001-4381.2019.000250 [本文引用: 1]

采用国产沥青基碳纤维与中间相沥青制备多孔碳/碳（C/C）复合材料，通过化学气相渗透法（CVI）与前驱体浸渍裂解法（PIP）复合工艺增密，经不同温度高温热处理（HTT）后制备单向C/C复合材料和两向正交C/C复合材料。利用SEM，XRD对不同温度热处理的材料进行微观结构分析，并结合导热机理，分析材料导热性能。结果表明：2300℃热处理后，高导热C/C复合材料结构致密，单向C/C复合材料X向（平行于碳纤维轴向）、两向正交C/C复合材料X向、Y向表现出优异的导热性能；3000℃热处理后，C/C复合材料石墨片层结构明显，石墨化度提高了18.84%，微晶尺寸增大，导热性能进一步提高。两向正交C/C复合材料X向、Y向导热系数可由单向C/C复合材料X向、Z向导热系数计算推导。

YAO

Yumin

, LI

Hong

, LIU

Zhengqi

, et al.

Microstructure and thermal conductivity of high thermal conductivity carbon/carbon composites

[J]. Journal of Materials Engineering, 2020, 48(11): 155-161.

DOI:10.11868/j.issn.1001-4381.2019.000250 [本文引用: 1]

Porous carbon/carbon (C/C) composites prepared by pitch-based carbon fiber and mesophase pitch were densified by chemical vapor infiltration (CVI) and precursor impregnation process (PIP). After different heat temperature treatment (HTT), the unidirectional C/C composites and bidirectional C/C composites were obtained. The microstructure of C/C composites was investigated by SEM, XRD, and the thermal conductivity was analyzed based on the thermal conductivity mechanism. The results show that unidirectional C/C composites and bidirectional C/C composites have dense structures and excellent thermal conductivity along the fiber axis. After 3000 ℃ treatment, the structure of graphite flat layers become more distinct and the graphitization degree is increased by 18.84%, leading to higher thermal conductivity. Furthermore, the thermal conductivity in X direction and Y direction of the bidirectional C/C composites can be calculated from that of unidirectional C/C composites in X direction and Z direction.

[2]

PIASECKA

Correlations for flow boiling heat transfer in minichannels with various orientations

[J]. International Journal of Heat and Mass Transfer, 2015, 81: 114-121.