带月池驳船式浮式风力机水动力性能

doi:10.16183/j.cnki.jsjtu.2022.521

带月池驳船式浮式风力机水动力性能

陈易人¹^,², 姚靳羽¹^,², 李明轩¹^,², 张新曙^,¹^,²

1.上海交通大学海洋工程国家重点实验室

2.高新船舶与深海开发装备协同创新中心,上海 200240

Hydrodynamic Performance of a Barge-Type Floating Offshore Wind Turbine with Moonpool

CHEN Yiren¹^,², YAO Jinyu¹^,², LI Mingxuan¹^,², ZHANG Xinshu^,¹^,²

1. State Key Laboratory of Ocean Engineering

2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 张新曙,研究员,博士生导师,电话(Tel.):021-34208359;E-mail:xinshuz@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-12-16 修回日期: 2023-04-13 接受日期: 2023-05-16

基金资助:

国家自然科学基金(52171269)
上海交通大学深蓝计划(SL2021PT205)

Received: 2022-12-16 Revised: 2023-04-13 Accepted: 2023-05-16

作者简介 About authors

陈易人(1997-),硕士,从事浮式风力机水动力性能研究及系泊设计.

摘要

参考Ideol-Floatgen相关设计,对带月池驳船式浮式风力机进行频域水动力性能研究,考虑了月池黏性阻尼的修正.首先对月池的共振模态进行分析,计算风力机在规则波下的水动力系数与不规则波下运动响应谱,并结合 DNV 相关规范对风力机的安全性进行了评估.结果表明,在作业工况与生存工况下,浮式风力机的动态纵倾与机舱加速度均符合安全性要求.通过对驳船式浮式风力机运动与月池共振的耦合作用的研究,发现风力机的运动会引起月池活塞共振频率的偏移与活塞共振幅值的减小,晃荡共振的频率基本不受影响,但一阶晃荡共振的幅值会增大.与无月池驳船式浮式风力机相比,月池可以降低风力机整体的运动响应,提升风力机整体的水动力性能.对浮式风力机驳船式平台的边长、月池边长与平台吃水进行参数化分析,将风力机的纵荡、垂荡、纵摇响应均方根(RMS)值与机舱加速度响应RMS值作为对比的指标,发现平台边长的增加可以有效降低风力机在作业工况与生存工况下的4项响应RMS值;月池边长的增加可以大幅降低平台生存工况下的4项响应RMS值;平台吃水的增加可以显著降低风力机在作业工况下的4项响应RMS值,并提高生存工况下的垂荡与纵摇响应RMS值.

关键词： 驳船式浮式风力机; 动力响应; 月池; 晃荡模态

Abstract

The hydrodynamic performance of a barge-type floating offshore wind turbine (FOWT) with a moonpool is studied in frequency domain with reference to the Ideol-Floatgen design. The correction of the viscous damping of the moonpool is considered. First, the resonance modes of the moonpool are analyzed. Then, the hydrodynamic coefficients of the FOWT under regular waves and the motion responses under irregular waves are investigated. Finally, the safety of the FOWT is verified with respect to the DNV standards. The results show that the dynamic pitch and nacelle acceleration of the barge-type FOWT meet the safety requirements under both operating and survival conditions. The investigation of the coupling effects of the platform motion and the moonpool resonance shows that the motion of the platform will cause the shift of the piston mode frequency of the moonpool and the reduction of the piston mode response amplitude, the frequency of the sloshing mode is basically unaffected, but the response amplitude of the first-order sloshing mode is increased. The motion responses of the barge-type FOWT with and without the moonpool are compared. It is found that the moonpool can reduce the motion response of the FOWT, and improve the overall hydrodynamic performance of the FOWT. The platform length, moonpool length and platform draught are parametrically analyzed. Surge, heave, pitch response RMS values and the nacelle acceleration response RMS value are used as the indicators of comparison. It is found that the increase of the platform length could effectively reduce the four response RMS values of the FOWT under both operating and survival conditions, the increase of the moonpool length will reduce the four response RMS values of the FOWT under the operating condition, and the increase of the platform draught could significantly reduce the four response RMS values of the FOWT under the survival condition, the heave and pitch response RMS values increase with the augmentation of the draught under the operating condition.

Keywords： barge-type floating offshore wind turbine (FOWT); dynamic response; moonpool; resonance mode

PDF (11548KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈易人, 姚靳羽, 李明轩, 张新曙. 带月池驳船式浮式风力机水动力性能[J]. 上海交通大学学报, 2024, 58(7): 965-982 doi:10.16183/j.cnki.jsjtu.2022.521

CHEN Yiren, YAO Jinyu, LI Mingxuan, ZHANG Xinshu. Hydrodynamic Performance of a Barge-Type Floating Offshore Wind Turbine with Moonpool[J]. Journal of Shanghai Jiaotong University, 2024, 58(7): 965-982 doi:10.16183/j.cnki.jsjtu.2022.521

近年来,为了加快国家能源结构的转型,我国大力发展海上风电相关产业.随着近海资源逐渐趋于饱和,海上风电正逐渐走向“深蓝”,漂浮式支承结构逐渐取代固定式支承结构,成为海上风电的主要支承结构形式.与固定式基础相比,漂浮式海上风力机突破了水深的限制,极大地拓展了海上风能资源的开发范围.这不仅可以降低深远海风电施工的难度与成本,也可以最大程度降低对海洋环境的破坏^[1].目前,业界一般认为,35 m以上水深可采用漂浮式基础,我国沿海大陆架平均水深小于100 m,根据国家发改委能源研究所《中国 2030 年风电发展展望》^[2],我国水深5~50 m、高度70 m的海上风电开发潜力约为500 MW.因此,对于我国漂浮式海上风电产业而言,35~50 m水深海域具有较高的开发价值,应作为投资和技术研发的重点方向.

美国国家可再生能源署(National Renewable Energy Laboratory)在2011年已经开展了浮式风力机(FOWT)的相关研究.针对频域和时域研究的局限性,Jonkman^[3]基于500 m口径球面射电望远镜 (FAST) 开发了空气动力水动力-伺服-弹性全耦合仿真工具,模拟漂浮式海上风力机的耦合动态响应,并应用于某驳船式海上风力机的环境载荷分析.Browning等^[4]对半潜式平台、张力腿平台和单立柱平台漂浮式风力机进行了数值仿真和试验研究.研究包括自由衰减测试,无风、周期性和不规则波浪条件下的静水测试,平流风与湍流风测试以及风-浪组合测试.通过对比数值计算与试验结果,验证了结果的可靠性.

美国麻省理工 (Massachusetts Institute of Technology) 机械工程学院也对漂浮式风力机的设计进行了大量研究.Lee^[5]设计了两种漂浮式风力机基础,对两者在风浪联合作用下的运动响应进行计算与分析,考虑了波浪激励力中的非线性问题,提出了一种新的计算方法.Tracy^[6]以NREL 5 MW风力机为模型,以海上油气行业的相关设计概念为基础,以结构和系泊系统的相关设计规范为依据,提出了一种参数化方法设计海上风力机漂浮式基础,得到了浮体的位移、结构和系泊载荷等多重驱动因素的帕累托优化解集.

半潜型浮式风力机以Principle Power的WindFloat为代表.Kvittem等^[7]以WindFloat半潜式浮式风力机为研究对象,通过SIMO-RIFLEX模拟水动力载荷,通过AeroDyn-TurbSim模拟空气动力载荷,开发了一种新的耦合计算工具.结果表明,与带有二次阻力的势流模型相比,采用Morison模型计算黏性阻力,最终得到的运动响应更为准确.国内也有较多学者对半潜型浮式风力机进行研究.张洪建等^[8]参考 OC4-DeepCwind 半潜式浮式风力机设计, 提出了一种新型的立柱倾斜的半潜式风力机设计, 基于势流理论计算了两者的水动力性能,并将频域结果与时域结果进行了比较.同时通过参数化分析,研究了系泊系统对风力机运动响应的影响,并对系泊系统进行了优化.刘一鸣等^[9]以搭载 DTU 10 MW风力机的 OO-Star 半潜型漂浮式风力机为研究模型,基于叶素动量理论和势流理论,模拟各种风浪耦合载荷下的漂浮型风力机动态响应,研究其响应特征在不同环境载荷入射角度下的变化.魏东泽等^[10]提出了一种新型半潜式浮式风力机概念, 对结构的主尺度进行设计,综合黏性阻尼和二阶波浪力的影响,计算了浮式风力机的水动力系数以及动力响应,进一步对不同风浪联合工况下浮式风力机的耦合动力响应展开研究.徐添等^[11]通过时域全耦合软件 OPENFAST,对 15 MW级大型半潜式浮式风力机进行建模与数值计算,分析了风力机在纵荡、垂荡和纵摇方向上的响应.

以Ideol为代表的带月池的混凝土驳船式平台吃水较小,仅为7 m左右,该型式的风力机漂浮式基础在我国海域具有较大应用潜力,近年来法国与日本学者对该型式的风力机漂浮式基础进行了较多研究.Beyer等^[12]与Borisade等^[13]通过CFD数值模拟与模型试验对Ideol-Floatgen浮式风力机的运动响应特性进行了研究.Ikoma等^[14]通过数值模拟对带月池驳船式浮式风力机水动力系数与载荷进行分析,发现增加月池开口数目相较于单口月池可以进一步提升驳船式平台的水动力性能.Tan等^[15]以四口月池驳船式浮式风力机为研究对象,通过WAMIT数值模拟与模型试验对驳船式平台所受平均二阶漂移力进行研究,发现月池结构可以降低平台在特定频率范围所受二阶平均漂移力.

目前国内浮式风力机领域的研究仍以半潜式与单立柱式风力机为主,关于驳船式浮式风力机的研究较少.易乾^[16]通过WAMIT-FAST研究了OC3-Hywind单立柱式、OC4-DeepCwind半潜式与ITI-Energy驳船式3种浮式风力机构型在风-浪耦合作用下的频域动力响应,针对南海海域的特点,设计对应工况条件,并计算分析了各工况下的最大运动响应.Ideol-Floatgen原平台搭载Vestas 2 MW 风力机,为了适应主流的5 MW风力机,我国台湾地区学者Yang等^[17]与Chuang等^[18]对驳船式浮式风力机主尺度进行优化,建立了1∶20试验模型,并通过AQWA软件进一步建立了数值模型,对台湾海峡台风海况下风力机整体的动力响应与系泊载荷进行了研究.

相较于半潜式与单立柱式风力机,驳船式浮式风力机对水深的适应性更加优越,建造与安装的成本更低.在驳船式平台上增设月池可进一步提高耐波性,且月池为镂空结构,可进一步减少平台整体用料、降低建造成本.此外,月池结构还赋予了平台多功能发展的可能性,未来可与网箱养殖、波浪能发电、海上制氢等相关设备相结合,提高资源利用率与经济效益.月池对风力机动力响应的影响机理尚不清楚,因此,对带月池驳船式浮式风力机进行动力响应研究与参数优化设计对于解决我国能源转型问题,提升可再生能源产业经济效益具有重要意义.

本文通过挪威船级社(DNV)商业软件SESAM对带月池驳船式浮式风力机的水动力性能进行分析,考虑了月池黏性阻尼的影响,对驳船式平台的主尺度进行参数化研究,并进一步分析了平台运动与月池内流体运动的耦合作用.

1 数值方法

1.1 理论基础

1.1.1 浮体运动方程

本文选择Chuang等^[18]所用的驳船式平台作为漂浮式基础.带月池驳船式浮式风力机整体构型和驳船式平台几何构型以及坐标系定义如图1所示.图中:H为平台型深;D为平台吃水;L₁为平台边长;L₂为月池边长;月池自由面中心处为坐标系原点.本研究采用商业软件SESAM对风力机进行频域水动力性能分析.基于三维无航速势流理论,浮式风力机的运动方程可以表达为

(1){-ω²[M_6×6+A_6×6(ω)]-iω[B_6×6(ω)+ΔB_6×6]+C_6×6}X_1×6(ω, β)=

{F^{e}}_{1 \times 6}

(ω, β)

式中:M为浮式风力机整体质量矩阵;ω与β分别为波浪频率与浪向角;A(ω)、B(ω)分别为附加质量系数与辐射阻尼系数矩阵;ΔB为线性化黏性阻尼系数矩阵;C为静水恢复力系数矩阵;X为风力机浮式基础的位移;F^e为风力机所受波浪激励力.

图1

新窗口打开| 下载原图ZIP| 生成PPT

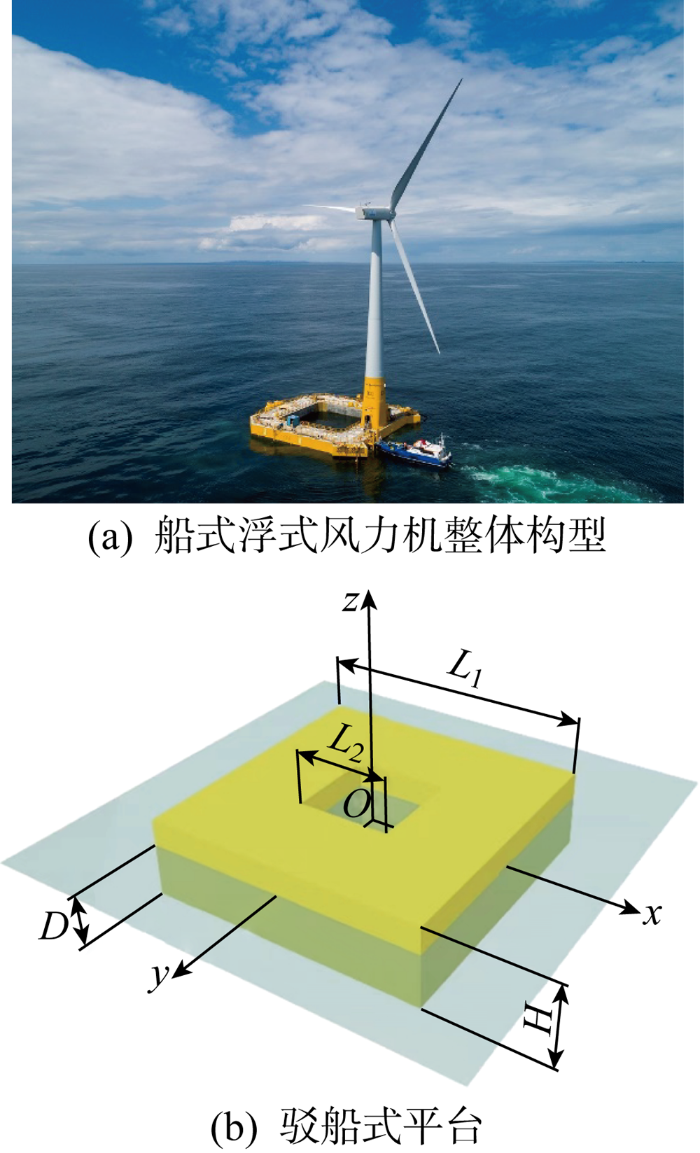
图1 驳船式浮式风力机整体及驳船式平台示意图

Fig.1 Illustrations of barge-type FOWT and barge platform

传统势流理论不考虑黏性,驳船式浮式风力机所受黏性阻尼力通过莫里森公式进行计算:

(2)F=M(1+C_a)a_w+

\frac{1}{2}

ρA_dC_DU

|U|

式中:M为浮体质量;C_a,C_D分别为浮体附加质量系数与拖曳力系数;a_w为水质点加速度;A_d为浮体截面面积;ρ为水的密度;U为流体相对浮体的速度.

1.1.2 不规则波下的响应谱计算

单位幅度规则波作用下的系统响应称为幅频响应函数,即幅值响应算子(RAO,H_RAO).不规则波可认为是由无穷个规则波叠加而成.因此,在不规则波作用下,结构物的运动响应同样可以求解.对于不规则风浪,响应变量和响应函数之间可以用谱密度函数来表达.谱分析方法认为:在线性系统中,响应谱密度S_R(ω)等于扰动谱密度S_ξ(ω) 乘以系统幅值响应算子H_RAO的平方,即

(3)S_R(ω)=S_ξ(ω)

H_{R A O}^{2}

=S_ξ(ω)

{|H (i ω)|}^{2}

式中:H(iω)为线性系统的频率响应函数.

对于不规则波下风力机的运动响应谱,定义均方根(RMS):

(4)

σ_{ζ}^{2}

\int_{0}^{\infty} {|H (i ω)|}^{2}

S_ξ(ω)dω=

\int_{0}^{\infty}

S_R(ω)dω

假设风力机浮体为线性响应系统,在足够长的时间内统计风力机浮体在随机波浪下的响应值,则响应值满足Rayleigh分布,该响应的最有可能最大值 (MPM,σ_MPM)可按下式计算:

(5)σ_MPM=

{(2 σ_{ζ}^{2} l n \frac{T}{T_{z}})}^{\frac{1}{2}}

式中:T为数值模拟的时长,通常取3 h;T_z为响应的平均过零周期.

1.2 数值模型

1.2.1 驳船式浮式风力机相关参数

漂浮式风力机由上部风力机、中部塔筒、下部漂浮式基础以及系泊系统4部分构成.风力机整机是实现风能与电能转换的关键机构,本文以NREL 5 MW机型为目标风力机,其主要结构和性能参数如表1所示.塔筒结构主要起连接作用, 塔筒结构的强度对于上部风力机的稳定运行至关重要.本文塔筒参考OC3-Hywind 形式的5 MW漂浮式风力机塔筒,采用中空的圆锥型结构,塔筒材质为Q345,塔筒的主要参数如表2所示.表中:I_xx,I_yy, I_zz为惯性矩;L_z为重心高度;M_z为包括压载在内的平台总质量.驳船式平台具体参数如表3所示.

表1 NREL 5 MW 风力机主要参数

Tab.1 Basic parameters of NREL 5 MW wind turbine

参数	取值	参数	取值
单机功率/MW	5	机舱质量/kg	240 000
叶轮直径/m	126	叶片质量/kg	17 740
桨毂中心高度/m	90	桨毂质量/kg	56 780
重心高度/m	64	风力机总质量/kg	314 520

新窗口打开| 下载CSV

表2 塔筒主要参数

Tab.2 Basic parameters of tower

参数	取值	参数	取值
塔筒高度/m	85	塔筒密度/(kg·m^-3)	8 500
塔筒重心高度/m	35.9	I_xx,I_yy/(kg·m²)	1.52×10⁸
塔筒总质量/kg	266 557	I_zz/(kg·m²)	1.86×10⁶

新窗口打开| 下载CSV

表3 驳船式平台主要参数

Tab.3 Basic parameters of barge platform

参数	取值	参数	取值
L₁/m	60	D/m	10
L₂/m	20	I_xx,I_yy/(kg·m²)	9.66×10⁹
L_z/m	-4.86	I_zz/(kg·m²)	1.93×10¹⁰
H/m	15	M_z/kg	32 200 282

新窗口打开| 下载CSV

1.2.2 计算模型

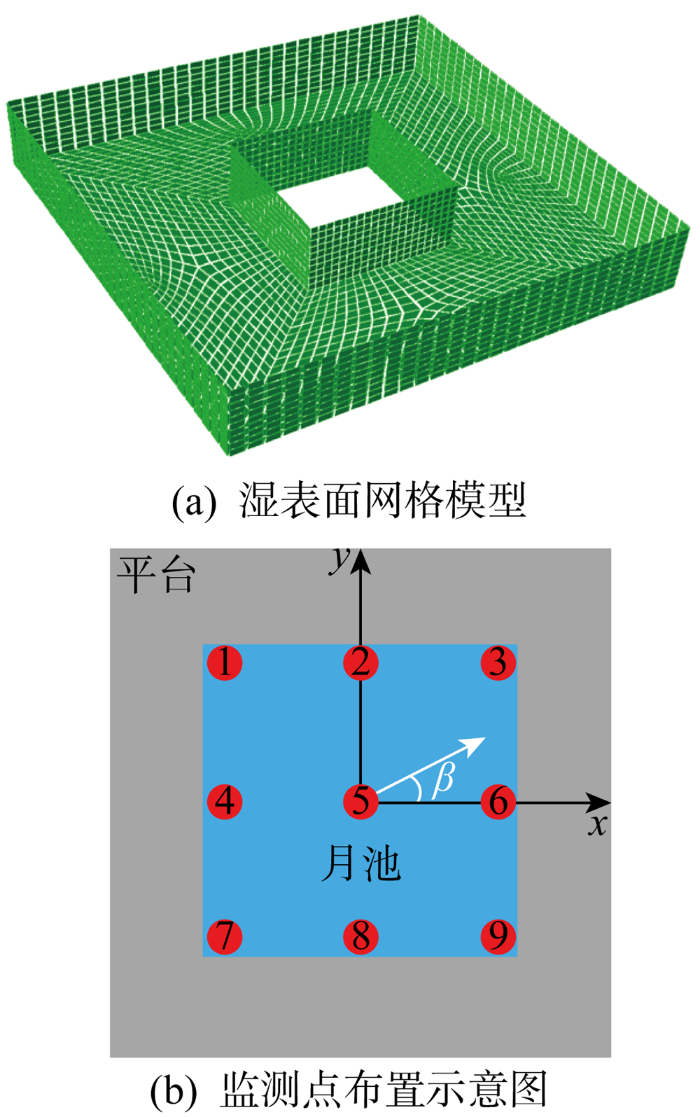
依据风力机设计参数初始值,可以对风力机进行建模.本文主要对风力机进行频域水动力分析,因此,仅对浮式风力机驳船式平台水下部分进行建模.基于质量累加与惯性矩等效原则,将驳船式风力机平台水上与水下部分的结构质量信息叠加,建立驳船式风力机平台等效计算模型.在后文研究中将分析月池的有无对驳船式风力机平台运动的影响,因此,表4与表5分别给出了有、无月池情况下驳船式风力机平台的参数.模型通过SESAM软件包中的GeniE模块建立,数值模型如图2所示.图2(a)展示了湿表面的面元网格模型.将上述模型导入HydroD模块中建立多体模型,选取β=0°,45°,90°,以0.05 rad/s为频率间隔在ω=0.05 ~2.5 rad/s区间内取点,并以0.01 rad/s为频率间隔在ω=0.6~0.8 rad/s区间内加密取点,总共选取66个频率进行计算.设置9个监测点对月池内部波面升高情况进行监测.监测点分布如图2(b) 所示,各点坐标如表6所示.按DNVGL^[19]相关规定定义环境工况,输入的海浪谱为JONSWAP谱,具体参数如表7所示.

表4 驳船式风力机平台等效计算模型主要参数

Tab.4 Basic parameters of equivalent calculation model of barge wind turbine platform

参数	取值	参数	取值
L₁/m	60	D/m	10
L₂/m	20	I_xx,I_yy/(kg·m²)	1.31×10¹⁰
L_z/m	-3.61	I_zz/(kg·m²)	1.93×10¹⁰
H/m	15	M_z/kg	32 781 359

新窗口打开| 下载CSV

表5 无月池驳船式风力机平台模型主要参数

Tab.5 Basic parameters of equivalent calculation model of barge wind turbine platform without the moonpool

参数	取值	参数	取值
L₁/m	60	D/m	10
L₂/m	20	I_xx,I_yy/(kg·m²)	1.33×10¹⁰
L_z/m	-3.60	I_zz/(kg·m²)	1.96×10¹⁰
H/m	15	M_z/kg	36 806 394

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 数值模型示意图

Fig.2 Sketches of numerical model

表6 月池内部监测点坐标

Tab.6 Coordinates of monitoring points in moonpool

监测点序号	坐标/m	监测点序号	坐标/m
1	(-9.5, 9.5, 0)	6	(9.5, 0, 0)
2	(0, 9.5, 0)	7	(-9.5,-9.5, 0)
3	(9.5, 9.5, 0)	8	(0,-9.5, 0)
4	(-9.5, 0, 0)	9	(9.5,-9.5, 0)
5	(0, 0, 0)

新窗口打开| 下载CSV

表7 不同工况下的JONSWAP谱参数

Tab.7 Values of JONSWAP spectral parameters under different working conditions

工况	有义波高,H_s/m	谱峰周期,T_p/s	形状因子,γ
作业工况LC1	2	5.5	3.6
生存工况LC2	10	12.5	3.3

新窗口打开| 下载CSV

2 动力性能计算和分析

2.1 收敛性分析

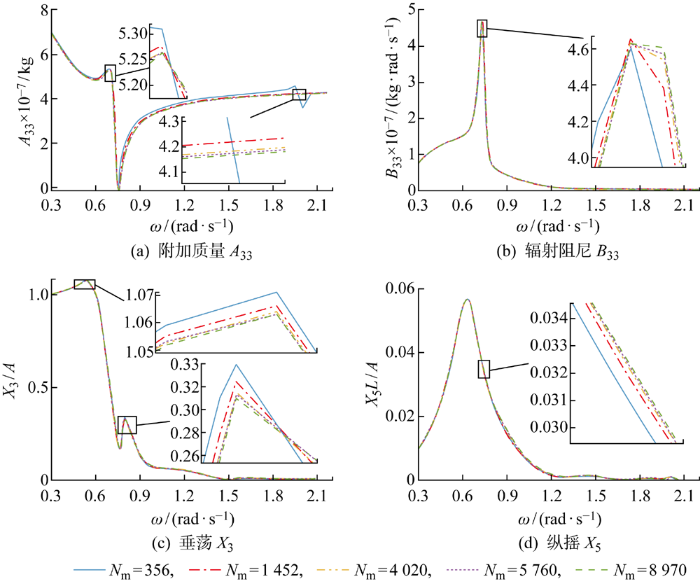
在进行运动响应分析之前,需要选取不同离散面元数目进行收敛性分析.本文建立了5个不同精度的面元模型,最小网格长度分别为3.33、1.67、1、0.83、0.67 m.对应面元数目N_m=356,1 452,4 020,5 760,8 970.图3对比了浮式风力机模型在不同网格精度下的水动力性能计算结果.图中:A为波浪高度;L为平台长度.从图中可以看到,随着面元数目的增加,垂荡方向上附加质量系数A₃₃、辐射阻尼系数B₃₃、垂荡运动响应X₃与纵摇运动响应X₅曲线逐渐趋向于收敛.垂荡和纵摇运动在ω>1.2 rad/s范围内趋于0,由ω=1.2 rad/s计算得到的波长与5个最小网格尺寸比值分别为13、26、43、52、64.当面元数目大于 5 760 时,面元数目增加对计算结果几乎不再产生影响.因此,为了兼顾计算准确性和高效性,在后续研究中的最小网格长度取为0.83 m.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 模型网格收敛性分析

Fig.3 Convergence analysis of panel model with respect to the number of panels

2.2 月池共振和晃荡模态

由于本文浮式风力机驳船式平台为对称结构,90°浪向角下,各监测点的波面升高响应与0°浪向角情况基本对称,以下仅对0°浪向角和45°浪向角共振模态进行分析.通过数值计算,得到0°浪向角下监测点4、5、6幅值曲线与相位曲线以及45°浪向角下监测点3、5、7幅值曲线与相位曲线,结果如图4所示.图中:η为响应幅值;φ为响应相位.不同浪向角、各点位的最大响应峰值频率均一致,出现在ω=0.75 rad/s左右,通过观察图4(b) 的响应相位可知,各点在该频率下相位均为-30° 左右,该频率称为月池的活塞共振频率,此时波浪升高幅值较大,浮式风力机驳船式平台的气隙将受到影响,需要引起注意.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 月池内波面运动响应

Fig.4 Motion responses of free surface in moonpool

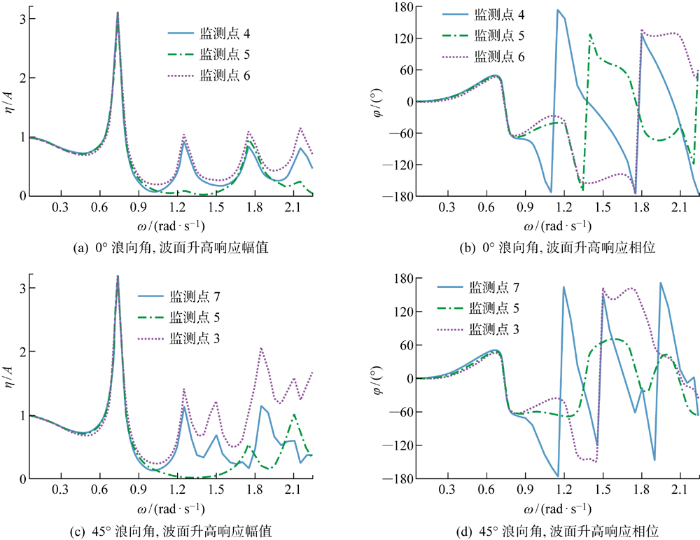
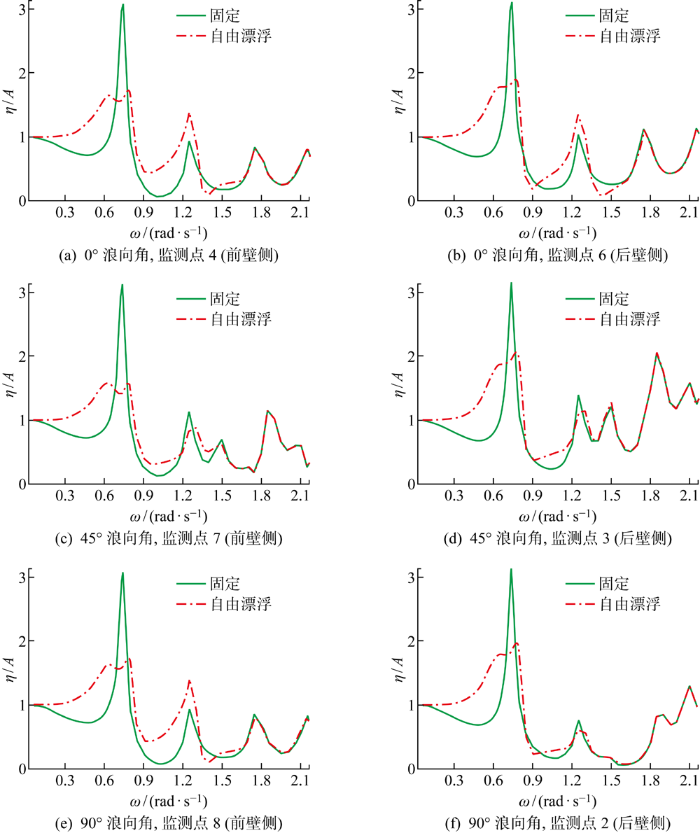
在较低波频段(0~0.8 rad/s),波面升高在不同浪向角下的响应趋势基本一致,而在较高波频段(>0.8 rad/s),不同浪向角下呈现不同的变化趋势.0°浪向角下,在1.25 rad/s处,监测点4、6均出现了较大的幅值,两者均为1左右,而监测点5响应幅值接近0,对比相位曲线可知,监测点5、6波面升高响应的相位均在-80°左右,监测点4的相位为100°,两者相差半个周期,此现象称为月池的一阶晃荡共振.

45°浪向角下,当波浪频率为1.25 rad/s时,监测点3、7均出现较大幅度波面升高响应,幅值分别为1.38、1.21,监测点5响应幅值几乎为0.通过对比相位差曲线发现,监测点3、5、7的相位分别为 -78°、-69°、102°,监测点3与7同样相差半个周期,该频率为45°浪向角下月池的一阶晃荡共振频率.通过类似的对比分析还可以确定月池45°浪向角下的二阶晃荡共振频率为1.5 rad/s.综合以上分析,将月池的共振频率汇总至表8.

表8 月池共振频率

Tab.8 Resonance frequencies of moonpool

β/(°)	活塞共振频率/ (rad·s^-1)	一阶晃荡共振频率/ (rad·s^-1)	二阶晃荡共振频率/ (rad·s^-1)
0	0.75	1.25	1.75
45	0.75	1.25	1.50

新窗口打开| 下载CSV

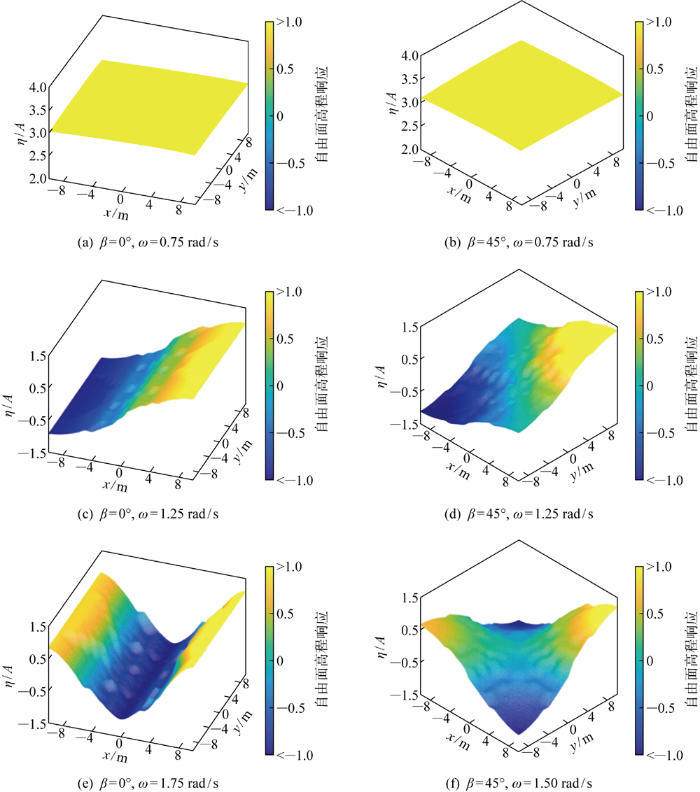
通过在月池内部加密布置21×21个监测点,计算上述月池共振频率的波面升高响应,可以得到0°浪向角与45°浪向角下月池共振模态如图5所示.图5(a)、5(b)展示了两个浪向角活塞共振频率下的模态,该频率下各点位响应幅值基本一致,为3.15左右,月池内各点处于同步、同幅振动.图5(c)、5(d)展示了两个浪向角一阶晃荡共振频率下的模态,月池前后壁水质点处于同频、同幅、反向振动.图 5(e)、5(f)展示了两个浪向角二阶晃荡共振频率下的模态,月池前后侧水质点基本处于同频、同幅、同向振动.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 月池共振模态

Fig.5 Resonance modes of moonpool

2.3 月池黏性阻尼的修正

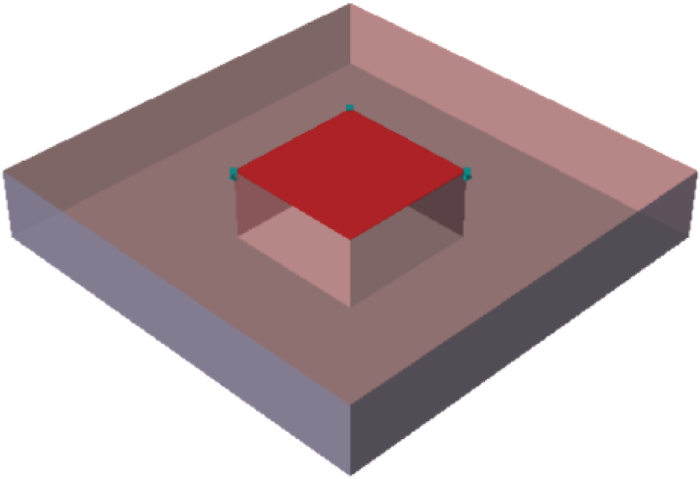
月池开口处的层流分离将产生相当大的黏性阻尼(Quadratic Damping),进而削弱月池中的共振响应.黏性阻尼大致与流速的平方成正比.传统线性势流理论不考虑黏性,导致其过度预测封闭水面区域(如月池区域)的自由面升高.为了考虑黏性阻尼的影响,本文通过阻尼盖(Damping Lid)对自由面过度升高进行抑制.如图6所示,月池阻尼盖(红色部分)设置在月池的自由表面上,月池线性自由面条件为

(6)ϕ_z-Kϕ=0|_z₌₀

式中:K=ω²/g,g为重力加速度;ϕ为速度势.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 阻尼盖示意图

Fig.6 Sketch of damping lid

加月池阻尼盖后,相应的自由表面条件改写为

(7)φ_z=Kϕ(1-2iε-ε²)

|_{S_{e}}

式中:ε为月池黏性阻尼系数;S_e为月池内部自由面.

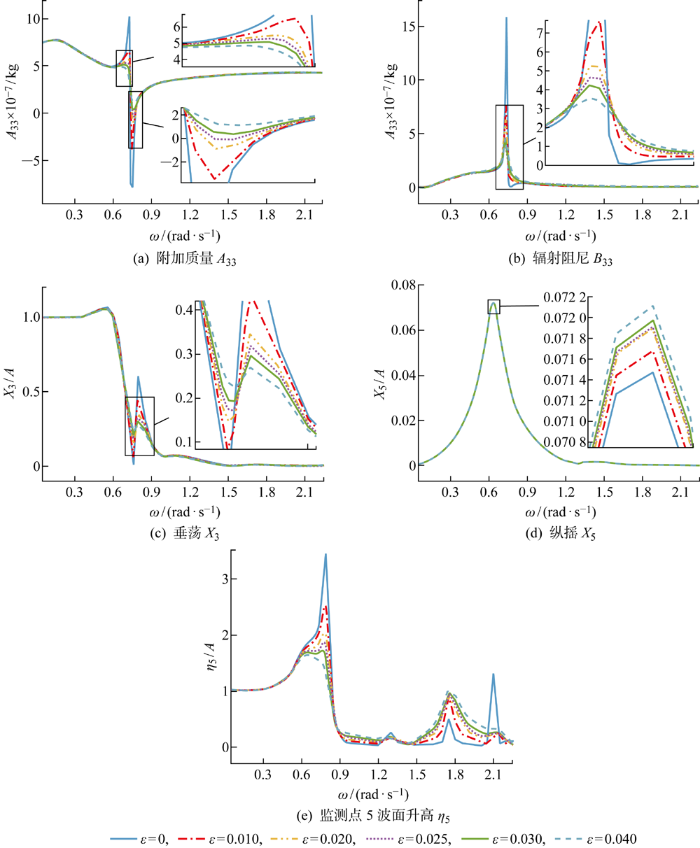
Tan等^[15]研究了不同阻尼系数对平均横荡漂移力的影响,并与试验所测平均横荡漂移力作了对比.本文参考Tan等^[15]研究,阻尼系数分别取ε= 0,0.01,0.02,0.025,0.03,0.04,计算对应情况下驳船式浮式风力机垂荡方向附加质量A₃₃、辐射阻尼B₃₃、垂荡响应X₃、纵摇响应X₅以及月池中心波面升高响应η₅.计算结果如图7所示.结果表明A₃₃与B₃₃在ω=0.75 rad/s处存在大幅突变,随着阻尼系数的增加,突变逐渐受到抑制.垂荡响应在ω=0.8 rad/s处存在极大值,随着附加阻尼系数的增加,该处峰值有减弱的趋势.纵摇响应在ω=0.65 rad/s处存在极大值,附加阻尼系数对极大值的影响不太显著,但仍能观察到峰值随附加阻尼系数的增加而减小的趋势.监测点5在ω=0.8 rad/s附近的波面升高随附加阻尼系数的增加而明显降低,在ω=1.75 rad/s附近的波面升高则随ε的增大而上升.值得注意的是,当ε=0.02,0.025时,波面升高在ω=0.65 rad/s与ω=0.8 rad/s附近可以看到较为明显的双峰现象.ω=0.65 rad/s为纵摇响应最大值所对应的频率,波面升高在ω=0.65 rad/s处产生峰值的原因与纵摇运动相关.波面升高在ω=0.8 rad/s处的峰值由活塞共振频率右移引发.驳船式浮式风力机在固定情况下时,月池的活塞共振频率为ω=0.75 rad/s(见表8);驳船式浮式风力机在自由运动情况下时,月池下的流体使附加质量减小,导致活塞共振频率增大(右移),波面升高在ω=0.8 rad/s处出现峰值^[20].当阻尼系数由0.025增大到0.04时,ω=0.65 rad/s对应峰值受影响程度较小,而 ω=0.8 rad/s对应峰值受到明显抑制,“双峰”现象逐渐消失,最大值对应频率出现了转移.综合考虑,本文所研究驳船式浮式风力机月池阻尼系数取0.025较为合适.此时,附加质量的突变与波面升高的过度响应得到适当的抑制,同时,也能观察到较为清晰的共振频率.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 月池自由面阻尼盖的影响

Fig.7 Influence of damping lid on free surface of moonpool

2.4 水动力系数

2.4.1 附加质量与辐射阻尼

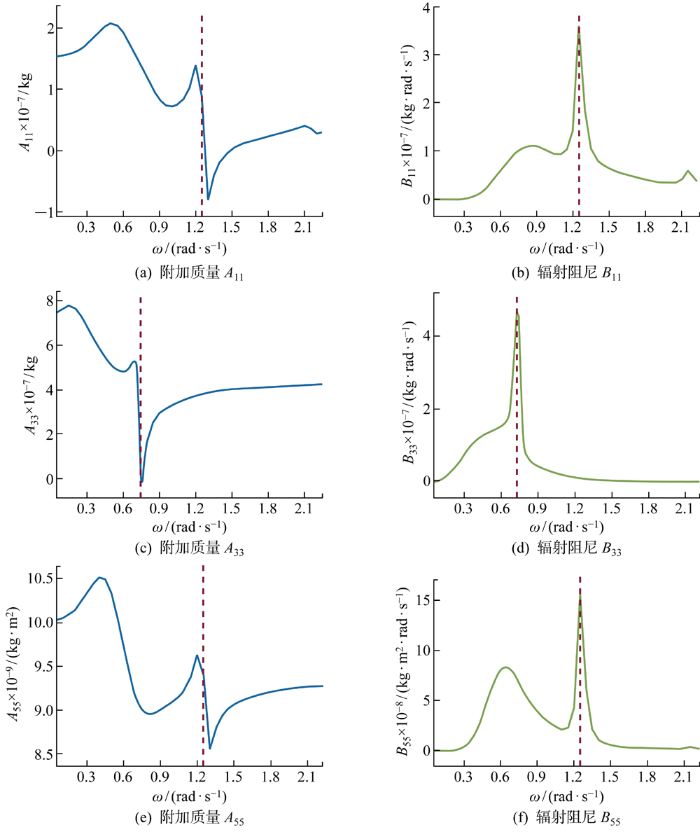
如图8所示,展示了驳船式浮式基础(浮体结构)在纵荡、垂荡、纵摇方向上的附加质量和辐射阻尼.纵荡与纵摇方向上的附加质量在ω=1.25 rad/s左右发生突变,垂荡方向上的附加质量在ω=0.75 rad/s左右出现骤降,呈现“V”字形,最后增加并逐渐趋于平稳.纵荡与纵摇方向的辐射阻尼在ω=1.25 rad/s左右出现突增,形成尖峰;垂荡方向上,辐射阻尼在ω=0.75 rad/s左右出现突起升高.垂荡方向上,附加质量与辐射阻尼突变的频率与月池的活塞共振频率较为接近.活塞共振频率下,月池内各点同步、同幅振动,且振动幅值大于0,驳船式浮式基础由运动导致的周围排开水的质量发生变化,从而垂荡方向上附加质量与辐射阻尼发生突变.纵荡与纵摇方向上的附加质量与辐射阻尼的突变频率则与月池的一阶晃荡共振频率基本一致.一阶晃荡共振频率下,监测点6所靠壁面处的模态幅值显著抬升,而监测点4所靠壁面处的模态幅值下降,导致纵荡与纵摇方向上的附加质量与辐射阻尼发生突变.综上所述,附加质量与辐射阻尼的突变与月池结构的晃荡共振模态存在相关性,显示出月池对驳船式浮式风力机的水动力性能具有较大的影响.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 驳船式浮式风力机附加质量系数与辐射阻尼系数

Fig.8 Added mass and potential damping coefficients of barge-type FOWT

2.4.2 RAO

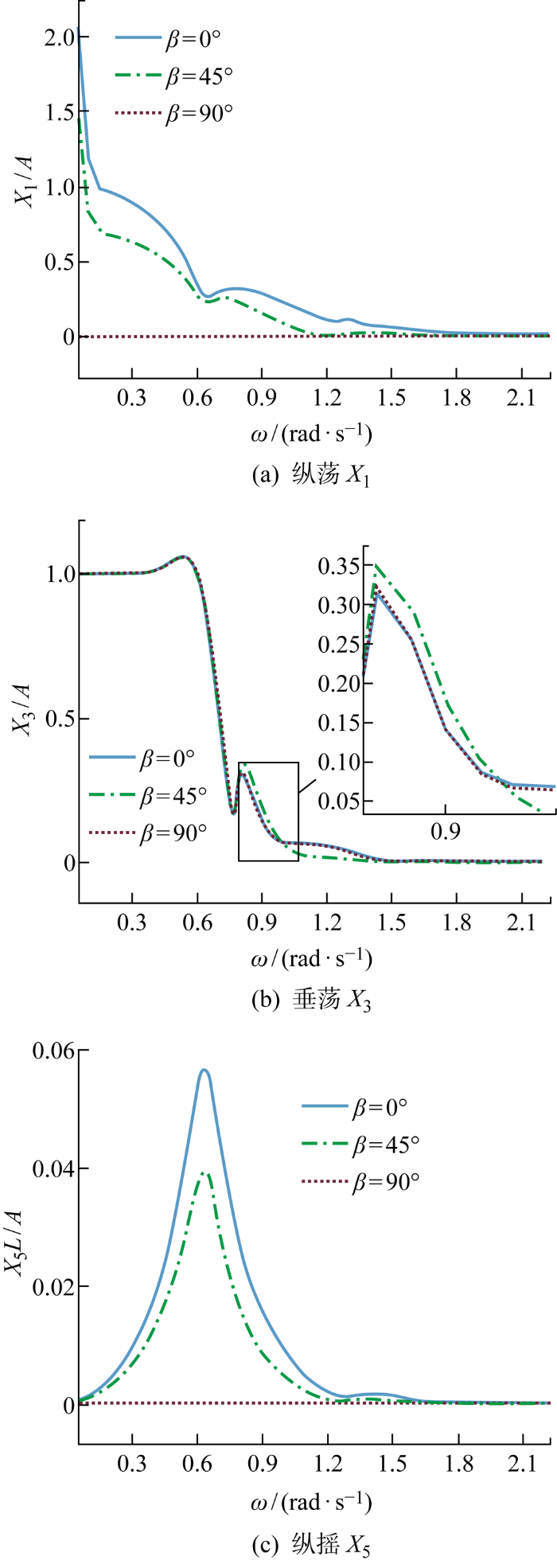
RAO是采用单位规则波计算得到的浮体频域运动响应与不同频率的规则波的关系.如图9所示,展示了驳船式浮式风力机在纵荡、垂荡与纵摇方向上的幅频响应特性曲线.纵荡随着波浪频率的增大先减小,在ω=0.65 rad/s左右小幅回升,随后不断减小并趋于0;垂荡总体上随着波浪频率的增大而减小,在ω=0.75~0.9 rad/s左右出现跃变上升.各浪向角下的曲线基本重合,垂荡基本不受浪向角的影响.纵摇随着波浪频率增大,呈现先增大后减小,最后趋于0的趋势,在ω=0.64 rad/s左右达到峰值.垂荡与纵摇可以观察到较为明显的固有频率,垂荡运动固有频率约为0.56 rad/s,纵摇运动的固有频率约为0.64 rad/s,两者均与自然界波浪能主要集中频率段较为接近,说明驳船式浮式风力机对波浪力较为敏感.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 驳船式浮式风力机运动响应

Fig.9 Motion responses of barge-type FOWT

为了论证数值模拟的准确性,将数值计算所得驳船式浮式风力机幅频响应曲线与Chuang等^[18]所提模型试验结果进行对比,如图10所示.图中:T为幅频曲线横轴各频率对应周期;H_R3为垂荡幅频响应算子;H_R5为纵摇幅频响应算子.从图中可以看出,数值模拟结果与试验结果基本吻合.试验所测纵摇幅值略小于数值模拟结果,这可能是由黏性效应所导致.与此同时,将数值模拟所得垂荡、横摇与纵摇的固有周期与试验结果进行对比,并计算两者的相对误差, 结果如表9所示,3项误差均较小, 其中垂荡与横摇固有周期误差小于2%,这从侧面进一步验证了本文计算结果的可靠性.

图10

新窗口打开| 下载原图ZIP| 生成PPT

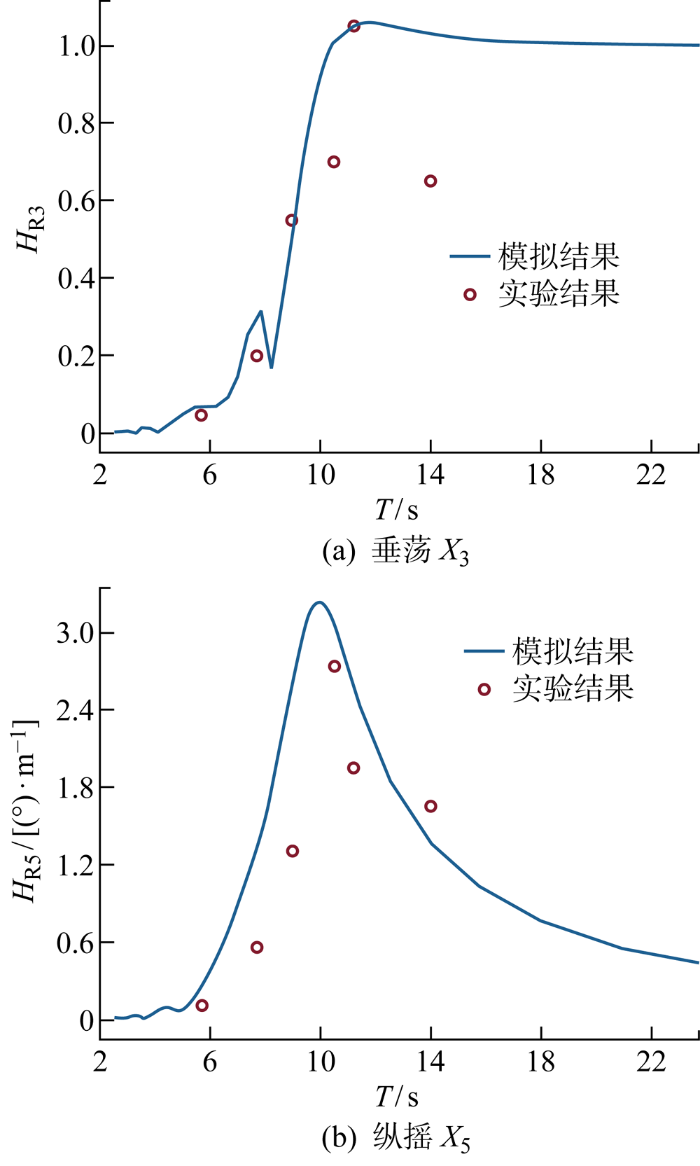
图10 H_RAO数值模拟结果与试验结果对比

Fig.10 Comparison of H_RAO of numerical simulations with H_RAO of experiments

表9 驳船式浮式风力机固有周期

Tab.9 Nature periods of barge-type FOWT

固有周期	模型试验结果/s	数值模拟结果/s	相对误差/%
垂荡	11.04	11.21	1.54
横摇	9.23	9.38	1.63
纵摇	9.29	9.82	5.71

新窗口打开| 下载CSV

2.5 响应谱分析

结合表7中对应工况条件的JONSWAP谱,可以进一步计算驳船式浮式风力机在两个工况下的运动响应谱.如图11所示,展示了驳船式浮式风力机在0°浪向角下,对应于两种工况的运动响应谱.右纵轴对应作业工况(LC1)取值,左纵轴对应生存工况(LC2)取值.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 运动响应谱

Fig.11 Response spectrums of motions

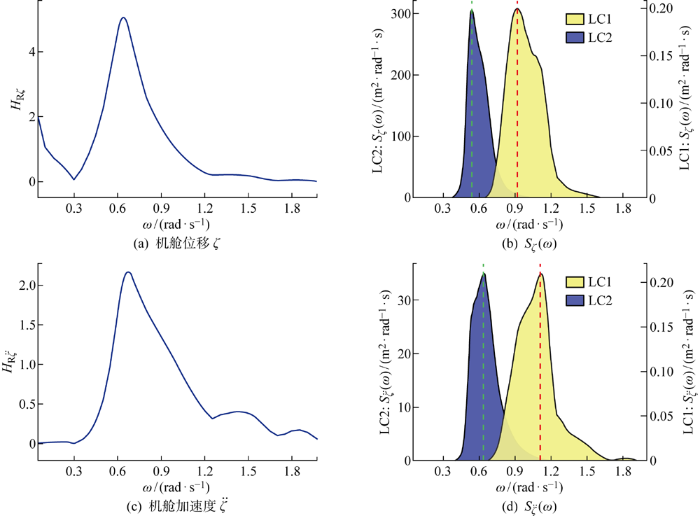
作业工况下,谱峰周期为5.5 s,对应频率为1.142 rad/s.风力机在纵荡与纵摇方向的响应谱峰值对应频率均为 1.130 rad/s 左右,与波浪谱的谱峰频率较为接近,表现出较强的相关性.垂荡响应谱出现了两处明显的峰值,分别位于ω=0.850 rad/s 和ω=1.152 rad/s,第1处峰值与月池的活塞共振频率较为接近,第2处峰值则与波浪谱的谱峰频率较为接近.生存工况下,谱峰周期为12.5 s,对应频率为0.503 rad/s.风力机纵荡、垂荡、纵摇3个自由度方向运动响应的峰值分别出现在ω=0.503 rad/s、ω=0.516 rad/s、ω=0.528 rad/s,与波浪谱的谱峰频率基本一致,显示出较强的关联性.

0°浪向角下,风力机运动响应谱均方根计算结果如表10所示.可知,风力机在作业工况下各自由度 RMS 值均较小,安全性较高,但在生存工况下,风力机的纵荡与垂荡 RMS 值分别达到了 1.30 m 与 2.28 m,纵摇的 RMS 值为5.31°.由于驳船式平台吃水较浅,水线面面积较 Spar 平台更大,重心较 Spar 平台更高,因此对波浪力更为敏感,运动响应也较大,需要优化系泊与相应的结构设计^[21].

表10 运动响应谱均方根

Tab.10 RMS values of motion responses

工况	σ(X₁)/m	σ(X₃)/m	σ(X₅)/(°)
LC1	6.56×10^-2	2.89×10^-2	1.31×10^-1
LC2	1.30	2.28	5.31

新窗口打开| 下载CSV

2.6 安全性评估

本文参考DNV关于浮式风力机耦合分析的指导意见,定义浮式风力机设计标准如表11所示^[22].

表11 挪威船级社浮式风力机设计标准^[22]

Tab.11 Design criteria of FOWT recommended by DNV^[22]

工况	最大动态纵倾/(°)	最大机舱加速度/(m·s^-2)
LC1	10	2.94
LC2	15	5.88

新窗口打开| 下载CSV

2.6.1 动态纵倾

Tracy^[23]提出风力机整体的动态纵倾可由下式计算:

(8)max

ξ_{5}^{d y m}

ξ_{5}^{s t a}

+σ_MPM(X₅)

式中: $ξ_{5}^{s t a}$ 为风力机的静态纵倾,

(9)C₅₅

ξ_{5}^{s t a}

=F_thrH_nac

F_thr为风力机所受推力;H_nac为风力机机舱距离水线面高度;C₅₅为纵摇方向静水恢复力系数.

风力机运行期间,风力机所受负荷增加,系统对稳性的要求更高,NREL的5 MW风力机的最大推力可达800 kN;生存工况下,风力机停机,风力机所受推力反而下降,一般低于400 kN,为保留安全冗余,本文取400 kN进行计算.经HydroD Stability 模块计算可得驳船式浮式风力机纵倾方向回复力系数C₅₅为1.07×10¹⁰ N·m/rad.进一步计算可得作业工况下,驳船式浮式风力机max $ξ_{5}^{d y m}$ = 0.39°+ 0.33°= 0.72°< 10°,满足动态纵倾安全性要求;在生存工况下,驳船式浮式风力机max $ξ_{5}^{d y m}$ = 0.19°+ 13.02°= 13.21°< 15°,同样满足动态纵倾安全性要求.

2.6.2 机舱处的加速度评估风力机性能的一个关键因素是风力机机舱的运动.机舱的大幅运动将导致风力机性能下降,并在极端情况下对设备造成损害.机舱的位移响应ζ算子H_R_ζ和加速度响应 $\ddot{ζ}$ 算子 $H_{R \ddot{ζ}}$ 表达式如下:

(10)

\begin{array}{l} H_{R ζ} (ω) = H_{R 1} + H_{n a c} H_{R 5} \\ H_{R \ddot{ζ}} (ω) = - ω^{2} (H_{R 1} + H_{n a c} H_{R 5}) \end{array}\}

式中:H_R1与H_R5分别为纵荡和纵摇幅频响应算子.

计算得到两者的幅频响应曲线与响应谱如图12所示.结果表明,机舱位移响应的峰值对应频率为 0.64 rad/s,机舱位移通过纵荡与纵摇进行计算,与图9(a) 与9 (c) 对比,可以发现机舱位移响应在低频段 (ω<0.3 rad /s) 的趋势与纵荡响应基本一致,此时机舱位移响应由风力机的纵荡运动主导,在中频段 (ω>0.3 rad/s)则与纵摇响应趋势基本一致,此时机舱位移响应则由风力机的纵摇运动主导.生存工况下,机舱位移响应谱峰频率与波浪谱谱峰频率基本一致,作业工况下,机舱位移响应谱峰频率为 0.92 rad/s,与纵摇响应谱峰频率较为接近.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 作业工况与生存工况下机舱的位移与加速度

Fig.12 Motion and acceleration responses of nacelle under the operating and survival conditions

机舱加速度响应的峰值频率为 0.67 rad/s.生存工况与作业工况下,机舱加速度响应谱峰频率与波浪谱的谱峰周期基本一致,从响应谱的纵坐标可以看出,机舱运动响应在生存工况下比作业工况下大 2 个数量级,有倾覆和损坏的风险.同时,计算得到0°浪向角下,机舱运动响应谱的 RMS 值(见表10).进一步计算可以得到,在作业工况与生存工况下,浮式风力机的机舱加速度σ_MPM分别为0.47 m/s² 与4.89 m/s²,两者均符合安全性要求.

3 月池共振与风力机动力响应的相互作用

3.1 月池对风力机整体性能的影响

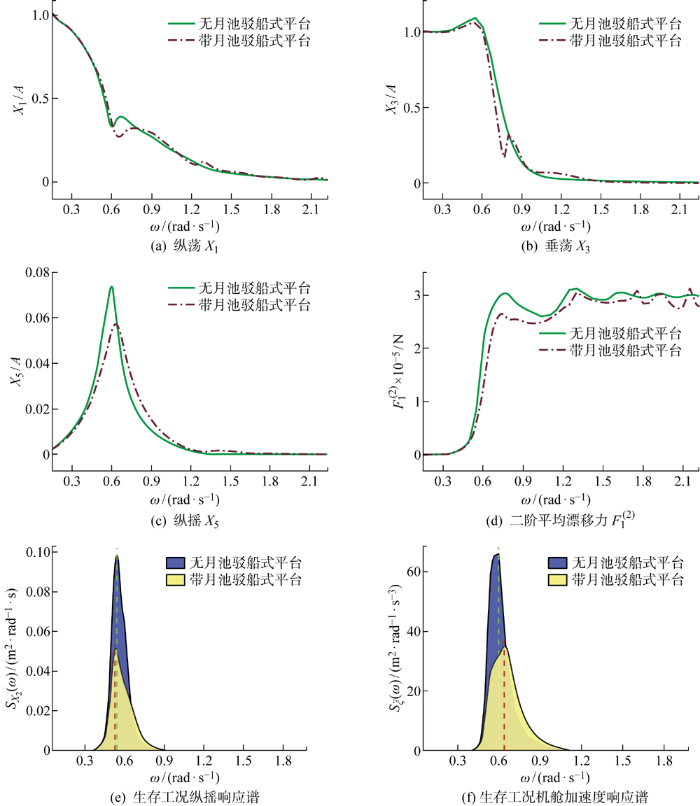
研究建立了相同尺寸无月池驳船式浮式风力机模型,将其与有月池模型进行性能对比.无月池模型的具体参数如表5所示,计算结果如图13所示.结果表明,有月池驳船式浮式风力机比无月池驳船式浮式风力机在纵荡、垂荡、纵摇方向的运动响应以及纵荡方向的水平漂移力4项指标上均有提升,浮式风力机的纵荡响应在ω=0.6~0.78 rad/s区间内有明显下降,垂荡响应同样在ω=0.6~0.8 rad/s区间内有下降,同时垂荡响应的峰值也小幅降低,纵摇的响应峰值减小但固有频率增大,平台纵荡方向所受水平漂移力在特定频率区间下降显著.最大动态纵倾与机舱最大加速度为浮式风力机设计的重要关注指标,两者的响应谱峰值均显著降低,进一步计算两者的RMS值,结果如表12所示,两者下降比分别达到了18.56% 与12.00%,表明月池结构显著提升了驳船式浮式风力机水动力性能.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 月池对风力机水动力性能的影响

Fig.13 Influence of moonpool on hydrodynamic performance of FOWT

表12 生存工况下纵摇响应与机舱加速度响应RMS值

Tab.12 RMS values of pitch response and acceleration response of nacelle under LC2

参数	LC2 RMS值		下降比例/%
参数	有月池	无月池	下降比例/%
σ(X₅)/(°)	6.65	5.31	18.56
σ( $\ddot{ζ}$ )/(m·s^-2)	2.25	1.98	12.00

新窗口打开| 下载CSV

3.2 风力机运动对月池共振模态的影响

驳船式浮式风力机的运动与月池内的水的运动会产生相互作用,从而影响整体的水动力性能.Xu等^[20]研究发现,浮体的运动会造成月池结构共振频率的偏移.通过对驳船式浮式风力机自由运动与固定两种状态下的月池波面升高响应进行计算,如图14所示,展示了 0°、45°与90°浪向角下前壁侧与后壁侧的波面升高响应情况.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 风力机运动对月池共振频率的影响

Fig.14 Influence of motions of FOWT on resonance frequencies of moonpool

结果表明,风力机固定状态下,0.63~0.80 rad/s频率范围内只有一处峰值,位于0.75 rad/s;而风力机自由运动状态下,月池波面升高在该频率范围内存在两处峰值,风力机的运动导致月池活塞共振频率出现了偏移.Ikoma等^[14]在关于带月池驳船式浮式风力机的研究中也发现了类似现象,且前壁侧的双峰分化现象较后壁侧更为显著.此外,风力机自由运动状态下,月池活塞共振模态对应波面升高幅值明显小于平台固定状态;0°与90°浪向角下,风力机自由运动状态与固定状态下一阶与二阶晃荡共振频率基本一致,而一阶晃荡共振的响应幅值得到增强;45° 浪向角下,一阶晃荡共振频率发生了微小偏移且响应幅值受到抑制.

4 浮式风力机驳船式平台主尺度参数化研究

浮式风力机驳船式平台的主要构型参数包括平台边长L₁、月池边长L₂、吃水D和平台高度H.在保证风力机高度一致的前提下(H=D+5 m)对前三者进行参数化研究,分别计算对应参数组合下,风力机纵荡响应、垂荡响应、纵摇响应以及机舱的加速度响应的RMS值,将结果进行归一化处理,计算4项响应的RMS值与初始设计(L₁=60 m,L₂=20 m,D=10 m)对应的RMS值的比例(σ/σ₀),进行对比分析.

4.1 平台边长的影响

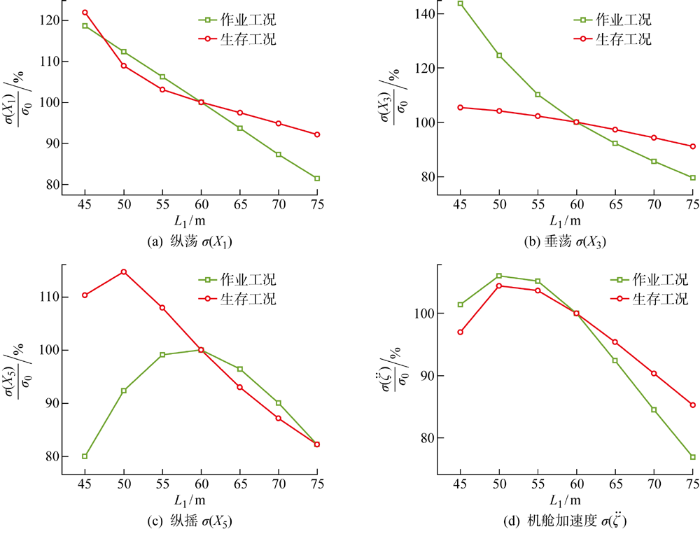
驳船式平台初始设计边长为60 m,平台边长从45 m到75 m每隔5 m均匀取点,共7个样本点.如图15所示,展示了风力机纵荡、垂荡、纵摇响应与机舱加速度响应RMS值随平台边长的变化.随着平台边长的增大,纵荡与垂荡响应 RMS 值均明显减小,作业工况下的下降幅度大于生存工况;纵摇响应 RMS 值先增大后减小,作业工况下,在平台边长为 60 m时有最大值,生存工况下,在平台边长为50 m时有最大值;机舱加速度RMS值同样先增大后减小,生存工况与作业工况下的最大值均出现在平台边长为50 m时.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 不同平台边长下风力机运动响应的变化

Fig.15 Computation of motion responses of FOWT to different lengths of barge platform

4.2 月池边长的影响

月池部分初始设计边长为20 m,月池边长从14 m到26 m每隔2 m均匀取点,共7个样本点,如图16所示,展示了风力机纵荡、垂荡、纵摇响应与机舱加速度响应RMS值随月池边长的变化.随着月池边长的增大,作业工况下,风力机纵荡响应RMS值先减小后增大,在月池宽度为20 m 时有最小值,生存工况下,纵荡响应RMS值逐渐减小,但变化幅度较小;风力机垂荡响应、纵摇响应与机舱加速度响应的 RMS 值在作业工况与生存工况下呈现相反的变化趋势,作业工况下,三者随月池边长的增加而上升,而生存工况下,三者则表现出不同程度的下降,纵摇响应与机舱加速度响应的RMS值变化幅度较小,均在3%以内.作业工况与生存工况下出现的相反变化趋势可归因于边长变化导致的驳船式平台H_RAO的变化.作业与生存工况下的JONSWAP谱谱峰频率分别为1.14 和0.50 rad/s,而垂荡与纵摇固有频率均位于两个JONSWAP谱谱峰频率中间.边长的变化使H_RAO的峰值与形状发生变化,导致作业工况与生存工况下的响应谱发生相反变化,从而出现不同的运动响应变化趋势.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 不同月池边长下风力机运动响应的变化

Fig.16 Computation of motion responses of FOWT to different widths of moonpool

4.3 平台吃水的影响

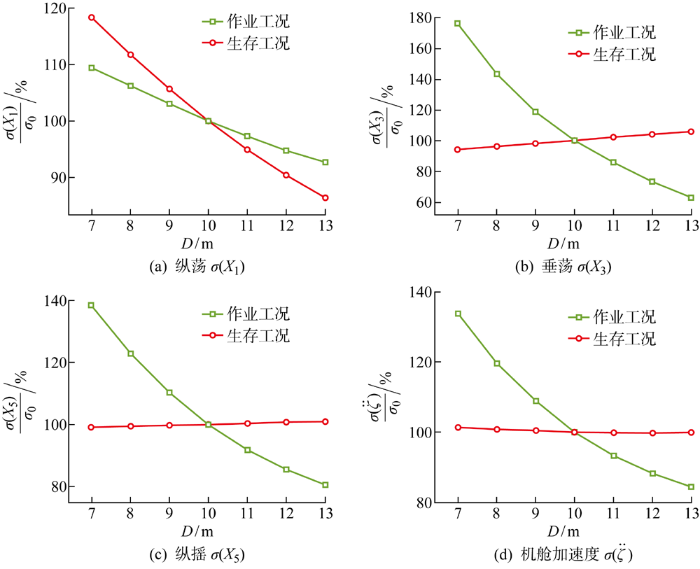
初始设计吃水为10 m,平台吃水从7 m到13 m每隔1 m均匀取点,共7个样本点.如图17所示,展示了风力机纵荡、垂荡、纵摇响应与机舱加速度响应RMS值随吃水的变化.随着平台吃水增加,作业工况下,4项响应的RMS值均显著下降,垂荡响应降低幅度最大,从初始值的175%降低至65%左右;生存工况下,纵荡响应RMS值与机舱加速度响应RMS值表现出不同程度降低,纵荡RMS值降幅较大,而机舱加速度降幅在2%以内,垂荡响应RMS值与纵摇响应RMS值逐渐增加,其中纵摇RMS值增幅较小,在2%以内.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 不同吃水下风力机运动响应的变化

Fig.17 Computation of motion responses of FOWT to different draughts

5 结论

本文对带月池驳船式浮式风力机建立数值模型,并进行频域水动力性能分析.主要的研究结论包括:

(1) 对于带月池的浮式风力机驳船式平台,月池阻尼盖模型可以有效防止月池内部过度共振.通过对驳船式浮式风力机的水动力性能分析,发现月池会导致水动力系数在共振频率处发生较大突变,风力机驳船式平台垂荡与纵摇响应固有周期均在自然界波浪能集中范围之内,对波浪较为敏感.结合DNV相关建议,通过响应谱分析对风力机的安全性进行了校核.结果表明,在作业工况与生存工况下,驳船式浮式风力机满足最大动态纵倾与最大机舱加速度限制,具有较高的安全性.

(2) 驳船式浮式风力机的运动会引起月池活塞共振频率的偏移,与风力机固定状态相比,风力机运动状态下,月池活塞共振频率增大,对应频率波面升高响应幅值降低;晃荡共振频率基本不受影响,一阶晃荡共振的幅值增大.与无月池驳船式浮式风力机相比,有月池驳船式浮式风力机纵荡、垂荡与纵摇响应有不同程度降低,风力机所受二阶平均漂移力明显减小,生存工况下风力机的最大动态纵倾与机舱最大加速度显著下降,风力机整体的水动力性能得到提升.

(3) 对平台边长、月池边长与平台吃水进行参数化分析,结果表明平台边长的增加可以有效降低风力机的纵荡响应与垂荡响应,且作业工况下降低的幅度明显大于生存工况下降低的幅度;月池边长的增加可以大幅降低风力机在生存工况下的运动响应,作业工况下,随着月池边长的增加,风力机运动响应有所增大,但仍远低于安全阈值.因此,可以适当增大月池边长,提升风力机生存工况下的安全性;吃水的增加可以有效降低风力机在作业工况下的运动响应,但在生存工况下会对风力机的垂荡与纵摇响应产生不利影响.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

周昊, 侯承宇, 李辉, 等.

我国海域漂浮式风电机组基础适用性分析

[J]. 风能, 2020(7): 102-105.