考虑竖向荷载作用时液化土中群桩基础水平动力响应

doi:10.16183/j.cnki.jsjtu.2023.007

考虑竖向荷载作用时液化土中群桩基础水平动力响应

胡安峰¹^,², 陈奕扬¹^,², 肖志荣^,³, 陈正⁴

1.浙江大学滨海和城市岩土工程研究中心, 杭州 310058

2.浙江大学浙江省城市地下空间开发工程技术研究中心, 杭州 310058

3.浙江科技学院土木与建筑工程学院,杭州 310023

4.浙江省建筑设计研究院,杭州 310006

Horizontal Dynamic Response of Pile Group Foundation in Liquefied Soil Under Vertical Load

HU Anfeng¹^,², CHEN Yiyang¹^,², XIAO Zhirong^,³, CHEN Zheng⁴

1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China

2. Engineering Research Center of Urban Underground Space Development of Zhejiang Province, Zhejiang University, Hangzhou 310058, China

3. School of Civil Engineering and Architecture, Zhejiang University of Science and Technology, Hangzhou 310023, China

4. Zhejiang Province Institute of Architectural Design and Research, Hangzhou 310006, China

通讯作者: 肖志荣,副教授;E-mail:100106@zust.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-01-9 修回日期: 2023-03-17 接受日期: 2023-03-24

基金资助:

国家自然科学基金(51978612)

Received: 2023-01-9 Revised: 2023-03-17 Accepted: 2023-03-24

作者简介 About authors

胡安峰(1974-),教授,博士生导师,从事桩基工程、软黏土力学研究.

摘要

基于Biot饱和多孔介质理论,考虑液化土的流动特性,建立考虑竖向荷载作用的部分埋入群桩水平振动模型,通过分离变量法、算子分解法,引入桩土耦合及位移连续条件,得到复杂条件下液化土中高桩桩间相互作用因子解和群桩水平动阻抗解.通过参数分析,表明液化土特性和竖向荷载对桩间水平相互作用因子、群桩动阻抗有显著影响,指出同一频率下,群桩水平动刚度随着表层液化土厚度的增加而下降,当液化厚度较大时,动刚度随频率上升显著下降,并出现负刚度;桩顶竖向荷载会降低液化土中的群桩动刚度,液化土厚度越大,削弱效果越明显.

关键词： 液化土; 高桩基础; 竖向荷载; 桩间水平相互作用

Abstract

The horizontal vibration model of partially buried pile group under vertical load is established based on Biot saturated porous media theory, considering the flow characteristics of liquefied soil. Considering the pile-soil coupling and continuous displacement conditions, the pile interaction factor solutions and the horizontal dynamic pile impedance solutions in liquefied soil under complex conditions are obtained using the variable separation method and the operator decomposition method. Parameter studies are conducted on liquefied soil characteristics and vertical loadings. The results show that at the same vibration frequency, the horizontal dynamic.pngfness of pile group decreases with the increase of surface liquefied soil thickness. When the liquefaction thickness is large, the dynamic.pngfness decreases significantly with the increase of frequency, and a negative.pngfness appears. Vertical pile top loading can reduce the dynamic.pngfness of pile group in liquefaction soils. The weakening effect becomes more obvious with the increase in the thickness of liquefied soil.

Keywords： liquefied soil; high-piled foundation; vertical load; horizontal interaction between piles

PDF (1797KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

胡安峰, 陈奕扬, 肖志荣, 陈正. 考虑竖向荷载作用时液化土中群桩基础水平动力响应[J]. 上海交通大学学报, 2024, 58(7): 1075-1085 doi:10.16183/j.cnki.jsjtu.2023.007

HU Anfeng, CHEN Yiyang, XIAO Zhirong, CHEN Zheng. Horizontal Dynamic Response of Pile Group Foundation in Liquefied Soil Under Vertical Load[J]. Journal of Shanghai Jiaotong University, 2024, 58(7): 1075-1085 doi:10.16183/j.cnki.jsjtu.2023.007

群桩动力响应特性一直是桩基研究领域的重要课题之一.部分埋入群桩作为一种常见的基础形式,多被应用于石油钻井平台、海上风力机等海工结构物中^[1].与完全埋入桩相比,海上高桩的工作环境更加特殊和复杂^[2].我国东南沿海是地震高发区域,广泛分布的海基表层天然泥沙沉积物^[3]在地震荷载作用下极易发生液化现象^[4-5],不仅会降低桩基抗压能力,还会导致桩侧约束减小,在承受波浪、地震等水平荷载作用时产生更大的水平位移.Novak等^[6]的试验结果指出,表层土性质对群桩振动特性有着重要的影响,因此需要重视液化土中的部分埋入群桩的动力响应问题.

国内外基于埋入桩的群桩振动响应特性已有一定的成果.Poulos等^[7-8]最早对群桩-土耦合模型进行了研究,在此基础上考虑静力荷载、动力荷载的作用,提出了桩-桩相互作用因子的概念,给出了群桩阻抗的计算方法.Dobry等^[9]进一步对动力Winkler地基模型中的群桩阻抗进行研究.国内学者任青等^[10]基于动力Winkler模型对考虑轴力的高桩群桩基础水平动力特性进行了研究.杨骁等^[11]采用Winkler模型模拟成层液化土地基,对带上部结构的桩土系统水平振动特性进行分析.刘圆圆^[12]基于简化饱和多孔介质理论,研究了高桩群桩基础振动阻抗.刘林超等^[13]等基于多孔介质理论研究了埋入管桩群桩的水平振动阻抗,但未考虑表层液化土的存在对桩基的影响.杨丰^[14]基于Winkler模型研究了液化土作用下群桩振动特性,通过假设被动桩埋入段的桩顶位移,结合位移叠加原理求得被动桩桩顶位移,定义了桩间相互影响因子.

目前基于Winkler地基法的完全埋入桩研究成果较为丰富,但对于液化土中部分埋入群桩基础的研究理论较少,并且在Winkler地基模型中,多采用强度折减法模拟液化土^[15],忽略了液化土的流动性.本文采用Biot饱和多孔介质理论描述海基非液化饱和土体,将上部液化土体视作无黏性不可压缩流体,充分考虑液化土的流动性,给出了复杂条件下的液化土中高桩桩间相互作用因子解和群桩水平动阻抗解,与Winkler地基中采用强度折减法模拟液化土的方法相比更符合实际.

1 计算模型及假定

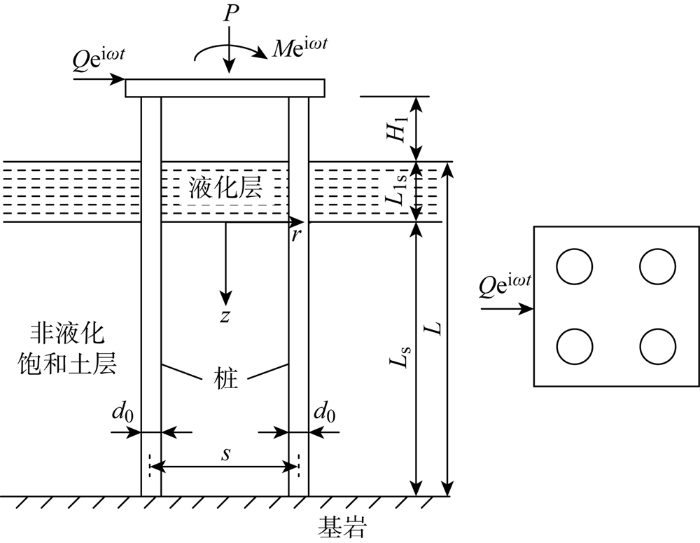
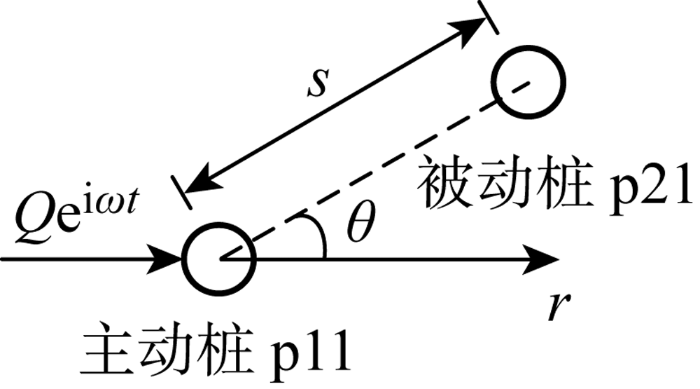
计算模型简图如图1所示.假定表层液化土体为无黏性流体,下部土层为饱和两相多孔介质,桩基为弹性均质圆杆.桩顶受到竖向荷载P、水平简谐荷载Qeⁱ^ωt、弯矩Meⁱ^ωt的共同耦合作用,ω为水平简谐荷载角频率,t为振动时间.主动桩与被动桩中心距为s,各桩半径均为r₀,桩径均为d₀,自上而下分为3段,上部自由段桩长为H₁,液化土中桩长为L_ls,非液化土中桩长为L_s.桩间相互作用模型如图2所示,主动桩和被动桩连线与受力方向的夹角为θ,r为径向坐标轴.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 液化土中群桩水平振动计算模型简图

Fig.1 Calculation model of horizontal vibration of group piles in liquefaction soil

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 桩间相互作用模型示意图

Fig.2 Model diagram of pile interaction

在对地震和波浪等荷载作用下的柔性桩进行动力响应分析时,由于其荷载频率一般较低,对群桩-土耦合系统模型可采用以下假定^{[16⇓⇓⇓-20]}:① 桩基为忽略剪切变形的线黏弹性等截面一维Euler-Bernoulli梁杆件,桩基底部为固定支撑,忽略桩侧摩阻力;② 液化土层为无黏性不可压缩流体,不考虑辐射阻尼影响,忽略自由表面波,在面上无限延伸,且初始无扰动;③ 桩周土为均匀饱和两相弹性介质,视作一系列沿纵向分布的土层,土层之间互相独立,土底为固定边界;④ 桩-土接触面良好,桩与液化土、非液化土不产生振动滑移,桩-土耦合体系振动为小变形;⑤ 各桩长度、半径不发生变化,且桩基表面不透水,不考虑桩基自重的影响.

2 单桩-土耦合系统振动方程求解

2.1 桩周土侧向压力

当桩受到圆频率为ω的水平简谐激振时,会沿水平方向作简谐运动,根据线性辐射波浪理论,桩周围的流体会以相同的频率ω做简谐运动,流体的速度势函数可表示为Φ(r, θ, z, t)=ϕ(r, θ, z)eⁱ^ωt.由于在水平简谐荷载作用下,桩-流体、桩-土系统均处于简谐振动状态,对应的状态项均包含时间因子eⁱ^ωt,为书写方便,以下推导过程中均省略eⁱ^ωt项.

由流体波动理论可以得到以速度势表示的无黏性不可压缩流体运动控制方程:

(1)

\frac{\partial^{2} ϕ (r, θ, z)}{\partial r^{2}}

\frac{1}{r} \frac{\partial ϕ (r, θ, z)}{\partial r}

\frac{1}{r^{2}} \frac{\partial^{2} ϕ (r, θ, z)}{\partial θ^{2}}

\frac{\partial^{2} ϕ (r, θ, z)}{\partial z^{2}}

液化土段满足以下边界条件.

(1) 液化土层底部、顶部边界条件:

(2)

{\frac{\partial ϕ (r, θ, z)}{\partial z}|}_{z = 0}

=0,

{ϕ (r, θ, z)|}_{z = - L_{l s}}

(2) 液化土无穷远处边界条件:

(3)

{ϕ (r, θ, z)|}_{r \to \infty}

(3) 桩-流体接触面处边界条件:

(4)

\frac{\partial ϕ (r, θ, z)}{\partial r}

{ω u_{p}^{1} c o s θ|}_{r = r_{0}}

式中: $u_{p}^{1}$ 为液化土段中的桩基水平位移.

采用参数分离法求解液化土振动控制方程,结合边界条件可得液化土在单位长度桩身上产生的反力q₁为

(5)q₁=

\overset{\infty}{\sum_{n = 1}}

A_nω²πr₀ρ_lscos(α_nz)K₁(α_nr)

式中:A_n为待定系数;ρ_ls为液化土层密度;α_n= $\frac{1 - 2 n}{2 L_{l s}}$ , n=1, 2, …;K_n(·)为n阶第二类修正Bessel函数.

基于Biot多孔介质理论与Novak薄层法,建立柱坐标下的非液化饱和振动控制方程:

(6)G^*Δ²u_r+(λ^*+α²M+G^*)

\frac{\partial e}{\partial r}

\frac{G^{*}}{r^{2}} (2 \frac{\partial u_{r}}{\partial θ} + u_{r})

-αM

\frac{\partial ξ}{\partial r}

=ρ

\frac{\partial^{2} u_{r}}{\partial t^{2}}

+ρ_f

\frac{\partial^{2} w_{r}}{\partial t^{2}}

(7)G^*Δ²u_θ+(λ^*+α²M+G^*)

\frac{\partial e}{r \partial θ}

\frac{G^{*}}{r^{2}} (u_{θ} - 2 \frac{\partial u_{r}}{\partial θ})

-αM

\frac{\partial ξ}{r \partial θ}

= ρ

\frac{\partial^{2} u_{θ}}{\partial t^{2}}

+ρ_f

\frac{\partial^{2} w_{θ}}{\partial t^{2}}

(8)αM

\frac{\partial e}{\partial r}

-M

\frac{\partial ξ}{\partial r}

=ρ_f

\frac{\partial^{2} u_{r}}{\partial t^{2}}

\frac{\partial^{2} w_{r}}{\partial t^{2}}

+b_pm

\frac{\partial w_{r}}{\partial t}

(9)αM

\frac{1}{r} \frac{\partial e}{\partial θ}

-M

\frac{1}{r} \frac{\partial ξ}{\partial θ}

= ρ _f

\frac{\partial^{2} u_{θ}}{\partial t^{2}}

\frac{\partial^{2} w_{θ}}{\partial t^{2}}

+b_pm

\frac{\partial w_{θ}}{\partial t}

式中:Δ²= $\frac{\partial^{2}}{\partial r^{2}}$ + $\frac{1}{r} \frac{\partial}{\partial r}$ + $\frac{1}{r^{2}} \frac{\partial^{2}}{\partial θ^{2}}$ ,e= $\frac{\partial u_{r}}{\partial r}$ + $\frac{u_{r}}{r}$ + $\frac{1}{r}$ × $\frac{\partial u_{θ}}{\partial θ}$ ,ξ=- $(\frac{\partial w_{r}}{\partial r} + \frac{w_{r}}{r} + \frac{1}{r} \frac{\partial w_{θ}}{\partial θ})$ ;u_r,u_θ分别代表土层的固相径向位移和切向位移;w_r,w_θ代表液相相对于固相的径向和切向位移;λ,μ为与土体相关的Lame常数,G为土体切变模量,ν为土骨架泊松比.当土体阻尼为滞回阻尼时,G^*=G(1+2ζi),λ^*=λ(1+2ζi),ζ为土体滞回阻尼;当土体为黏性阻尼土时,G^*=G+2c_i $\frac{\partial}{\partial t}$ ,λ^*=λ+2c_i $\frac{\partial}{\partial t}$ ,c_i为黏性阻尼系数;α,M为土骨架和流体压缩性相关的Biot参数;ρ为土体密度,ρ=ρ_s(1-n₀)+n₀ρ_f,ρ_s与ρ_f分别为土颗粒、流体密度,n₀为土体孔隙率;m=ρ_f/n₀,b_p=ρ_fg/k_d,k_d为桩周土体的渗透系数.

非液化饱和土层段满足以下边界条件.

(1) 土体位移边界条件:

(10)

\begin{array}{l} {u_{r}|}_{r \to \infty} = 0, {u_{θ}|}_{r \to \infty} = 0 \\ {w_{r}|}_{r \to \infty} = 0, {w_{θ}|}_{r \to \infty} = 0 \end{array}\}

(2) 桩底位移边界条件:

(11)

{u_{p}^{s}|}_{z = L_{s}}

=0,

{φ_{p}^{s}|}_{z = L_{s}}

=0°

(3) 桩-饱和土接触边界条件:

(12)

{u_{r}|}_{r = r_{0}}

u_{p}^{s}

cos θ,

{u_{θ}|}_{r = r_{0}}

u_{p}^{s}

sin θ

(13)

{w_{r}|}_{r = r_{0}}

式中: $u_{p}^{s}$ 为饱和土段中的桩基水平位移.

引入势函数解耦,根据微分算子分解法、分离变量法与边界条件可以得到非液化土中土骨架的径向位移以及环向位移表达式:

(14)

\begin{array}{l} u_{r} = [F_{2} (K_{1} (β_{1} r))' + H_{2} (K_{1} (β_{2} r))' + \\ J_{2} \frac{1}{r} K_{1} (β_{3} r)] c o s θ \\ u_{θ} = - [F_{2} \frac{1}{r} K_{1} (β_{1} r) + H_{2} \frac{1}{r} K_{1} (β_{2} r) + \\ J_{2} (K_{1} (β_{3} r))'] s i n θ \end{array}\}

式中:

β₁= $\frac{e_{1} + \sqrt{e_{1} - 4 e_{2}}}{2}$ ,β₂= $\frac{e_{1} - \sqrt{e_{1} - 4 e_{2}}}{2}$

β₃= $\frac{ρ_{f}^{2} ω^{4} - ρ ω^{2} (m ω^{2} - b_{p} ω i)}{G^{*} (m ω^{2} - b_{p} ω i)}$

e₁= $\frac{- (λ^{*} + α^{2} M + 2 G^{*}) (m ω^{2} - b_{p} ω i)}{(λ^{*} + 2 G^{*}) M}$ + $\frac{2 α ρ_{f} ω^{2} - ρ ω^{2}}{λ^{*} + 2 G^{*}}$

e₂= $\frac{ρ ω^{2} (m ω^{2} - b_{p} ω i) - ρ_{f}^{2} ω^{4}}{(λ^{*} + 2 G^{*}) M}$

$(K_{1} (β_{n} r))$ '= $\frac{\partial K_{1} (β_{n} r)}{\partial r}$ ; F₂, H₂, J₂为待定系数.

基于饱和多孔介质理论中的土体本构关系,可以得到非液化土中桩段周围土体的水平动反力q_s,表示为

(15)q_s=δF₂δ=-πr₀{(λ^*+2G^*)(

β_{1}^{2}

K₁(β₁r₀)+

β_{2}^{2}

m₁K₁(β₂r₀))+αM[(α+f₁)

β_{1}^{2}

K₁(β₁r₀)+(α+h)

β_{2}^{2}

m₁K₁(β₂r₀)]+G^*

β_{3}^{2}

m₂K₁(β₃r₀)}

式中: $\frac{H_{2}}{F_{2}}$ =m₁, $\frac{J_{2}}{F_{2}}$ =m₂; m₁= $\frac{τ_{11} τ_{23} - τ_{13} τ_{21}}{τ_{13} τ_{22} - τ_{12} τ_{23}}$ , m₂= $\frac{τ_{12} τ_{21} - τ_{11} τ_{22}}{τ_{13} τ_{22} - τ_{12} τ_{23}}$ ; τ₁₁= $(K_{1} (β_{1} r_{0}))$ '- $\frac{1}{r_{0}}$ K₁(β₁r₀), τ₁₂= $(K_{1} (β_{2} r_{0}))$ '- $\frac{1}{r_{0}}$ K₁(β₂r₀), τ₁₃= $\frac{1}{r_{0}}$ K₁(β₃r₀)- $(K_{1} (β_{3} r_{0}))$ ';τ₂₁=f₁ $(K_{1} (β_{1} r_{0}))$ ', τ₂₂=h $(K_{1} (β_{2} r_{0}))$ ', τ₂₃=j $\frac{1}{r_{0}} (K_{1} (β_{2} r_{0}))$ ; f₁= $\frac{α M β_{1}^{2} + ρ_{f} ω^{2}}{b_{p} ω i - M β_{1}^{2} - m ω^{2}}$ , h= $\frac{α M β_{2}^{2} + ρ_{f} ω^{2}}{b_{p} ω i - M β_{2}^{2} - m ω^{2}}$ , j= $\frac{ρ_{f} ω^{2}}{b_{p} ω i - m ω}$ .

2.2 桩顶阻抗求解

由动力平衡条件可以得到不同介质中桩体的自由振动控制方程:

(16)

E_{p}^{*}

I_p

\frac{\partial^{4} u_{p}^{i}}{\partial z^{4}}

\frac{\partial^{2} u_{p}^{i}}{\partial z^{2}}

-m_pω²

u_{p}^{i}

+q_i=0

式中:q_i(i=1, 2, s)分别为桩液化土、空气、饱和土段的动反力; $u_{p}^{i}$ (i=1, 2, s)分别为液化土中段、自由段、非液化土中段桩基水平位移;E_p为桩体弹性模量,当桩体存在滞回阻尼ζ_p时, $E_{p}^{*}$ =E_p(1+2ζ_pi);P为桩顶所受竖向荷载;I_p为桩段截面惯性矩;m_p为桩段单位长度质量.

可用S_i(z)表示桩身的变形和受力情况:

S_i(z)= $[\begin{array}{l} u_{p}^{i} (z) \\ φ_{p}^{i} (z) \\ M_{p}^{i} (z) \\ Q_{p}^{i} (z) \end{array}]$ =X_i(z) $[\begin{array}{l} N_{1}^{i} \\ N_{2}^{i} \\ N_{3}^{i} \\ N_{4}^{i} \end{array}]$

式中:X_i(z)为关系矩阵; $φ_{p}^{i}$ , $M_{p}^{i}$ , $Q_{p}^{i}$ (i=1, 2, s)分别为桩身液化土中段、自由段、非液化土中段的转角、弯矩和剪力; $N_{1}^{i}$ , $N_{2}^{i}$ , $N_{3}^{i}$ , $N_{4}^{i}$ (i=1, 2, s)为待定系数.

将液化土的侧向土压力表达式(5)代入式(16),结合三角函数正交性,可得液化土中段的桩基水平位移.进一步地,由Euler-Bernoulli梁理论,可得液化土桩身段的关系矩阵X₁(z)为

X₁(z)= $[\begin{array}{l} c o s γ_{1} z - \overset{\infty}{\sum_{n = 1}} C_{1} η c o s (α_{n} z) & s i n γ_{1} z - \overset{\infty}{\sum_{n = 1}} C_{2} η c o s (α_{n} z) \\ γ_{1} s i n γ_{1} z - \overset{\infty}{\sum_{n = 1}} C_{1} η α_{n} s i n (α_{n} z) & - γ_{1} c o s γ_{1} z - \overset{\infty}{\sum_{n = 1}} C_{2} η α_{n} s i n (α_{n} z) \\ E_{p}^{*} I_{p} [- γ_{1}^{2} c o s γ_{1} z + \overset{\infty}{\sum_{n = 1}} C_{1} η α_{n}^{2} c o s (α_{n} z)] & E_{p}^{*} I_{p} [- γ_{1}^{2} s i n γ_{1} z + \overset{\infty}{\sum_{n = 1}} C_{2} η α_{n}^{2} c o s (α_{n} z)] \\ E_{p}^{*} I_{p} [γ_{1}^{3} s i n γ_{1} z - \overset{\infty}{\sum_{n = 1}} C_{1} η α_{n}^{3} s i n (α_{n} z)] & E_{p}^{*} I_{p} [- γ_{1}^{3} c o s γ_{1} z - \overset{\infty}{\sum_{n = 1}} C_{2} η α_{n}^{3} c o s (α_{n} z)] \end{array}$

(17)

\begin{array}{l} c o s h γ_{2} z - \overset{\infty}{\sum_{n = 1}} C_{3} η c o s (α_{n} z) & s i n h γ_{2} z - \overset{\infty}{\sum_{n = 1}} C_{4} η c o s (α_{n} z) \\ - γ_{2} s i n h γ_{2} z - \overset{\infty}{\sum_{n = 1}} C_{3} η α_{n} s i n (α_{n} z) & - γ_{2} c o s h γ_{2} z - \overset{\infty}{\sum_{n = 1}} C_{4} η α_{n} s i n (α_{n} z) \\ E_{p}^{*} I_{p} [γ_{2}^{2} c o s h γ_{2} z + \overset{\infty}{\sum_{n = 1}} C_{3} η α_{n}^{2} c o s (α_{n} z)] & E_{p}^{*} I_{p} [γ_{2}^{2} s i n h γ_{2} z + \overset{\infty}{\sum_{n = 1}} C_{4} η α_{n}^{2} c o s (α_{n} z)] \\ E_{p}^{*} I_{p} [γ_{2}^{3} s i n h γ_{2} z - \overset{\infty}{\sum_{n = 1}} C_{3} η α_{n}^{3} s i n (α_{n} z)] & E_{p}^{*} I_{p} [γ_{2}^{3} c o s h γ_{2} z - \overset{\infty}{\sum_{n = 1}} C_{4} η α_{n}^{3} s i n (α_{n} z)] \end{array}]

式中:η= $\frac{2}{L_{l s}}$ (πr₀ρ_lsω²K₁(α_nr₀)) /[ $E_{p}^{*}$ I_p( $α_{n}^{4}$ -d⁴- $α_{n}^{2}$ b²)(K₁(α_nr))'+πρ_lsω²K₁(α_nr₀)r₀];γ₁= $\sqrt[4]{\frac{b_{1}^{2} + \sqrt{b_{1}^{2} + d_{1}^{4}}}{E_{p}^{*} I_{p}}}$ , γ₂= $\sqrt[4]{\frac{- b_{1}^{2} + \sqrt{b_{1}^{4} + d_{1}^{4}}}{E_{p}^{*} I_{p}}}$ ; $b_{1}^{2}$ = $\frac{P}{E_{p}^{*} I_{p}}$ , $d_{1}^{2}$ = $\frac{m_{p} ω^{2}}{E_{p}^{*} I_{p}}$ ;

C₁= $\int_{- L_{1}}^{0}$ cos(γ₁z) cos(α_nz)dz

C₂= $\int_{- L_{1}}^{0}$ sin(γ₁z) cos(α_nz)dz

C₃= $\int_{- L_{1}}^{0}$ cosh(γ₂z) cos(α_nz)dz

C₄= $\int_{- L_{1}}^{0}$ sinh(γ₂z) cos(α_nz)dz

自由段的桩体关系矩阵X₂(z)可通过式(17)中的各元素仅保留第1项退化得到.

同理,当桩段周围为非液化饱和土时,可以得非液化土段的关系矩阵X_s(z)为

(18)X_s(z)=

[\begin{array}{l} c o s γ_{5} z & s i n γ_{5} z & c o s h γ_{6} z & s i n h γ_{6} z \\ γ_{5} s i n γ_{5} z & - γ_{5} c o s γ_{5} z & - γ_{6} s i n h γ_{6} z & - γ_{6} c o s h γ_{6} z \\ - γ_{5}^{2} E_{p}^{*} I_{p} c o s γ_{5} z & - γ_{5}^{2} E_{p}^{*} I_{p} s i n γ_{5} z & γ_{6}^{2} E_{p}^{*} I_{p} c o s h γ_{6} z & γ_{6}^{2} E_{p}^{*} I_{p} s i n h γ_{6} z \\ γ_{5}^{3} E_{p}^{*} I_{p} s i n γ_{5} z & - γ_{5}^{3} E_{p}^{*} I_{p} c o s γ_{5} z & γ_{6}^{3} E_{p}^{*} I_{p} s i n h γ_{6} z & γ_{6}^{3} E_{p}^{*} I_{p} c o s h γ_{6} z \end{array}]

式中:γ₅= $\sqrt[4]{\frac{b_{3}^{2} + \sqrt{b_{3}^{2} + d_{3}^{4}}}{E_{p}^{*} I_{p}}}$ , γ₆= $\sqrt[4]{\frac{- b_{3}^{2} + \sqrt{b_{3}^{4} + d_{3}^{4}}}{E_{p}^{*} I_{p}}}$ ; $b_{3}^{2}$ = $\frac{P}{E_{p}^{*} I_{p}}$ , $d_{3}^{4}$ = $\frac{m_{p} ω^{2} - k_{s}}{E_{p}^{*} I_{p}}$ ,k_s= $\frac{δ}{ξ}$ ;ξ可由前文边界条件求得.

由桩身变形位移连续条件S_s(0)=S₁(0)和S₁(-L_ls)=S₂(-L_ls),采用矩阵传递法,可得到完整桩桩底与桩顶的位移、转角、弯矩、剪力间的关系:

(19)

[\begin{array}{l} u_{p} (L_{s}) \\ ϕ_{p} (L_{s}) \\ M_{p} (L_{s}) \\ Q_{p} (L_{s}) \end{array}]

[\begin{array}{l} u_{p} [- (L_{l s} + H_{1})] \\ φ_{p} [- (L_{l s} + H_{1})] \\ M_{p} [- (L_{l s} + H_{1})] \\ Q_{p} [- (L_{l s} + H_{1})] \end{array}]

式中: T=X_s(L_s) $X_{s}^{- 1}$ (0)X₁(0)X₁(-L_ls)X₂(-L_ls) $X_{2}^{- 1}$ [-(L_ls+H₁)].

已知桩的底部为刚性支承,因此桩底处的位移为0、转角为0°,进一步得到桩顶的位移、转角、弯矩、剪力间的阻抗关系矩阵:

(20)

[\begin{array}{l} M_{p} [- (L_{l s} + H_{1})] \\ Q_{p} [- (L_{l s} + H_{1})] \end{array}]

[\begin{array}{l} u_{p} [- (L_{l s} + H_{1})] \\ φ_{p} [- (L_{l s} + H_{1})] \end{array}]

式中:K为单桩阻抗矩阵,且

K=- ${[\begin{array}{l} T (1, 3) & T (1, 4) \\ T (2, 3) & T (2, 4) \end{array}]}^{- 1} [\begin{array}{l} T (1, 1) & T (1, 2) \\ T (2, 1) & T (2, 2) \end{array}]$ .

可得桩顶水平阻抗为

(21)K_h=

\frac{Q_{p} [- (L_{l s} + H_{1})]}{u_{p} [- (L_{l s} + H_{1})]}

=K(2, 1)

3 群桩相互作用分析

3.1 桩间相互作用因子

高桩主动桩p11在受到桩顶竖向荷载、水平荷载及弯矩等耦合作用时,会产生相应的位移变形,非液化土中主动桩桩身的位移变形会挤压桩周土体,使得土体产生向四周扩散的应力波,并传播到被动桩p21附近,使被动桩桩体与非液化土产生动力相互作用,不考虑被动桩振动产生次生波对主动桩的影响.假定主动桩p11与被动桩p21满足以下边界条件.

(1) 主动桩p11桩顶弯矩、剪切力不为0,桩底位移为0、转角为0°:

(22)

\begin{array}{l} {M_{p 11}|}_{z = - (H_{1} + L_{l s})} = M_{0}, {Q_{p 11}|}_{z = - (H_{1} + L_{l s})} = Q_{0} \\ {u_{p 11}|}_{z = L_{s}} = 0, {φ_{p 11}|}_{z = L_{s}} = 0 ° \end{array}\}

(2) 被动桩p21桩顶弯矩、剪切力为0,桩底位移为0、转角为0°:

(23)

\begin{array}{l} {M_{p 21}|}_{z = - (H_{1} + L_{l s})} = 0, {Q_{p 21}|}_{z = - (H_{1} + L_{l s})} = 0 \\ {u_{p 21}|}_{z = L_{s}} = 0, {φ_{p 21}|}_{z = L_{s}} = 0 ° \end{array}\}

(3) 主动桩p11与被动桩p21桩顶与刚性承台固接,因此桩顶边界条件满足:

(24)

{φ_{p 11}|}_{z = - (H_{1} + L_{l s})}

{φ_{p 21}|}_{z = - (H_{1} + L_{l s})}

=0°

根据式(14),由土体的切向位移u_θ与径向位移u_r可求得桩周土体水平位移u_x:

(25)

\begin{array}{l} u_{x} = u_{r} c o s θ - u_{θ} s i n θ = \\ (Γ_{1} (r) c o s^{2} θ - Γ_{2} (r) s i n^{2} θ) F_{2} \\ Γ_{1} (r) = β_{1} \frac{K_{2} (β_{1} r) + K_{0} (β_{1} r)}{2} + \\ m_{1} β_{2} \frac{K_{2} (β_{2} r) + K_{0} (β_{2} r)}{2} + \\ m_{2} \frac{K_{1} (β_{3} r)}{r} \\ Γ_{2} (r) = - (\frac{1}{r} K_{1} (β_{1} r) + m_{1} \frac{1}{r} K_{1} (β_{2} r) + \\ m_{2} β_{3} \frac{K_{2} (β_{3} r) + K_{0} (β_{3} r)}{2}) \end{array}\}

当主动桩发生位移时,桩周土体以辐射波的形式向四周扩散,主动桩附近土体的位移受到该点与主动桩的距离s和激振荷载入射夹角θ控制.因此可定义主动桩周边不同位置处的土体水平位移衰减函数Ψ:

(26)Ψ(s, θ)=

\frac{u (s)}{u (r_{0})}

\frac{Γ_{1} (s) c o s^{2} θ - Γ_{2} (s) s i n^{2} θ}{Γ_{1} (r_{0}) c o s^{2} θ - Γ_{2} (r_{0}) s i n^{2} θ}

位于非液化土中的被动桩段水平振动控制方程:

(27)E_pI_p

\frac{\partial^{4} u_{p 21}^{s}}{\partial z^{4}}

\frac{\partial^{2} u_{p 21}^{s}}{\partial z^{2}}

-m_pω²

u_{p 21}^{s}

+k_s(

u_{p 21}^{s}

-Ψ

u_{p 11}^{s}

)=0

该方程的特解为

(28)

\begin{array}{l} u_{p 21}^{s} (z) = u_{p 21}^{s (1)} (z) + u_{p 21}^{s (2)} (z) \\ u_{p 21}^{s (1)} (z) = {R^{s}}_{1} c o s γ_{5} z + {R^{s}}_{2} s i n γ_{5} z + \\ {R^{s}}_{3} c o s h γ_{6} z + {R^{s}}_{4} s i n h γ_{6} z \\ u_{p 21}^{s (2)} (z) = ε_{1} (z) {N^{s}}_{1} + ε_{2} (z) {N^{s}}_{2} + \\ ε_{3} (z) {N^{s}}_{3} + ε_{4} (z) {N^{s}}_{4} \end{array}\}

式中: $R_{1}^{s}$ , $R_{2}^{s}$ , $R_{3}^{s}$ , $R_{4}^{s}$ 为待定系数;γ₅,γ₆计算方法与式(18)一致,并且

(29)

\begin{array}{l} ε_{1} (z) = - \frac{k_{s} Ψ}{E_{p}^{*} I_{p}} \frac{z}{2 \sqrt{b_{3}^{4} + 4 d_{3}^{4}} γ_{5}} s i n γ_{5} z \\ ε_{2} (z) = \frac{k_{s} Ψ}{E_{p}^{*} I_{p}} \frac{z}{2 \sqrt{b_{3}^{4} + 4 d_{3}^{4}} γ_{5}} c o s γ_{5} z \\ ε_{3} (z) = \frac{k_{s} Ψ}{E_{p}^{*} I_{p}} \frac{z}{2 \sqrt{b_{3}^{4} + 4 d_{3}^{4}} γ_{6}} s i n h γ_{6} z \\ ε_{4} (z) = \frac{k_{s} Ψ}{E_{p}^{*} I_{p}} \frac{z}{2 \sqrt{b_{3}^{4} + 4 d_{3}^{4}} γ_{6}} c o s h γ_{6} z \end{array}\}

令:

(30)X_s2(z)=

[\begin{array}{l} ε_{1} (z) & ε_{2} (z) & ε_{3} (z) & ε_{4} (z) \\ - ε'_{1} (z) & - ε'_{2} (z) & - ε'_{3} (z) & - ε'_{4} (z) \\ ε ″_{1} (z) E_{p}^{*} I_{p} & ε ″_{2} (z) E_{p}^{*} I_{p} & ε ″_{3} (z) E_{p}^{*} I_{p} & ε ″_{4} (z) E_{p}^{*} I_{p} \\ ε ‴_{1} (z) E_{p}^{*} I_{p} & ε ‴_{2} (z) E_{p}^{*} I_{p} & ε ‴_{3} (z) E_{p}^{*} I_{p} & ε ‴_{4} (z) E_{p}^{*} I_{p} \end{array}]

则被动桩p21的桩身变形和受力的矩阵表达式可写作:

(31)S_p21(z)=X_s(z)R_s+X_s2(z)N_s

式中:R_s= ${[\begin{array}{l} {R^{s}}_{1} & {R^{s}}_{2} & {R^{s}}_{3} & {R^{s}}_{4} \end{array}]}^{T}$ 和N_s= ${[\begin{array}{l} {N^{s}}_{1} & {N^{s}}_{2} & {N^{s}}_{3} & {N^{s}}_{4} \end{array}]}^{T}$ 均为待定系数向量;S_p21(z)= ${[\begin{array}{l} u_{p 21}^{s} (z) & φ_{p 21}^{s} (z) & M_{p 21}^{s} (z) & Q_{p 21}^{s} (z) \end{array}]}^{T}$ .

可以得到非液化土中被动桩桩底与被动桩桩顶、主动桩桩顶的受力变形矩阵关系式:

(32)S_p21(L_s)=

[\begin{array}{l} u_{p 21}^{s} (L_{s}) \\ φ_{p 21}^{s} (L_{s}) \\ M_{p 21}^{s} (L_{s}) \\ Q_{p 21}^{s} (L_{s}) \end{array}]

= T₂

[\begin{array}{l} u_{p 21}^{s} (0) \\ ϕ_{p 21}^{s} (0) \\ M_{p 21}^{s} (0) \\ Q_{p 21}^{s} (0) \end{array}]

+T₁

[\begin{array}{l} u_{p 11}^{s} (0) \\ φ_{p 11}^{s} (0) \\ M_{p 11}^{s} (0) \\ Q_{p 11}^{s} (0) \end{array}]

式中:T₂=X_s(L_s) $X_{s}^{- 1}$ (0);T₁可通过被动桩桩顶、桩底的表达式变形得到T₁=X_s2(L_ls) $X_{s 2}^{- 1}$ (0)-T₂X_s2(0) $X_{s 2}^{- 1}$ (0).

结合桩体自由段、液化段、非液化段的位移连续条件,由刚度矩阵传递可得:

(33)

[\begin{array}{l} u_{p 21}^{s} (L_{s}) \\ φ_{p 21}^{s} (L_{s}) \\ M_{p 21}^{s} (L_{s}) \\ Q_{p 21}^{s} (L_{s}) \end{array}]

=T₂T₀

[\begin{array}{l} u_{p 21}^{2} [- (L_{l s} + H_{1})] \\ φ_{p 21}^{2} [- (L_{l s} + H_{1})] \\ M_{p 21}^{2} [- (L_{l s} + H_{1})] \\ Q_{p 21}^{2} [- (L_{l s} + H_{1})] \end{array}]

+ T₁T₀

[\begin{array}{l} u_{p 11}^{2} [- (L_{l s} + H_{1})] \\ φ_{p 11}^{2} [- (L_{l s} + H_{1})] \\ M_{p 11}^{2} [- (L_{l s} + H_{1})] \\ Q_{p 11}^{2} [- (L_{l s} + H_{1})] \end{array}]

式中:T₀=X₁(0) $X_{1}^{- 1}$ (-L_ls)X₂(-L_ls) $X_{2}^{- 1}$ [-(L_ls+H₁)].

令T₄=T₂T₀,T₃=T₁T₀,结合被动桩桩底边界条件,可以得到被动桩与主动桩间的相互作用关系矩阵:

(34)

[\begin{array}{l} u_{p 21}^{2} [- (L_{l s} + H_{1})] \\ φ_{p 21}^{2} [- (L_{l s} + H_{1})] \end{array}]

[\begin{array}{l} u_{p 11}^{2} [- (L_{l s} + H_{1})] \\ φ_{p 11}^{2} [- (L_{l s} + H_{1})] \end{array}]

式中:A=- ${[\begin{array}{l} T_{4} (1, 1) & T_{4} (1, 2) \\ T_{4} (2, 1) & T_{4} (2, 2) \end{array}]}^{- 1}$ × $([\begin{array}{l} T_{4} (1, 1) & T_{4} (1, 2) \\ T_{4} (2, 1) & T_{4} (2, 2) \end{array}]$ + $[\begin{array}{l} T_{4} (1, 3) & T_{4} (1, 4) \\ T_{4} (2, 3) & T_{4} (2, 4) \end{array}] K)$ ,具体求解方法可参考文献[10].进而得到以位移定义的桩间水平相互作用因子α_up:

(35)α_up=

\frac{u_{p 21} [- (L_{l s} + H_{1})]}{u_{p 11} [- (L_{l s} + H_{1})]}

\frac{A (1, 1) f^{s} (1, 1) + A (1, 2) f^{s} (2, 1)}{f^{s} (1, 1)}

式中:f^s=K^-1.

3.2 群桩阻抗求解

承台水平荷载由各桩共同承担:

(36)Q=

\overset{N}{\sum_{j = 1}}

Q_j

由位移叠加原理可知:

(37)u_g=u_i=

\overset{N}{\sum_{j = 1}}

α_iju_j=

\overset{N}{\sum_{j = 1}}

α_ij

\frac{Q_{j}}{K_{h}}

式中:u_g为群桩的桩头水平位移;u_j, u_i分别为主动桩P_j和被动桩P_i的桩头位移;α_ij为主动桩P_j与被动桩P_i间的水平动力相互作用因子,当i=j时,α_ij=1;Q_j为桩j分担的水平荷载.

式(36)和式(37)可写为矩阵形式:

(38)

[\begin{array}{l} Q \\ 0 \\ ︙ \\ 0 \\ 0 \end{array}]

[\begin{array}{l} 1 & 1 & \dots & 1 & 0 \\ \frac{1}{K_{h}} & \frac{α_{12}}{K_{h}} & \dots & \frac{α_{1 N}}{K_{h}} & - 1 \\ \frac{α_{21}}{K_{h}} & \frac{1}{K_{h}} & \dots & \frac{α_{2 N}}{K_{h}} & - 1 \\ ︙ & ︙ & ⋱ & ︙ & ︙ \\ \frac{α_{N 1}}{K_{h}} & \frac{α_{N 2}}{K_{h}} & \dots & \frac{1}{K_{h}} & - 1 \end{array}] [\begin{array}{l} Q_{1} \\ Q_{2} \\ ︙ \\ Q_{N} \\ u_{g} \end{array}]

通过矩阵求逆运算即可得到群桩中各单桩所受水平力Q_i和群桩位移u_g.将计算结果代入群桩水平阻抗K_gh的计算公式:K_gh=Q/u_g,最终可得到无量纲群桩桩顶水平阻抗:

(39)k_gh=

\frac{r_{0}^{3}}{E_{p} I_{p}}

Re(K_gh), c_gh=

\frac{r_{0}^{3}}{E_{p} I_{p}}

lm(K_gh)

式中:k_gh为无量纲群桩水平动刚度;c_gh为反映群桩能量耗散的无量纲水平动阻尼:Re代表实部;Im代表虚部.

4 模型有效性分析

数值计算参数如下:r₀=0.5 m,L=20 m,α=1,M=4.6 GPa,ν=0.3,n₀=0.3,ρ_s=2 700 kg/m³,ρ_p=2 500 kg/m³,G=10 MPa,E_p=40 GPa,k_d=10^-6 m/s,ζ=0,ζ_p=0,s=5d₀.本节频率均采用无量纲频率a₀=2ωr₀/ $\sqrt{G / ρ}$ .

将本文解退化为不考虑竖向荷载时饱和地基中桩顶阻抗解(L_ls=0 m,P=0 kN),与Kaynia等^[21]、刘圆圆^[12]所给出的群桩解进行对比,结果如图3所示.分别对完全埋入桩和高桩桩间水平相互作用因子的结果进行对比,可以看到退化解与已有解的结果吻合度较好,完全埋入桩相互作用因子与已有解略有差异,这是由于两者所采取的衰减函数形式以及采用的理论模型不同,但变化趋势吻合,验证了本文解的合理性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 桩间水平相互作用因子的对比验证

Fig.3 Comparative verification of interaction factors of horizontal piles

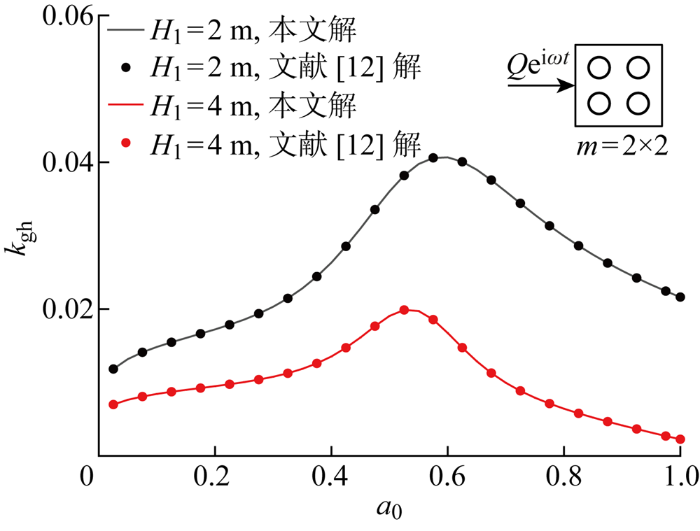
将桩基退化为无竖向荷载、无液化土中的部分埋入群桩水平振动解,与已有忽略孔隙流体压缩性的群桩水平振动解进行对比(n₀=0.4,E_p=30 GPa,其余参数取值同上),结果如图4所示.可以看到不同埋入比下的群桩(m=2×2)水平复阻抗解吻合较好,m为群桩排列方式.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 群桩阻抗退化解的对比验证

Fig.4 Comparative verification of group pile impedance degenerate solution

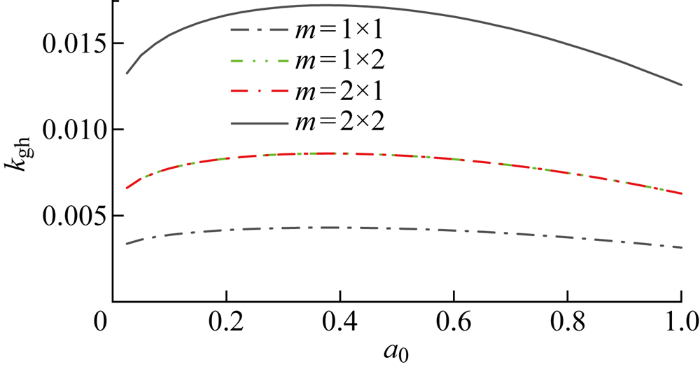
栾鲁宝^[22]已有研究指出,桩间相互作用随着桩间距的增大而减小.因此,只要桩间距无限大时,可以忽略群桩间的相互作用,群桩阻抗可视作各单桩阻抗之和.取桩间距s/d₀=2 000,对比不同桩数时群桩阻抗的大小,结果如图5所示.可以看出当桩间距离足够大时,同一频率下群桩阻抗接近于单桩阻抗的桩数倍,验证了本文解的合理性.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 大桩间距下不同桩数群桩基础水平动刚度对比

Fig.5 Comparison of horizontal dynamic.pngfness of pile foundation with different pile groups under large pile spacing condition

5 算例分析

针对影响液化土中的群桩水平动力特性的参数分析中,n₀=0.4,E_p=30 GPa,ζ=0.02,P=1 000 kN,其余参数同前.

5.1 桩间水平相互作用因子参数分析

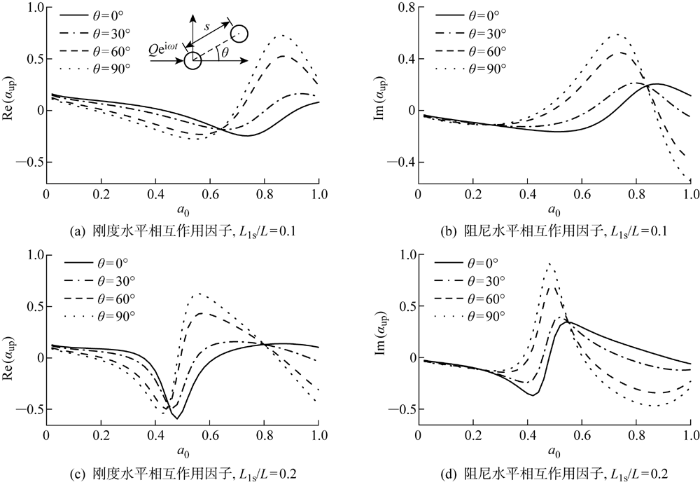
设水平激振作用方向与两桩的夹角θ=0°,液化土厚度占比L_ls/L=0,0.05,0.1,0.2.图6反映了在竖向荷载作用下,不同厚度的表层液化土中高桩桩间相互作用因子随水平荷载频率的变化规律,相互作用因子的实部和虚部都会随着频率的变化呈现出一定的振荡特性.在a₀<0.2的低频范围内,随着液化土厚度的增大,桩间水平相互作用因子实部减小,说明在低频范围内土体液化会导致桩-桩相互作用效应减弱.在高频范围内,相互作用因子的振荡幅值随着液化土相对厚度的增大逐渐增大,其中峰谷位置朝低频方向移动,且波峰波谷间的距离缩短.这是由于表面土体液化导致桩-土-桩系统的整体刚度下降,系统的共振频率随之发生下降,达到相互作用因子的极值所需要的频率也随之下降.液化层厚度比越高的地基中高桩桩间相互作用因子更具频率敏感性,传统的动刚度放大法将不再适用.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 液化层厚度比对桩间相互作用因子的影响

Fig.6 Effect of liquefied layer thickness ratio on piles interaction factor

图7反映了在常见的水平荷载范围内,水平激振作用方向与桩间连线的夹角θ对高桩桩间水平相互作用因子的影响.取θ=0°,30°,60°,90°,其余参数与前文一致.如图7所示, 在低频阶段, 桩基水平相互作用因子实部随着夹角的增大而减小,虚部受夹角变化的影响较小.这是由于主动桩振动生成的应力波在各个方向上的大小不同,与荷载的夹角较小的方向应力波较大,所以也对应着较高的相互作用因子.在高频阶段,随着荷载作用夹角的增大,桩间水平相互作用因子波动的幅值不断增大,更具频率敏感性.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 荷载作用夹角对桩间相互作用因子的影响

Fig.7 Effect of load angle on piles interaction factor

5.2 群桩水平动阻抗参数分析

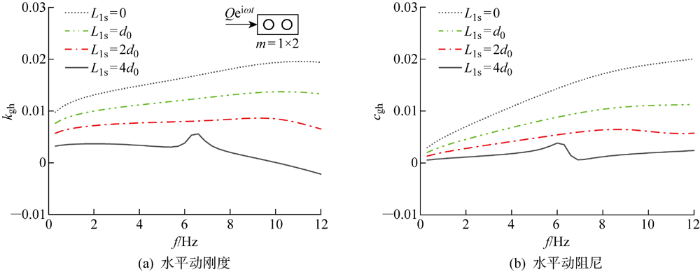
控制液化土密度不变,液化土厚度L_ls=0,d₀,2d₀,4d₀,其余参数与前文一致.图8反映了无竖向荷载作用时,不同厚度表层液化土中高桩群桩(1×2)水平阻抗随荷载频率的变化.如图8所示,同一频率下,群桩阻抗随着表层液化土厚度的增加而下降.液化土越厚,群桩阻抗波动性越明显,阻抗峰值所处的频率进一步减小,在较高频率下变为负刚度,这要求在工程设计时严格控制可液化深度.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同厚度液化土中群桩基础水平阻抗

Fig.8 Horizontal impedance of pile group in liquefied soil of different thicknesses

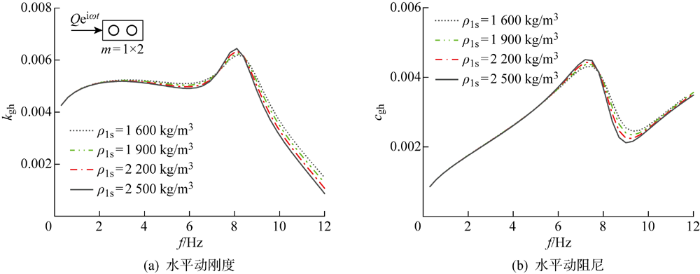
进一步探究液化土密度对群桩阻抗的影响,保持液化土深度L_ls=3d₀不变,自由段桩基H₁=1 m.表层液化土密度分别取:ρ_ls=1 600,1 900,2 200,2 500 kg/m³,其余参数同前,如图9所示.在低频范围内,桩周液化土密度对群桩阻抗的影响不显著.随着激振频率的提高,由液化土密度产生的群桩阻抗结果差异性得以显现:① 当激振频率达到 6 Hz 以上时,液化土密度才对群桩动阻尼产生明显效果;② 液化土密度越大,群桩阻抗峰值越大,波动性越大.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同液化土密度对群桩水平阻抗的影响

Fig.9 Effect of different density of liquefied soil on horizontal impedance of pile group

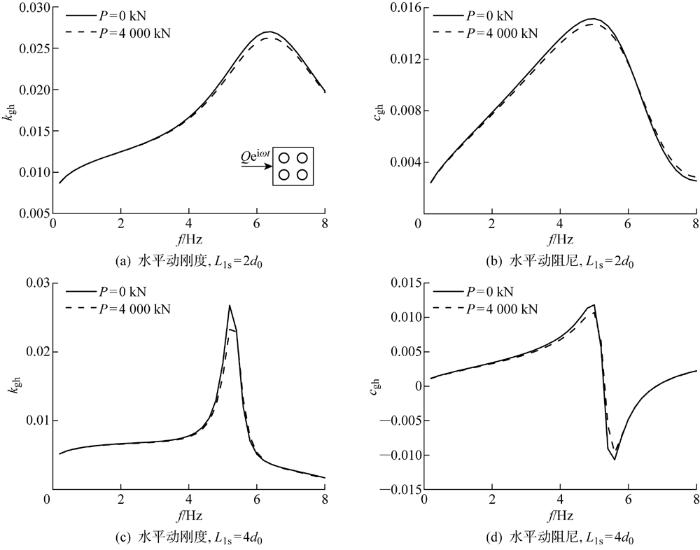
进一步分析海洋工程中常见的2×2群桩基础桩顶阻抗特性,保持桩间距不变,竖向荷载P=0,4 000 kN.高桩上部自由段高度取d₀,液化土深度L_ls=2d₀,4d₀,如图10所示.竖向荷载的存在减小了水平阻抗曲线的波动程度.对于水平动刚度而言,竖向荷载使全频率范围内桩顶水平动刚度降低,这是由于竖向荷载在桩内产生了P-Δ效应(Δ为水平位移),在轴力较小,不考虑失稳破坏时,P-Δ效应产生的附加弯矩将增大桩基的水平位移,从而使得水平动刚度相较于无轴力条件时发生下降.并且,在波动峰值时竖向荷载的影响效果最为显著,一般认为,群桩动力效应的存在造成动刚度频域曲线的波峰出现,而竖向荷载作为一种边界约束条件,会造成群桩动力效应减弱,在波峰处表现为相对较大程度的刚度下降.随着液化土厚度的增大,波峰处的刚度下降幅度更加明显,而且增大效应所对应的频率范围变小,会对工程安全产生不利影响.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 桩顶竖向荷载对群桩水平阻抗的影响

Fig.10 Effect of vertical load on horizontal impedance of pile group

6 结论

本文基于Biot饱和多孔介质理论,结合海洋表层土易液化的特点,对表层液化地基中承受竖向-水平耦合荷载作用的高桩水平振动特性进行了研究.将上部液化土视作完全流体,通过矩阵传递法求得被动桩桩顶受力变形解,由水平位移定义的高桩桩间相互作用因子,求得液化土中群桩桩顶水平阻抗的表达式.得到以下结论:

(1) 低频范围内,随着液化层厚度比增大,桩间相互作用效应减弱,在高频范围内,液化层厚度比越高的地基中桩间相互作用因子对激振频率更敏感,且由于系统整体刚度的减小,相互作用因子将在更低的频率下到达峰值.

(2) 同一频率下,群桩水平动刚度随着表层液化土厚度的增加而下降,当液化层厚度比越高时,动刚度随着频率的上升显著下降,并出现负刚度;在高频阶段,液化土密度产生的群桩阻抗结果差异性得以显现.

(3) 在低频范围内,桩周液化土密度对群桩阻抗影响不显著,随着激振频率的提高,密度对群桩动阻尼的产生明显影响,液化土密度越大,群桩阻抗峰值越大.

(4) 桩顶竖向荷载会在桩内产生P-Δ效应,导致液化土中的群桩水平动刚度下降,且液化土厚度越大,削弱效果越明显.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ZHANG

, WANG

Development of offshore wind power and foundation technology for offshore wind turbines in China

[J]. Ocean Engineering, 2022, 266: 113256.