船舶碰撞事故不仅严重危害船舶航行安全,还会造成经济损失、环境污染及人员伤亡等严重后果.为了降低此类事故发生所造成的损失,需对船舶的抗碰撞能力进行研究,以期提出更合理的抗碰撞结构设计方案.船舶碰撞损伤研究方法主要有:简化解析方法、数值模拟方法、试验方法及经验方法[1].相对于其他方法,能够快速预报船体结构耐撞性能的简化解析方法得到了研究人员的广泛关注.
针对球形物撞击船体结构的情形,许多学者做了相关的研究,Wang等[2]将固支圆板的变形模式假定为球形与直线相结合,并认为板的变形抗力主要由膜拉伸作用产生,推导出了板发生大变形时的变形抗力-横向变形的关系式.刘敬喜等[3]讨论了单壳舷侧结构的破坏模式,并提出了计算舷侧构件梁和板耐撞性的解析方法.庄科挺等[4]提出了考虑摩擦力影响的固支加筋板结构的简化解析方法,并详细讨论了球形物体撞击下舷侧加筋板的损伤渐进过程.Gong等[5]对固支圆板的塑性大变形进行了详细讨论,假定其变形模式为球面、抛物面与对数曲面的组合形式,推导了板的抵抗力-横向变形的关系式.张敏等[6]给出了以抛物形式模拟板及其附连加强筋变形模式的理论模型,基于塑性力学理论,得到了球形物体作用下加筋板的撞击力计算公式.
随着研究的不断深入,不少学者开始关注船舶结构设计常见的楔形船艏撞击船体结构的耐撞性分析.Cho等[7]在以系列加筋板为撞击对象,楔形物为撞击物的试验基础上,提出了针对加筋板的理论计算模型,将板受面载荷作用所形成的塑性铰划分为轴对称的4个区域,分区域推导得到一套简化解析方法.Sun等[8]将前倾型船艏视为刚性楔形撞头,提出了倾斜船艏撞击下船体板及舷侧骨材变形模式的理论模型,考虑变形区域的主要能量耗散形式,推导了倾斜楔形艏撞击船体板、舷侧骨材及纵桁的解析计算公式.Zhang等[9]基于矩形板受楔形平头撞头撞击的变形响应试验研究,给出了矩形板在面载荷作用下发生大变形的抵抗力计算公式.黄东等[10]将矩形板的塑性变形区域分为4个板块,在以抛物曲面模拟其变形模式的假定基础上,推导了固支矩形板受楔形物压载的抵抗力与横向变形之间的关系式.加筋板结构作为船舶舷侧主要结构,在抵抗碰撞中发挥重要作用,因此,对加筋板结构进行耐撞性研究是十分必要的.然而,目前针对楔形物偏心垂向作用下加筋板产生的变形抗力的计算公式较少.
1 简化解析方法
1.1 矩形板在楔形物作用下的简化解析方法
在实际的船体结构中,船体板的周界通常由纵横强构件作为它的支撑,因此在船舶结构碰撞分析中将船体板看作四周固支矩形板处理是合理的,这就为船体板的耐撞性分析带来了极大的简化.与文献[9]有所不同的是,在本文的分析中考虑楔形物偏离矩形板中心垂向压载作用于固支矩形板.
由于实际结构变形可能会十分复杂,所以为保证解析计算模型的可靠性并对推导过程进行简化,做出如下假定:
(1) 忽略材料的弹性效应,假定材料为理想刚塑性材料,遵循Mises屈服条件.
(2) 忽略构件之间的耦合作用,假定结构各构件单独作用,且结构变形时所涉及的不同能量耗散机制之间互不影响.
(3) 忽略局部凹陷对变形模式的影响,假定结构变形模式为直线形式.
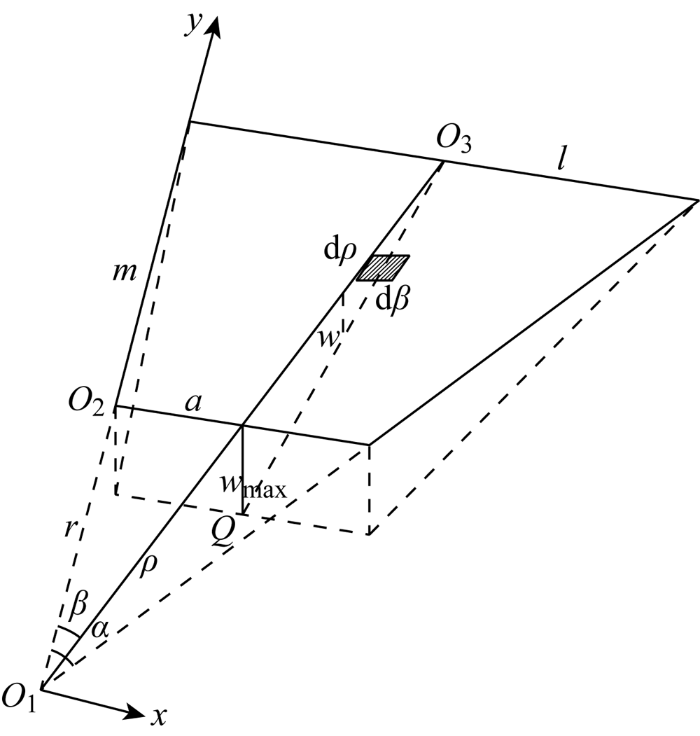
楔形加载头垂向压载作用于固支矩形板任意位置的变形模式如图1所示.图中:以楔形头尖端中点为坐标原点,建立xOy直角坐标系;矩形板尺寸为2l×2m(l和m分别为矩形板的半长和半宽);楔形加载头尺寸为2a(a为楔形加载头的半长);夹角为2θ;l1、l2为矩形板的长边被加载头中线分开的两侧长度;m1、m2为矩形板的短边被加载头尖端长度方向轴线分开的两侧宽度;wmax为最大横向位移;①~⑧为矩形板被分成的8个区域的编号.
图1
考虑楔形加载头与矩形板接触部分的形状,可视矩形板受到线载荷偏心压载作用.假设在加载头压载过程中,矩形板与楔形加载头接触的部分是固定不变的,同时将楔形加载头视为刚性.因此,直角坐标系中第一象限的板可被楔形加载头与矩形板顶点的斜连线划分为两部分,即区域①和区域②.其他象限同理,则可将整个矩形板分为8个部分.分别推导矩形板8个部分的变形抗力与最大横向变形之间的关系式,随后根据文献[13]中的叠加原理对矩形板8个部分的结果进行线性叠加,即可得到矩形板受楔形加载头偏心垂向作用的整体变形抗力与最大横向变形之间的关系曲线.
图2
本文假设矩形板受压载形成的塑性绞线的变形模式为直线形式,以区域①两侧边延长线的交点O1为坐标原点,建立xO1y直角坐标系,则在区域①中任意转角β下的线O1O3的变形表达式可以写为
式中:c1和c2为待定系数.
由几何关系可知:
式中:r为线O1O2的长度.因此,可以由边界条件确定c1和c2,整理后得到板的变形表达式为
矩形板在变形过程中的主要通过膜拉伸作用进行能量耗散,因此考虑板的膜拉伸作用,拉伸应变εp可由公式εp=
故区域①的矩形板在变形过程中的膜拉伸能量率
式中:σ0,p为板的塑性流动应力,σ0, p=
根据上限定理,外力功的功率与结构变形能量耗散率相等,则有:
式中:P1为①区域处的矩形板的变形抗力.
将各表达式代入式(9),整理后可以得到区域①的变形抗力P1与最大横向位移wmax的关系如下:
同理,可以得到矩形板的区域②至区域⑧所对应的变形抗力与最大横向位移的关系式如下:
矩形板在楔形加载头偏心准静态压载作用下的整体变形抗力P可以通过线性叠加各区域的变形抗力得到,其表达式为
1.2 骨材在楔形物作用下的简化解析方法
图3
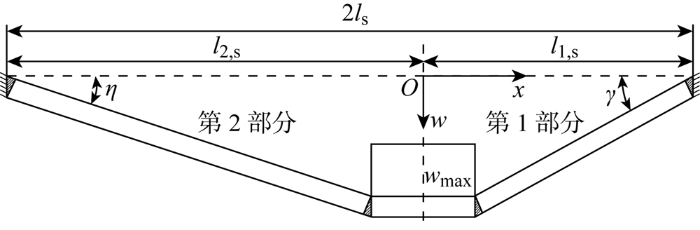
在楔形加载头压载作用下,梁会同时承受拉伸作用和弯曲作用.与矩形板的分析类似,由楔形加载头中轴线将梁分为两个部分,分别推导梁各个部分在楔形加载头偏心压载作用下的变形抗力后线性叠加即可得到梁的整体变形抗力.梁在进入塑性阶段之后,假设其变形模式为:在梁与楔形加载头接触区域(0≤x≤a),梁的上表面紧贴加载头,未发生变形;在梁与楔形加载头非接触区域产生拉伸作用(-l2,s≤x≤-a, a≤x≤l1,s),采用直线形式进行简化,弯曲作用集中在梁的端部及与楔形加载头的交界处,用阴影表示.此外,文献[13]中研究表明梁在受压载过程中会发生不同程度的侧偏,但侧偏程度大小对变形抗力的影响不大,因此,为了简化分析,假设梁在大变形过程中不发生侧偏.
将梁置于xOw直角坐标系中.梁在有限变形过程中第1部分端部的转角γ可表示为
则可以得到梁的角速度
那么,第1部分梁的弯曲能量率
式中:σ0,s是梁的塑性流动应力,σ0,s=
梁的拉伸应变ε1,s和拉伸应变率
第1部分梁的膜拉伸能量率
式中:S1,s是梁第1部分受到拉伸作用的面积,S1,s=xhs.
根据上限定理,外力功的功率与结构的应变能量耗散率相等,则有:
式中:F1为第1部分梁的变形抗力.
结合式(21)及式(24),可以得到第1部分梁的变形抗力与最大横向位移的关系表达式为
第2部分梁的变形抗力与第1部分梁的求解过程相同,因此可以得到第2部分梁的转角和变形抗力F2与最大横向变形之间的关系式为
那么,刚塑性梁在楔形加载头偏心准静态压载作用下的整体变形抗力F为
2 简化解析方法的验证与结果分析
2.1 仿真技术与试验结果对比
本文采用非线性有限元软件Abaqus进行有限元仿真计算,采用S4R壳单元进行建模,采用显示动力学方法进行准静态压载计算.
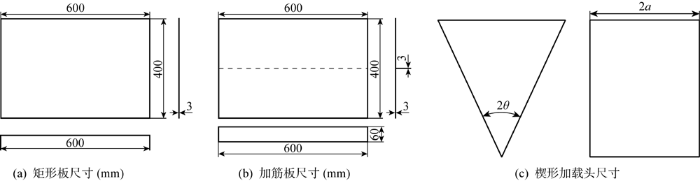
在进行有限元仿真计算分析前,为了验证本文所使用的非线性有限元技术及计算的准确性,根据已有的外壳光板受球形加载头准静态压载试验[15]进行了有限元仿真模拟.有限元仿真模拟中使用的矩形板尺寸(2l×2m)为600 mm×600 mm,厚度为3.15 mm,球形加载头半径为75 mm.有限元仿真模拟中采用的网格尺寸划分为3 mm,约束矩形板四周节点6个方向的自由度,即边界条件为四周刚性固定,整体模型设置全局接触,静摩擦因数设定为0.3,失效应变为0.6,压载至模型发生断裂破坏.为使有限元模拟更接近真实情况且更好地验证解析解,本文选取文献[15]中得到的材料真实应力应变关系作为有限元模拟的输入条件,其表达式为
式中:σeq和εeq分别为材料的等效应力和等效应变;σy是材料的屈服应力;εplat是材料屈服阶段结束时的应变值;k是材料的强化系数;n是材料的应变硬化指数.那么,本文有限元模拟中输入的材料力学性能参数如下:弹性模量E=207 GPa,σy=302.8 MPa,抗拉强度σu=408.4 MPa,断裂应变εf=0.306,εplat=0.019 2,k=690.2 MPa,n=0.2.
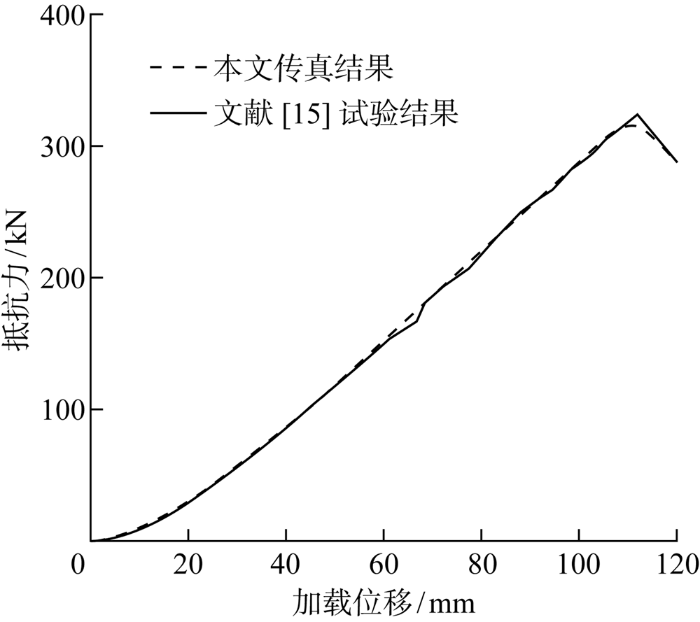
外壳光板受球形加载头作用的抵抗力-加载位移曲线如图4所示.曲线峰值处,即结构失去承载能力时,有限元模拟结果与文献中试验结果的误差为2.48%,曲线整体吻合良好.因此,本文采用的有限元仿真模拟方法用于后续的仿真模拟计算是适合且合理的.
图4
图4
球形加载头作用下变形抗力-加载位移曲线
Fig.4
Resistance-penetration curves under sphere impact
2.2 简化解析公式的验证
图5
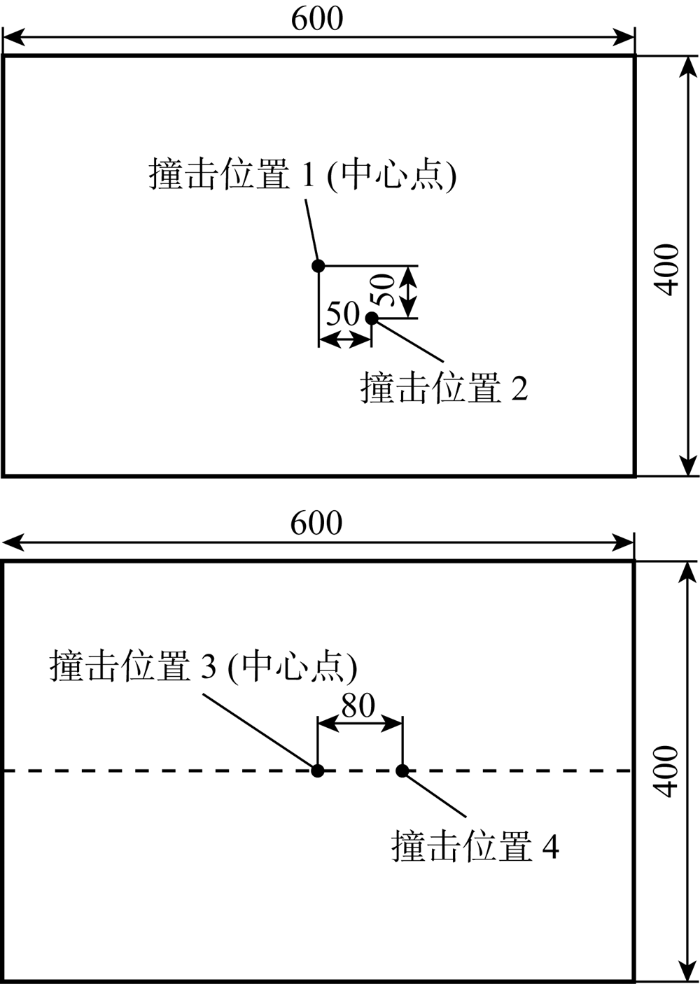
表1 有限元模拟工况设计
Tab.1
| 工况 | 模型尺寸 | 撞击 位置 | |||
|---|---|---|---|---|---|
| 2l×2m/ (mm×mm) | 2a/mm | 2ls×hs/ (mm×mm) | ts/mm | ||
| A1 | 600×400 | 80 | — | — | 1 |
| A2 | 600×400 | 160 | — | — | 1 |
| A3 | 600×400 | 240 | — | — | 1 |
| AD2 | 600×400 | 160 | — | — | 2 |
| B1 | 600×400 | 80 | 600×60 | 3 | 3 |
| B2 | 600×400 | 160 | 600×60 | 3 | 3 |
| B3 | 600×400 | 240 | 600×60 | 3 | 3 |
| BD2 | 600×400 | 160 | 600×60 | 3 | 4 |
| C1 | 600×400 | 160 | 600×40 | 3 | 3 |
| C2 | 600×400 | 160 | 600×80 | 3 | 3 |
| D1 | 600×400 | 160 | 600×60 | 2 | 3 |
| D2 | 600×400 | 160 | 600×60 | 4 | 3 |
图6
图7
2.3 结果对比与分析
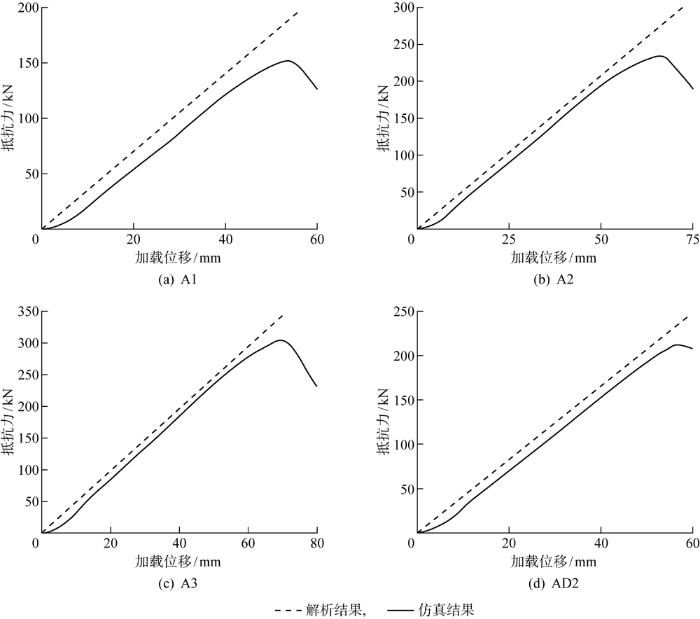
由式(18)计算矩形板不同区域的变形抗力并进行叠加得到整个矩形板模型的抵抗力-加载位移曲线,如图8所示,为了方便比较分析,图中也给出了相应的工况通过有限元仿真计算得到的抵抗力-加载位移曲线.
图8
图8
矩形板模型抵抗力-加载位移曲线
Fig.8
Resistance-penetration curves of rectangular plate models
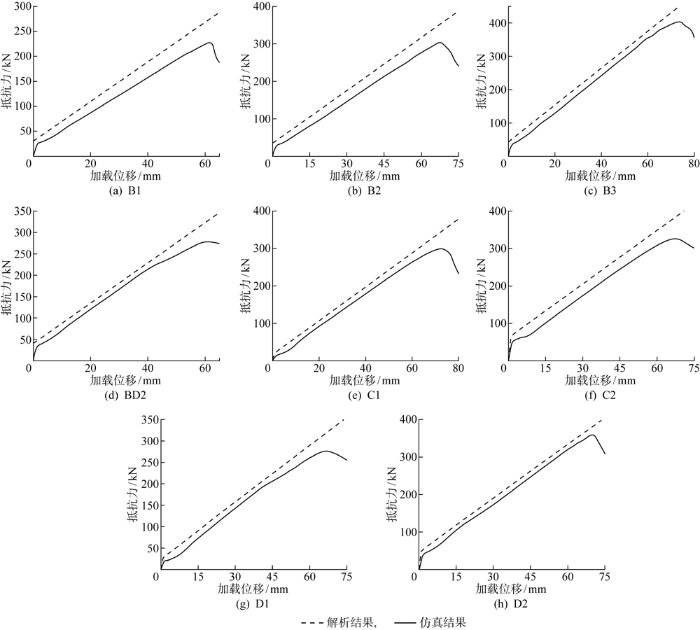
在船舶低速碰撞分析中,加筋板结构受准静态压载变形损伤主要通过板中面内的膜力和骨材截面的轴力进行能量耗散,为简化计算,将矩形板与骨材视为单独作用,忽略其中弯矩与剪力的相互传递.因此,在矩形板不同区域的变形抗力计算结果的基础上,根据式(29)计算加强筋不同部分的变形抗力并与矩形板的变形抗力结果叠加得到整个单筋加筋板的抵抗力-加载位移曲线,如图9所示,为了方便比较分析,图中也给出了相应的工况通过有限元仿真计算得到的抵抗力-加载位移曲线.
图9
图9
单筋加筋板模型抵抗力-加载位移曲线
Fig.9
Resistance-penetration curves of single-reinforced.pngfened plate models
矩形板及单筋加筋板结构在楔形加载头作用下失去承载能力时的数据与简化解析方法计算得到的变形抗力结果如表2所示.
表2 有限元模拟与理论计算结果
Tab.2
| 模型 编号 | 结构失效时数据 | 解析计算 变形抗力/kN | 误差/% | |
|---|---|---|---|---|
| 加载位移/mm | 抵抗力/kN | |||
| A1 | 53.5 | 151.4 | 187.5 | 23.8 |
| A2 | 66.1 | 234.8 | 274.6 | 17.0 |
| A3 | 69.3 | 304.2 | 340.1 | 11.8 |
| AD2 | 56.4 | 211.8 | 233.1 | 10.1 |
| B1 | 61.9 | 227.1 | 275.3 | 21.2 |
| B2 | 67.5 | 303.2 | 351.5 | 15.9 |
| B3 | 73.6 | 403.5 | 449.9 | 11.5 |
| BD2 | 58.8 | 276.8 | 317.8 | 14.8 |
| C1 | 71.9 | 299.0 | 340.7 | 13.9 |
| C2 | 67.0 | 326.1 | 386.2 | 18.4 |
| D1 | 66.5 | 276.1 | 318.7 | 15.4 |
| D2 | 69.8 | 359.9 | 380.8 | 5.8 |
据图8中矩形板的简化解析计算结果与有限元模拟结果对比可知,4种工况下的简化解析计算结果与有限元模拟结果趋势相同且误差较小,说明本文提出的简化解析方法能较好地预报矩形板受楔形加载头对心或偏心垂向作用的变形抗力.分析矩形板受楔形加载头作用下的抵抗力-加载位移曲线可以发现,其在初始阶段斜率较小,上升较缓,这是因为此阶段矩形板主要在楔形加载头尖端附近产生变形,即以局部变形为主;之后,抵抗力曲线斜率迅速增大,表明矩形板发生整体变形;同时矩形板发生整体变形时对应的有限元模拟结果曲线与简化解析方法计算结果曲线几乎平行,说明在前文推导中只考虑矩形板整体变形的假设是合理的.
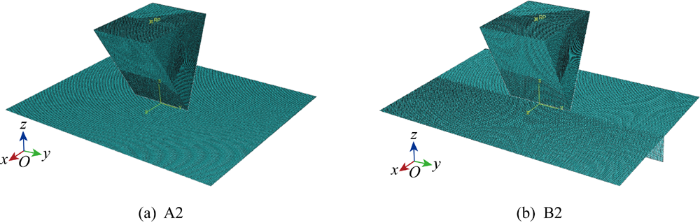
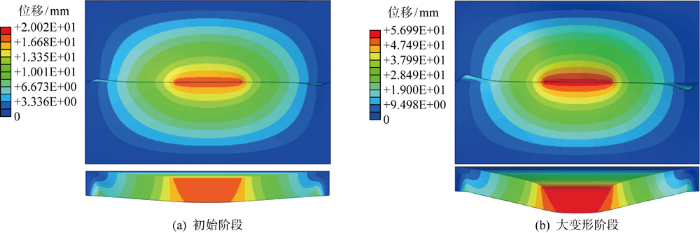
单筋加筋板模型有限元仿真变形如图10所示.据图9中单筋加筋板的简化解析计算结果与有限元模拟结果对比可知,8种工况下的简化解析计算结果与有限元模拟结果趋势相同且误差较小,说明本文提出的简化解析方法能较好地预报骨材受楔形加载头对心或偏心垂向作用的变形抗力.分析单筋加筋板受楔形加载头作用下的抵抗力-加载位移曲线可以发现,其在初始阶段上升速度比后期快,究其原因,考虑为加强筋的屈曲变形导致,且屈曲变形主要集中在加强筋的端部固支处,单筋加筋板初始阶段的变形图可证实上述分析,如图10(a)所示;之后,抵抗力曲线上升速度降低,表明此阶段加强筋在楔形加载头作用下随矩形板主要发生整体大变形,如图10(b)所示.此外,图10(b)中可以看出此时加强筋端部翘曲变形较初始阶段明显,但中部并未发生明显的侧偏,说明在简化解析方法的推导中假设其在大变形过程中不发生侧偏是合理的.
图10
图10
单筋加筋板模型有限元仿真变形
Fig.10
Deformation of finite element simulation of single-reinforced.pngfened plate model
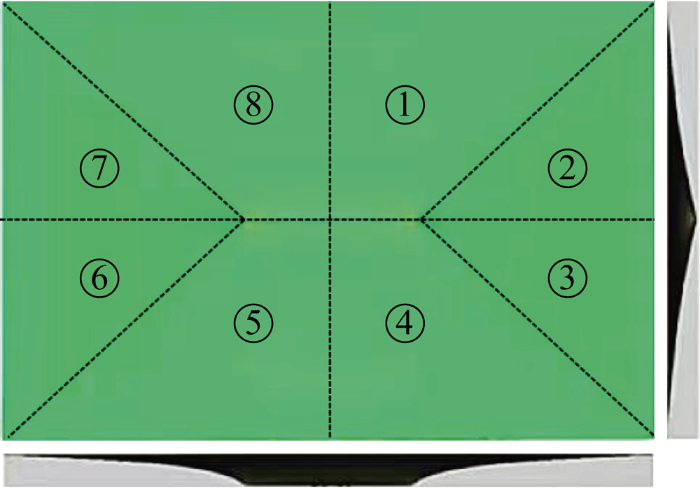
由表2可知,当加载头长度2a=80 mm时,简化解析方法与有限元模拟结果的计算误差超过20%;随着加载头长度的增加,简化解析方法与有限元模拟结果的计算误差减小.对矩形板的变形情况进行分析,本文针对矩形板不同区域均采用线性函数作为其变形产生的塑性铰线的理论表达,以此来保证变形的连续性,而矩形板的真实变形可由文献[9]中矩形板试验模型的真实变形三维扫描图表明,如图11所示,图中可以看出区域①、区域④、区域⑤及区域⑧的变形曲率较小,与假定的直线变形模式接近,区域②、区域③、区域⑥及区域⑦的变形曲率较大,并且越靠近加载头处变形梯度越大,与假定的变形模式存在误差.随着加载头长度的增加,矩形板中变形曲率较大的区域随之减少,故使得误差有所降低.此外,随着加载头长度的增加,变形区域更加靠近边界,有限元模拟中固支边界对周围单元的约束会使抗力稍有提升,对误差的减小也会造成一定的影响.另外,本文的简化解析方法采用塑性流动应力进行计算,便于实际工程应用,但未考虑结构在变形时的变形量对应力的影响,这是导致简化解析结果比有限元模拟结果大的原因.通过比较表2中模型B2与C1、C2以及B2与D1、D2的数据可以发现,单筋加筋板的抵抗能力会随着加强筋的高度或厚度的增大而提升,这与简化解析公式中变形抗力F与骨材的高度hs及骨材的厚度ts呈正相关相符合.
图11
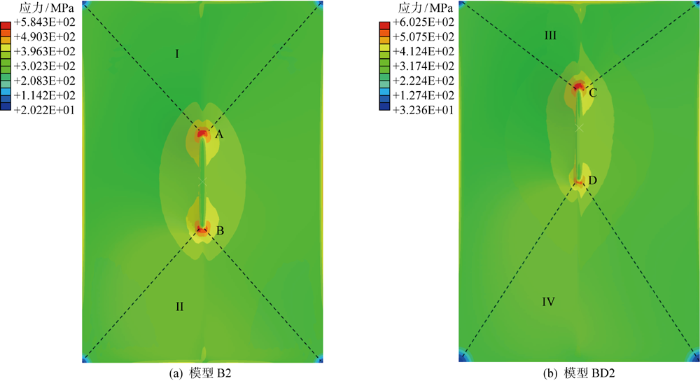
还需要指出的是,楔形加载头偏心作用下不仅加筋板的结构抗力会发生变化,结构失去承载能力时的横向位移也稍有减小,这是压载位置的偏移使得结构变形不对称导致的.相同横向位移下的结构Mises应力分布如图12所示,从中可以看出,与模型B2的 I 区域相比,模型BD2的 III 区域参与抵抗压载的面积减少,相同横向位移下此区域中单位面积的结构受到的应力增加,应变增大,也就导致C点的应力集中现象较A点更加明显,更快达到结构的失效应变从而发生破裂,最终影响加筋板的结构抗力及结构失去承载能力时的横向位移.
图12
图12
相同横向位移下模型B2与BD2应力分布
Fig.12
Stress distribution of Model B2 and BD2 in the same lateral displacement
3 结论
(1) 本文提出了一种新的用于计算加筋板结构受楔形物偏心垂向准静态压载作用时变形抗力的简化解析方法.该解析方法的特点是忽略加筋板中矩形板与骨材的耦合作用,对给定横向位移下矩形板的变形抗力与骨材的变形抗力分别进行计算,然后线性叠加得到整个加筋板结构的变形抗力,从而简化了船舶舷侧加筋板结构受压载变形损伤的计算.该方法虽忽略了板与骨材的耦合作用,但就船舶低速碰撞分析而言,加筋板结构变形主要通过板中面内的膜力和梁截面的轴力进行能量耗散,将矩形板、骨材分开单独计算不会给整体的变形抗力计算结果带来重要的影响.本文关于简化解析方法计算结果与有限元模拟结果之间的比较表明该方法有较高的计算精度,亦证实了上述论断的合理性和正确性.
(2) 在楔形物作用下,单筋加筋板的骨材首先在端部发生屈曲变形,抵抗力迅速增长直至骨材随矩形板发生整体大变形,抵抗力上升速度放缓.骨材的端部翘曲会随着横向变形的增大愈加明显,但大变形过程中骨材中部未发生明显侧偏.
(3) 本文提出的简化解析方法考虑了楔形物偏心作用的影响.分析表明,偏心垂向作用会对结构的耐撞能力造成一定的影响.上述结论已被有限元模拟结果证实,从而为加筋板结构受楔形物偏心垂向准静态压载作用的抵抗能力评估提供了指导,同样为球形物体准静态压载作用于船体舷侧结构的情况提供了有意义的参考.
参考文献
Large deflection of a rigid-plastic circular plate pressed by a rigid sphere
[J].
单壳船舷侧结构的碰撞分析
[J].
The analysis of singlehull structure’s crashworthiness
[J].
船舶加筋板结构耐撞性能分析
[J].
Analysis on the crashworthiness behavior of ship.pngfened plate
[J].
Deflection and fracture of a clamped plate under lateral indentation by a sphere
[J].
船体加筋板耐撞性解析预报方法研究
[J].
Analytical prediction method for crashworthiness of ship.pngfened panels
[J].
Experimental and analytical investigations on the response of.pngfened plates subjected to lateral collisions
[J].
An analytical method for predicting the ship side structure response in raked bow collisions
[J].
On resistance of a rectangular thin plate under lateral indentation by a wedge indenter
[J].
楔形撞头作用下固支矩形板的耐撞性
[J].
Crashworthiness of clamped rectangular plates under wedge impact
[J].
Y型浮式生产储油轮船侧结构耐撞性
[J].
Research on the crashworthiness of a Y-shape side structure design for FPSO
[J].
Dynamic plastic response of thin circular plates struck transversely by nonblunt masses
[J].