基于滑移线法的黏土海床中浅基础固结承载力分析

doi:10.16183/j.cnki.jsjtu.2022.468

基于滑移线法的黏土海床中浅基础固结承载力分析

李志坚¹^,², 廖晨聪^,¹^,², 张璐璐¹^,², 叶冠林¹^,²

1.上海交通大学海洋工程国家实验室,上海 200240

2.上海市公共建筑和基础设施数字化运维重点实验室,上海 200240

Analysis of Consolidated Bearing Capacity of Shallow Foundations Based on Characteristics Method

LI Zhijian¹^,², LIAO Chencong^,¹^,², ZHANG Lulu¹^,², YE Guanlin¹^,²

1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Shanghai Key Laboratory for Digital Operation and Maintenance of Buildings and Infrastructure, Shanghai 200240, China

通讯作者: 廖晨聪,副教授,博士生导师;E-mail:billaday@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-11-21 修回日期: 2023-01-24 接受日期: 2023-03-9

基金资助:

国家自然科学基金(52279106)
上海市晨光计划(20CG15)
上海市教委科研创新计划(2021-01-07-00-02-E00089)

Received: 2022-11-21 Revised: 2023-01-24 Accepted: 2023-03-9

作者简介 About authors

李志坚(1998-),硕士生,主要从事海底浅基础承载力方面的研究.

摘要

为评估海底浅基础服役过程的承载力时变规律,推导了预载作用下黏土海床完全固结后的不排水抗剪强度分布,利用滑移线法给出了应力特征线方程并求解出浅基础固结承载力,研究了预载比、土体不均匀性、有效内摩擦角和基础尺寸对浅基础固结承载力的影响.结果表明:浅基础固结承载力的相对增长幅度和预载比近似呈线性关系,由土体不均匀因子和有效内摩擦角共同决定,不受基础尺寸的影响.通过与水土耦合有限元分析结果进行比较,对所提方法的准确性进行了严格的验证,表明了该方法的有效性.最后,根据有限元结果分析了滑移线解的误差来源,发现孔压计算差异是导致固结承载力预测结果产生误差的主要原因.该滑移线解可快速准确地预估浅基础固结承载力的增长规律,为海底浅基础的优化设计提供重要参考.

关键词： 黏土海床; 浅基础; 固结承载力; 滑移线法; 预载作用

Abstract

To evaluate the bearing capacity evolution of subsea shallow foundations during operation, an undrained shear strength distribution of clay seabed following full consolidation due to preloading was deduced. The characteristics method was used to derive the stress characteristics equation and to evaluate the consolidated bearing capacity of shallow foundations. The influence of preloading ratio, soil inhomogeneity, effective internal friction angle, and foundation dimension on the consolidated bearing capacity of shallow foundations was investigated. The result shows that the relationship between the relative gain in the consolidated bearing capacity of shallow foundations and the preloading ratio is approximately linear. Meanwhile, the relative gain in consolidated bearing capacity is jointly determined by soil inhomogeneity and effective internal friction angle and is not affected by the foundation dimension individually. The accuracy and effectiveness of the proposed method were verified by comparing it with the results of soil-water coupled finite element analysis. Finally, possible errors between the characteristics solution and finite element model (FEM) results were analyzed. It was found that the discrepancy in the pore pressure calculation was the main reason for the disparity in the prediction of consolidated bearing capacity obtained by two methods. This characteristics solution can quickly and accurately predict the growth of consolidated bearing capacity of shallow foundations, which provides important reference for the optimal design of subsea shallow foundations.

Keywords： clay seabed; shallow foundation; consolidated bearing capacity; characteristics method; preloading

PDF (3909KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李志坚, 廖晨聪, 张璐璐, 叶冠林. 基于滑移线法的黏土海床中浅基础固结承载力分析[J]. 上海交通大学学报, 2024, 58(7): 1047-1056 doi:10.16183/j.cnki.jsjtu.2022.468

LI Zhijian, LIAO Chencong, ZHANG Lulu, YE Guanlin. Analysis of Consolidated Bearing Capacity of Shallow Foundations Based on Characteristics Method[J]. Journal of Shanghai Jiaotong University, 2024, 58(7): 1047-1056 doi:10.16183/j.cnki.jsjtu.2022.468

由于陆上空间和资源有限,开发利用海洋资源逐渐成为全球的研究热点,各类海洋基础也因此得到了大力发展.沉垫、防沉板等用于海上能源开发的移动式浅基础,可利用大底面站稳在浅层承载力较低的软土层上,降低了对土体的承载力要求,尤其适合在我国沿海的软土海床上开展作业.现有规范对黏土海床中浅基础承载力的计算一般基于土的原位应力状态,通过原位测试得到的抗剪强度估算基础的未固结不排水承载力V_uu(以下简称为未固结承载力).这种方法忽略了由上部结构、基础自重和环境荷载产生预载作用下基础下部土体固结导致的强度增长,是一个保守的结果.

特别地,在近海海域进行作业如边际油田的开发、海洋牧场网箱养殖、海底管道的安装作业时,浅基础的工作时间可能达到几周、几个月甚至更长^[1-2].在基础服役的过程中,由于基础离地表较近、排水路径短且表层沉积物渗透性较好^[3-4],基础以下土层由于预载作用会发生显著的排水固结效应,导致土体强度提高,地基承载力明显增大.海床土层因预载作用完全固结时的地基承载力可称为基础的固结不排水承载力V_cu(以下简称为固结承载力).考虑到当前设计规范均未给出海底浅基础固结承载力的评估方法,继续沿用传统的设计方法势必会低估基础的承载力,造成设计冗余.

基于经典的浅基础承载力问题,过去学者已开展了大量研究,并涌现出了很多不同的方法.Terzaghi、Skempton等根据极限平衡法提出了计算砂土和黏土中基础极限承载力的经验公式,在工程实践中被广泛应用.陈希有等^[5]通过滑移线法研究了各向异性和非均质地基上条形基础的承载力.黄茂松等^[6-7]通过极限分析法对黏土和c-φ型土中的基础承载力分别进行了上限分析和下限分析.Gourvenec等^[8]基于有限元和有限元极限分析,提出了一套考虑基础埋深比、地基-土界面粗糙度和土体不均匀性的统一承载力系数.罗强等^[9]在鼓式离心机中进行了方形和圆形浅基础的模型试验,根据试验结果比较了两种基础形式承载力系数的不同.

对于基础的固结承载力,由于涉及渗流固结过程求解,所以目前的研究成果主要集中于考虑水土耦合的有限元方法,计算过程较为繁琐.Bransby^[10]通过有限元分析发现长期竖向荷载作用后,地基水平和竖向承载力均得到显著提高,其中水平承载力提升更大.Zdravkovic等^[11]研究了预载固结效应对正常和超固结土中粗糙和光滑基础不排水承载力的影响,结果表明超固结土中基础承载力增长更小.Gourvenec等^[12]基于临界状态理论,根据小应变有限元分析的结果,将预载水平和固结时间作为变量,提出了一个可以预测浅基础固结承载力的理论框架,并可同时适用于正常固结和超固结黏土.Fu等^[13]开展了一系列离心机试验,提出了一种预测固结承载力的方法,但具体的参数仍需要通过耦合有限元分析确定.Gaone等^[14]、Lehane等^[15]的现场测试试验结果表明,长期预载作用后,基础的固结承载力较未固结承载力得到了显著提升,甚至会超过有限元预测的增长幅度.

可以看到,经典的浅基础承载力研究已经较为完善,但其计算理论主要针对均匀或者线性分布的原位地层强度.对于沉垫、防沉板这类有限服役时间的可移动式海底浅基础,忽视固结效应将导致其承载力评估较为保守,因此需要提出新方法对浅基础的固结承载力进行评估.现有研究在计算基础固结承载力时大都需要使用有限元方法,并根据有限元结果拟合得出经验公式,工作量大,流程繁琐,使用起来有一些局限性和经验性.为了克服以上不足,本文对固结后土体的不排水抗剪强度分布进行了简化计算,推导了固结后土体的应力特征线方程,并采用有限差分法编制了对应计算程序,可快速准确地计算浅基础的固结承载力.此外,本文综合考虑了预载比、土体不均匀性、土体有效内摩擦角及基础尺寸对浅基础固结承载力的影响,分析了固结承载力的相对增长规律.最后,将滑移线计算结果与水土耦合有限元计算结果进行对比,分析了滑移线法可能的误差来源及范围.

1 固结承载力的滑移线解法

1.1 固结后土体不排水抗剪强度分布

正常固结黏土海床处于原位应力状态时,一般认为其不排水抗剪强度沿深度线性增长.基础就位预载施加后,土体会产生超孔压并在随后的固结过程中逐渐消散,有效应力和抗剪强度随之增加,形成固结后的不排水抗剪强度分布.该分布极不规律且非线性,需采用合理的假设和简化进行推导.

首先根据土体的原位应力状态确定海床的不排水抗剪强度分布.对于平面应变条件,Worth^[16]基于临界状态理论,推导出了正常固结黏土层的不排水抗剪强度S_u和竖向有效应力σ'_v之间存在以下关系式:

(1)

\frac{S_{u}}{σ'_{v}}

\frac{2}{\sqrt{3}} \frac{s i n φ'}{2 a} {(\frac{1 + a^{2}}{2})}^{1 - \frac{κ}{λ}}

(2)a=

\frac{3 - s i n φ'}{2 (3 - 2 s i n φ')}

式中:φ'为有效内摩擦角;λ为压缩系数;κ为回弹系数.对于正常固结黏土,κ/λ取值一般为0.2左右,变化范围不大.

对于给定的黏土,式(1)右端为一常数,可简化为

(3)

\frac{S_{u}}{σ'_{v}}

本研究选用黏土的有效内摩擦角φ'= 30°,κ/λ=0.2,对应的不排水抗剪强度比R = 0.345.

实际工程中基础一般都有一定的埋深,而浅基础因其埋深较浅,故可将作用在基础底面以上的土体简化为初始超载σ'_v₀.规定基础底面处z=0,则土体的初始竖向有效应力分布为

(4)σ'_v=σ'_v₀+γ'z

式中:γ'为土体有效重度.

根据式(3)和(4)可推导出土体初始不排水抗剪强度的分布为

(5)S_u=S_u₀+k_suz

式中:S_u代表深度z处土体的不排水抗剪强度;S_u0代表基础底面处土体的不排水抗剪强度;k_su代表土体不排水抗剪强度随深度增加的速率.

土体孔压响应计算示意图如图1所示.图中:以基础左边缘为原点O;V_p为预载水平;B为基础宽度;x为计算点和原点O之间的水平距离;z为计算点和原点O之间的垂直距离.预载V_p作用后,基础底面压力往往不是均匀分布,同时由于土体不是简单的弹性体,产生的真实孔压响应较为复杂,需要通过一些假定来进行简化分析.首先假定预载作用后基础底面的压力分布是均匀的,并视土体为均匀的各向同性的半无限弹性体.满足以上两个假定后可根据Boussinesq解求得不同预载作用下土体中任意一点的孔压响应为

(6)Δu_w=

\frac{V_{p}}{π B}

[arctan

\frac{x}{z}

-arctan

\frac{x - B}{z}

\frac{x z}{x^{2} + z^{2}}

\frac{(x - B) z}{{(x - B)}^{2} + z^{2}}

]

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 土体孔压响应计算示意图

Fig.1 Schematic graph for calculating the pore pressure response of soil

固结完成后,认为孔压完全消散,根据有效应力原理可知消散的孔压将转为由土体承担,则可近似认为土体竖向应力增量为

(7)Δσ'_v=Δu_w

对于固结后土体不排水抗剪强度增量和竖向有效应力增量可近似采用式(3)计算:

(8)ΔS_u=RΔσ'_v

则固结后土体的不排水抗剪强度分布为

(9)S_u(x, z)=S_u₀+k_suz+RΔσ'_v

需要注意的是,预载作用后土体的固结严格上不再满足K₀固结的条件,但为了简化计算仍采用式(3)近似计算,该假定会带来较小的误差,详见后文说明.

1.2 应力特征线方程

浅基础极限承载力问题可简化为平面应变情况进行求解,土中任意一点的正应力和切应力满足以下平衡方程:

(10)

\begin{array}{l} \frac{\partial σ_{x}}{\partial x} + \frac{\partial τ_{x z}}{\partial z} = 0 \\ \frac{\partial σ_{z}}{\partial z} + \frac{\partial τ_{x z}}{\partial x} = γ \end{array}\}

式中:σ_x 和σ_z分别为x、z方向的正应力;τ_xz为平面内切应力;γ为土体天然重度.

假定土体强度为任意分布且满足Tresca屈服条件:

(11)

{(\frac{σ_{x} - σ_{z}}{2})}^{2}

τ_{x z}^{2}

S_{u}^{2}

式中:S_u为土体不排水抗剪强度,是关于x,z的分布函数S_u(x, z),由式(9)决定.

图2给出了土体中任意一点主应力和滑移线方向,该点的应力莫尔圆情况如图3所示.为了计算简便,取特征应力σ = (σ₁ +σ₃)/2,规定大主应力σ₁与z轴夹角为θ,则土体中任意一点处的应力分量σ_x, σ_z和τ_xz可表示为

(12)

\begin{array}{l} σ_{x} = σ - S_{u} c o s 2 θ \\ σ_{z} = σ + S_{u} c o s 2 θ \\ τ_{x z} = S_{u} s i n 2 θ \end{array}\}

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 主应力与滑移线方向

Fig.2 Orientation of principal stresses and characteristics

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 应力莫尔圆

Fig.3 Stress Mohr circle

将式(12)代入式(10)并结合滑移线理论,可推导出两组不同族的应力特征线微分方程.

S₁线:

(13)

\begin{array}{l} \frac{d x}{d z} = t a n (θ + ε) \\ d σ + 2 S_{u} d θ = γ d z - \frac{\partial S_{u}}{\partial z} d x - \frac{\partial S_{u}}{\partial x} d z \end{array}\}

S₂线:

(14)

\begin{array}{l} \frac{d x}{d z} = t a n (θ - ε) \\ d σ - 2 S_{u} d θ = γ d z + \frac{\partial S_{u}}{\partial z} d x + \frac{\partial S_{u}}{\partial x} d z \end{array}\}

式中:ε=π/4为大主应力方向与特征线方向的夹角.

将式(9)代入式(13)和(14)即可求得土体固结后的应力特征线方程.需要注意的是,当求解未固结承载力时,式(13)和(14)中S_u为均匀或线性分布,相应的特征线方程会有一定程度的简化,但当求解固结承载力时,式(13)和(14)中S_u为式(9)所示的复杂的非线性分布函数,特征线方程的求解难度更大.对于式(13)和(14)这种形式的特征线方程,暂时无法求得其解析解,但可采用数值方法求得其近似解^[17-18].本文利用MATLAB编制了相应的计算程序求解浅基础固结承载力,主要流程归纳如下:

(1) 确定土体初始应力状态,根据Boussinesq解求出土体的孔压响应,推导不排水抗剪强度增量,给出完全固结后土体不排水抗剪强度分布.

(2) 在已知完全固结后土体不排水抗剪强度分布的基础上,基于滑移线理论给出固结后土体的应力特征线方程.

(3) 采用数学方法(如有限差分法)求解应力特征线方程,编制对应的计算程序用于求解不同预载作用后土体的固结承载力.

2 浅基础的固结承载力分析

2.1 滑移线解的验证

对于未固结承载力V_uu,为了方便将本文结果与已有研究结果进行对比,通过承载力系数N_cv将未固结承载力V_uu与基础底面处土体强度S_u0联系起来:

(15)N_cv=

\frac{V_{u u}}{B S_{u 0}}

同时引入无量纲因子ξ来表征土体强度分布的不均匀性:

(16)ξ=k_suB/S_u₀

表1给出了未固结条件下本文滑移线结果和其他学者研究结果的对比^[19-20].可以看到,本文滑移线方法得到的未固结承载力计算结果与Martin^[20]几乎完全一致,这验证了本文滑移线解法的准确性.Gourvenec等^[19]的有限元结果虽然比本文的计算结果略大,但误差也很小,均在3%以内,考虑到有限元结果是在位移承载力曲线上取值得到的,这样小的误差是完全可以接受的.此外,进一步提高本文数值程序的精度如进一步收紧收敛标准、细分网格等,可以进一步缩小误差,但本文并非需要得到一个完全精确的解,只是提供一个足够精确的近似参考解,考虑到计算成本的问题,认为本研究的精度可以满足要求.

表1 未固结承载力系数N_cv对比

Tab.1 Comparison of unconsolidated undrained bearing capacity factor N_cv

数据来源	N_cv
数据来源	ξ=1	ξ=2	ξ=4	ξ=10	ξ=20
本文	6.62	7.59	9.13	12.65	17.39
Gourvenec等^[19]	6.70	7.71	9.24	12.95	—
Martin^[20]	6.61	7.60	9.13	12.66	17.40

新窗口打开| 下载CSV

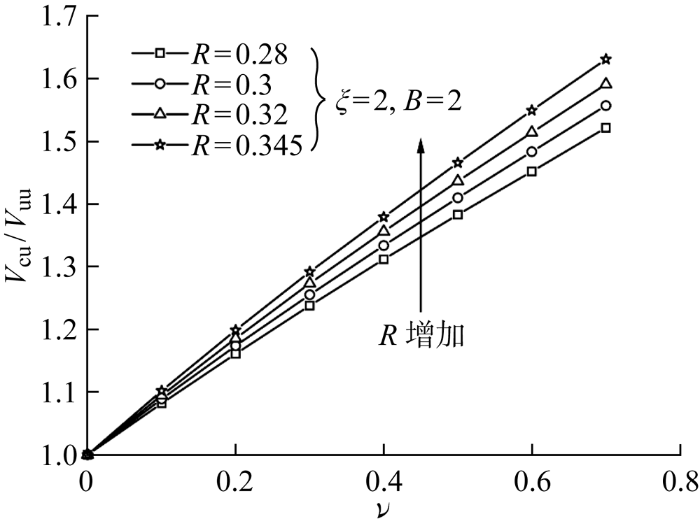
2.2 土体不均匀性ξ对固结承载力的影响

本文研究的预载主要指由于上部结构自重和环境荷载产生的竖向荷载,为了使研究结果更具有普遍性,将预载和基础未固结承载力的比值V_p/V_uu定义为预载比ν.根据实际情况,考虑了预载比ν=0.1~0.7时基础的竖向固结承载力.

浅基础归一化固结承载力的相对增长趋势如图4所示.可以看到,随着预载比的增大,基础的固结承载力增长非常明显,且其相对增长幅度与预载比大小近似存在线性关系(V_cu/V_uu~V_p/V_uu).从图4中还可以看出,当ξ不同时,固结承载力的相对增长也不相同,且ξ越大,固结承载力的相对增长越大,这种趋势可以根据土体固结后不排水抗剪强度的相对增长(S_u,con/S_u,ini)情况进行解释.图5对比了预载比为0.7、土体不均匀性不同时,土体固结后不排水抗剪强度的相对增长情况.可以看到,ξ越大则滑动破坏区(如图中红线所示)越局限于土体浅层,滑裂面经过土体强度相对增长较大的区域,相应的基础固结承载力的相对增长也会越大.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 归一化固结承载力的相对增长

Fig.4 Relative gain in normalized consolidated undrained capacity

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 ξ对不排水抗剪强度相对增长的影响(ν=0.7)

Fig.5 Effect of ξ on relative gains in undrained shear strength (ν=0.7)

2.3 基础宽度B和不排水抗剪强度比R对固结承载力的影响

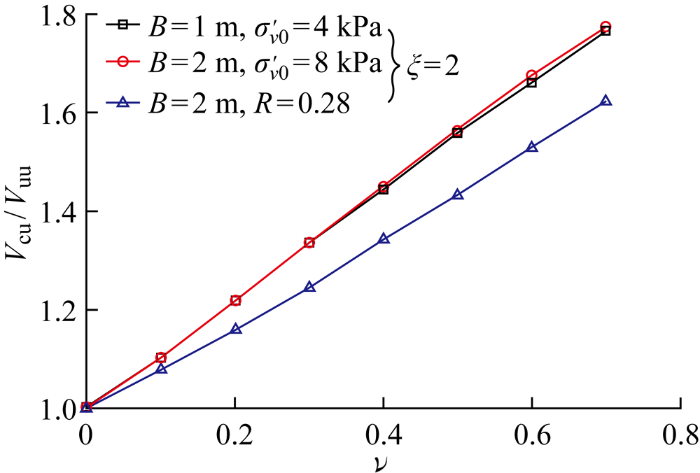
图6、7分别给出了基础宽度B和不排水抗剪强度比R(由有效内摩擦角决定)对固结承载力相对增长趋势的影响.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 ξ相同时固结承载力的相对增长趋势(B不同)

Fig.6 Relative gain in consolidated undrained bearing capacity with various B

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 ξ相同时固结承载力的相对增长趋势(R不同)

Fig.7 Relative gain in consolidated undrained bearing capacity with various R values

如图6所示,ξ、R相同而B不同时,固结承载力的相对增长相同.从图7则可以发现,ξ、B相同而R不同时,固结承载力的相对增长不同,且R越大,固结承载力的相对增长越大.这些结果表明当土体不均匀性为常数时,固结承载力的增长与基础尺寸无关,而受R的控制.这一规律也与Vulpe等^[21]有限元分析的结果相吻合,下面根据2.1节中的推导结果进行解释.

将式(6)简化为

(17)Δu_w=α

\frac{ν N_{c v} S_{u 0}}{π B}

式中:α为应力系数,是关于x, z的函数.则式(9)可改写为

(18)

\frac{S_{u, c o n}}{S_{u, i n i}}

=1+

\frac{α ν N_{c v}}{π (B + ξ z)}

已有研究结果表明^[8],未固结承载力系数N_cv由ξ决定,ξ相同时则N_cv也相同.故当B和相同时,R越大则土体中任意一点固结后不排水抗剪强度的相对增长就越大,相应的固结承载力的相对增长也就越大.需要注意的是,当R和ν相同时,B越大则土体中任意一点固结后不排水抗剪强度的相对增长越小,但是B增大的同时会导致破坏滑动区的增大,因此不能直接判断其对固结承载力相对增长的影响,而仅改变R时不会导致破坏面形状发生变化.综合图4~7的结果可知,固结承载力的相对增长由土体不均匀性和R共同控制,不单独受基础尺寸的影响.

3 滑移线法与有限元法的对比分析

本文在推导固结承载力的滑移线解时,对土体中的孔压响应和不排水抗剪强度的增长做出了一些简化假定,导致滑移线解存在一定误差.为厘清本文滑移线解的误差来源和范围,在商业有限元软件Abaqus中,采用水土耦合有限元方法(FEM)对浅基础固结承载力进行分析,并与本文滑移线结果进行比较,验证滑移线解的有效性.

3.1 有限元模型

在Abaqus中进行子程序二次开发来开展相关的有限元计算.假定基础为刚体且基础与土体间接触面为完全粗糙的情况,基础宽度B=2 m,通过基础底面中心处的荷载参考点(RP)进行加载.土体从基础底面中心处向左右各延伸5B,在垂直方向延伸10B,以避免边界效应的干扰.限制土体两侧的法向位移和底面处所有方向的位移,土体自由表面(除基础占据部分)设定为排水边界,其余边界均为不排水边界.黏土本构为修正剑桥模型,土体参数的取值参考了典型海洋软土的相关研究^[22],如表2所示.为了考虑固结效应的影响,采用了C3DP8单元,并在基础附近对网格进行了局部加密以提高计算精度,最小网格尺寸为0.025B,图8展示了本研究中所采用的典型有限元模型网格划分方法.

表2 土体参数

Tab.2 Parameters of soil

参数	取值
初始参考孔隙比,e	1.2
泊松比,μ	0.3
临界状态线线斜率,M	1.2
λ	0.2
κ	0.04
渗透系数,k/(m·s^-1)	4×10^-8
土体饱和重度,γ_sat/(kN·m^-3)	18

新窗口打开| 下载CSV

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 有限元模型

Fig.8 Finite element model

3.2 滑移线法和有限元法的结果对比

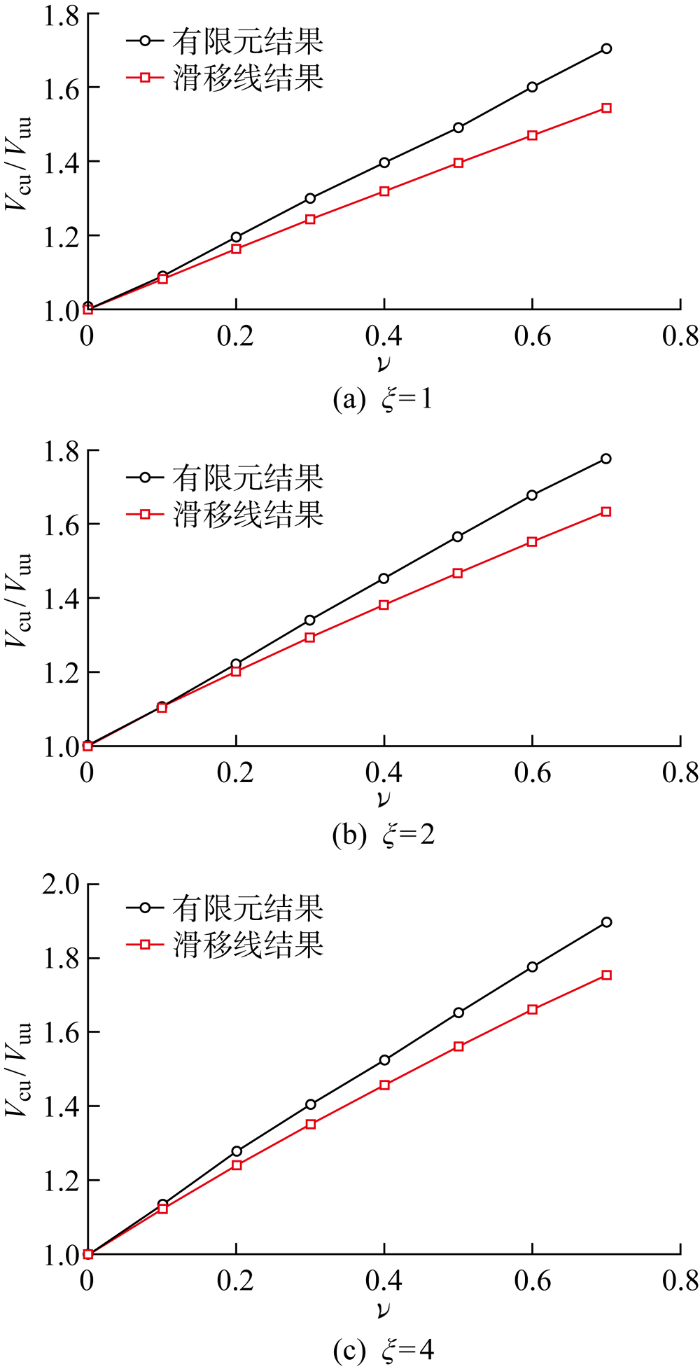
采用和3.2节中相同的分析条件,对浅基础固结承载力开展水土耦合有限元分析,有限元结果和滑移线结果的对比如图9所示.结果表明滑移线法计算得到的固结承载力相对增长趋势与有限元结果一致:随着预载比的增大,固结承载力显著增大,且两者之间近似存在线性关系.但滑移线法计算得到的固结承载力相对增长幅度略小于有限元结果,且该差异随着预载比增大而逐渐增大.当预载比小于0.7时,两种方法的差别不超过10%,误差产生的原因将在下一节中进行详细分析.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 滑移线和有限元结果对比

Fig.9 Comparison of characteristics and FEM results

对于3.3节中研究的基础宽度B和不排水抗剪强度比R对固结承载力的影响,在相同的分析条件下,同样采用有限元法进行分析,结果如图10所示.可以看到,根据有限元结果得到的规律和滑移线法同样一致,即土体不均匀性相同时,固结承载力的相对增长只受R的影响而不单独受基础尺寸的影响.需要注意的是,在这些条件下,滑移线法预测得到的结果仍略小于有限元结果(见图6、7、9).

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 ξ相同时固结承载力相对增长趋势(有限元法)

Fig.10 Relative gain in consolidated undrained bearing capacity at different ξ values (FEM)

综上所述,滑移线法预测得到的固结承载力相对增长趋势和有限元结果可以较好地吻合,两者都反映了土体不均匀性ξ和不排水抗剪强度比R对固结承载力的影响.此外,与需要较多分析参数、分析过程复杂的水土耦合有限元法相比,滑移线法预测固结承载力的一大显著优势在于: 只需要获取土体的初始强度和有效内摩擦角两个基本土工参数,即可对不同预载作用后基础的固结承载力进行计算,简单方便.虽然其计算的结果略小于有限元结果,但误差小且较为保守,可为海底浅基础的设计提供参考.

3.3 滑移线解法的误差分析

3.3.1 土体孔压响应的误差分析

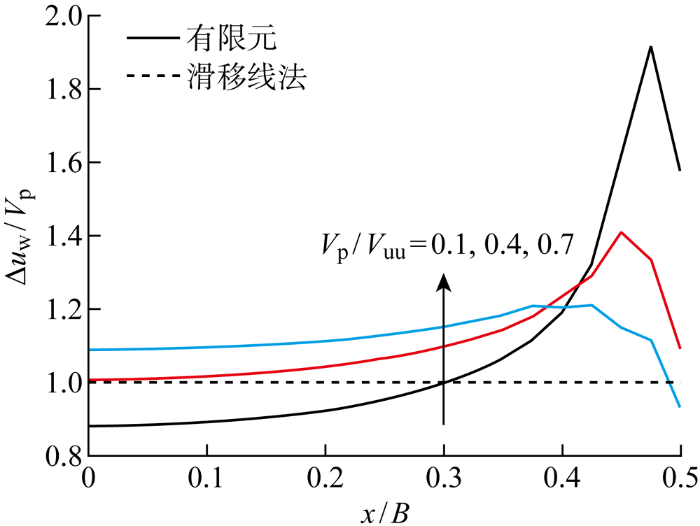
通过式(6)推导预载作用后土体的孔压响应时,应用了一些假定,下面将对这些假定产生的误差进行分析.首先,本研究中的基础为刚性基础,预载作用后基础底面附加应力的分布形状较为复杂,不符合式(6)所假定的均匀分布,图11将滑移线法假定的基础底面归一化超孔压(Δu_w/V_p)分布和有限元结果进行了比较.可以看到,有限元中基础底面的超孔压大体呈马鞍形分布,并在基础边缘处突然下降,该下降现象的出现主要是因为粗糙基础的角点处会率先发生屈服.其次,式(6)来源于Boussinesq解,是根据半无限空间中的各向同性弹性体假定推导而来,但事实上土体为各向异性的弹塑性体,这必然会导致滑移线法计算得到的孔压响应产生一定误差.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 基础底面处归一化超孔压分布

Fig.11 Normalized excess pore pressure distribution beneath foundation

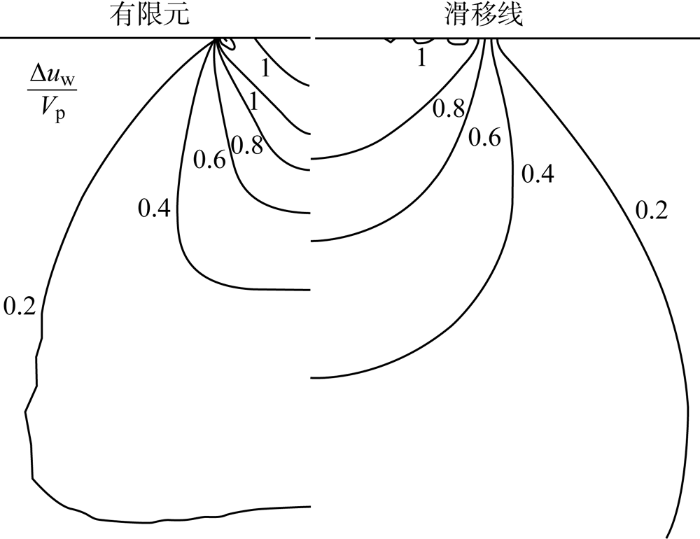
图12通过等值线图的方式比较了两种方法得到土体中归一化超孔压的分布情况.相比于有限元法,当深度较浅时,滑移线法得到的超孔压较小,而当到达一定深度时,滑移线法得到的超孔压则会反超有限元法.当土体充分固结后,超孔压完全转化为土体有效应力,则在浅层处,有限元法得到的土体有效应力增长更大,不排水抗剪强度增长更大.又因为本文研究的是浅基础,浅层土体对基础承载力的贡献更大,结合上述讨论可知有限元法得到的固结承载力相对增长将更大,且这种差距会随着预载比增长而增大,与前文的结果相吻合.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 归一化超孔压分布等值线图(有限元和滑移线法)

Fig.12 Contours of normalized excess pore pressure distribution (FEM and characteristics method)

由此可知,滑移线法孔压计算结果的误差导致了其预测的固结承载力偏低,且这种误差在预载比较大、土体不均匀性较小时更为明显(见图8).为此,引入孔压修正因子f_p对式(6)修正:

(19)Δu_w=

\frac{f_{p} V_{p}}{π B}

[arctan

\frac{x}{z}

-arctan

\frac{x - B}{z}

\frac{x z}{x^{2} + z^{2}}

\frac{(x - B) z}{{(x - B)}^{2} + z^{2}}

]

由上述分析可知,两种方法的超孔压误差大小和预载比、土体不均匀性均存在一定关系,本文建议孔压修正因子采用下式来进行取值:

(20)f_p=1+β

\frac{V_{p}}{V_{u u}}

式中:β为关于土体不均匀性ξ的函数.根据有限元结果,可得出β与ξ的对应关系如表3所示.

表3 β与ξ的对应关系

Tab.3 Relationship between β and ξ

ξ	β	ξ	β
1	0.60	6	0.34
2	0.49	8	0.33
4	0.41	10	0.27

新窗口打开| 下载CSV

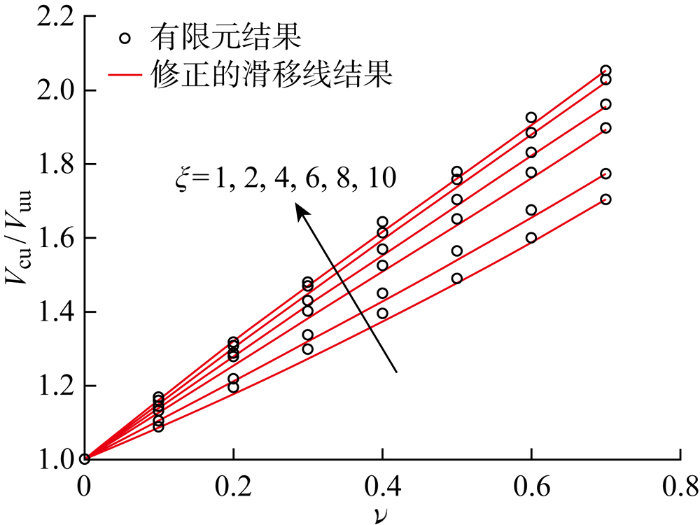
采用修正后的孔压响应计算式(19)重新计算固结承载力,并与有限元结果进行对比,结果如图13所示,可以看到,修正后的滑移线结果和有限元结果较为吻合,误差可控制在2%以内.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 修正后的滑移线和有限元结果对比

Fig.13 Comparison of modified characteristics and FEM results

3.3.2 不排水抗剪强度增长的误差分析

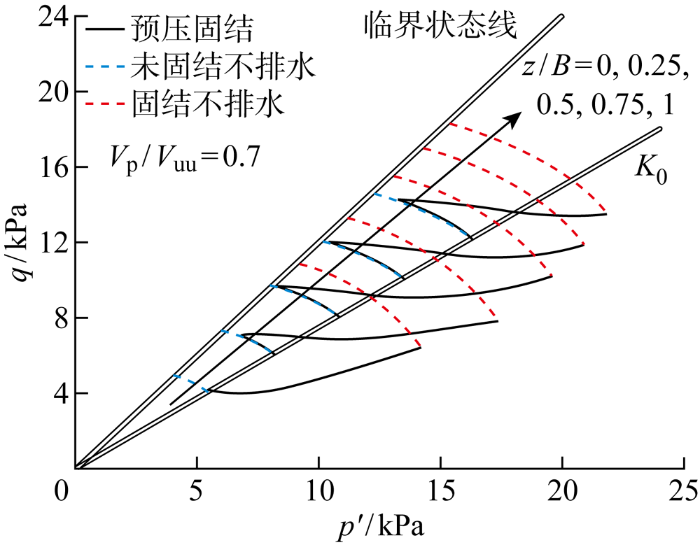
式(1)是基于临界状态理论推导的K₀固结条件下正常固结黏土的竖向有效应力和不排水抗剪强度之间的关系,而土体在受预载作用后固结的过程显然不再严格满足K₀固结的条件,因此根据式(7)和(8)并不能简单推导出式(9).但由于预载作用后土体的固结效应比较复杂难以给出精确解,所以本文进行了近似处理,即认为固结后土体不排水抗剪强度增长和竖向有效应力增长的比值仍满足式(3).为分析这一近似处理带来的误差,建立不排水剪切试验的单元模型进行研究.提取基础底面中心点以下0~2 m处土体固结前和固结后的有效应力和孔隙比,将其作为初始条件进行分析.ξ=2,V_p/V_uu=0.7时的典型结果如图14所示.图中:q为偏应力;p'为平均偏应力.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 固结不排水和未固结不排水土体有效应力路径

Fig.14 Effective stress path for consolidated undrained and unconsolidated undrained soil

由图14可知,预载作用时,除基础底面以下 0 m 处土体由于处于弹性区内未发生明显剪切,基础底面以下其他深度处土体均受到不同程度的剪切作用,表现出初期的有效应力路径与未固结不排水剪切试验得到的应力路径重合.当预载作用结束、固结开始后,土体有效应力增加,有效应力路径则逐渐向右上发展.此外,还可以看到固结不排水剪切试验的有效应力路径较未固结不排水条件近似等向扩张,土体的不排水抗剪强度显著提升.

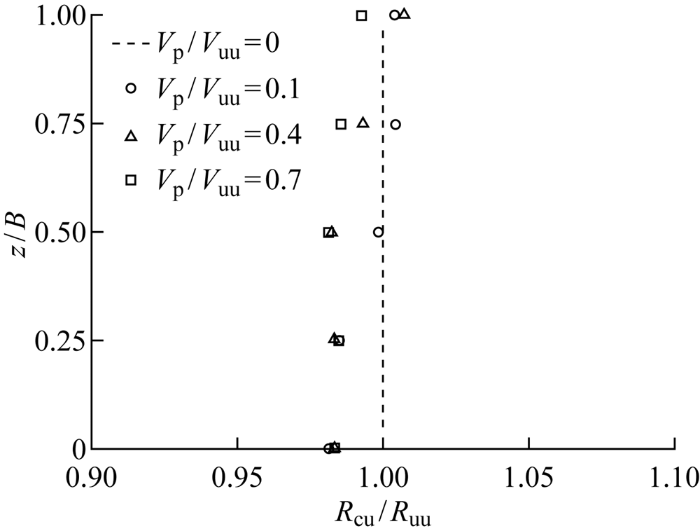
将根据不同有效应力路径得到的不排水抗剪强度和对应的竖向有效应力作比,结果即为R.其中根据未固结不排水应力路径得到的R相同,规定其为R_uu,规定固结不排水应力路径得到的R为R_cu,再进行归一化处理,得到不同预载作用下固结前后R的变化,如图15所示.结果表明,固结后R略微减小,但最多也不超过3%,故可认为式(8)的近似处理是合理的.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 固结前后R值的变化

Fig.15 Variation in R value due to consolidation

4 结论

本文推导了完全固结后土体的不排水抗剪强度分布,根据滑移线理论和有限差分法编制了浅基础固结承载力的计算程序,并与有限元结果进行了对比,分析了误差的来源,得到的主要结论如下:

(1) 为了评估预载固结效应导致的承载力增长,基于滑移线理论,考虑土体强度非线性变化,给出了一种浅基础固结承载力的计算方法.预载作用后,浅基础的固结承载力较未固结承载力有显著增长,只有采用考虑预载固结效应的新方法才能对浅基础的承载力时变规律做出合理预估,避免设计冗余.

(2) 浅基础固结承载力的相对增长和预载比近似呈线性关系,受土体不均匀性ξ和不排水抗剪强度比R共同控制.R相同,ξ越大,固结承载力的相对增长越大;ξ相同,R越大,固结承载力的相对增长越大.

(3) 水土耦合有限元分析结果表明,滑移线法的孔压计算结果偏低,进而导致了根据滑移线法计算得到的固结承载力小于有限元方法.引入孔压修正因子f_p对滑移线解进行修正,并给出了f_p的取值公式,可进一步将滑移线解和有限元解的误差控制在2%以内,精度较高.

(4) 预测浅基础固结承载力时,水土耦合有限元法需要较多的分析参数,分析过程也较为繁琐.滑移线法只需获取海床的初始强度和有效内摩擦角便可对不同预载作用后浅基础的固结承载力进行计算,简单方便,具有较好的应用价值,可为实际工程设计提供重要参考.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

谭越, 王春升, 陈国龙.

可移动生产储油平台的应用与发展

[J]. 中国造船, 2011, 52 (Sup.1): 159-165.