基于预期动态方程的含高比例可再生能源孤岛运行微电网负荷频率控制

doi:10.16183/j.cnki.jsjtu.2022.459

基于预期动态方程的含高比例可再生能源孤岛运行微电网负荷频率控制

吴振龙¹, 刘艳红^,¹, 薛亚丽², 李东海², CHEN Yangquan³

1.郑州大学电气与信息工程学院,郑州 450001

2.清华大学能源与动力工程系,北京 100084

3.加州大学默塞德分校工程学院, 美国默塞德 CA 95343

Load Frequency Control of Islanding Micro-Grid with High-Proportional Renewable Energy Based on Desired Dynamics Equation

WU Zhenlong¹, LIU Yanhong^,¹, XUE Yali², LI Donghai², CHEN Yangquan³

1. School of Electrical and Information Engineering, Zhengzhou University, Zhengzhou 450001, China

2. Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China

3. School of Engineering, University of California, Merced CA 95343, USA

通讯作者: 刘艳红,教授,博士生导师,电话(Tel.):0371-67783113;E-mail:liuyh@zzu.edu.cn.

责任编辑: 王历历

收稿日期: 2022-11-15 修回日期: 2023-03-8 接受日期: 2023-03-10

基金资助:

国家自然科学基金项目(52106030)
河南省科技攻关项目(212102311052)
电力系统国家重点实验室开放课题(SKLD21KM14)
郑州大学教授团队助力企业创新驱动发展专项资助项目(JSZLQY2022016)

Received: 2022-11-15 Revised: 2023-03-8 Accepted: 2023-03-10

作者简介 About authors

吴振龙(1992-),副教授,从事PID控制、自抗扰控制及其在热力系统和电力系统中的应用研究.

摘要

针对高比例可再生能源并入微电网带来的负荷频率控制问题,提出基于预期动态方程的比例-积分-微分(PID)控制策略.在分析微电网负荷频率控制模型和控制难点的基础上,设计基于预期动态方程的PID控制策略,采用单一变量法分析控制器参数对控制效果的影响,总结了简单、实用的参数整定流程,并在微电网负荷频率控制系统中应用.在不同工况下与多种控制器进行仿真对比,结果表明:所提控制策略能够在保证鲁棒性的前提下取得最佳控制效果,展现出很高的工程应用价值.

关键词： 微电网; 负荷频率控制; 预期动态方程; 比例-积分-微分; 参数整定

Abstract

A proportional-integral-derivative (PID) control strategy based on desired dynamics equation is proposed to solve the problem of load frequency control in micro-grid integrated with a large proportion of renewable energy. Based on the analysis of the load frequency control model and control difficulties of the micro-grid, a PID control strategy based on desired dynamics equation is designed. By analyzing the influence of controller parameters on the control performance using the single variable method, a simple and practical parameter procedure is summarized and the proposed controller strategy is applied to the load frequency control of the micro-grid. The simulation comparison with various controllers under different conditions show that the proposed control strategy can obtain the best control performance with good robustness and have a significant value for engineering application.

Keywords： micro-grid; load frequency control; desired dynamics equation; proportional-integral-derivative (PID); parameter tuning

PDF (4809KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

吴振龙, 刘艳红, 薛亚丽, 李东海, CHEN Yangquan. 基于预期动态方程的含高比例可再生能源孤岛运行微电网负荷频率控制[J]. 上海交通大学学报, 2024, 58(6): 954-964 doi:10.16183/j.cnki.jsjtu.2022.459

WU Zhenlong, LIU Yanhong, XUE Yali, LI Donghai, CHEN Yangquan. Load Frequency Control of Islanding Micro-Grid with High-Proportional Renewable Energy Based on Desired Dynamics Equation[J]. Journal of Shanghai Jiaotong University, 2024, 58(6): 954-964 doi:10.16183/j.cnki.jsjtu.2022.459

随着“碳达峰”和“碳中和”目标的提出,传统电力供应模式受到一定的挑战.为了降低电力系统的碳排放,具有灵活性、清洁性、环境友好等优点的微电网得到越来越多的应用^[1].具有随机性、暂态性和不确定性的风电、太阳能等新能源大规模接入微电网^[2-3]对微电网的负荷频率带来较大冲击,此外,随时变化的用户负荷也会给微电网的负荷频率带来扰动^[4].

为提高微电网负荷频率的控制品质,许多学者设计了多种控制策略.文献[5 ⇓-7]中分别设计了不依赖精确数学模型的比例积分微分(Proportional-Integral-Derivative, PID)控制策略、分数阶PID控制策略和自抗扰控制策略.上述控制策略通过仿真验证了各自控制策略在负荷频率控制中的扰动抑制能力.文献[8-9]中针对可再生电力系统中的时滞难点设计滑模控制策略,用于提高可再生电力系统的稳定性.文献[10-11]中考虑不同风电渗透率情况设计模型预测控制,并通过仿真验证模型预测控制在维持系统频率的优势.然而,模型预测控制的模型依赖性使得系统在偏离标称工况时控制品质下降^[12].随着人工智能技术的发展,强化学习控制策略也被尝试应用于微电网负荷频率的控制^[13-14].然而,在实际工程应用中,强化学习控制策略面临着工程实施难度高、计算量大等挑战.

PID由于结构简单、控制效果稳定等优点在负荷频率控制中应用广泛^[15],但是PID存在扰动抑制能力较弱的缺陷^[12].为了克服上述缺陷,一种基于预期动态方程的二自由度PID得到越来越多的关注^[16],基于预期动态方程的PID控制律设计能够很好地兼顾跟踪和抗干扰能力,并保留了PID结构简单、参数易于整定的优点.针对微电网负荷频率控制的难点,应用基于预期动态方程的PID提高系统的扰动抑制能力.首先,介绍微电网负荷频率的控制模型并分析该模型的控制难点;然后,介绍基于预期动态方程的PID并通过单一变量法分析控制器参数对于控制效果的影响,从而总结出简单、适用和实用的整定流程;最后,将基于预期动态方程的PID在太阳能、风电功率和用户负荷阶跃变化工况,太阳能、风电功率随机波动和用户负荷阶跃变化工况,太阳能、风电功率和用户负荷随机波动工况和微电网负荷频率控制系统存在不确定性工况分别与常规PID进行对比,仿真结果表明:基于预期动态方程的PID能够在保证较强的鲁棒性的同时取得最佳控制效果.

1 微电网负荷频率模型

高比例可再生能源微电网如图1所示,主要包括太阳能发电系统、风力发电系统、飞轮储能系统、电池储能系统、燃料电池系统和内燃机系统^[17].图中:DC、AC分别表示直流、交流电.当太阳能发电系统和风力发电系统具有输出功率时,优先使用二者产生的电能,飞轮储能系统和电池储能系统通过充放电进行负荷的瞬时消纳和补充.燃料电池系统和内燃机系统提供基础的负荷供应.

图1

新窗口打开| 下载原图ZIP| 生成PPT

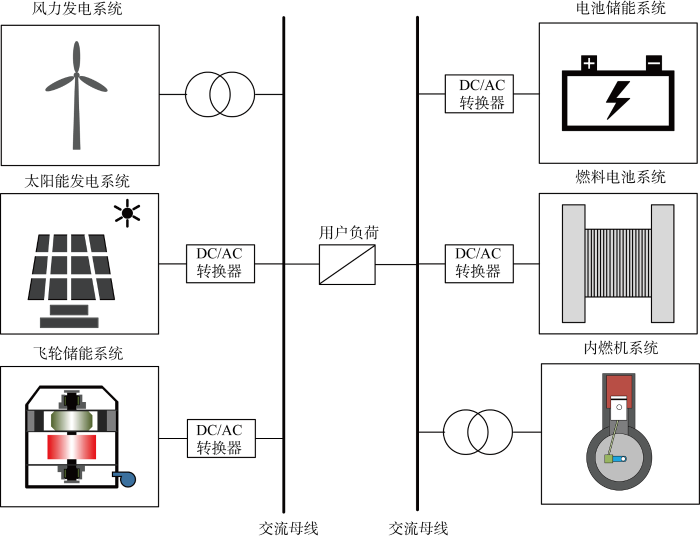
图1 高比例可再生能源微电网的组成示意图

Fig.1 Diagram of high-proportional renewable energy micro-grid

1.1 太阳能发电系统

太阳能发电系统由多个光伏板组成,每个光伏板由多个太阳能电池组成.因此,太阳能电池是太阳能发电的基本组成部分.常用太阳能电池的电学模型由电流源、并联二极管、并联电阻和串联电阻组成.基于其电路结构,可以得到其等效电路为

(1)

\begin{matrix} I = I_{P V} - I_{d} - I_{s h} \end{matrix}

式中:I、I_PV、I_d和I_sh分别为流过负载的电流、光伏在光照下产生的光电电流、二极管电流和流过并联电阻的电流.

二极管电流可以通过下式进行计算:

(2)

\begin{matrix} I_{d} = I_{0} (e^{\frac{V_{j 1}}{n V_{T}}} - 1) \end{matrix}

式中:I₀、V_T、V_j1和n分别为反向饱和电流、热电压、二极管和电阻之间的电压和二极管理想因数.

此外,I_sh可以通过下式计算:

(3)

\begin{matrix} I_{s h} = \frac{V + I R_{s}}{R_{S H}} \end{matrix}

式中:V为光伏电压;R_s、R_SH分别为光伏串联电阻和光伏并联电阻.

此时,太阳能发电系统流过负载的电流可以表示为^[5]

(4)

\begin{matrix} I = I_{P V} - I_{0} (e^{\frac{V_{j}}{n V_{T}}} - 1) - \frac{V + I R_{s}}{R_{S H}} \end{matrix}

结合式(1)~(4),太阳能发电系统的线性模型可以光伏矩阵传递函数G_PV(s)和逆变器传递函数G_IC(s)表示^[17]:

(5)

\begin{matrix} G_{P V} (s) = \frac{1}{T_{P V} s + 1} \end{matrix}

(6)

G_{I C} (s) = \frac{1}{T_{I C} s + 1}

式中:T_PV、T_IC分别为G_PV(s)和G_IC(s)的时间常数,T_PV=0.04 s,T_IC=0.004 s;s为拉普拉斯算子.

1.2 风力发电系统

风力发电系统主要包括变桨控制机构、液压变桨机构、执行机构等,其传递函数可以表示为^[16]

(7)

\begin{matrix} G_{W} (s) = \frac{1}{T_{W} s + 1} \end{matrix}

式中:T_W为风力发电系统的时间常数,T_W=1.5 s.

1.3 飞轮储能系统

飞轮储能系统将能量存储在飞轮的惯性中,在用电低谷时,电能用于运行飞轮,使其保持高速运转;在用电高峰时,飞轮带动发电机运转,对外输出电能.一般来说,飞轮储能系统是快速作用装置,可以很容易地消除较小的负载干扰.一般通过一阶传递函数表示为

(8)

\begin{matrix} G_{F E S} (s) = \frac{1}{T_{F E S} s + 1} \end{matrix}

式中:T_FES为飞轮储能系统的时间常数,T_FES=0.1 s.

1.4 电池储能系统

电池储能系统充电时,能量以化学离子的形式存储,当连接到负载时,电能被释放.随着技术的发展,电池与电力转换器结合使用,将直流电转换为交流电,能够抑制系统产生的谐波.电池储能系统一般通过一阶传递函数^[17]表示为

(9)

\begin{matrix} G_{B E S} (s) = \frac{1}{T_{B E S} s + 1} \end{matrix}

式中:T_BES为电池储能系统的时间常数,T_BES=0.1 s.

1.5 燃料电池系统

燃料电池是一种将燃料具有的化学能直接转换成电能的化学装置,是静态能量转换装置.燃料电池系统可以为微电网提供高效率和高可靠性的电量输出,通过一阶传递函数表示为

(10)

\begin{matrix} G_{F C} (s) = \frac{1}{T_{F C} s + 1} \end{matrix}

式中:T_FC为燃料电池系统的时间常数,T_FC=0.26 s.此外,燃料电池系统还需要逆变器和电源转换器设备,其传递函数分别为

(11)

\begin{matrix} G_{F C - I} (s) = \frac{1}{T_{F C - I} s + 1} \end{matrix}

(12)

G_{F C - I C} (s) = \frac{1}{T_{F C - I C} s + 1}

式中:T_FC-I、T_FC-IC分别为逆变器和电源转换器设备传递函数的时间常数,T_FC-I=0.04 s 和T_FC-IC=0.004 s.

1.6 内燃机系统

当储能系统和燃料电池系统不能满足负荷需求时,内燃机系统通过持续工作对外输出负荷.内燃机系统主要包括调速器和发电机,传递函数^[17]分别为

(13)

\begin{matrix} G_{t} (s) = \frac{1}{T_{t} s + 1} \end{matrix}

(14)

G_{g} (s) = \frac{1}{T_{g} s + 1}

式中:T_t、T_g分别为调速器和发电机传递函数的时间常数,T_t=0.4 s和T_g=0.08 s.

需要说明的是,风力发电系统和内燃机系统在建模时一般采用高阶模型进行描述,为简化分析,本文建立的微电网负荷频率控制模型中风力发电系统和内燃机系统分别采用一阶模型和二阶模型进行描述,在保证一定的模型精度下,能够有效降低分析难度.该简化模型适用于负荷频率控制分析,在其他电力系统控制分析如调压等特性分析时,建议使用高阶模型进行描述.

将分布式电源来连接到交流母线,组成对外提供电负荷的微电网,电负荷的计算表达式为

(15)

\begin{array}{l} P_{L o a d} = P_{P V} + P_{W} \pm P_{F E S} \pm P_{B E S} + \\ P_{F C} + P_{D E G} \end{array}

式中:P_Load、P_PV、P_W、P_FES、P_BES、P_FC、P_DEG分别为电负荷、太阳能发电系统功率、风力发电系统功率、飞轮储能系统功率、电池储能系统功率、燃料电池系统功率、内燃机系统功率.需要说明的是,P_FES和P_BES储能时功率为负,反之为正,其输出范围为 $[- 0.11, 0.11]$ .P_FC和P_DEG的功率只能为正,其输出范围分别为 $[0, 0.48]$ 和 $[0, 0.45]$ .上述功率均为标幺值.

为了保证用电量的平衡,可以得到:

(16)

\begin{array}{l} Δ P_{L o a d} + Δ P_{P V} + Δ P_{W} + Δ P_{F E S} + Δ P_{B E S} + \\ Δ P_{F C} + Δ P_{D E G} = 0 \end{array}

式中:ΔP_Load、ΔP_PV、ΔP_W、ΔP_FES、ΔP_BES、ΔP_FC、ΔP_DEG分别为电负荷变化量、太阳能发电系统功率变化量、风力发电系统功率变化量、飞轮储能系统功率变化量、电池储能系统功率变化量、燃料电池系统功率变化量、内燃机系统功率变化量.

电负荷与微电网频率可以通过下式进行等价:

(17)

\begin{matrix} G_{M D} (s) = 1 / (M s + D) \end{matrix}

式中:M和D分别是发电机的转动惯量和发电机的阻尼系数,M=0.166 7 s和D=0.001 5,其输出为频率偏差Δf.

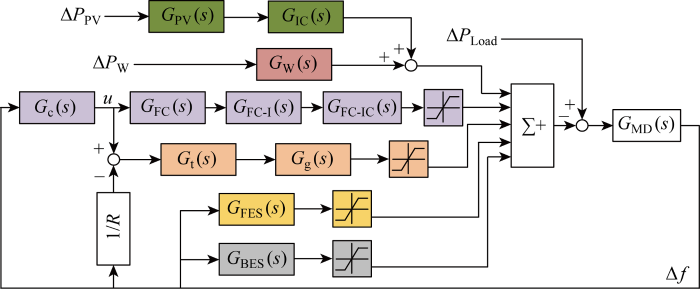
当用户负荷或者风能、光伏等功率发生变化时,微电网频率产生波动,通过调整燃料电池系统和内燃机系统的输出负荷实现负荷频率的稳定控制,其控制框图如图2所示.图中:G_c(s)为荷频率控制的反馈控制器;u为控制量;R为调速器的速度跌落系数.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 微电网负荷频率控制框图

Fig.2 Diagram of load frequency control of micro-grid

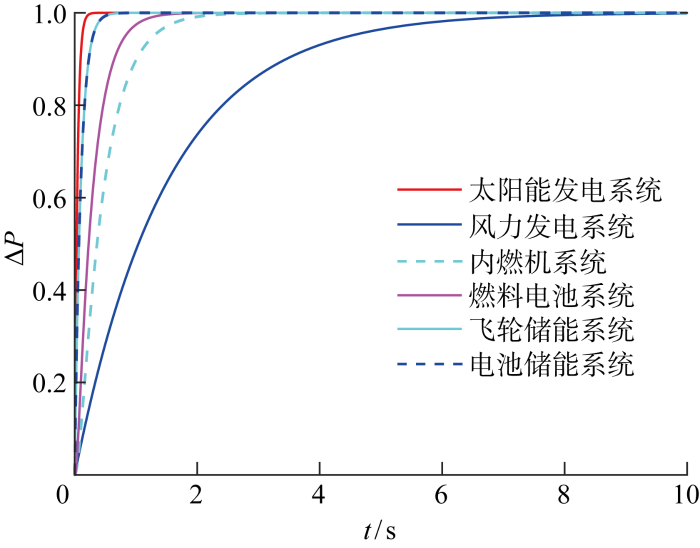
为了分析上述不同子系统的动态特性,对太阳能发电系统、风力发电系统等子系统进行幅值为1的输入,可以得到各子系统的阶跃响应输出如图3所示.图中:ΔP为功率变化量;t为时间.由图可知风力发电系统、太阳能发电系统分别具有最慢和最快的动态特性,二者的差距比较大,其他子系统的动态特性也较大.这意味着该微电网负荷频率控制的扰动存在快慢特性,其自身系统的响应也有较为明显的区别,这就要求反馈控制器具有较强的抗干扰性能,并且要具有较强的工况适应能力,即鲁棒性要足够强.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 微电网子系统的开环阶跃响应

Fig.3 Open loop step responses of all subsystems in micro-grid

不考虑微电网负荷频率控制模型中的输出限幅环节时,利用梅森变换公式可以得到频率偏差Δf的计算如下:

(18)

\begin{array}{l} Δ f = [Δ P_{L o a d} - G_{P V} (s) G_{I C} (s) Δ P_{P V} - G_{W} (s) Δ P_{W} - (G_{F C} (s) G_{F C - I} (s) G_{F C - I C} (s) + G_{t} (s) G_{t} (s)) u - \\ (G_{F E S} (s) + G_{B E S} (s) - \frac{G_{t} (s) G_{t} (s)}{R}) Δ f] G_{M D} (s) \end{array}

得到等价微电网模型的等效传递函数,即从控制量u到频率偏差:

(19)

\begin{matrix} Δ f = G_{e q} (s) u = - \frac{G_{M D} (s) (G_{F C} (s) G_{F C - I} (s) G_{F C - I C} (s) + G_{t} (s) G_{g} (s))}{1 + G_{M D} (s) (G_{F E S} (s) + G_{B E S} (s) - \frac{G_{t} (s) G_{g} (s)}{R})} u \end{matrix}

将式(5)~(16)中具体的传递函数代入式(19),可以得到G_eq(s)是一个相对阶为3、分子和分母阶次分别为8和11的高阶传递函数模型.下面关于控制器的稳定性分析和鲁棒性计算均基于该等效传递函数G_eq(s)展开.

2 基于预期动态方程的PID控制器设计

基于预期动态方程的PID控制器详细设计原理见文献[16],其典型的二自由度结构如图4所示,其中 $G_{p} (s) 为被控对象, b_{f} = k h_{1} / l$ 为前馈控制系数.此时基于预期动态方程的PID参数计算如下:

(20)

\begin{matrix} \begin{array}{l} k_{p} = \frac{k h_{1} + h_{0}}{l} \\ k_{i} = \frac{k h_{0}}{l} \\ k_{d} = \frac{k + h_{1}}{l} \\ b_{f} = \frac{k h_{1}}{l} \end{array}\} \end{matrix}

式中:l为与系统增益符号相同的参数;k为设计的增益参数;k_p、k_i和k_d分别为PID控制器的比例增益、积分增益和微分增益;h₁、h₀为设计的预期动态方程 $\ddot{y}$ +h₁ $\overset{\cdot}{y}$ +h₀y=h₀r的参数,y为闭环系统的输出,r为闭环系统设定值.

图4

新窗口打开| 下载原图ZIP| 生成PPT

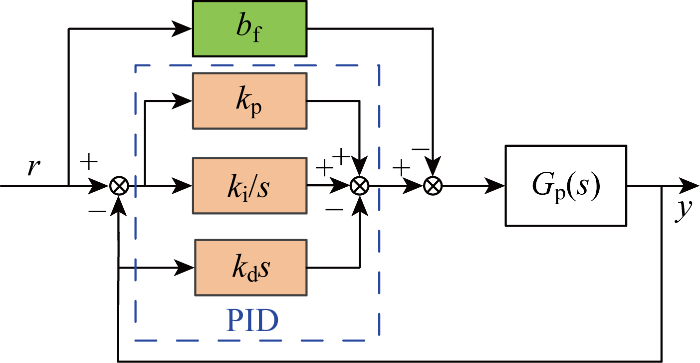
图4 预期动态方程PID的控制结构

Fig.4 Control structure of PID based on desired dynamic equation

基于预期动态方程的PID需要整定的参数为h₁、h₀、k和l,其中h₁和h₀为设计的预期动态方程的参数,可以根据预期动态方程进行调整.k和l为可调参数,接下来分析k和l对控制效果的影响.定义观测器的观测误差为Δf= $\bar{f}$ -f(z, w, u).其中z为系统状态,w为外部扰动.根据观测器的定义可以得到:

(21)

\begin{matrix} \bar{f} = k z_{2} - \frac{k^{2} z_{2} + k l u}{k + s} = \frac{k z_{2} s - k l u}{k + s} \end{matrix}

式中:z₂为预期动态方程中的一个变量.

根据f(z, w, u)=z₂s-lu,可以得到:

(22)

\begin{array}{l} Δ f = \frac{s}{k + s} (- z_{2} s + l u) = \\ \frac{s}{k + s} (- y s^{2} + l u) \end{array}

由于式(18)中表示实际被控对象,系统输出和控制量均连续且有界,即 $\ddot{y}$ 和u都是有界的,则误差Δf收敛于0的速度取决于k和l值,当l不变时k值越大收敛速度越快,此时系统的响应更加接近预期动态方程.当k值不变时,l值越小收敛速度越快,此时系统的响应更加接近预期动态方程.

闭环系统的预期动态方程 $\ddot{y} + h_{1} \overset{\cdot}{y} + h_{0} y = h_{0} r$ 可以等效为

(23)

\begin{matrix} y (s) = \frac{h_{0}}{s^{2} + h_{1} s + h_{0}} r (s) \end{matrix}

为了简化参数整定和减少参数的数量,可以将预期动态方程的参数设置为

(24)

\begin{matrix} \begin{array}{l} h_{0} = ω_{d}^{2} \\ h_{1} = 2 ω_{d} \end{array}\} \end{matrix}

式中:ω_d为预期动态方程的带宽.ω_d越大意味着闭环系统的动态响应越快,反之亦然.此时,需要整定的参数变为

(25)

\begin{matrix} \begin{array}{l} k_{p} = \frac{2 k ω_{d} + ω_{d}^{2}}{l} \\ k_{i} = \frac{k ω_{d}^{2}}{l} \\ k_{d} = \frac{k + 2 ω_{d}}{l} \\ b_{f} = \frac{2 k ω_{d}}{l} \end{array}\} \end{matrix}

为了分析基于预期动态方程的PID参数对于控制效果的影响,采用单一变量法分析控制效果,选择被控对象为G_p(s)= $\frac{1}{(2 s + 1) (3 s + 1)}$ ,整定参数ω_d=0.6、k=40和l=5.改变单一变量并保持其他参数不变化,可以得到系统的输出y和控制量u如图5~7所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

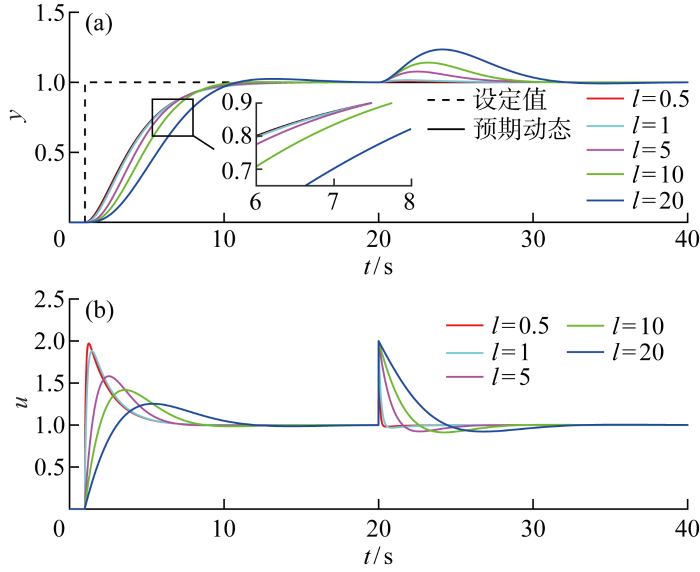
图5 ω_d和k保持不变时随着l变化的系统输出和控制量

Fig.5 Outputs and control signals versus l with ω_d and k remaining unchanged

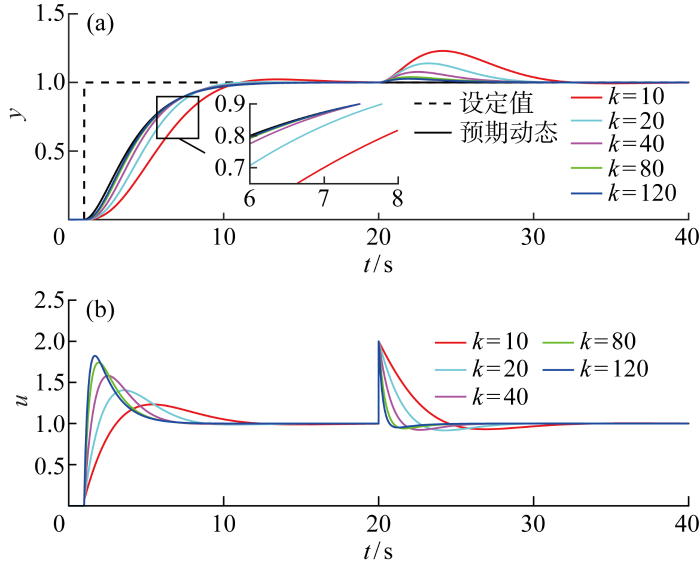
图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 ω_d和l保持不变时随着k变化的系统输出和控制量

Fig.6 Outputs and control signals versus k with ω_d and l remaining unchanged

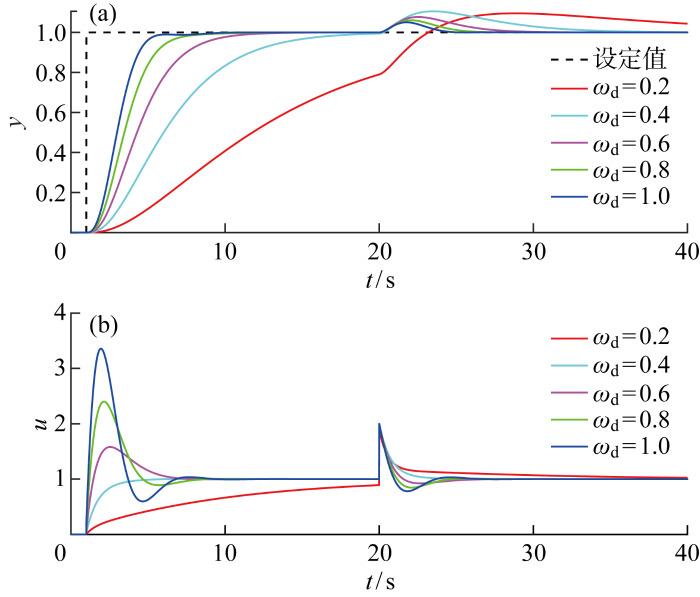
图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 l和k保持不变时随着ω_d变化的系统输出和控制量

Fig.7 Outputs and control signals versus ω_d with l and k remaining unchanged

从图5可知,随着l的减小,闭环系统的跟踪能力和抗干扰能力均增强,且越来越接近预期动态方程的响应,l减小到一定程度后闭环系统的跟踪能力和抗干扰能力变化不明显,此外,l的减小会带来控制量的增加.从图6可知,随着k的增大,闭环系统的跟踪能力和抗干扰能力均增强,且越来越接近预期动态方程的响应;k增大到一定程度后闭环系统的跟踪能力和抗干扰能力变化不明显,此外,k的增大会造成控制量的增加.k和l的仿真结果与上述理论分析保持一致.从图7可知,随着ω_d的增大,闭环系统的跟踪能力和抗干扰能力均增强.上述参数整定过程中需要注意由于微电网限幅环节造成的控制性能下降,尽可能减少控制量在限幅边界值的作用时间.

基于 $ω_{d} 、 k 和 l$ 对于控制效果的影响分析以及大量仿真,可以总结基于预期动态方程的PID参数整定流程如下:

(1) 结合系统的动态特性,选择合适的预期动态方程带宽ω_d,建议开始时选择ω_d保守一些,即选择较小ω_d作为初值.

(2) 在k∈[ω_d, 100ω_d]的范围内,逐步增加k值,k值不宜过大,需要兼顾控制量的限幅作用.

(3) 在l∈ $[H α_{0} / β_{2}, 100 H α_{0} / β_{2}]$ 的范围内,逐步减小l值,l值不宜过小,同样需要兼顾控制量的限幅作用,其中H、α₀、β₂为被控对象参数^[16].

(4) 判断闭环系统是否取得满意的控制效果,如果取得满意的控制效果则中止参数整定流程;反之,则重复步骤(1)~(4).

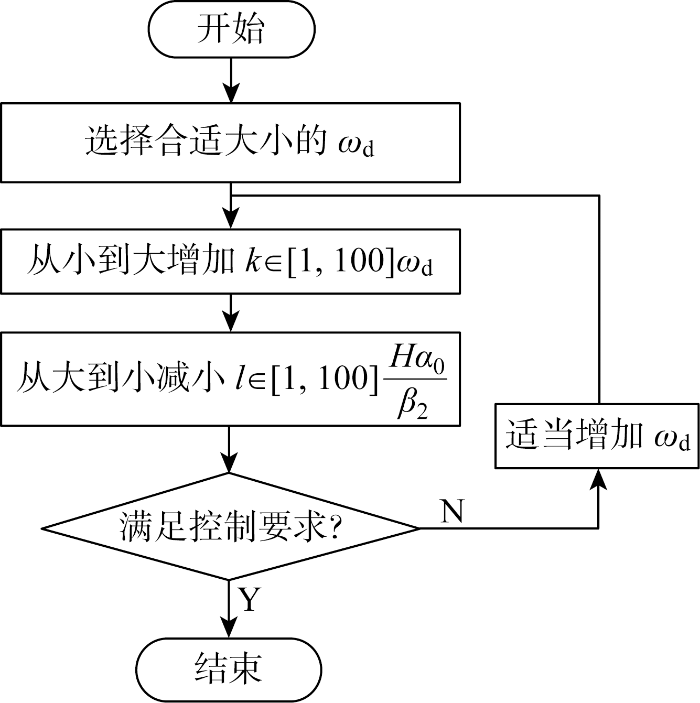
上述参数整定流程可以整理为图8,需要说明的是,该流程是一种经验试凑的方法,需要进行不断调整达到理想的控制效果,但该方法具有简单、实用和可工程化的优点,有很好的应用潜力.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 基于预期动态方程的PID参数整定流程

Fig.8 Parameter tuning procedure of the PID based on desired dynamic equation

接下来通过对基于预期动态方程的PID稳定域的计算与分析,进一步探究上述参数与k_p、k_i和k_d之间的关系.

图4所示二自由度PID的稳定域可以通过D-分割法求解,得到其稳定域的表达式:

(26)

\begin{matrix} \begin{array}{l} ω + k_{p} a (ω) ω + (k_{i} - k_{d} ω^{2}) b (ω) = 0 \\ k_{p} b (ω) ω + (k_{i} - k_{d} ω^{2}) a (ω) = 0 \\ k_{i} = 0 \end{array}\} \end{matrix}

式中:ω为频域频率;a(ω)、b(ω)分别为被控对象频域的实部和虚部.将式(25)代入式(26),可以得到基于预期动态方程的PID稳定域的计算表达式为

(27)

\begin{matrix} \begin{array}{l} ω + \frac{2 k ω_{d} + ω_{d}^{2}}{l} a (ω) ω + \\ (\frac{k ω_{d}^{2}}{l} - \frac{k + 2 ω_{d}}{l} ω^{2}) b (ω) = 0 \\ \frac{2 k ω_{d} + ω_{d}^{2}}{l} b (ω) ω + \\ (\frac{k ω_{d}^{2}}{l} - \frac{k + 2 ω_{d}}{l} ω^{2}) a (ω) = 0 \\ \frac{k ω_{d}^{2}}{l} = 0 \end{array}\} \end{matrix}

针对图5中被控对象,基于式(26)可以得到PID稳定域 $\{k_{p}, k_{i}, k_{d}\}$ 的分布如图9所示.基于式(27)可以得到基于预期动态方程PID稳定域 $\{ω_{d}, k, l\}$ 的分布如图10所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

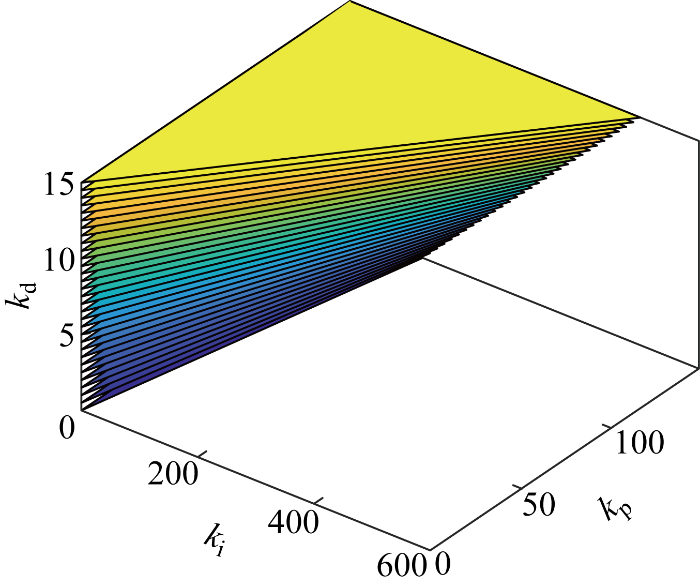
图9 PID稳定域 $\{k_{p}, k_{i}, k_{d}\}$ 的分布

Fig.9 Distributions of $\{k_{p}, k_{i}, k_{d}\}$ in PID stability region

图10

新窗口打开| 下载原图ZIP| 生成PPT

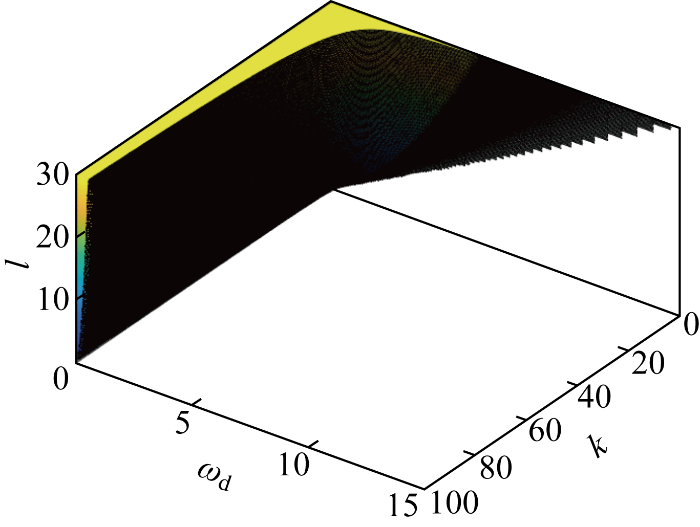
图10 基于预期动态方程的PID参数 $\{ω_{d}, k, l\}$ 的分布

Fig.10 Distributions of $\{ω_{d}, k, l\}$ in PID stability region based on desired dynamic equation

考虑实际系统存在一定的延迟,被控对象变为G_p₁(s)=G_p(s)e^-0^.⁵^s, 可以得到图11和图12所示的结果.对比分析可知,基于预期动态方程的PID参数稳定域分布与 $\{k_{p}, k_{i}, k_{d}\}$ 的分布规律有明显不同, $\{k_{p}, k_{i}, k_{d}\}$ 和 $\{ω_{d}, k, l\}$ 的边界趋势不同,前者会随着纯滞后的出现快速收敛于k_i所在的轴,后者的边界趋向但不收敛于ω_d和k所在的轴.综上所述,纯滞后的存在大大降低了参数的稳定域范围.

图11

新窗口打开| 下载原图ZIP| 生成PPT

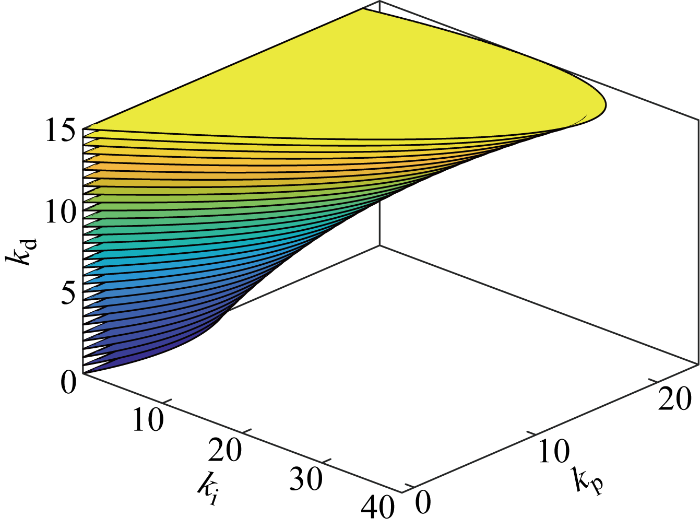
图11 系统存在纯滞后时PID稳定域 $\{k_{p}, k_{i}, k_{d}\}$ 的分布

Fig.11 Distributions of $\{k_{p}, k_{i}, k_{d}\}$ in PID stability region with delay time

图12

新窗口打开| 下载原图ZIP| 生成PPT

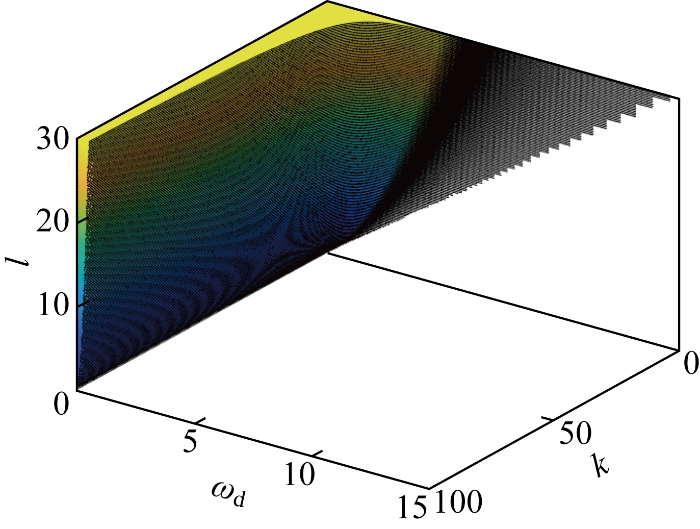
图12 系统存在纯滞后时基于预期动态方程的PID参数 $\{ω_{d}, k, l\}$ 的分布

Fig.12 Distributions of $\{ω_{d}, k, l\}$ in PID stability region based on desired dynamic equation with delay time

此时,通过合适的参数整定,闭环系统和预期动态方程 $\ddot{y} + h_{1} \overset{\cdot}{y} + h_{0} y = h_{0} r$ 有很接近的动态特性.基于预期动态方程PID的优势在于:

(1) 通过二自由度结构的PID参数调整能够使得闭环系统的动态方程与预期动态方程保持一致.

(2) 基于预期动态方程的PID具有的二自由度结构使得扰动抑制性能和跟踪性的设计能在一定程度上解耦,通过参数优化调整可以增强系统的扰动抑制能力.

(3) 建立PID与预期动态方程之间的定量化参数关系,使得参数物理意义更加明确.

(4) 由于前馈控制系数b_f的存在,使得反馈PID控制器主要用于随机性的太阳能、风电以及用户负荷的频率等扰动抑制,能够提高微电网的频率控制品质.

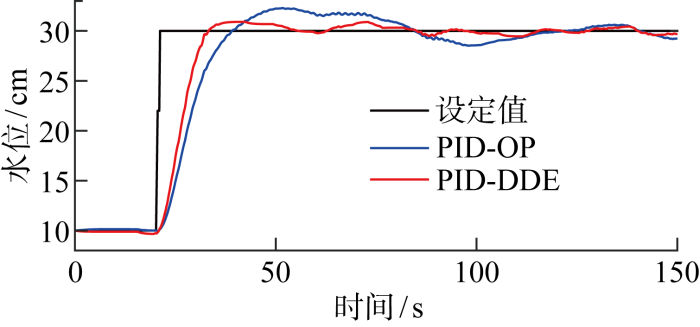
为了验证基于预期动态方程PID的控制效果,将基于预期动态方程的PID(PID-DDE)应用在Feedback公司生产的水箱实验台.此外,对比控制器为采用遗传算法以误差绝对值积分(Integral Absolute Error,IAE)作为适应度函数优化的PID(PID-OP),可以得到图13所示的结果.由图可见,PID-DDE能够用更快的速度达到稳态,且具有更小的超调;PID-OP跟踪速度较慢,且具有较大的超调.该水箱实验台验证了PID-DDE对于性能的提升能力,为PID-DDE在微电网负荷频率控制中应用提供基础.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 水位设定值阶跃变化的跟踪效果

Fig.13 Tracking performance of water level with step change

3 仿真验证

根据上面的分析可知,该微电网负荷频率控制的扰动具有快慢特性.为了能够较好地抑制风力发电系统和太阳能发电系统的扰动,结合基于预期动态方程的PID在抗干扰能力的优势,将其应用于图2所示的微电网负荷频率控制系统中,参数整定时的性能要求:①Δf的输出尽可能光滑;②外部扰动发生时,Δf能够尽可能快地恢复到稳态值并且Δf的峰值尽可能小.选择文献[16]中设计的适用的PID参数(PID-O)作为对比.此外,针对该微电网负荷频率控制采用基于遗传算法以IAE作为适应度函数对PID参数进行优化.PID-DDE、PID-O和PID-OP的参数如表1所示.需要说明的是,为了降低噪声等信号对于控制量的影响,PID中的微分均采用实际微分的形式, 即k_d $\frac{N}{1 + N / s}$ ,其中滤波器系数均取值N=100.该微电网负荷频率控制模型如图2所示,对应的模型参数均在微电网负荷频率模型介绍中给出,系统的稳定性分析见附录A.

表1 PID-DDE、PID-O和PID-OP参数

Tab.1 Parameters of PID-DDE, PID-O, and PID-OP

控制器	参数
PID-DDE	ω_d=3.5, k=20, l=20
PID-O	k_p=3.712, k_i=1.391, k_d=0.333
PID-OP	k_p=3.997 1, k_i=6.632 5, k_d=2.400 0

新窗口打开| 下载CSV

3.1 工况1:太阳能、风电功率和用户负荷阶跃变化时的控制效果

该工况下,不考虑太阳能、风电功率和用户负荷的随机性,只考虑太阳能、风电功率和用户负荷发生阶跃变化时负荷频率的控制效果.采用表1中控制器参数,太阳能、风电功率和用户负荷分别在合适的时间进行一定的幅值变化,如图14(a)所示,p.u.表示标幺值,可以得到图14(b)中负荷频率变化的情况.由图可见,太阳能、风电功率和用户负荷扰动发生时PID-DDE具有最好抑制效果,能够最快将负荷频率偏差控制到0,并且负荷频率的波动较PID-OP更小.

图14

新窗口打开| 下载原图ZIP| 生成PPT

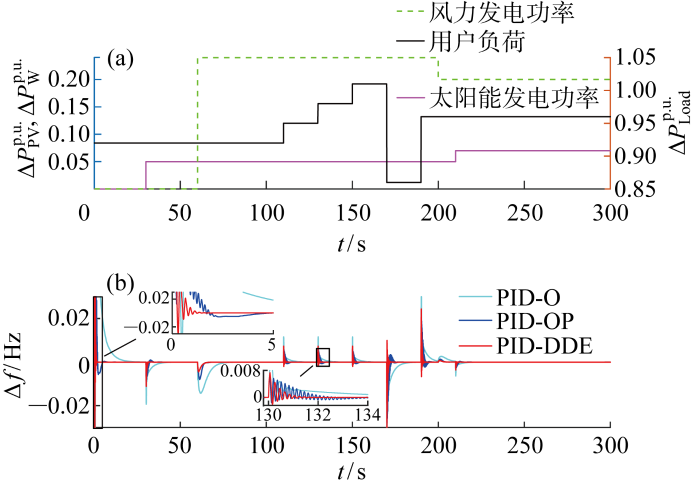
图14 太阳能、风电功率和用户负荷阶跃变化时的控制效果

Fig.14 Control performance with step changes in solar power, wind power, and consumer load

为了定量地衡量控制效果, IAE、误差绝对值时间积分(Integral of Time Absolute Error, ITAE)、误差积分(Integral of Error, IE)、误差平方积分(Integral of Squared Error, ISE)和误差平方时间积分(Integral of Time Squared Error, ITSE)作为性能指标进行计算,计算公式见附录B,可以得到表2所示的结果.由表可见,PID-DDE的各性能指标均有明显优势,进一步证明了该方法在微电网负荷频率控制中的优势.

表2 工况1的控制性能指标统计

Tab.2 Control performance index statistics under working Condition 1

控制器	IAE	ITAE	IE	ISE	ITSE
PID-DDE	0.0773	4.3578	0.0282	0.0058	0.0398
PID-OP	0.1623	9.2692	0.0520	0.0071	0.0736
PID-O	0.5975	31.9650	0.2480	0.0373	0.2851

新窗口打开| 下载CSV

3.2 工况2:太阳能、风电功率随机波动和用户负荷阶跃变化时的控制效果

该工况下,考虑阶跃变化的用户负荷和随机波动的太阳能、风电功率.依旧采用表1中控制器参数,用户负荷在合适的时间进行一定的幅值变化,太阳能和风电功率在随机波动中进行阶跃变化,如图15(a)所示,可以得到图15(b)中负荷频率变化的情况.由图可见,在随机扰动即太阳能、风电功率和用户负荷阶跃扰动下,PID-DDE具有最佳负荷频率控制效果,尽管PID-O的波动最小,但其波动幅值最大且需要最长时间才能达到稳态.PID-DDE具有比PID-OP更小的波动,且所需时间最短.

图15

新窗口打开| 下载原图ZIP| 生成PPT

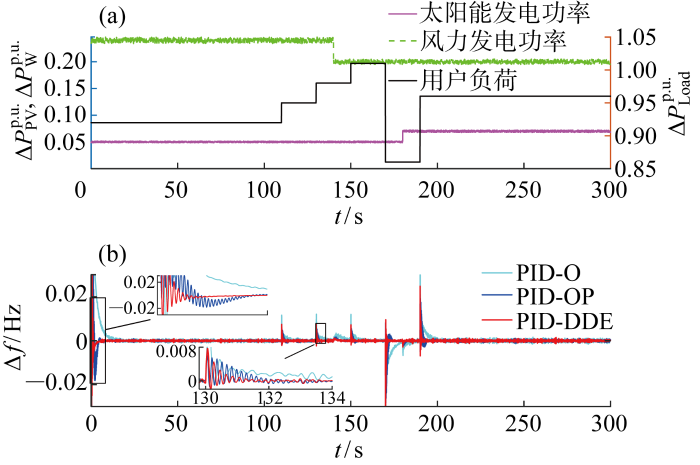
图15 太阳能、风电功率随机波动和用户负荷阶跃变化时的控制效果

Fig.15 Control performance with random fluctuation in solar and wind power and step changes in consumer load

计算图15(b)中的各项性能指标如表3所示,可知PID-DDE的各性能指标较PID-OP和PID-OP仍然有明显的优势.PID-OP具有次于PID-DDE的控制性能.PID-DDE的IAE、ITAE、IE、ISE和ITSE分别占 PID-OP 的65.79%、73.61%、54.13%、 83.61%和57.78%.PID-DDE在该工况下仍可以保证最佳控制效果.

表3 工况2的控制性能指标统计

Tab.3 Control performance index statistics under working Condition 2

控制器	IAE	ITAE	IE	ISE	ITSE
PID-DDE	0.1254	12.7179	0.0282	0.0051	0.0412
PID-OP	0.1906	17.2774	0.0521	0.0061	0.0713
PID-O	0.4578	37.7171	0.2482	0.0261	0.2264

新窗口打开| 下载CSV

3.3 工况3:太阳能、风电功率和用户负荷随机波动时的控制效果

该工况下,考虑随机波动的太阳能、风电功率和用户负荷.保持表1中控制器参数不变,在图16(a)的太阳能、风电功率和用户负荷扰动下,可以得到图16(b)所示的控制效果.从图16(b)可知PID-DDE的负荷频率波动范围较PID-OP和PID-OP更小.该工况下的控制性能指标如表4所示,由表可见,随机波动的太阳能、风电功率和用户负荷下PID-DDE的负荷频率性能指标更小,PID-DDE仍然具有最佳外部扰动抑制能力.

图16

新窗口打开| 下载原图ZIP| 生成PPT

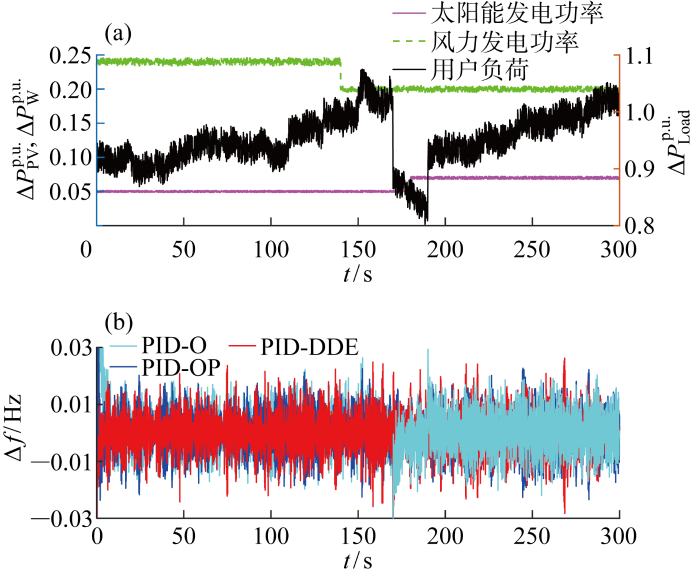
图16 太阳能、风电功率和用户负荷随机波动时的控制效果

Fig.16 Control performance with step changes in solar power, wind power, and consumer load

表4 工况3的控制性能指标统计

Tab.4 Control performance index statistics under working Condition 3

控制器	IAE	ITAE	IE	ISE	ITSE
PID-DDE	1.2947	192.4833	0.0302	0.0145	1.5637
PID-OP	1.5951	236.5464	0.0557	0.0179	1.9389
PID-O	1.8713	254.9701	0.2689	0.0383	2.2728

新窗口打开| 下载CSV

3.4 工况4:应对不确定性系统的控制效果

由于微电网建模过程中存在必要的简化和近似,且工况变化时系统动态发生变化,必须考虑控制器的鲁棒性,即控制器应对系统不确定性的能力.

为比较上述控制器的鲁棒性,采用蒙特卡洛实验进行分析比较,图2所示系统的时间常数与增益在标称值±10%范围随机摄动,在保持控制器参数不改变提前下,重复工况1~3仿真各200次,并统计每次仿真的性能指标,可以得到图17~19所示的控制性能分布结果.

图17

新窗口打开| 下载原图ZIP| 生成PPT

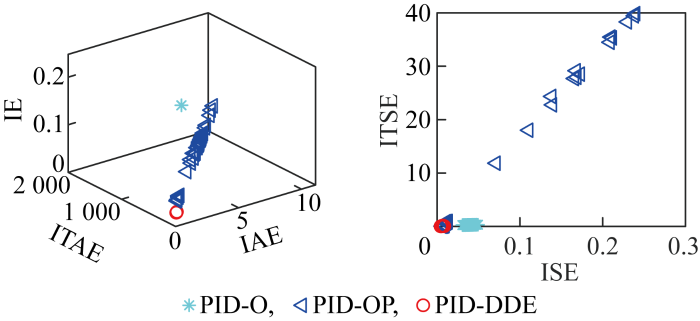
图17 工况1的蒙特卡洛实验结果

Fig.17 Monte Carlo experimental results under working Condition 1

图18

新窗口打开| 下载原图ZIP| 生成PPT

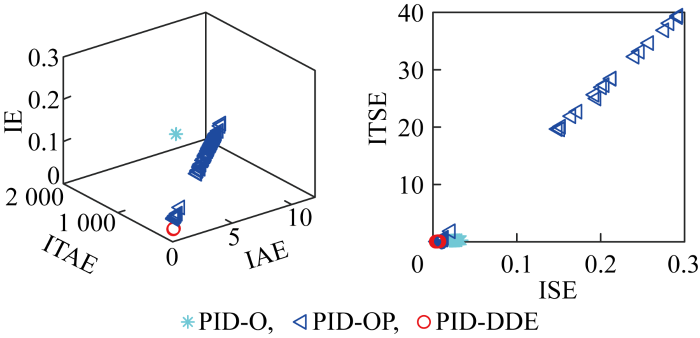
图18 工况2的蒙特卡洛实验结果

Fig.18 Monte Carlo experimental results under working Condition 2

图19

新窗口打开| 下载原图ZIP| 生成PPT

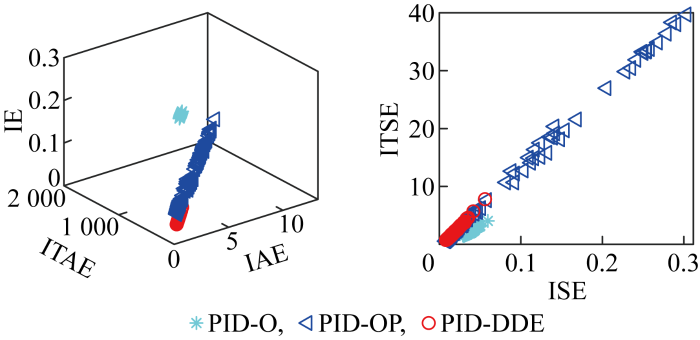
图19 工况3的蒙特卡洛实验结果

Fig.19 Monte Carlo experimental results under working Condition 3

性能指标越集中意味着随着对象变化控制器的鲁棒性越强,性能指标越小意味着控制性能越好.从图17~19可知,PID-DDE和PID-O的性能指标分布较PID-OP更加集中,即意味着PID-DDE和PID-O的鲁棒性更强.PID-DDE的各个性能指标均集中于更小的位置,这意味着PID-DDE能够在保证较强的鲁棒性下具有最佳的控制效果.此外,最大灵敏度函数也用于比较系统的鲁棒性指标,其计算公式^[18]如下:

(28)

\begin{matrix} M_{s} = \underset{0 \leq ω < \infty}{m a x} |\frac{1}{1 + G_{c} (j ω) G_{e q} (j ω)}| \end{matrix}

式中: $G_{c} (j ω) 、 G_{e q} (j ω)$ 分别为控制器和微电网模型等效传递函数的频率响应.M_s越小意味着闭环系统的鲁棒性越强,反之亦然,推荐范围为[1.2,2.0].计算得到PID-DDE、PID-O和PID-OP的M_s值分别为1.56、1.31和1.92,均在推荐范围内.PID-OP鲁棒性最弱,与图17~19结果一致.尽管PID-DDE的M_s值比PID-O的大,但仍具有足够好的鲁棒性.

通过上述分析可知,PID-DDE不仅能够保证微电网系统在标称工况下的控制效果,在微电网系统存在不确定性时,也能够取得令人满意的控制效果.需要说明的是,可以采用遗传算法对基于预期动态方程PID三个参数进一步优化,进一步提高微电网系统的控制性能.

4 结论

风电、太阳能的随机性和暂态性给高比例可再生能源并入微电网带来较大的负荷频率控制挑战.针对微电网负荷频率控制面临的多源不确定性扰动问题,提出基于预期动态方程的PID控制策略.主要工作如下:

(1) 在分析微电网负荷频率控制模型和控制难点的基础上设计基于预期动态方程的PID控制策略,并通过单一变量法分析控制器参数对控制效果的影响,总结了简单、实用的参数整定流程.

(2) 与其他控制策略相比,所提方法能够在太阳能、风电功率和用户负荷随机波动等多个工况中具有抗干扰能力最强、频率偏差最小,恢复到稳态值所需时间最短等优势.在微电网系统存在不确定性时仍具有最佳控制性能.

基于预期动态方程的PID控制策略能够提高包含高比例可再生能源微电网的负荷稳定性,对电网安全运行具有重要意义.在未来工作中,将进一步完成实验台的验证和现场的应用,通过实验对比数据以及在现场运行数据进一步验证该方法的有效性.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2024/1006-2467/1006-2467-58-06-0954.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘吉臻, 王玮, 胡阳, 等.

新能源电力系统控制与优化

[J]. 控制理论与应用, 2016: 33(12): 1555-1561.