考虑阶梯碳奖惩和综合需求响应的楼宇低碳规划

doi:10.16183/j.cnki.jsjtu.2022.527

考虑阶梯碳奖惩和综合需求响应的楼宇低碳规划

尚梦琪, 高红均, 贺帅佳^,, 刘俊勇

四川大学电气工程学院,成都 610065

Low-Carbon Planning for Buildings Considering Ladder Carbon Reward and Punishment and Integrated Demand Response

SHANG Mengqi, GAO Hongjun, HE Shuaijia^,, LIU Junyong

College of Electrical Engineering, Sichuan University, Chengdu 610065, China

通讯作者: 贺帅佳,副研究员,电话(Tel.):028-85405614;E-mail:shuaijiahe@scu.edu.cn.

责任编辑: 王历历

收稿日期: 2022-12-21 修回日期: 2023-03-2 接受日期: 2023-03-31

基金资助:

国家自然科学基金资助项目(52077146)
中央高校基本科研业务费专项资金资助项目(YJ202252)

Received: 2022-12-21 Revised: 2023-03-2 Accepted: 2023-03-31

作者简介 About authors

尚梦琪(1998-),硕士生,从事智能楼宇规划研究.

摘要

近年来,商业综合体的发展趋势迅猛,楼宇建筑的能源消耗以及碳排放持续增长.在此背景下,对包含购物、餐饮、办公和住宿等多种功能的商业综合体楼宇低碳规划进行研究,建立楼宇低碳规划模型,同时考虑引入上级电网购电分时碳计量模型的阶梯碳奖惩和考虑楼宇各功能区域差异化预测平均指标(PMV)的综合需求响应(IDR).首先,引入上级网络购电分时碳计量模型,利用其评估楼宇等效碳排放,并构建阶梯碳奖惩模型衡量楼宇碳排放.同时,根据所规划商业综合体的特点构建考虑负荷时间转移和用能削减、终端用能设备替代及上级能源端用能种类转换的IDR.其次,以计及楼宇碳奖惩费用的楼宇年总规划成本最优为目标函数,考虑楼宇各功能区域差异化PMV,建立楼宇低碳规划模型来决策楼宇中各能源设备的型号及台数.然后,利用基于Kullback-Leibler散度的分布鲁棒优化方法应对接入的屋顶分布式光伏及光伏幕墙出力波动性.最后,通过算例分析引入上级电网购电分时碳计量模型的阶梯碳奖惩、考虑楼宇各功能区域差异化PMV的IDR及接入光伏出力波动性对楼宇规划的影响,验证所提规划模型可以有效减少楼宇能耗以及降低碳排放.

关键词： 商业综合体; 楼宇规划; 阶梯碳奖惩; 综合需求响应; 低碳

Abstract

With the rapid development of commercial complexes in recent years, energy consumption and carbon emissions of buildings are growing continuously. In this context, the low-carbon planning of commercial complexes is studied including shopping, restaurants, offices, and accommodation. In addition, a low-carbon planning model for building considering ladder carbon reward and punishment with the introduction of the time-sharing carbon measurement model of superior network power purchase and an integrated demand response (IDR) considering the differentiated predicted mean vote (PMV) of each functional area of the building is established. First, the time-sharing carbon measurement model of superior network power purchase is introduced to evaluate the equivalent carbon emissions of the building. Then, a ladder carbon reward and punishment model is built to measure the carbon emissions of the building. Based on the characteristics of the commercial complex planned in this paper, the IDR considering load time shifting and energy use reduction, end-use energy equipment substitution, and energy use type conversion at the superior energy end is constructed. Afterwards, a low-carbon planning model for building is established to determine the equipment type and capacity considering the PMV for each functional area of the building. Especially, the objective function is to optimize the total annual planning cost of the building by taking into account carbon reward and punishment costs of the building. A distributionally robust optimization model based on Kullback-Leibler divergence is proposed to cope with the output volatility of the connected distributed photovoltaic and photovoltaic curtain wall. Finally, the effects of the ladder carbon reward and punishment mechanism of the time-sharing carbon measurement model of superior network power purchase, the IDR of the differentiated PMV of each functional area of the building, and the volatility of the connected photovoltaic output on the building planning are analyzed to verify the effectiveness of the planning model proposed for energy saving and emission reduction in the building.

Keywords： commercial complex; building planning; ladder carbon reward and punishment; integrated demand response (IDR); low-carbon

PDF (3083KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

尚梦琪, 高红均, 贺帅佳, 刘俊勇. 考虑阶梯碳奖惩和综合需求响应的楼宇低碳规划[J]. 上海交通大学学报, 2024, 58(6): 926-940 doi:10.16183/j.cnki.jsjtu.2022.527

SHANG Mengqi, GAO Hongjun, HE Shuaijia, LIU Junyong. Low-Carbon Planning for Buildings Considering Ladder Carbon Reward and Punishment and Integrated Demand Response[J]. Journal of Shanghai Jiaotong University, 2024, 58(6): 926-940 doi:10.16183/j.cnki.jsjtu.2022.527

随着我国楼宇建筑能源消耗及碳排放的持续增长^[1],如何利用碳奖惩机制降低楼宇系统的碳排放,实现楼宇低碳规划,已经成为当前研究热点^[2].另外,楼宇作为商业综合体,涵盖办公、餐饮、零售、娱乐等多种用户,对多种类型的能源均有需求^[3],这导致传统电力需求响应逐步向综合需求响应(Integrated Demand Response,IDR)转变^[4].若能利用IDR充分挖掘商业综合体楼宇的用能潜力,引导用户合理用能,可以有效降低能源消耗.因此,考虑碳奖惩和IDR的商业综合体楼宇低碳规划具有重要研究意义.

目前,已有许多学者针对单一用户类型的楼宇规划问题^[5-6]进行研究,但对于商业综合体楼宇的多能规划涉及较少.另外,规划方案会在很大程度上决定楼宇能源系统未来很长时间的碳排放强度.基于碳配额的碳奖惩机制是控制碳排放强度的主要手段之一,不仅欧盟、英国、韩国、新西兰、美国等都已经采用该方法,北京、天津、上海、重庆等国内城市也已开展试点工作,具有良好的应用前景.因此,已有许多学者在能源系统规划中引入碳奖惩机制,将原来系统的外部碳排放成本内部化来降低能源系统碳排放^[7].文献[8-9]中采取固定碳奖惩机制考虑外部碳奖惩效益,利用统一奖励或惩罚价格对不足或超出碳配额部分碳排放进行奖惩,并运用到综合能源系统规划中.文献[10-11]中在固定碳奖惩机制的基础上引入阶梯碳奖惩机制,采用阶梯奖惩价格对不足或超出碳配额部分碳排放进行奖惩,建立计及碳奖惩费用的综合能源系统规划模型.上述文献表明,将固定碳奖惩改为阶梯碳奖惩,系统减少碳排放的作用更明显,控碳效果更显著.但上述文献中外购电能均采用固定碳排放计量因子,无法充分反映不同时刻上级电网发电机组组成成分的差异^[12],从而未能充分挖掘系统碳减排潜力与用能潜力.此外,上述文献的算例结果表明,采用碳奖惩机制虽然在降低碳排放上起到良好的效果,但系统的经济性有一定下降.因此,如何考虑上级电网发电机组组成成分的差异,从而充分挖掘系统碳减排潜力,保证降碳的同时具有一定经济性,对于低碳楼宇规划十分重要.

IDR可以通过需求侧负荷在横向上的时间转移和用能削减与纵向上用能种类的转换提升系统经济性^[4].比如,文献[13]中考虑电、气、热负荷灵活的响应能力构建IDR模型.文献[14]中建立电、热需求响应模型,平滑电热负荷曲线.文献[15]中构建用户冷、热、电负荷的IDR精细化模型.上述文献通过算例分析验证了IDR能够减少综合能源系统的能耗,提升系统经济性,但都局限于单一电、气、冷、热负荷之间的弹性调节,未考虑终端用能设备之间的替代.除此以外,上述文献未考虑用户舒适度或在考虑用户舒适度时将室内温度利用直接给出的上下限进行约束.文献[16]中的模糊舒适度冷负荷需求响应模型利用预测平均指标(Predicted Mean Vote,PMV)表征用户对环境温度的感觉.文献[17]中也引入PMV表征容许的温度范围,从而量化冷、热负荷的可调度潜力.但上述文献中PMV指标值均直接指定,未考虑该区域影响人体舒适度感觉的物理环境与个体行为差异影响因素,会扩大或缩小实际的温度调节范围,使得室温约束不够精确.因此,有必要使用构建楼宇各功能区域差异化PMV约束不同区域的室内温度,并将其融入IDR模型,保证楼宇低碳规划方案的合理性.

此外,楼宇规划设备中光伏装置的出力很大程度上受到环境的影响,具有不确定性^[18-19].目前,不确定性处理方法主要有随机规划 (Stochastic Programming,SP)方法、鲁棒优化 (Robust Optimization,RO) 方法与分布鲁棒优化 (Distributionally Robust Optimization,DRO) 方法^[20-21].SP中不确定性参数的准确概率分布难以获取,RO在不确定参数最恶劣情况下进行决策,结果过于保守,而DRO弥补了这些缺陷^[20],在不确定参数最恶劣概率分布情况下进行决策.并且,Kullback-Leibler(KL)散度可以构建DRO中包含所有实际场景概率分布的不确定性集,量化实际概率分布与经验性分布之间的差异性,提高实际概率分布描述的准确性^[22-23].基于此,利用基于KL散度的DRO方法应对光伏出力的不确定性,以求最终决策方案兼顾经济性和鲁棒性.

因此,同时引入考虑上级网络购电分时碳计量模型的阶梯碳奖惩和考虑楼宇各功能区域差异化PMV的IDR,建立包含购物、餐饮、办公和住宿等多种功能的商业综合体楼宇的低碳规划模型,并且利用基于KL散度的DRO方法应对光伏的不确定性,保证楼宇规划低碳性能的同时还具有一定经济性.算例结果验证了所构建的考虑阶梯碳奖惩和IDR的楼宇规划模型可以有效减少楼宇能耗以及降低碳排放.本研究创新之处在于:①为降低阶梯碳奖惩机制导致的系统经济性能变差,结合IDR改变楼宇用能习惯,提升系统经济性;②为降低楼宇综合能源系统碳排放,在构建阶梯碳奖惩机制的基础上引入上级网络分时碳计量模型,充分挖掘楼宇降碳潜力;③根据楼宇各功能区域影响人体舒适度感觉的物理环境与个体行为差异影响因素,建立考虑楼宇各功能区域差异化PMV的IDR,在使得室内温度约束更合理的前提下,充分挖掘楼宇用能潜力.

1 考虑阶梯碳奖惩和IDR的楼宇低碳系统框架

1.1 楼宇低碳规划系统结构

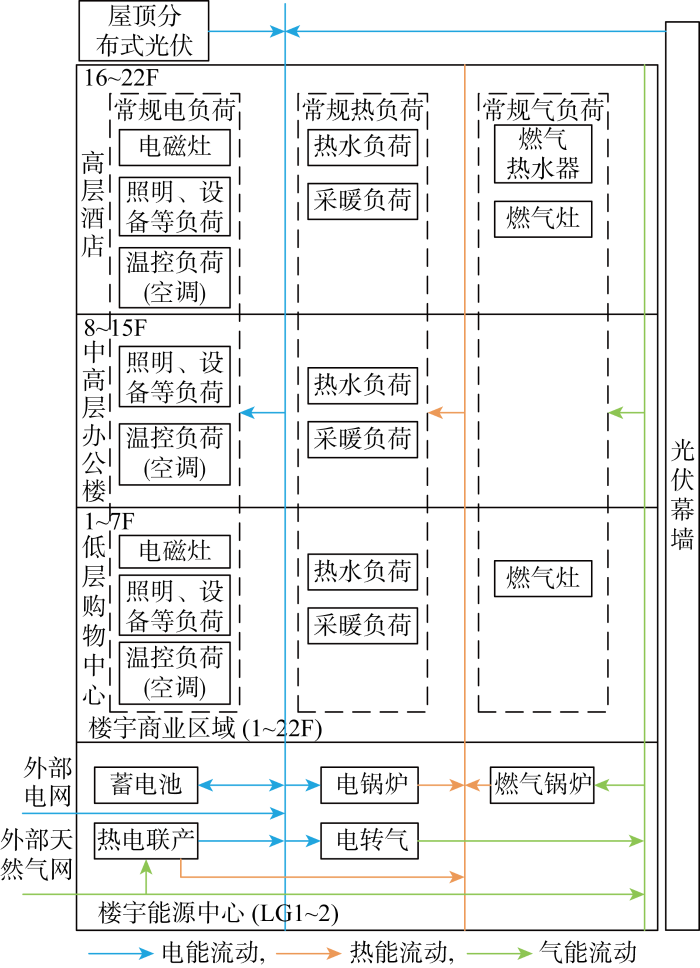
所规划的楼宇综合能源系统结构和能流示意图如图1所示.该楼宇系统根据供用能关系分为楼宇能源中心和楼宇商业区域两部分.拟通过规划楼宇能源中心的能源设备、屋顶分布式光伏(Distributed Photovoltaic,DPV)以及光伏幕墙(Photovoltaic Curtain Wall,PVCW)的型号及台数来满足商业区域的电、气、热能需求.楼宇商业区域根据其使用功能不同分为3部分,低层购物中心(1~7F)对电、气、热负荷均有需求,中高层办公楼(8~15F)对气负荷无需求,对电、热负荷具有需求,高层酒店(16~22F)对电、气、热负荷均有需求.根据楼宇商业中心的功能特性,常规电负荷(照明、设备、温控负荷)、常规热负荷(热水、采暖负荷)在功能不同的3部分区域都具备;具有餐饮功能的购物中心和酒店配备电磁灶以及燃气灶;办公楼则无需消耗气能,因此没有气负荷;酒店需要随时供应热水,配备燃气热水器.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 楼宇综合能源系统结构和能流示意图

Fig.1 Schematic of structure and energy flow of integrated energy system of buildings

1.2 阶梯碳奖惩模型

1.2.1 购电碳排放分时计量模型

传统的上级电网发电碳排放计量因子是固定的,没有考虑上级电网发电侧能源供应的不同发电机组,如火电机组、水电机组、风电机组等,在不同时段出力占比不同.假设清洁能源机组未直接产生碳排放,实时产生碳排放的机组主要为火电机组,因此只考虑火电机组的发电占比与碳排放计量因子.而电价的变化与不同发电机组出力占比也有关系^[24],将其关联起来,把购电碳排放分时计量因子与分时电价的时段定为一致^[12].

上级购电碳排放分时计量模型如下所示:

(1)

\begin{matrix} \begin{array}{l} {M^{E}}_{t} = {ε^{E}}_{t} {P^{E}}_{t} \\ {ε^{E}}_{t} = {R^{S}}_{t} χ^{S} \end{array}\} \end{matrix}

式中: ${M^{E}}_{t}$ 、 ${ε^{E}}_{t}$ 、 ${P^{E}}_{t}$ 分别为上级电网在t时刻的购电等效碳排放、碳排放计量因子、与楼宇的交互功率; ${R^{S}}_{t}$ 、χ^S分别为火电机组在t时刻的单位发电量占比、单位发电碳排放计量因子.

1.2.2 阶梯碳奖惩模型

基于碳排放配额构建阶梯碳排放奖惩模型,当碳排放量小于碳配额时,碳排放量与碳配额的差值区间越大,碳排放奖励系数越大,此时楼宇系统可以出售碳配额获取利润;当碳排放量大于碳配额时,碳排放量与碳配额的差值区间越大,碳排放惩罚系数越大^[25],此时楼宇系统要购买一定碳配额.对于楼宇系统,由于天然气在生产传输中所产生的碳排放很小,只计及其由热电联产(Combined Heat and Power,CHP)机组和燃气锅炉(Gas Boiler,GB)产生的碳排放;而电能需要计及其在上级电网产生的碳排放.此外,电转气(Power to Gas,P2G)设备在电转气过程中会消耗一定CO₂,可以作为碳减排装置.

(2)

M^{C O_{2}} = \sum_{t} M_{t}^{C O_{2}}

(3)

M_{t}^{C O_{2}} = {M^{E}}_{t} + {M^{G}}_{t} - M_{t}^{P 2 G}

(4)

M_{t}^{G} = ε^{G B} G_{t}^{G B} + ε^{G T} G_{t}^{G T}

(5)

\begin{array}{l} G_{t}^{P 2 G} = η^{P 2 G} P_{t}^{P 2 G} \\ V_{t}^{P 2 G} = G_{t}^{P 2 G} / β \\ M_{t}^{P 2 G} = V_{t}^{P 2 G} m^{C O_{2}} \end{array}\}

(6)

\begin{matrix} C^{C O_{2}} = \{\begin{array}{l} - ϕ (E^{C O_{2}} - M^{C O_{2}}), & E^{C O_{2}} - h < M^{C O_{2}} \leq E^{C O_{2}} \\ ϕ m - (ϕ + m) (E^{C O_{2}} - M^{C O_{2}}), & E^{C O_{2}} - 2 h < M^{C O_{2}} \leq E^{C O_{2}} - h \\ 3 m h - (ϕ + 2 m) (E^{C O_{2}} - M^{C O_{2}}), & E^{C O_{2}} - 3 h < M^{C O_{2}} \leq E^{C O_{2}} - 2 h \\ \dots & \dots \\ φ (M^{C O_{2}} - E^{C O_{2}}), & E^{C O_{2}} < M^{C O_{2}} \leq E^{C O_{2}} + h \\ - φ n + (φ + n) (M^{C O_{2}} - E^{C O_{2}}), & E^{C O_{2}} + h < M^{C O_{2}} \leq E^{C O_{2}} + 2 h \\ - 3 n h + (φ + 2 n) (M^{C O_{2}} - E^{C O_{2}}), & E^{C O_{2}} + 2 h < M^{C O_{2}} \leq E^{C O_{2}} + 3 h \\ \dots & \dots \end{array} \end{matrix}

式中: $M^{C O_{2}}$ 为一段时间内的楼宇碳排放总量; $M_{t}^{C O_{2}}$ 为楼宇在t时刻的碳排放总量; ${M^{G}}_{t}$ 为消耗的天然气在t时刻产生的等效碳排放; $M_{t}^{P 2 G}$ 为P2G设备在t时刻消耗的CO₂量;ε^GB、ε^GT分别为燃气锅炉、燃气轮机(Gas Turbine, GT)消耗天然气的等效碳排放计量因子; $G_{t}^{G B}$ 、 $G_{t}^{G T}$ 为燃气锅炉、燃气轮机在t时刻消耗的天然气功率; $P_{t}^{P 2 G}$ 、 $G_{t}^{P 2 G}$ 分别为t时刻P2G设备输入功率、制取天然气功率;η^P²^G为P2G设备电制气的转换效率;β为天然气的热值; $V_{t}^{P 2 G}$ 为t时刻P2G设备的消耗的CO₂体积; $m^{C O_{2}}$ 为CO₂质量和体积的转换系数; $C^{C O_{2}}$ 为楼宇系统碳奖惩成本; $E^{C O_{2}}$ 为楼宇所拥有的碳排放额度;h为碳排放阶梯区间长度;ϕ、φ分别为单位碳排放奖励、惩罚基数;m、n分别为碳排放奖励、惩罚阶梯增长系数.

1.3 综合需求响应

构建楼宇各功能区域差异化PMV可以约束不同区域的室内温度范围从而量化热负荷的可调度潜力,因此将其融入IDR模型,保证楼宇低碳规划方案的合理性.

1.3.1 各功能区域差异化PMV模型

PMV舒适度指标是由影响人体舒适度感觉的物理环境与个体行为差异,即人体新陈代谢率、服装热阻、平均辐射温度、空气流速等多方面因素共同作用的综合性指标,可量化用户冷热舒适度,几乎包含所有影响人体舒适度的因素^[26].PMV舒适度指标λ^PMV公式及相关参数如下:

(7)

\begin{array}{l} λ^{P M V} = [0.303 e x p (- 0.036 M) + 0.028] {(M - W) - 3.05 \times 10^{- 3} [5 733 - 6.99 (M - W) - \\ p_{a}] - 0.42 [(M - W) - 58.15] - 1.7 \times 10^{- 5} M (5 867 - p_{a}) - 0.001 4 M (34 - T_{a}) - \\ 3.96 \times 10^{- 8} f_{c l} [{(T}_{c l} {+ 273)}^{4} - {\bar{(T}}_{r} {+ 273)}^{4}] - f_{c l} h_{c} (T_{c l} - T_{a})} \\ T_{c l} = 35.7 - 0.028 (M - W) - I_{c l} {3.96 \times 10^{- 8} f_{c l} [{(T}_{c l} {+ 273)}^{4} - {\bar{(T}}_{r} {+ 273)}^{4}] + f_{c l} h_{c} (T_{c l} - T_{a})} \\ h_{c} = \{\begin{array}{l} 2.38 | T_{c l} - T_{a} |^{0.25}, & 2.38 | T_{c l} - T_{a} |^{0.25} > 12.1 \sqrt{v_{a r}} \\ 12.1 \sqrt{v_{a r}}, & 2.38 | T_{c l} - T_{a} |^{0.25} \leq 12.1 \sqrt{v_{a r}} \end{array} \\ f_{c l} = \{\begin{array}{l} 1 + 1.29 I_{c l}, & I_{c l} \leq 0.078 m^{2} \cdot K / W \\ 1.05 + 0.645 I_{c l}, & I_{c l} > 0.078 m^{2} \cdot K / W \end{array} \end{array}\}

式中:M 为人体新陈代谢率;W 为人体活动所产生的机械功;p_a为环境中水蒸气压力;T_a为环境空气温度;f_cl为衣着系数;T_cl为着装人体表面温度; ${\bar{T}}_{r}$ 为平均辐射温度;h_c为空气对流热传递系数;I_cl为服装热阻;v_ar为空气流速.

根据定义,当PMV舒适度指标λ^PMV值离0越远,用户的舒适度感觉越低.定义PMV指标参考值±λ^{PMV, ref}到0的距离为PMV可调裕度δ^PMV,δ^PMV表示λ^PMV的可调节范围:

(8)

\begin{matrix} - | λ^{P M V, r e f} | \leq δ^{P M V} \leq + | λ^{P M V, r e f} | \end{matrix}

受物理环境与个体行为差异的影响,楼宇各功能区域包括购物中心、办公区域、高层酒店影响人体舒适度感觉的各方面因素不完全相同(见附录A),因此各区域PMV指标参考值λ^PMV,ref存在差异,PMV可调裕度δ^PMV也不相同.

1.3.2 综合需求响应

外部电能供应价格采用分时电价,当外部能源价格发生改变时,楼宇商业区域会根据价格变化在一定程度上对用能负荷进行调整,即电、气、热负荷发生不同程度横向上的增减、平移及纵向上终端用能设备替代.表示为

(9)

[\begin{array}{l} {L^{e}}_{t} \\ {L^{g}}_{t} \\ {L^{h}}_{t} \end{array}] = [\begin{array}{l} L_{t}^{e, 0} \\ L_{t}^{g, 0} \\ L_{t}^{h, 0} \end{array}] + [\begin{array}{l} Δ {L^{e}}_{t} \\ Δ {L^{g}}_{t} \\ Δ {L^{h}}_{t} \end{array}] + [\begin{array}{l} S_{t}^{e c h} + S_{t}^{e c g} - {S^{e}}_{t} \\ S_{t}^{g c h} + S_{t}^{g c e} - {S^{g}}_{t} \\ - {S^{h}}_{t} \end{array}]

式中: ${L^{e}}_{t}$ 、 ${L^{g}}_{t}$ 、 ${L^{h}}_{t}$ 分别为楼宇商业区域在t时刻IDR后的电、气、热负荷; $L_{t}^{e, 0}$ 、 $L_{t}^{g, 0}$ 、 $L_{t}^{h, 0}$ 分别为IDR前的电、气、热负荷; Δ ${L^{e}}_{t}$ 、Δ ${L^{g}}_{t}$ 、Δ ${L^{h}}_{t}$ 分别为IDR导致的电、气、热负荷弹性可调节部分变化量; $S_{t}^{e c h}$ 、 $S_{t}^{g c h}$ 、 ${S^{h}}_{t}$ 、 $S_{t}^{e c g}$ 、 $S_{t}^{g c e}$ 、 ${S^{e}}_{t}$ 、 ${S^{g}}_{t}$ 分别为由于电替热导致的电负荷增加量、气替热导致的气负荷增加量、能源替代导致的热负荷减少量、电气互相替代的电能增加量、电气互相替代的气能增加量、电气互相替代的电能减少量、电气互相替代的气能减少量.

2 楼宇系统模型构建

2.1 楼宇能源中心模型

2.1.1 光伏发电系统模型

光伏发电系统与楼宇结合已经成为光伏系统在城市的主要应用方式.楼宇系统在楼宇屋顶安放分布式光伏阵列以及楼宇的外墙表面铺设光伏组件.表示为

(10)

\begin{matrix} \begin{array}{l} P_{t}^{P V, m a x} = S^{P V} η^{P V} η^{l o s s} I_{t}^{P V} \\ η^{l o s s} = 1 - 0.004 5 (T_{t}^{o u t} - 25) \\ 0 \leq P_{t}^{P V} \leq P_{t}^{P V, m a x} \end{array}\} \end{matrix}

式中: $P_{t}^{P V}$ 、 $P_{t}^{P V, m a x}$ 分别为在t时刻光伏发电系统的实际出力、最大可输出功率; S^PV为光伏面板的面积;η^PV、η^loss分别为光伏系统的发电效率与光伏系统由于温度升高导致功率损耗后的效率; $I_{t}^{P V}$ 为在t时刻单位面积所获取的太阳能辐照量; $T_{t}^{o u t}$ 为在t时刻的环境温度.

2.1.2 电转气设备模型

利用P2G技术可以加强光伏的消纳以及电价低谷时期电能的灵活应用,制取的甲烷可以直接注入天然气网络以供使用.能量转换表达式见式(5).

2.1.3 蓄电池模型

蓄电池(Energy Storage System,ESS)在楼宇系统中的应用可以实现电能在时间尺度上的平移,平抑负荷供能波动,减少峰时段来自上级电网的购电量.

(11)

\begin{array}{l} E_{t}^{E S S} = E_{t - 1}^{E S S} + Δ E_{t}^{E S S} \\ Δ E_{t}^{E S S} = (P_{t}^{E S S, c h} η^{E S S, c h} - P_{t}^{E S S, d i s} / η^{E S S, d i s}) Δ t \\ 0.2 E^{E S S, m a x} \leq E_{t}^{E S S} \leq 0.9 E^{E S S, m a x} \\ E_{1}^{E S S} = E_{24}^{E S S} \end{array}\}

(12)

\begin{array}{l} 0 \leq P_{t}^{E S S, c h} \leq x_{t}^{E S S, c h} P^{E S S, c h m a x} \\ 0 \leq P_{t}^{E S S, d i s} \leq x_{t}^{E S S, d i s} P^{E S S, d i s m a x} \\ x_{t}^{E S S, c h} + x_{t}^{E S S, d i s} \leq 1 \\ P_{t}^{E S S} = P_{t}^{E S S, c h} - P_{t}^{E S S, d i s} \end{array}\}

式中: $E_{t}^{E S S}$ 为蓄电池t时刻的储电量; $P_{t}^{E S S, c h}$ 、 $P_{t}^{E S S, d i s}$ 分别为t时刻蓄电池的充电、放电功率;η^{ESS, ch}、η^{ESS, dis}分别为充电、放电效率;E^{ESS, max}为蓄电池的最大安装容量; P^{ESS, chmax}、P^{ESS, dismax}分别为蓄电池充、放电功率的上限; $x_{t}^{E S S, c h}$ 、 $x_{t}^{E S S, d i s}$ 为0或1变量,分别为蓄电池的充电、放电状态变量; $P_{t}^{E S S}$ 为t时刻蓄电池的功率.

2.1.4 CHP机组、燃气锅炉、电锅炉模型

楼宇配备含GT、余热锅炉(Heat Recovery Boiler,HB)、燃气锅炉以及电锅炉(Electric Boiler,EB)的小型CHP机组进行生活热水供应及部分电能供应.

(13)

\begin{matrix} \begin{array}{l} P_{t}^{C H P} = η^{G T, e} G_{t}^{C H P} \\ H_{t}^{C H P} = η^{H B} η^{G T, h} G_{t}^{C H P} \end{array}\} \end{matrix}

式中: $P_{t}^{C H P} 、 H_{t}^{C H P}$ 分别为CHP机组在t时刻的发电功率、产热功率;η^{GT, e}、η^{GT, h}分别为燃气轮机的发电、制热效率;η^HB为余热锅炉的制热效率; $G_{t}^{C H P}$ 为CHP机组的天然气功率.

燃气锅炉与电锅炉的能量转换表达式与上式类似.

2.2 楼宇能源中心模型

2.2.1 中央空调模型

中央空调是常见的温控负荷,根据楼宇用户的舒适度要求运行并调节制热量,可以在夏季进行制冷、冬季进行供暖,使得用户侧可利用电能满足热能需求.表示为

(14)

\begin{matrix} \begin{array}{l} M_{i, t}^{a c} = P_{i, t}^{a c} η^{H, a c} \\ Q_{i, t}^{a c} = P_{i, t}^{a c} η^{C, a c} \end{array}\} \end{matrix}

(15)

H_{i, t}^{a c} = M_{i, t}^{a c} - Q_{i, t}^{a c}

式中: $M_{i, t}^{a c}$ 、 $Q_{i, t}^{a c}$ 、 $P_{i, t}^{a c}$ 、 $H_{i, t}^{a c}$ 分别为在t时段中央空调i的制热量、制冷量、耗电量、产热量;η^H^,^ac、η^C^,^ac分别为中央空调i的制热能效比、制冷能效比.

空调频繁的启停会影响设备寿命与用户体验,对空调最小运行时间作一定的约束^[27].表示为

(16)

\begin{matrix} \begin{array}{l} x_{i, t}^{a c, o n} + x_{i, t}^{a c, o f f} \leq 1 \\ x_{i, t}^{a c, o n} + \overset{m i n (T_{l, t}^{o f f} + τ_{o n}^{a c} - 1)}{\sum_{v = t + 1}} x_{i, v}^{a c, o f f} \leq 1 \\ w_{i, t}^{a c} - w_{i, t - 1}^{a c} = x_{i, t - 1}^{a c, o n} - x_{i, t - 1}^{a c, o f f} \end{array}\} \end{matrix}

式中: $x_{i, t}^{a c, o n}$ 、 $x_{i, t}^{a c, o f f}$ 为0或1变量,分别表示中央空调i在t时段末的开、关状态变量; $T_{l, t}^{o f f}$ 为t时段该楼宇商业功能区域l的营业结束时间; $τ_{o n}^{a c}$ 为中央空调i的最小运行时间; $w_{i, t}^{a c}$ 为0或1变量,表示中央空调i在t时段的运行状态.

2.2.2 燃气热水器

高层酒店可以通过燃气热水器获得生活热水,使用户侧可用天然气满足热能需求.表示为

(17)

\begin{matrix} H_{p, t}^{G H} = G_{p, t}^{G H} η^{G H} \end{matrix}

式中: $G_{p, t}^{G H}$ 、 $H_{p, t}^{G H}$ 分别为t时刻燃气热水器p消耗的气能、供热量;η^GH为燃气热水器p的效率.

2.2.3 电磁灶

需要烹饪的场所如购物中心的餐饮场所、酒店里的高级餐厅配备电磁灶及燃气灶,用户可以根据电能和气能的价格进行选择,实现电能和气能在用户侧的相互替代.表示为

(18)

\begin{matrix} \begin{array}{l} P_{q, t}^{E G} η^{E G} = G_{q, t}^{G E} η^{G E} \\ P_{q, t}^{E G} = G_{q, t}^{G E} η^{G E} / η^{E G} \\ G_{q, t}^{G E} = P_{q, t}^{E G} η^{E G} / η^{G E} \end{array}\} \end{matrix}

式中: $P_{q, t}^{E G}$ 为在t时刻电磁灶q的耗电功率,也是燃气灶q替代的电功率; $G_{q, t}^{G E}$ 为在t时刻燃气灶q的燃气功率,也是电磁灶q替代的气功率;η^EG、η^GE分别为电磁灶、燃气灶的效率.

3 考虑阶梯碳奖惩和IDR的楼宇规划模型

3.1 目标函数

采用等年值法将投资成本转化成设备寿命周期内的等效年投资成本,以单年的等效投资成本和运行成本最低为优化目标,在初始年进行规划.规划模型的目标函数可以表示为

(19)

\begin{matrix} m i n C = m i n (C^{i n v} + C^{o p e}) \end{matrix}

式中:C为年总规划成本;C^inv、C^ope分别为年化设备投资成本、系统运营成本.表示为

(20)

C^{i n v} = \sum_{k_{j} \in k, k \in Ω} u_{k_{j}} n_{k_{j}} C_{k_{j}} \frac{r {(1 + r)}^{T_{k_{j}}}}{{(1 + r)}^{T_{k_{j}}} - 1}

(21)

C^{o p e} = 365 \sum_{s} θ_{s} (C^{o m} + C^{e n e r y} + C^{u n c}) + C^{C O_{2}}

(22)

\begin{array}{l} C^{o m} = \sum_{k_{j} \in k, k \in Ω} \overset{24}{\sum_{t = 1}} c_{k j}^{o m} P_{k j, t} Δ t \\ C^{e n e r y} = \overset{24}{\sum_{t = 1}} ({c^{E}}_{t} {P^{E}}_{t} + {c^{G}}_{t} {G^{G}}_{t}) Δ t \\ C^{u n c} = \overset{24}{\sum_{t = 1}} ε^{u n c} (T_{t}^{i n} - T^{s e t}) Δ t \end{array}\}

式中:Ω={DPV,PVCW,ESS,EB,P2G,GB,GT,HB},k={k₁,k₂,……,k_o}; $u_{k_{j}}$ 为0或1变量,表示是否配置设备k的第j种类型,j=1, 2, …, o; $n_{k_{j}}$ 为配置设备k_j的台数; $C_{k_{j}}$ 为设备k_j的成本;r为折现率; $T_{k_{j}}$ 为设备k_j的寿命周期;C^om、C^enery、C^unc分别为楼宇系统的设备运行维护成本、与外部能源网交互的购能费用、室内温度不舒适惩罚费用;θ_s为s类典型日在全年的占比; $c_{k_{j}}^{o m}$ 为设备k_j的单位功率输出运行维护成本; $P_{k_{j}, t}$ 为设备k_j在t时刻的出力; ${c^{E}}_{t}$ 、 ${c^{G}}_{t}$ 分别为在t时刻电能购入、气能购入价格; ${G^{G}}_{t}$ 为在t时刻购入天然气功率;ε^unc为室内温度不舒适成本系数; $T_{t}^{i n}$ 、T^set分别为t时刻的室内温度、室内温度设定值.

3.2 约束条件

3.2.1 设备选型定容约束

设备约束可见式(5)、式(10)~(13),楼宇能源中心的可安装设备类型约束条件如下:

(23)

\begin{array}{l} u_{k_{1}} + u_{k_{2}} + \dots + u_{k_{o}} \leq 1, k_{j} \in k, k \in Ω \\ 0 \leq n_{k_{j}} \leq n_{k_{j}, m a x} \end{array}\}

式中: $n_{k_{j}, m a x} 为设备 k 第 j$ 种类型的最大台数.

3.2.2 室内热平衡约束

楼宇具有一定蓄热特性,因此有一定储能特性.其蓄热特性的表达式如下^[28]:

(24)

Δ H_{t}^{r o o m} Δ t = ρ^{a i r} c^{a i r} V^{r o o m} (T_{t}^{i n} - T_{t - 1}^{i n})

(25)

\begin{array}{l} Δ H_{t}^{r o o m} = H_{t}^{1} + H_{t}^{2} + H_{t}^{3} + {L^{h}}_{t} \\ H_{t}^{1} = k^{w a l l} F^{w a l l} (T_{t}^{o u t} - T_{t}^{i n}) \\ H_{t}^{2} = k^{w i n} F^{w i n} (T_{t}^{o u t} - T_{t}^{i n}) \\ H_{t}^{3} = λ^{S C} I_{t}^{s u n} F^{w i n} \end{array}\}

式中: $H_{t}^{r o o m}$ 为t时刻楼宇的蓄热量;ρ^air、c^air分别为空气的密度、比热容;V^room为室内空气体积; $T_{t}^{i n}$ 为在t时刻的室内温度; $H_{t}^{1}$ 、 $H_{t}^{2}$ 、 $H_{t}^{3}$ 分别为t时刻楼宇建筑外墙与室外传递的热量、楼宇建筑外窗与室外传递的热量、太阳热辐射传递的热量;k^wall、k^win分别为楼宇建筑外墙、外窗的传热系数;F^wall、F^win分别为楼宇建筑外墙、外窗的面积; $T_{t}^{o u t}$ 为t时刻的室外温度;λ^SC为遮阳系数; $I_{t}^{s u n}$ 为t时刻的太阳辐射功率.

3.2.3 楼宇室内温度约束

为了方便计算可对t时刻PMV进行简化,简化模型^[26]为

(26)

\begin{matrix} λ_{t}^{P M V} = 2.43 - \frac{3.76 (T^{b o d y} - T_{t}^{i n})}{M (I_{c l} + 0.1)} \end{matrix}

式中: $T^{b o d y}$ 为人体感觉舒适时的皮肤体表温度.

由式(26)可得t时刻室内温度与PMV舒适度指标的关系为

(27)

T_{t}^{i n} = T^{b o d y} - \frac{(2.43 - λ_{t}^{P M V}) (I_{c l} + 0.1) M}{3.76}

根据各区域的差异化PMV指标参考值λ^{PMV, ref},将PMV可调裕度δ^PMV所包含的±|λ^PMV|作为 $λ_{t}^{P M V}$ 上下限作为一个调节范围代入式(27),可得出楼宇各区域温度的上下界:

(28)

\begin{matrix} T_{t}^{i n, m i n} \leq T_{t}^{i n} \leq T_{t}^{i n, m a x} \end{matrix}

式中: $T_{t}^{i n, m i n}$ 、 $T_{t}^{i n, m a x}$ 分别为根据PMV取值范围算出的室内温度下限、上限.

3.2.4 供需平衡约束

楼宇能源中心向楼宇商业区域供应的电功率、气功率和热功率供需平衡约束为

(29)

\begin{array}{l} P_{t}^{c o m} = {P^{E}}_{t} + P_{t}^{P V} + P_{t}^{C H P} - P_{t}^{E S S} - P_{t}^{P 2 G} - P_{t}^{E B} \\ G_{t}^{c o m} = G_{t}^{P 2 G} + {G^{G}}_{t} - G_{t}^{C H P} - G_{t}^{G B} \\ H_{t}^{c o m} = H_{t}^{E B} + H_{t}^{G B} + H_{t}^{C H P} \end{array}\}

式中: $P_{t}^{c o m}$ 、 $G_{t}^{c o m}$ 、 $H_{t}^{c o m}$ 分别为楼宇能源中心向楼宇商业中心所供给的电能、气能、热能; $P_{t}^{E B}$ 、 $G_{t}^{G B}$ 分别为电锅炉、燃气锅炉所消耗的电能、气能; $H_{t}^{E B}$ 、 $H_{t}^{G B}$ 分别为电锅炉、燃气锅炉所产生的热能.

3.2.5 用能平衡约束

(1) 横向IDR.当外部能源价格发生变化时,楼宇商业区域发生价格响应,电、气、热负荷发生不同程度的增减、平移.可转移电、气负荷指每个时段的可转移电、气负荷在一定范围内,一天内电、气负荷总量不变.可转移热负荷指短时间内室内温度在合理范围内小幅度变化,用户的热舒适度也不会受到很大影响.表示为

(30)

\begin{matrix} \begin{array}{l} - Δ L_{t}^{e / g, m a x} \leq Δ L_{t}^{e / g} \leq Δ L_{t}^{e / g, m a x} \\ \overset{T}{\sum_{t = 1}} Δ L_{t}^{e / g} = 0 \end{array}\} \end{matrix}

(31)

\begin{array}{l} {L^{h}}_{t} = H_{t}^{i n} + H_{t}^{a c} \\ L_{t}^{h, 0} = H_{t}^{i n, 0} + H_{t}^{a c, 0} \\ Δ {L^{h}}_{t} = {L^{h}}_{t} - L_{t}^{h, 0} \end{array}\}

式中:Δ $L_{t}^{e / g, m a x}$ 为t时刻时可转移电、气负荷的最大值; $H_{t}^{i n, 0}$ 、 $H_{t}^{i n}$ 分别为IDR前、后的室内热源; $H_{t}^{a c, 0}$ 为IDR前中央空调的产热量.

(2) 纵向IDR.电替热和气替热导致的电能和气能需求增量、电气互相替代导致的能源变化量、能源替代导致的热能减少量如下:

(32)

\begin{matrix} \begin{array}{l} S_{t}^{e c h} = P_{t}^{a c} \\ S_{t}^{g c h} = G_{t}^{G H} \\ S_{t}^{e c g} = P_{t}^{E G} \\ S_{t}^{g c e} = G_{t}^{G E} \\ {S^{e}}_{t} = G_{t}^{G E} η^{G E} / η^{E G} \\ {S^{g}}_{t} = P_{t}^{G E} η^{E G} / η^{G E} \\ {S^{h}}_{t} = H_{t}^{a c} + H_{t}^{G H} \end{array}\} \end{matrix}

3.3 分布鲁棒优化模型

3.3.1 分布鲁棒优化模型

由于所规划的设备里只有光伏装置出力很大程度上受到环境的影响,具有不确定性,其他设备的出力都灵活可控,且目前负荷预测精度较高^[29].因此,仅考虑规划设备中新能源出力的不确定性,负荷的不确定性暂未考虑.影响光伏发电装置的光照强度和温度在每个时段都不断波动,通常光伏出力采用Beta分布的概率分布模型来描述,然而一方面获取精确的Beta分布的系数很困难;另一方面,Beta分布仅是光伏出力的经验分布,光伏出力的精确概率分布实际上难以获取.因此,采用基于KL散度的DRO方法处理光伏出力的概率分布不确定性,以经验设置或预测所得的一组场景概率分布 $p_{s'}^{0}$ 为基础,通过KL散度限制不确定性场景概率分布p_s与 $p_{s}^{0}$ 之间的距离,进而构成场景概率分布不确定集,最后在该不确定性集内寻找最恶劣场景下的规划决策方案,实现规划决策结果在经济性和鲁棒性之间的平衡.

采用KL散度刻画光伏不确定集ψ的边界,场景s下光伏不确定参数的概率值p_s满足下式约束:

(33)$\psi=\left\{\left\{p_{s^{\prime}}\right\}\left|\begin{array}{l}\sum_{s^{\prime}=1}^{N_s}p_{s^{\prime}}=1\\\\p_{s^{\prime}}\geq0,s^{\prime}=1,2,\cdots,N_s\\\\\sum_{s^{\prime}=1}^{N_s}p_{s^{\prime}}\ln\left(\frac{p_{s^{\prime}}}{p_{s^{\prime}}^0}\right)\leqslant\lambda\end{array}\right.\right\}$

式中:N_s为不确定性场景总数; $p_{s'}^{0}$ 为第s'个光伏场景概率的基础概率值;λ为实际概率分布与经验性概率分布的允许最大误差水平.

将规划决策变量作为第一阶段变量,将运行决策变量作为第二阶段变量,进而构建出与前文确定性双层规划模型相对应的 “min-max-min”形式的两阶段三层DRO规划模型^[30].其目标函数如下:

(34)

\begin{matrix} \underset{x \in X}{m i n} a^{T} x + \underset{{p_{s'}} \in ψ}{m a x} \overset{N_{s}}{\sum_{s' = 1}} p_{s'} \underset{y_{s} \in Y {x, ζ_{s'}}}{m i n} b^{T} y_{s} \end{matrix}

式中:a^Tx为投资变量{x}所对应楼宇规划投资目标函数式(20);b^Ty_s为运行变量{y_s}对应楼宇规划运行目标函数式(21);ζ_s'为运行层决策变量.

3.3.2 模型求解

针对式(34)中所构建的“min-max-min”形式的两阶段三层规划模型,采用列和约束生成算法对模型进行转化和求解,将其分解为主问题和子问题,对原目标函数设定上下界限,通过主问题和子问题反复迭代得出最优解.

4 算例分析

4.1 算例数据

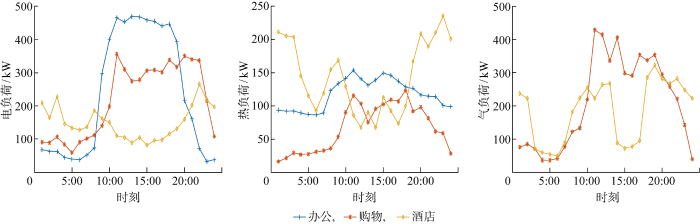
楼宇为一个商业综合体,通过配置楼宇能源设备的型号及台数可实现对楼宇商业区域能源供应的需求.办公楼层每个时段电负荷可转出上限为该时段负荷总量的12%,其他区域可转出电、气负荷上限为15%.碳奖惩成本在年末结算,区间长度为h=400 t,单位碳排放奖励基数与惩罚基数的关系为ϕ=0.6φ,碳排放奖励、惩罚阶梯增长系数m=0.32ϕ,n=0.32φ.上级电网火电实际发电量占比及分时碳计量因子见文献[12]和[31].楼宇各功能区域负荷数据来自某配电楼宇的实测数据,选取典型场景日负荷数据绘制成图,如图2所示.购电电价则按照单一制工商业峰谷电价^[32]计算,天然气价格为3.8元/m³.选择在楼宇屋顶以及光照最好的立面铺设光伏面板.拟选择的设备参数^{[6,33⇓⇓⇓ -37]}见附录B.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 典型场景日楼宇商业区域电、热、气负荷

Fig.2 Typical scenario of daily electrical, thermal, and gas load of commercial area of buildings

4.2 算例结果与分析

针对构建的考虑阶梯碳奖惩和IDR的楼宇低碳规划模型,分6种情形进行对比.在碳奖惩力度上,阶梯碳奖惩机制大于固定碳奖惩机制.

案例1:不计及IDR,不进行碳排放奖惩,但用阶梯碳奖惩机制衡量碳排放;案例2:不计及IDR,以固定碳奖惩机制进行碳排放奖惩;案例3:不计及IDR,以阶梯碳奖惩机制进行碳排放奖惩;案例4:计及IDR,不进行碳排放奖惩,但用阶梯碳奖惩机制衡量碳排放;案例5:计及IDR,以固定碳奖惩机制进行碳排放奖惩;案例6:计及IDR,以阶梯碳奖惩机制进行碳排放奖惩.

4.2.1 模型求解

(1) 楼宇低碳规划结果分析.如表1所示,从整体上看,碳奖惩机制会加大楼宇系统的年总规划成本并大幅度降低系统的碳排放,降低其经济性、改善环境效益;而计及IDR可以降低楼宇系统成本,提升经济性,对系统碳排放也有一定程度改善.

表1 楼宇低碳规划结果

Tab.1 Results of low-carbon planning of buildings

案例	C/万元	C^inv/ 万元	C^ope/ 万元	$C^{C O_{2}}$ / 万元	$M^{C O_{2}}$ /t
1	546.02	70.50	475.52	168.51	2755.15
2	606.47	110.78	495.69	52.55	2034.92
3	652.62	144.87	507.74	63.73	1325.80
4	510.50	55.51	454.99	154.61	2565.56
5	552.74	92.37	460.37	27.22	1248.89
6	574.75	117.15	457.60	32.25	849.21

新窗口打开| 下载CSV

经济性比较:从不采用到采用碳排放奖惩机制(1→2、4→5),年总规划成本分别增加 60.45 万元 (11.07%)、42.24万元(8.27%);采用固定碳奖惩机制到阶梯碳奖惩机制(2→3、5→6),年总规划成本分别增加46.15万元(7.61%)、22.01万元(3.98%).除此以外,楼宇系统年化设备投资成本、碳奖惩费用从整体上看均有增加趋势.其中,结合表2所示楼宇低碳规划方案可知,加大碳奖惩力度会增大楼宇大部分设备的投资容量,导致年化设备投资成本大幅上升;从碳奖惩费用来看,阶梯碳奖惩机制下的碳奖惩费用稍高于固定碳奖惩机制,不考虑碳奖惩机制时,楼宇碳排放没有限制,碳排放极大,此时若用阶梯碳排放进行衡量,碳奖惩费用极大.

表2 楼宇低碳规划方案

Tab.2 Low-carbon planning schemes of buildings

案例	P/kW							E/(kW·h)
案例	DPV	PVCW	EB	GB	P2G	GT	HB	ESS
1	450.56	526.50	150	150	0	200	160	750
2	605.44	614.25	150	170	0	200	160	1000
3	689.92	666.90	100	220	200	160	120	1000
4	450.56	421.20	180	130	0	200	160	500
5	605.44	526.50	130	150	0	160	120	750
6	661.76	614.25	130	180	100	120	100	750

新窗口打开| 下载CSV

此外,从不计及IDR到计及IDR(1→4、2→5、3→6),楼宇系统年总规划成本分别下降35.52万元(6.51%)、53.73万元(8.86%)、77.87万元(11.93%).并且,年化设备投资成本、碳奖惩费用从整体上看均有下降趋势.结合表2,计及IDR时,大部分设备规划容量呈现下降趋势,年化设备投资成本有下降趋势.计及IDR时,碳排放降低,碳奖惩费用下降.

碳排放比较:从不采用到采用碳奖惩机制(1→2、4→5),年碳排放总量分别下降720.23 t(26.14%)、1316.67 t(51.32%);采用固定碳奖惩机制到阶梯碳奖惩机制(2→3、5→6),年碳排放总量分别下降709.12 t(34.85%)、399.68 t(32.00%).由此可见,采取碳奖惩机制,尤其是阶梯碳奖惩机制,对降低楼宇系统碳排放可以起到显著效果.

此外,从不计及IDR到计及IDR (1→4、2→5、3→6),年碳排放总量分别下降189.59 t(6.88%)、786.03 t(38.63%)、476.59 t(35.95%).从整体上看,考虑IDR可以不同幅度降低楼宇系统碳排放量.

(2) 楼宇低碳规划方案分析.如表2所示,从整体上看,从不采用碳奖惩到固定碳奖惩再到阶梯碳奖惩,即(1→2→3、4→5→6),屋顶光伏、光伏幕墙、蓄电池、燃气锅炉、P2G的规划容量呈现增加的趋势,电锅炉、CHP的规划容量呈现降低的趋势.此时,由于碳奖惩费用增加,为了衡量经济性与环境效益,选择一定程度上加大能减少碳排放的设备的容量,降低碳排放较大的设备容量,牺牲部分经济换取环境效益.从不计及IDR到计及IDR (1→4、2→5、3→6),屋顶光伏、光伏幕墙、蓄电池、燃气锅炉、P2G、包含燃气轮机、余热锅炉的CHP规划容量呈现下降趋势,电锅炉的规划容量大致呈现上升趋势.计及IDR可以使各时段的负荷需求发生改变,使得用能曲线较为平缓,此时在保障楼宇负荷能源供应的基础上可以适当降低绝大部分楼宇能源中心设备的装机容量.从整体上看,IDR可以降低由碳奖惩机制造成的楼宇设备规划容量增大的影响.

4.2.2 碳奖惩机制影响分析

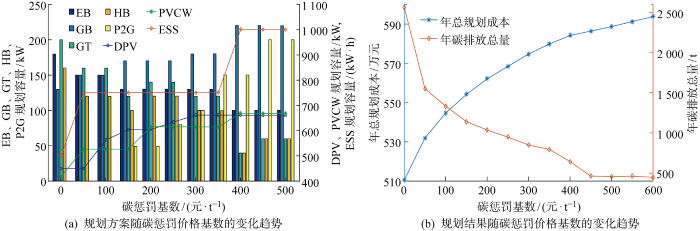
(1) 阶梯碳惩罚价格基数影响分析.从图3(a)来看,随着碳惩罚价格基数的增大,屋顶光伏、光伏幕墙、蓄电池、燃气锅炉、P2G的规划容量加大,电锅炉、CHP的规划容量减少.这与从不采用碳奖惩机制到采用碳奖惩机制、采用固定碳奖惩机制到阶梯碳奖惩机制的变化趋势一致,因为阶梯碳奖惩机制碳惩罚价格基数增大本质上也是碳奖惩力度增大.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 规划方案和结果随碳惩罚价格基数的变化趋势

Fig.3 Trends of changes in planning schemes and results with carbon penalty price base

从图3(b)来看,随着碳惩罚价格基数的增大,年总规划成本呈现增长趋势,而碳排放量呈现下降趋势.从不考虑碳奖惩机制到考虑碳奖惩机制时,年总规划成本和年碳排放总量的变化幅度最为明显;而随着碳奖惩机制碳惩罚价格基数增长到一定幅度,年总规划成本和年碳排放总量基本不变,呈现饱和状态.

(2) 购电碳排放分时计量模型影响分析.表3中,a表示不采用购电碳排放分时计量模型;b表示采用购电碳排放分时计量模型.由表可知,采用购电碳排放分时计量模型比不采用时减少8.11万元(20.09%)碳奖惩费用,降低137.11 t(13.90%)的碳排放量,可见采用购电碳排放分时计量模型对楼宇系统规划在降低碳排放上起到良好作用.

表3 购电碳排放分时计量模型影响的规划结果

Tab.3 Planning results of influence of time-sharing metering model on carbon emission from electricity purchase

方案	C/万元	C^ope/ 万元	$C^{C O_{2}}$ / 万元	$M^{C O_{2}}$ /t
a	578.99	461.97	40.36	986.32
b	574.75	457.60	32.25	849.21

新窗口打开| 下载CSV

如表4所示,采用购电碳排放分时计量模型,加大了对电锅炉、P2G设备的投资,减少了对CHP设备的投资.P2G设备在电转气的过程中需要吸收CO₂,其装机容量的增大也意味着吸碳能力增大,碳排放减少.CHP设备较为昂贵且产热效率低,电锅炉相反,增大电锅炉投资降低CHP设备的投资,可以降低单位热能生产的成本.

表4 购电碳排放分时计量模型影响的规划方案

Tab.4 Planning scheme of influence of time-sharing metering model on carbon emission from electricity purchase

方案	P/kW							E/(kW·h)
方案	DPV	PVCW	EB	GB	P2G	GT	HB	ESS
a	661.76	614.25	60	180	80	140	120	750
b	661.76	614.25	130	180	100	120	100	750

新窗口打开| 下载CSV

4.2.3 IDR影响分析

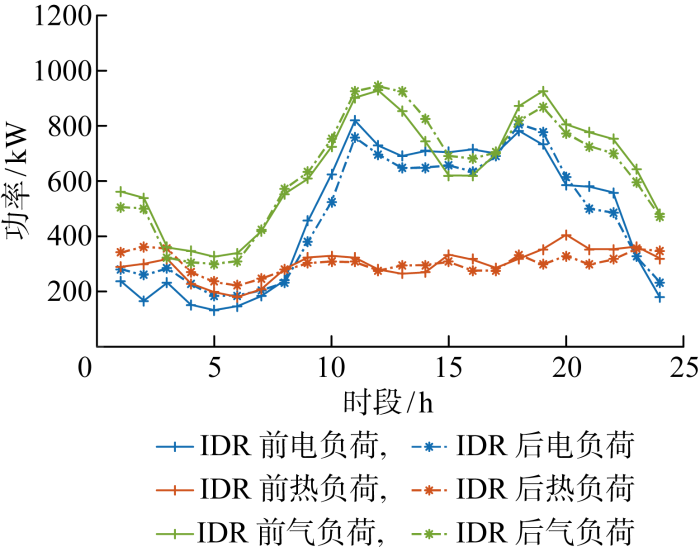
(1) IDR影响分析.如图4所示,电、气、热3类负荷在IDR作用后在各时间段有不同程度的改变.0:00—8:00电、热负荷在IDR后均有不同程度增加,气负荷则不同程度地减少;8:00—17:00电负荷减少,气负荷增加;17:00—23:00电负荷先增加再减少,气、热负荷均减少.综上所述,IDR可以使用户在电价变化时根据实际情况改变三类负荷的使用程度.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 IDR前后电、气、热负荷曲线

Fig.4 Curves of electric, thermal, and gas load before and after IDR

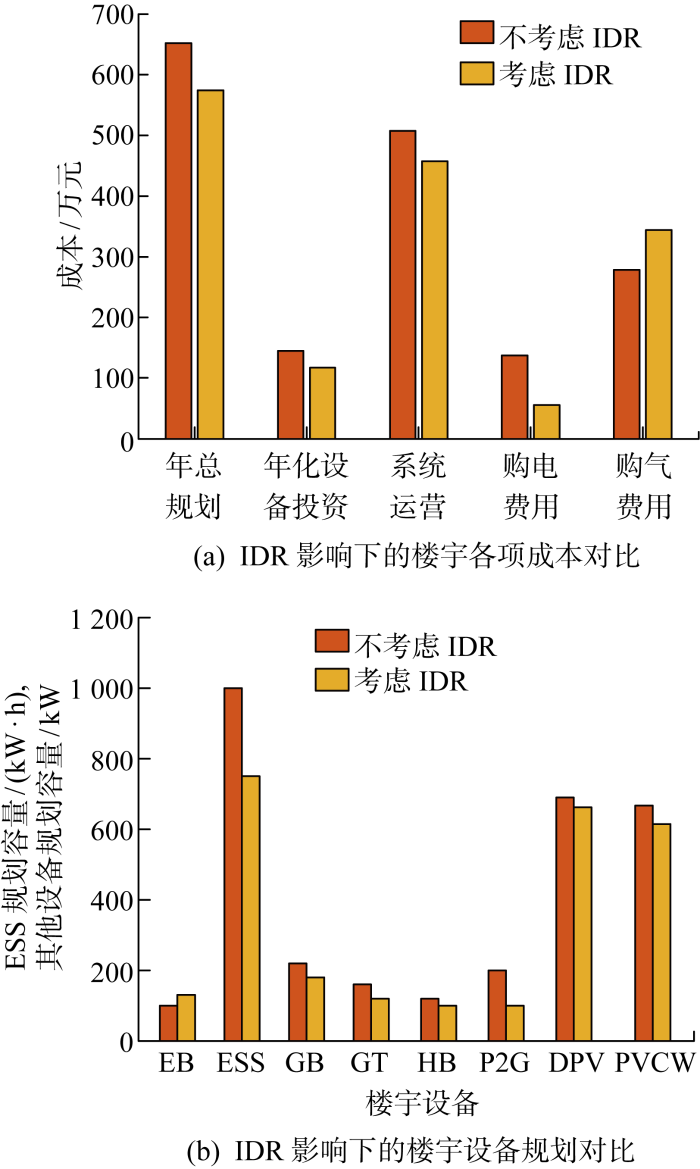
从图5(a)中可知,考虑IDR后楼宇各项成本除购气费用以外均有不同程度下降,购气成本上升是考虑IDR以后气价在部分电价较高时段发生的气替电行为.由图4可见,考虑IDR后各时段的负荷需求会发生改变,用能曲线变得平缓,楼宇能源中心设备装机容量有一定程度降低,设备规划容量减少,如图5(b)所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 IDR影响下的楼宇各项成本、设备规划对比

Fig.5 Comparison of cost and equipment planning of building with the influence of IDR

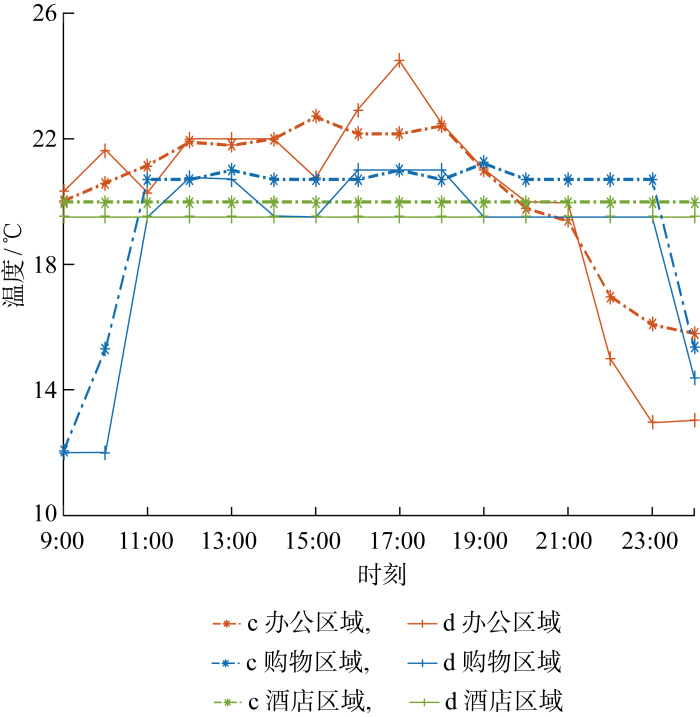
(2) PMV可调裕度影响分析.楼宇商业区域包含购物中心、办公区域、酒店3个部分,各部分的物理环境与个体行为差异,即人体新陈代谢率、服装热阻、平均辐射温度、空气流速有一定差异, 按照正态分布N(μ, σ²)选取典型参数,μ为期望,σ为标准差,具体见附录B.ISO7730标准中提出PMV在-0.5~0.5时,室内热环境达到人体可接受的舒适要求.在此条件下对两种情况下的PMV可调裕度进行对比分析,如图6所示.图中:c代表情况为采用区域差异化PMV;d代表情况为将PMV可调裕度限制在-0.5~0.5.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同PMV可调裕度下的楼宇商业区域室内温度

Fig.6 Indoor temperature in commercial area of buildings at different PMV adjustable margins

楼宇商业区域各部分在营业时间对温度要求较严格,非营业时间要求较低.综合考虑用能成本和温度舒适度成本后,在不同方案PMV可调裕度下,可见采用区域差异化PMV会使得楼宇商业区域室内温度变化更为平缓,更接近楼宇舒适温度,用户感觉会更舒适.

如表5所示,采用区域差异化PMV比直接限定PMV可调裕度的楼宇规划年碳排放量降低94.55 t(10.02%),减少5.1万元(13.65%)碳奖惩费用与8.28万元(1.78%)的系统运营成本,可见更精准地计算PMV可调裕度可以起到减少系统碳排放,降低碳奖惩费用,适当降低系统运营成本的作用.

表5 PMV舒适度指标影响的规划结果

Tab.5 Planning results of impacts of PMV comfort index

方案	C/万元	C^ope/ 万元	$C^{C O_{2}}$ / 万元	$M^{C O_{2}}$ /t
c	574.75	457.60	32.25	849.21
d	582.33	465.88	37.35	943.76

新窗口打开| 下载CSV

如表6所示,采用区域差异化PMV的楼宇规划,加大对电锅炉、燃气锅炉、P2G设备的投资,减少对CHP设备的投资.采用区域差异化PMV使得楼宇商业区域室内温度更接近楼宇舒适温度,对热能需求小幅增加,于是加大产热效率高的电锅炉、燃气锅炉设备投资,减少产热效率低的CHP设备投资;与此同时,系统碳排放增大;为了降低系统碳排放,加大P2G设备的装机容量,吸碳能力增大,碳排放减少.

表6 PMV舒适度指标影响的规划方案

Tab.6 Planning scheme of impacts of PMV comfort index

方案	P/kW							E/(kW·h)
方案	DPV	PVCW	EB	GB	P2G	GT	HB	ESS
c	661.76	614.25	130	180	100	120	100	750
d	661.76	614.25	100	160	80	160	120	750

新窗口打开| 下载CSV

4.2.4 不确定性分析

设置4种方法进行对比:e为确定性规划方法;f为随机规划方法;g为鲁棒优化规划方法;h为分布鲁棒优化规划方法.

如表7所示,所采用的分布鲁棒优化规划方法较鲁棒优化规划方法而言,其规划结果经济性更好,因为鲁棒规划优化方法是不考虑概率分布下寻求最恶劣场景的优化结果,而分布鲁棒会考虑概率分布,所以改进了鲁棒规划优化方法过于保守的问题;但与随机规划方法对比,经济性略差,因为分布鲁棒规划是考虑包含经验性概率的不确定性集合而求解得到的最恶劣概率分布下的优化结果,所以其鲁棒性较随机规划更好.可见,所采用的分布鲁棒规划优化方法可以兼顾经济性和鲁棒性.

表7 不同优化规划方法下考虑光伏出力波动影响的规划结果

Tab.7 Planning results of different optimal planning methods considering PV output fluctuation

方法	C/万元	C^inv/ 万元	C^ope/ 万元	$C^{C O_{2}}$ / 万元	$M^{C O_{2}}$ /t
e	568.48	110.57	457.91	31.17	948.15
f	569.77	110.57	459.21	31.67	956.47
g	575.36	109.69	465.67	36.30	1041.16
h	570.65	109.93	460.72	32.25	965.91

新窗口打开| 下载CSV

考虑光伏出力波动之后,如表8所示,对楼宇设备规划结果几乎没有影响;由表7可知,对楼宇系统运行具有一定的影响.就分布鲁棒优化规划方法与确定性优化规划方法对比来看,年碳排放总量增加17.76 t (1.87%),碳奖惩费用增加 1.08 万元(3.46%), 系统运营成本增加2.75万元(0.60%).虽然分布鲁棒优化规划方法比确定性优化规划方法结果差,但是考虑光伏出力的波动性更符合实际情况.

表8 不同优化规划方法下考虑光伏出力波动影响的规划方案

Tab.8 Planning scheme of different optimal planning methods considering PV output fluctuation

方法	P/kW							E/(kW·h)
方法	DPV	PVCW	EB	GB	P2G	GT	HB	ESS
e	633.6	614.25	130	170	80	140	120	750
f	633.6	614.25	130	170	80	140	120	750
g	633.6	614.25	130	170	50	140	120	750
h	633.6	614.25	130	170	80	120	100	750

新窗口打开| 下载CSV

5 结论

以商业综合体为对象,建立考虑引入上级网络购电分时碳计量模型的阶梯碳奖惩机制和考虑楼宇各功能区域差异化PMV的IDR的商业综合体楼宇低碳规划模型.通过算例分析得出以下结论:

(1) 碳奖惩机制通过将碳排放量转换成成本来控制楼宇的碳排放量,改变楼宇规划方案.考虑阶梯碳奖惩机制的规划方案碳排放大幅降低,采用购电碳排放分时计量模型时碳排放量小幅降低,可见购电碳排放分时计量模型在降低碳排放上可以起到一定作用.但考虑阶梯碳奖惩机制时年规划成本增加,证明阶梯碳奖惩机制会牺牲部分经济性从而换取碳减排性能.

(2) IDR作用在楼宇能源调度期间,使得用能曲线更加平缓,从而影响楼宇设备规划.在考虑阶梯碳奖惩机制的前提下,考虑IDR可以降低年总规划成本.采用区域差异化PMV的楼宇规划也可小幅降低楼宇成本,可见其可以进一步挖掘楼宇用能潜力.证明IDR结合阶梯碳奖惩机制在节能减排上的有效性.

(3) 构建的基于KL散度的分布鲁棒规划模型能够很好地应对光伏不确定性.考虑不确定性对于楼宇系统设备规划几乎没有影响,但是楼宇运行情况出现小幅度变差,考虑不确定性更符合真实情况.

本文仅研究规划设备中新能源出力的不确定性与分时电价机制下的需求响应,负荷的不确定性与激励型需求响应暂未考虑.后续将在楼宇低碳规划模型中融入其他类型的需求响应,并考虑负荷及用户响应行为不确定性对规划方案的影响,以得到更加合理的楼宇低碳规划方案.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2024/1006-2467/1006-2467-58-06-0926.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

中国建筑节能协会. 中国建筑能耗研究报告2020[R]. 北京: 中国建筑节能协会, 2021.