风电-光伏-抽蓄-电制氢多主体能源系统增益的合作博弈分配策略

doi:10.16183/j.cnki.jsjtu.2022.531

风电-光伏-抽蓄-电制氢多主体能源系统增益的合作博弈分配策略

段佳南, 谢俊^,, 邢单玺

河海大学能源与电气学院,南京 211100

A Cooperative Game Allocation Strategy for Wind-Solar-Pumped Storage-Hydrogen Multi-Stakeholder Energy System

DUAN Jia’nan, XIE Jun^,, XING Shanxi

College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, China

通讯作者: 谢俊,教授,博士生导师,电话(Tel.):025-85099097;E-mail:eejxie@163.com.

责任编辑: 王历历

收稿日期: 2022-12-26 修回日期: 2023-03-27 接受日期: 2023-03-31

基金资助:

国家自然科学基金(U1965104)
国家重点研发计划(2019YFE0105200)

Received: 2022-12-26 Revised: 2023-03-27 Accepted: 2023-03-31

作者简介 About authors

段佳南(1999-),硕士生,从事电力市场与电力系统经济运行研究.

摘要

根据清洁能源示范基地的建设需求,提出基于合作博弈论的风电-光伏-抽蓄-电制氢多主体能源系统联合优化运行的增益分配策略.为兼顾系统运行安全性,构建上网出力互补性评价指标.风电、光伏、抽蓄、电制氢利益主体通过内部电量交易进行合作,以系统运行收益最大为优化目标构建联合优化调度模型.根据调度结果,应用合作博弈论中的最大最小成本法分配系统合作增量收益.利用风电-光伏-抽蓄-电制氢清洁能源示范基地12利益主体系统算例进行仿真验证,结果表明联合优化运行可实现各利益主体自身收益正增长,抽蓄库容、上网电价以及运行安全性需求会影响系统的合作增量收益.

关键词： 风电-光伏-抽蓄-电制氢多主体能源系统; 短期调度; 增益分配策略; 合作博弈论; 最大最小成本法

Abstract

To meet the construction demand of clean energy demonstration bases, a gain allocation strategy for the joint optimization operation of wind-solar-pumped storage-hydrogen multi-stakeholder energy system based on the cooperative game theory is proposed. In order to take into consideration the security of system operation, evaluation indicators for the complementarity of on-grid output are constructed. The stakeholders of wind, solar, pumped storage, and power-to-hydrogen cooperate through the internal electricity transaction to construct a joint scheduling model with the optimization goal of maximizing the operation benefits. Then, the minimum cost remaining saving (MCRS) method in the cooperative game theory is applied to allocate the synergistic benefits based on the scheduling results. The simulation results of a 12-stakeholder wind-solar-pumped storage-hydrogen clean energy demonstration base show that each stakeholder can derive positive gains through joint operation, and the reservoir capacity of pumped storage station, on-grid price and operation security demand will affect the cooperative synergistic benefits of the system.

Keywords： wind-solar-pumped storage-hydrogen multi-stakeholder energy system; short term dispatch; allocation mechanism of synergistic gains; cooperative game theory; minimum cost remaining saving (MCRS) method

PDF (1400KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

段佳南, 谢俊, 邢单玺. 风电-光伏-抽蓄-电制氢多主体能源系统增益的合作博弈分配策略[J]. 上海交通大学学报, 2024, 58(6): 872-880 doi:10.16183/j.cnki.jsjtu.2022.531

DUAN Jia’nan, XIE Jun, XING Shanxi. A Cooperative Game Allocation Strategy for Wind-Solar-Pumped Storage-Hydrogen Multi-Stakeholder Energy System[J]. Journal of Shanghai Jiaotong University, 2024, 58(6): 872-880 doi:10.16183/j.cnki.jsjtu.2022.531

电力系统脱碳是中国实现“双碳”目标的关键,氢能与电力系统的互补协同运行将成为未来能源系统的发展趋势,对支撑“双碳”目标具有重要意义^[1].随着可再生能源装机容量不断扩大,大规模风电、光伏并网时,其出力波动性、不确定性特征将为系统安全运行带来严峻挑战^[2].储能电站是有效平抑风光出力波动性的重要手段,抽水蓄能(抽蓄)电站作为电力系统中技术成熟、成本低廉的大容量储能设施,与风电、光伏协同运行可提高风光消纳水平^[3⇓-5].

目前,含风电、光伏、抽蓄、电制氢的多能源系统优化调度已成为研究热点^[6⇓-8].对于含抽蓄的多能互补系统,文献[9]中建立一种含抽蓄电站的日前及实时调度模型,火电机组平衡波动性功率,抽蓄电站为预测误差提供旋转备用,两类电源分工互济实现电网功率平衡;文献[10]中以火电运行的经济性和平稳性最优、清洁能源消纳量最大、风电入网后负荷波动最小为目标构建风蓄水火多目标协调短期优化调度模型,该模型能够实现多能互补综合效能的最大化.对于含电制氢的多能互补系统,文献[11]中提出一种风电与氢燃料电站联合优化调度方法,通过合作可降低氢燃料电站的制氢成本;文献[12]中构建一种可再生能源制氢的综合能源应用系统,可再生能源向电网供电的同时向储氢单元充电,可电转氢、氢转电运行,但电-氢-电存在转换效率较低的问题.上述研究为多主体能源系统的联合优化运行提供参考技术路线,但目前鲜见风电-光伏-抽蓄-电制氢多能源系统联合优化调度的研究,在制定联合运行策略时亟需兼顾系统运行的经济性与安全性.

目前,基于合作博弈理论的增量效益(增益)分配方法因其分配公平性被广泛应用^[13⇓-15].Shapley值法、核仁法作为经典的合作博弈分配法在实际的大规模系统应用中存在计算复杂、低效的问题.针对这一问题,在保留传统博弈特性的基础上寻求更高效的求解方法^[16-17].其中,最大最小成本(Minimum Cost Remaining Saving,MCRS)法因原理简单、求解高效被应用于大规模系统的增益分配问题中^[18-19],上述研究为风电-光伏-抽蓄-电制氢系统联合优化运行的增益分配方法提供参考技术路线.

在上述研究背景下,提出一种风电-光伏-抽蓄-电制氢多主体能源系统的联合优化调度及其合作增益分配策略.首先,构建风电-光伏-抽蓄-电制氢优化调度模型,并构建系统上网出力互补性指标以兼顾系统运行经济性与安全性;随后,基于MCRS法构建系统的合作增益分配模型;最后,利用12利益主体系统算例验证所提模型的有效性,并分析影响风电-光伏-抽蓄-电制氢系统合作增益的关键影响因素.

1 风电-光伏-抽蓄-电制氢多主体能源系统优化调度模型

假设含n个利益主体的风电-光伏-抽蓄-电制氢多能源合作运行联盟,记为大联盟N.基于合作博弈论的增益分配方法除需获取大联盟N的优化调度结果外,还需求得各利益主体非合作运行模式以及各子联盟合作运行模式下的优化调度结果.下面建立对n利益主体风电-光伏-抽蓄-电制氢多能源系统优化调度模型.

1.1 目标函数

非合作运行模式下,风电和光伏按照自然资源多寡进行发电,发电量全部上网;电制氢站制氢所需用电量全部从电网购买;抽蓄电站单独运行时与电网交易,利用抽发差价获取自身收益.合作运行模式下,一方面风、光、抽蓄通过互补发电产生合作增益电量,另一方面发电利益主体可向电制氢站售卖电量进行合作,系统剩余电量打捆上网.风电-光伏-抽蓄-电制氢合作运行系统结构示意图见附录A, 忽略系统线路阻塞.记独立联盟以及子合作联盟为S(S⊆N, |S|=2ⁿ-1),分别记风电、光伏、抽蓄和电制氢利益主体集合为S_WD、S_PV、S_PS和S_HG.在调度周期T内以Δt为间隔共划分t个调度时段,以联盟收益F_S最大为优化目标建立如下目标函数:

(1)

m a x F_{S} = \sum_{i \in S} (F_{i, W D} + F_{i, P V} + F_{i, P S} + F_{i, H G})

(2)

\begin{array}{l} F_{i, W D} = R_{i, W D 2 G} + R_{i, W D 2 H} + R_{i, W D 2 P S} - \\ C_{i, W D, o p} - C_{i, W D, g} \\ F_{i, P V} = R_{i, P V 2 G} + R_{i, P V 2 H} + R_{i, P V 2 P S} - \\ C_{i, P V, o p} - C_{i, P V, g} \\ F_{i, P S} = R_{i, P S 2 G} + R_{i, P S 2 H} - C_{i, P S P} - \\ C_{i, P S, o p} - C_{i, P S, g} \\ F_{i, H G} = - (R_{i, W D 2 H} + R_{i, P V 2 H} + R_{i, P S 2 H} + \\ C_{i, G 2 H} + C_{i, H G, o p}) \end{array}\}

式中:当利益主体i不属于当前联盟S时,其相关变量为0;风电总收益F_i,_WD由上网收益R_i,_WD₂_G、售氢收益R_i,_WD₂_H、储能收益R_i,_WD₂_PS、运行维护成本C_i,_WD_,_op和过网费C_i,_WD_,_g构成;光伏总收益F_i,_PV由上网收益R_i,_PV₂_G、售氢收益R_i,_PV₂_H、储能收益R_i,_PV₂_PS、运行维护成本C_i,_PV_,_op和过网费C_i,_PV_,_g构成;抽蓄总收益F_i,_PS由上网收益R_i,_PS₂_G、售氢收益R_i,_PS₂_H、抽水成本C_i,_PSP、运行成本C_i,_PS_,_op和过网费C_i,_PS_,_g构成;电制氢总收益即负的总成本F_i,_HG由向风、光、抽蓄、电网购电成本R_i,_WD₂_H、R_i,_PV₂_H、R_i,_PS₂_H、C_i,_G₂_H和运行维护成本C_i,_HG_,_op构成.

1.2 约束条件

1.2.1 风电/光伏运行约束

假设风、光各利益主体出力服从正态分布,为保证95%的风光利用率^[20],采用置信区间法描述风光的不确定问题:

(3)

\begin{matrix} \begin{array}{l} 0 \leq P_{i, t}^{W D / P V} \leq P_{i, m a x}^{W D / P V} \\ {\bar{P}}_{i, m i n}^{W D / P V} \leq P_{i, t}^{W D / P V} \leq {\bar{P}}_{i, m a x}^{W D / P V} \\ {\bar{P}}_{i, m a x}^{W D / P V} = μ_{i, t}^{W D / P V} + 1.96 σ_{i, t}^{W D / P V} \\ {\bar{P}}_{i, m i n}^{W D / P V} = μ_{i, t}^{W D / P V} - 1.96 σ_{i, t}^{W D / P V} \end{array}\} \end{matrix}

式中: $P_{i, t}^{W D / P V}$ 为风/光出力, $P_{i, m a x}^{W D / P V}$ 为其技术出力上限; ${\bar{P}}_{i, m a x}^{W D / P V}$ 、 ${\bar{P}}_{i, m i n}^{W D / P V}$ 分别为风/光95%置信区间上下限; $μ_{i, t}^{W D / P V}$ 、 $σ_{i, t}^{W D / P V}$ 分别为出力预测均值和标准差.

收益与成本相关约束如下:

(4)

\begin{matrix} \begin{array}{l} R_{i, W D / P V 2 G} = \overset{T}{\sum_{t = 1}} λ_{i, t}^{W D / P V 2 G} P_{i, t}^{W D / P V 2 G} Δ t \\ R_{i, W D / P V 2 H} = \overset{T}{\sum_{t = 1}} λ_{i, t}^{W D / P V 2 H} P_{i, t}^{W D / P V 2 H} Δ t \\ R_{i, W D / P V 2 P S} = \overset{T}{\sum_{t = 1}} λ_{i, t}^{W D / P V 2 P S} P_{i, t}^{W D / P V 2 P S} Δ t \\ C_{i, W D / P V, o p} = \overset{T}{\sum_{t = 1}} γ_{i, t}^{W D / P V, o p} P_{i, t}^{W D / P V} Δ t \\ C_{i, W D / P V, g} = \overset{T}{\sum_{t = 1}} γ_{i, t}^{W D / P V 2 H} P_{i, t}^{W D / P V 2 H} Δ t \\ γ_{i, t}^{W D / P V 2 H} = α (P_{i, t}^{W D / P V 2 H})^{2} + β P_{i, t}^{W D / P V 2 H} \end{array}\} \end{matrix}

式中: $P_{i, t}^{W D / P V 2 G}$ 为风/光上网功率, $λ_{i, t}^{W D / P V 2 G}$ 为其单位上网电价; $P_{i, t}^{W D / P V 2 H}$ 为风/光向电制氢系统售电功率, $λ_{i, t}^{W D / P V 2 H}$ 为其单位售氢电价; $P_{i, t}^{W D / P V 2 P S}$ 为风/光向抽蓄提供的抽水功率, $λ_{i, t}^{W D / P V 2 P S}$ 为其单位抽水电价; $γ_{i, t}^{W D / P V, o p}$ 为风/光单位运行维护成本; $γ_{i, t}^{W D / P V 2 H}$ 为风/光单位过网费成本;α、β为过网费系数.

1.2.2 抽蓄运行约束

抽蓄机组的抽/发功率约束如下:

(5)

\begin{matrix} \begin{array}{l} {I^{g}}_{i, t} P_{i, m i n}^{P S, g} \leq P_{i, t}^{P S, g} \leq {I^{g}}_{i, t} P_{i, m a x}^{P S, g} \\ {I^{p}}_{i, t} P_{i, m i n}^{P S, p} \leq P_{i, t}^{P S, p} \leq {I^{p}}_{i, t} P_{i, m a x}^{P S, p} \end{array}\} \end{matrix}

式中: $P_{i, t}^{P S, g}$ 、 $P_{i, t}^{P S, p}$ 分别为发电和抽水功率; $P_{i, m a x}^{P S, g / p}$ 、 $P_{i, m i n}^{P S, g / p}$ 分别为发电/抽水功率上下限值; ${I^{g}}_{i, t}$ 、 ${I^{p}}_{i, t}$ 分别为发电/抽水工况下机组启停状态的二元整型变量.

分别对抽蓄机组单台机和多台机的运行工况进行约束:

(6)

\begin{matrix} \begin{array}{l} {I^{g}}_{i, t} + {I^{p}}_{i, t} \leq 1 \\ \sum_{i \in S_{P S}} {I^{g}}_{i, t} \sum_{i \in S_{P S}} {I^{p}}_{i, t} = 0 \end{array}\} \end{matrix}

水库需满足水量平衡、库容约束以及循环约束:

(7)

\begin{matrix} \begin{array}{l} E_{t} = E_{t - 1} + \sum_{i \in P S} (\frac{P_{i, t}^{P S, p}}{{η^{p}}_{i}} - \frac{P_{i, t}^{P S, g}}{{η^{g}}_{i}}) \\ E_{m i n} \leq E_{t} \leq E_{m a x} \\ E_{T} = E_{0} \end{array}\} \end{matrix}

式中:E_t为水库容量;E_max、E_min分别为库容上下限值; ${η^{g}}_{i}$ 、 ${η^{p}}_{i}$ 分别为机组发电/抽水工况运行效率;E₀、E_T分别为始末时段库容.

抽蓄机组在抽水和发电工况下分别可为风光提供上下旋转备用如下:

(8)

\begin{array}{l} (P_{i, t}^{P S, g} + R_{i, t}^{g u}) {I^{g}}_{i, t} \leq P_{i, m a x}^{P S, g} {I^{g}}_{i, t} \\ (P_{i, t}^{P S, g} - R_{i, t}^{g d}) {I^{g}}_{i, t} \geq P_{i, m i n}^{P S, g} {I^{g}}_{i, t} \\ (P_{i, t}^{P S, p} + R_{i, t}^{p u}) {I^{p}}_{i, t} \leq P_{i, m a x}^{P S, p} {I^{p}}_{i, t} \\ (P_{i, t}^{P S, p} - R_{i, t}^{p d}) {I^{p}}_{i, t} \geq P_{i, m i n}^{P S, p} {I^{p}}_{i, t} \end{array}\}

(9)

\begin{array}{l} \sum_{i \in S_{P S}} (R_{i, t}^{g u} + R_{i, t}^{p d}) \geq \sum_{i \in S_{W D}} (P_{i, t}^{W D} - {\bar{P}}_{i, m i n}^{W D}) + \\ \sum_{i \in S_{P V}} (P_{i, t}^{P V} - {\bar{P}}_{i, m i n}^{P V}) \\ \sum_{i \in S_{P S}} (R_{i, t}^{g d} + R_{i, t}^{p u}) \geq \sum_{i \in S_{W D}} ({\bar{P}}_{i, m a x}^{W D} - P_{i, t}^{W D}) + \\ \sum_{i \in S_{P V}} ({\bar{P}}_{i, m a x}^{P V} - P_{i, t}^{P V}) \\ S_{P S} ⋂ S \neq ⌀ \end{array}\}

式中: $R_{i, t}^{g u}$ 、 $R_{i, t}^{g d}$ 分别为发电工况下的上下旋转备用容量; $R_{i, t}^{p u}$ 、 $R_{i, t}^{p d}$ 分别为抽水工况下的上下旋转备用容量.其中式(9)规定联盟S中无抽蓄机组消纳风光波动出力时,不考虑下旋转备用约束式,由上旋转备用约束式定义可知此时风光只按下限出力;收益与成本相关约束为

(10)

\begin{matrix} \begin{array}{l} R_{i, P S 2 G} = \overset{T}{\sum_{t = 1}} (P_{i, t}^{P S 2 G} λ_{i, t}^{P S 2 G}) Δ t \\ R_{i, P S 2 H} = \overset{T}{\sum_{t = 1}} (P_{i, t}^{P S 2 H} λ_{i, t}^{P S 2 H}) Δ t \\ C_{i, P S P} = \overset{T}{\sum_{t = 1}} (λ_{i, t}^{W D / P V 2 P S} P_{i, t}^{W D / P V 2 P S} + \\ γ_{i, t}^{G 2 P S} P_{i, t}^{G 2 P S}) Δ t \\ C_{i, P S, o p} = \overset{T}{\sum_{t = 1}} [γ^{P S, g} {I^{g}}_{i, t} (1 - {I^{g}}_{i, t - 1}) + \\ γ^{P S, p} {I^{p}}_{i, t} (1 - {I^{p}}_{i, t - 1})] \\ C_{i, P S, g} = \overset{T}{\sum_{t = 1}} γ_{i, t}^{P S 2 H} P_{i, t}^{P S 2 H} Δ t \\ γ_{i, t}^{P S 2 H} = α (P_{i, t}^{P S 2 H})^{2} + β P_{i, t}^{P S 2 H} \end{array}\} \end{matrix}

式中: $P_{i, t}^{P S 2 G}$ 为抽蓄上网功率, $λ_{i, t}^{P S 2 G}$ 为其单位上网电价; $P_{i, t}^{P S 2 H}$ 为抽蓄向电制氢系统售电功率, $λ_{i, t}^{P S 2 H}$ 为其单位售氢电价; $P_{i, t}^{G 2 P S}$ 为电网向抽蓄提供的抽水功率, $γ_{i, t}^{G 2 P S}$ 为其单位抽水电价;γ^PS^,^g、γ^PS^,^p分别为发电/抽水工况下的启动成本系数; $γ_{i, t}^{P S 2 H}$ 为抽蓄单位过网费成本.

1.2.3 电制氢站运行约束

电制氢站主要考虑电解槽、储氢罐两部分结构,调度周期内氢气负荷总需求量给定,各时段需求量可根据系统出力灵活调节.下式为电解槽输入功率与爬坡功率约束,其中输入功率由风/光/抽蓄/电网购电功率构成:

(11)

\begin{matrix} \begin{array}{l} 0 \leq P_{i, t}^{H G, e l} \leq P_{m a x}^{H G, e l} \\ | P_{i, t + 1}^{H G, e l} - P_{i, t}^{H G, e l} | \leq P_{i, r u}^{H G, e l} \end{array}\} \end{matrix}

式中: $P_{i, t}^{H G, e l}$ 为电解槽输入功率; $P_{m a x}^{H G, e l}$ 为输入功率上限值; $P_{i, r u}^{H G, e l}$ 为爬坡功率上限值.

电-氢转换关系、储氢罐气量平衡、容量约束、循环约束以及需求量平衡约束为

(12)

\begin{matrix} \begin{array}{l} Q_{i, t}^{e - h} = η_{e l} ρ^{e - h} P_{i, t}^{H G, e l} \\ V_{i, t + 1}^{H G} = V_{i, t}^{H G} + Q_{i, t}^{e - h} - L_{i, t} \\ V_{m i n}^{H G} \leq V_{i, t}^{H G} \leq V_{m a x}^{H G} \\ V_{i, 0}^{H G} = V_{i, T}^{H G} \\ \sum_{t \in T} L_{i, t} = L_{i}^{t o t a l} \end{array}\} \end{matrix}

式中: $Q_{i, t}^{e - h}$ 为制气量;η_el为电解槽工作效率;ρ^e-h为电-氢转换系数; $V_{i, t}^{H G}$ 为储氢罐容量; $V_{m a x}^{H G}$ 、 $V_{m i n}^{H G}$ 分别为容量上下限值; $V_{i, 0}^{H G}$ 、 $V_{i, T}^{H G}$ 分别为始末时段容量;L_i_,_t、 $L_{i}^{t o t a l}$ 分别为各时段负荷需求以及调度周期内总负荷需求.

成本相关约束如下:

(13)

\begin{matrix} \begin{array}{l} C_{i, H G, o p} = \overset{T}{\sum_{t = 1}} γ_{i, t}^{H G, o p} P_{i, t}^{H G, e l} \\ C_{i, G 2 H} = \overset{T}{\sum_{t = 1}} γ_{i, t}^{G 2 H G} P_{i, t}^{G 2 H G} \end{array}\} \end{matrix}

式中: $γ_{i, t}^{H G, o p}$ 为电制氢系统的单位运行维护成本; $P_{i, t}^{G 2 H G}$ 为电制氢系统向电网购电的功率; $γ_{i, t}^{G 2 H G}$ 为对应购电时段的工业电价.

1.2.4 上网出力互补约束

发电利益主体与电制氢站利益主体通过电量交易开展合作,剩余电量打捆上网,为保证系统运行安全性,可利用资源间的互补特性解决风电-光伏-抽蓄上网出力的平稳性问题.

由相邻时段出力之差建立风、光、抽蓄上网出力变化率 $β_{W D}^{t} 、 β_{P V}^{t} 、 β_{P S}^{t},$ 得到聚合电源上网出力变化率β^t:

(14)

\begin{matrix} \begin{array}{l} β_{W D}^{t} = (P_{i, t + 1}^{W D 2 G} - P_{i, t}^{W D 2 G}) / Δ t \\ β_{P V}^{t} = (P_{i, t + 1}^{P V 2 G} - P_{i, t}^{P V 2 G}) / Δ t \\ β_{P S}^{t} = (P_{i, t + 1}^{P S 2 G} - P_{i, t}^{P S 2 G}) / Δ t \\ β^{t} = β_{W D}^{t} + β_{P V}^{t} + β_{P S}^{t} \end{array}\} \end{matrix}

聚合电源各时段上网出力 $P_{t}^{m i x}$ 与调度周期内平均上网出力P^ave分别表示为

(15)

\begin{matrix} \begin{array}{l} P_{t}^{m i x} = P_{i, t}^{W D 2 G} + P_{i, t}^{P V 2 G} + P_{i, t}^{P S 2 G} \\ P^{a v e} = \frac{1}{T} \overset{T}{\sum_{t = 1}} P_{t}^{m i x} \end{array}\} \end{matrix}

以上网出力曲线变化率、曲线峰值上限、谷值上限为上网出力互补评价指标^[21]建立上网出力互补约束:

(16)

\begin{matrix} \begin{array}{l} |\frac{β^{t}}{P^{a v e}}| \leq C_{r} \\ |\frac{m a x P_{t}^{m i x} - P^{a v e}}{P^{a v e}}| \leq C_{p} \\ |\frac{m i n P_{t}^{m i x} - P^{a v e}}{P^{a v e}}| \leq C_{v} \end{array}\} \end{matrix}

式中:C_r、C_p、C_v分别为上网出力曲线变化比例以及曲线峰、谷上限值.

2 合作增益分配模型

在应对大规模利益主体风电-光伏-抽蓄-电制氢多能源系统的增益分配问题时,经典合作博弈分配法如Shapley值法、核仁法所需求解的子联盟运行场景数呈指数级增长,计算量与耗时大幅增加^[22].因此,采用MCRS法对多主体能源系统合作增益进行分配.

为实现公平分配,MCRS法将个体的边际贡献价值作为分配衡量标准,按照各利益主体参与合作的最大收益x_i,_max与最小收益x_i,_min差值占比进行增益分配.规定最大收益为利益主体i加入大联盟N所带来的边际增益,由加入与未加入联盟所获收益之差决定;最小收益为利益主体i独立优化运行所获收益:

(17)

\begin{matrix} \begin{array}{l} x_{i, m i n} = F_{i} \\ x_{i, m a x} = F_{N} - F_{N \ {i}} \end{array}\} \end{matrix}

式中:F_i为利益主体i的独立运行收益;F_N为大联盟N的合作运行总收益;F_N\_{_i_}为利益主体i未加入大联盟N时的联盟总收益.

抽蓄、风、光、氢各利益主体i采用MCRS法所分得合作增益可表述为

(18)

\begin{array}{l} x_{i}^{M C R S} = x_{i, m i n} + \frac{|x_{i, m a x} - x_{i, m i n}|}{\sum_{j \in N} |x_{j, m a x} - x_{j, m i n}|} \times \\ (F_{N} - \sum_{j \in N} x_{j, m i n}) \end{array}

式中:j为任一利益主体.

3 算例分析

算例的12利益主体系统数据选取我国西部某风电-光伏-抽蓄-电制氢清洁能源示范基地规划水平年相关数据,联盟包含风电场(WD1~3)、光伏电站(PV1~3)以及电制氢站(HG1~3)各3个,抽蓄电站选取3台机组(PS1~3)投入运行.以1 h为间隔,对全天共24个时段进行优化调度,算例涉及数据如下.

(1) 风电场参数.每座风电场包含风电机组若干台,总装机容量分别为50、60和65 MW;出力均值与标准差数据见附录B;上网电价按照2020年国家发改委公布的 II 类资源区域指导价格设置为0.34元/(kW·h),单位运行维护成本取0.008元/(kW·h),过网费系数α为3×10^-5,β为0.01.

(2) 光伏电站参数.每个光伏电站包含光伏发电板若干块,总装机容量均为150 MW,出力均值与标准差数据见附录C;上网电价按照2020年国家发改委公布的 II 类资源区域指导价格设置为0.40元/(kW·h),单位运行维护成本设置为 0.008 5元/(kW·h),过网费系数取值同风电.

(3) 抽蓄机组参数.抽蓄机组技术参数设置见附录D,水库容量上下限值分别为1×10⁷和1.5×10⁶ m³,将上下限值之差的2/3处设定为初始库容;发电上网电价参照标杆煤电电价取0.391元/(kW·h),抽水电价设置为发电电价的75%;抽水和发电工况下的启动成本系数均为500;过网费系数取值同风电.

(4) 电制氢站参数.电制氢站技术参数见附录E,单位运行维护成本设置为0.022元/(kW·h),规定电制氢站按照工业电价向电网购电,工业电价谷段(01:00—07:00,23:00—24:00)为 0.337 6元/(kW·h),峰段(12:00—14:00,19:00—22:00)为 0.865 4 元/(kW·h),平段(08:00—11:00,15:00—18:00)为 0.598 0 元/(kW·h).

对系统的合作运行增量收益、增益分配结果以及合作增益的场景影响因素展开分析.由于风电-光伏-抽蓄-电制氢多利益主体优化调度为混合整数非线性规划问题,所以采用MATLAB R2016a软件调用Gurobi对各联盟的优化调度模型进行求解.

3.1 不同运行模式下合作增益分析

3.1.1 合作增益分摊结果分析

以基础场景为例,暂不考虑上网出力风互补指标,即不考虑约束式(14)~(16),对风电-光伏-抽蓄-电制氢12利益主体系统进行联合优化调度,并采用MCRS法分配合作增益.

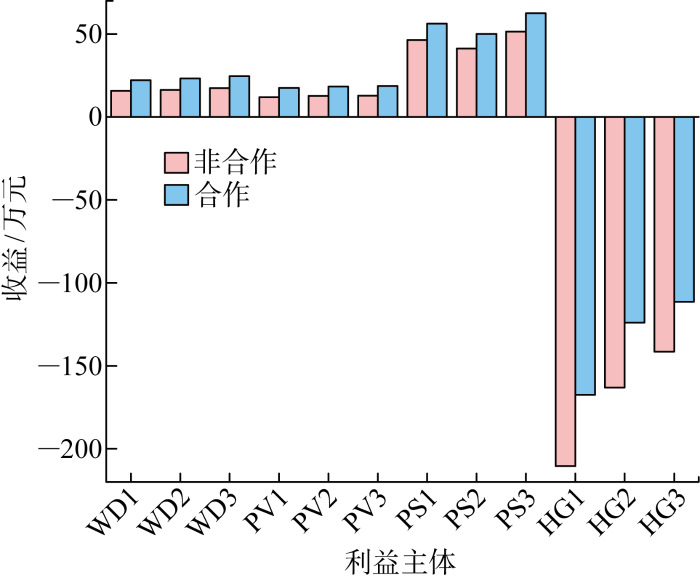
计算结果如图1所示,风电-光伏-抽蓄-电制氢12利益主体系统通过联合优化运行,相较合作前大联盟共增收179 万元.根据边际贡献价值采用MCRS对增益进行分配,可见各利益主体在非合作运行模式的基础上均获得一定比例的收益提升,发电利益主体(抽蓄、风、光)增加了自身收益,用电利益主体(电制氢)降低了自身用电成本,分配结果满足个体理性和整体理性.风、光增益的总增收占比较少,约为3%~4%;电制氢站增益的总增收占比最多,约为16%~24%;抽蓄机组增益的总增收占比次之,约为5%~6%.抽蓄机组为风光提供旋转备用容量,可消纳波动的风光出力,使大联盟获取电量增益.电制氢的加入使得发电利益主体在电量增益的基础上利用电价互补特性在系统内部通过电量交易与之开展合作,边际贡献较高,因此所分得增益占比最多.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 不同运行模式下各利益主体的收益

Fig.1 Benefits of each stakeholder in different operation modes

3.1.2 风光消纳能力分析

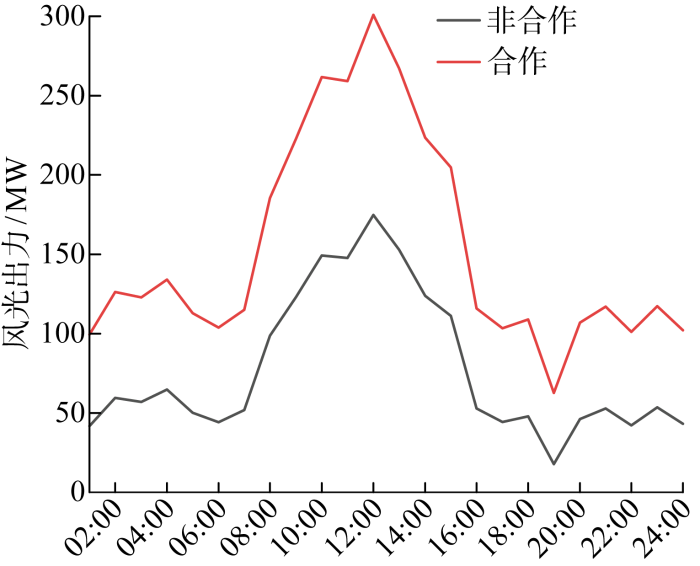
非合作运行模式下,无抽蓄机组向风光提供备用,风光只能按照下限进行出力.在合作运行模式下,由式(9)可知,抽蓄机组可向波动的风光提供备用支撑,因此提高了风光消纳水平.如图2所示,通过联合优化运行,风电-光伏-抽蓄-电制氢12利益主体系统中风光利益主体较非合作运行模式共增加发电功率 1 244 MW,通过风电-光伏-抽蓄-电制氢多能互补产生的增益电量可进一步为系统带来额外增量收益.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不同运行模式下的风光出力

Fig.2 Output of wind and PV power in different operation modes

3.1.3 电量调度情况分析

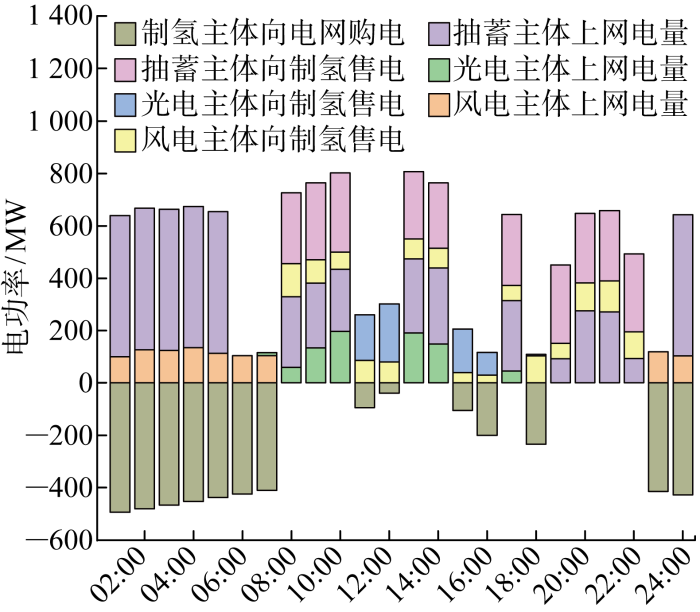
为方便分析,合并同类型利益主体的电量调度情况,绘制风电-光伏-抽蓄-电制氢站在合作运行模式下的电量调度情况如图3所示.由图可见,01:00—07:00以及23:00—24:00工业电价最低,风电、光伏和抽蓄上网电价均高于工业电价,风电全部上网;光伏于07:00上网;抽蓄机组于06:00—07:00和23:00抽水进行储能,其余时刻发电上网;此时电制氢主体的用电需求由电网满足,以较低的工业电价大量购入需求电量.08:00—22:00 工业电价较高,风、光、抽蓄上网电价较低,因此电制氢主体向风、光、抽蓄购入需求电量,各发电利益主体在满足制氢需求量的前提下,将多余发电量上网.其中,抽蓄机组于11:00—12:00、15:00—16:00 以及18:00抽水储能,风、光、抽蓄所能提供的制氢电量有限,因此电制氢主体向电网购入少部分电量以满足制氢计划需求,其余时段制氢需求电量均由风、光、抽蓄提供.各调度时段内发、用电利益主体双方各自选择获益更高的方式进行电量调度,以内部电量交易的形式开展合作,最大化联盟的经济效益.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 电量调度结果

Fig.3 Results of power dispatching

3.2 不同场景因素下合作增益分析

3.2.1 抽蓄库容对合作增益的影响

以基础场景参数为1倍库容,保持其余参数不变,在此基础上将抽蓄库容按一定系数扩大或缩小,探究风电-光伏-抽蓄-电制氢12利益主体系统的合作增益变化情况,计算结果如表1所示.由表可见,随着抽蓄库容扩大,系统的合作总收益呈增长趋势, 即库容越大,合作总收益越多.与合作前相比,合作增益随库容扩大呈先增长后不变的趋势.风光装机容量一定,当抽蓄库容很小时,所能提供的旋转备用裕度有限,只能消纳部分风光,合作增益较少;风光消纳能力随库容扩大而增强,因此库容扩大时,合作增益首先呈现上升趋势;随着库容继续扩大,风光消纳能力进一步增强直至风光被全部消纳,此时合作增益不再继续增长.综上,在风电-光伏-抽蓄-电制氢联合优化系统中,风光装机规模与抽蓄库容的容量配比需优化选择,否则资源过度浪费不仅无法带来增益增长,还会存在过度投资的经济性问题.

表1 不同抽蓄库容下的合作增量收益

Tab.1 Incremental benefits with different reservoir capacities of pumped storage station

抽蓄库容缩放系数	合作前收益/ 万元	合作后收益/ 万元	增量收益/ 万元
0.1	-413.90	-278.77	135.13
0.2	-399.96	-246.04	153.93
0.3	-386.03	-218.32	167.71
0.5	-358.16	-177.29	179.13
1.0	-288.48	-109.35	179.13
1.5	-218.80	-40.16	179.13

新窗口打开| 下载CSV

3.2.2 上网电价对合作增益的影响

当风光上网电价不变时,以基础场景抽蓄上网电价为基准,将其分别增减0.5元/(kW·h),分析不同上网电价场景下系统的合作增益,计算结果如表2所示.由表可见,系统总收益随上网电价降低而降低,但与合作前相比,上网电价越低,风电-光伏-抽蓄-电制氢系统所创造的合作增益越多,即各利益主体可分得的个体增益也越多.较低的上网电价导致各利益主体合作增益增加.

表2 不同上网电价下的合作增量收益

Tab.2 Incremental benefits at different on-grid prices

上网电价场景设置	合作前收益/ 万元	合作后收益/ 万元	增量收益/ 万元
增加0.5元/(kW·h)	-288.30	-109.32	178.98
基础场景	-288.48	-109.35	179.13
减少0.5元/(kW·h)	-288.66	-109.38	179.27

新窗口打开| 下载CSV

进一步分析抽蓄分时上网电价对系统合作增益的影响.分别设置抽蓄的上网电价与工业电价变化趋势呈正或负相关,且日内平均上网电价均为0.391元/(kW·h),系统合作增益计算结果如表3所示.由表可见,当上网电价与工业电价变化趋势呈负相关时,在工业电价较低、抽蓄上网电价较高的时段,电制氢站向电网购入低价电,而抽蓄电站以较高的价格发电上网;在工业电价较高、抽蓄上网电价较低的时段,抽蓄电站抽水储能,电制氢站与其合作购入所需制氢电量,风电-光伏-抽蓄-电制氢多主体联合优化的合作增益更多.若上网电价与工业电价变化趋势呈正相关,则抽蓄电站可能在工业电价较高的时段将更多出力用于上网以最大化自身收益,弱化内部合作,因此系统合作增益较少.

表3 不同分时上网电价下的合作增量收益

Tab.3 Incremental benefits at different time-of-day on-grid prices

上网电价场景设置	合作前收益/ 万元	合作后收益/ 万元	增量收益/ 万元
与工业电价正相关	-255.54	-107.03	148.52
与工业电价负相关	-247.73	-94.59	153.13

新窗口打开| 下载CSV

3.2.3 上网安全约束对合作增益的影响

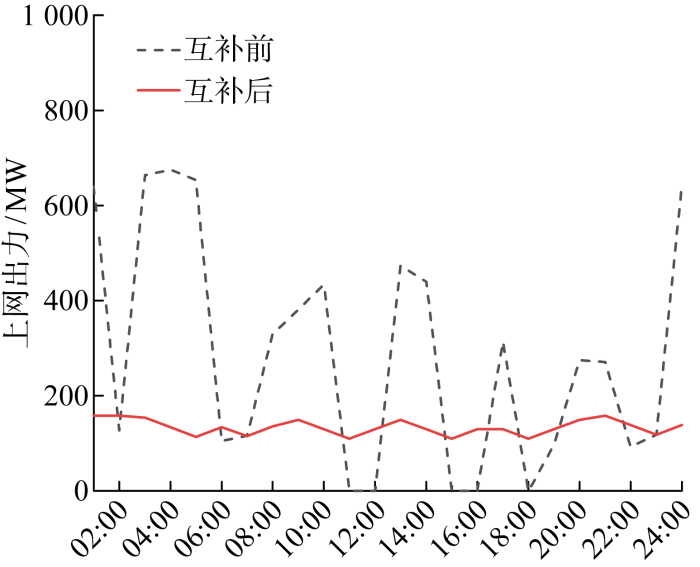
考虑上网出力互补指标约束式(14)~(16),在保证风电-光伏-抽蓄-电制氢系统经济性最优的同时兼顾系统电量上网的安全性.以基础场景为例,设置上网出力互补指标分别为C_r=0.15、C_p=C_v=0.18,绘制互补前后的上网出力曲线如图4所示.由图可见,在仅考虑系统经济性最优的联合调度中,系统上网出力变化幅度很大, 04:00出力最高为675 MW,11:00—12:00、15:00—16:00和18:00无上网出力.进一步考虑上网出力互补指标约束后,如图中红色实线所示,系统上网出力曲线波动性大幅降低,日内上网出力在100~160 MW小范围波动,峰谷差值较先前降低92.9%,极大程度提升了系统出力安全上网的平稳性要求.另一方面,互补前系统内部交易电量为 4 650 MW·h,互补后提升至 6 893 MW·h,一定程度上促进了系统进行内部合作.但为保证系统安全运行,系统内部电量需重新优化调度,由于原先调度结果已在最大收益运行点,重新调度后的系统合作收益为-143.64万元,较先前降低了31.4%.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 互补前后系统上网出力

Fig.4 On-grid power before and after complementation

进一步探究互补约束对系统合作总收益的影响,其余因素不变,将3个互补指标同时扩大和缩小0.02与基础场景进行对比.当互补指标同时扩大0.02,即互补性要求降低时,合作收益上升至-143.09万元;当互补指标同时缩小0.02,即互补性要求提高时,合作收益下降至-144.78万元.由此可见,上网出力互补性要求越高,系统合作总收益越低,即当系统运行的安全性要求越高时,系统运行的经济性会有所下降.

3.3 不同分配方法下计算高效性分析

MCRS法与经典合作博弈分配法中的Shapley值法均以各利益主体的边际贡献价值作为分配的衡量标准,分配结果差异较小^[19].以风电-光伏-抽蓄-电制氢12利益主体系统联盟求解数量以及计算总耗时作为计算高效性的衡量标准,将MCRS法与Shapley值法进行对比,如表4所示.由表可知,本算例中Shapley值法除需求解12个利益主体的独立运行及其联合运行结果外,还需计算出12个利益主体在各种组合方式下的联合运行收益,共计4 095种调度场景,求解复杂度高,计算耗时长.由式(17)可知,MCRS法在求得12个利益主体独立运行及其联合运行结果的基础上,仅需对除去个体成员的12种联合运行模式进行求解,所需求解联盟数量大幅减少,计算效率显著提升.

表4 MCRS法与Shapley值法计算高效性对比

Tab.4 Comparison of calculation efficiency of MCRS method and Shapley value method

分配方法	n主体系统理论联盟求解数量/个	本算例实际联盟求解数量/个	计算耗时/s
Shapley值法	2ⁿ-1	4095	85285
MCRS法	2n+1	25	304

新窗口打开| 下载CSV

对于一个n主体的风电-光伏-抽蓄-电制氢联合系统,由表4中联盟求解数量值可知,随着系统规模不断扩大,Shapley值法的计算复杂度呈指数级快速增长,出现组合爆炸问题,难以应用;而 MCRS法计算复杂度呈线性缓慢增长,当系统规模越大,即联盟成员数越多时,MCRS法的计算高效性优势将越明显,因此能较好地克服大规模系统合作增益分配时的组合爆炸问题.

4 结论

基于合作博弈论中的MCRS法,提出一种风电-光伏-抽蓄-电制氢多利益主体系统合作运行增益分配策略.对所提调度模型及增益分配模型进行仿真验证,得出以下结论:

(1) 风电-光伏-抽蓄-电制氢多利益主体通过资源互补特性为联合优化运行带来合作增量收益;基于MCRS法的分配策略可实现合作增益在各利益主体间的高效公平分配.

(2) 抽蓄库容影响系统合作增益.风光装机容量一定时,库容越大,抽蓄所能支撑的风光波动出力越多,风光消纳能力越强,系统合作增益随库容扩大而增长,直至消纳全部风光后不变.需合理规划风光装机与抽蓄库容的容量配比,避免配比过大时资源的不充分以及配比过小时资源浪费带来的过度投资问题.

(3) 上网电价影响系统合作增益.上网电价越低,系统的合作增益越多,即各利益主体所能分得的增益越多.此外,当上网电价与工业电价变化趋势呈负相关时,系统能实现更高的合作增益.

(4) 运行安全性需求影响系统合作增益.除内部交易电量外,将系统剩余电量打捆作为大电源上网时,上网出力波动性越低,系统运行安全性越强.为平稳上网出力,内部交易电量增加,因此考虑上网出力互补性指标在一定程度上能够促进多能源系统进行内部合作.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2024/1006-2467/1006-2467-58-06-0872.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李佳琪, 徐潇源, 严正.

大规模新能源汽车接入背景下的电氢能源与交通系统耦合研究综述

[J]. 上海交通大学学报, 2022, 56(3): 253-266.

DOI:10.16183/j.cnki.jsjtu.2021.464 [本文引用: 1]

新能源的大规模开发利用是实现“双碳”目标的重要手段.可再生能源发电耦合制氢技术在提高可再生能源消纳率的同时,加速了新能源汽车的普及.未来,电氢能源系统与交通系统的耦合将会更加密切.以大规模新能源汽车接入为背景,首先综述了电氢能源系统的发展现状,并对耦合系统制氢、出力波动平抑以及参与电力系统优化运行3种工作模式进行了介绍.在此基础上,从不同能源角度出发,分别对电力-交通耦合系统中的联合规划与优化运行研究现状以及氢能-交通耦合系统中的加氢站优化与氢能运输相关问题进行了总结分析.最后,结合当前研究中存在的瓶颈,从动态模型构建、不确定性因素影响等方面对未来可行研究方向进行了展望.

Jiaqi

, XU

Xiaoyuan

, YAN

Zheng

A review of coupled electricity and hydrogen energy system with transportation system under the background of large-scale new energy vehicles access

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(3): 253-266.