考虑碳交易量自适应决策的输电网两阶段鲁棒规划

doi:10.16183/j.cnki.jsjtu.2022.473

考虑碳交易量自适应决策的输电网两阶段鲁棒规划

蒋标¹, 刘佳^,¹, 曾平良¹, 唐早¹, 李亚楼²

1.杭州电子科技大学自动化学院,杭州 310018

2.中国电力科学研究院有限公司,北京 100192

Two-Stage Robust Planning for Transmission Network Considering Adaptive Decision of Carbon Trading Volume

JIANG Biao¹, LIU Jia^,¹, ZENG Pingliang¹, TANG Zao¹, LI Yalou²

1. School of Automation, Hangzhou Dianzi University, Hangzhou 310018, China

2. China Electric Power Research Institute, Beijing 100192, China

通讯作者: 刘佳,讲师,电话(Tel.):0571-86919086;E-mail:sjtu_lj@hdu.edu.cn.

责任编辑: 王历历

收稿日期: 2022-11-25 修回日期: 2023-03-13 接受日期: 2023-03-14

基金资助:

国家自然科学基金(U2166211)
2022年度电网安全与节能国家重点实验室开放基金(XTB51202201509)

Received: 2022-11-25 Revised: 2023-03-13 Accepted: 2023-03-14

作者简介 About authors

蒋标(1998-),硕士生,从事电力系统规划研究.

摘要

低碳化是新型电力系统未来发展趋势,在规划层面模拟水平年碳交易量对实现未来电网低碳经济运行具有重要作用.基于此,提出考虑碳交易量自适应决策的输电网鲁棒规划方法.首先,构建基于基准线法的碳配额交易成本计量方法,并考虑碳交易量约束,建立考虑风电和负荷不确定性的两阶段鲁棒规划模型.其次,利用松-紧解耦法将子问题按时间解耦为安全可行性检测子问题和低碳可行性检测子问题,并采用列和约束生成算法求解两阶段鲁棒规划模型,根据安全约束与碳配额交易量约束在各不确定场景下反馈的割信息,分析模型可行解空间与碳配额交易量阈值参数设置的映射关系,自适应决策碳交易量上下限.最后,以改进的IEEE-RTS 24节点系统进行算例仿真,分析低碳规划模型、碳配额交易量、碳价对规划结果的影响.结果表明所提模型实现了规划方案在经济性和低碳性方面的协同优化.

关键词： 鲁棒优化; 输电网; 碳交易; 碳配额; 时间解耦

Abstract

Low carbon is the future development trend of new power system, and the simulation of horizontal annual carbon trading volume at the planning level plays an important role in realizing the low-carbon economic operation of future power grid. Based on this understanding, a robust planning method for transmission network considering adaptive decision-making of carbon trading volume is proposed. First, a measurement method of carbon quota trading cost based on the baseline method is constructed, and a two-stage robust programming model considering the uncertainty of wind power and load is established considering the constraint of carbon trading volume. Then, the relax-and-enforce decoupling method is used to decouple the sub-problem into security feasibility detection sub-problem and low carbon feasibility detection sub-problem according to time, and the two-stage robust programming model is solved by using the column and constraint generation algorithm. Based on the cut information feedback from the security constraint and the carbon quota trading volume constraint in each uncertain scenario, the mapping relationship between the feasible solution space of the model and the setting of the threshold parameter of carbon quota trading volume is analyzed, and the upper and lower limits of carbon trading volume are adaptively decided. Finally, the improved IEEE-RTS 24-node system is simulated to analyze the impacts of the low-carbon planning model, carbon quota trading volume, and carbon price on the planning results. The results show that the proposed model realizes the coordinated optimization of the planning scheme in terms of economy and low carbon.

Keywords： robust optimization; transmission network; carbon trading; carbon quota; time decoupling

PDF (1824KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

蒋标, 刘佳, 曾平良, 唐早, 李亚楼. 考虑碳交易量自适应决策的输电网两阶段鲁棒规划[J]. 上海交通大学学报, 2024, 58(6): 826-835 doi:10.16183/j.cnki.jsjtu.2022.473

JIANG Biao, LIU Jia, ZENG Pingliang, TANG Zao, LI Yalou. Two-Stage Robust Planning for Transmission Network Considering Adaptive Decision of Carbon Trading Volume[J]. Journal of Shanghai Jiaotong University, 2024, 58(6): 826-835 doi:10.16183/j.cnki.jsjtu.2022.473

近年来气候问题越来越受国际关注,为应对全球变暖,我国提出“力争2030年前实现碳达峰、2060年前实现碳中和”的目标^[1].我国作为能源消费大国,电力在我国能源消费与碳排放中占据重要地位,电力行业作为二氧化碳排放的主要来源,碳排放占比超过40%^[2].因此,加快实现电力脱碳对构建新型电力系统、实现双碳目标具有重要意义.

目前,针对电力系统规划已有丰富的研究成果.文献[3]中针对风电出力和负荷不确定性,建立输电网结构和储能联合鲁棒规划模型.文献[4]中针对高比例可再生能源问题,提出电网运行状态后校验的方法评估电网结构的适用性指标,建立多目标电力系统规划模型,保证系统高效、安全、稳定的运行.文献[5]中针对输电网长期和短期不确定性问题建立鲁棒规划模型,并采用Benders算法对模型进行求解.文献[6 ⇓-8]中考虑输配协同的电网规划,将输配电网联络线处功率作为耦合变量建立模型,并利用分布式算法对其求解,保证输配电网实现最优运行.文献[9]中建立基于线路传输能力的电网灵活性评价指标,并综合考虑灵活性与经济性因素的相互影响,提出一种输电网多目标扩展规划模型.以上文献处理电力系统深度脱碳过程中的不确定性和灵活性等问题,未计及碳排放对电力系统规划结果的影响.

在低碳电力系统方面,现有研究中低碳电力规划的一般思路是在传统规划模型的基础上引入碳排放约束以及考虑多种低碳电力技术与减排策略的协同优化.文献[10]中将低碳电力技术的成本和所涉及碳交易机制的交易费用纳入目标函数,并将二氧化碳减排目标纳入约束条件,以低碳经济条件下规划期内整体互联效益最大化为目标函数,建立互联规划模型.文献[11]中提出一种考虑碳排放约束的发电计划优化模型,建立虚拟电力系统来验证模型有效性,所提方法仅考虑电源规划,仍有一定的应用局限性.文献[12]中在我国“3060”背景下,考虑火电机组在保障可再生能源占比较高的电力系统中的作用,并在此基础上建立以碳减排为目标的电力系统模型.文献[13 ⇓-15]中利用碳捕集系统减少系统碳排放量,建立低碳规划模型.文献[16]中提出一种利用模糊风力发电实现低碳经济的输电网络扩展规划具体方法,并开发了一种评估输电容量不足导致风能溢出的方法和发电机低碳调整策略,以应对过载问题.文献[17]中提出考虑经济性、低碳、储能寿命的多目标电力系统低碳经济调度优化模型,并基于参数规划及工程博弈给出一种多目标优化问题的求解方法.文献[18]中提出考虑碳排放流理论和需求响应的低碳调度模型,将碳排放责任归算到负荷侧,体现负荷所对应的碳排放量.文献[19]中从电力系统发电结构转型的角度出发,基于系统动力学,构建双碳目标下电力系统供给侧形态发展的推演模型.

综上所述,现有研究一般在传统规划的基础上引入碳排放约束以及考虑低碳电力技术与减排策略的协同优化,在如何设定碳交易量或碳减排目标临界值方面的研究较少.因此,在传统电力系统规划研究的基础上提出考虑碳交易量自适应决策的输电网鲁棒规划模型,引入碳交易机制实现模型在经济性和低碳性的协同优化,并通过安全性检测保证不确定条件下的安全性.然后,给出计算碳交易量上限和下限求解模型,为制定碳排放指标提供参考.最后,以改进的IEEE-RTS 24节点系统验证所提模型的经济性与低碳性.

主要工作为:①提出基于碳配额交易机制的两阶段鲁棒规划模型,将碳交易成本引入到目标函数,并考虑模型碳交易总量约束;②综合利用松-紧解耦^[20-21](Relax-and-Enforce Decoupling,R&ED)法和列和约束生成(Column and Constraints Generation,C&CG)算法在保证规划安全可行性的同时,求解碳配额交易量上限、下限.

1 基于碳配额交易机制的两阶段鲁棒规划模型

两阶段鲁棒规划模型旨在寻找预测场景下最优方案的线路规划和运行方案,使得该方案不仅能满足预测场景也能在不确定条件下调整系统运行方案.两阶段鲁棒优化的主问题模型包括投资建设和运行模拟,子问题是对主问题产生的线路规划和调度方案进行可行性检测的问题.其具体形式如下:

(1)

\begin{matrix} (x, y) = a r g [\underset{x, y}{m i n} C (x, y) \underset{q}{m a x} \underset{v_{w} v_{l}}{m i n} v] \end{matrix}

式中:x、y分别为新建线路的0或1变量和运行策略;C为总成本;q为不确定量集合;v为极端场景下的运行偏差;v_w、v_l为安全约束松弛变量.

1.1 碳配额交易机制

现有碳配额分配方法有“有偿分配”和“免费分配”两种,其中免费分配又包含“历史法”和“基准线法”^[22].我国碳交易市场仍处于初级阶段,为调动市场活力、激励企业减排,电力行业主要采取免费分配的基准线法^[23],即碳排放配额与发电量成正比,而且基准线法具有方向性确定、减排幅度可控的优点.基准线法的免费配额量为

(2)

\begin{matrix} E^{b} = \sum_{t \in T} \sum_{i \in N} \sum_{f \in G_{i}} η P_{i, t, f} \end{matrix}

式中:t为时段;T为时长;N为节点集合;G_i为节点i处连接的发电机组集合;η为区域碳排放配额基准值;P_i_,_t_,_f为节点i处t时火电机组f的发电量.

系统的碳排放量模型为

(3)

E^{a} = \sum_{t \in T} \sum_{i \in N} \sum_{g, h \in G_{i}} (p_{i}^{c o_{2}} P_{i, t, g}^{G e n} + q_{i}^{c o_{2}} P_{i, t, h}^{G a s})

式中:E^a为系统的碳排放量; $p_{i}^{c o_{2}}$ 、 $q_{i}^{c o_{2}}$ 分别为节点i处燃煤机组和燃气机组产生单位有功的碳排放量; $P_{i, t, g}^{G e n}$ 、 $P_{i, t, h}^{G a s}$ 分别为节点i处t时燃煤机组g和燃气机组h的出力.

碳配额交易量为

(4)

\begin{matrix} E = E^{a} - E^{b} \end{matrix}

碳配额交易成本为

(5)

\begin{matrix} C_{c} = c_{c o_{2}} E \end{matrix}

式中: $c_{c o_{2}}$ 为单位碳排放配额的交易成本.

当E>0,说明机组系统碳排放量已经超出碳配额,需要购买超出的排放指标并支付费用,增加了系统的运行成本;当E≤0,说明机组系统碳排放量未超出碳配额,不需要购买排放额,并且可以把剩余配额量向市场出售获利,降低系统的运行成本.

1.2 主问题模型

1.2.1 目标函数

主问题以包括线路投资成本、发电机出力成本、切负荷惩罚成本和碳配额交易成本在内的规划总成本最小为目标函数.具体形式如下:

(6)

m i n C = C_{I n v} + C_{G e n} + C_{G a s} + C_{L} + C_{c}

式中:C_Inv为投资成本;C_Gen为燃煤机组出力成本;C_Gas为燃气机组出力成本;C_L为切负荷惩罚成本.各成本可具体表示为

(7)

C_{I n v} = \frac{r_{0} (1 + r_{0})^{m}}{(1 + r_{0})^{m} - 1} \sum_{(i, j) \in Ω} \sum_{k \in K_{i j}^{+}} c_{i j, k} I_{i j, k} l_{i j, k}

(8)

C_{G e n} = \sum_{t \in T} \sum_{i \in N} \sum_{g \in G_{i}} [a_{i, g} + b_{i, g} P_{i, t, g}^{G e n} + c_{i, g} (P_{i, t, g}^{G e n})^{2}]

(9)

C_{G a s} = \sum_{t \in T} \sum_{i \in N} \sum_{h \in G_{i}} [α_{i, h} + β_{i, h} P_{i, t, h}^{G a s} + γ_{i, h} (P_{i, t, h}^{G a s})^{2}]

(10)

\begin{matrix} C_{L} = \sum_{t \in T} \sum_{i \in N} {c^{L}}_{i} {P^{L}}_{i, t} \end{matrix}

式中:(i, j)∈Ω为输电线路走廊集合; $K_{i j}^{+}$ 为待建支路集合;r₀为贴现率;m为线路运行年限;I_ij_,_k为节点i、j之间第k条线路是否投建的决策变量,I_ij_,_k=1表示线路投建,I_ij_,_k=0表示线路不投建;c_ij_,_k为线路单位长度投资成本;l_ij_,_k为线路长度;a_i_,_g、b_i_,_g、c_i_,_g为节点i处燃煤机组g的耗量特性曲线参数;α_i_,_h、β_i_,_h、γ_i_,_h为节点i处燃气机组h的耗量特性曲线参数; ${c^{L}}_{i}$ 为节点i处单位切负荷成本; ${P^{L}}_{i, t}$ 为节点i处t时的切负荷量.

1.2.2 约束条件

具体为

(1) 已建线路潮流约束:

(11)

\begin{array}{l} f_{i j, t, k} = b_{i j, k} (θ_{i, t} - θ_{j, t}), \\ \begin{matrix} (i, j) \in Ω, k \in K_{i j}^{-} \end{matrix} \end{array}

式中:f_ij_,_t_,_k为节点i、j第k条线路在t时的有功潮流;b_ij_,_k为节点i、j第k条线路的电纳;θ_i_,_t、θ_j_,_t分别为节点i、j处t时的电压相角; $K_{i j}^{-}$ 为已有支路集合.

(2) 待建线路潮流约束:

(12)

\begin{array}{l} f_{i j, t, k} = I_{i j, k} b_{i j, k} (θ_{i, t} - θ_{j, t}), \\ \begin{matrix} (i, j) \in Ω, k \in K_{i j}^{+} \end{matrix} \end{array}

(3) 已建线路潮流容量约束:

(13)

\begin{array}{l} F_{i j, m i n} \leq f_{i j, t, k} \leq F_{i j, m a x}, \\ \begin{matrix} (i, j) \in Ω, k \in K_{i j}^{-} \end{matrix} \end{array}

式中:F_ij_,min为节点i、j之间线路潮流容量最小值;F_ij_,max为节点i、j之间线路潮流容量最大值,一般来说,F_ij_,min=-F_ij_,max.

(4) 待建线路潮流容量约束:

(14)

\begin{array}{l} I_{i j, k} F_{i j, m i n} \leq f_{i j, t, k} \leq I_{i j, k} F_{i j, m a x}, \\ \begin{matrix} (i, j) \in Ω, k \in K_{i j}^{+} \end{matrix} \end{array}

(5) 发电机组出力上下限约束:

(15)

\begin{matrix} \begin{array}{l} P_{i, g, m i n}^{G e n} \leq P_{i, t, g}^{G e n} \leq P_{i, g, m a x}^{G e n} \\ P_{i, h, m i n}^{G a s} \leq P_{i, t, h}^{G a s} \leq P_{i, h, m a x}^{G a s} \\ i \in N, g, h \in G_{i} \end{array}\} \end{matrix}

式中: $P_{i, g, m i n}^{G e n}$ 、 $P_{i, h, m i n}^{G a s}$ 为与节点i相连燃煤机组g、燃气机组h出力的最小值; $P_{i, g, m a x}^{G e n}$ 、 $P_{i, h, m a x}^{G a s}$ 为与节点i相连燃煤机组g、燃气机组h出力的最大值.

(6) 切负荷约束:

(16)

\begin{matrix} 0 \leq {P^{L}}_{i, t} \leq {P^{L}}_{i, t, m a x}, i \in N \end{matrix}

式中: ${P^{L}}_{i, t, m a x}$ 为节点i处t时允许切负荷量最大值.

(7) 节点功率约束:

(17)

\begin{array}{l} \sum_{g \in G_{i}} P_{i, t, g}^{G e n} + \sum_{h \in G_{i}} P_{i, t, h}^{G a s} + \sum_{j \in Ω_{2} (i)} \sum_{k \in K_{i j}} f_{i j, t, k} + \\ \sum_{w \in W_{i}} {P^{W}}_{i, t, w} = {P^{L}}_{i, t, l} - {P^{L}}_{i, t} + \sum_{j \in Ω_{1} (i)} \sum_{k \in K_{i j}} f_{i j, t, k} \end{array}

式中: ${P^{W}}_{i, t, w}$ 为节点i处风电机组w在t时出力; ${P^{L}}_{i, t, l}$ 为t时与节点i相连的负荷的需求量;Ω₂(i)为以节点i为末端的线路集合;Ω₁(i)为以节点i为首端线路集合;K_ij为可存线路集合;W_i为节点i处连接风电机组集合.

(8) 碳配额交易量约束:

(18)

\begin{matrix} E^{a} - E^{b} \leq E^{m} \end{matrix}

采用式(18)约束条件对碳配额交易量进行约束,约束值为E^m,也即间接对系统碳排放总量进行约束.但是,如果E^m设置过高,则不能对碳排放量起到约束作用,如果设置过低则可能导致系统不存在可行解,影响系统的安全运行.

1.2.3 约束松弛

在约束条件式(12)中,由于布尔变量I_ij_,_k与θ_i_,_t和θ_j_,_t都为决策变量,所以待建线路潮流约束为非线性约束,为了将其转化为线性约束,采用大M法对其进行线性化,将约束松弛为

(19)

\begin{array}{l} b_{i j, k} (θ_{i, t} - θ_{j, t}) - f_{i j, t, k} + (1 - I_{i j, k}) M \geq 0 \\ b_{i j, k} (θ_{i, t} - θ_{j, t}) - f_{i j, t, k} + (1 - I_{i j, k}) M \leq 0 \end{array}\}

式中:M为一个非常大的数.

若I_ij_,_k为1,1-I_ij_,_k为0,则满足支路约束潮流,即f_ij_,_t_,_k=b_ij_,_k(θ_i_,_t-θ_j_,_t).若I_ij_,_k为0,由于M是一个非常大的数,则该潮流约束被松弛,该项约束不起作用.

1.3 子问题模型

子问题的目标函数为最小化偏离系统安全运行的程度^[20],即

(20)

\begin{array}{l} v = \\ \underset{P_{i, t, l}^{L u}, P_{i, t}^{W u}}{m a x} \underset{P_{i, t, g}^{u G e n}, P_{i, t, h}^{u G a s}, P_{i, t, w}^{W u}, {v^{u}}_{w, t}, {v^{u}}_{l, t}}{m i n} \sum_{t \in T} ({v^{u}}_{w, t} + {v^{u}}_{l, t}) \end{array}

约束条件具体形式如下:

(21)

{f^{u}}_{i j, t, k} = b_{i j, k} ({θ^{u}}_{i, t} - {θ^{u}}_{j, t})

(22)

F_{i j, m i n} \leq {f^{u}}_{i j, t, k} \leq F_{i j, m a x}

(23)

\begin{array}{l} P_{i, g, m i n}^{G e n} \leq P_{i, t, g}^{u G e n} \leq P_{i, g, m a x}^{G e n} \\ P_{i, h, m i n}^{G a s} \leq P_{i, t, h}^{u G a s} \leq P_{i, h, m a x}^{G a s} \end{array}\}

(24)

0 \leq P_{i, t}^{L u} \leq {P^{L}}_{i, t, m a x}

(25)

$\sum_{g \in G_{i}} P_{i, t, g}^{u G e n} + \sum_{h \in G_{i}} P_{i, t, h}^{u G a s} + \sum_{j \in Ω_{2} (i)} \sum_{k \in K_{i j}} {f^{u}}_{i j, t, k} +$

$\sum_{w \in W_{i}} P_{i, t, w}^{W u} + {v^{u}}_{w, t} - {v^{u}}_{l, t} =$

P_{i, t, l}^{L u} - P_{i, t}^{L u} + \sum_{j \in Ω_{1} (i)} \sum_{k \in K_{i j}} {f^{u}}_{i j, t, k}

(26)

E^{a u} - E^{b u} \leq E^{m}

(27)

E^{a u} = \sum_{t \in T} \sum_{i \in N} \sum_{g, h \in G_{i}} (p_{i}^{c o_{2}} P_{i, t, g}^{u G e n} + q_{i}^{c o_{2}} P_{i, t, h}^{u G a s})

(28)

E^{b u} = \sum_{t \in T} \sum_{i \in N} \sum_{f \in G_{i}} η {P^{u}}_{i, t, f}

式中: $P_{i, t, w}^{W u}$ 、 $P_{i, t, g}^{u G e n}$ 、 $P_{i, t, h}^{u G a s}$ 分别为风电机组、燃煤机组、燃气机组出力的实际值;上标u表示偏离系统安全程度的实际值; ${v^{u}}_{w, t}$ 、 ${v^{u}}_{l, t}$ 分别为风电和负荷偏离程度; ${P^{u}}_{i, t, f}$ 为节点i处t时火电机组f的实际发电量;E^au、E^bu分别为系统实际的碳排放量与碳配额量.式(21)为线路潮流约束;式(22)为线路容量约束;式(23)为常规机组出力约束;式(24)为切负荷约束;式(25)为节点功率平衡约束;式(26)~(28)为碳配额交易量约束.

1.4 不确定集合

以多面体不确定集合描述风电预测误差和负荷预测误差:

(29)

q = \{\begin{array}{l} \sum_{i} \frac{{\bar{u}}_{i, t} - u_{i, t}}{ε_{i, t}} \leq Γ, & \forall t \\ u_{i, t} - ε_{i, t} \leq {\bar{u}}_{i, t} \leq u_{i, t} + ε_{i, t}, & \forall i, \forall t \end{array}

式中: ${\bar{u}}_{i, t}$ 为不确定量预测值;u_i_,_t为不确定参数;ε_i_,_t为最大预测误差;Γ为不确定度.

2 模型求解方法

2.1 子问题模型的时间解耦

智能优化算法求解结果具有随机性并且易陷入局部最优,因此采用具有确定性的C&CG算法^[24]求解上述主问题模型与子问题模型,并用R&ED法将原始问题的子问题基于时间解耦.其基本思想为将原始时间耦合问题分解为时间间隔更小的时间解耦子问题,然后分别求解.分解情况如下:将子问题分解为SP-1与SP-2.其中SP-1为安全可行性检测子问题,具体形式同式(20),其约束条件包括式 (21)~(25);SP-2为低碳可行性检测子问题,其具体形式如下:

(30)

s = \underset{P_{i, t, l}^{L u}, P_{i, t}^{W u}}{m a x} \underset{P_{i, t, g}^{u G e n}, P_{i, t, h}^{u G a s}, P_{i, t, w}^{W u}}{m i n} (E^{a u} - E^{b u} - E^{m})

其约束条件包括忽略松弛变量的式(21)~(25)和式(27)~(28).

将子问题SP-1与SP-2基于时间解耦得到SP-1-t与SP-2-t:

(31)

v_{t}^{n} = \underset{P_{i, t, l}^{L u}, P_{i, t}^{W u}}{m a x} \underset{P_{i, t, g}^{u G e n}, P_{i, t, h}^{u G a s}, P_{i, t, w}^{W u}, {v^{u}}_{w, t}, {v^{u}}_{l, t}}{m i n} ({v^{u}}_{w, t} + {v^{u}}_{l, t})

(32)

s_{t}^{n} = \underset{P_{i, t, l}^{L u}, P_{i, t}^{W u}}{m a x} \underset{P_{i, t, g}^{u G e n}, P_{i, t, h}^{u G a s}, P_{i, t, w}^{W u}}{m i n} (E^{a u} - E^{b u})

式中:n为迭代次数.式(31)的约束条件为与时间t相对应的式(21)~(25);式(32)的约束条件包括忽略松弛变量的式(21)~(25)、式(27)~(28).

2.2 求解流程

双层问题不易求解,因此在求解上述最大值-最小值问题时,采用强对偶理论将其转化为单层最大化问题.主问题模型与子问题模型关系在于:主问题模型在满足预测场景和最坏场景相关约束情况下寻求最优方案,其中最坏场景在主问题得到的最优方案下由子问题求得,主问题与子问题迭代求解直到满足收敛条件为止.

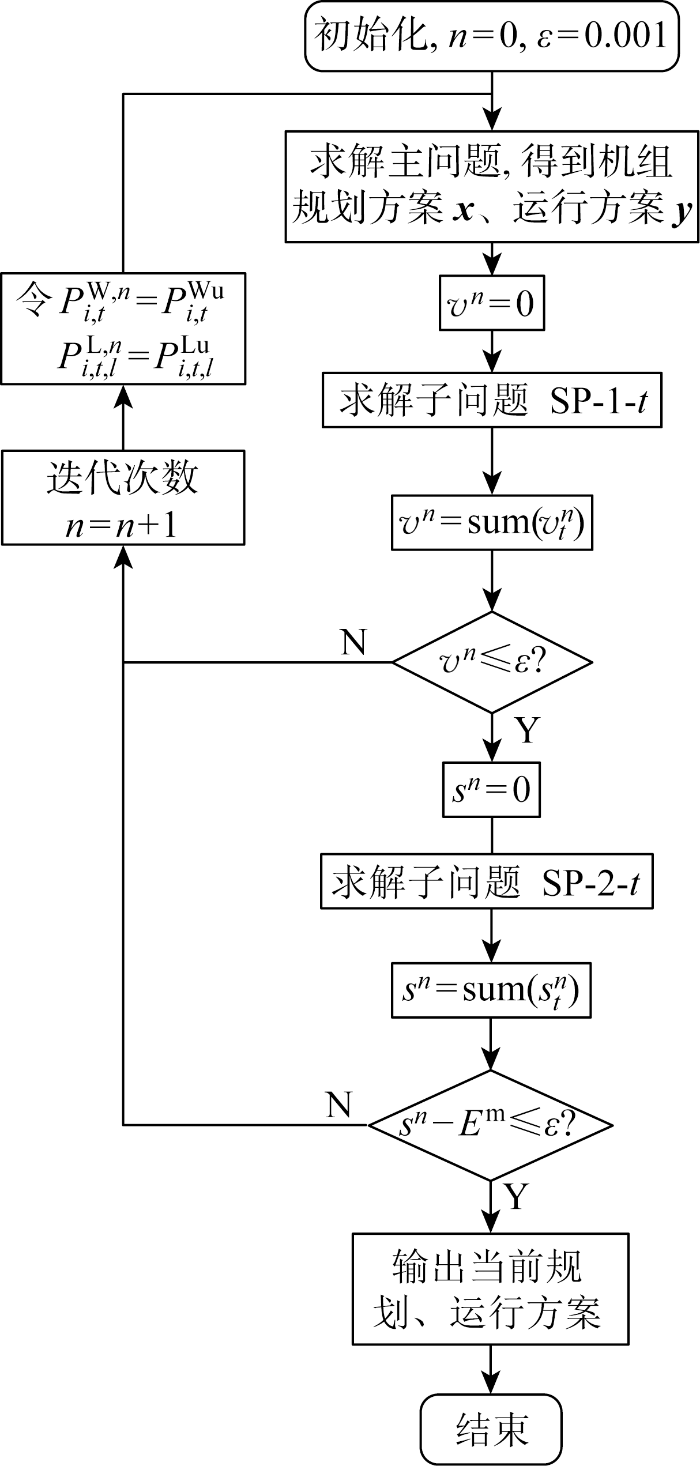
基于时间解耦之后的两阶段鲁棒规划模型求解流程如图1所示.具体求解步骤如下:

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 两阶段鲁棒规划模型求解流程

Fig.1 Flow chart of two stage robust planning model

步骤1 初始化.令n=0,设置收敛精度ε=0.001.

步骤2 求解主问题模型得到线路规划方案和运行方案.

步骤3 根据步骤2得到的线路规划方案和运行方案,分别计算子问题SP-1-t,并计算目标函数 $v_{t}^{n}$ 之和得到vⁿ,若vⁿ≤ε,则转步骤4,否则令 $P_{i, t}^{W, n}$ = $P_{i, t}^{W u}$ , $P_{i, t, l}^{L, n}$ = $P_{i, t, l}^{L u}$ ,n=n+1返回步骤2.

步骤4 根据主问题得出的线路规划方案和运行方案,分别计算子问题SP-2-t,并计算目标函数 $s_{t}^{n}$ 之和得到sⁿ;若sⁿ-E^m≤ε,则当前规划结果和运行方案为最优解,转步骤5;若sⁿ-E^m>ε,则令 $P_{i, t}^{W, n}$ = $P_{i, t}^{W u}$ , $P_{i, t, l}^{L, n}$ = $P_{i, t, l}^{L u}$ ,n=n+1返回步骤2.

步骤5 输出结果,结束.

3 碳配额交易量上下限计算

合理设置碳配额交易量E^m有利于降低系统碳排放总量,如果设置不合理,则可能导致该约束不起作用或者导致模型不存在可行解.因此,主要计算碳配额交易量的上限 $E_{m a x}^{m}$ 和下限 $E_{m i n}^{m}$ .

3.1 碳配额交易量上限

碳配额交易量上限定义为当碳配额交易E^m≤ $E_{m a x}^{m}$ 时,随着碳配额交易量的上升,总成本随之减少;当E^m> $E_{m a x}^{m}$ 时,总成本保持不变,即碳配额交易量相关的约束不起作用.

碳配额交易量上限计算流程如下:

步骤1 忽略约束式(18)、式(26)和子问题模型SP-2-t,使主问题模型MP与子问题模型SP-1-t迭代求解,得到最优投资方案与运行方案以及主模型得到的目标函数值C,并计算此时的碳配额交易量,记为 $E_{m a x, 1}^{m}$ .

步骤2 根据步骤1计算得到的投资方案和运行方案,求解子问题模型SP-2-t,得到最优函数值 $s_{t}^{n}$ 并对其求和得到sⁿ,记当前场景为最坏场景,并记 $E_{m a x, 2}^{m}$ =sⁿ.

步骤3 记 $E_{m a x}^{m}$ =max{ $E_{m a x, 1}^{m}$ , $E_{m a x, 2}^{m}$ }即为碳配额交易量的上限.

3.2 碳配额交易量下限

碳配额交易量下限定义为碳配额交易量E^m< $E_{m i n}^{m}$ 时,由于碳排放限值过低而使系统模型不存在可行解;当E^m≥ $E_{m i n}^{m}$ 时,目标函数总费用将随E^m的增大而减小,此时的碳交易量称为碳交易量下限,记为 $E_{m i n}^{m}$ .

根据定义可以得到计算碳交易量下限的模型MP-1为

(33)

\begin{matrix} E_{m i n} = m i n (E^{a} - E^{b}) \end{matrix}

其约束条件包括式(2)~(3)和式(11)~(17)、(19).

碳配额交易量下限计算流程如下:

步骤1 初始化,令n=0.

步骤2 求解模型MP-1,得到规划方案和运行方案,MP-1表示碳交易成本.

步骤3 将步骤2得到的规划方案和运行方案代入SP-1-t中;若 $v^{n} > ε, 则令 P_{i, t}^{W, n} = P_{i, t}^{W u}, P_{i, t, l}^{L, n} = P_{i, t, l}^{L u}$ 为最坏场景,继续求解MP-1,令 $n = n + 1; 若 v^{n} \leq ε,$ 则转下一步.

步骤4 令E^m= $E_{m i n}^{n}$ ,将步骤2得到的规划方案、运行方案代入SP-2-t中计算;若sⁿ-E^m>ε, 则令 $P_{i, t}^{W, n}$ = $P_{i, t}^{W u}$ , $P_{i, t, l}^{L, n}$ = $P_{i, t, l}^{L u}$ 为最坏场景,继续求解MP-1,令n=n+1;若sⁿ-E^m≤ε,则输出当前结果 $E_{m i n}^{n}$ ,并令E^m= $E_{m i n}^{n}$ ,即为碳配额交易量下限.

4 算例分析

以改进的IEEE-RTS 24节点系统^[25]进行案例分析,来验证所提模型与方法的有效性.在该案例中,规划目标年为10年,贴现率取0.12,规划年的负荷在原有基础上扩大1.25倍,备选线路走廊为已有廊道,新建线路上限为3条,每千米造价为60万美元,在母线节点1和母线节点2处分别增加一个100 MW的燃气机组,在母线节点3、10、19、22处分别增加一个100 MW的风电机组.风电、负荷预测误差分别为30%、20%.设区域碳排放额因子为0.8 t/(MW·h);对于传统燃煤机组来说装机容量越大单位电量二氧化碳排放量相对越小,装机容量300 MW以上的机组单位发电量二氧化碳排放量为0.83 t/(MW·h),300 MW以下的机组单位二氧化碳排放量为0.979 t/(MW·h);燃气机组单位二氧化碳排放量为0.4 t/(MW·h),碳交易价格为25 美元/t,节点切负荷成本为100 美元/(MW·h),机组出力成本系数参考文献[26].求解在MATLAB 2021a平台上完成,并调用Gurobi求解器辅助求解.

4.1 方案对比分析

首先将碳交易量约束松弛,分析以下两种情况:①传统规划模型为在规划模型的目标函数中不计入碳交易成本与碳排放相关约束,而是在规划后计算模型的碳交易与碳排情况,并将碳交易成本计入总成本中;② 低碳规划模型为在规划时模拟水平年的碳交易情况与碳排情况,即目标函数中计入碳交易成本.两种方案结果对比如表1所示.

表1 传统规划和低碳规划对比

Tab.1 Comparison between traditional planning and low carbon planning

模型类别	线路规划方案	投资成本/ 万美元	机组运行成本 ×10^-6/美元	切负荷成本/ 万美元	碳交易成本/ 万美元	总成本 ×10^-6/美元
传统规划	1~2,1~5,6~10,7~8,14~16,21~22	1 391	360.55	166	2 366	399.78
低碳规划	1~5,6~10,7~8,14~16,21~22	1 359	363.44	216	1 717	396.36

新窗口打开| 下载CSV

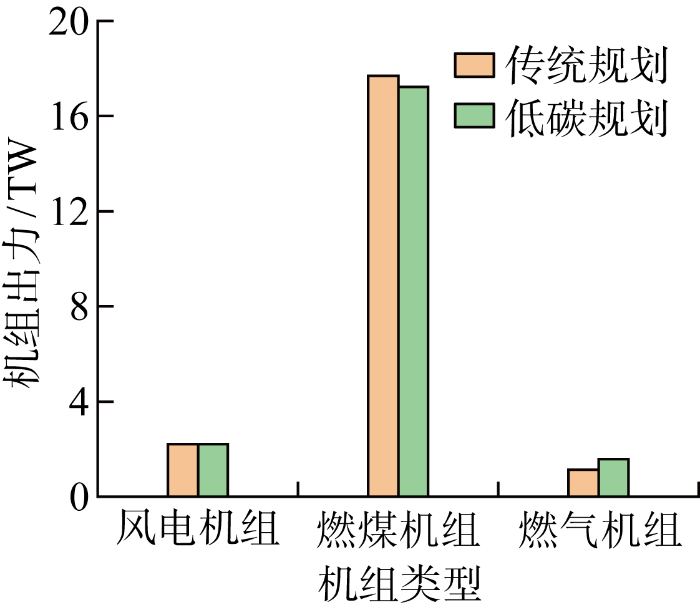
表1中传统规划结果和低碳规划结果是模拟运行一年所对应的等年值费用.在传统规划中新建线路6条,低碳规划中新建线路为5条,传统规划中比低碳规划增加线路1~2.在运行成本上,低碳规划机组运行成本比传统规划运行成本高出289万美元,切负荷成本高出50万美元,但是由于碳交易成本降低649万美元,线路投资成本低32万美元,所以在总成本上低碳规划比传统规划降低342万美元.低碳规划中机组运行成本增高的原因从图2可以看出,在计及碳交易成本时单位电量碳排放较低的燃气机组出力增大,但是其发电成本高导致低碳规划的机组运行成本高.由对比结果可得出,考虑计及碳交易的低碳规划具有明显的经济性.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 各类机组出力

Fig.2 Output of various units

4.2 碳配额交易量对规划结果的影响

根据第3节中对碳配额交易量的计算,得出在本文考虑的模型中碳交易量的上限为 686 868.6 t,下限为 559 890.7 t.

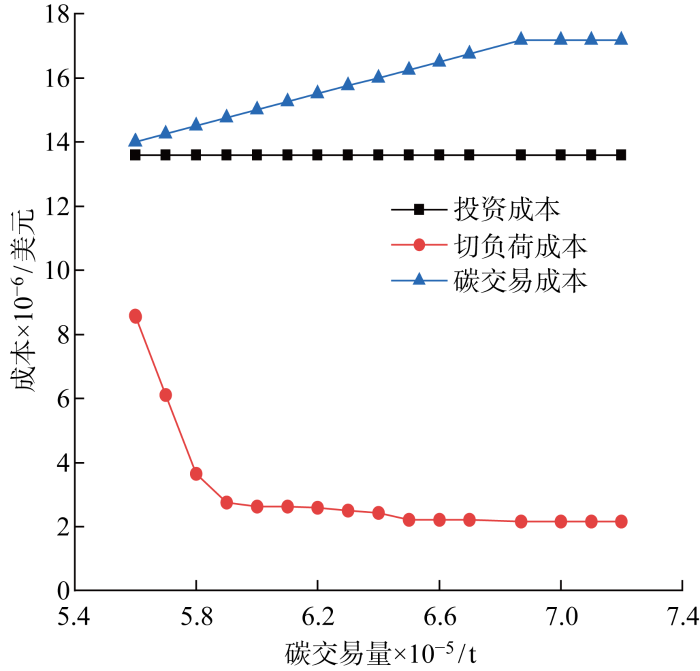
在此范围内选取不同的碳配额交易量E^m,分析不同的碳配额交易量E^m对结果的影响.由于单位碳配额交易成本是固定系数,所以在图3中随着碳配额交易量的不断增加,碳配额交易成本呈线性增加;线路投资成本一直保持不变;切负荷惩罚成本随着碳配额交易量增大而减小,说明切负荷量也在减小,保证了系统的可靠性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同碳配额交易量下各类成本

Fig.3 Cost at different trading carbon quotas

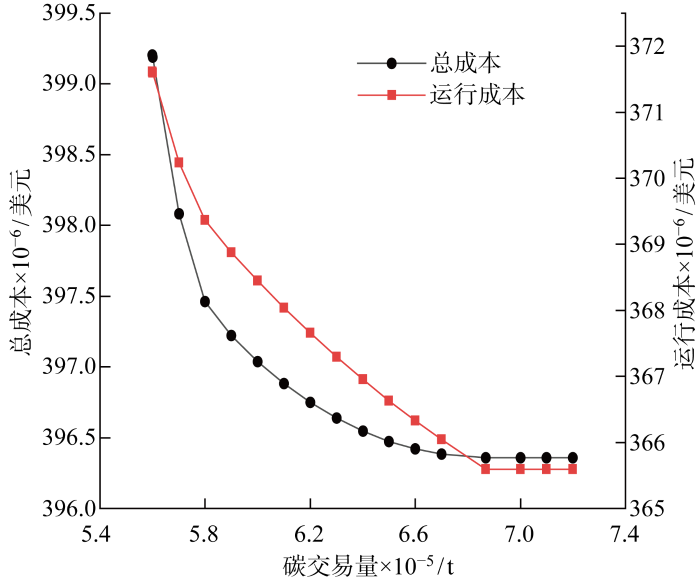
为验证第3节所提碳交易量计算模型,如图4所示,在碳配额交易量E^m大于下限 559 890.7 t、小于上限 686 868.6 t 时,随着碳配额交易量E^m的增加,系统的总成本与运行成本随之减小,在交易量达到上限 686 868.6 t 后保持不变.总成本的变化趋势证明所提模型的可靠性.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同碳配额交易量时运行成本和总成本

Fig.4 Operating cost and total cost at different carbon quota trading volumes

如图3~4所示,当碳配额交易量达到上限时,投资成本、切负荷成本、碳交易成本、运行成本、总成本不再随碳配额交易量变化,即碳配额交易量约束被松弛.

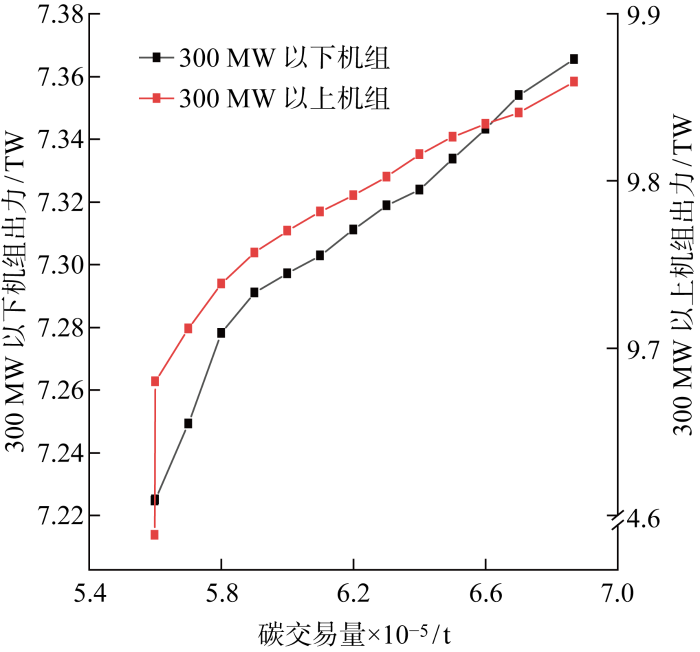
由于300 MW以下机组单位碳排放量和平均成本比300 MW以上的机组高、燃气机组比传统燃煤机组单位发电量碳排放量低但成本高,所以从图5~6中可以看出,随着碳配额交易量的增加,为了达到最优结果,出力成本较高的燃气机组出力降低,燃煤机组出力增加;由于风电出力不计成本和碳排放量,所以风电出力无变化.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 风电和燃气机组出力

Fig.5 Output of wind and gas units

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 燃煤机组出力

Fig.6 Output of coal-fired unit

4.3 不同碳交易价格对规划结果的影响

进行碳交易价格分析时不需考虑交易量约束,因为碳交易价格不同时,模型碳配额交易量的上下限不一致,参数设置不合理可能会造成模型无解的情况发生.

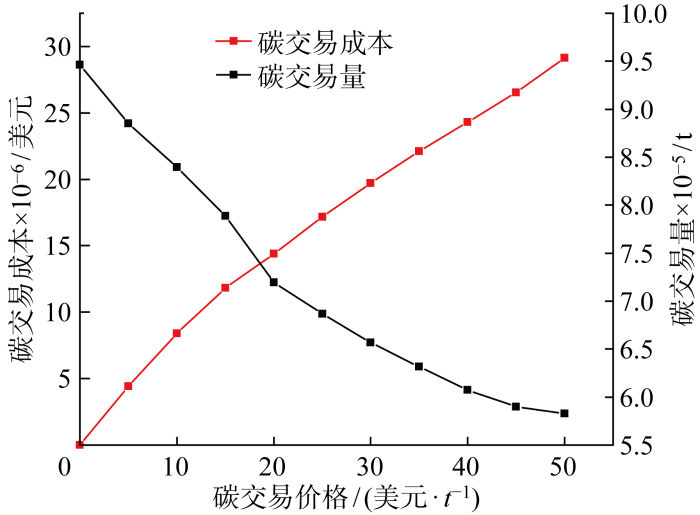
当碳交易价格不同时,在最优目标值处的碳交易量也不同.从图7可以看出,随着碳交易价格提升,碳配额交易量逐渐减少,但是由于价格升高,而且单位发电量碳排放量较低的机组出力调节范围有限,所以碳配额交易成本逐渐增加.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同碳价格对碳交易量的影响

Fig.7 Influence of different carbon prices on carbon trading volume

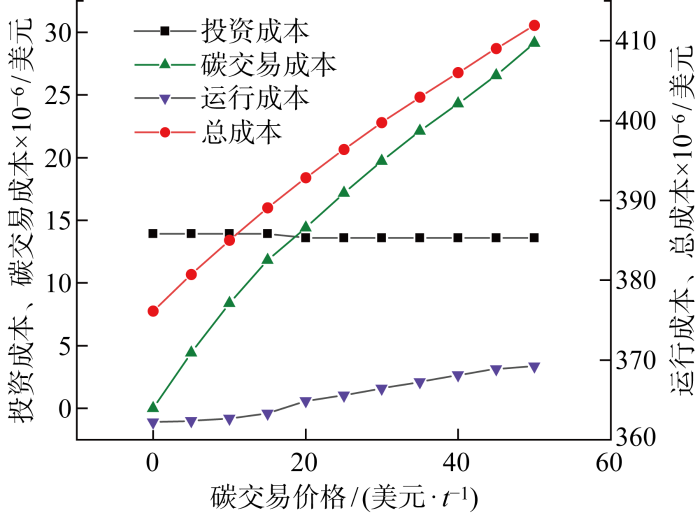
同时,不同碳交易价格也会影响系统的各项成本.如图8所示,随着碳交易价格的增加,投资成本在碳交易价格为15美元/t 之后下降然后保持不变;碳交易成本、运行成本呈增加趋势.因为投资成本变化趋势较小,所以在总成本上呈增加趋势.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同碳交易价格对规划结果影响

Fig.8 Influence of different carbon trading prices on the planning results

5 结论

主要研究考虑碳交易的输电网规划模型.首先,以两阶段鲁棒规划模型处理不确定性,利用R&ED法对子问题解耦加快求解速度,再用C&CG算法求解两阶段鲁棒模型.其次,在考虑碳配额交易量约束时,可能会因为约束参数设置的不合理导致模型无解或者约束被松弛不起作用,对此考虑风-荷不确定的同时对碳配额交易量上下限进行计算.最后,以改进的经典算例系统进行验证分析,得出结论如下:

(1) 相比于传统的规划方案,考虑碳交易量自适应决策的输电网鲁棒规划模型实现了规划方案在经济性和低碳性方面的协同优化.

(2) 所提模型的碳交易量上限为 686 868.6 t、下限为 559 890.7 t,在此范围内随着碳交易量的增加,总成本随之降低,同时也提高了系统的可靠性,从而验证了所提模型的有效性.

(3) 碳交易价格也会对系统的碳排放量有影响,确定合理的价格有助于平衡低碳性和经济性.

本研究为固定碳交易价格下的电力系统规划,未来将在阶梯碳交易价格和低碳电源规划方面进一步研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

习近平

在第七十五届联合国大会一般性辩论上的讲话

[EB/OL]. (2020-09-22)[2022-11-22]. https://baijiahao.baidu.com/s?id=1678546728556033497&wfr=spider&for=pc.

URL [本文引用: 1]

Jinping

Speech at the general debate of the 75th session of United Nations General Assembly

[EB/OL]. (2020-09-22)[2022-11-22]. https://baijiahao.baidu.com/s?id=1678546728556033497&wfr=spider&for=pc.

URL [本文引用: 1]

[2]

康重庆, 杜尔顺, 李姚旺, 等.

新型电力系统的“碳视角”: 科学问题与研究框架

[J]. 电网技术, 2022, 46(3): 821-833.