锂离子电池具有能量密度高、循环寿命长等优点,在新能源电力系统的产能-储能-供能工业链中承担着能量存储、功率缓冲、稳压等多项重要任务.时刻掌握锂离子电池的健康状态(State of Health,SOH),不仅有助于保障电池系统安全运行,还能推断出储能系统最大储能容量,指导新能源电力系统中发电、用电环节的能量调度规划,最大限度发挥电池系统的储能潜力.SOH通常被定义为电池当前最大可用容量与额定容量的比值,目前SOH估计方法主要分为基于模型的方法和数据驱动方法.
基于模型的方法根据锂离子电池物理或化学原理建立电池模型,通过辨识模型中的某些关键参数推断电池的健康信息.现有研究中常用的模型为电化学模型[1]和等效电路模型(Equivalent Circuit Model,ECM)[2],其中等效电路模型方法通常使用带有遗忘因子的递归最小二乘(Forgetting Factor Recursive Least Square,FFRLS)算法辨识模型参数[3],例如文献[4-5]中使用FFRLS算法辨识一阶Thevenin模型参数,结合线性模型推算SOH.文献[6]中使用在线电化学阻抗谱(Electrochemical Impedance Spectroscopy,EIS)技术识别电池内部阻抗,并建立了以电池欧姆内阻、第一和第二极化电阻以及温度为输入的非线性SOH估计模型.
借助深度学习模型的自动特征提取能力,深度学习方法无需显式地提取健康因子便能完成SOH估计.事实上,只要将可测量数据组织成合适的数据结构,几乎所有的深度学习模型都可用于SOH估计[15],例如文献[16]中以恒流-恒压充电过程中的电压、电流、温度曲线为卷积神经网络(Convolutional Neural Network,CNN)的输入,以容量为输出进行SOH估计,文献[17]中搭建以充电时间节点和电压曲线线下面积为输入,SOH为输出的长短期记忆-全连接(Long Short-Term Memory-Fully Connect,LSTM-FC)网络.深度学习方法无需额外的数据预处理或健康因子提取,集成度较高.
基于模型的方法根据实时采集的信号在线辨识模型参数,适合在线应用,但由于缺乏必要的泛化手段,通常仅适用于特定工况.数据驱动方法的准确性依赖于大量高质量训练数据,应用阶段则必需得到有效完整的测量数据才能提取可靠的健康因子.然而,现实中很难保证在每个充放电循环都能采集到完备的数据,特别是电动汽车(Electric Vehicles,EVs)和移动电子设备,充电和放电时长通常是随机和短暂的,这导致了众多数据驱动算法不适用于随机的荷电状态(State of Charge,SOC)范围[18].综合而言,基于模型的方法和数据驱动方法都对工况具有一定的敏感性,导致SOH估计精度不足或适用范围受限.
针对上述问题,提出一种基于模型和数据驱动融合的锂离子电池SOH估计方法,该方法在保证估计精度的同时,对随机的SOC范围具有较强的容忍性.相比于放电过程,充电过程更加稳定,可控性更好,因此基于恒流充电过程估计电池SOH,具体为利用两个在线滤波器辨识二阶Thevenin模型的各项参数,据此构建一种工况不敏感的新型动态健康因子,结合稀疏高斯过程回归(Sparse Gaussian Process Regression,SGPR),以较低的计算复杂度实现SOH的在线估计.
1 实验设计及引用数据集
1.1 镍锰钴酸锂电池老化实验
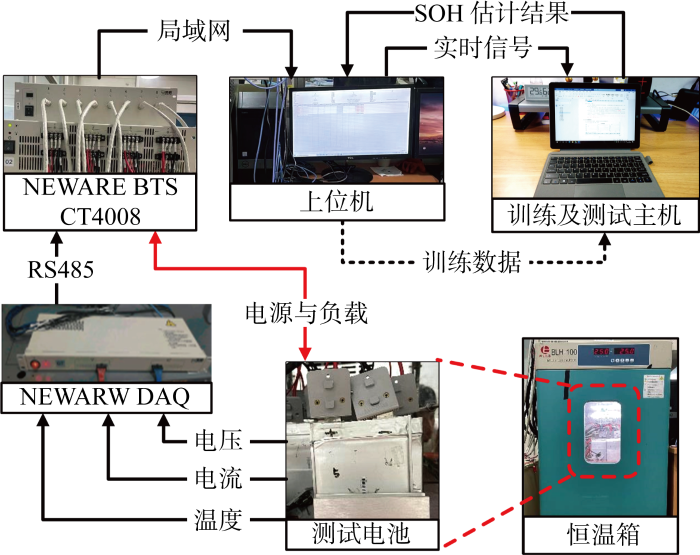
实验室搭建的锂离子电池老化实验台架由博翎BLH-100电池测试恒温箱、Neware CT-4008-5 V 20 A 电池测试系统、上位机等设备组成,其拓扑结构如图1所示.
图1
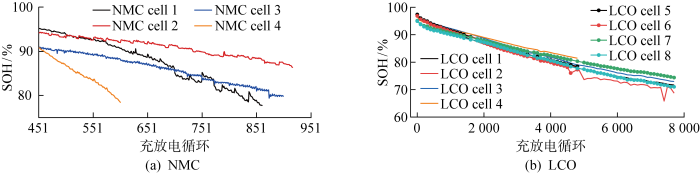
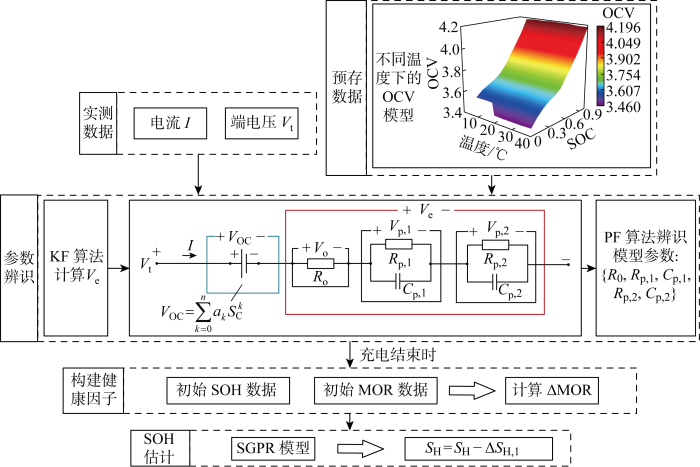
测试电池为4节镍锰钴酸锂(Lithium Nickel Manganese Cobalt Oxide,NMC)软包电池,额定电压为3.7 V,额定容量为10 A·h.4个电池分别编号为NMC cell 1、cell 2、cell 3和cell 4.老化实验开始之前,在环境温度为5和25℃的条件下进行伪开路电压(Open Circuit Voltage,OCV)测试,用于确定该型号电池在不同温度下的OCV模型.实验中,首先将4个电池串联,循环充放电以加速老化.450次循环后解除串联,按恒流(Constant Current,CC)模式充电、放电,各自独立地执行老化循环,恒流充电截止电压为4.2 V,恒流放电截止电压为3.0 V,4个电池的充放电倍率及环境温度各不相同,如表1所示.每次充电和放电切换时将电池静置15 min,使其达到近稳态.数据采集模块将各电池端电压、电流和温度等信息发送到上位机, 上位机通过安培-时间积分计算出电池实际容量,从而确定电池的真实SOH.
表1 NMC电池老化工况
Tab.1
| 电池编号 | 充电 电流/A | 放电 电流/A | 环境 温度/℃ | 循环次数 |
|---|---|---|---|---|
| NMC cell 1 | 5 | 10 | 25 | 410 |
| NMC cell 2 | 5 | 20 | 25 | 466 |
| NMC cell 3 | 10 | 10 | 25 | 446 |
| NMC cell 4 | 5 | 10 | 5 | 150 |
1.2 LCO电池老化实验数据集
图2
2 动态健康因子提取
2.1 等效电路模型参数辨识
式中:VOC为开路电压,即电池正负极之间的电势差;SC为荷电状态;多项式参数α= [α0… αk… αn]由小电流OCV测试和多项式拟合确定;n为OCV模型阶数集合.需要注意的是,电池在不同温度下的OCV存在差异,因此需要在不同温度下进行OCV测试,记录多个OCV模型,在实际计算中视环境温度选取相应的OCV模型[22].定义恒流充电过程中的SOC为
式中:q 为电池当前存储的电量;q0为电池充电前的初始电量;CR为额定容量;I为恒定的充电电流;t为充电时间;恒流充电中q与t呈线性关系.受电池内部阻抗影响,电池端电压Vt和OCV之间存在差异,记该电压差异为Ve,可得到如下抽象电压模型:
Ve 综合反映了电池的内部阻抗特征,引入Ve的多项式模型:
式中:m为Ve多项式模型阶数集合.结合式(3)和(4),将多项式参数向量β=[β0β1 … βm]T 作为状态向量,Vt作为观测变量,Δq为步长,可得到如下状态空间方程,包括状态转移和观测方程:
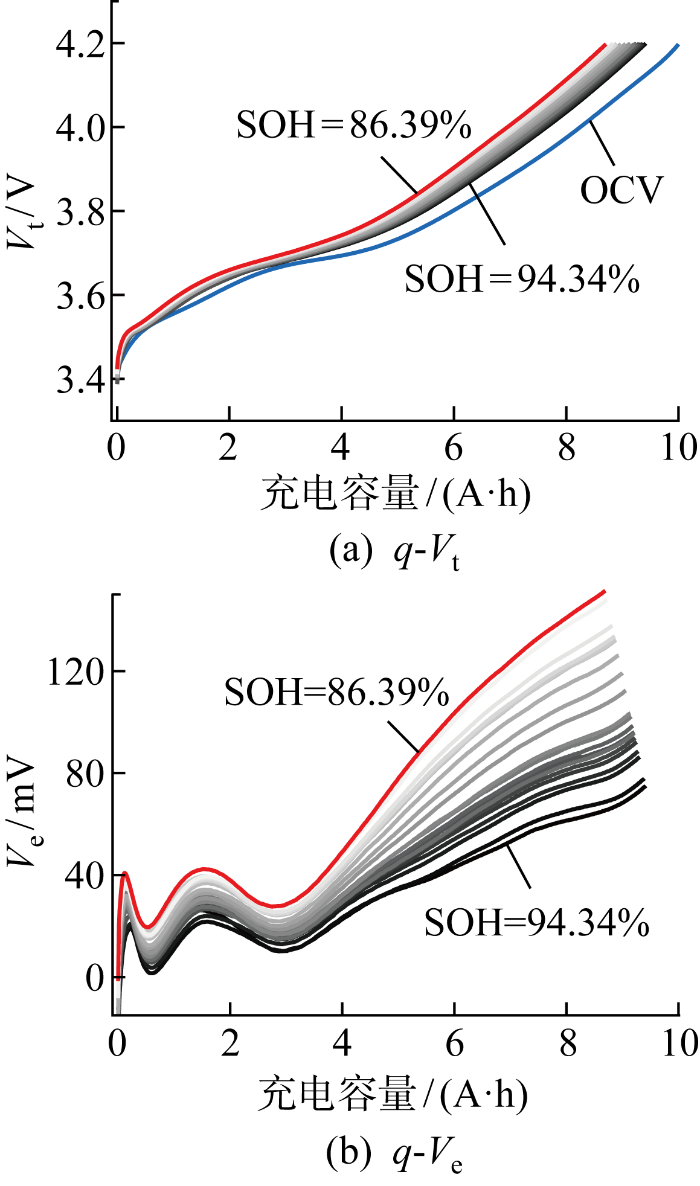
式中:Im+1表示m+1阶单位矩阵;步长Δq = IΔt,Δt为信号采集系统的采样周期;过程噪声ω和观测噪声ν均为高斯白噪声.式(5)和(6)构成了简单的线性时变系统,为保证在强烈测量噪声干扰下仍能获得光滑的Ve曲线,使用卡尔曼滤波(Kalman Filter,KF)算法对上述系统进行滤波处理.取OCV模型阶数n和Ve多项式模型阶数m为9,不同SOH下经KF滤波后的q-Vt和q-Ve曲线如图3所示,其中图3(a)中包括本文使用的NMC电池OCV模型(NMC cell 1).可以看到,随着SOH的降低,Vt更快地达到截止电压,q-Ve曲线的整体轮廓不断上移,显然,q-Ve曲线与SOH之间存在隐含联系.
图3
图3
q-Vt和q-Ve曲线变化趋势(NMC cell 1)
Fig.3
Changing trend of q-Vt and q-Ve curves (NMC cell 1)
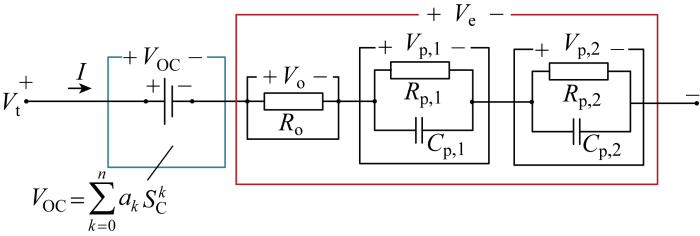
Ve的变化轨迹十分复杂,实验结果表明一阶Thevenin模型无法很好地模拟Ve的变化轨迹,因此采用二阶Thevenin模型对Ve进行物理建模,如图4所示.模型中各组成部分的含义如下:Ro、Rp, 1和Rp, 2分别为欧姆内阻、第一和第二极化电阻;Cp, 1和Cp, 2分别为第一和第二极化电容;Vo、Vp,1和Vp,2分别为欧姆内阻电压、第一和第二极化电压.
图4
将外界施加的恒定充电电流视作对图4所示系统的阶跃激励,可以得到Ve的阶跃响应函数:
式中:Vp(0)为充电开始前的极化电压,如果电池在充电前被充分搁置并达到稳态,Vp,1(0)和Vp,2(0)可视为0.以等效电路模型的参数向量x=[R0Rp,1Cp,1Rp,2Cp,2]T为状态向量,Ve为观测变量,将t替换为q,Δq为步长,可写出如下状态转移和观测方程:
考虑式(9)的强非线性,使用粒子滤波算法(Particle Filter,PF)在线辨识参数向量x,具体计算流程及算法1如下:
(1) 初始化.q=q0,即t=0时,生成N=200个粒子(N为训练样本个数):X'(q0)=
(2) 权重更新.计算每个粒子的权重wi(q)=exp[-(Ve(q)-
(3) 重采样.计算有效样本量Neff=1/
(4) 状态输出.输出状态向量期望值
算法1 残差重采样
输入:X'={xi,
1. 计算各粒子被复制次数:
2. 计算复制后的粒子总数:Nc=
3. 复制粒子,得到新的粒子集合:
4. 计算剩余粒子数:Nr=N-Nc.
5. 各粒子残差权值
6. 生成Nr个均匀随机数:uk∈
7. 若
输出:
基于KF-PF的模型参数辨识算法有着较强的鲁棒性,即使在强烈的噪声干扰下,KF算法依然能够很好地滤除Ve的噪声,使得PF算法始终在无噪或低噪环境下完成参数辨识.
2.2 动态健康因子提取
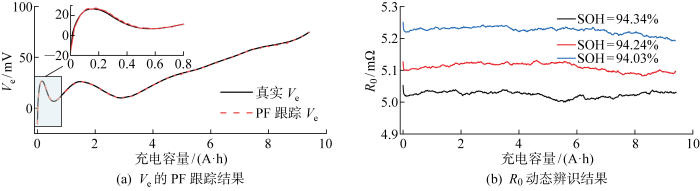
图5(a)显示了NMC cell 1第451次循环Ve的PF轨迹跟踪结果.可以看到,PF算法跟踪得到的q-Ve 曲线与实际的q-Ve曲线高度契合,说明二阶Thevenin模型配合PF算法能够很好地捕捉到电池内部阻抗的变化情况.文献[3]中通过FFRLS算法辨识出动态工况下的R0,发现q-R0曲线随着SOH的减小呈现上升趋势,本文也得到了相同结论,如图5(b)所示.电池负极的固体电解质界面膜(Solid Electrolyte Interphase,SEI)增厚是R0增大的主要原因之一,而生成SEI膜需要消耗一定数量活性锂离子,导致了电池容量不可逆衰减[23].可见,根据R0估计SOH直接而有效.
图5
图5
Ve跟踪结果及R0辨识结果(NMC cell 1)
Fig.5
Tracking result of Ve and identification results of R0 (NMC cell 1)
从图5(b)可以看到,R0的数值随着q的变化不断波动,取一定SOC范围内R0的平均值(Mean Ohmic Resistance,MOR)作为考察对象以缓解这种波动,定义为
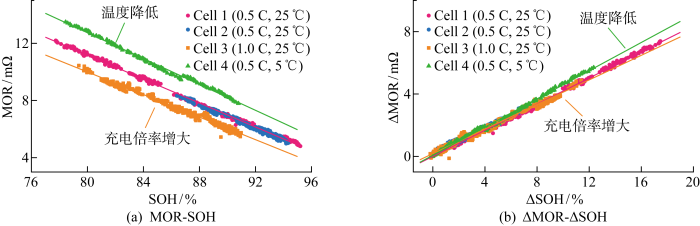
式中:n=(q-q0)/Δq,由式(2)可以方便地将q换算为SOC.虽然MOR可以直接用于SOH估计,但MOR受充电倍率和环境温度影响较大,不同工况下的MOR与SOH之间的映射关系存在差异,如图6(a)所示,即基于MOR的SOH估计方法对工况具有敏感性.为弱化MOR对工况的敏感性,使用MOR的增量ΔMOR作为健康因子,容量衰减率ΔSOH为估计目标,定义方法分别为
式中:RM, i(q1~q2)为第i次循环时电池电量在 q1~q2之间的MOR;RM,1(q1~q2)为电池在初次使用时电量在q1~q2之间的MOR;SH,1为电池初次使用时的SOH;C1为初始容量.
图6
在前450次循环中,4个电池被串联进行充放电,将第451次循环作为初始循环,并不影响算法推理的正确性.不同工况下ΔMOR-ΔSOH的线性关系如图6(b)所示.
使用皮尔逊相关系数评估ΔMOR与ΔSOH之间的线性相关性,其计算公式为
表2 健康因子的相关性分析结果
Tab.2
| SOC范围/% | 工况 | ||
|---|---|---|---|
| 0.5 C,25 ℃ | 1 C,25 ℃ | 0.5 C,5 ℃ | |
| [10,20) | 0.9911 | 0.9909 | 0.9910 |
| [20,30) | 0.9921 | 0.9930 | 0.9951 |
| [40,50) | 0.9938 | 0.9931 | 0.9955 |
| [50,60) | 0.9938 | 0.9931 | 0.9955 |
| [20,40) | 0.9938 | 0.9931 | 0.9955 |
| [40,60) | 0.9938 | 0.9931 | 0.9955 |
| [20,50) | 0.9937 | 0.9930 | 0.9955 |
| [30,80) | 0.9938 | 0.9931 | 0.9953 |
3 基于稀疏高斯过程回归的SOH估计
GPR作为一种非参数概率预测模型,在锂离子电池SOH估计领域取得了成功应用.从一次充电过程中,按不同SOC范围可以提取不同的ΔMOR,直接使用GPR模型进行SOH在线估计时计算成本过大.因此使用SGPR模型作为在线映射模型,降低算法的计算复杂度.该模型以ΔMOR为输入变量x,以ΔSOH为预测变量y.从标准工况下的锂离子电池老化数据集中提取ΔMOR和ΔSOH,构建训练样本集,记为{XN×1,YN×1}.
3.1 高斯过程回归
考察如下带噪声的抽象回归模型:
式中:f为x与y之间的隐含函数,在GPR中,f被视为一个高斯过程;σn为噪声标准差.假设f的均值函数为零函数,则对于训练样本集{X,Y},由高维高斯分布的可加性可得:
式中:KX,X为Y的协方差矩阵.本文选用平方指数协方差函数计算KX,X,即
式中:k(xi, xj)为KX,X的第i行第j列元素;
式中:IN表示N阶单位矩阵.使用共轭梯度法可方便地优化Θ.GPR模型训练完成后,可根据新的输入x*得到y的预测y*.首先建立Y和y*的联合概率分布:
根据贝叶斯定理,可求得y*的后验概率分布:
式中:
y*的点估计由μ*给出,并且可计算出f*的区间估计,95%置信区间为
3.2 稀疏高斯过程回归
式(17)包含N×N方阵求逆,GPR模型的训练时间复杂度为O(N3),式(20)和(21)包含3个N阶矩阵连乘,单次预测时间复杂度到达了O(N2),空间复杂度为O(N2)[24].为降低在线预测复杂度,SGPR从训练样本中挑选少量诱导点集替代完整训练集合,求y的无噪预测f(x*)的后验概率分布,记诱导点集为
诱导点集的位置可以均匀地分布在训练输入X的范围内,引入诱导输入假设:在给定U的情况下, f(X)和f(x*)条件独立[24](以下简记为f和f*),从而f、f*和U的联合概率分布为
上式右侧3项均为指数函数,其乘积也是指数函数,另外为f引入完全独立训练条件(Fully Independent Training Condition,FITC)假设[25],可得f、f*和U的联合概率分布具体形式:
结合贝叶斯定理和矩阵求逆引理,可得到f*的近似分布:
式中:
3.3 基于ΔMOR和SGPR的SOH估计流程
基于ΔMOR和SGPR的SOH估计方法包括离线训练和在线应用两个阶段.离线训练阶段收集标准工况下锂离子电池老化实验数据,从中提取多种SOC范围内的ΔMOR,计算每个循环的ΔSOH,构建训练数据集合,并完成GPR模型超参数优化.在训练阶段使用全部训练样本,保证超参数得到充分优化,优化后的参数可直接用于SGPR模型.在线应用阶段根据实测的q-Vt曲线辨识ΔMOR,充电结束时将其输入SGPR模型,得到ΔSOH估计值,经过式(12)换算即可完成SOH在线估计,在线实施流程如图7所示.
图7
4 结果与讨论
使用平均绝对误差(Mean Absolute Error,MAE)和均方根误差(Root Mean Squared Error,RMSE)评价计算结果的准确性,计算方法为
式中:
4.1 标准工况验证
使用NMC cell 1作为训练电池,提取该电池每个循环中8种典型SOC范围内的ΔMOR作为训练数据输入集,其对应循环的ΔSOH作为训练数据输出集,使用MATLAB GPML[26]训练模型超参数,SGPR模型诱导点个数设置为500.
表3 GPR和SGPR模型计算耗时及误差统计
Tab.3
| 指标 | 训练 | 测试 | |
|---|---|---|---|
| 常规GPR | SGPR | ||
| 样本数 | 410×8 | 466×8 | 466×8 |
| 计算时长/s | 552 | 639 | 8 |
| MAE/% | 0.1573 | 0.2631 | 0.2629 |
| RMSE/% | 0.2027 | 0.3183 | 0.3182 |
图8
图8
标准工况下GPR和SGPR的估计结果(NMC cell 2)
Fig.8
Estimation results of GPR and SGPR under standard working condition (NMC cell 2)
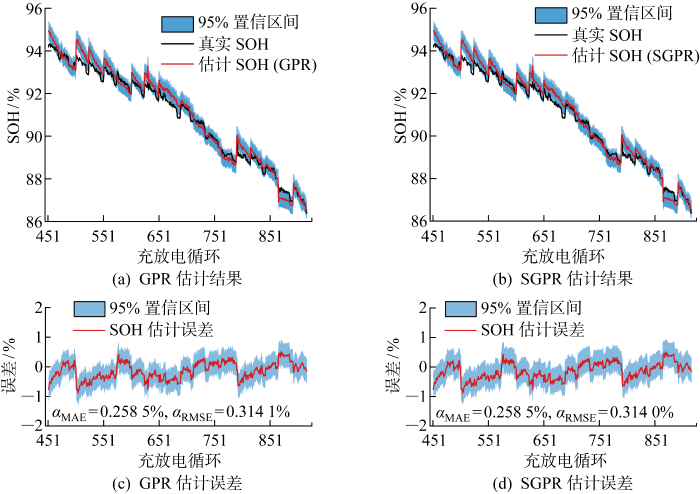
GPR模型预测结果的MAE和RMSE分别为 0.263 1% 和 0.318 3%,SGPR模型分别为 0.262 9% 和 0.318 2%,与常规GPR模型相比几乎没有变化.训练样本数达到了 3 280 个,GPR模型每次预测都面临巨大的计算量,而SGPR模型每次预测仅需考虑500个诱导点,其预测总时间比GPR模型减少了98%以上.可见,对于大规模数据样本,SGPR模型不仅有着与GPR模型相当的预测精度,而且在计算效率上获得了巨大提升.
4.2 1 C充电倍率和5 ℃环境温度下的适用性
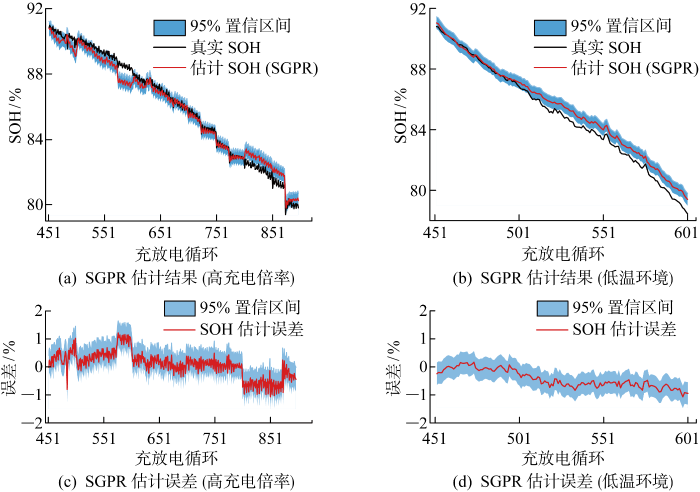
NMC cell 3 在1 C充电倍率和25 ℃环境温度下老化,可用于验证方法在高充电倍率下的适用性.NMC cell 4 在0.5 C的充电倍率和5 ℃环境温度下老化,可用于验证方法在低温环境下的适用性.沿用NMC cell 1训练的SGPR模型,20%~50%的SOC范围内的SOH估计结果及其95%置信区间如图9所示.
图9
图9
不同工况下SOH估计结果(NMC cell 3和4)
Fig.9
Estimation results of GPR and SGPR under different working conditions (NMC cell 3 and 4)
3个测试电池在8种典型SOC范围SOH估计误差统计结果如表4所示.可以看到,相比于标准工况,高倍率和低温环境下的SOH估计误差显著增大,但MAE均未超过0.46%,RMSE未超过0.54%.结合图6(b)可知,高充电倍率和低温环境下的电池老化速率存在差异,ΔMOR与ΔSOH之间的函数关系随工况变化发生了一定的偏移,由此导致了误差增大.总体而言,在无需额外训练新回归模型的前提下,基于ΔMOR和SGPR模型的SOH估计方法在1 C充电倍率和5 ℃环境温度下仍然适用.同时可以看到,SOC范围对SOH估计结果影响甚微,这显示了ΔMOR对SOC范围具有很好的鲁棒性,本文SOH估计方法在多种SOC范围内具有普遍适用性.与同领域的其他算法相比,SGPR模型的估计精度已经达到了领先水平[16,27 -28].
表4 不同工况下SOH估计误差统计
Tab.4
| SOC范围/% | MAE/% | RMSE/% | |||||
|---|---|---|---|---|---|---|---|
| 0.5 C, 25 ℃ | 1 C, 25 ℃ | 0.5 C, 5 ℃ | 0.5C, 25 ℃ | 1 C, 25 ℃ | 0.5 C, 5 ℃ | ||
| [10, 20) | 0.269 8 | 0.399 4 | 0.458 9 | 0.329 8 | 0.516 2 | 0.538 8 | |
| [20, 30) | 0.267 6 | 0.398 6 | 0.457 0 | 0.326 5 | 0.515 5 | 0.536 7 | |
| [40, 50] | 0.265 4 | 0.397 8 | 0.455 1 | 0.323 4 | 0.514 9 | 0.534 6 | |
| (50, 60] | 0.263 3 | 0.397 0 | 0.453 4 | 0.320 4 | 0.514 2 | 0.532 7 | |
| [20, 40) | 0.261 5 | 0.396 3 | 0.452 3 | 0.317 7 | 0.513 6 | 0.531 9 | |
| [40, 60) | 0.259 8 | 0.395 6 | 0.450 6 | 0.315 6 | 0.513 2 | 0.530 7 | |
| [20, 50) | 0.258 5 | 0.395 3 | 0.449 4 | 0.314 0 | 0.512 9 | 0.530 4 | |
| [30, 80) | 0.257 6 | 0.395 2 | 0.448 9 | 0.312 9 | 0.512 7 | 0.530 4 | |
4.3 对不同电池类型的适用性
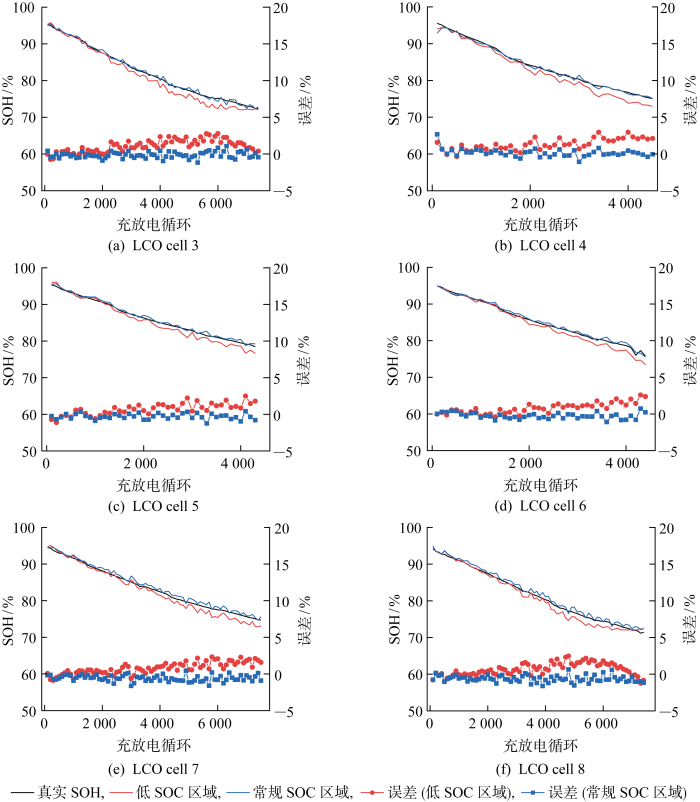
牛津大学LCO电池在1 C充电倍率和40 ℃环境温度下老化,使用该数据集验证方法对LCO类型电池的适用性.使用LCO cell 1和cell 2作为训练电池,LCO cell 3 ~ 8用作测试电池.特征提取和数据预处理方法与4.1节相同,训练数据共包含 1208 个样本(2个训练电池共151个循环,每个循环提取8种SOC范围内的ΔMOR),测试数据共包括 2928 个样本(6个测试电池共366个循环,每个循环提取8个SOC范围内的ΔMOR). 将SGPR模型的诱导点个数调整为200,其余参数与4.1节一致.10%~20%和50%~60%的SOC范围内,6个测试电池的SOH估计结果如图10所示,详细的误差统计结果如表5所示.
图10
表5 LCO电池SOH估计误差统计
Tab.5
| 电池编号 | 10%~20% SOC | 50%~60% SOC | |||
|---|---|---|---|---|---|
| MAE/% | RMSE/% | MAE/% | RMSE/% | ||
| LCO cell 3 | 0.8013 | 0.9870 | 0.3432 | 0.4223 | |
| LCO cell 4 | 0.9398 | 1.1011 | 0.3692 | 0.4622 | |
| LCO cell 5 | 0.9081 | 1.0812 | 0.3643 | 0.4511 | |
| LCO cell 6 | 0.8733 | 1.0893 | 0.3904 | 0.4654 | |
| LCO cell 7 | 0.9209 | 1.1196 | 0.4047 | 0.5120 | |
| LCO cell 8 | 0.8405 | 1.0691 | 0.4392 | 0.5416 | |
可以看到,在常规SOC范围内(50%~60%),本文SOH估计算法在多个LCO电池上均取得了较低的估计误差,最大的MAE和RMSE分别为LCO cell 8的 0.439 2% 和 0.541 6%.当SOC范围较低时(10%~20%),LCO电池的SOH估计精度大幅下降,最大的MAE和RMSE分别达到了LCO cell 4的 0.939 8% 和LCO cell 7的 1.119 6%.通过分析LCO电池的端电压曲线、Ve曲线以及增量容量曲线发现,LCO电池在一定次数循环约SH<81%后,端电压曲线和Ve曲线的轮廓发生明显变化, IC曲线在3.55 V(约SC=15%)附近的峰消失,这导致低SOC区域内,ΔMOR的辨识结果在SH=81%前后存在巨大差异,最终导致了SOH估计结果出现偏差,较宽的SOC区间或高SOC区域内的ΔMOR则不存在该问题.可见对于LCO电池,应尽可能在较宽SOC区间或高SOC范围内进行SOH估计,以避免出现较大误差.
4.4 与其他SOH估计算法相比
式中:T表示记录间隔,本文取T=10,即每10个采样点计算一次IC.使用两层滑动平均滤波处理IC曲线,窗口宽度经反复调试后选为13和5.分别以上述两类健康因子作为输入向量,SOH作为输出训练GPR模型.另外以ΔMOR为输入,ΔSOH为输出训练线性回归(Linear Regression,LR)模型、SVR模型、GPR模型和SGPR模型,其中LR和SVR使用MATLAB Regression Learner训练, GPR和SGPR使用MATLAB GPML训练,SVR、GPR和SGPR均选用平方指数核函数.上述6种方法的训练电池均为LCO cell 1和cell 2,测试电池均为LCO cell 3~cell 8.一条完整的充电曲线仅能提取一个ICP和CTEVI特征向量,因此基于这两类健康因子的SOH估计方法的测试样本仅有366个,基于ΔMOR的方法的测试样本共 2 928 个.图11为所述6种方法测试结果绝对误差的箱线图.此外,引用文献[16]中的研究成果作为深度学习方法的参考:完整的充电电压、电流和温度曲线为输入, SOH为输出,CNN为特征提取模型,测试电池为LCO cell 4和cell 8,共123个测试样本.上述7种SOH估计方法的误差统计[10,29]如表6所示.由表6可见,在健康因子方面,基于ICP和CTEVI特征向量的SOH估计方法有着较低的估计误差,但需要较宽的电压区间,不适用于随机电压区间情况[18,29],而基于ΔMOR的方法有着较强的工况容忍性.在特征映射算法方面,SGPR模型的精度高于LR、SVR,略高于GPR模型,这与NMC电池的计算结果一致,SGPR模型在精度上的可靠性再次得到验证.
图11
图11
不同SOH估计方法的误差分布(LCO cell 3~8)
Fig.11
Error distribution of different SOH estimation methods (LCO cell 3~8)
| 方法 | 编号 | 测试 样本量 | 所需电压 区间/V | MAE/ % | RMSE/ % |
|---|---|---|---|---|---|
| ICP+GPR | 1 | 366 | 3.2~4.1 | 0.4091 | 0.5331 |
| CTEVI+GPR | 2 | 366 | 3.55~4.15 | 0.2726 | 0.3212 |
| ΔMOR+LR | 3 | 2928 | — | 0.5593 | 0.7574 |
| ΔMOR+SVR | 4 | 2928 | — | 0.6013 | 0.7749 |
| ΔMOR+GPR | 5 | 2928 | — | 0.5163 | 0.6590 |
| ΔMOR+SGPR | 6 | 2928 | — | 0.4543 | 0.6108 |
| CNN | 7 | 123 | 3.0~4.2 | 0.9400 | - |
5 结语
针对以往锂离子电池SOH估计方法在可变工况下失效的问题,提出一种基于ECM和SGPR算法的SOH估计方法,并通过实验验证了该方法在多种充电工况下的适用性.首先采用KF-PF算法,在恒流充电过程中动态地辨识锂离子电池二阶Thevenin模型的各项参数,在此基础上提取可变SOC范围内平均欧姆内阻的增量为动态健康因子.皮尔逊相关性分析表明,ΔMOR在多种SOC范围内、0.5 C/1 C充电倍率以及25 ℃/5 ℃环境温度下与ΔSOH有着一致的线性相关性,由此提出了以ΔMOR为输入、ΔSOH为输出和SGPR为特征映射模型的在线SOH估计框架.为验证方法的准确性和鲁棒性,在不同工况下进行了算法测试.NMC和LCO电池的算法测试结果表明,该方法同时适用于0.5 C、1 C充电倍率和5、25、40 ℃环境温度工况,在最恶劣的情况下,本文方法的MAE不超过0.94%,RMSE不超过1.12%,与常规GPR模型相比,SGPR模型的计算时间减少了98%以上.该SOH估计方法兼具较高的准确性和较强的鲁棒性,与以往多种SOH估计算法相比,具有最佳的综合性能.
参考文献
Online capacity estimation for lithium-ion battery cells via an electrochemical model-based adaptive interconnected observer
[J].
Capacity attenuation mechanism modeling and health assessment of lithium-ion batteries
[J].
Online estimating state of health of lithium-ion batteries using hierarchical extreme learning machine
[J].
A novel data-model fusion state-of-health estimation approach for lithium-ion batteries
[J].
State-of-health estimation for LiFePO4 battery system on real-world electric vehicles considering aging stage
[J].
基于特征频率阻抗的锂离子电池健康状态评估
[J].
Health assessment of lithium-ion batteries based on characteristic frequency impedance
[J].
退役动力电池健康状态特征提取及评估方法综述
[J].
Research on feature extraction and SOH evaluation methods for retired power battery
[J].
Review on state-of-health of lithium-ion batteries: Characterizations, estimations and applications
[J].
Battery health prediction using fusion-based feature selection and machine learning
[J].
一种基于数据驱动与经验模型组合的锂电池在线健康状态预测方法
[J].
An online state of health prediction method for lithium batteries based on combination of data-driven and empirical model
[J].
Multistage state of health estimation of lithium-ion battery with high tolerance to heavily partial charging
[J].
基于双充电状态的锂离子电池健康状态估计
[J].
DOI:10.16183/j.cnki.jsjtu.2021.027
[本文引用: 1]

针对锂离子电池实际应用中存在不完全充放电而导致的充电起始点及截止点不确定问题,提出一种基于双充电状态因子的电池健康状态估计方法.搭建电池老化实验台架,采用8块镍钴锰锂离子电池进行老化实验;区别于传统单状态因子估计,选取不同老化阶段下恒压充电状态前端等时间差的电流平均值,以及恒流充电状态末端等幅值电压的充电时间构造健康因子;分析不同老化阶段实验电池的荷电状态-开路电压对应关系,通过理论推导及实验结果证明健康因子的正确性;建立具备强泛化能力的改进支持向量回归模型,并通过粒子群算法优化模型超参数.实验结果表明:所提双充电状态健康因子与电池老化衰减密切相关,所建立的改进支持向量回归模型可实时估计不同老化状态下的电池健康状态,具备容量局部回弹变化的表征能力,可作为一种有效的嵌入式电池管理系统健康状态估计方法.
State of health estimation of lithium-ion batteries based on dual charging state
[J].
Online state-of-health estimation of lithium-ion battery based on dynamic parameter identification at multi timescale and support vector regression
[J].
Data-driven battery state of health estimation based on random partial charging data
[J].
Convolutional neural network based capacity estimation using random segments of the charging curves for lithium-ion batteries
[J].
基于卷积神经网络的锂离子电池SOH估算
[J].
An approach to lithium-ion battery SOH estimation based on convolutional neural network
[J].
Transfer learning with long short-term memory network for state-of-health prediction of lithium-ion batteries
[J].
An adaptive battery capacity estimation method suitable for random charging voltage range in electric vehicles
[J].
Oxford battery degradation dataset 1
[DB/OL]. (
锂离子电池开路电压快速估计研究
[J].
DOI:10.3901/JME.2022.08.227
[本文引用: 1]

提出了一种离线式锂离子电池开路电压快速估计方法,在短时间内完成对需要经过长时间搁置才能稳定的开路电压的预估。建立了一个带有权重的电压弛豫模型并利用短时间内搁置电压数据和模型预估值构造损失函数,通过优化算法对损失函数中的参数进行寻优。电池开路电压预估流程包括对电池进行放电,搁置和开路电压预估,整个过程所需时间为30~40 min,即通过30~40 min就可以完成对需要进行数小时静置后才能稳定的开路电压的预估。为了检验此模型的适用性,设计了三元锂电池在不同电池荷电状态(State of charge,SOC)下、不同温度下和以不同的放电倍率放电下开路电压预估的试验,以及设计了电池容量循环衰减试验,并在电池容量衰减后继续对电池开路电压进行预估。试验结果表明,此模型可以通过短时间搁置便能精确地预测电池在不同SOC和不同温度下以及电池容量衰减后的开路电压。提出的离线式锂离子电池开路电压快速估计方法能够快速、准确地预估电池稳定开路电压,在电池SOC以及电池健康状态(State of health,SOH)等状态估计及电池容量估计方面有重要作用,能够大大缩短预估时间。
Fast estimation of open circuit voltage for lithium-ion batteries
[J].
DOI:10.3901/JME.2022.08.227
[本文引用: 1]

An off-line quick battery open circuit voltage estimation method which can be used to estimate the open circuit voltage that need to be stored for a long time to be stable in a short time was proposed. A voltage relaxation model with weights is established and the loss function is constructed by using the voltage data and the model estimated value to be put in a short period of time. Optimizing the parameters in the loss function by using optimization algorithm. The battery open circuit voltage estimation process including discharging, shelving, and estimating the open circuit voltage. The whole process about 30-40 min, that is, the estimation of the open circuit voltage that can be stable after several hours of standing can be completed in 30-40 min. In order to test the feasibility of this model, an experiment was designed for the open-circuit voltage estimation of LiNixCoyMn1-x-y battery under different state of charge(SOC), different temperature and different discharge rate, then an experiment was designed for the cyclic attenuation of battery capacity, and the open-circuit voltage of the battery was further estimated after the battery aging. The results show that the model can well estimate the open circuit voltage of the battery under different SOC and different temperature. The fast estimation method of battery open-circuit voltage proposed can predict the stable open-circuit voltage rapidly and accurately, which is of great significance in SOC, state of health(SOH) and battery capacity estimation and can greatly shorten the time of estimation.
State-of-health estimation of lithium-ion batteries by fusing an open circuit voltage model and incremental capacity analysis
[J].
A study on the dependency of the open-circuit voltage on temperature and actual aging state of lithium-ion batteries
[J].
High-temperature storage and cycling of C-LiFePO4/graphite Li-ion cells
[J].
A unifying view of sparse approximate Gaussian process regression
[J].
Online sparse Gaussian process regression using FITC and PITC approximations
[J].
Documentation for GPML Matlab Code version 4.2
[CP/OL]. (2020-07-14)[2022-06-10]. http://gaussianprocess.org/gpml/code/matlab/doc/.
Online state-of-health estimation of lithium-ion battery based on dynamic parameter identification at multi timescale and support vector regression
[J].
A hybrid drive method for capacity prediction of lithium-ion batteries
[J].
Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging condition
[J].