基于安全深度强化学习的电网有功频率协同优化控制

doi:10.16183/j.cnki.jsjtu.2022.358

基于安全深度强化学习的电网有功频率协同优化控制

周毅¹, 周良才^,¹, 史迪², 赵小英², 闪鑫³

1.国家电网有限公司华东分部,上海 200002

2. AINERGY, 美国圣塔克拉拉 95051

3.国电南瑞科技股份有限公司,南京 210024

Coordinated Active Power-Frequency Control Based on Safe Deep Reinforcement Learning

ZHOU Yi¹, ZHOU Liangcai^,¹, SHI Di², ZHAO Xiaoying², SHAN Xin³

1. State Grid East China Branch, Shanghai 200002, China

2. AINERGY, Santa Clara 95051, USA

3. NARI Technology Development Co., Ltd., Nanjing 210024, China

通讯作者: 周良才,高级工程师;E-mail:liangcaizhou@163.com.

责任编辑: 王历历

收稿日期: 2022-09-13 修回日期: 2023-02-15 接受日期: 2023-02-24

基金资助:

国家电网有限公司华东分部科技项目(SGHD0000DKJS2100235)

Received: 2022-09-13 Revised: 2023-02-15 Accepted: 2023-02-24

作者简介 About authors

周毅(1982-),高级工程师,主要从事电网调度、电力系统自动化研究.

摘要

可再生能源占比不断增加给互联电网频率控制带来严峻考验.由于常规的自动发电控制(AGC)策略没有考虑电网潮流安全约束,所以传统方法根据专家知识和经验进行尝试性发电机功率调整,需耗费较多时间;基于最优电力潮流的互联电网AGC优化模型由于非凸性和大规模性,求解时间较长且存在收敛性问题.鉴于常规深度强化学习具有“离线训练、在线端对端形成策略”的优点,但在动作探索过程中无法保证系统安全性,提出一种基于安全深度强化学习的电网有功频率协同优化控制方法.首先,将电网频率控制建模为约束马尔可夫决策过程,对决策过程添加相关安全约束进行智能体设计;然后,基于华东电网实际系统算例对智能体进行训练和性能提升;最后,对比智能体决策与常规AGC策略效果.结果表明:所提方法在多种运行方式下可快速生成有功频率控制策略,且保证系统频率恢复过程中电网的安全性,可辅助调度员在线决策.

关键词： 有功频率协同控制; 人工智能; 深度强化学习; 约束马尔可夫决策过程; 智能体

Abstract

The continuous increase in renewables penetration poses a severe challenge to the frequency control of interconnected power grid. Since the conventional automatic generation control (AGC) strategy does not consider the power flow constraints of the network, the traditional approach is to make tentative generator power adjustments based on expert knowledge and experience, which is time consuming. The optimal power flow-based AGC optimization model has a long solution time and convergence issues due to its non-convexity and large size. Deep reinforcement learning has the advantage of “offline training and online end-to-end strategy formation”, which yet cannot ensure the security of artificial intelligence (AI) in power grid applications. A coordinated optimal control method is proposed for active power and frequency control based on safe deep reinforcement learning. First, the method models the frequency control problem as a constrained Markov decision process, and an agent is designed by considering various safety constraints. Then, the agent is trained using the example of East China Power Grid through continuous interactions with the grid. Finally, the effect of the agent and the conventional AGC strategy is compared. The results show that the proposed approach can quickly generate control strategies under various operating conditions, and can assist dispatchers to make decisions online.

Keywords： coordinated power and frequency control; artificial intelligence (AI); safe deep reinforcement learning; constrained Markov decision process; agent

PDF (2823KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

周毅, 周良才, 史迪, 赵小英, 闪鑫. 基于安全深度强化学习的电网有功频率协同优化控制[J]. 上海交通大学学报, 2024, 58(5): 682-692 doi:10.16183/j.cnki.jsjtu.2022.358

ZHOU Yi, ZHOU Liangcai, SHI Di, ZHAO Xiaoying, SHAN Xin. Coordinated Active Power-Frequency Control Based on Safe Deep Reinforcement Learning[J]. Journal of Shanghai Jiaotong University, 2024, 58(5): 682-692 doi:10.16183/j.cnki.jsjtu.2022.358

随着新能源和有源化负荷比例不断增大、电力市场改革持续深化,电网运行的不确定性、动态性和多元性显著增强,给电网的频率控制带来严峻考验^[1-2].

太阳能和风力发电具有显著的随机性和间歇性,随着大量常规机组被替代,系统转动惯量持续降低,电网频率波动率不断增大,潮流随机性不断增强.大区联网扩大了潮流波动的影响范围并带来联络线功率窜动问题,基于预设“临界”运行工况以及调度员经验指定的传统调控措施难以适应快速变化的系统状态.由于常规自动发电控制(Automatic Generation Control, AGC)策略没有考虑其对电网潮流安全约束的影响,此时仅依靠常规AGC滞后控制很难将系统频率和联络线功率维持在运行范围内^[3].目前调度实践中,系统频率控制和潮流控制相对独立,频率调整过程中经常出现潮流越限运行.尤其是发生特高压直流双极闭锁时,系统频率大幅扰动的同时系统潮流大范围转移,各省市按照规定预留的旋转备用比例分摊功率缺额^[1],可能导致多个断面越限,局部电网甚至需要采取负荷控制措施才能确保电网安全运行.现有基于日前离线分析和灵敏度计算的调控方法速度和精度不够,在多断面同时越限情况下缺乏有效优化手段.

基于最优电力潮流(Optimal Power Flow, OPF)的互联电网AGC优化模型由于具有非凸性和大规模性,通常较难求解,在国内区域互联电网缺少成功的工程实践应用^[4⇓-6].亟需更加精细化、能够辅助调度员快速在线决策的频率和潮流协同优化控制方法.

近年来,以深度强化学习(Deep Reinforcement Learning, DRL)为代表的人工智能技术在多个领域获得应用^[7⇓⇓-10].利用其强大的感知和逻辑推演能力来解决电网调控问题成为新兴研究热点和应用方向.国内外学者对DRL在电力系统中的应用做了大量探索.文献[11]中提出基于深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)的低频振荡控制策略;文献[12]中提出基于深度Q网络和DDPG的无功电压控制方法;文献[13]中将强化学习用于短期负荷预测;文献[14]中将双深度Q网络应用于负荷模型辨识;文献[15]中提出基于近端策略优化的电网潮流优化控制框架;文献[16]中提出基于竞争深度Q网络的电网拓扑实时优化方法;文献[17]中将深度强化学习技术应用于最优潮流快速求解.在电网频率控制领域,文献[18]中提出基于深度强化学习的负荷频率控制方法并将其应用在单区域小系统;文献[19]中将强化学习算法应用在微电网频率控制;文献[20]中提出基于DDPG的分布式负荷频率控制算法.上述工作以恢复电网频率为控制目标,未考虑网络安全约束,因此适用范围为小系统和微网.此外,由于这些方法未考虑系统级优化目标,如控制成本、网损、系统平衡度等,所以对于区域互联电网,其控制措施容易成本过高从而在实践中不可行.

针对上述问题,提出基于安全深度强化学习的电网有功频率协同优化控制方法,对现有AGC控制模型进行优化.将实时发电控制过程建模为约束马尔可夫决策过程,在互联电网频率控制过程中同时考虑联络线和断面潮流约束,且在控制动作搜索过程中保证系统各电气量及其轨迹满足安全约束条件.训练好的智能体可在线辅助调度员进行决策,在保证电网安全的情况下快速实现频率恢复.

1 互联电网有功频率协同优化

常规AGC策略没有考虑网络安全约束,其主要原因是传统的水火电源互联电力系统中,系统负荷短时的随机波动及相应的系统功率缺额不大,导致AGC机组的调节量较小,对电网的安全性影响不大.但是,随着新能源大量接入,系统的不确定性功率波动及功率缺额大幅度增加.为了满足频率和联络线功率的约束,AGC机组的调节量也会大幅度增加,由此经常导致线路和断面功率过载从而影响互联电网的安全运行.针对含大规模新能源互联电力系统的潮流和频率协同控制问题,需要对AGC模型进行优化,其数学模型如下.

以优化系统生产成本为例,目标函数定义为

(1)min

\sum_{i \in S_{G}}

(c₂_i

P_{G i}^{2}

+c₁_iP_G_i+c₀_i)

式中:S_G为所有参与调频的AGC机组集合;c₀_i、c₁_i、c₂_i为第i台机组发电成本系数;P_G_i为第i台发电机发电量.

对应的等式约束条件为节点功率平衡方程:

(2)

\begin{array}{l} P_{i} - P_{G i} + P_{D i} = 0 \\ Q_{i} - Q_{G i} + Q_{D i} = 0 \end{array}\}

(3)

\begin{array}{l} P_{i} = \overset{n}{\sum_{j = 1}} [e_{i} (G_{i j} e_{j} - B_{i j} f_{j}) + \\ f_{i} (G_{i j} f_{j} - B_{i j} e_{j})] \\ Q_{i} = \overset{n}{\sum_{j = 1}} [f_{i} (G_{i j} e_{j} - B_{i j} f_{j}) - \\ e_{i} (G_{i j} f_{j} + B_{i j} e_{j})] \end{array}\}

式中:假设第i台发电机对应i节点,Q_G_i为第i台发电机输出的无功功率;P_D_i、Q_D_i分别为节点i的负荷有功和无功功率;P_i、Q_i分别为节点i的注入有功和无功功率;G_ij、B_ij 分别为节点导纳矩阵中第i行第j列元素的实部和虚部;e_i、f_i 分别为节点i电压向量的实部和虚部;e_j、f_j分别为节点j电压向量的实部和虚部.

发电机出力和负荷功率计及机组和负荷的静态频率调节特性如下:

(4)P_G_i=P_G_i0-K_G_i(f-f_N)+P_Gr_i

(5)

\begin{array}{l} P_{D i} = [1 + K_{P f i} (f - f_{N}) / f_{N}] P_{D N i} \\ Q_{D i} = [1 + K_{Q f i} (f - f_{N}) / f_{N}] Q_{D N i} \end{array}\}

式中:f、f_N分别为系统频率和额定频率;P_DN_i、Q_DN_i分别为节点i在额定电压和频率条件下的有功和无功负荷;P_G_i0为第i台AGC机组当前计划发电值;P_Gr_i为第i台AGC机组的二次调频量;K_G_i为第i台发电机的有功-频率静特性系数;K_Pf_i、K_Qf_i分别为负荷模型的静态频率特性系数.

优化模型的不等式约束包括:

(6)

V_{i, m i n}^{2}

≤

V_{i}^{2}

≤

V_{i, m a x}^{2}

(7)P_G_i,_min≤P_G_i≤P_G_i,_max

(8)Q_G_i,_min≤Q_G_i≤Q_G_i,_max

(9)-S_ij,_max≤S_ij≤S_ij,_max

(10)P_t_m,_min≤

\sum_{i j \in S_{l i n k, m}}

P_ij_,_m≤P_t_m,_max, m∈S_t

式中:V_i为节点i的电压幅值;S_ij为线路ij传输的视在功率; S_link_{, m}为第m个断面所包含的联络线集合;P_ij_,_m为第m个断面上线路ij传输的有功功率;P_t_m为第m个断面传输的有功功率; S_t为断面集合;下标max和min分别表示相应变量的上下限.

由于基于OPF的AGC优化模型非凸且规模较大^[21],其求解速度无法满足在线决策和控制的要求,所以采用深度强化学习算法求解互联电网有功功率协同问题.

2 深度强化学习SAC模型

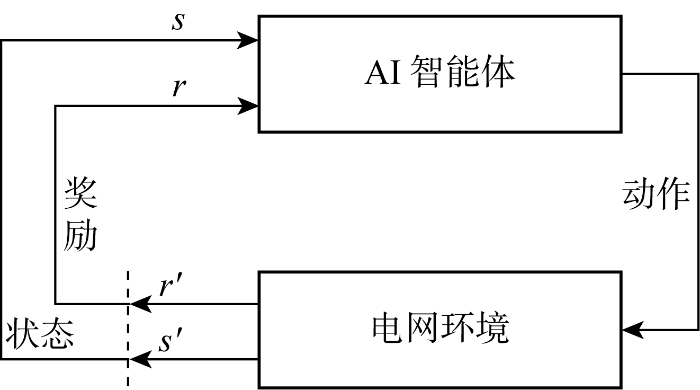
强化学习是解决智能体在动态变化环境中如何获取最大累计奖励的一类机器学习方法,可用于解决复杂信息物理系统的优化控制和决策问题.强化学习智能体与电网环境交互过程如图1所示.电网每执行一个智能体建议的动作,会返回新的系统状态s'并计算相应奖励值r';智能体根据当前状态s,以最大化奖励r期望值为目标,在不断与电网交互过程中学习并改进动作策略.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 智能体与电网环境交互过程

Fig.1 Interaction between agent and grid environment

深度强化学习是深度学习和强化学习的结合,通过不断与环境交互迭代,智能体可逐步提高决策、推理、预测能力,不断提升控制效果.

深度强化学习算法可根据价值函数或网络更新所使用方法的不同分为既定策略和新策略两大类.在电力系统相关应用中,由于生成海量数据样本的成本较高,提升采样效率十分关键,所以使用新策略类算法较合适^[18].考虑到大电网有功频率协同优化控制问题的复杂性以及系统状态和动作空间的特点,对比各算法的优缺点发现,软演员-评论家(Soft Actor-Critic, SAC)算法适合于状态和动作空间均较大的优化控制问题,其鲁棒性和收敛性能优异^[22-23].

SAC算法中控制策略最大化预期回报和未来熵的和,更新最优策略的过程可表示为

(11)π^*=arg

\underset{π}{m a x}

E_{(s_{t}, a_{t}) ~ π}

[

\overset{T}{\sum_{t = 0}}

γ^t(R(s_t, a_t)+αH(π(·|s_t)))]

式中:E(·)为期望函数;H(π(·|s_t))为控制策略π在状态为s_t时刻的熵值;γ为折现率;R(s_t, a_t)为在系统状态为s_t时采取动作a_t获得的奖励值;α为探索新策略与采用已有控制策略之间的权衡系数,也称温度参数.状态值函数V^π(s_t)与动作值函数Q^π(s_t, a_t)存在下述关系,即

(12)V^π(s_t)=

E_{a_{t} ~ π}

(Q^π(s_t, a_t))+αH(π(·|s_t))

SAC智能体训练过程中,对于控制策略的评估和提升采用带有随机梯度的深度神经网络.构造所需状态值函数 $V_{ψ}^{π}$ (s_t)和动作值函数 $Q_{θ}^{π}$ (s_t, a_t)时,对应神经网络的参数可以用ψ和θ来表示,策略网络π_ϕ(a_t, s_t)对应的参数由ϕ表示.SAC算法中采用两套值函数,其中一个值函数称为“软”值函数,用来逐步更新策略,以提升算法的稳定性和可靠性.软V函数的参数可以通过最小化下式中的残差进行更新:

(13)L_V(ψ)=

E_{s_{t} ~ D}

{

\frac{1}{2}

[

V_{ψ}^{π}

(s_t)-

E_{a_{t} ~ π_{θ}}

(

Q_{θ}^{π}

(s_t, a_t)-αlg π_ϕ(a_t|s_t))]²}

式中:D为已采样样本的分布.概率梯度 ${\hat{Δ}}_{ψ}$ L_V(ψ)可以用下式计算,即

(14)

{\hat{Δ}}_{ψ}

L_V(ψ)=Δ_ψ

V_{ψ}^{π}

(s_t)(

V_{ψ}^{π}

(s_t)-

Q_{θ}^{π}

(s_t, a_t)+αlg π_ϕ(a_t|s_t))

类似地,可通过最小化贝尔曼残差的方式来更新软Q函数的网络参数,即

(15)

\begin{array}{l} L_{Q} (θ) = E_{(s_{t}, a_{t}) ~ D} [\frac{1}{2} (Q_{θ}^{π} (s_{t}, a_{t}) - \\ \hat{Q} (s_{t}, a_{t} {))}^{2}] \\ \hat{Q} (s_{t}, a_{t}) = R (s_{t}, a_{t}) + γ E_{s_{t + 1} ~ p} (V_{\bar{ψ}}^{π} (s_{t + 1})) \end{array}\}

式中: $\hat{Q}$ (s_t, a_t)为状态-动作函数的估计; $E_{s_{t + 1} ~ p}$ 为状态s_t₊₁的概率分布为p的期望; $\bar{ψ}$ 为值函数网络参数在移动窗口内的平均值.其求解可根据概率梯度 ${\frac{\frac{^}{}}{Δ}}_{θ}$ L_Q(θ)进行迭代,即

(16)

{\hat{Δ}}_{θ}

L_Q(θ)=Δ_θ

Q_{θ}^{π}

(s_t, a_t)(

Q_{θ}^{π}

(s_t, a_t)-R(s_t, a_t)-γ

V_{\bar{ψ}}^{π}

(s_t₊₁))

SAC算法的策略由带有平均值和协方差的随机高斯分布所表示,其参数可通过最小化预期Kullback-Leibler(KL)偏差而得到,即

(17)L_π(ϕ)=

E_{s_{t} ~ D}

[

E_{a_{t} ~ π_{ϕ}}

(αlg π_ϕ(a_t|s_t)-

Q_{θ}^{π}

(s_t, a_t)]

其优化求解过程可根据概率梯度 ${\hat{Δ}}_{ϕ}$ L_π(ϕ)进行迭代:

(18)

{\hat{Δ}}_{ϕ}

L_π(ϕ)=αΔ_ϕlg π _ϕ(a_t|s_t)+(α

Δ_{a_{t}}

lg π _ϕ(a_t|s_t)-

Δ_{a_{t}} Q_{θ}^{π}

(s_t, a_t))Δ_ϕf_ϕ(ε_t;s_t)

式中: $Δ_{a_{t}}$ 为控制动作a_t的梯度;ε_t为输入向量误差;a_t可由神经网络变换f_ϕ(ε_t; s_t)获得.

3 基于安全SAC算法的有功频率协同优化算法设计

由于深度强化学习在训练过程中有试错的特点,智能体探索出的控制动作具有一定的随机性,动作执行后可能会违反电网的安全约束,这在实际系统中无法接受.智能体训练过程中应自始至终保证电网各项安全约束条件得到满足.由于常规的SAC算法无法直接处理大量安全约束条件,如果简单地将所有约束条件体现在奖惩函数中,则得到的解会偏保守或不可行^[24],所以必须对算法进行改进.

在标准SAC算法基础上改进并提出考虑网络安全约束的安全SAC(Safe SAC, SSAC)算法,将有功频率协同控制建模成约束马尔可夫决策过程( Constrained Markov Decision Process, CMDP),将互联电网的网络安全约束在CMDP中进行建模,保证了智能体训练和策略生成过程中式(6)~(10)所示的安全约束得到满足.

3.1 CMDP模型

CMDP可以用5维元组(S, A, P_a, R_a, C)描述,其中S为系统状态空间;A为动作集;P_a(s, s')为系统采取动作a后由状态s转移到s'的概率;R_a(s, s')为在状态s采取动作a后转移到新状态s'所得到的奖励值;C为安全约束方程.

该过程的每组轨迹都对应一个回报,该过程的求解目标是策略π,即建立起系统状态与动作之间的对应关系,从而使得策略执行过程中系统状态满足约束条件且预期回报J(π)最大,亦为目标函数:

(19)

\underset{π}{m a x}

(\overset{T}{\sum_{t = 0}} γ^{t} R_{t})

, s.t. C^π(s)≤

\bar{C}

式中:C^π(s)为成本函数; $\bar{C}$ 为成本上限;R_t为 $R_{a_{t}}$ (s, s')缩写.

在该过程的一组轨迹中,目标函数与初始状态s相关,可以定义状态值函数V^π(s),即智能体由状态s开始,按照策略π决定后续动作所得回报的数学期望:

(20)V^π(s)=E_τ~π

(\overset{T}{\sum_{t = 0}} γ^{t} R_{t} |s)

式中:变量τ为一段轨迹.同理,定义Q^π(s, a)为动作值函数,即从给定状态s和动作a后采用策略π所得回报的期望,可以用来评估控制策略的好坏,具体定义为

(21)Q^π(s, a)=E_τ~π

(\overset{T}{\sum_{t = 0}} γ^{t} R_{t} |s, a)

CMDP中的动作和状态值函数满足贝尔曼方程^[25],即有

(22)V^π(s_t)=

E_{s_{t + 1} ~ P_{a}}^{a_{t} ~ π} (R_{t} + γ V^{π} (s_{t + 1}))

(23)Q^π(s_t, a_t)=

E_{s_{t + 1} ~ P_{a}}^{a_{t + 1} ~ π} (R_{t} + γ Q^{π} (s_{t + 1}, a_{t + 1}))

3.2 考虑网络安全约束的SSAC算法

在智能体训练过程中,动作执行前后应使得系统电压和网络潮流在约束范围内,即F_{limit_L}≤F_t≤F_{limit_H}.其中,F_t代表式(6)~(9)中的电压和功率,F_{limit_H}、F_{limit_L}为F_t对应的上下限.根据式(19),选择成本函数为系统电压和网络潮流越限个数,其表达式如下:

(24)C^π(s)=E_τ~π(

\overset{T}{\sum_{t = 0}}

γ^tc_t(s))=E_τ~π[

\overset{T}{\sum_{t = 0}}

γ^t

\overset{K}{\sum_{i = 1}}

(Π(

F_{t + 1}^{i}

F_{l i m i t_H}^{i}

)+Π(

F_{t + 1}^{i}

F_{l i m i t_L}^{i}

))]

(25)

\bar{C}

\frac{1 - γ^{T}}{1 - γ} \bar{c}

式中:c_t(s)为t时刻的成本函数; $\bar{c}$ 为单步成本上限;Π(·)为指示函数;K为式(6)~(9)中不等式约束条件个数.如还有其他约束条件,也可以类似方式处理.

结合式(11)、(19)、(24)~(25),有功潮流协同优化对应的CMDP问题可通过下式求解:

(26)

\begin{array}{l} \underset{π}{m a x} E_{s ~ D} [\overset{T}{\sum_{t = 0}} γ^{t} (R (s_{t}, a_{t}) + α H (π (\cdot | s_{t})))] \\ s . t . E_{s ~ D} (\overset{T}{\sum_{t = 0}} γ^{t} c_{t} (s)) \leq \bar{C} \end{array}\}

将上述含约束条件的优化问题转化为无约束条件的优化问题,其对应的拉格朗日方程为

(27)L(π, λ)=E_s~D

[\overset{T}{\sum_{t = 0}} γ^{t} (R (s_{t}, a_{t}) + α H (π (\cdot | s_{t})))]

+λ(

\bar{C}

-E_s~D(

\overset{T}{\sum_{t = 0}}

γ^tc_t(s)))

上式可以通过拉格朗日乘数法进行求解,即分别对相关变量求梯度后形成多个联立方程进而求解.其中,拉格朗日乘子λ在给定初值的情况下,可以通过迭代求解:

(28)λ^k⁺¹=λ^k-σ_λΔ_λL(π, λ)

式中:k为更新步数.同理,两个值函数网络和策略网络参数也可以进行迭代更新,其中σ_λ为拉格朗日乘子迭代更新时采用的步长,具体流程与式(13)~(18)类似.

按照本文所提SSAC算法,智能体的训练流程如算法1所示.

算法1 SSAC智能体训练流程

1. 初始化策略网络π参数ϕ、状态值函数V网络参数ψ和 $\bar{ψ}$ 、动作值函数Q网络参数θ₁和θ₂;初始化拉格朗日乘数λ、更新权重τ;初始化回放缓存D

2. for:对所有样本逐个执行

3. for:根据控制迭代次数,执行

4. 获取系统状态并计算控制动作 a_t~π(·|s_t)

5. 执行动作a_t, 获取状态s_t₊₁、奖励值r_t、c_t和结束信号done

6. 储存元组(s_t, a_t, r_t, c_t, s_t₊₁, done)在回放缓存D中

7. s_t=s_t₊₁

8. if 满足梯度更新条件,则

9. for 根据所需更新次数,执行

10. 从D中随机采样一批N个数据

(s_t, a_t, r_t, c_t, s_t₊₁, done)

11. 更新V当前网络参数 ψ

12. 更新Q网络参数 θ_i (i=1, 2)

13. 更新策略π网络参数 ϕ

14. 更新V目标网络数 $\bar{ψ}$ ←τψ+(1-τ) $\bar{ψ}$

15. 更新拉格朗日乘子λ

16. end for

17. end if

18. end for

19. end for

3.3 SSAC智能体设计

针对互联电网有功频率协同优化问题,SSAC智能体的训练环境设为真实电网或其高精度仿真器D5000或PSD-BPA.智能体与环境的接口为电网断面数据文件,智能体应能从中获取频率偏差和功率缺额.

离线训练和测试样本可从电网断面潮流文件中获得,应尽量选取有代表意义的电网运行工况.当历史断面中电网拓扑结构发生重大变化时,该变化可直接反映在历史的海量断面潮流文件中,用于智能体的训练.若针对未来规划中的拓扑结构变化训练智能体,则需将该变化反映在样本中.

SSAC智能体的状态变量包括母线电压V^bus、线路潮流(P_L, Q_L)、发电机出力(P_g, Q_g)、系统频率偏差f-f_N或功率缺额P_loss.状态空间S定义为

(29)S={

V_{1}^{b u s}

V_{2}^{b u s}

, …,

V_{N_{b}}^{b u s}

P_{L_{1}}

Q_{L_{1}}

, …,

P_{L_{M}}

Q_{L_{M}}

P_{g_{1}}

Q_{g_{1}}

, …,

P_{g_{n}}

Q_{g_{n}}

, P_loss}

式中:N_b、M、n分别为系统母线、线路、发电机的个数.

SSAC智能体可选择的控制动作包括发电机出力调节、切负荷等.动作空间A定义为

(30)A={Δ

P_{g_{1}}

, Δ

P_{g_{2}}

, …, Δ

P_{g_{n}}

, Δ

P_{L_{1}}

, Δ

P_{L_{2}}

, …, Δ

P_{L_{o}}

}

式中:o为可切负荷个数.

奖惩机制的设定对SSAC智能体的优化控制性能至关重要.值得注意的是,奖惩函数的设计可根据优化目标的不同而改变.以尽快完成系统频率恢复为例,即最少迭代次数为目标进行说明.奖励值R_t的定义如下:

(31)C_sys=

\overset{n}{\sum_{i = 1}}

(c₂_i

P_{G i}^{2}

+c₁_iP_G_i+c₀_i)

(32)D_ovf=

\overset{l}{\sum_{i = 1}}

(max {

\sum_{i j \in S_{l i n k, m}}

P_ij_,_m-P_t_m_{, max}, 0}+min {

\sum_{i j \in S_{l i n k, m}}

P_ij_,_m-P_t_m_{, min}, 0})²

(33)D_p=

|\overset{n}{\sum_{i = 1}} Δ P_{g i} - \overset{m}{\sum_{i = 1}} Δ P_{L_{i}} - P_{l o s s}|

(34)R_t=

\{\begin{array}{l} E_{1} - \frac{C_{s y s}}{E_{2}}, & D_{o v f} = 0 \\ - \frac{D_{o v f}}{E_{3}} - \frac{D_{p}}{E_{4}}, & D_{o v f} > 0 \end{array}

式中:C_sys为电网生产成本;l为系统断面个数;D_ovf为系统断面潮流越限量的平方和;D_p为系统功率差额;E₁为一个正的偏移系数,其作用是使得对应条件满足时奖励为正;E₂~E₄为正的常数,作用是调节各自成分之间的比例以及限制奖励的取值范围.若采用某个控制决策导致系统监测的所有断面潮流越限问题得以解决,即D_ovf=0时,选择合适的常数E₁和E₂的值以使该步奖励值R_t始终为正数,同时该步奖励值与系统网损或生产成本C_sys负相关,即在解决稳定断面潮流越限问题情况下,网损或生产成本越高,奖励值越小,在引导智能体解决问题的同时促进网损或生产成本优化目标的实现;若采用某个控制策略后系统稳定断面潮流越限仍然存在,即D_ovf>0,则该步的奖励值R_t为负,选择合适的常数E₃和E₄以平衡潮流越限和功率净调节量所占的比例大小,在对未实现控制目标的策略进行惩罚的基础上平衡潮流越限和功率调节两个因素所占比例.根据奖惩函数的定义,智能体在学习过程中将会尽快完成优化控制目标.

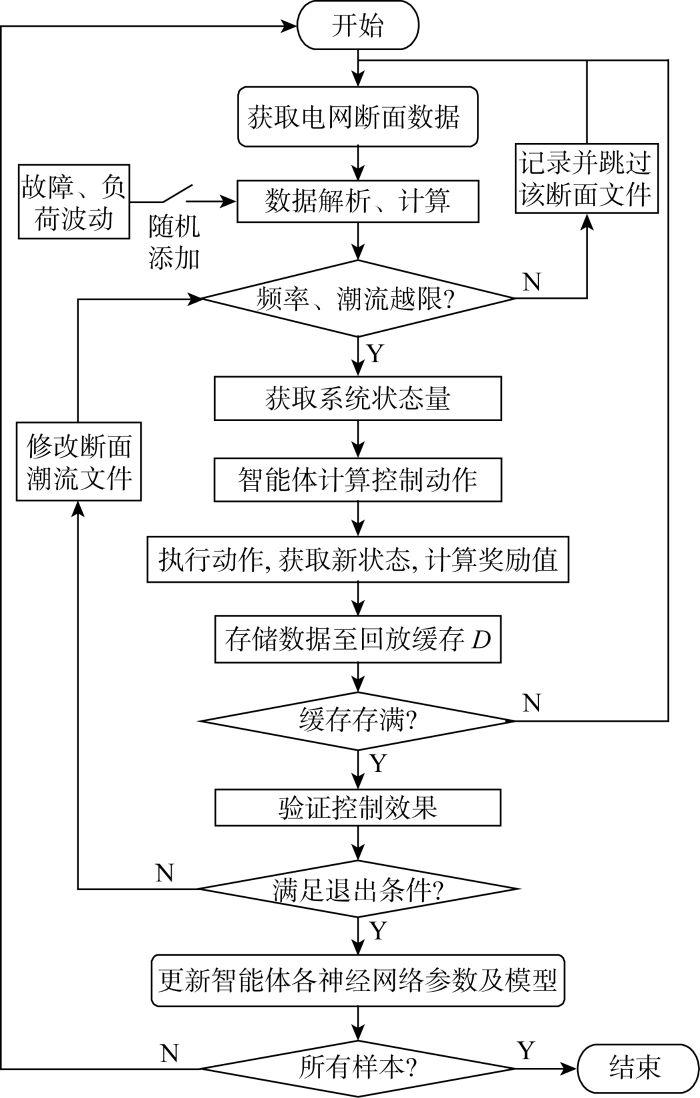
SSAC智能体训练流程如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 智能体训练流程图

Fig.2 Flow chart of the training process of an agent

4 算例分析

4.1 典型场景选取和仿真环境建立

利用2021年6月的华东电网实际断面数据,通过大量数值实验对提出的有功频率协同优化控制方法进行验证.实验分两步进行: ①验证提出的协同优化控制框架和智能体训练方法,并在此基础上评估智能体的性能和决策质量;②使用时域仿真,对比基于智能体决策和华东电网现有功率分摊两种控制方法的动态曲线,进而验证所提方法的优势.

实验中使用的华东电网断面数据包含 4 463 条母线,其中220 kV及以上母线共 2 913 条,5 686 条输电线路,2 051 台变压器,216个发电厂共579台发电机,49个重点关注的稳定断面.为了生成更多训练和测试数据,对华东电网实际断面数据的负荷进行随机扰动,按能包住两回特高压直流同时失去带来的波动,扰动范围为90%~110%,在此基础上考虑“锦苏”“灵绍”两条直流线路发生单极或双极闭锁,产生功率缺失,共生成12万个系统断面数据.在实验过程中,控制措施以调整发电机出力为主要手段,尽量避免切除负荷.训练过程中,智能体控制措施的执行以发电厂为单位,发电厂内的发电机按照各自备用容量进行分摊.

4.2 SSAC智能体性能评估

将产生的12万个华东电网断面数据分为两部分,其中10万个样本用于智能体的训练,剩下的2万个样本用于对训练好的智能体进行性能测试.训练和测试阶段的主要区别在于:①测试阶段采用训练好的智能体并固定其各项参数,整个测试过程中不做智能体中深度神经网络参数的更新;②训练阶段采用随机性策略,而测试阶段采用确定性策略.

智能体训练过程使用的相关参数设置如下:隐藏层层数为3;隐藏层神经元个数为(2 048, 1 024, 512);批量大小为256;学习率为0.001;折现率为0.99;温度参数为0.006;最大熵值为0.1;拉格朗日乘数初值为0.0;回放缓存大小为 50 000;隐藏层激活函数为ReLU;优化器为Adam.

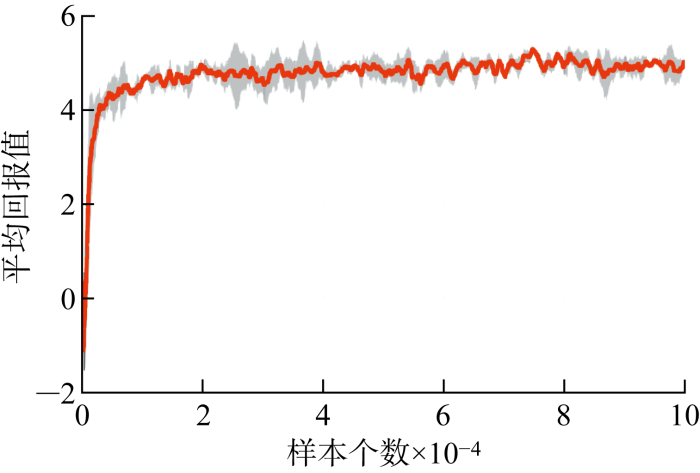
使用5个不同的随机数种子(8,10,18,22,28)训练5个智能体实例,每500个环境步骤对智能体进行1次评估.训练过程中智能体获得的平均回报值变化趋势如图3所示.图中实线对应于奖励值均值,阴影区域对应于奖励值的99%置信区间(3σ),智能体最初的回报值为负,随着训练样本数的增加,很快变成正值.根据奖励值的定义,正回报表示控制目标得到实现.在训练过程中,总回报不断提升,且其波动量逐渐减小.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 训练阶段智能体平均回报值

Fig.3 Average total return in training stage

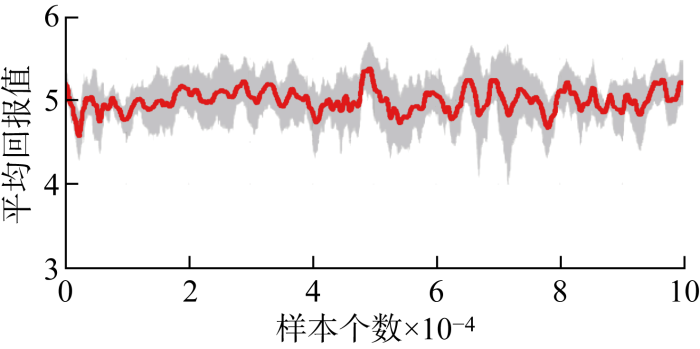
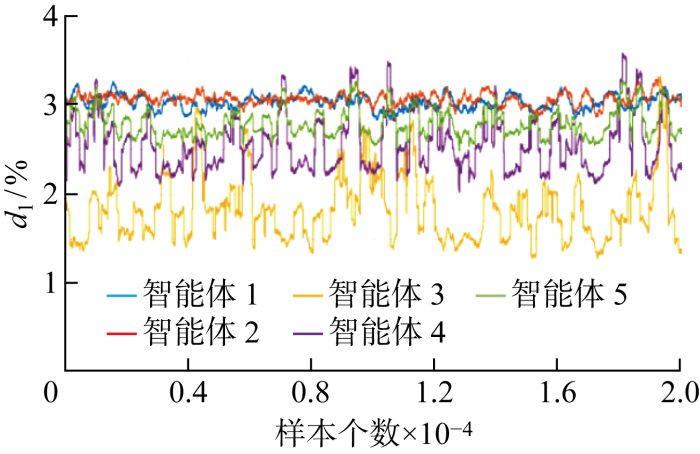
使用剩下的2万个断面数据对经过训练的智能体进行测试,测试平台硬件和系统参数为Intel i9-7920 CPU@2.9 GHz, 128 GB RAM, Ubuntu 20.04.2LTS, 4×Nvidia Titan V.测试阶段的平均回报如图4所示,5个智能体的测试结果总结如表1所示.对于前2个智能体,系统频率和稳定断面越限问题均得到100%的解决.对于后3个智能体,所有频率问题都得到100%的解决,但分别有68、86和16个样本数据在智能体采取控制措施后仍然存在越限问题.最后3个智能体的成功率仍然非常高,为99.57%~99.66%.对于所有样本数据,5个智能体均可在 20 ms 内给出优化控制决策.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 测试阶段智能体平均回报值

Fig.4 Average total return in testing stage

表1 智能体测试结果小结

Tab.1 Summary of agent testing results

编号	总样本数	断面潮流越限的样本个数	成功率/%	平均决策时间/ms
1	20 000	0	100	15.178
2	20 000	0	100	16.290
3	20 000	68	99.66	19.703
4	20 000	86	99.57	16.842
5	20 000	16	99.92	17.633

新窗口打开| 下载CSV

为了进一步测试和验证智能体决策,将智能体决策结果与华东电网功率缺额情况下各省市按比例分摊的控制策略进行对比.根据华东现有电网频率调控体系,大扰动情况下五省市的功率分摊按照如下比例进行:11.6%沪、31.26%苏、22.56%浙、17.32%皖、17.24%闽.在数值实验中,发电机出力按照所在省市的分摊总量和省内各发电机备用比例进行调整以补偿系统功率缺额,并将该场景设置为基准场景.重点比较样本中的稳定断面潮流越限个数以及网损.表2总结了样本中的稳定断面潮流越限个数:在基准场景下,2万个样本均有稳定断面潮流越限,越限个数在1~3个不等.利用所提控制框架,这些越限均可被解决,前两个智能体取得100%的成功率,后3个智能体实现大于99.57%的成功率.

表2 断面潮流越限情况统计

Tab.2 Statistics of numbers of snapshots with overflows

智能体	样本数
智能体	无断面越限	1个断面越限	2个断面越限	3个断面越限
基准场景	0	17 213	2 434	353
智能体1	20 000	0	0	0
智能体2	20 000	0	0	0
智能体3	19 932	68	0	0
智能体4	19 914	74	11	1
智能体5	19 984	15	1	0

新窗口打开| 下载CSV

提出方法对系统网损优化的效果可以降损率为指标进行评估,降损率的定义如下:

(35)d_l=

\frac{L_{2} - L_{1}}{L_{2}}

式中:L₁、L₂分别为采用智能体决策后的系统网损和对应的基准场景下的系统网损.5个智能体的降损率如图5所示,所有智能体均改善了系统网损,这验证了降低网损这一控制目标得到实现.与基准场景相比,智能体1和2的降损率高于智能体3~5.由图5可知,5个智能体的平均降损率分别为3.033%、3.071%、1.826%、2.556%和2.801%.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 测试阶段各智能体的网损差别率

Fig.5 Difference in system loss in the testing stage

需要指出的是,由于人工智能和机器学习算法的统计性质和随机性,使用相同参数训练的智能体可能在性能上出现细微差异.因此,训练多个智能体、评估和比较它们的性能并选择其中一个或多个性能更好的智能体是一个好的解决方法.对于在线推理,最好使用多个智能体并发进行决策,并在执行控制动作前综合或验证解的有效性.

4.3 SSAC智能体决策与常规AGC策略对比

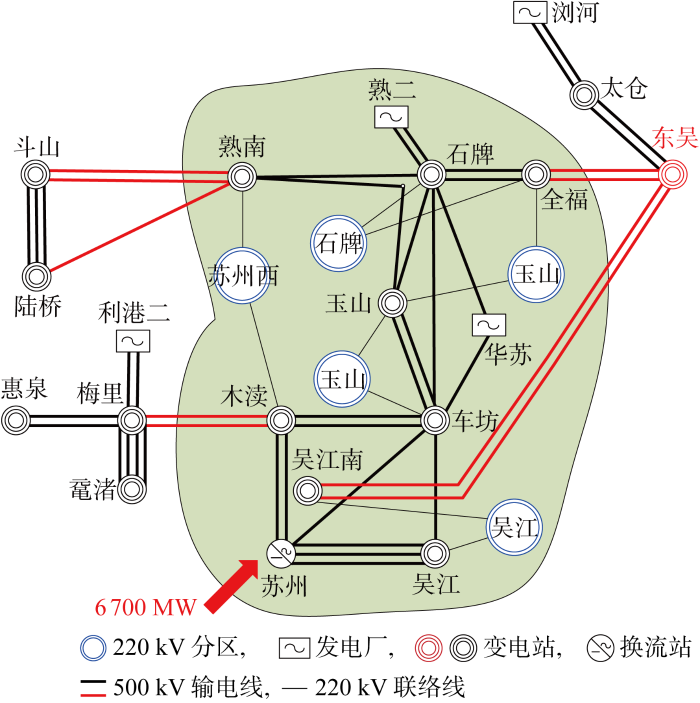
上述基于华东电网实际数据的系列数值实验验证了所提方法的有效性,在电网扰动场景下很好地实现了有功频率协同优化控制.为进一步验证智能体性能,选取苏州南部电网(见图6)作为典型研究场景,利用训练好的智能体进行决策,并与现有AGC策略进行对比.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 苏州南部电网示意图

Fig.6 Suzhou southern power grid

苏州南部电网通过锦苏直流及3个交流通道(斗山-常熟南、梅里-木渎、东吴送出)受电,若发生锦苏直流双极闭锁,按照现有频率防控体系,在频率协控系统和动态区域控制误差系统动作后,剩余功率缺额由五省市按照固定比例分摊,且江苏优先加足苏州南部电网出力,苏州南部交流受电断面仍将越限,且受制于斗山-常熟南断面最先越限,苏州南部电网在大负荷方式下存在事故拉电风险.而如何调整包括苏州南部电网机组在内全部华东全网机组出力,尽量将3个交流通道能力用足,降低事故拉电风险是调度实践中存在的难题.

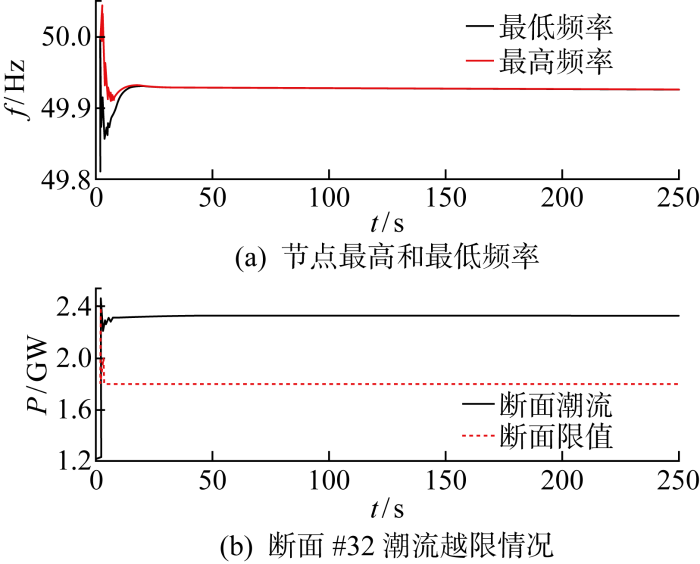
利用PSD-ST暂态稳定程序,通过时域动态仿真的方式来对智能体决策和常规AGC策略进行对比.首先,使用2021年6月25日21:00的华东电网实际断面数据,即系统总负荷约为219.7 GW,锦苏直流功率约为 5 912 MW,在t=2 s时添加锦苏直流双极闭锁故障,在仅依靠发电机一次调频能力情况下的系统频率如图7(a)所示,直流双极闭锁后系统最低频率降至49.81 Hz,稍后在一次调频的作用下恢复至49.92 Hz.关注的49个稳定断面中的第32个断面即斗山-常数南断面功率(P)越限,如图7(b)所示,该断面在闭锁前潮流为 1 226 MW,闭锁后升至 2 321.5 MW,该断面的稳定限值在第2 s和第3 s先后发生阶跃变化,原因是分档条件发生变化.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 仅一次调频作用情况下系统动态曲线

Fig.7 Dynamic simulation results with only primary frequency control

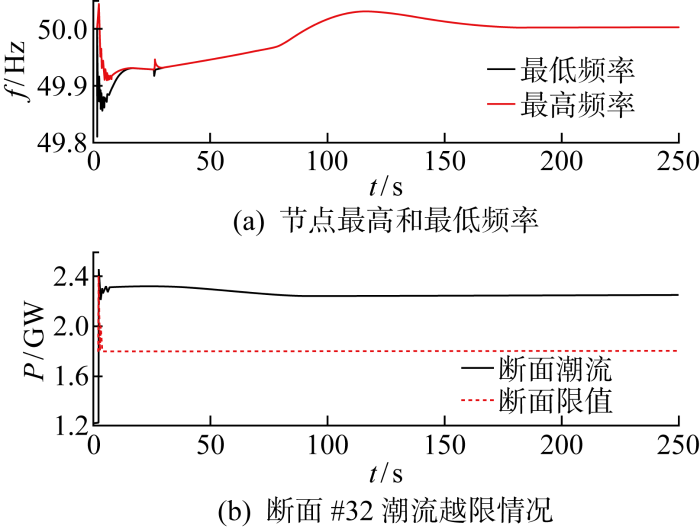
根据华东电网现有频率调控实践,五省市按照本节先前讨论的比例和发电机备用容量进行功率缺额分摊,重复上述动态仿真实验.在t=2 s时切除锦苏直流,在t=25~80 s时通过PSD-ST暂态稳定程序IGV/IGV+卡改变各发电机调速器的功率参考信号,以线性方式增加至新的功率参考值,进而实现功率分摊,时域动态仿真结果如图8所示.由图可见,系统频率在直流闭锁后降至49.81 Hz,经过系统一次调频后恢复至49.92 Hz,在25 s后开始增加,最高达到50.03 Hz后开始逐渐降低,在190 s左右达到50.00 Hz,其后保持稳定.在系统各发电机功率调整过程中,断面32的潮流存在越限情况,断面限值在第2 s和第3 s分别发生阶跃变化.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 各省市发电机按照备用比例分摊情况下系统动态曲线

Fig.8 Dynamic simulation results with generators adjusted based on backup capacity for each province

然后,重复上述实验并以智能体决策结果取代之前的发电机出力调整策略,时域动态仿真结果如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 采用智能体控制策略情况下系统动态曲线

Fig.9 Dynamic simulation results with control actions generated by the agent

由图可见,系统频率在锦苏双极闭锁后跌落至49.81 Hz并在一次调频完成后恢复至49.92 Hz,在25 s后开始增加,最高达到50.03 Hz后开始逐渐降低,在170 s左右达到50.00 Hz,其后保持稳定.在发电机出力调整过程中,断面32的越限情况得到消除.时域仿真实验结果再次验证了提出方法的有效性.

5 结论

提出一种基于安全深度强化学习的电网有功频率协同优化方法,通过分析和算例验证,得到结论如下.

(1) 提出的模型和方法,在系统扰动情况下,可端对端快速形成发电机调整策略,解决系统频率波动和网络潮流越限问题,对各种运行方式有较好的适应性.

(2) 针对常规的深度强化学习在动作探索即试错过程中无法保证系统安全性的问题,在标准SAC算法基础上改进并提出考虑网络安全约束的SSAC算法,保证了智能体训练过程中电网的安全性.

(3) 与常规AGC策略进行对比,所提方法在决策速度、保证网络潮流安全方面更有优势.

针对当前研究进展,下一步工作将研究基于多智能体技术的分布式频率控制问题,另外,将针对SSAC算法应用于时域性强、变化速率高的暂态预防控制问题进行探索.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

周毅, 钱学东.

华东电网动态区域控制误差应用分析

[J]. 电力系统自动化, 2010, 34(8): 106-110.

[本文引用: 2]

ZHOU

, QIAN

Xuedong

Applications analysis of dynamic ACE in East China power grid

[J]. Automation of Electric Power Systems, 2010, 34(8): 106-110.

[本文引用: 2]

[2]

李兆伟, 吴雪莲, 庄侃沁, 等.

“9·19”锦苏直流双极闭锁事故华东电网频率特性分析及思考

[J]. 电力系统自动化, 2017, 41(7): 149-155.