基于Luenberger观测器的不确定系统鲁棒状态反馈设计

doi:10.16183/j.cnki.jsjtu.2022.328

基于Luenberger观测器的不确定系统鲁棒状态反馈设计

赵东东, 闫磊, 周兴文, 耿宗盛, 阎石^,

兰州大学信息科学与工程学院,兰州 730000

Robust State Feedback Design for Uncertain Systems Based on Luenberger Observer

ZHAO Dongdong, YAN Lei, ZHOU Xingwen, GENG Zongsheng, YAN Shi^,

School of Information Science and Engineering, Lanzhou University, Lanzhou 730000, China

通讯作者: 阎石,教授,博士生导师,电话(Tel.):093-18912778;E-mail:yanshi@lzu.edu.cn.

责任编辑: 李博文

收稿日期: 2022-08-26 修回日期: 2022-09-14 接受日期: 2022-09-19

基金资助:

国家自然科学基金项目(U22B2040)
国家自然科学基金项目(62233003)
甘肃省自然科学基金项目(20JR10RA638)
中央高校基本科研业务费(lzujbky-2021-67)

Received: 2022-08-26 Revised: 2022-09-14 Accepted: 2022-09-19

作者简介 About authors

赵东东(1989-),副教授,主要研究方向为不确定性动态系统、机器人、机器学习.

摘要

针对不确定系统测量输出矩阵含有不确定参数的问题,提出一种基于新龙伯格(Luenberger)类型观测器的鲁棒状态反馈设计方法.首先,针对实践中状态变量难以测量的问题,通过观测状态的反馈来进行观测器设计,考虑不确定系统中测量输出矩阵含有不确定参数的情况,设计一种新龙伯格类型观测器;其次,在新龙伯格类型观测器基础上,结合多仿射表示和松弛变量框架,得到与李亚普诺夫函数相关的凸线性矩阵不等式(LMI)条件,进而对闭环系统进行基于线性矩阵不等式组的鲁棒稳定性分析;最后,通过实验检验上述条件的可行性,证明该方法的实用性和有效性.

关键词： 不确定系统; 龙伯格观测器; 多仿射表示; 鲁棒设计; 观测状态

Abstract

This paper proposes a robust state feedback design method based on a new Luenberger observer for uncertain systems with measurement output matrices containing uncertain parameters. First, in view of the problem that it is challenging to measure state variables in practice, an observer is designed through the feedback of the observation state. Considering the situation that the measurement output matrix contains uncertain parameters in the uncertain system, a new Luenberger observer is designed. Then, based on the new Luenberger observer, and combined with the multi-affine representation and the slack variable framework, the convex linear matrix inequality condition related to the Lyapunov function is obtained, and the robust stability analysis based on linear matrix inequalities is conducted for the closed-loop system. Finally, the feasibility of the above condition is tested by an experiment to show the applicability and effectiveness of the proposed method.

Keywords： uncertain systems; Luenberger observer; multi-affine representations; robust design; observed-state

PDF (1042KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

赵东东, 闫磊, 周兴文, 耿宗盛, 阎石. 基于Luenberger观测器的不确定系统鲁棒状态反馈设计[J]. 上海交通大学学报, 2024, 58(4): 492-497 doi:10.16183/j.cnki.jsjtu.2022.328

ZHAO Dongdong, YAN Lei, ZHOU Xingwen, GENG Zongsheng, YAN Shi. Robust State Feedback Design for Uncertain Systems Based on Luenberger Observer[J]. Journal of Shanghai Jiaotong University, 2024, 58(4): 492-497 doi:10.16183/j.cnki.jsjtu.2022.328

许多物理系统包含固有不确定性,例如电力系统^[1]、切换系统^[2]、多智能体系统^[3]、机器人系统^[4-5],而不确定性会严重影响系统的稳定性和闭环系统性能^[2⇓⇓-5],因此对系统进行控制设计时有必要考虑其不确定性.为此,许多学者提出了不同的鲁棒控制设计方法,其中一种代表性设计思路是反馈控制^[6⇓⇓-9].

对不确定系统的反馈控制大致分为输出反馈控制和状态反馈控制两大类.输出反馈直接通过测量输出进行反馈以便于工程应用,得到许多研究者的青睐,文献[6]中提出一种关于多面体系统的H₂和H_∞输出反馈控制方法,文献[8]中通过鲁棒稳定函数来实现鲁棒静态输出反馈控制器.这些控制方案大多应用二次稳定性的概念,只需线性矩阵不等式(LMI)在多面体的顶点上收敛,以保证系统稳定性.状态反馈在实践中状态变量难以测量,往往需要借助观测器,文献[9]中提出基于观测器不确定系统的鲁棒性LMI优化控制方法,能保证不确定系统的稳定性.但当涉及到不确定有理参数时,系统基于观测器的线性矩阵不等式组(LMIs)设计,大多为非凸的^[7]、保守的^[9]或需要计算和操纵特征多项式的参数相关系数^[8].

为此,文献[10]中提出一种基于凸LMIs的启发式算法,其中详细描述的描述符多仿射表示(DMAR)和松弛变量(S)方法对不确定的有理参数具有效性.同时,基于多仿射的性质和S变量的框架,可得到凸的LMIs及可行解.但当与测量输出相关的矩阵含有不确定参数时,其鲁棒反馈设计更为复杂.因鲁棒观测状态反馈设计需涉及观测器矩阵C是一个待求参数,而不再是系统自身的测量输出矩阵,这使S变量LMIs框架更加复杂,此问题仍是一个挑战^[10-11].

为解决上述问题,提出一种基于新龙伯格(Luenberger)类型观测器的鲁棒状态反馈设计方法.首先,针对实践中状态数据难以测量的问题及测量输出相关矩阵含有不确定性的情况,设计一种新龙伯格类型观测器;其次,基于新龙伯格类型观测器,结合DMAR和S变量框架,得到与李亚普诺夫函数相关的凸LMI条件,并对闭环系统进行基于LMIs的鲁棒稳定性分析;最后,通过实验检验上述条件的可行性,证明方法的实用性和有效性.

符号说明:A^T是矩阵A的转置;A^ξ表示对称矩阵A^T+A;A≻B是矩阵不等式,表示A-B是对称正定的.如果N(X)在决策变量X中是仿射的,则称N(X)≻0型的一个矩阵不等式是一个LMI. $Ξ_{\bar{v}} = \{ξ_{v = 1, \dots, \bar{v}} \geq 0, \overset{\bar{v}}{\sum_{v = 1}} ξ_{v} = 1\}$ 是 $R^{\bar{v}}$ 中的单纯形,ξ_v为 $\bar{v}$ 维中每个维度的加权.对于离散时间信号v_k_≥0, ${(v)}_{2}^{2} = \overset{\infty}{\sum_{k = 0} {v^{T}}_{k}} v_{k}$ 是L₂范数平方, ${(v)}_{2, \bar{k}}^{2} = \overset{\bar{k}}{\sum_{k = 0} {v^{T}}_{k}} v_{k}$ 是截断范数平方, ${(v)}_{p}$ =sup_k_≥0( ${v^{T}}_{k}$ v_k)¹^/²是欧几里得范数随时间变化的峰值.

1 问题提出及状态反馈设计

考虑如下不确定系统^[10]:

(1)$\begin{matrix} & {{x}_{k}}_{+1}={{A}_{r}}(\theta ){{x}_{k}}+{{B}_{r}}(\theta ){{u}_{k}}+{{B}_{rw}}(\theta ){{w}_{k}} \\ & {{z}_{k}}={{C}_{rz}}(\theta ){{x}_{k}}+{{D}_{rzu}}(\theta ){{u}_{k}}+{{D}_{rzw}}(\theta ){{w}_{k}} \\ & {{y}_{k}}={{C}_{ry}}(\theta ){{x}_{k}} \\ \end{matrix}$

式中:x_k∈Rⁿ为状态向量;y_k∈R^p为测量输出;u_k∈R^m是控制输入向量;w_k∈R^v是扰动输入;z_k∈R^q是受控输出;矩阵A_r(θ)∈Rⁿ^×ⁿ(θ), B_r(θ)∈Rⁿ^×^m(θ), B_rw(θ)∈Rⁿ^×^v(θ), C_rz(θ)∈R^q^×ⁿ(θ), D_rzu(θ)∈R^q^×^m(θ), D_rzw(θ)∈R^q^×^v(θ), C_ry(θ)∈R^p^×ⁿ(θ)都是关于不确定参数θ的有理矩阵.假设参数θ位于集合Θ中,定义集合Θ为 $\bar{p}$ 个集合的交叉积,则连续不确定参数θ∈Θ={(θ₁, …, $θ_{\bar{p}}$ )∈Θ₁×…× $Θ_{\bar{p}}$ },其中θ的 $\bar{p}$ 个分量是 $R^{m_{p}}$ 的独立分量.假设每个集合Θ_p是具有 ${\bar{v}}_{p}$ 个来自集合V_p的顶点组成的多面体,V_p={ $θ_{p}^{[1]}$ , …, $θ_{p}^{[{\bar{v}}_{p}]}$ }.Θ_p是顶点的凸组合,Θ_p=Co(V_p)={θ_p= $\overset{{\bar{v}}_{p}}{\sum_{v_{p} = 1}} ξ_{p, v_{p}} θ_{p}^{[v_{p}]}$ : ξ_p∈ $Ξ_{{\bar{v}}_{p}}$ }.V=V₁×…× $V_{\bar{p}}$ 是参数的所有极值的集合,V的一个通用元素将用θ^[^v^]表示,其中v=[v₁ … $v_{\bar{p}}$ ]表示每个分量的顶点索引向量,后文使用ℓ表示所有v向量的集合^[10].验证集合V和ℓ的基数为, $\overset{=}{v} = \prod_{p = 1}^{\bar{p}} {\bar{v}}_{p}$ .

注1 文献[10]中仅考虑输出矩阵C_ry(θ)为一个常数的情形,而本文中输出矩阵C_ry(θ)是关于不确定参数θ的有理多项式矩阵,文献[10]中的研究仅为本文的特例,并不能解决本文所面对的问题.

首先,引入多仿射概念.如矩阵在每个θ_p中都是仿射的,则在参数θ中是多仿射的.同时,每个多仿射矩阵M_i(θ)可写成V中顶点的凸组合,M_i(θ)= $\overset{\overset{=}{v}}{\sum_{v = 1}}$ ξ_i_,_vM_i(θ^[^v^]),ξ_i∈ $Ξ_{\overset{=}{v}}$ .矩阵M(θ)也是多仿射的,M(θ)中的每个元素可表示为

(2)

m (θ) = \sum_{k_{1}, \dots, k_{N} \in {0,1}} α_{k_{1}, \dots, k_{N}} θ_{1}^{k_{1}} \dots θ_{N}^{k_{N}}

式中: $α_{k_{1}, \dots, k_{N}}$ ∈R;k₁, …, k_N∈{0,1}.

对上述不确定系统式(1),可重写为

(3)

[\begin{array}{l} x_{k + 1} \\ z_{k} \\ y_{k} \end{array}] = R (θ) [\begin{array}{l} x_{k} \\ u_{k} \\ w_{k} \end{array}]

式中:

(4)

R (θ) : = [\begin{array}{l} A_{r} (θ) & B_{r} (θ) & B_{r w} (θ) \\ C_{r z} (θ) & D_{r z u} (θ) & D_{r z w} (θ) \\ C_{r y} (θ) & 0 & 0 \end{array}] \in R^{(n + q + p) \times (n + m + v)} (θ)

将式(4)中R(θ)表示为如下DMAR形式^[10]:

(5)

R (θ) = [\begin{array}{l} E_{x} (θ) \\ E_{y} (θ) \\ E_{z} (θ) \end{array}] E_{π}^{- 1} (θ) M_{3} (θ)

式中:E_x(θ)∈Rⁿ^×^t(θ);E_y(θ)∈R^q^×^t(θ);E_z(θ)∈R^p^×^t(θ);E_π(θ)∈R^t^×^t(θ);M₃(θ)=[A(θ) B(θ) B_w(θ)]∈R^t^×(ⁿ⁺^m⁺^v⁾(θ).

假设基于系统式(1)的DMAR,构建新龙伯格类型的动态观测器与观测状态反馈器,以确保系统的鲁棒稳定性和输入/输出H_∞性能.动态观测器和观测状态反馈器分别表示为

(6)${{\hat{x}}_{k+1}}={{A}_{o}}{{\hat{x}}_{\text{k}}}+{{B}_{o}}{{u}_{k}}+L({{C}_{o}}{{\hat{x}}_{\text{k}}}-{{y}_{k}})$

(7)${{u}_{k}}=K{{\hat{x}}_{k}}$

式中: ${\hat{x}}_{k}$ ∈Rⁿ为观测状态;L为观测器增益;A_o、B_o、C_o为待求矩阵.

注2 构建的新龙伯格类型的动态观测器与传统龙伯格类型观测器的不同在于传统观测器中的C_o直接来自于不确定系统的已知输出矩阵,为研究对象自身的测量输出矩阵^[10,12].由于本研究中的系统测量输出矩阵不确定,故新构建的龙伯格类型观测器中含有对测量输出进行估计的待求参数C_o.

设计状态反馈增益K,使其具有状态反馈u_k=Kx_k的闭环系统,满足鲁棒稳定性和输入/输出H_∞性能.设计K的过程详见文献[10]的引理2和定理5.

2 鲁棒观测器设计

由于理想状态通常不可测量,所以在实践中状态反馈控制是基于状态估计 $\hat{x}$ 的反馈${{u}_{k}}=K{{\hat{x}}_{k}}$.基于此观测状态反馈,设计龙伯格类型的观测器如下:

(8)${{\hat{x}}_{k+1}}={{A}_{o}} ~ {{\hat{x}}_{\text{k}}}+{{B}_{o}}{{u}_{k}}+L({{C}_{o}}{{\hat{x}}_{\text{k}}}-{{y}_{k}})$

定义理想状态和估计状态的误差e_k=x_k- ${\hat{x}}_{k}$ ,以及$\epsilon_{k}=Ke_{k}$.为求取新龙伯格类型的观测器待求参数,提出新的系统的等价性引理和稳定性定理.

基于DMAR和S变量框架,得出以下与观测器设计相关的引理.

引理1 在DMAR式(5)下,设 ${\hat{A}}_{o}$ =A_o+B_oK+LC_o, ${η^{T}}_{o, k} = [\begin{array}{l} {e^{T}}_{k + 1} & {π^{T}}_{o 1, k} & {π^{T}}_{o 2, k} & {e^{T}}_{k} & {x^{T}}_{k} \end{array}]$ 和 $E_{o} (θ) = [\begin{array}{l} I & E_{x} (θ) & L E_{z} (θ) & - {\hat{A}}_{o} & {\hat{A}}_{o} \\ 0 & E_{π} (θ) & 0 & - B (θ) K & A (θ) + B (θ) K \\ 0 & 0 & E_{π} (θ) & 0 & A (θ) \end{array}]$ 对于由式(7)和式(8)定义的龙伯格观测器,E_o(θ)η_o_,_k=0的稳定性和输入/输出性能分别对应误差e_k=x_k- ${\hat{x}}_{k}$ 的稳定性和从x_k到$\epsilon_{k}$的转移性能.

注3 提出的引理1基于上述新龙伯格类型的观测器,结合DMAR和S变量框架得到,是下文引理和定理的基础.

证明在扰动w_k=0的情况下,联立式(1)、式(7)和式(8)进行简单操作,得到理想状态x_k和观测状态 ${\hat{x}}_{k}$ 之间的误差:

$\begin{matrix} & {{e}_{k}}_{+1}=({{{{\hat{A}}}}_{\text{o}}}-{{B}_{r}}(\theta )K){{e}_{k}}+({{A}_{r}}(\theta )+ \\ & {{B}_{r}}(\theta )K+L{{C}_{ry}}(\theta )-{{{{\hat{A}}}}_{\text{o}}}){{x}_{k}}= \\ & {{{{\hat{A}}}}_{\text{o}}}{{e}_{k}}-{{{{\hat{A}}}}_{\text{o}}}{{x}_{k}}+L{{E}_{z}}(\theta )E_{\pi }^{-1}(\theta )A(\theta ){{x}_{k}}+ \\ & {{E}_{x}}(\theta )E_{\pi }^{-1}(\theta )[(A(\theta )+B(\theta )K){{x}_{k}}-B(\theta )K{{e}_{k}}] \\ \end{matrix}$

由式(5)得到精确的E_o(θ)η_o_,_k=0,其中:

${{\pi }_{o}}_{1,k}=E_{\pi }^{-1}~(\theta )[B(\theta )K{{e}_{k}}-(A(\theta )+B(\theta )K){{x}_{k}}]$

${{\pi }_{o}}_{2,k}=-E_{\pi }^{-1}(\theta )A(\theta ){{x}_{k}}$

进行观测器设计前,为保持动态尽可能相似,需对预期的状态轨迹进行估计.文献[10]定理6中,理想状态x通过 ${(W x)}_{2}$ ≤使控制信号$\epsilon$的有界误差有界,其中Wx为观测状态轨迹,W=Q¹^/².

设计观测器的目标是提供一个估计 ${\hat{x}}_{k}$ ,使理想状态反馈控制的Kx_k与实际控制 ${\hat{K x}}_{k}$ 之间的误差$\epsilon_{k}$最小化,假设反馈增益K和状态x_k的可能轨迹矩阵Q固定,进行观测器矩阵A_o、 B_o、 C_o、 L的设计.

定义如下矩阵,在决策变量中是仿射的,在不确定性θ中为多仿射:

${{{\hat{S}}}_{\text{a}}}={{S}_{a}}+{{S}_{b}}K+{{S}_{lc}}$

N_{x} (θ) = [\begin{array}{l} S_{x} & S_{x} E_{x} (θ) & S_{l} E_{z} (θ) & - {\hat{S}}_{a} & {\hat{S}}_{a} \end{array}]

N_{π} (θ) = [\begin{array}{l} 0 & E_{π} (θ) & 0 & - B (θ) K & A (θ) + B (θ) K \\ 0 & 0 & E_{π} (θ) & 0 & A (θ) \end{array}]

定理1 假设存在2 $\overset{=}{v}$ 个对称正定矩阵 $P_{2}^{[v]}$ ≻0, $P_{p}^{[v]}$ ⪰K^TK和适当维数的矩阵S_x、S_a、S_b、S_l、S_lc、S₂_π、S_pπ使得下列LMIs对所有的v∈ℓ同时成立:

(9a)$\begin{matrix} & \text{diag}(P_{2}^{\left[ \text{v} \right]},0,{{K}^{T}}K-P_{2}^{\left[ \text{v} \right]},-\gamma _{2}^{2}Q)\prec \\ & {{\left( \left[ \begin{array}{*{35}{l}} I \\ 0 \\\end{array} \right]{{N}_{x}}\left( {{\theta }^{\left[ v \right]}} \right) \right)}^{\xi }}+{{\left( {{S}_{2 \pi }}{{N}_{\pi }}\left( {{\theta }^{\left[ v \right]}} \right) \right)}^{\xi }} \\ \end{matrix}$

(9b)$\begin{matrix} & \text{diag}(P_{p}^{\left[ \text{v} \right]},0,-P_{p}^{\left[ \text{v} \right]},-\gamma _{p}^{2}Q)\prec \\ & {{\left( \left[ \begin{array}{*{35}{l}} I \\ 0 \\\end{array} \right]{{N}_{x}}\left( {{\theta }^{\left[ v \right]}} \right) \right)}^{\xi }}+{{\left( {{S}_{\text{p }\!\!\pi }}{{N}_{\pi }}\left( {{\theta }^{\left[ v \right]}} \right) \right)}^{\xi }} \\ \end{matrix}$

那么,A_o= $S_{x}^{- 1}$ S_a, B_o= $S_{x}^{- 1}$ S_b, L= $S_{x}^{- 1}$ S_l, C_o= $S_{l}^{- 1}$ S_lc定义了一个形式为式(8)的观测器,保证下列两个范数到范数和范数到峰值的特性:≤γ₂ ${(W x)}_{2}$ , ≤γ_p $(W x)$ ,其中$\epsilon_{k}=Ke_{k}$.这些特性包括所有有界状态x和所有不确定性θ∈Θ.

证明由于矩阵不等式的凸性和参数相关矩阵的多仿射性质,当且仅当上述公式中的θ^[^v^]被θ取代, $P_{2}^{[v]}$ 、 $P_{p}^{[v]}$ 分别替换为P₂(θ)、 P_p(θ)后,相似公式对所有的θ∈Θ同时成立,故LMIs式(9a)和(9b)可行.同时,有S_a=S_xA_o, S_b=S_xB_o, S_l=S_xL, S_lc=S_lC_o,这些变量替换后的LMIs为

(10)$\text{diag}({{P}_{2}}(\theta ),0,{{K}^{T}}K-{{P}_{2}}(\theta ),-\gamma _{2}^{2}Q)\prec {{({{S}_{2}}{{E}_{o}}(\theta ))}^{\xi }}$

(11)$\text{diag}({{P}_{p}}(\theta ),0,-{{P}_{p}}(\theta ),-\gamma _{p}^{2}Q)\prec {{\left( {{S}_{p}}{{E}_{o}}\left( \theta \right) \right)}^{\xi }}$

式中: $S_{2} = [\begin{array}{l} \begin{array}{l} S_{x} \\ 0 \end{array} & | S_{2 π} \end{array}]$ ; $S_{p} = [\begin{array}{l} \begin{array}{l} S_{x} \\ 0 \end{array} & | S_{p π} \end{array}]$ .通过向量η_o_,_k≠0对这两个不等式进行同余运算,得到的观测误差同时满足以下两个公式:

(12)$\begin{gathered}\boldsymbol{e}_{k+1}^{\mathrm{T}} \boldsymbol{P}_2(\boldsymbol{\theta}) \boldsymbol{e}_{k+1}-\boldsymbol{e}_k^{\mathrm{T}} \boldsymbol{P}_2(\boldsymbol{\theta}) \boldsymbol{e}_k+ \\ \boldsymbol{\epsilon}_k^{\mathrm{T}} \boldsymbol{\epsilon}_k-\gamma_2^2 \boldsymbol{x}_k^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{x}_k<0 \end{gathered}$

(13)${{e}^{\text{T}}}_{\text{k}+1}{{P}_{p}}(\theta ){{e}_{k}}_{+1}-{{e}^{\text{T}}}_{k}{{P}_{p}}(\theta ){{e}_{k}}-\gamma _{p}^{2}{{x}^{\text{T}}}_{k}Q{{x}_{k}}<0$

由上述两式可知,系统是渐进稳定且满足≤γ₂ ${(W x)}_{2}$ , ≤γ_p $(W x)$ 的,具体证明过程见文献[10].

3 闭环系统的稳定性分析

因分离原理不适用于不确定系统,故需首先考虑小增益定理,对整体观测状态反馈设计进行鲁棒稳定性分析.与文献[10]类似, ${(W x)}_{2}$ ≤保证以$\epsilon_{k}$为输入,以 ${\tilde{x}}_{k}$ =Wx_k为输出的第1个系统的L₂诱导范数小于1.同时,定理1保证了以 ${\tilde{x}}_{k}$ 为输入,以$\epsilon_{k}$为输出的第2个系统的L₂诱导范数小于γ₂.根据小增益定理,如γ₂<1,则闭环系统稳定.由于上界对所有不确定性θ∈Θ都有效,所以稳定性是鲁棒的.

上述关于闭环稳定的理论是保守的,γ₂≥1时,闭环也可能是稳定的^[10].对具有观测状态反馈控制的闭环系统进行基于LMIs的鲁棒稳定性分析.

引理2 在DMAR式(5)下,假设

${η^{T}}_{c, k} = [\begin{array}{l} {\hat{x}}^{T}_{k + 1} & {x^{T}}_{k + 1} & {z^{T}}_{k} & {π^{T}}_{c 1, k} & {π^{T}}_{c 2, k} & {\hat{x}}^{T}_{k} & {x^{T}}_{k} & {w^{T}}_{k} \end{array}]$

$E_{c} (θ) = [\begin{array}{l} I & 0 & 0 & 0 & - L E_{z} (θ) & - {\hat{A}}_{o} & 0 & 0 \\ 0 & I & 0 & E_{x} (θ) & 0 & 0 & 0 & 0 \\ 0 & 0 & I & E_{y} (θ) & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & E_{π} (θ) & 0 & B (θ) K & A (θ) & B_{w} (θ) \\ 0 & 0 & 0 & 0 & E_{π} (θ) & 0 & A (θ) & 0 \end{array}]$

E_c(θ)η_c_,_k=0的稳定性和输入/输出性能相当于系统式(1)、观测器式(8)和反馈u_k=K ${\hat{x}}^{T}_{k}$ 组成的闭环系统的稳定性和输入/输出性能.证明可由文献[10]的引理2和本文的引理1得到.

定理2 假设存在 $\overset{=}{v}$ 个对称正定矩阵 $P_{c}^{[v]}$ ≻0和一个具有适当维数的矩阵S_c,使得下列LMIs对所有v∈ℓ同时成立:

(14)$\text{diag}(P_{c}^{\left[ \text{v} \right]},I,0,0,-P_{c}^{\left[ \text{v} \right]},-\mu _{c}^{2}I)\prec {{\left( {{S}_{c}}{{E}_{c}}\left( {{\theta }^{\left[ v \right]}} \right) \right)}^{\xi }}$

则系统式(1)、式(7)和式(8)组成的闭环系统是鲁棒稳定的,所有θ∈Θ,其H_∞性能小于μ_c.

4 数值例子

例1 通过下例证明上述设计程序的有效性:

${{x}_{k}}_{+1}=\left[ \begin{array}{*{35}{l}} -\theta _{1}^{2}/{{\theta }_{2}} & -{{\theta }_{1}} \\ 1 & 0 \\ \end{array} \right]{{x}_{k}}+\left[ \begin{array}{*{35}{l}} 0 \\ {{\theta }_{2}} \\ \end{array} \right]{{u}_{k}}+\left[ \begin{array}{*{35}{l}} {{\theta }_{1}} \\ 0 \\ \end{array} \right]{{w}_{k}}$

${{z}_{k}}=\left[ \begin{array}{*{35}{l}} 1 & 0 \\ \end{array} \right]{{x}_{k}}+{{\theta }_{2}}{{u}_{k}},{{y}_{k}}=\left[ \begin{array}{*{35}{l}} {{\theta }_{2}} & 0 \\ \end{array} \right]{{x}_{k}}$

可以得到一个如下的DMAR:

${{E}_{x}}=\left[ \begin{array}{*{35}{l}} {{\theta }_{1}} & 0 \\ 0 & 1 \\ \end{array} \right],{{E}_{y}}=\left[ \begin{array}{*{35}{l}} 0 & 1 \\ \end{array} \right],{{E}_{z}}=\left[ \begin{array}{*{35}{l}} 0 & {{\theta }_{2}} \\ \end{array} \right]$

${{E}_{\pi }}=\left[ \begin{array}{*{35}{l}} {{\theta }_{2}} & 0 \\ 0 & 1 \\ \end{array} \right],A=\left[ \begin{array}{*{35}{l}} -{{\theta }_{1}} & -{{\theta }_{2}} \\ 1 & 0 \\ \end{array} \right]$

$B=\left[ \begin{array}{*{35}{l}} 0 \\ {{\theta }_{2}} \\ \end{array} \right],{{B}_{w}}=\left[ \begin{array}{*{35}{l}} {{\theta }_{2}} \\ 0 \\ \end{array} \right]$

其中不确定参数在标称值 1 附近,差异为δ₁、 δ₂的间隔内,即θ₁∈[1-δ₁, 1+δ₁]和θ₂∈[1-δ₂, 1+δ₂].δ₁、 δ₂表示参数变化的范围,是对现实中电阻(容、抗)、速度等不确定范围的数学简单描述.

本例目的是为上述含有不确定有理参数的不稳定开环系统设计一个观测状态反馈控制器,使其闭环系统稳定且满足一定性能.需特别指出的是,文献[10]中的方法仅适用于系统测量输出矩阵为常数不确定性系统,因此不能对上述不确定系统进行鲁棒状态反馈设计.

使用所提出的设计方案设计控制器.取不同差异和优化设置的结果如表1所示.β₂、 β_p分别为收敛速度和误差(受控输出)峰值加权,其中差异(δ₁, δ₂)=(0, 0)表示没有不确定.当(δ₁, δ₂)=(0, 0) 时,取μ_d=10;其余取值时,最小化μ_d.所有LMIs都通过YALMIP解析器^[13]构建并使用SDPT3求解器^[14]进行求解.

表1 不同差异和优化设置的结果

Tab.1 Results of different diffs and optimization settings

差异(δ₁, δ₂)	加权因子 (β₂, β_p)	转移特性(γ₂, γ_p)	H_∞性能μ_c
(0, 0)	(1, 1)	(1.5×10^-4, 1.5×10^-4)	1.0561
(0.1, 0)	(1, 1)	(0.421 8, 0.397 0)	1.6531
(0, 0.1)	(1, 1)	(0.038 4, 0.038 4)	1.5573
(0.1, 0.1)	(1, 1)	(0.481 9, 0.428 9)	2.3533
(0.2, 0.2)	(10, 1)	(3.845 1, 3.703 4)	13.3457
(0.2, 0.2)	(1, 1)	(3.939 4, 3.515 5)	无可行解
(0.2, 0.2)	(1, 10)	(4.879 7, 3.137 5)	9.6805

新窗口打开| 下载CSV

由表1可知,不同差异和优化设置的结果可以得到不同的转移特性和H_∞性能μ_c,证明测量输出矩阵含有不确定参数的不确定系统设计的程序确实有效.

为直观表现控制效果,对δ₁=δ₂=0.2, β₂=1, β_p=1进行测试,可得以下观测矩阵:

$Q = [\begin{array}{l} 0.117 & 0.067 \\ 0.067 & 0.052 \end{array}]$

$A_{o} = [\begin{array}{l} - 0.434 & - 0.909 \\ 0.650 & 1.031 \end{array}]$ , $B_{o} = [\begin{array}{l} 0.869 \\ - 0.612 \end{array}]$

$C_{o} = [\begin{array}{l} - 0.7723 & - 1.0927 \end{array}]$ , $L = [\begin{array}{l} 0.525 \\ - 0.828 \end{array}]$

$K = [\begin{array}{l} 0.690 & 1.274 \end{array}]$

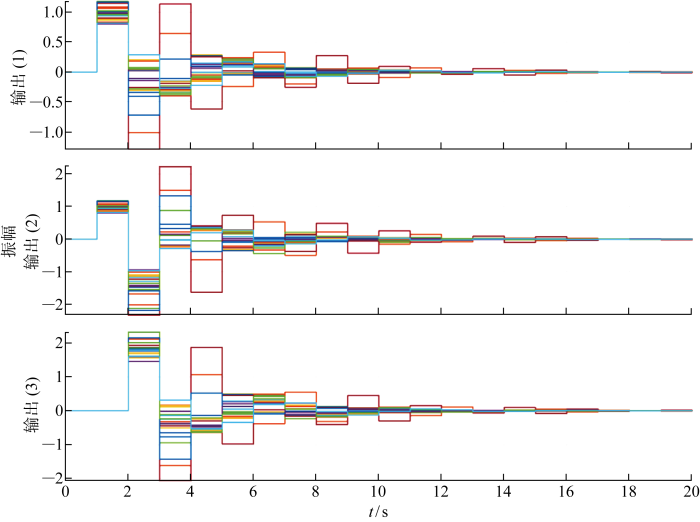
得出含有鲁棒观测状态反馈控制的闭环冲激响应如图1所示,其中,输出(1)是z_k,输出(2)、(3)是理想状态和观测状态之间的误差e_k.取20个随机选择的不确定性值得到冲激响应,可知不论是输出z_k,还是理想状态和观测状态之间的误差e_k都是收敛的,说明闭环系统呈渐进稳定趋势.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 冲激响应

Fig.1 Impulse response

5 结语

提出一种基于新龙伯格类型观测器的鲁棒状态反馈设计方法.通过实验可知,此观测器适用于测量输出矩阵含有不确定参数的不确定系统模型.同时,基于此类型观测器结合DMAR和S变量框架,提出数值可处理的与李亚普诺夫函数相关的LMIs条件.综上所述,提出的基于新龙伯格类型观测器的鲁棒观测状态反馈设计方法研究了更为一般的不确定性系统,可以得到与文献[10]中相似的结论.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

金鹏, 马倩, 周国鹏.

负荷扰动互联电力系统模糊自适应输出跟踪与干扰抗御

[J]. 控制理论与应用, 2021, 38(5): 571-577.

[本文引用: 1]

JIN

Peng

, MA

Qian

, ZHOU

Guopeng

Fuzzy adaptive output tracking and disturbance rejection for interconnected power systems with load disturbance

[J]. Control Theory & Applications, 2021, 38(5): 571-577.

[本文引用: 1]

[2]

陈龙胜, 王琦, 何国毅.

非仿射纯反馈非线性切换系统自适应控制

[J]. 上海交通大学学报, 2020, 54(9): 981-986.

DOI:10.16183/j.cnki.jsjtu.2020.137 [本文引用: 2]

针对一类单输入单输出的非仿射纯反馈非线性切换系统,研究了一种在任意切换下的自适应控制策略.首先,引入中值定理处理系统的非仿射特性问题,并利用径向基函数神经网络逼近系统的未知非线性动态.然后,采用 Nussbaum函数处理系统控制增益未知的问题,且在反演设计的每一步引入低通滤波器以解决“微分爆炸”问题.最后,基于共同Lyapunov函数设计状态反馈控制器,并分析闭环系统的稳定性.所设计的控制器避免了切换发生时控制参数跳变和调节参数过多的问题,减少了计算负荷,可以保证闭环系统所有信号半全局一致有界,且跟踪误差可收敛到原点的一个较小邻域.仿真结果验证了控制策略的有效性.

CHEN

Longsheng

, WANG

, HE

Guoyi

Adaptive control of non-affine pure feedback nonlinear switching systems

[J]. Journal of Shanghai Jiao Tong University, 2020, 54(9): 981-986.

[本文引用: 2]

[3]

陈刚, 李志勇.

集合约束下多智能体系统分布式固定时间优化控制

[J]. 自动化学报, 2022, 48(9): 2254-2264.

[本文引用: 2]

CHEN

Gang

, LI

Zhiyong

Distributed fixed-time optimal control of multi-agent system with set constraints

[J]. Acta Automatica Sinica, 2022, 48(9): 2254-2264.

[本文引用: 2]

[4]

Z J

, XIA

Y Q

, WANG

D H

, et al.

Neural network-based control of networked trilateral teleoperation with geometrically unknown constraints

[J]. IEEE Transactions on Cybernetics, 2016, 46(5): 1051-1064.

DOI:10.1109/TCYB.2015.2422785 PMID:25956001 [本文引用: 2]

Most studies on bilateral teleoperation assume known system kinematics and only consider dynamical uncertainties. However, many practical applications involve tasks with both kinematics and dynamics uncertainties. In this paper, trilateral teleoperation systems with dual-master-single-slave framework are investigated, where a single robotic manipulator constrained by an unknown geometrical environment is controlled by dual masters. The network delay in the teleoperation system is modeled as Markov chain-based stochastic delay, then asymmetric stochastic time-varying delays, kinematics and dynamics uncertainties are all considered in the force-motion control design. First, a unified dynamical model is introduced by incorporating unknown environmental constraints. Then, by exact identification of constraint Jacobian matrix, adaptive neural network approximation method is employed, and the motion/force synchronization with time delays are achieved without persistency of excitation condition. The neural networks and parameter adaptive mechanism are combined to deal with the system uncertainties and unknown kinematics. It is shown that the system is stable with the strict linear matrix inequality-based controllers. Finally, the extensive simulation experiment studies are provided to demonstrate the performance of the proposed approach.

[5]

SHANG

W W

, XIE

, ZHANG

, et al.

Adaptive cross-coupled control of cable-driven parallel robots with model uncertainties

[J]. IEEE Robotics and Automation Letters, 2020, 5(3): 4110-4117.

DOI:10.1109/LSP.2016. URL [本文引用: 2]

[6]

GEROMEL

J C

, KOROGUI

R H

, BERNUSSOU

H₂ and H_∞ robust output feedback control for continuous time polytopic systems

[J]. IET Control Theory Applications, 2007, 1(5): 1541-1549.

DOI:10.1049/iet-cta:20060460 URL [本文引用: 2]

[7]

S S

, LI

Z J

Robust adaptive control for a class of MIMO nonlinear systems by state and output feedback

[J]. IEEE Transactions on Automatic Control, 2014, 59(6): 1624-1629.

DOI:10.1109/TAC.9 URL [本文引用: 2]

[8]

CHESI

H₂ and H_∞ robust output feedback control for continuous time polytopic systems

[J]. IEEE Transactions on Automatic Control, 2014, 59(6): 1618-1623.

DOI:10.1109/TAC.2013.2293453 URL [本文引用: 3]

[9]

LIEN

C H

, YU

K W

LMI optimization approach on robustness and H_∞ control analysis for observer-based control of uncertain systems

[J]. Chaos, Solitons & Fractals, 2008, 36(3): 617-627.

DOI:10.1016/j.chaos.2006.06.076 URL [本文引用: 3]

[10]

PEAUCELLE

, EBIHARA

, HOSOE

Robust observed-state feedback design for discrete-time systems rational in the uncertainties

[J]. Automatica, 2017, 76: 96-102.

DOI:10.1016/j.automatica.2016.10.003 URL [本文引用: 16]

[11]

PEREIRA

R L

, DE

OLIVEIRA M S

On robust stabilization of discrete-time LPV/LFR systems

[J]. IEEE Transactions on Automatic Control, 2023, 68(1): 448-453.

DOI:10.1109/TAC.2022.3140255 URL [本文引用: 1]

[12]

LUENBERGER

An introduction to observers

[J]. IEEE Transactions on Automatic Control, 1971, 16(6): 596-602.

DOI:10.1109/TAC.1971.1099826 URL [本文引用: 1]

[13]

LOFBERG

YALMIP: A toolbox for modeling and optimization in MATLAB

[C]// 2004 IEEE International Conference on Robotics and Automation. Taipei, China: IEEE, 2004: 284-289.

[本文引用: 1]

[14]

TOH

K C

, TODD

M J

, TÜTÜNCÜ

R H

. On the Implementation and usage of SDPT3-A Matlab software package for semidefinite-quadratic-linear programming, version 4.0[M]//Handbook on semidefinite, conic and polynomial optimization. Boston, MA: Springer, 2012: 715-754.

[本文引用: 1]

负荷扰动互联电力系统模糊自适应输出跟踪与干扰抗御

2021

... 许多物理系统包含固有不确定性,例如电力系统^[1]、切换系统^[2]、多智能体系统^[3]、机器人系统^[4-5],而不确定性会严重影响系统的稳定性和闭环系统性能^[2⇓⇓-5],因此对系统进行控制设计时有必要考虑其不确定性.为此,许多学者提出了不同的鲁棒控制设计方法,其中一种代表性设计思路是反馈控制^[6⇓⇓-9]. ...

Fuzzy adaptive output tracking and disturbance rejection for interconnected power systems with load disturbance

2021

非仿射纯反馈非线性切换系统自适应控制

2020

... [2⇓⇓-5],因此对系统进行控制设计时有必要考虑其不确定性.为此,许多学者提出了不同的鲁棒控制设计方法,其中一种代表性设计思路是反馈控制^[6⇓⇓-9]. ...

Adaptive control of non-affine pure feedback nonlinear switching systems

2020

集合约束下多智能体系统分布式固定时间优化控制

2022

... ⇓⇓-5],因此对系统进行控制设计时有必要考虑其不确定性.为此,许多学者提出了不同的鲁棒控制设计方法,其中一种代表性设计思路是反馈控制^[6⇓⇓-9]. ...

Distributed fixed-time optimal control of multi-agent system with set constraints

2022

Neural network-based control of networked trilateral teleoperation with geometrically unknown constraints

2016

... ⇓-5],因此对系统进行控制设计时有必要考虑其不确定性.为此,许多学者提出了不同的鲁棒控制设计方法,其中一种代表性设计思路是反馈控制^[6⇓⇓-9]. ...

Adaptive cross-coupled control of cable-driven parallel robots with model uncertainties

2020

... -5],因此对系统进行控制设计时有必要考虑其不确定性.为此,许多学者提出了不同的鲁棒控制设计方法,其中一种代表性设计思路是反馈控制^[6⇓⇓-9]. ...

H₂ and H_∞ robust output feedback control for continuous time polytopic systems

2007

... 对不确定系统的反馈控制大致分为输出反馈控制和状态反馈控制两大类.输出反馈直接通过测量输出进行反馈以便于工程应用,得到许多研究者的青睐,文献[6]中提出一种关于多面体系统的H₂和H_∞输出反馈控制方法,文献[8]中通过鲁棒稳定函数来实现鲁棒静态输出反馈控制器.这些控制方案大多应用二次稳定性的概念,只需线性矩阵不等式(LMI)在多面体的顶点上收敛,以保证系统稳定性.状态反馈在实践中状态变量难以测量,往往需要借助观测器,文献[9]中提出基于观测器不确定系统的鲁棒性LMI优化控制方法,能保证不确定系统的稳定性.但当涉及到不确定有理参数时,系统基于观测器的线性矩阵不等式组(LMIs)设计,大多为非凸的^[7]、保守的^[9]或需要计算和操纵特征多项式的参数相关系数^[8]. ...

Robust adaptive control for a class of MIMO nonlinear systems by state and output feedback

2014

H₂ and H_∞ robust output feedback control for continuous time polytopic systems

2014

... [8]. ...

LMI optimization approach on robustness and H_∞ control analysis for observer-based control of uncertain systems

2008

... [9]或需要计算和操纵特征多项式的参数相关系数^[8]. ...

Robust observed-state feedback design for discrete-time systems rational in the uncertainties

2017

... 为此,文献[10]中提出一种基于凸LMIs的启发式算法,其中详细描述的描述符多仿射表示(DMAR)和松弛变量(S)方法对不确定的有理参数具有效性.同时,基于多仿射的性质和S变量的框架,可得到凸的LMIs及可行解.但当与测量输出相关的矩阵含有不确定参数时,其鲁棒反馈设计更为复杂.因鲁棒观测状态反馈设计需涉及观测器矩阵C是一个待求参数,而不再是系统自身的测量输出矩阵,这使S变量LMIs框架更加复杂,此问题仍是一个挑战^[10-11]. ...

... [10-11]. ...

... 考虑如下不确定系统^[10]: ...

... 式中:x_k∈Rⁿ为状态向量;y_k∈R^p为测量输出;u_k∈R^m是控制输入向量;w_k∈R^v是扰动输入;z_k∈R^q是受控输出;矩阵A_r(θ)∈Rⁿ^×ⁿ(θ), B_r(θ)∈Rⁿ^×^m(θ), B_rw(θ)∈Rⁿ^×^v(θ), C_rz(θ)∈R^q^×ⁿ(θ), D_rzu(θ)∈R^q^×^m(θ), D_rzw(θ)∈R^q^×^v(θ), C_ry(θ)∈R^p^×ⁿ(θ)都是关于不确定参数θ的有理矩阵.假设参数θ位于集合Θ中,定义集合Θ为

\bar{p}

个集合的交叉积,则连续不确定参数θ∈Θ={(θ₁, …,

θ_{\bar{p}}

)∈Θ₁×…×

Θ_{\bar{p}}

},其中θ的

\bar{p}

个分量是

R^{m_{p}}

的独立分量.假设每个集合Θ_p是具有

{\bar{v}}_{p}

个来自集合V_p的顶点组成的多面体,V_p={

θ_{p}^{[1]}

, …,

θ_{p}^{[{\bar{v}}_{p}]}

}.Θ_p是顶点的凸组合,Θ_p=Co(V_p)={θ_p=

\overset{{\bar{v}}_{p}}{\sum_{v_{p} = 1}} ξ_{p, v_{p}} θ_{p}^{[v_{p}]}

: ξ_p∈

Ξ_{{\bar{v}}_{p}}

}.V=V₁×…×

V_{\bar{p}}

是参数的所有极值的集合,V的一个通用元素将用θ^[^v^]表示,其中v=[v₁ …

v_{\bar{p}}

]表示每个分量的顶点索引向量,后文使用ℓ表示所有v向量的集合^[10].验证集合V和ℓ的基数为,

\overset{=}{v} = \prod_{p = 1}^{\bar{p}} {\bar{v}}_{p}

. ...

... 注1 文献[10]中仅考虑输出矩阵C_ry(θ)为一个常数的情形,而本文中输出矩阵C_ry(θ)是关于不确定参数θ的有理多项式矩阵,文献[10]中的研究仅为本文的特例,并不能解决本文所面对的问题. ...

... 的有理多项式矩阵,文献[10]中的研究仅为本文的特例,并不能解决本文所面对的问题. ...

... 将式(4)中R(θ)表示为如下DMAR形式^[10]: ...

... 注2 构建的新龙伯格类型的动态观测器与传统龙伯格类型观测器的不同在于传统观测器中的C_o直接来自于不确定系统的已知输出矩阵,为研究对象自身的测量输出矩阵^[10,12].由于本研究中的系统测量输出矩阵不确定,故新构建的龙伯格类型观测器中含有对测量输出进行估计的待求参数C_o. ...

... 设计状态反馈增益K,使其具有状态反馈u_k=Kx_k的闭环系统,满足鲁棒稳定性和输入/输出H_∞性能.设计K的过程详见文献[10]的引理2和定理5. ...

... 进行观测器设计前,为保持动态尽可能相似,需对预期的状态轨迹进行估计.文献[10]定理6中,理想状态x通过

{(W x)}_{2}

≤使控制信号

$\epsilon$

的有界误差有界,其中Wx为观测状态轨迹,W=Q¹^/². ...

... 由上述两式可知,系统是渐进稳定且满足≤γ₂

{(W x)}_{2}

, ≤γ_p

(W x)

的,具体证明过程见文献[10]. ...

... 因分离原理不适用于不确定系统,故需首先考虑小增益定理,对整体观测状态反馈设计进行鲁棒稳定性分析.与文献[10]类似,

{(W x)}_{2}

≤保证以

$\epsilon_{k}$

为输入,以

{\tilde{x}}_{k}

=Wx_k为输出的第1个系统的L₂诱导范数小于1.同时,定理1保证了以

{\tilde{x}}_{k}

为输入,以

$\epsilon_{k}$

为输出的第2个系统的L₂诱导范数小于γ₂.根据小增益定理,如γ₂<1,则闭环系统稳定.由于上界对所有不确定性θ∈Θ都有效,所以稳定性是鲁棒的. ...

... 上述关于闭环稳定的理论是保守的,γ₂≥1时,闭环也可能是稳定的^[10].对具有观测状态反馈控制的闭环系统进行基于LMIs的鲁棒稳定性分析. ...

... E_c(θ)η_c_,_k=0的稳定性和输入/输出性能相当于系统式(1)、观测器式(8)和反馈u_k=K

{\hat{x}}^{T}_{k}

组成的闭环系统的稳定性和输入/输出性能.证明可由文献[10]的引理2和本文的引理1得到. ...

... 本例目的是为上述含有不确定有理参数的不稳定开环系统设计一个观测状态反馈控制器,使其闭环系统稳定且满足一定性能.需特别指出的是,文献[10]中的方法仅适用于系统测量输出矩阵为常数不确定性系统,因此不能对上述不确定系统进行鲁棒状态反馈设计. ...

... 提出一种基于新龙伯格类型观测器的鲁棒状态反馈设计方法.通过实验可知,此观测器适用于测量输出矩阵含有不确定参数的不确定系统模型.同时,基于此类型观测器结合DMAR和S变量框架,提出数值可处理的与李亚普诺夫函数相关的LMIs条件.综上所述,提出的基于新龙伯格类型观测器的鲁棒观测状态反馈设计方法研究了更为一般的不确定性系统,可以得到与文献[10]中相似的结论. ...

On robust stabilization of discrete-time LPV/LFR systems

2023

An introduction to observers

1971

YALMIP: A toolbox for modeling and optimization in MATLAB

2004

... 使用所提出的设计方案设计控制器.取不同差异和优化设置的结果如表1所示.β₂、 β_p分别为收敛速度和误差(受控输出)峰值加权,其中差异(δ₁, δ₂)=(0, 0)表示没有不确定.当(δ₁, δ₂)=(0, 0) 时,取μ_d=10;其余取值时,最小化μ_d.所有LMIs都通过YALMIP解析器^[13]构建并使用SDPT3求解器^[14]进行求解. ...

2012

〈

〉