圆柱薄膜振动特性

doi:10.16183/j.cnki.jsjtu.2022.396

圆柱薄膜振动特性

黄涛¹^,², 何泽青^,¹^,², 宋林¹

1.中国科学院空天信息创新研究院, 北京 100094

2.中国科学院大学航空宇航学院, 北京 100040

Vibration Characteristics of Cylindrical Membrane

HUANG Tao¹^,², HE Zeqing^,¹^,², SONG Lin¹

1. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China

2. School of Aeronautics and Astronautics, University of Chinese Academy of Sciences, Beijing 100040, China

通讯作者: 何泽青,高级工程师;E-mail:zqhe@aoe.ac.cn.

责任编辑: 王一凡

收稿日期: 2022-10-8 修回日期: 2022-12-18 接受日期: 2023-01-6

Received: 2022-10-8 Revised: 2022-12-18 Accepted: 2023-01-6

作者简介 About authors

黄涛(1997-),硕士生,从事飞行器结构动力学研究.

摘要

根据达朗贝尔原理建立圆柱状薄膜非线性振动方程并对其展开分析与试验验证.建立圆柱膜振动问题的控制方程组,依据薄膜振动物理方程与边界条件简化方程组并求解;得到圆柱膜非线性振动频率解析解,并通过有限元仿真对其线性解析解进行验证.结果表明,理论计算与数值仿真结果误差较小,有限元方法适用于柔性薄膜结构模态分析.采用三维激光扫描式测振系统测试圆柱膜在空气环境中的振动频率,利用有限元分析软件获得圆柱膜干模态和湿模态振动频率并提取空气附加质量系数.结果表明,圆柱膜振动湿模态测试结果与数值分析结果具有良好的一致性,地面空气附加质量对圆柱膜振动的影响与薄膜自身质量处于同一量级.

关键词： 非线性振动; 湿模态; 空气附加质量; 曲率薄膜

Abstract

Based on the principle of D’Alembert, the nonlinear vibration equation of cylindrical membrane is established, and the analysis and experimental verification of it are conducted. The control equation system for cylindrical membrane vibration problems is established, and the equation system according to the physical equations and boundary conditions of thin diaphragms is simplified and solved, the analytical solution of nonlinear vibration frequency of cylindrical membrane is obtained, and the linear analytical solution is verified by finite element simulation, which shows that the error between theoretical calculation and numerical simulation is small, and the applicability of finite element method to the modal analysis of flexible membrane structure is verified. A 3D laser scanning vibration measurement system is used to test the vibration frequency of cylindrical membranes in the air environment. The finite element analysis software is used to obtain the dry mode and wet mode vibration frequencies of cylindrical membranes and extract the additional mass coefficients of air. The results showed that the test results of the vibration in wet mode have a good consistency with the numerical analysis results, and the influence of the additional quality of the ground air on the cylindrical membrane is in the same order of magnitude as its own mass.

Keywords： nonlinear vibration; wet modal; additional mass of air; curvature membrane

PDF (4517KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄涛, 何泽青, 宋林. 圆柱薄膜振动特性[J]. 上海交通大学学报, 2024, 58(4): 428-437 doi:10.16183/j.cnki.jsjtu.2022.396

HUANG Tao, HE Zeqing, SONG Lin. Vibration Characteristics of Cylindrical Membrane[J]. Journal of Shanghai Jiaotong University, 2024, 58(4): 428-437 doi:10.16183/j.cnki.jsjtu.2022.396

薄膜结构具有质量轻、易折叠、高强度、化学稳定等特点,在浮空器、新兴建筑和航天等领域有着广泛的应用前景^[1].薄膜结构主要应用场景以大跨度、小质量为主,使其普遍存在大变形的振动特性,为有效避免系留气球、飞艇、航天充气舱等大型薄膜结构的共振现象出现,研究曲率薄膜结构自振特性显得尤为重要.

当前对于膜结构振动特性的研究对象主要以平面薄膜结构为主.邱慧等^[2]对多花边平面薄膜结构湿模态展开有限元仿真和试验测试,分析了绳索拉力和花边半径对膜结构基频的影响;张祎贝等^[3]提出采用网格膜作为矩形膜面的等效替代以减小地面空气附加质量的影响,进行动力学试验并建立了等效准则;Xiao等^[4]对膜结构预应力导入方式及预应力对膜结构模态的影响进行了分析和试验;张宇等^[5]构建了应用于软式飞艇、高空气球等薄膜结构的非定常显示动力学流固耦合分析框架,表明飞艇振动主频与其内外压差存在近似线性;Tatematsu 等^[6]通过试验分析不同尺寸薄膜结构相似关系的影响因素;陈宇峰等^[7]利用兰索斯法对25 m平流层验证飞艇为基本分析对象进行模态数值分析,表明膜结构外形尺寸、内外压差和周围空气附加质量是模态的重要影响因素;张祎贝等^[8]制备了低真空试验装置,其试验结果与仿真分析有良好的对应关系,并验证了模态分析中常用的Lancoz法和随机子空间法的一致性;Li等^[9]利用振型分区方法分析了平面圆形膜和空间三角形膜的振动特性;何泽青等^[10]基于大挠度理论建立了正交异性平面薄膜的动力学方程,利用伽辽金法得到薄膜非线性振动频率的近似解并验证了其精确度,为膜结构工程设计提供了理论计算依据;Timoshenko等^[11]对具有规则外形的矩形膜和圆形膜的振动频率和振型进行了理论求解;Lee等^[12]利用共旋有限元壳单元方法,分析了流固耦合效应微型薄膜翼面的影响.

以上模态分析主要以平面薄膜结构为基础进行,但在薄膜结构的主要应用中,例如大型飞艇、系留气球、高空科学气球等场景中,薄膜都呈现为非平面状态.本文参考圆柱薄壳非线性振动,结合薄膜振动无矩无剪力的特点,建立圆柱形曲率薄膜法向自由振动的动力学控制方程组,引入边界条件得到其自由振动及具有初始挠度的振动频率的解析解,分析非线性因素对圆柱膜振动的影响.在空气环境中测试圆柱膜自由振动频率,并结合圆柱膜湿模态仿真结果提取空气附加质量系数,验证试验测试、仿真分析和理论计算的准确性,同时掌握空气附加质量对圆柱膜自由振动的影响程度,以提升圆柱膜振动特性研究在工程应用中的便利性.

1 圆柱膜振动方程推导

1.1 振动微分方程

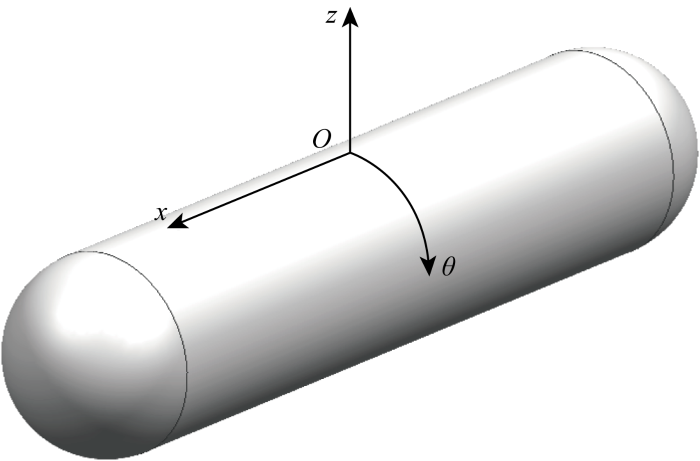
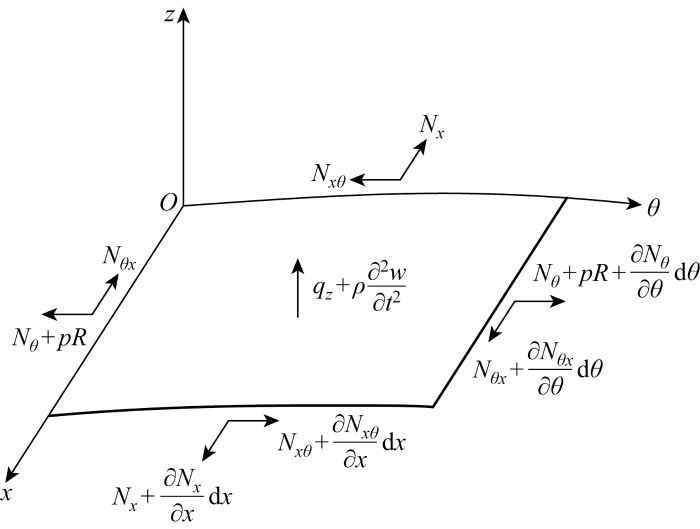
图1所示为有限长闭合圆柱膜结构,两端同为半径为R的半球形状.在圆柱段薄膜上截取一弧长分别为dx和Rdθ的微元并对其展开分析,截取的微元如图2所示.首先在圆柱膜上选择正交曲线坐标系Oxθz,其中x轴与圆柱轴线平行.微元上作用有4个应力分量:N_x、N_θ、N_xθ和N_θx,其中N_x和N_θ分别为垂直于x轴和θ轴截面的单位长度上的切应力,N_xθ和N_θx分别为垂直于x轴和θ轴截面的单位长度上的平行于θ轴和x轴的切应力,图上箭头均表示各分量的正方向.假设圆柱状膜结构受到压差p的作用,闭合膜结构会受压成型且有一定刚度,并在微元上产生环向切应力pR和轴向切应力 $\frac{p R}{2}$ .薄膜微元上还有轴向惯性力项ρ $\frac{\partial^{2} u}{\partial t^{2}}$ 、切向惯性力项ρ $\frac{\partial^{2} v}{\partial t^{2}}$ 、法向惯性力项ρ $\frac{\partial^{2} w}{\partial t^{2}}$ ,其中ρ为薄膜面密度,u、v、w分别为轴向位移、切向位移和法向位移,假设薄膜同时受法向外载荷力q_z的作用.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 圆柱膜模型

Fig.1 Model of cylindrical membrane

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 微元受力分析

Fig.2 Force analysis of micro-element

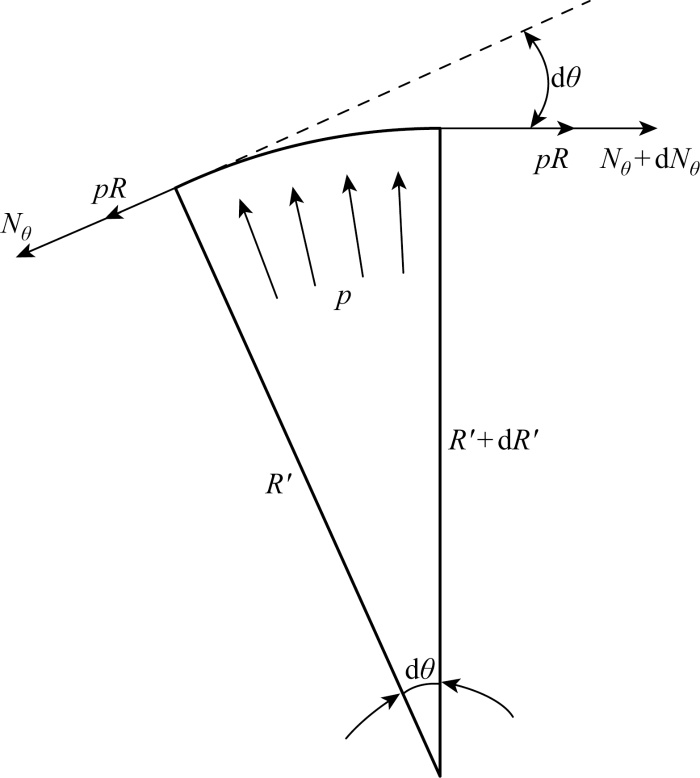
图3给出了从圆柱膜中提取的微元的环向受力情况.在压差p的作用下,薄膜微元将产生大小为pR的环向切应力,并取法向外载荷力q_z=0,圆柱膜微元的环向切应力在dθ处的外法向的力应为

(1)$(pR+{{N}_{\theta }})\sin \text{ }d\theta dx=(pR+{{N}_{\theta }})d\theta dx$

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 微元切向受力分析

Fig.3 Tangential force analysis of micro-element

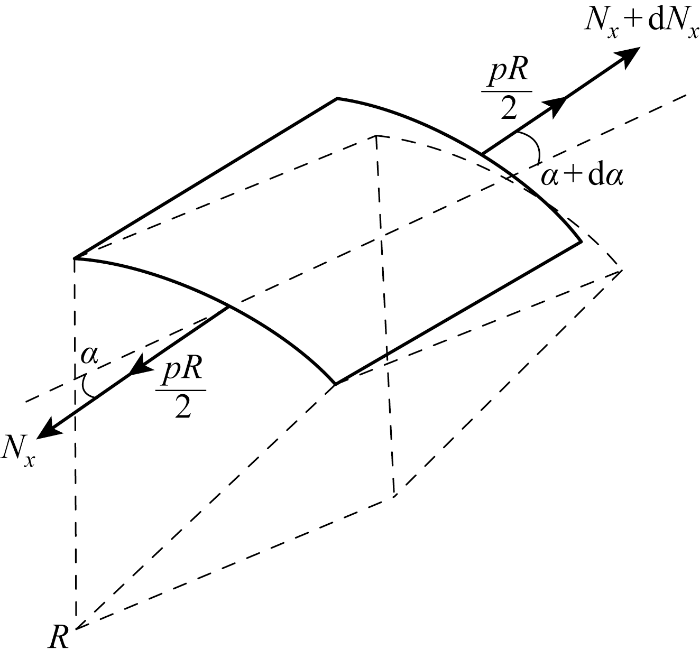
图4给出了从圆柱膜中提取的微元的轴向受力情况,在压差p的作用下,薄膜微元将产生大小为 $\frac{p R}{2}$ 的轴向切应力,振动变形时薄膜微元与x轴的夹角为α.圆柱膜微元的轴向切应力在薄膜外法向分量为

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 微元轴向受力分析

Fig.4 Axial force analysis of micro-element

(2)

[N_{x} s i n (α + d α) - N_{x} s i n α] R d θ = (N_{x} {(\frac{\partial w}{\partial x})}_{x + d x} - N_{x} {(\frac{\partial w}{\partial x})}_{x}) R d θ = N_{x} \frac{\partial^{2} w}{\partial x^{2}} R d x d θ

根据达朗贝尔原理^[13],膜面无矩无剪力假设^[14],略去切应力N_xθ,综合式(1)、式(2)和法向惯性力项后可以得到薄膜微元法向动力学微分方程:

(3)

(N_{θ} + p R) d x d θ + N_{x} \frac{\partial^{2} w}{\partial x^{2}} R' d x d θ = (p + ρ \frac{\partial^{2} w}{\partial t^{2}}) R' d x d θ

化简后,法向振动微分方程变为

(4)$\frac{1}{R'}({{N}_{\theta }}+pR)+{{N}_{x}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}=p+\rho \frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}$

式中:R'为瞬时的截面半径.

由圆柱膜结构截面几何变形关系得^[15]:

(5)

\frac{R}{R'} = 1 + \frac{1}{R} (\frac{\partial^{2} w}{\partial θ^{2}} + 2 w)

将式(5)代入式(4),化简后的圆柱膜微元法向振动微分方程变为

(6)

ρ \frac{\partial^{2} w}{\partial t^{2}} - (N_{x} + \frac{p R}{2}) \frac{\partial^{2} w}{\partial x^{2}} - \frac{N_{θ}}{R} - \frac{p}{R} (\frac{\partial^{2} w}{\partial θ^{2}} + 2 w) = 0

1.2 应变方程与物理方程

薄膜振动通常具有大变形的特点^[16],即薄膜振动产生的最大挠度与其厚度处于同一量级甚至远大于薄膜厚度,属于强非线性.基于板壳理论^[17],并考虑到薄膜应变的特点,圆柱薄膜结构在大挠度振动时的位移应包括线性和非线性两部分,线性部分主要由薄膜面内位移u、v引起,非线性部分主要由w引起,具体的应变关系为

(7)

\begin{array}{l} ε_{x} = \frac{\partial u}{\partial x} + \frac{1}{2} {(\frac{\partial w}{\partial x})}^{2} \\ ε_{θ} = \frac{1}{R} (\frac{\partial v}{\partial θ} - w) + \frac{1}{2} {(\frac{\partial w}{R \partial θ})}^{2} \\ ε_{x θ} = \frac{\partial v}{\partial x} + \frac{1}{R} \frac{\partial u}{\partial θ} + \frac{\partial w}{\partial x} \frac{\partial w}{R \partial θ} \end{array}\}

式中:ε_x为微元沿轴向的应变;ε_θ为微元沿周向的应变;ε_xθ为切应变.

对式(7)可进一步化简,消去u、v后得相容方程:

(8)

\frac{1}{R} \frac{\partial^{2} ε_{x}}{\partial θ^{2}} + R \frac{\partial^{2} ε_{θ}}{\partial x^{2}} - \frac{\partial^{2} ε_{x θ}}{\partial x \partial θ} = \frac{1}{R} {(\frac{\partial^{2} w}{\partial x \partial θ})}^{2} - \frac{\partial^{2} w}{\partial x^{2}} - \frac{1}{R} \frac{\partial^{2} w}{\partial x^{2}} \frac{\partial^{2} w}{\partial θ^{2}}

假设薄膜材料的力学性能均匀且为各向同性,根据应力应变物理方程可以得到:

(9)

\begin{array}{l} ε_{x} = \frac{1}{E h} N_{x} - \frac{μ}{E h} N_{θ} \\ ε_{θ} = \frac{1}{E h} N_{θ} - \frac{μ}{E h} N_{x} \\ ε_{x θ} = \frac{1}{G h} N_{x θ} \end{array}\}

式中:E为薄膜材料弹性模量;μ为薄膜材料泊松比;h为薄膜材料厚度; $G = \frac{E}{2 (1 + μ)}$ .

根据膜面无矩无剪力假设,引入艾里应力函数φ(x, θ, t),各应力分量可表示为

(10)

\begin{array}{l} N_{x} = \frac{h}{R^{2}} \frac{\partial^{2} φ}{\partial θ^{2}} \\ N_{θ} = h \frac{\partial^{2} φ}{\partial x^{2}} \\ N_{x θ} = - \frac{h}{R} \frac{\partial^{2} φ}{\partial x \partial θ} \end{array}\}

联立式(8)~(10),可以得到由应力函数φ和w表示的相容方程:

(11)

\frac{1}{E R^{4}} \frac{\partial^{4} φ}{\partial θ^{4}} + \frac{1}{E} \frac{\partial^{4} φ}{\partial x^{4}} + \frac{1}{G R^{2}} \frac{\partial^{4} φ}{\partial x^{2} \partial θ^{2}} = \frac{1}{R^{2}} {(\frac{\partial^{2} w}{\partial x \partial θ})}^{2} - \frac{1}{R} \frac{\partial^{2} w}{\partial x^{2}} - \frac{1}{R^{2}} \frac{\partial^{2} w}{\partial x^{2}} \frac{\partial^{2} w}{\partial θ^{2}}

1.3 振动控制方程组

通过以上分析,结合式(6)和式(11),可以得到圆柱膜法向自由振动的控制方程组:

(12)

\begin{array}{l} ρ \frac{\partial^{2} w}{\partial t^{2}} - (N_{x} + \frac{p R}{2}) \frac{\partial^{2} w}{\partial x^{2}} - \frac{N_{θ}}{R} - \\ \frac{p}{R} (\frac{\partial^{2} w}{\partial θ^{2}} + 2 w) = 0 \\ \frac{1}{E R^{4}} \frac{\partial^{4} φ}{\partial θ^{4}} + \frac{1}{E} \frac{\partial^{4} φ}{\partial x^{4}} + \frac{1}{G R^{2}} \frac{\partial^{4} φ}{\partial x^{2} \partial θ^{2}} = \\ \frac{1}{R^{2}} {(\frac{\partial^{2} w}{\partial x \partial θ})}^{2} - \frac{1}{R} \frac{\partial^{2} w}{\partial x^{2}} - \frac{1}{R^{2}} \frac{\partial^{2} w}{\partial x^{2}} \frac{\partial^{2} w}{\partial θ^{2}} \end{array}\}

2 振动方程简化与求解

2.1 边界条件

以两端自由约束的闭合圆柱膜为对象进行振动方程求解,为了计算方便,将薄膜的部分边界条件进行部分简化.将圆柱段薄膜的两端在振动过程中的应力视为0,并在后续部分对简化结果的准确度和工程适用性进行验证.简化后的圆柱段薄膜应满足如下边界条件.

x=0或x=l时应满足:

(13)

\begin{array}{l} N_{x |_{x = 0, l}} = 0 \\ N_{θ |_{x = 0, l}} = 0 \end{array}\}

同时应满足周期性条件:

(14)

\begin{array}{l} N_{x |_{θ = 0}} = N_{x |_{θ = 2 π}} \\ N_{θ |_{θ = 0}} = N_{θ |_{θ = 2 π}} \end{array}\}

且t=0时应满足:

(15)

{\frac{\partial w (x, θ, t)}{\partial t}|}_{t = 0} = 0

设满足边界条件的位移函数为

(16)$w(x,\theta,t)=\sum{\sin \lambda x\cos n\theta X}(t)$

式中:w(x, θ, t)为薄膜法向位移;λ=mπ/l,m为轴向半波数;n为节径数;l为圆柱膜长度;X(t)为膜面位移最大值的时间函数.

2.2 方程简化

进行计算时,位移函数首先按照w(x, θ, t)=sin λxcos nθX(t)计算,再将最终结果求和即可.通过式(12)第2项可以得到:

(17)$\begin{matrix} & \frac{1}{E{{R}^{4}}}\frac{{{\partial }^{4}}\varphi }{\partial {{\theta }^{4}}}+\frac{1}{E}\frac{{{\partial }^{4}}\varphi }{\partial {{x}^{4}}}+\frac{1}{G{{R}^{2}}}\frac{{{\partial }^{4}}\varphi }{\partial {{x}^{2}}\partial {{\theta }^{2}}} \\ & =\frac{{{\lambda }^{2}}{{n}^{2}}}{2{{R}^{2}}}~(\cos \text{ }2\lambda x-\cos \text{ }2n\theta ){{X}^{2}}(t)+ \\ & \frac{{{\lambda }^{2}}}{R}\sin \lambda x\cos n\theta X(t) \\ \end{matrix}$

对比式(17)中等号的左边和右边,可以得到应力函数结构应为

(18)$\varphi (x,\theta,t)={{f}_{1}}(x,\theta ){{X}^{2}}(t)+{{f}_{2}}(x,\theta )X(t)$

式中:f₁(x, θ)和f₂(x, θ)表示系数.

上述应力函数应包含cos 2λx、cos 2nθ和 sin λxcos nθ 等项,且其幂次最高为3.于是设满足上述条件的应力函数φ(x, θ, t)表达式为

(19)$\begin{matrix} & \varphi (x,\theta,t)=({{k}_{1}}cos\text{ }2\lambda x+{{k}_{2}}cos\text{ }2n\theta +{{k}_{3}}{{x}^{3}}+{{k}_{4}}{{x}^{2}} \\ & +{{k}_{5}}{{R}^{3}}{{\theta }^{3}}+{{k}_{6}}{{R}^{2}}{{\theta }^{2}}+{{k}_{7}}R{{x}^{2}}\theta +{{k}_{8}}{{R}^{2}}x{{\theta }^{2}}+{{k}_{9}}Rx\theta ) \\ & {{X}^{2}}(t)+({{j}_{1}}sin\lambda xcosn\theta +{{j}_{3}}{{x}^{3}}+{{j}_{4}}{{x}^{2}}+{{j}_{5}}{{R}^{3}}{{\theta }^{3}}+ \\ & {{j}_{6}}{{R}^{2}}{{\theta }^{2}}+{{j}_{7}}R{{x}^{2}}\theta +{{j}_{8}}{{R}^{2}}x{{\theta }^{2}}+{{j}_{9}}Rx\theta )X(t) \\ \end{matrix}$

式中:k₁~k₉、j₁~j₉分别表示待解系数.

将式(19)代入式(17)并比对系数可得:

(20)

\begin{array}{l} k_{1} = \frac{E n^{2}}{32 λ^{2} R^{2}} \\ k_{2} = - \frac{E λ^{2} R^{2}}{32 n^{2}} \\ j_{1} = \frac{λ^{2}}{R (\frac{n^{4}}{E R^{4}} + \frac{λ^{4}}{E} + \frac{λ^{2} n^{2}}{G R^{2}})} \end{array}\}

继续引入式(13)和(14)的边界条件可得:

(21)

\begin{array}{l} k_{4} = 2 λ^{2} k_{1}, k_{6} = \frac{2 n^{2}}{R^{2}} k_{2} c o s 2 n θ \\ k_{3} = k_{5} = k_{7} = k_{8} = k_{9} = 0 \\ j_{3} = j_{4} = j_{5} = j_{6} = j_{7} = j_{8} = j_{9} = 0 \end{array}\}

进而得到应力函数φ(x, θ, t)表达式为

(22)$\begin{matrix} & \varphi (x,\theta,t)=({{k}_{1}}cos\text{ }2\lambda x+{{k}_{2}}cos\text{ }2n\theta +2{{k}_{1}}{{\lambda }^{2}}{{x}^{2}}+ \\ & {{k}_{6}}{{R}^{2}}{{\theta }^{2}}){{X}^{2}}(t)+{{j}_{1}}sin\lambda xcosn\theta X(t) \\ \end{matrix}$

令位移函数w(x, θ, t)=sin λxcos nθX(t)=WX(t),联立式(10)、(12)、(22),可得薄膜非线性振动频率方程的表达式:

(23)$\begin{matrix} & -\frac{h{{\lambda }^{2}}}{{{R}^{2}}}[8{{n}^{2}}{{k}_{2}}(2n\theta \sin \text{ }2n\theta + \\ & {{n}^{2}}{{\theta }^{2}}\cos \text{ }2n\theta ){{X}^{2}}(t)+{{n}^{2}}{{j}_{1}}WX(t)]WX(t)- \\ & \frac{h}{R}[4{{\lambda }^{2}}{{k}_{1}}(1-\cos \text{ }2\lambda x){{X}^{2}}(t)-{{\lambda }^{2}}{{j}_{1}}WX(t)]- \\ & \frac{p}{R}(2-{{n}^{2}})WX(t)+\rho W\ddot{X}(t)=0 \\ \end{matrix}$

对式(23)采用Ritz-Galerkin法进行求解^[18],取权函数为W,构造积分方程为

(24)$\begin{matrix} & \underset{0}{\overset{l}{\mathop \int }}\, ~ \underset{0}{\overset{2\pi }{\mathop \int }}\, ~ \left\{ \rho W\ddot{X} \right.(t)-\frac{h{{\lambda }^{2}}}{{{R}^{2}}}[8{{n}^{2}}{{k}_{2}}(2n\theta \sin \text{ }2n\theta + \\ & {{n}^{2}}{{\theta }^{2}}\cos \text{ }2n\theta )W{{X}^{3}}(t)+{{n}^{2}}{{j}_{1}}{{W}^{2}}{{X}^{2}}(t)]- \\ & \frac{h}{R}[4{{\lambda }^{2}}{{k}_{1}}(1-\cos \text{ }2\lambda x){{X}^{2}}(t)-{{\lambda }^{2}}{{j}_{1}}WX(t)]- \\ & \frac{p}{R}\left. (2-{{n}^{2}})WX(t) \right\}Wdxd\theta =0 \\ \end{matrix}$

式(24)化简后得到:

(25)$\ddot{X}~(t)+KX(t)+B{{X}^{3}}(t)=0$

K = \frac{h λ^{2} j_{1} + p (n^{2} - 2)}{R ρ}

B = - \frac{8 λ^{2} n^{2} h k_{2}}{R^{2} ρ} \frac{768 π^{2} n^{2} - 888}{1 152}

可以看出式(25)属于强非线性方程,说明圆柱膜振动时通常处于非线性状态.

2.3 方程求解

当圆柱膜振动时,不考虑高次项系数,薄膜线性振动频率即为

(26)

f = \frac{ω}{2 π} = \frac{\sqrt{K}}{2 π}

式中:ω为圆频率.

对于薄膜在初始位移条件下的非线性振动,式(25)积分可以得到:

(27)${{(\dot{X}(t))}^{2}}+K{{X}^{2}}(t)+\frac{1}{2}B{{X}^{4}}(t)=C$

设t=0时刻膜面挠度处于最大值A,则有 $\overset{\cdot}{X}$ (0)=0,根据边界条件还可以得到w(x, θ, 0)=Asin λxcos nθ.将 $\overset{\cdot}{X}$ (0)=0代入式(27)可得:

(28)C=KA²+BA⁴/2

联立式(27)和(28)得到:

(29)

d t = {(K A^{2} + \frac{1}{2} B A^{4} - K X^{2} (t) - \frac{1}{2} B X^{4} (t))}^{- \frac{1}{2}} d X

薄膜振动时,挠度从0直接变化到A需要经历 $\frac{1}{4}$ 周期,于是可以得到周期T为

(30)$\frac{T}{4}=\underset{0}{\overset{\frac{T}{4}}{\mathop \int }}\, ~\!\!\text{ d}t= ~ \underset{0}{\overset{A}{\mathop \int }}\, ~ {{\left( K{{A}^{2}}+\frac{1}{2}B{{A}^{4}}-K{{X}^{2}}(t)-\frac{1}{2}B{{X}^{4}}(t) \right)}^{-\frac{1}{2}}}\text{d}X$

进而得到振动频率表达式:

(31)

f = \frac{1}{T} = \frac{1}{{4 \int_{0}^{A} (K A^{2} + \frac{B A^{4}}{2} - K X^{2} (t) - \frac{B X^{4} (t)}{2})}^{- \frac{1}{2}} d X}

式(31)可通过MATLAB对上述推导过程创建函数,再输入薄膜材料等相关参数后进行数值求解.式(31)即为有限长闭合圆柱状膜结构在具有初始挠度A时的干模态自由振动的频率公式,可以看出圆柱膜干模态振动频率的非线性解包含振频率的线性解部分.当A趋于0时,通过式(31)得到的结果为初始挠度为0的频率值.由上式可见,圆柱膜干模态振动频率与薄膜承受的气压、长度、面密度和半径参数等有关,而且受薄膜振动初始位移的影响.

3 算例分析

以图1所示的两端简支的圆柱膜为例,薄膜各项参数为:圆柱段长为l=1.8 m,半径为R=0.25 m,成型薄膜总长为2.3 m,薄膜面密度为ρ=0.14 kg/m²,薄膜厚度为h=0.2 mm,薄膜弹性模量E=10 GPa,薄膜泊松比为0.3,圆柱膜内外压差取10 kPa.采用有限元仿真软件分析符合上述参数圆柱膜的振动特性,并将仿真结果与理论计算值比较.利用仿真软件展开分析时,首先建立闭合圆柱膜模型,然后输入上述薄膜材料参数及载荷条件,设置模型处于自由约束状态,并选用八节点四边形膜单元和Lanczos求解器开展仿真分析.此处理论计算和仿真分析的振动频率都不考虑空气的干模态频率.圆柱膜计算值与仿真值的比较如表1所示.

表1 计算频率和仿真频率对比一

Tab.1 Comparison of calculation frequency and simulation frequency in the first group

模态	m, n	计算值/Hz	仿真值/Hz	相对误差/%
一阶	m=1, n=2	163.74	152.34	7.483
二阶	m=1, n=3	231.96	232.18	0.094
三阶	m=1, n=4	320.63	320.88	0.078
四阶	m=1, n=5	409.24	408.97	0.066
五阶	m=1, n=6	496.90	496.03	0.042

新窗口打开| 下载CSV

从表1中可以看到,除一阶频率有较大误差以外,其余阶数的计算频率和仿真频率有很好的一致性,说明边界条件的简化主要会对一阶频率的计算造成一定的误差.上述特征尺寸的薄膜结构符合试验测试使用的薄膜结构,但与薄膜实际工程应用场景,例如应用于飞艇等浮空器时,形状有较大差异.继续对比分析圆柱段长度l=50 m,半径为R=8 m,压差为2 kPa,且其余参数与上述数值一致的圆柱膜结构自振频率的计算值和仿真值,具体数据如表2所示.

表2 计算频率和仿真频率对比二

Tab.2 Comparison of calculation frequency and simulation frequency in the second group

模态	m, n	计算值/Hz	仿真值/Hz	相对误差/%
一阶	m=1, n=2	10.747	10.879	1.21
二阶	m=1, n=3	18.069	18.173	0.57
三阶	m=1, n=4	25.305	25.340	0.14
四阶	m=1, n=5	32.352	32.346	0.02
五阶	m=1, n=6	39.292	39.248	0.11

新窗口打开| 下载CSV

表2的结果也显示仅一阶频率有一定误差,其余数据的一致性较好.综合表1和表2的误差分析可知,计算值与仿真分析结果的总体误差较小,其中仅一阶频率的误差较大,这一误差主要来源于2.1节中边界条件的应力简化.利用有限元软件对薄膜圆柱段两端部进行静力分析,结果显示该部位应力并不为0,但该部位应力值较难计算,且若按照实际应力值计算将导致应力函数极难求到,使整体推导难度增大.同时为了提升工程应用的便捷程度,且该误差范围也满足于飞艇等一般工程应用的需求,表明采用式的简化边界条件是可行的.从表1和表2的数据也可以看出计算结果和仿真结果有较好的吻合程度,这说明了有限元方法对于柔性薄膜结构模态分析同样适用,可以利用有限元软件对薄膜振动特性进一步分析.

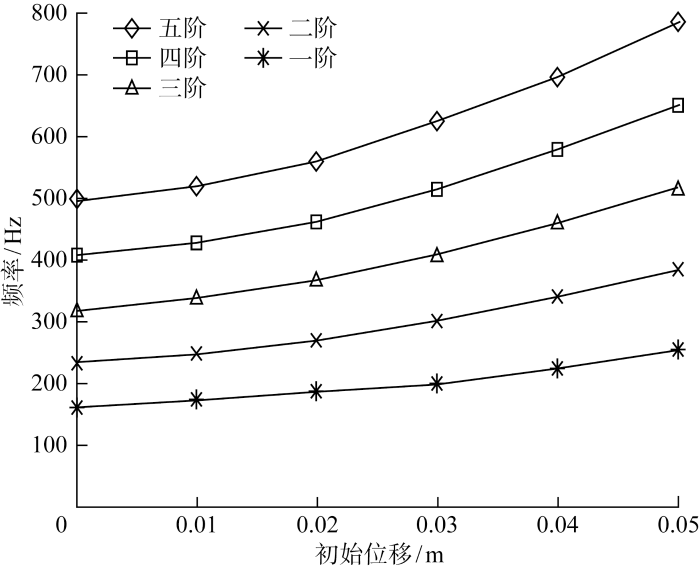
进一步采用表1的薄膜参数讨论圆柱膜随着初始位移变化时的各阶振动频率的解析值变化,具体如表3和图5所示.

表3 自振频率的非线性解

Tab.3 Nonlinear solution of natural frequency

模态	频率/Hz
模态	A=0 m	A=0.01 m	A=0.02 m	A=0.03 m	A=0.04 m	A=0.05 m
一阶	161.63	174.58	187.58	199.59	226.47	257.25
二阶	230.47	248.43	270.33	301.57	340.73	384.99
三阶	319.56	340.28	368.75	409.48	461.72	519.75
四阶	408.39	429.12	463.29	515.36	579.01	651.85
五阶	496.21	519.27	561.48	625.50	697.39	784.62

新窗口打开| 下载CSV

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 初始位移对频率的影响

Fig.5 Effect of initial displacement on frequency

从图5可以看出,随着初始位移的增加,圆柱膜自由振动的各阶频率也逐渐增加,初始位移越大对振动频率的影响越明显,这种影响对于圆柱膜高阶振动更为显著.初始位移能对圆柱膜振动频率产生较大影响的原因是初始位移的产生增大了圆柱膜面内应力,这与增大圆柱膜内气压的效果类似,从K的表达式可以看出,圆柱膜的刚度会明显变大,从而引起其振动频率的增加.

但解析表达式(31)仅是针对真空状态时得到的干模态频率计算公式,但受其形状、尺寸、固定机构和成本等因素的限制,进行膜结构振频试验时往往难以在真空及低真空环境内进行,解析表达式用于快速验证的现实场景将受到极大的限制.为此,可以通过试验测试探究地面空气附加质量对圆柱膜各阶振动频率的影响系数.

4 试验测试与分析

由于理论计算中引入的边界条件存在一定程度的简化,造成的误差会使计算和分析的结果与真实情况出现一定范围的偏差.为了验证湿模态仿真分析方法的正确性,了解空气附加质量对于圆柱膜各阶频率的影响程度,探讨频率计算公式应用于湿模态分析的可行性,设计了试验测试圆柱膜湿模态振动频率,圆柱膜放置方式如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 圆柱膜试验装置

Fig.6 Experimental device for cylindrical membranes

4.1 试验内容

试验以两端闭合的圆柱状薄膜结构为对象进行,在空旷场所且处于空气环境中试验测试圆柱膜结构的湿模态频率.由于圆柱膜质量较小,可通过两根细绳将圆柱膜横向悬挂模拟膜结构自由约束状态,圆柱膜两端面分别连接充气管和压差测量气管,用于将闭合圆柱膜结构充至所需气压并对压差进行监测.为了减少两端褶皱对振动频率的影响, 需要将圆柱膜的长径比设计的相对较大.所选用的薄膜参数与3.1节介绍的薄膜参数相同.

4.2 测试数据及结果分析

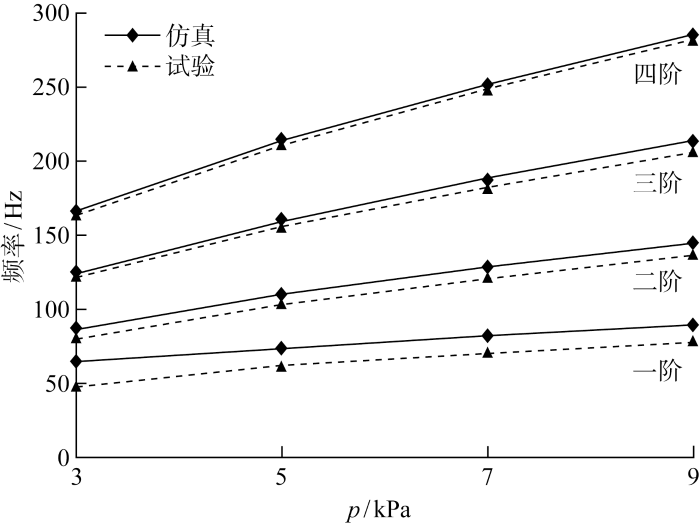
分别对压差为3、5、7和9 kPa的圆柱膜结构展开振动频率测量,选用Ploytec公司的PSV-500-3D激光测振仪进行测量,对每组数据进行3次有效测量,并选取3个有效数据的平均值进行分析.利用Abaqus有限元分析软件对上述圆柱膜结构在真空和空气中进行模态分析.用仿真软件进行湿模态分析时,空气介质采用声学无限单元法来模拟,圆柱膜内外的空气被近似为声音介质.薄膜材料继续选用八节点四边形膜单元,空气介质选用八结点二次表面插值声学无限单元,利用Lanczos求解器开展仿真分析,结合空气温度和大气压强,计算得到空气密度为1.23 kg/m³,体积压缩模量取0.142 MPa.试验结果和仿真分析的频率如表4所示.

表4 湿模态试验频率和仿真频率比较

Tab.4 Comparison of test frequency and simulation frequency in wet mode

p/kPa	一阶频率/Hz		二阶频率/Hz		三阶频率/Hz		四阶频率/Hz
p/kPa	试验	仿真	试验	仿真	试验	仿真	试验	仿真
3	49.3	64.5	81.3	87.5	122.6	125.3	165.1	166.5
5	62.1	73.9	104.2	110.6	155.9	160.8	212.4	214.3
7	71.3	81.7	121.3	128.8	182.7	188.7	249.5	252.0
9	79.1	89.2	137.6	145.4	207.1	213.8	283.1	285.7

新窗口打开| 下载CSV

图7中的4组曲线从下往上分别表示一到四阶频率.从图7可以看出,随着压差的增加,圆柱膜各阶频率都平稳增加,符合实际规律;测试频率和分析频率总体吻合程度较好,但低阶频率存在较大误差,相较于一阶频率试验值,仿真值平均有19.3%的误差,而二阶、三阶和四阶测试频率的平均误差分别为6.40%、2.97%和0.92%,低压差条件下各阶仿真和试验频率误差相对更大,主要原因是压差的大小和圆柱膜结构的刚度有密切关联,较小的压差使膜结构整体刚度偏小,实验测试得到的频率受充气管、压差管等试验辅助用品的影响更大.表4的结果显示,试验测试和仿真分析的频率值在较高阶数趋于收敛,且二者结果十分接近,这说明了圆柱膜结构湿模态仿真的正确性.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 湿模态试验频率和仿真频率误差对比

Fig.7 Error comparison of test frequency and simulation frequency in wet mode

造成低阶频率差异较大的原因有以下几点:实际的空气密度测量难度较大,计算得到的空气密度没有引入空气湿度和温度变化等因素,这会有一定误差从而影响仿真结果;试验时圆柱膜结构连接有充气管和压差管,这会对系统低阶频率产生一定影响;圆柱膜结构加工过程使用了一些辅材以保证抗压和气密性能,使圆柱膜整体质量产生较小变化,以及受加工工艺的限制,圆柱段两端在成型后会出现褶皱,从而影响边界的应力分布.

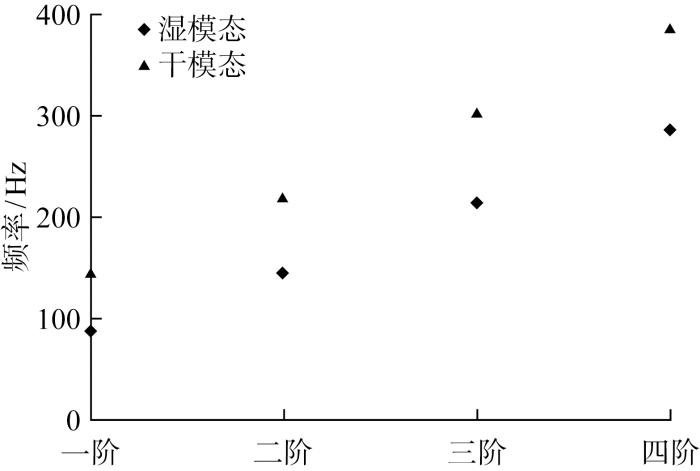
4.3 空气对膜振动的影响

以压差9 kPa为例,将湿模态仿真中的空气密度设为0后进行仿真可以得到干模态振动频率,具体结果如图8所示.干模态和湿模态结果的巨大差异说明空气对圆柱膜模态有较大的影响,在空气环境进行薄膜振动试验时空气附加质量是仿真分析不可忽略的因素,圆柱膜处于地面空气环境时的一阶振动频率仅约为真空状态时的60%.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 干湿模态频率趋势

Fig.8 Frequency trends in dry and wet modes

根据Maheri等^[19]的研究结论,对于质量分布规则的薄膜材料,假设附加质量均匀分布,那么考虑了附加质量的圆柱膜结构的质量也分布均匀,则广义质量之比等于实际质量之比.引入经典频率计算公式后可以得到:

(32)

C_{a} = \frac{m_{a} + m_{s}}{m_{s}} = {(\frac{ω_{s}}{ω_{t}})}^{2}

式中:m_a为空气附加质量;m_s为薄膜结构的质量;ω_s为膜结构干模态频率;ω_t为膜结构湿模态频率;并设无量纲系数C_a为附加质量系数.

将表5的数据代入式(32)后可以计算得到9 kPa 压差条件下一到四阶收缩模态附加质量系数,并通过以上方法计算 3、5、7 kPa 等压差条件下的各阶模态的附加质量系数,得到的数据整理在表5中.从表5的数据可以看出,地面空气附加质量对圆柱膜振动特性的影响极其明显,还能看出压差对各阶模态的空气附加质量系数的影响不大,而且随着压差的不断增大,附加质量系数的变化幅度有越来越小的趋势.

表5 不同压差的空气附加质量系数

Tab.5 Additional mass factor for air at different pressures

p/kPa	C_a
p/kPa	一阶	二阶	三阶	四阶
3	2.640	2.254	1.989	1.810
5	2.650	2.266	1.998	1.817
7	2.692	2.254	2.024	1.838
9	2.697	2.300	2.024	1.838

新窗口打开| 下载CSV

从表5中可以提取前4阶模态的附加质量系数,分别提取各阶平均数,具体为2.67、2.27、2.01和1.83,并将以上系数用于为1~10 kPa压差的附加质量快速计算.以上系数乘以薄膜面密度ρ后得到新的含各阶模态附加质量的薄膜面密度ρ',用ρ'代替ρ参与式(26)的计算得到处于地面空气环境的湿模态频率.以压差9 kPa为例,将计算湿模态频率、仿真湿模态频率和试验湿模态频率做比较,具体如表6所示.

表6 湿模态频率比较

Tab.6 Comparison of wet mode frequencies

模态	模态频率/Hz
模态	计算	仿真	试验
一阶	97.33	89.2	79.1
二阶	146.42	145.4	137.6
三阶	214.64	213.8	207.1
四阶	287.02	285.7	283.1

新窗口打开| 下载CSV

从表6的结果可以看出,一阶频率的计算值和实验值有较大误差,这主要是由于计算过程中边界条件的简化,以及仿真模型与试验对象有一定出入导致的.二阶、三阶和四阶湿模态频率的计算值和实验值的吻合程度较好,不仅说明了表5中计算得到的各阶模态附加质量系数是可靠的,还能验证将附加质量整合在薄膜自身质量上来分析湿模态振动频率的方法是可行的.

空气附加质量主要影响低阶频率,上述分析中影响一、二阶模态频率的空气附加质量均大于薄膜自身质量,随着阶数的增加影响逐渐减弱,但其影响依旧明显.由此说明分析薄膜结构振动特性时,必须要考虑空气附加质量的影响,但受限于环境、试验件尺寸、设备、成本等因素,薄膜结构真空状态模态试验通常难以开展.表5的数据可以为薄膜结构干模态和湿模态测试值的关系提供一定的判断依据,但这判断依据不是精确的,还需进行多种薄膜结构的试验测试和分析才能掌握更为科学客观的依据.

5 结论

本文通过建立闭合圆柱膜的非线性动力学微分方程,在自由约束条件下得到了其在初始位移条件下的振动频率理论解,对近似自由约束的闭合圆柱膜结构湿模态频率进行试验测试,利用有限元软件分析圆柱膜结构干模态和湿模态频率并提取空气附加质量影响系数,对比发现计算结果与分析结果以及试验结果一致性较好.另外,还得到了以下结论:

(1) 初始位移对于圆柱膜振动频率具有较大影响,圆柱膜线性振动分析仅在小挠度条件下适用.

(2) 有限元分析方法对于柔性薄膜结构模态分析具有良好的适用性,可以采用声固耦合的方法模拟结构周围的空气介质并进行湿模态分析.

(3) 空气附加质量对圆柱膜振动的影响极为明显,在圆柱膜结构低阶振动时,空气附加质量与结构自身质量处于同一量级.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

黄宛宁, 张晓军, 李智斌, 等.

临近空间科学技术的发展现状及应用前景

[J]. 科技导报, 2019, 37(21): 46-62.

DOI:10.3981/j.issn.1000-7857.2019.21.005 [本文引用: 1]

介绍了临近空间的特殊空间位置以及典型气象特征，梳理了国内外通过天基、地基、原位平台对临近空间进行科学探索和研究的情况，针对目前对临近空间认知不足的现状，提出应该以临近空间飞行器为主要平台对临近空间进行科学探索及应用；回顾了国内外临近空间飞行器（包括高空气球、平流层飞艇和高空太阳能长航时无人机）的技术发展及其在军用和民用市场中的应用现状，总结了亟需关注的关键问题，并提出了中国临近空间科技发展和应用的具体建议。

HUANG

Wanning

, ZHANG

Xiaojun

, LI

Zhibin

, et al.

Development status and application prospect of near space science and technology

[J]. Science & Technology Review, 2019, 37(21): 46-62.