上海交通大学学报

上海交通大学学报, 2024, 58(4): 419-427 doi: 10.16183/j.cnki.jsjtu.2022.414

航空航天

水滴在气流中变形破碎过程的数值模拟研究

桑旭1, 金哲岩,1,2, 杨志刚2, 余放3,4

1.同济大学 航空航天与力学学院,上海 200092

2.上海市地面交通工具空气动力学与热环境模拟重点实验室,上海 201804

3.同济大学 机械与能源工程学院,上海 201804

4.中国航发商用航空发动机有限责任公司,上海 201108

Numerical Study of Deformation and Breakup Processes of Water Droplets in Air Flow

SANG Xu1, JIN Zheyan,1,2, YANG Zhigang2, YU Fang3,4

1. School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China

2. Shanghai Key Laboratory of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Shanghai 201804, China

3. School of Mechanical Engineering, Tongji University, Shanghai 201804, China

4. AECC Commercial Aircraft Engine Co., Ltd., Shanghai 201108, China

通讯作者: 金哲岩,副教授,博士生导师,电话(Tel.):021-65982651;E-mail:zheyanjin@tongji.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-10-20   修回日期: 2023-03-6   接受日期: 2023-03-24  

基金资助: 国家数值风洞工程项目(NNW2019ZT2-B26)

Received: 2022-10-20   Revised: 2023-03-6   Accepted: 2023-03-24  

作者简介 About authors

桑旭(2000-),硕士生,从事飞行器结冰机理研究.

摘要

针对水滴在结冰风洞实验中加速过程内易发生破碎而导致试验段内水滴粒径分布难以符合结冰气象条件的问题,利用流体体积(VOF)方法,模拟了直径为100、200、400、600、800、1 000 μm 以及 1 200 μm 的水滴在不同气流速度作用下(20、50、80 m/s)的变形破碎情况.结果表明:在20 m/s气流作用下,直径为600 μm的水滴不发生破碎;当风速为50 m/s时,直径为100 μm的水滴不发生破碎;随着韦伯数增加,最大不稳定波波长也随之增大,水滴的破碎模式从袋状破碎变为包-蕊状破碎,随后转变为蕊-层状破碎,进一步转变为剪切破碎.水滴的破碎形式包括袋状破碎、包-蕊状破碎、蕊-层状破碎及剪切破碎,会对面积最大的液滴与初始液滴面积之比有较大影响.在初始水滴直径相同的条件下,入口速度越大,破碎后的面积比越大.

关键词： 过冷大水滴; 变形破碎; 气液两相流; 流体体积方法

Abstract

Aimed at the problem that water droplets are easy to break up during the acceleration process in icing wind tunnel experiment, which makes it difficult for the particle size distribution of water droplets in the test section to conform to the icing weather conditions, the deformation and breakup regime of water droplets with a diameter of 100, 200, 400, 600, 800, 1 000 and 1 200 μm under the action of different air velocities(20, 50, and 80 m/s) are simulated by using the volume of fluid (VOF) method. The results show that under the action of 20 m/s air flow, the water droplet with a diameter of 600 μm does not break. Under the action of 50 m/s air flow, the water droplet with a diameter of 100 μm does not break. With the increase of Weber number, the wavelength of the most destructive wave also increases, and the breakup regime of water droplets changes from bag breakup to bag-plume breakup, to plume-shear breakup, and to shear breakup successively. The droplet breakup regime, including the bag breakup, bag/plume breakup, the plume/sheet-thinning breakup, and the shear breakup, has a significant effect on the ratio of the area of the largest droplet to the initial droplet. Under the condition that the initial drop diameter is the same, as the inlet velocity increases, the area ratio after breakup increases.

Keywords： supercooled large drop (SLD); deformation and breakup; gas-liquid flow; volume of fluid (VOF) method

PDF (2771KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

桑旭, 金哲岩, 杨志刚, 余放. 水滴在气流中变形破碎过程的数值模拟研究[J]. 上海交通大学学报, 2024, 58(4): 419-427 doi:10.16183/j.cnki.jsjtu.2022.414

SANG Xu, JIN Zheyan, YANG Zhigang, YU Fang. Numerical Study of Deformation and Breakup Processes of Water Droplets in Air Flow[J]. Journal of Shanghai Jiaotong University, 2024, 58(4): 419-427 doi:10.16183/j.cnki.jsjtu.2022.414

结冰风洞是一种研究飞机结冰的地面实验设备,常见的回流式冰风洞通过制冷系统以及喷雾系统来模拟云层中的低温和云雾环境[1].在云雾环境的模拟内容中,需要将冰风洞试验段内水滴的中位体积直径(MVD)以及液态水含量(LWC)等模拟参数的范围涵盖适航所规定的结冰气象条件[2].近年来,随着附录O[3]的提出,过冷大水滴(SLD)的结冰条件对结冰风洞的模拟能力提出了新的要求,SLD通常是指直径大于40 μm的过冷水滴,在冻雨环境[4⇓-6]中可能达到 2 000 μm.因此,满足SLD结冰条件的粒径分布特性对冰风洞的喷雾系统以及收缩段对SLD的加速控制提出了新的挑战.

为了探究结冰风洞中水滴的参数沿程变化规律,学者们利用数值模拟以及实验的方法开展了大量研究[7⇓⇓⇓-11].其中,李晓峰等[8]利用拉格朗日法,结合水滴蒸发及凝固模型,得到了三维条件下冰风洞内单个水滴速度、温度、直径等参数沿程变化.为了满足SLD的颗粒度分布具有明显的双峰分布[10]这一特性,符澄等[11]在实验的基础上采用离散型模型,对具有Rosin-Rammler分布特性的喷雾通过湍流混合形成具有双峰特性的SLD云雾场的过程进行模拟,发现小液滴的蒸发以及大液滴的二次破碎是影响混合滴谱的主要因素.

针对液滴的变形破碎,学者们通过实验得到了液滴的不同破碎模式,并研究了液滴发生不同破碎模式的机理[12⇓⇓⇓-16].其中,金仁瀚等[13]研究了直径为3 mm 左右的航空煤油液滴,发现液滴的初始直径会影响其变形破碎模式的转变,且气流速度越大,破碎情况越剧烈复杂.Jackiw等[14]将垂坠的直径在 1.5~2.0 mm左右的水滴暴露在高速气流中进行实验,并利用内部流动机理进行数学建模,发现液滴边缘的膨胀与袋子的生长有关,而边缘的破碎与Rayleigh-Taylor不稳定性(下文简称R-T不稳定性)相关.

此外,在数值模拟方面,学者们致力于研究参数变化导致液滴破碎模式不同的原因[17⇓⇓⇓-21],数值模拟在调整参数及流场可视化方面具有便利性.楼建峰等[17]利用流体体积(VOF)方法和标准k-ε湍流模型对直径为1.2 mm的液滴在气流中的破碎进行模拟,发现韦伯数We对液滴变形破碎起促进作用,奥内佐格数Oh和液气密度比起阻碍抑制作用.Jain等[18]对流场中的液滴建立二维轴对称模型,发现在中等We(20~120)条件下液气密度比对液滴的变形破碎影响较大,证明了在高液气密度比(>150)条件下R-T不稳定性的确是导致袋状破碎的原因.樊玉光等[20]采用CLSVOF方法进行模拟,发现在同一We条件下,液化天然气液滴的破碎时间随初始直径的增大而减小后趋于平缓,初始直径为400 μm时,液滴发生剪切破碎的临界We在80左右.

综上所述,目前国内外对冰风洞内水滴参数的研究均基于球形液滴假设,并没有考虑水滴的变形破碎效应,即没有考虑水滴变形破碎后导致风洞试验段内水滴的MVD变化,影响风洞实验人员对喷雾系统的调整,导致错误的结冰输入参数.针对液滴变形破碎的研究,学者们对直径在100~1 200 μm 水滴的研究结果较少,且没有对水滴破碎后的面积变化进行统计.由于风洞试验段内水滴粒径分布要求的特殊性,水滴在风洞加速段内的破碎会导致试验段内的粒径分布变化,导致无法利用该破碎结果来指导风洞实验参数的调整,进而难以得到符合云雾参数的试验段数据.因此,研究云雾模拟条件中主要粒径分布的水滴的破碎情况以及破碎后的面积变化对于指导风洞实验参数调整具有重要意义.

与文献中的数值模拟相比,本文全面系统地分析了100~1 200 μm直径范围内水滴在20、50、80 m/s 入口速度条件下的变形破碎情况.根据SLD粒径的主要分布范围探究不同直径的水滴发生破碎的条件,并对不同直径水滴的破碎结果进行分析,包括流场情况以及破碎后的面积比,为风洞实验参数调整提供了宝贵的参考数据.

1 物理模型与数值方法

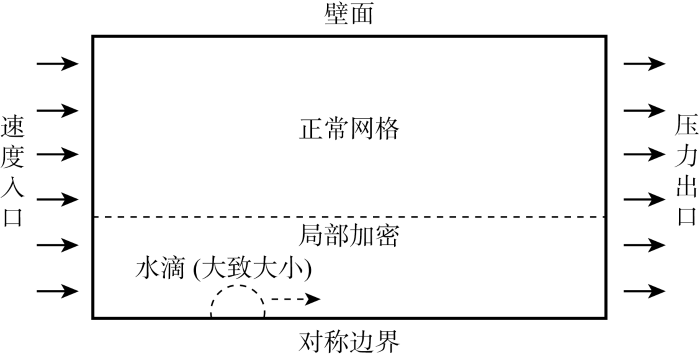
本文所研究的气流中水滴的变形破碎属于气液两相流的范畴,而VOF模型是一种在固定的欧拉网格下的表面跟踪方法,该方法可以得到一种或多种互不相融流体间的交界面[22-23].

针对水滴在空气流场中的变形破碎模拟,建立了如图1所示的计算模型.边界条件如下:左侧为速度入口,右侧为压力出口,上侧为壁面,下侧为对称边界(本文经过多次模拟验证,不影响水滴的变形和破碎情况).经过模拟验证,需要将水滴中心位置距离入口6d (d为水滴初始直径),距离壁面10d以确保不受入口边界和壁面的影响.在网格设置方面,在距离对称边界3d的范围内进行局部加密,网格大小h=0.02d.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   计算模型示意图

Fig.1   Schematic diagram of the calculation model


在下文研究结果中,时间t*以无量纲形式[20]呈现,表示为

t*=Ugdρl/ρgt

式中:Ug为气流入口速度(速度尺度);t为气流流动时间(时间尺度);ρl为水的密度;ρg为空气的密度.

在求解设置中,采用瞬态模拟,选择基于压力的求解器.选择压力的隐式算子分割(PISO)算法作为压力速度耦合的方法,压力计算采用PRESTO格式,其他物理量采用一阶迎风格式离散[24-25].

2 网格收敛性与模型有效性验证

通过多次对网格无关性的验证(见图2),模拟了直径为1 000 μm的水滴在入口速度为50 m/s条件下的变形情况.在保证计算结果准确性的基础上尽量节约计算资源与时间,确定了一套较为完善的网格划分方法,在计算域内,网格的大小h=0.02d,随后对VOF相界面区域进行自适应网格加密[26].

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   网格无关性验证

Fig.2   Verification of grid independence


为了验证该计算模型的准确性,利用VOF方法以及realizable k-ε湍流模型对文献[17]中给出的数据进行模拟.该模型模拟的是 1 200 μm的液滴在气流中剪切破碎的状态,入口速度为33.83 m/s,该工况下,We=78.68,雷诺数Re=2 850.液滴以及气相物性参数详细情况参见文献[17].

剪切破碎的数值模拟如图3所示,分别与文献[17]和[19]中的数值模拟以及文献[19]实验结果对比.图3(a)为在本文计算模型下的液滴变形破碎情况,图3(b)[17]、图3(c)[19]是文献中得出的模拟结果,图3(d)为文献[19]实验结果(实验条件与数值模拟计算条件相同).从图中可以看出,本文模型的计算结果图3(a)与文献模拟结果图3(b)、3(c)相近,能够较好地模拟出液滴变形破碎的过程,验证了本文计算模型的有效性及准确性.与实验结果图3(d) 对比,变形有较为明显的不同,这是由于受到实验环境的不稳定性以及重力、实验风速不均的影响.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   剪切破碎条件下的结果对比

Fig.3   Comparison of results under shear breakup conditions


3 结果与讨论

随着We的增加,液滴的破碎模式可以分为振荡变形(破碎)、袋状破碎、多模式破碎、剪切破碎和灾难性破碎[27].本文主要模拟了直径为100、200、400、600、800、1 000、1 200 μm大小的水滴在不同气流速度(20、50、80 m/s)作用下的变形破碎情况.

3.1 入口风速为20 m/s条件下的变形及破碎结果

如图4~6所示,当风速为20 m/s,直径 d=1 200 μm时,在空气动力作用下,水滴的迎风面开始变形.紧接着,水滴沿垂直于气流的方向逐渐变形,形成圆盘状结构. 同时,水滴的主体部分向边缘移动,形成一个液环.液滴中心附近形成袋状结构,气流作用下,袋状液膜继续变薄,最终破裂.同样的结果出现在d=1 000 μm中,不同之处在于水滴直径为 1 000 μm时形成的袋状结构较 1 200 μm直径的滴小.当水滴直径为600 μm时,其在足够长的计算域内仅发生了振荡变形.袋状破碎的整个过程与Zhao等[28]的实验结果以及张文英等[29]的数值模拟结果吻合较好.

图4

新窗口打开| 下载原图ZIP| 生成PPT

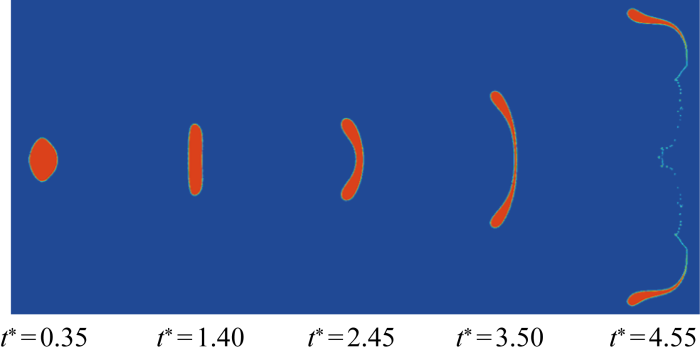
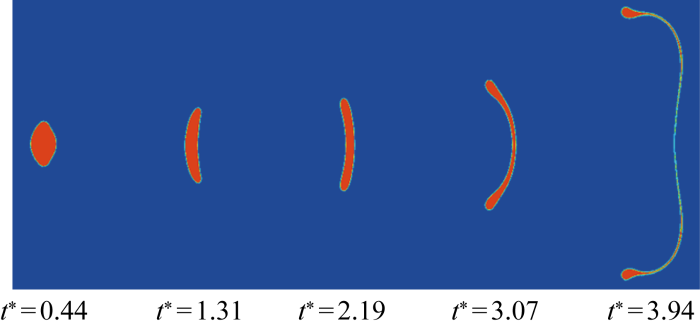
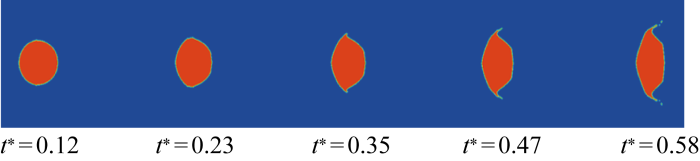
图4   入口风速为20 m/s,直径为1 200 μm,We = 8.05时的水滴变形破碎情况

Fig.4   Deformation and breakup of water droplets at an inlet velocity of 20 m/s, a diameter of 1 200 μm, and We=8.05


图5

新窗口打开| 下载原图ZIP| 生成PPT

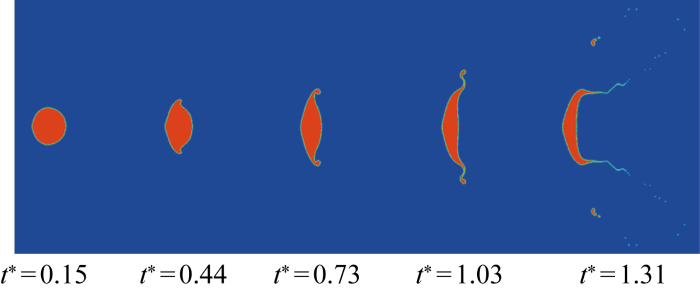
图5   入口风速为20 m/s,直径为1 000 μm,We=6.70时的水滴变形破碎情况

Fig.5   Deformation and breakup of water droplets at an inlet velocity of 20 m/s, a diameter of 1 000 μm, and We=6.70


图6

新窗口打开| 下载原图ZIP| 生成PPT

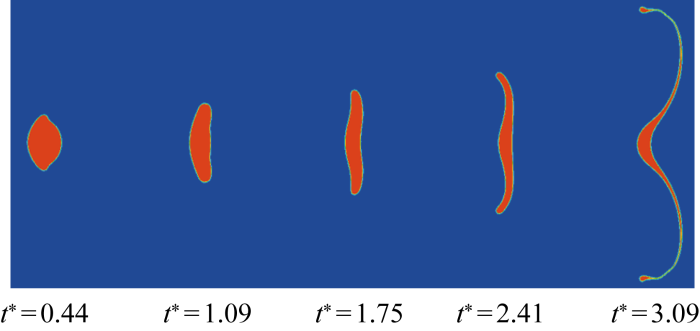
图6   入口风速为20 m/s,直径为600 μm,We=4.03时的水滴变形破碎情况

Fig.6   Deformation and breakup of water droplets at an inlet velocity of 20 m/s, a diameter of 600 μm, and We=4.03


3.2 入口风速为50 m/s条件下的变形及破碎结果

水滴破碎具有多模式破碎的特征,多模式破碎通过水滴边缘特征又可以区分为包-蕊状破碎和蕊-层状破碎[30].如图7~11所示,当风速为50 m/s、水滴直径为 1 200 μm时,水滴边缘几乎没有袋状结构形成,属于蕊-层状破碎.当水滴直径为800 μm时,与前者不同的是在水滴边缘处形成了明显的袋状结构,液滴两侧的边缘部位呈现出袋状的形式,并且袋状部分慢慢变薄,直至破裂,属于包-蕊状破碎.与前者的相同点在于,液滴的中心部分明显向上游突起(向左侧突起),形成一个较大的液核,且水滴初始直径越大,形成的液核越大.当水滴直径为400 μm时,破碎形式同样为包-蕊状破碎,水滴两侧形成的袋状结构更为明显.多模式破碎的模拟结果与Zhao等[28]的实验结果相符较好.当水滴直径为200 μm时,水滴的破碎形式转换为袋状破碎.当水滴直径为100 μm时,水滴发生振荡变形不发生破碎.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   入口风速为50 m/s,直径为1200 μm,We = 50.34 时的水滴变形破碎情况

Fig.7   Deformation and breakup of water droplets at an inlet velocity of 50 m/s, a diameter of 1 200 μm, and We=50.34


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   入口风速为50 m/s,直径为800 μm,We=33.56 时的水滴变形破碎情况

Fig.8   Deformation and breakup of water droplets at an inlet velocity of 50 m/s, a diameter of 800 μm, and We=33.56


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   入口风速为50 m/s,直径为400 μm,We=16.78 时的水滴变形破碎情况

Fig.9   Deformation and breakup of water droplets at an inlet velocity of 50 m/s, a diameter of 400 μm, and We=16.78


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   入口风速为50 m/s,直径为200 μm,We=8.39 时的水滴变形破碎情况

Fig.10   Deformation and breakup of water droplets at an inlet velocity of 50 m/s, a diameter of 200 μm, and We=8.39


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   入口风速为50 m/s,直径为100 μm,We=4.19 时的水滴变形破碎情况

Fig.11   Deformation and breakup of water droplets at an inlet velocity is 50 m/s, a diameter of 100 μm, and We=4.19


3.3 入口风速为80 m/s条件下的变形及破碎结果

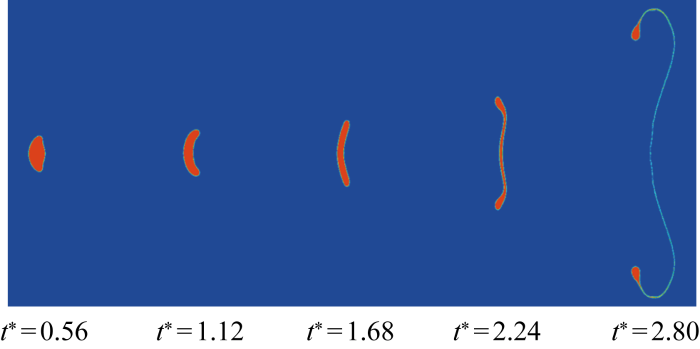
从图12~15中可以看出,当风速为80 m/s、d=1 200 μm时,在气流速度较大的条件下,水滴两侧不断有小液滴被剥离出去,且刚剥离时,液核比多模式破碎更大,符合剪切破碎的特征.在小水滴被剥离出去的过程中,液核逐渐被气流压扁,水滴边缘部分形成很小的袋状膜,袋状膜逐渐变薄直至破碎,袋状膜破碎后,袋膜处的小液滴不断被剥离出去.剪切破碎的模拟结果与Xu等[16]的实验结果相符较好.与蕊-层状破碎相比,剪切破碎在初期水分向边缘移动时几乎没有汇聚过程,由于水滴边缘气流速度较大,移动到液滴边缘的水滴直接被剥离出去,这是可以区分剪切破碎与蕊-层状破碎的方法.当d=600 μm 时,水滴的破碎方式转换为蕊-层状破碎.当d=200 μm时,水滴的破碎方式变为包-蕊状破碎.当d=100 μm时,水滴的破碎方式变为袋状破碎.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   入口风速为80 m/s,直径为 1 200 μm,We = 128.88 时的水滴变形破碎情况

Fig.12   Deformation and breakup of water droplets at an inlet velocity of 80 m/s, a diameter of 1 200 μm,and We=128.88


图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   入口风速为80 m/s,直径600 μm,We=64.44 时的水滴变形破碎情况

Fig.13   Deformation and breakup of water droplets at an inlet velocity of 80 m/s, a diameter of 600 μm, and We=64.44


图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   入口风速为80 m/s,直径200 μm,We=21.48 时的水滴变形破碎情况

Fig.14   Deformation and breakup of water droplets at an inlet velocity of 80 m/s, a diameter of 200 μm, and We=21.48


图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   入口风速为80 m/s,直径100 μm,We=10.74 时的水滴变形破碎情况

Fig.15   Deformation and breakup of water droplets at an inlet velocity of 80 m/s, a diameter of 100 μm, and We=10.74


3.4 表面波对具体分裂模式的影响

在对液滴分裂模式的研究中,表面波是一个重要的物理量.当气流吹向水滴表面时,水滴迎风面在气体压力的作用下会产生表面波.Theofanous等[31]根据R-T不稳定性理论,提出了最大不稳定波长λmax与水滴最大直径dmax的关系:

dmaxλmax=14πdmaxd2CDWe

式中:CD为液滴的阻力系数,CD/CD-s=1+2.632y,CD-s为圆柱绕流的阻力系数,y=1-(d/dmax)2 [32].该式假设初始时刻的液滴在外部气流的作用下被压扁成为一个直径为dmax的圆盘.

当Oh<0.1时,由Hsiang等[33]根据实验得到的经验公式:

dmaxd=1+0.19We

将式(3)代入式(2)中即可得到最大不稳定波长λmax与We的关系.根据实验以及数值结果,当Re较小时(Re<5 000),CD-s取值0.4[30].

得到水滴破碎模式与表面波的关系如图16所示,随着We的增大,液滴垂直于气流流向的直径dcro与λmax的比值增大,表面波的波长λmax逐渐减小.同时可以发现,在二者比值增加的过程中,液滴的破碎模式发生转变.根据本文数值模拟的结果,表面波与We以及破碎模式的关系统计结果如表1所示,dcro/λmax表示液滴垂直于气流流向的直径与最大不稳定波长的比值,这与Guildenbecher等[34]的分析计算结果基本一致.

图16

新窗口打开| 下载原图ZIP| 生成PPT

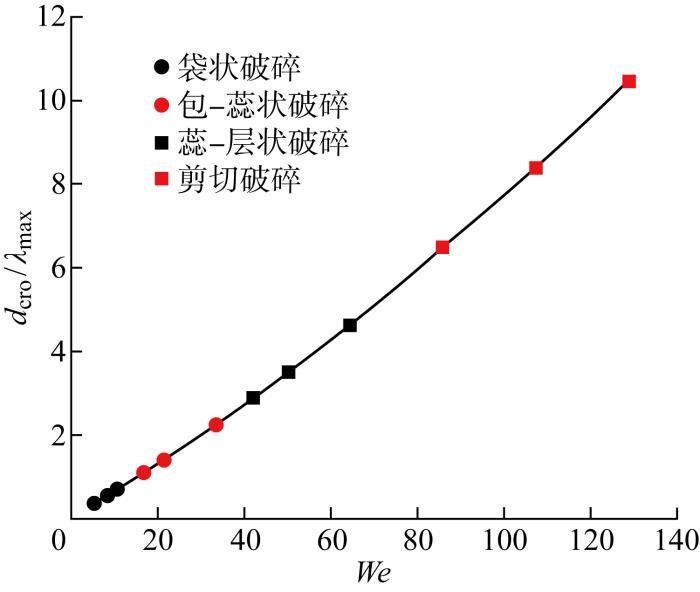
图16   水滴破碎模式与表面波的关系

Fig.16   Relationship between water droplets breakup modes and surface wave


表1   破碎模式与We以及表面波波长的关系

Tab.1  Relationship between water droplets breakup modes, We, and surface wave

破碎模式Wedcro/λmax
袋状破碎5~160.3~1
包-蕊状破碎16~501~3
蕊-层状破碎50~853~6
剪切破碎>85>6

新窗口打开| 下载CSV


3.5 不同入口速度条件下水滴初次破碎后的结果统计

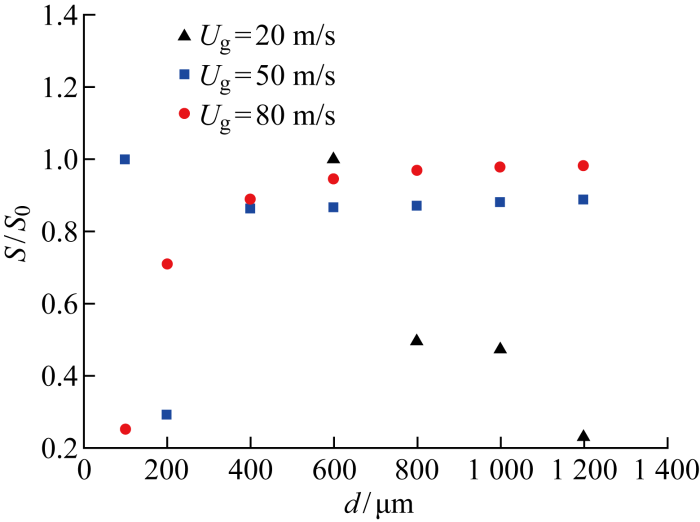
对水滴初次破碎后的主液滴(面积最大的液滴)面积S和球形水滴初始面积S0进行统计,得到面积比S/S0与水滴直径d的关系,如图17所示.当入口速度为20 m/s时,水滴在600 μm直径条件下不发生破碎,在800、1 000 和1 200 μm直径条件下均表现出袋状破碎,袋状破碎由于其破碎形式的特殊性,没有位于中部的母液滴,只有居于两侧的子液滴,所以面积比小于0.5,且随着水滴直径增大,初次破碎后的主液滴与初始液滴面积之比减小;当入口速度为50 m/s时,水滴在100 μm直径条件下不发生破碎,在200 μm直径条件下发生袋状破碎,在400、600、800 μm直径条件下发生包-蕊状破碎,在1 000、1 200 μm直径条件下发生蕊-层状破碎,蕊-层状破碎后的面积比整体大于包-蕊状破碎,且随着直径的增大,面积比略微增大;当入口速度为80 m/s时,水滴在100 μm直径条件下发生袋状破碎,在200 μm直径条件下发生包-蕊状破碎,在400、600 μm 直径条件下发生蕊-层状破碎,在800、1 000、1 200 μm直径条件下发生剪切破碎,4种破碎模式下的面积比呈现出如下规律:

S/S0(剪切破碎)>S/S0(蕊-层状破碎)>S/S0(包-蕊状破碎)>S/S0(袋状破碎)

以水滴破碎为前提,在相同直径条件下,入口速度越大,破碎后的面积比越大.以 1 200 μm直径的水滴为例,当Ug=20 m/s时,S/S0=0.229;当 Ug=50 m/s时,S/S0=0.888;当Ug=80 m/s时,S/S0=0.982.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17   水滴初次破碎后的面积比与水滴直径的关系

Fig.17   Relationship between the area ratio of water droplets after initial crushing and the diameter of water droplets


4 结论

本文主要分析了在常用低速风洞条件下可能产生的3种主要破碎模式,为袋状破碎、多模式破碎以及剪切破碎,指出了3种不同破碎模式的区别与联系.通过对水滴的表面波和We的量化分析,得到了二者与破碎模式之间的关系.得出的主要结论如下:

(1) 在相同气流速度条件下,不同直径水滴的破碎模式不同.随着水滴直径减小,We值减小.在 20 m/s 气流作用下,直径为600 μm的水滴不发生破碎;当风速为50 m/s时,直径为100 μm的水滴不发生破碎.

(2) 多模式破碎可以分为包-蕊状破碎和蕊-层状破碎,二者的区别在于包-蕊状破碎在水滴两侧会形成较为明显的袋状结构,而蕊-层状破碎两侧则没有明显的袋状结构,在剪切力的作用下小水滴被逐渐剥离出去,且发生蕊-层状破碎的水滴在中部形成的液核比包-蕊状破碎形成的液核占比更大.

(3) 随着We增加,水滴垂直于气流流向的直径与最大不稳定表面波波长的比值增大,最大不稳定表面波波长逐渐减小.水滴的破碎形式会对水滴破碎后形成的最大液滴的面积与初始液滴的面积之比有较大影响.在初始水滴直径相同的条件下,入口速度越大,破碎后的面积比越大.

受模拟计算方法及其他条件的限制,针对水滴破碎后小水滴(除母液滴之外)的等效直径、速度等参数有待进一步统计.

参考文献

战培国.

美国NASA结冰试验设备体系综述

[J]. 航空科学技术, 2021, 32(5): 1-6.

[本文引用: 1]

ZHAN Peiguo.

Review on the system of icing facilities in NASA

[J]. Aeronautical Science & Technology, 2021, 32(5): 1-6.

[本文引用: 1]

符澄, 宋文萍, 彭强, 等.

结冰风洞过冷大水滴结冰条件模拟能力综述

[J]. 实验流体力学, 2017, 31(4): 1-7.

[本文引用: 1]

FU Cheng, SONG Wenping, PENG Qiang, et al.

An overview of supercooled large droplets icing condition simulation capability in icing wind tunnels

[J]. Journal of Experiment in Fluid Mechanics, 2017, 31(4): 1-7.

[本文引用: 1]

Federal Aviation Administration. Airplane and engine certification requirements in supercooled large drop, mixed phase, and ice crystal icing conditions[S]. Washington: FAA, 2014.

[本文引用: 1]

陈舒越, 郭向东, 王梓旭, 等.

结冰风洞过冷大水滴粒径测量初步研究

[J]. 实验流体力学, 2021, 35(3): 22-29.

[本文引用: 1]

CHEN Shuyue, GUO Xiangdong, WANG Zixu, et al.

Preliminary reasearch on size measurement of supercooled large droplet in icing wind tunnel

[J]. Journal Experiments in Fluid Mechanics, 2021, 35(3): 22-29.

[本文引用: 1]

陈勇, 孔维梁, 刘洪.

飞机过冷大水滴结冰气象条件运行设计挑战

[J]. 航空学报, 2023, 44(1): 15.

[本文引用: 1]

CHEN Yong, KONG Weiliang, LIU Hong.

The challenge of aircraft design under operational conditions of supercooled large water droplets icing

[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(1): 15.

[本文引用: 1]

LANKFORD T T. 飞机结冰[M]. 上海: 上海交通大学出版社, 2020: 20-32.

[本文引用: 1]

LANKFORD T T. Aircraft icing[M]. Shanghai: Shanghai Jiao Tong University Press, 2020: 20-32.

[本文引用: 1]

易贤, 马洪林, 王开春, 等.

结冰风洞液滴运动及传质传热特性分析

[J]. 四川大学学报(工程科学版), 2012, 44 (Sup.2): 132-135.

[本文引用: 1]

YI Xian, MA Honglin, WANG Kaichun, et al.

Analysis of water droplet movement and heat/mass transfer in an icing wind tunnel

[J]. Journal of Sichuan University (Engineer Science Edition), 2012, 44 (Sup.2): 132-135.

[本文引用: 1]

李晓峰, 常士楠, 冷梦尧.

冰风洞内水滴参数沿程变化的数值模拟

[J]. 计算机仿真, 2018, 35(10): 66-71.

[本文引用: 2]

LI Xiaofeng, CHANG Shinan, LENG Mengyao.

Numerical simulation of water droplet parameters variation along the icing wind tunnel

[J]. Computer Simulation, 2018, 35(10): 66-71.

[本文引用: 2]

郭向东, 王梓旭, 李明, 等.

结冰风洞中液滴相变效应数值模拟

[J]. 航空学报, 2018, 39(3): 36-48.

[本文引用: 1]

GUO Xiangdong, WANG Zixu, LI Ming et al.

Numerical investigation of phase transition effects of droplet in icing wind tunnel

[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(3): 36-48.

[本文引用: 1]

POTAPCZUK M G, TSAO J.

Bimodal SLD ice accretion on swept NACA 0012 airfoil models: AIAA 2020-2814

[R]. VIRTUAL EVENT: AIAA, 2020.

[本文引用: 2]

符澄, 徐兵兵, 彭强, 等.

结冰风洞中SLD模拟方法及其实验验证研究

[C]// 中国力学大会论文集. 杭州: CCTAM, 2019: 2851-2857.

[本文引用: 2]

FU Cheng, XU Bingbing, PENG Qiang, et al.

The SLD simulation method and experiment study of icing wind tunnel

[C]// Proceedings of the Chinese Congress of Theoretical and Applied Mechanics. Hangzhou, China: CCTAM, 2019: 2851-2857.

[本文引用: 2]

孔上峰, 封锋, 邓寒玉.

高韦伯数下煤油液滴的破碎机理研究

[J]. 实验流体力学, 2017, 31(1): 20-25.

[本文引用: 1]

KONG Shangfeng, FENG Feng, DENG Hanyu.

Breakup of a kerosene droplet at high Weber numbers

[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(1): 20-25.

[本文引用: 1]

金仁瀚, 刘勇, 王锁芳.

单液滴羽状/液膜稀释破碎特性研究

[J]. 推进技术, 2017, 38(4): 885-895.

[本文引用: 2]

JIN Renhan, LIU Yong, WANG Suofang.

Experimental investigations of breakup characteristic of single droplet in plume/sheet-thinning breakup regime in airflow

[J]. Journal of Propulsion Technology, 2017, 38(4): 885-895.

[本文引用: 2]

JACKIW I M, ASHGRIZ N.

On aerodynamic droplet breakup

[J]. Journal of Fluid Mechanics, 2021, 913(433): A33-A33.

[本文引用: 2]

ZHAO H, NGUYEN D, DUKE D J, et al.

Effect of turbulence on drop breakup in counter air flow

[J]. International Journal of Multiphase Flow, 2019, 120: 103108.

DOI:10.1016/j.ijmultiphaseflow.2019.103108      URL     [本文引用: 1]

XU Z K, WANG T Y, CHE Z Z.

Droplet breakup in airflow with strong shear effect

[J]. Journal of Fluid Mechanics, 2022, 941(454): A54.

DOI:10.1017/jfm.2022.326      URL     [本文引用: 2]

The deformation and breakup of droplets in airflows is important in spray and atomisation processes, but the shear effect in non-uniform airflow is rarely reported. In this study, the deformation and breakup of droplets in a shear flow of air is investigated experimentally using high-speed imaging, digital image processing and particle image velocimetry. The results show that in airflow with a strong shear effect, the droplet breakup exhibits unique features due to the uplift and stretching produced by the interaction between the deformed droplet and the shear layer. The breakup process can be divided into three stages according to the droplet morphology and the breakup mechanism, namely the sheet breakup, the swing breakup and the rim breakup stages. Theoretical analysis reveals that the swing breakup is governed by the transverse Rayleigh–Taylor instability. A regime map of the droplet breakup is produced, and the transitions between different regimes are obtained theoretically. The stretching liquid film during the droplet deformation and the fragment size distribution after droplet breakup are analysed quantitatively, and the results show that they are determined by the competition of breakup at different stages affected by the shear. Finally, the effect of the droplet viscosity is investigated, and the viscosity inhibits the droplet breakup in a strong shear airflow.

楼建锋, 洪滔, 朱建士.

液滴在气体介质中剪切破碎的数值模拟研究

[J]. 计算力学学报, 2011, 28(2): 210-213.

[本文引用: 6]

LOU Jianfeng, HONG Tao, ZHU Jianshi.

Numerical study on shearing breakup of liquid droplet in gas medium

[J]. Chinese Journal of Computational Mechanics, 2011, 28(2): 210-213.

[本文引用: 6]

JAIN S S, TYAGI N, PRAKASH R S, et al.

Secondary breakup of drops at moderate Weber numbers: Effect of density ratio and Reynolds number

[J]. International Journal of Multiphase Flow, 2019, 117: 25-41.

DOI:10.1016/j.ijmultiphaseflow.2019.04.026      URL     [本文引用: 2]

LIANG P Y, EASTES T W, GHARAKHARI A, et al.

Computer simulations of drop deformation and drop breakup

[C]// 24th Joint Propulsion Conference. Boston, MA, USA: AIAA, 1988: 1-7.

[本文引用: 5]

樊玉光, 宋光辉, 袁淑霞, 等.

气流中液化天然气液滴破碎数值模拟研究

[J]. 石油化工, 2021, 50(3): 224-229.

DOI:10.3969/j.issn.1000-8144.2021.03.004      [本文引用: 3]

基于流体体积法和k-ε湍流模型对液化天然气单液滴在气流中的变形破碎情况进行模拟研究。研究不同We对液滴形态和破碎模式的影响,分析液滴形态变化过程中速度、加速度和阻力系数随时间的变化趋势,并研究不同流场下液滴变形破碎情况。结果表明,不同的We下,液滴呈现出不同的破碎模式,液滴发生剪切破碎的临界We为80左右,同一We下不同直径的液滴临界破碎时间有所不同;随着气液相对速度的We的增大,液滴的无量纲变形时间先递减后趋向于平缓;液滴变形破碎过程中,速度随着时间的延长而增加,加速度和阻力系数随着时间的延长先增后减;与普通流场相比,带挡板的流场中液滴变形破碎时间明显缩短。

FAN Yuguang, SONG Guanghui, YUAN Shuxia, et al.

Numerical simulation of liquid natural gas droplet breakup in gas phase flow

[J]. Petrochemical Technology, 2021, 50(3): 224-229.

DOI:10.3969/j.issn.1000-8144.2021.03.004      [本文引用: 3]

The deformation and breakup of a single liquified natural gas droplet is simulated in gas phase flow by using the volume of fluid method and k-ε turbulence model. The influence of We on droplet morphology and breakup mode was investigated,and the change tendencies of velocity,acceleration and drag coefficient with time during the process of droplet morphology change were studied. In addition,the droplet deformation and breakup in different flow fields were compared. The results indicate that the droplet shows different breakup modes in different We. The critical We of shear breakup is about 80,and the critical breakup time of different droplet diameter is different under the same We. With the increase in We at relative gas-liquid velocity,the curve of dimensionless deformation time of droplet decreases firstly and then tends to be flat. In the process of droplet deformation and breakup,the velocity keeps increasing,while the acceleration and drag coefficient increase firstly and then decrease with the increase in time. Compared with the original flow field,the deformation and breaking time of droplets in the flow field with baffle plates are significantly reduced.

LI W, WANG J X, ZHU C L, et al.

Deformation and acceleration of water droplet in continuous airflow

[J]. Physics of Fluids, 2022, 34(3): 033313.

[本文引用: 1]

刘全忠, 李小斌. 高等流体力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2018: 179-180.

[本文引用: 1]

LIU Quanzhong, LI Xiaobin. Advanced fluid mechancs[M]. Harbin: Harbin Institute of Technology Press, 2018: 179-180.

[本文引用: 1]

ZEESHAN A K, NASEEM A, MARIYAM S, et al.

Cell alternation algorithm for simulating bubble growth in boiling flows through volume of fluid (VOF) method in fluent

[J]. Alexandria Engineering Journal, 2022, 61(12): 13051-13066.

DOI:10.1016/j.aej.2022.06.059      URL     [本文引用: 1]

凌桂龙. Fluent2020流体计算从入门到精通[M]. 北京: 电子工业出版社, 2021: 110-113.

[本文引用: 1]

LING Guilong. Fluent2020 fluid computing from beginner to proficient[M]. Beijing: Publishing House of Electronics Industry, 2021: 110-113.

[本文引用: 1]

潘丽萍, 王强. 实用多相流数值模拟[M]. 北京: 科学出版社, 2021: 11-15.

[本文引用: 1]

PAN Liping, WANG Qiang. Practical numerical simulation of multiphase flow[M]. Beijing: China Science Publishing, 2021: 11-15.

[本文引用: 1]

杨威, 贾明, 孙凯, 等.

液滴变形-袋式-多模式破碎转换研究

[J]. 工程热物理学报, 2017, 38(2): 416-420.

[本文引用: 1]

YANG Wei, JIA Ming, SUN Kai, et al.

Investigation on transtions of deformation-bag-multimode breakup for liquid droplets

[J]. Journal of Engineering Thermophysics, 2017, 38(2): 416-420.

[本文引用: 1]

杨威, 贾明, 孙凯, 等.

液滴在连续气流作用下的变形与破碎

[J]. 内燃机学报, 2018, 36(3): 230-236.

[本文引用: 1]

YANG Wei, JIA Ming, SUN Kai, et al.

Droplet deformation and breakup in a continuous gas flow

[J]. Transactions of CSICE, 2018, 36(3): 230-236.

[本文引用: 1]

ZHAO H, WU Z W, LI W F, et al.

Transition Weber number between surfactant-laden drop bag breakup and shear breakup of secondary atomization

[J]. Fuel, 2018, 221: 138-143.

DOI:10.1016/j.fuel.2018.02.119      URL     [本文引用: 2]

张文英, 常士楠, 蒋斌, 等.

基于VOF方法的大水滴袋状破碎的仿真研究

[J]. 空气动力学学报, 2018, 36(4): 605-612.

[本文引用: 1]

ZHANG Wenying, CHANG Shinan, JIANG Bin, et al.

Numerical simulation of large droplets in bag breakup regime based on VOF method

[J]. Acta Aerodynamica Sinica, 2018, 36(4): 605-612.

[本文引用: 1]

张雨树, 薛雷平.

液滴二次雾化破碎模式数值模拟

[J]. 力学季刊, 2015, 36(4): 574-585.

DOI:10.15959/j.cnki.0254-0053.2015.04.003      [本文引用: 2]

在许多现代工程领域中，二次雾化对于增强液体雾化以及提高混合率都起到了关键的作用．基于SIMPLE方法对这个问题进行了数值模拟，VOF方法与Level-Set方法耦合捕捉界面，自适应网格的运用平衡了对提高计算精度以及降低计算成本两方面的要求．在Oh数较低(Oh &lt; 0.1)的情况下，通过数值模拟得到了四种典型的液滴分裂模式，并且对其中相对复杂的第二第三种分裂模式进行了详细的分析与比较．得出了该模式形成的条件与相关特性．最后，将以上结果与前人的实验结果作了对比，在大多数重要特征方面，两者有非常好的一致性．

ZHANG Yushu, XUE Leiping.

Numerical simulation of droplet breakup regimes in secondary atomization

[J]. Chinese Quarterly of Mechanics, 2015, 36(4): 574-585.

DOI:10.15959/j.cnki.0254-0053.2015.04.003      [本文引用: 2]

The secondary atomization plays a key role in increasing both evaporation and mixing rates in a variety of engineering applications. The phenomenon was studied by numerical simulation based on SIMPLE scheme. The VOF method, coupled with the Level-Set method, was used to capture the boundary; the adaptive mesh strategy was taken to balance the demands for raising accuracy of calculation and for reducing computational expenditures. In the case of low Oh number, when Oh &lt; 0.1, four typical regimes of droplet breakup are observed in the simulation; and the comparatively more complicated the second and the third modes had undergone detailed analysis and comparison. The condition for the occurance of these modes and the pertinent features were obtained. Finally, comparison between these results and those of past experiments were made; in most part of significant aspects the two have very good agreement.

THEOFANOUS T G, LI G J, DINH T N, et al.

Aerobreakup in rarefied supersonic gas flows

[J]. Journal of Fluids Engineering, 2004, 126(4): 516-527.

DOI:10.1115/1.1777234      URL     [本文引用: 1]

We present new experimental results on the interfacial instabilities and breakup of Newtonian liquid drops suddenly exposed to rarefied, high-speed (Mach 3) air flows. The experimental approach allows for the first time detailed observation of interfacial phenomena and mixing throughout the breakup cycle over a wide range of Weber numbers. Key findings are that Rayleigh-Taylor instability alone is the active mechanism for freestream Weber numbers as low as 28 for low viscosity liquids and that stripping rather than piercing is the asymptotic regime as We→∞. This and other detailed visual evidence over 26&lt;We&lt;2,600 are uniquely suitable for testing Computational Fluid Dynamics (CFD) simulations on the way to basic understanding of aerobreakup over a broad range of conditions.

LIU A B, MATHER D, REITZ R D. Modeling the effects of drop drag and breakup on fuel sprays[DB/OL]. (1993-03-01) [2022-10-20]. https://ui.adsabs.harvard.edu/abs/1993STIN...9329388L .

URL     [本文引用: 1]

HSIANG L, FAETH G.

Near-limit drop deformation and secondary breakup

[J]. International Journal of Multiphase Flow, 1992, 18(5): 635-652.

DOI:10.1016/0301-9322(92)90036-G      URL     [本文引用: 1]

GUILDENBECHER D R, RIVERA C L, SOJKA P E, et al.

Secondary atomization

[J]. Experiments in Fluids, 2009, 46(3): 371-402.

DOI:10.1007/s00348-008-0593-2      URL     [本文引用: 1]

/

〈 〉