柴油机活塞缸套摩擦副润滑和多柔体动力学耦合特性

doi:10.16183/j.cnki.jsjtu.2022.357

柴油机活塞缸套摩擦副润滑和多柔体动力学耦合特性

翟旭茂¹, 田新伟¹, 张传斌², 李玉娟¹, 刘硕², 崔毅^,²

1.潍柴动力股份有限公司,山东潍坊 261061

2.上海交通大学动力机械与工程教育部重点实验室,上海 200240

Coupling Characteristics of Lubrication and Flexible Multibody Dynamics of Piston-Liner Pairs in Diesel Engines

ZHAI Xumao¹, TIAN Xinwei¹, ZHANG Chuanbin², LI Yujuan¹, LIU Shuo², CUI Yi^,²

1. Weichai Power Co., Ltd., Weifang 261061, Shandong, China

2. Key Laboratory for Power Machinery and Engineering of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 崔毅,研究员,博士生导师,电话(Tel.):021-34206861;E-mail:ycui@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-09-13 修回日期: 2022-11-14 接受日期: 2022-11-21

基金资助:

国家自然科学基金(52171315)

Received: 2022-09-13 Revised: 2022-11-14 Accepted: 2022-11-21

作者简介 About authors

翟旭茂(1986-),硕士,高级工程师,从事柴油机润滑动力学及NVH开发研究.

摘要

为研究四冲程车用柴油机活塞-缸套摩擦副的动力学及润滑特性,提出了一种新的活塞-缸套摩擦动力学耦合模型.模型中采用绝对节点坐标公式(ANCF)描述活塞-连杆-曲轴多柔体动力系统,采用平均雷诺方程和微凸体接触理论描述混合润滑模型,基于商用软件结合二次开发程序实现仿真计算.对活塞缸套摩擦副的润滑动力学计算分析表明,由于缸内压力和活塞敲击作用,缸套会产生最大值为23.6 μm的瞬时变形.与刚体模型相比,考虑部件的弹性变形不仅会使活塞横向位移增加40%,还会使得活塞润滑域出现油膜压力的局部集中.另外,柔体模型的循环平均功耗更小,与刚体模型相比相差17.7%.

关键词： 活塞-缸套摩擦副; 润滑动力学; 多柔体系统; 有限元法; 柴油机

Abstract

In this paper, a new piston-liner tribo-dynamic coupling model is proposed to study the dynamics and lubrication characteristics of the piston-liner friction pair of four-stroke vehicle diesel engines. In the model, the piston-rod-crankshaft flexible multibody dynamic system is described by absolute nodal coordinate formulation (ANCF), and the lubrication behavior is described by the averaged Reynolds equation and the Greenwood-Tripp asperity contact theory. The simulation is realized based on commercial software combined with self-developed codes. The results show that the liner has a maximum transient deformation of 23.6 μm due to cylinder pressure and piston knocking behavior. Compared with the rigid model, the proposed model considering the elastic deformation increases lateral displacement of piston by 40% with oil film pressure concentration in lubrication domain. In addition, the friction power loss of flexible model in one cycle is smaller and 17.7% lower than that of rigid model.

Keywords： piston-liner pairs; tribo-dynamics; flexible multibody system; finite element method; diesel engines

PDF (11548KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

翟旭茂, 田新伟, 张传斌, 李玉娟, 刘硕, 崔毅. 柴油机活塞缸套摩擦副润滑和多柔体动力学耦合特性[J]. 上海交通大学学报, 2024, 58(3): 324-332 doi:10.16183/j.cnki.jsjtu.2022.357

ZHAI Xumao, TIAN Xinwei, ZHANG Chuanbin, LI Yujuan, LIU Shuo, CUI Yi. Coupling Characteristics of Lubrication and Flexible Multibody Dynamics of Piston-Liner Pairs in Diesel Engines[J]. Journal of Shanghai Jiaotong University, 2024, 58(3): 324-332 doi:10.16183/j.cnki.jsjtu.2022.357

随着国际能源日益紧张,排放指标愈发严格,现代内燃机正在向高效、节能、环保的方向发展.活塞缸套系统作为内燃机中将热能转换为机械能的主要部件,其摩擦损失占柴油机总摩擦损失的55%~65%^[1].降低内燃机的摩擦损耗对于提高内燃机的经济性、可靠性均有重要作用^[2].

内燃机工作时,活塞在气体燃烧压力的推动下沿缸套的轴线方向做往复运动,机体受到的侧向力主要来自于活塞,活塞的换向过程是噪声的重要来源.伴随着活塞的往复运动,活塞在配合间隙中还会进行横向移动和转动,即二阶运动.活塞缸套摩擦副的润滑状况同时受活塞二阶运动和摩擦副振动的影响.研究表明,适当减小活塞与缸套之间的间隙,能够提高润滑效率,又可以在一定程度上减少活塞的二阶运动和冲击振动^[3-4].此外,表面形貌、结构参数、润滑油特性、内燃机转速和负荷等一系列因素也会影响其摩擦学和动力学性能^{[3,5⇓⇓⇓ -9]}.因此,充分考虑活塞的润滑和动力学相互影响,建立合理的缸套活塞摩擦副摩擦动力学模型,对于内燃机的减摩降噪设计尤为重要.

Tian等^[3]考虑由活塞的弹性变形和热变形引起的活塞裙和缸套的动态间隙,建立了一种新的仿真模型,并对比了柔性活塞和刚性活塞对活塞敲击力的影响.研究表明,为得到更准确的活塞敲击力,在仿真模型中必须考虑由弹性变形和热变形引起的动态间隙.张桂昌^[10]考虑热负荷和机械负荷的共同作用,并建立活塞-连杆-曲柄多体动力学模型,其中活塞被视为弹性体,连杆和曲轴为刚性体,研究了活塞敲击噪声产生机理.方聪聪^[11]建立活塞-缸套的混合润滑和活塞-连杆-曲轴系统的多刚体动力学耦合模型,从活塞裙表面结构参数和工况条件等方面探究了活塞-缸套系统的润滑机理及活塞的二阶动力学特性,并基于活塞热变形补偿给出了裙部型线的优化方案.总的来说,现有研究往往将活塞和缸套视为刚体,忽略了缸套变形与活塞润滑行为的耦合影响,针对柴油机活塞缸套摩擦副多柔体建模分析的研究较少.随着内燃机强化程度提高和轻量化设计需求,润滑组件的弹性变形和表面振动对润滑的影响越来越受到重视,将摩擦副组件视为柔性体是研究的趋势^[3,12].

本文以四冲程车用柴油机的活塞-缸套运动副为研究对象,通过耦合活塞-连杆-曲轴多柔体系统动力学模型和缸套-活塞混合润滑模型,建立了新的活塞-缸套润滑动力学模型.模型考虑活塞-缸套运动副的弹性变形,采用绝对节点坐标公式(Absolute Nodal Coordinate Formulation,ANCF)描述柔性多体系统;采用平均Reynolds方程和Greenwood-Tripp粗糙接触理论描述润滑行为.统一采用有限元方法(Finite Element Method, FEM)进行求解.对比了刚体、柔性体润滑动力学结果差异,分析了活塞缸套动力学及润滑的相互影响特性.

1 活塞-缸套摩擦副润滑动力学耦合

模型

考虑表面粗糙度的影响,采用Patir等^[13⇓-15]提出的平均Reynolds方程来描述活塞和缸套之间的混合润滑,无量纲化的方程可表示为

(1)$ \begin{array}{r} \frac{\partial}{\partial \bar{x}}\left(\phi_{x} \bar{h}^{3} \frac{\partial \bar{p}}{\partial \bar{x}}\right)+\frac{\partial}{\partial \bar{y}}\left(\phi_{y} \bar{h}^{3} \frac{\partial \bar{p}}{\partial \bar{y}}\right)= \\ \bar{u}\left(\phi_{\mathrm{c}} \frac{\partial \bar{h}}{\partial \bar{y}}+\sigma \frac{\partial \phi_{\mathrm{s}}}{\partial \bar{y}}\right)+\phi_{\mathrm{c}} \frac{\partial \bar{h}}{\partial \bar{t}} \end{array}$

(2) $\left.\begin{array}{l} \bar{x}=\frac{x}{R}, \quad \bar{y}=\frac{y}{R}, \quad \bar{h}=\frac{h}{c}, \quad \bar{\sigma}=\frac{\sigma}{c} \\ \bar{u}=\frac{u}{r \omega}, \quad \bar{p}=\frac{p c^{2}}{6 \mu r \omega R}, \quad \bar{t}=\frac{\operatorname{tr} \omega}{2 R} \end{array}\right\}$

式中:x为沿活塞润滑域圆周的局部坐标轴,y为沿活塞润滑域轴向的局部坐标轴,如图1所示;h为油膜厚度;p为油膜压力;u为活塞的往复运动速度;μ为润滑油的动力黏度;t为时间;c为活塞和缸套间的名义径向间隙;R为活塞半径;r为曲柄半径;ω为曲轴角速度;σ为活塞和缸套的综合表面粗糙度;ϕ_x和ϕ_y分别为沿x和y方向的压力流量系数;ϕ_s和ϕ_c分别为剪切流量系数和接触系数^[13⇓-15].考虑油膜压力的对称性,活塞润滑的边界条件可表示为

(3)p(x,y)=0, (x,y)∈Γ

式中:Γ为图1(a)所示的活塞裙润滑域边界.通过活塞和缸套之间的相对位置和弹性形变得到的油膜厚度分布可以表示为

(4)$ \begin{aligned} h(x, y)= & c+h_{\mathrm{p}}(x, y)+\left[e_{0}+\left(y-a_{0}\right) \gamma\right] \times \\ & \cos \alpha+d_{1}(x, y, t)+d_{2}(x, y, t) \end{aligned}$

式中:h_p为活塞型面;式(4)的第3项表示活塞二阶运动导致的膜厚变化,其中e₀为活塞销中心在间隙中的横向位移,a₀为活塞销中心到活塞裙部上边界的垂直距离,α为角坐标,γ为活塞二阶运动的转动角度,如图1(b)所示,图中TS、ATS分别表示主、副推力侧;d₁(x, y, t)和d₂(x, y, t)分别表示在不同时刻由于活塞和缸套的表面振动和弹性变形引起的油膜厚度变化.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 活塞-缸套摩擦副

Fig.1 Piston-liner friction pair

本文中的平均Reynolds方程是一个二阶非齐次椭圆型偏微分方程,因此采用标准Galerkin有限元方法求解,其在处理不规则润滑域时更具灵活性.式(1)可写成:

(5)

\frac{\partial}{\partial \bar{x}} (ξ_{x} \frac{\partial \bar{p}}{\partial \bar{x}})

\frac{\partial}{\partial \bar{y}} (ξ_{y} \frac{\partial \bar{p}}{\partial \bar{y}})

-ψ=0

(6)

\begin{array}{l} ψ = \bar{u} (ϕ_{c} \frac{\partial \bar{h}}{\partial \bar{y}} + σ \frac{\partial ϕ_{s}}{\partial \bar{y}}) + ϕ_{c} \frac{\partial \bar{h}}{\partial \bar{t}} \\ ξ_{x} = ϕ_{x} {\bar{h}}^{3}, ξ_{y} = ϕ_{y} {\bar{h}}^{3} \end{array}\}

对润滑域划分有限元网格,根据Galerkin理论,在式(5)两边同时乘以单元形函数N并在润滑域Ω内对其积分,则第i个内部单元 $Ω_{i}^{e}$ 中平均Reynolds方程的弱形式可写为

(7)

K_{i}^{e} p_{i}^{e}

F_{i}^{e}

式中: $K_{i}^{e}$ 是第i个内部单元的刚度矩阵; $p_{i}^{e}$ 是第i个内部单元的无量纲节点压力向量; $F_{i}^{e}$ 是第i个内部单元的节点力向量.其中 $K_{i}^{e}$ 和 $F_{i}^{e}$ 可分别表示为

(8)

\begin{array}{l} K_{i}^{e} = - \int \int_{Ω_{i}^{e}} (ξ_{x} \frac{\partial N_{i}^{e}}{\partial \bar{x}} \frac{\partial N_{i}^{e T}}{\partial \bar{x}} + ξ_{y} \frac{\partial N_{i}^{e}}{\partial \bar{y}} \frac{\partial N_{i}^{e T}}{\partial \bar{y}}) \bar{d x} \bar{d y} \\ F_{i}^{e} = \int \int_{Ω_{i}^{e}} N_{i}^{e} ψ \bar{d x} \bar{d y} \end{array}\}

据此,将单元代数方程式(8)进行装配,得到整个润滑求解域Ω的稀疏求解方程:

(9)

\bar{K p}

结合边界条件,通过求解式(9)即可得到流体动力油膜压力.对于活塞-缸套摩擦副的润滑而言,若膜厚比H_σ(定义为h/σ)小于4.0,则油膜的润滑状态会由液体动压润滑转变为边界润滑.此时,可以通过Greenwood和Tripp提出的G-T模型计算微凸体接触压力 ${p_{c}}^{[16]}$ .作用在活塞上的压力包括液体动压p和微凸体接触压力p_c;而摩擦力则包括油膜切应力τ和微凸体切应力τ_c.其中,τ和τ_c可分别表示为

(10)τ=-

\frac{μ u}{h}

(ϕ_f+ϕ_fs)-ϕ_fp

\frac{h}{2} \frac{\partial p}{\partial y}

(11)τ_c=sign(-u)μ_fp_c

式中:ϕ_f、ϕ_fs、ϕ_fp均为切应力系数,取值见文献[13 ⇓-15];μ_f为微凸体接触摩擦因数.

由活塞、连杆和曲轴组成的动力学系统如图2所示.图中:XYZ为系统的全局坐标系.系统中缸套与机体绑定,作为一个柔性整体进行分析,对机体底座施加固定约束;缸套-活塞定义为混合润滑接触副;活塞-活塞销、连杆小端轴承、连杆大端轴承以及主轴承均定义为理想的旋转关节接触副.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 活塞-连杆-曲轴多体系统

Fig.2 Piston-rod-crankshaft multibody dynamic system

为描述活塞-连杆-曲轴约束多体系统的动态响应,采用Shabana等^[17-18]提出的ANCF统一建立刚柔多体系统的运动方程,表示为如下微分-代数方程组:

(12)

\begin{array}{l} \ddot{M q} + {Φ^{T}}_{q} (q) λ = Q (q, \overset{\cdot}{q}, t) \\ Φ (q, t) = 0 \end{array}\}

式中:M为该系统有限元离散后的质量矩阵,不随时间变化;q为系统离散后节点的广义坐标向量;λ为考虑该系统运动约束方程的拉格朗日乘子向量;Q为包含爆压、油膜接触力、弹性力以及阻尼力等的广义外力向量;Ф为考虑系统运动副约束关系的向量;Ф_q=∂Ф/∂q为约束向量Ф的雅可比矩阵.对于由活塞、活塞销、连杆、曲轴和缸套组成的多体系统而言,活塞缸套为柔体,其余部分视作刚体.

润滑模型为多体系统中相连接的两个部件施加相反的广义外力.引入方程 $\overset{\cdot}{q}$ =s,将式(12)的微分代数方程组转化为如下形式.最后采用向后差分公式(BDF)方法求解下式:

(13)

\begin{array}{l} \overset{\cdot}{M s} = Q (q, s, t) - {Φ^{T}}_{q} (q) λ \\ \overset{\cdot}{q} = s \\ Φ (q, t) = 0 \end{array}\}

该润滑动力学模型的计算流程如图3所示.图中:p_m为所有网格节点的平均油膜压力;T_p为周期时长.在初始条件中,将活塞位于上止点作为初始位置,初始速度和初始油膜压力均为0.在t时刻迭代求解摩擦学和动力学两个物理场:润滑模型中,采用标准Galerkin有限元法求解平均Reynolds方程,向动力学模型传递油膜压力、摩擦力和微凸体接触压力;动力学模型中,将润滑模型中传递的力组装在广义外力矢量Q中,用以求解约束多体系统的运动响应,并向润滑模型传递活塞的二阶运动以及活塞和缸套的变形,从而在润滑模型中计算由于摩擦副表面振动和弹性变形引起的膜厚变化.在每个时间步内,迭代求解上述物理场,直至满足收敛条件,进而向下一时刻推进.重复计算直到相邻循环结果收敛.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 计算摩擦动力学耦合模型的算法流程图

Fig.3 Flow chart of computational algorithm for the tribo-dynamic model

2 4缸柴油机缸套活塞润滑动力学性能分析

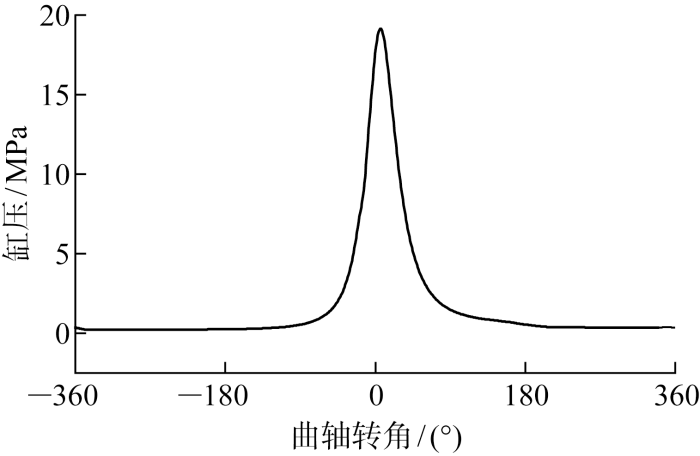
基于上述多物理场耦合方法,对潍柴某款4缸车用柴油机建立缸套活塞摩擦副润滑动力学分析模型(见图2).模型共有40万单元,网格节点数为11万.柴油机参数如表1所示,气缸压力如图4所示.

表1 柴油机和模型参数

Tab.1 Parameters of diesel engine and the model

参数	取值
标定转速/(r·min^-1)	2 600
标定功率/kW	140
缸径/mm	105
缸套弹性模量/GPa	117
缸套泊松比	0.26
活塞弹性模量/GPa	79
活塞泊松比	0.32
连杆长度/mm	190
曲柄半径/mm	59
活塞和缸套间名义径向间隙/μm	50
活塞缸套综合表面粗糙度/μm	5.07
润滑油动力黏度/(Pa·s)	0.008
微凸体接触摩擦因数	0.12
弹性系数	1.198×10^-4

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 标定工况下气缸压力

Fig.4 Cylinder pressure under rated condition

2.1 动力学性能分析对比

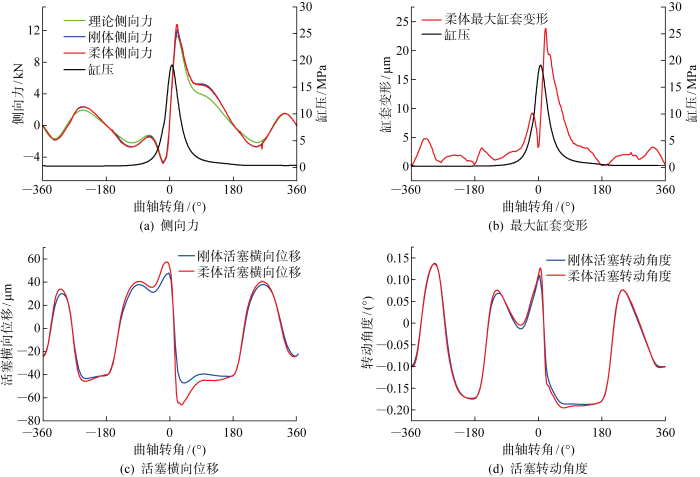
文献[7]和[16]中基于平面刚体动力学和润滑模型,研究了活塞-缸套摩擦副的润滑动力学行为.计算结果与文献相比,活塞二阶运动趋势相似、数量级相同;由于柴油机参数和缸压等的不同,膜厚结果存在一定差异,但整体趋势相似,动力学与摩擦学的计算结果相对可靠.活塞缸套摩擦副在标定转速的动力学不同分析方法结果对比如图5所示.图5(a)中,理论侧向力不考虑间隙和变形,由一阶和二阶往复惯性力以及气体力的横向分量计算获得.刚体与柔体不同建模方法得到的活塞侧向力基本一致,0° 曲轴转角后受缸压影响侧向力急剧增大,并在20° 曲轴转角时达到峰值.与理论侧向力相比,计算得到的侧向力数值和趋势总体相同,仅在70°~100° 曲轴转角期间在数值上略有差异,考虑到理论计算中连杆往复质量的分布差异,这一误差可以接受,侧向力计算结果与理论值相吻合.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 刚体和柔体模型的动力学结果对比

Fig.5 Dynamic results of rigid and flexible models

图5(b)给出了柔体计算得到的缸套最大变形.当活塞在第一个冲程的下行过程中,主推力侧方向的缸套受到来自活塞传递的侧向力而弯曲变形.20° 曲轴转角左右时,受爆压影响,侧向力达到峰值,缸套变形也相应达到最大值,为23.6 μm.后续分析可知,缸套活塞最小油膜厚度可低至4.62 μm,缸套变形明显大于最小油膜厚度,因此摩擦副的弹性变形不容忽视.

图5(c)和图5(d)分别给出了一个周期内活塞横向位移和转动角度的对比,其中,转动角度为正值表示活塞进行顺时针旋转.两种建模方法的活塞横向位移均在30°~50° 曲轴转角处达到最大值,此时活塞仍然处于做功冲程(0°~180° 曲轴转角)的下行阶段.受缸套弯曲变形影响,与刚体模型相比,柔体模型的活塞最大横向位移和最大转动角度均有所增大.具体而言,两种模型的最大横向位移相差40%;最大转动角度相差4.3%,而在5° 曲轴转角左右处,两种建模方式得到的转动角度差异也达到了15.5%.

综上而言,柔体模型中活塞侧向力与刚体模型基本一致,但受缸套弯曲变形影响,采用柔体建模使得活塞横向位移和转动角度等明显增大,活塞二阶运动更加剧烈.

2.2 摩擦学性能分析对比

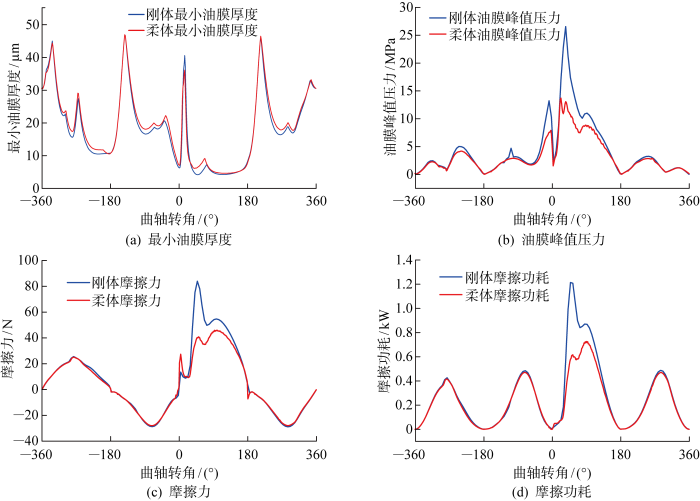
活塞缸套摩擦副在标定转速下的润滑结果对比如图6所示.图6(a)为一个周期内活塞裙部的最小油膜厚度(Minimum Oil Film Thickness, MOFT).由于活塞受到缸内气体力和往复惯性力的共同作用,力的侧向分量将活塞压向缸套,造成活塞和缸套的弹性变形,使得运动副局部间隙增大.因此可以发现,一个周期内柔体条件下的最小油膜厚度普遍大于刚体条件下得到的膜厚.图6(b)、图6(c)和图6(d)分别为活塞裙部润滑域的峰值压力、摩擦力和摩擦功耗的对比.柔体条件下活塞与缸套之间的局部间隙增大,活塞裙部的油膜厚度增加,会带来更好的润滑条件.因此活塞裙部润滑油膜的局部压力降低,一个周期内的摩擦力和摩擦功耗同样得到降低,平均摩擦功耗的差异为17.7%.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 刚体和柔体模型的摩擦学结果对比

Fig.6 Lubrication results of rigid and flexible models

在做功冲程,刚体与柔体模型下摩擦学结果的差异更为明显.在做功上止点换向后,柔体模型计算得到的峰值压力、摩擦力和摩擦功耗比刚体模型分别低48%、51%、51%.这是由于在燃烧冲程中,缸内气体力的作用使得活塞侧向力远大于其他冲程,柔体条件下活塞和缸套有着更大的弹性变形,导致两种模型摩擦学结果的差异在这一冲程更为明显.

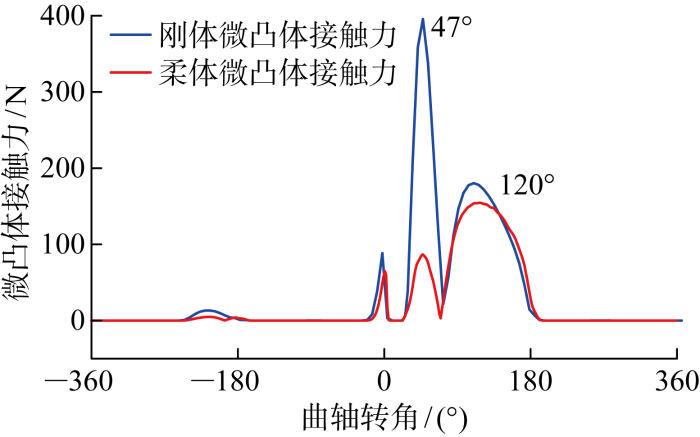
无论是刚体模型还是柔体模型,其达到最小油膜厚度时,膜厚比均小于4.这意味着活塞缸套在一个循环中会发生粗糙接触,如图7所示.由于柔体模型对应着更好的润滑条件,因此从图中可知,一个周期内柔体条件下的微凸体接触力普遍小于刚体条件下得到的微凸体接触力.在活塞换向后的50° 曲轴转角附近,缸内气体力爆压使得活塞侧向力远大于其他冲程,活塞和缸套的弹性变形使得局部油膜厚度增大,造成50° 曲轴转角附近柔体建模型下的微凸体接触力大幅低于刚体建模的结果,仅为刚体模型的25%.因此,可以得出结论:在柔体模型中,缸套的弹性变形使得最小油膜厚度增大,摩擦力和微凸体力减小,并降低一个周期内的平均摩擦功耗.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 刚体和柔体模型的微凸体接触力结果对比

Fig.7 Asperity contact results of rigid and flexible model

2.3 活塞最大侧向力时刻场量对比

如图5(a)所示,20° 曲轴转角为侧向力最大的时刻,该时刻刚体模型和柔体模型计算得到的侧向力相同,但其油膜力有很大的差距.因此,提取20° 曲轴转角时的油膜厚度分布以及油膜压力分布,以进一步分析柔体建模对动力学和摩擦学性能的影响.图8给出了20° 曲轴转角时的缸套变形.此时活塞接近上止点,倾斜角度为逆时针,且被推向主推力侧,其传递给缸套的侧向力使得主推力面方向的缸套发生弯曲变形,最大变形为23.6 μm.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 20° 曲轴转角时的缸套变形

Fig.8 Deformation of liner at 20° crank angle

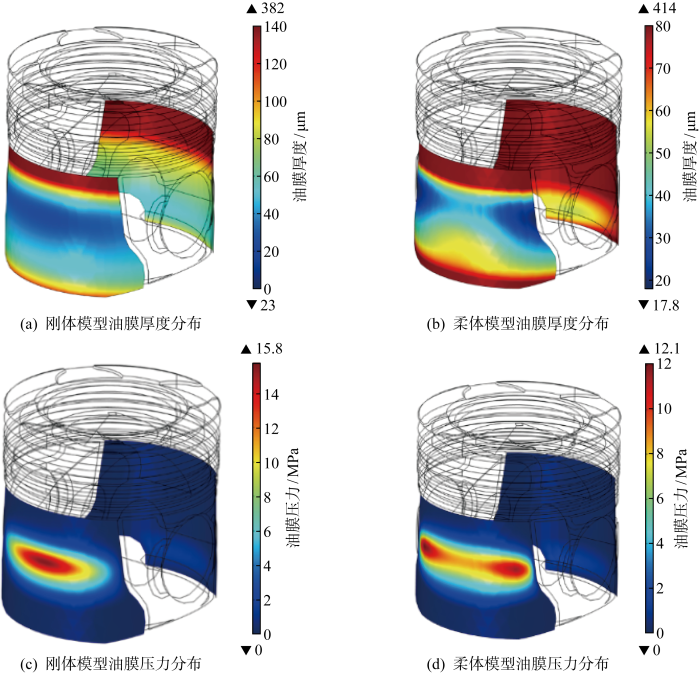
图9给出了20° 曲轴转角时两种建模方式计算得到油膜厚度和压力分布对比.其中,图9(a)和图9(b)分别给出了20° 曲轴转角时刚体模型和柔体模型中活塞润滑域主推力侧的油膜厚度分布.刚体模型中活塞润滑域主推力侧的油膜厚度为23~382 μm,最小油膜厚度出现在中间位置,即受活塞裙部型线影响的活塞裙部半径最大的位置.而柔体模型中的油膜厚度为17.8~414 μm,与刚体模型不同的是,在中间位置的左右两侧存在相对更小的油膜厚度,且两侧的最小油膜厚度小于刚体模型.出现这一现象的原因是,在刚体模型中,油膜集中在中间位置,该位置油膜压力最大;而在柔体模型中,此处集中的油膜压力以及活塞的二阶运动都使得缸套产生弯曲变形,进而使得中心位置的油量增加,油膜变厚,而最小油膜厚度则出现在缸套变形的两侧边缘.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 20° 曲轴转角时油膜厚度和油膜压力分布对比

Fig.9 Comparison of oil film thickness and oil film pressure distribution in different models at 20° crank angle

图9(c)和图9(d)分别给出了刚体模型和柔体模型在20° 曲轴转角时活塞润滑域主推力侧的油膜压力分布.可以看出,刚体模型中,油膜峰值压力出现在活塞裙部的核心润滑区域,压力由峰值区域向外均匀减小.而在柔体模型中,油膜峰值压力出现在前文所述的局部油膜厚度相对更小的位置,即左侧和右侧各有一个油膜压力的峰值区域47° 曲轴转角左右时两个模型计算的微凸体力均达到峰值,但二者差异却十分大,因此图10对比了刚体模型和柔体模型的微凸体接触压力分布.其中,图10(a)给出了刚体模型的微凸体压力分布,图10(b)为柔体模型的微凸体压力分布.由于微凸体接触压力和膜厚直接相关,因此,微凸体接触压力的分布情况和油膜压力的分布相似.刚体模型中,微凸体压力出现在活塞裙部的核心润滑区域,压力由峰值区域向外均匀减小;而在柔体模型中,在膜厚更小的左右两侧出现微凸体压力峰值区域.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 20° 曲轴转角时微凸体接触压力分布对比

Fig.10 Comparison of asperity contact pressure distribution at 20° crank angle

总的来说,柔体模型中缸套的变形不仅使得油膜厚度增大,同时使原本油膜压力最集中的中间位置油量增大,导致在缸套变形边缘的左右两侧出现油膜压力和微凸体接触压力的峰值区域.

3 结论

本文通过耦合缸套-活塞混合润滑模型和活塞-连杆-曲轴多柔体系统动力学模型,针对某款车用4缸柴油机,建立了活塞-缸套摩擦副润滑动力学模型,对比了刚体柔体模型结果差异,分析了摩擦副的动力学及润滑特性,得到了以下结论:

(1) 与刚体模型相比,柔体模型中活塞侧向力与刚体模型基本一致,但主推力侧缸套的最大变形达23.6 μm.缸套的弯曲变形使得活塞横向位移和转动角度等明显增大,活塞二阶运动更加剧烈,其中,最大活塞横向位移增加40%.

(2) 缸套变形和更加剧烈的活塞二阶运动使得最小油膜厚度增大,摩擦力、微凸体力以及摩擦功耗均减小,其中,循环平均摩擦功耗相差17.7%.另外,缸套的变形使原本油膜压力最集中的中间位置油量增多,导致油膜压力和微凸体接触压力的峰值区域出现在变形边缘的左右两侧.

(3) 采用柔体模型对活塞缸套摩擦副进行建模分析可以更准确地描述活塞的二阶运动,从而为摩擦学计算提供更准确的边界条件.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

成东康.

基于流固耦合传热的活塞缸套摩擦性能仿真与实验研究[D]. 天津: 河北工业大学, 2018.