数据驱动法一般包含特征参数选取和SOH回归估计两大步骤.提取出能够充分表征SOH的特征参数是近年来的一个研究热点,文献[8]中从充放电曲线中获取增量容量(Incremental Capacity, IC)曲线,研究了IC曲线随循环次数的变化趋势,并验证IC峰值、IC峰值位置等特征与SOH之间的相关性,但不同型号电池的IC峰值数量并不一致,所用特征并不适用于所用电池.文献[9]中进一步研究不同型号电池包含多个IC峰值的情况.但在IC曲线的提取过程中必须设计复杂的滤波算法来平滑原始电压测量值,同时,IC峰值位置会随着电池老化而逐渐偏移;并且要获得所有老化周期下的IC特性,需要在较大的电压范围内进行采样,十分耗时.针对这个问题,文献[10]中从放电电压曲线及温度曲线中获取放电平均电压和平均温度作为外部特征,估算SOH.但在实际应用中,电池放电深度不一致导致平均电压变化且温度受环境影响较大.为此,文献[11]中选择从恒压充电曲线中获取平均电流等作为外部特征,并用等效电路模型表征恒压曲线中的电池老化现象.上述锂电池特征参数提取的最新研究较大程度上推动了基于数据驱动的锂电池SOH估计的发展.但上述研究有一个共性不足——都是基于恒流恒压充电策略下进行的锂电池充放电实验,所用数据均为单一充电策略下所得数据,未考虑不同充电策略或锂电池实际放电情况等问题,在实际应用中缺乏普适性.研究高效准确的适用不同充电策略的锂电池特征参数选择方法是迫切的现实需求.
获得与SOH高度相关的特征参数之后,需要建立所获取特征参数与SOH之间的映射关系,其本质是一类多元回归问题.诸多机器学习方法可以用于解决这类问题.反向传播(BP)神经网络、支持向量机、高斯回归、决策树等方法相继被用来建立SOH的回归估计模型[4].如文献[12]中搭建BP神经网络对锂电池SOH进行在线估计;文献[3]中采用粒子群优化的支持向量回归模型实时估计不同老化状态下的电池SOH;文献[13]中基于高斯过程回归(Gaussian Process Regression, GPR)建立SOH估算模型,取得较精确的估算精度;文献[10]中搭建布谷鸟搜索支持向量模型实现锂离子电池的SOH快速估计.结合前述特征参数选取方法,上述回归估计模型在特定条件下能够较为精确地估计SOH值,但上述研究所采用的SOH估计模型均为点估计方法.实际工作环境中锂电池剩余容量存在容量回升效应[14],随着循环次数的推移,锂电池剩余容量会有一定幅度的波动甚至上升,导致在某一时刻的SOH估计结果无法充分揭示SOH的退化趋势.同时,在实际运行中电动汽车工作环境复杂、负载波动较大,导致锂电池退化模式不固定,SOH估计结果具有一定的不确定性[15],传统点估计方法无法对锂电池退化过程进行合理量化.
针对锂电池SOH估计的不确定性量化估计问题,近年来有研究人员提出两类方法来构建电池SOH的预测区间.第一类为理论方法,基于以下假设:预测误差遵循具有零均值的确定分布,通常为正态分布或拉普拉斯分布[16].文献[17]中开发了一个基于平均熵和相关向量机的多步预测模型,并将其应用于电池的SOH评估和剩余寿命预测,该方法基于高斯分布构造95%的预测结果置信区间.但实测的锂电池充放电数据涉及复杂过程和噪声干扰,很难确保满足高斯假设.第二类为神经网络方法,该类方法无需考虑误差分布,因此受到研究者青睐.如文献[18]中构建了一个改进的上下边界估计神经网络对锂电池SOH进行区间估计.但此算法需要大量数据集进行训练,而锂电池全生命期,即SOH从100%退化到80%,一般循环次数不超过 2 000,属于典型的小样本问题,这类方法效果有限.
针对当前有关锂电池SOH估计方面的研究在特征参数选取普适性和SOH估计不确定性量化两方面的不足,提出一种适用于多种充电策略的锂电池SOH不确定量化估计方法.该方法充分考虑当前常用充电策略下充放电曲线的变化,从电压、电流及IC曲线中提取出多个外部特征,再通过交叉验证方法自动选取出适用于不同充电策略的个性化最优特征组合.首次提出使用支持向量分位数回归(Support Vector Quantile Regression, SVQR)模型进行锂电池SOH区间估计.所采用的SVQR方法利用分位数回归(Quantile Regression, QR)模型解决了区间分布问题,同时,支持向量回归(Support Vector Regression, SVR)模型在小样本充放电数据下具有较好的泛化性能.将所提方法在常用的3种不同充电策略的锂电池数据集上进行验证,并与QR、分位数回归神经网络(Quantile Regression Neural Network,QRNN)及GPR进行对比,验证了所提方法的优越性.
1 所提方法的总体框架
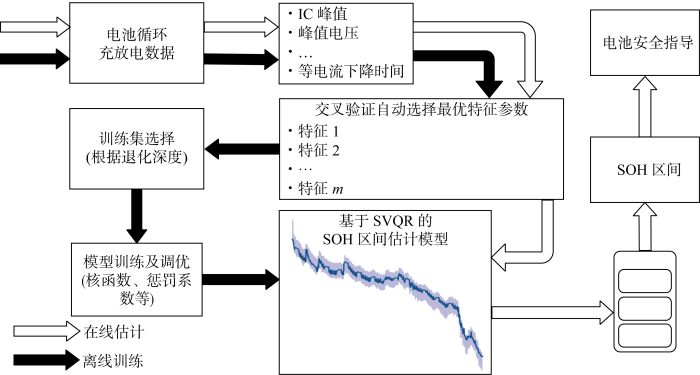
所提方法的总体流程如图1所示,分为离线训练和在线评估两个阶段.在离线训练阶段,首先从循环电压曲线、电流曲线及IC曲线中提取多个通用特征参数,然后采用交叉验证方法自动选择与SOH相关性最好的最优特征参数组合,并将其输入SVQR模型进行训练.在线阶段将充放电数据输入训练好的SVQR模型,实现电池SOH的在线区间估计,从而给出锂电池使用安全指导建议.
图1
图1
所提SOH区间估计方法流程
Fig.1
Flow chart of the proposed SOH interval estimation method
2 考虑不同充电策略的锂电池SOH区间估计方法
2.1 锂电池常用充电策略及其特点
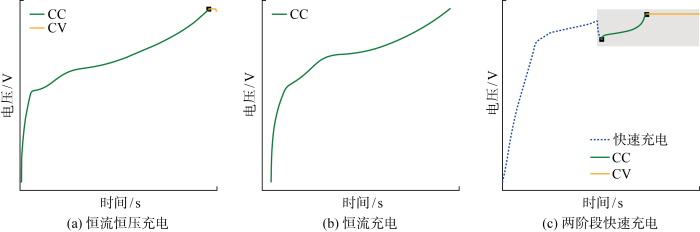
锂电池充电速度是制约电动汽车进一步发展的主要瓶颈之一[19].人们希望提高充电速度,但充电速度的提高会造成温度的快速升高和电池寿命的快速衰退.因此,探索能够兼顾充电快速性、温度控制与合理寿命预期的充电策略一直是一个研究热点[20].目前锂电池充电策略已由最初的恒压充电、恒流充电,发展到恒压恒流充电结合的多阶段充电[21].结合当前锂电池充电策略发展的现状,重点考虑如下3类常用的充电策略.第一类为恒流恒压(Constant Current Constant Voltage, CC-CV)充电.CC-CV充电第一阶段以恒定电流充电;当电压达到预定值时转入第二阶段进行恒压充电,此时电流逐渐减小;当充电电流下降到0时,蓄电池完全充满.该充电策略可有效避免电池极化效应,但充电时间较长;第二类为恒流(Constant Current, CC)充电.CC充电采用恒定电流对电池进行充电.由于电流一般较大,电池会快速达到截止电压,充电时间较短,但控制不得当则会增大电芯的极化;第三类为两阶段快速充电(Two Step Fast Charge, 2-step).该充电策略历经两个充电阶段.充电过程可表达为“C1(Q1)-C2”,其中C1和C2分别代表两个充电阶段,Q1代表充电电流切换时电池的荷电状态(State of Charge, SOC),第一个阶段采用恒流充电至SOC为Q1结束;第二个阶段采用CC-CV方式直至电池充满.上述3种充电策略的电压变化曲线如图2所示.
图2
2.2 SOH特征选择
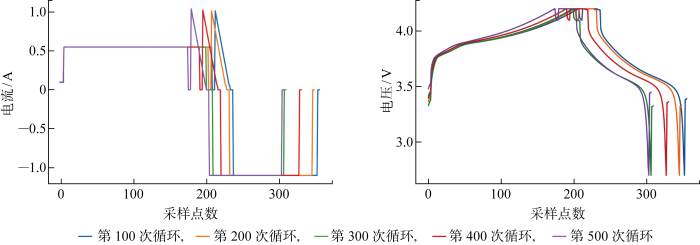
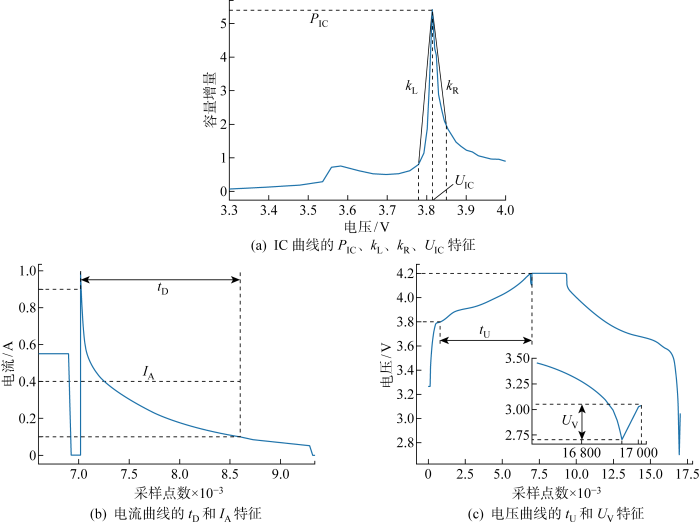
锂电池充放电曲线中蕴含丰富的电池老化信息.图3为某单体电池不同循环次数下电压、电流变化曲线.可见,随着循环次数增多,充放电电压曲线和电流曲线也随之变化,充放电曲线的形状与电池的老化情况高度相关.如何从充放电曲线中提取出与SOH高度敏感的特征参数是SOH估计的关键.但不同充电策略所对应的敏感特征参数可能不同,很难找到普适于多个充电策略的特征参数.当前有关锂电池SOH估计方法大多针对某一特定充电策略,没有考虑充电策略的不同及其进一步发展.为此,提出一种更泛化的特征参数提取流程.首先,充分分析不同充电策略的单体电池在不同循环次数下电压、电流、IC曲线变化特性,并参考文献[2,6,15]中的结论,从IC曲线提取IC曲线峰值(PIC)、IC曲线峰值对应电压(UIC)、IC曲线峰左斜率(kL)、IC曲线峰右斜率(kR) 4个特征,如图4(a)所示;从电流曲线提取CV充电下降到给定电流所用时间(tD)和CV充电过程最后阶段的平均电流(IA),如图4(b)所示;从电压曲线提取CC充电上升到给定电压所用时间(tU)和单次循环后静置时间内的电压回升数值(UV),如图4(c)所示.然后,为了适应不同充电策略,采用交叉验证方法自动选择针对特定充电策略的个性化最优特征参数.交叉验证方法在上述所提取的通用特征集中遍历所有可能的特征参数组合, 然后对各个特征组合的估计结果进行排序以选出最优特征参数组合.
图3
图3
某单体电池充放电曲线在不同循环周期下的变化情况
Fig.3
Change of voltage and current in charging and discharging of a single battery of different cycles
图4
图4
电流、电压和IC曲线的提取特征
Fig.4
Extracted features from current, voltage, and IC curve
2.3 分位数回归
QR最初由Koenker和Bassett[22]提出.把传统方法的均值回归推广到QR,可以更详细地描述响应变量的全局特征,且不易受离群点影响,结果更稳健.尤为重要的是QR不需要回归残差满足正态分布、随机独立、方差齐同等均值回归方法的基本假设.这对于解决锂电池SOH估计这类实际工程问题十分有利,原因在于锂电池实际工作中受多变工况、运行环境等因素影响,监测数据很难满足正态分布的假设.给定训练集T=(xi, yi
式中:xi=[xi,1xi,2 … xi,d]为包含d个分量的独立变量,xi,j是xi的第j个分量, j=1, 2, …, d;yi为对应xi的因变量;qτ(xi)为因变量yi在自变量xi下的第τ分位数,对于任意分位数0<τ<1,β(τ)=[β1(τ) β2(τ) … βd(τ)]'为τ分位数下的回归系数.β(τ)的估计值通过最小化检验函数ρτ(σ)获得.
检验函数ρτ(σ)为一分段线性函数,定义为
式中:I(σ)为一个指示函数,定义为
2.4 支持向量分位数回归
尽管QR方法可以更详细地描述响应变量的全局特征,无需所描述对象服从特定分布,但从1.3节可见,QR本质上还是针对线性问题的回归分析.在实际工程问题中,自变量和因变量之间的关系往往非线性,且难以确定显性的函数形式.考虑到SVR[23]可以通过核函数技巧隐式地把低维非线性数据映射到高维特征空间中做线性回归,且基于结构风险最小化原理,其在解决小样本、非线性问题上具有独特优势,自然地结合SVR与QR并充分利用二者优势将是很好的选择.Takeuchi等[24]首次提出SVQR模型,较好地解决了经济系统中的非线性结构与经济行为在不同尾部的异质性.Shim等[25]利用半参数方法,得到更为简单的SVQR模型.仍以训练集(xi, yi
式中:w为权重向量;λ为惩罚参数;φ(x)为非线性映射函数,可将d维输入向量x隐式地映射到高维特征空间来求解;b为阈值.同SVR的求解过程一样,通过引入松弛变量ξi、
Shim等[25]采用半参数方法通过构造拉格朗日函数的方法对式(6)优化问题进行求解,即
式中:U为一个设计矩阵,由(1,
式中:xs、xt为任意变量;σK为核函数的宽度.采用广义近似交叉验证准则[26]获得最优超参数组合,即
式中:θ=[λ
3 实验设计
3.1 实验设置
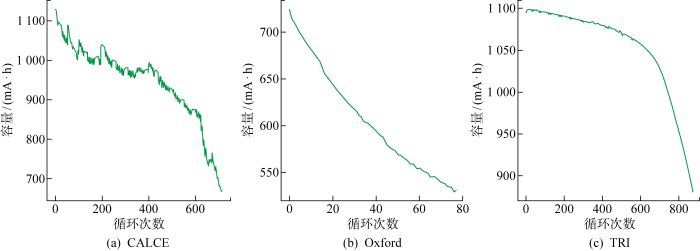
表1 3个数据集的基本信息
Tab.1
| 数据集 | 充电协议 | 标称电压/V | 标称容量/(mA·h) |
|---|---|---|---|
| CALCE | CC-CV | 4.2 | 1100 |
| Oxford | CC | 3.7 | 740 |
| TRI | 2-step | 3.3 | 1100 |
图5
图5
CALCE、Oxford、TRI数据集电池容量变化
Fig.5
Battery capacity change of CALCE, Oxford and TRI datasets
在每个数据集中选用1个放电程度较深的单体电池充放电数据作为训练集,在其余单体电池中任选3个作为测试集来验证所提方法的性能.所选训练集和测试集的情况如表2所示.
表2 训练集和测试集情况
Tab.2
| 数据集 数据划分 | CALCE | Oxford | TRI | |||||
|---|---|---|---|---|---|---|---|---|
| 训练集 | 测试集 | 训练集 | 测试集 | 训练集 | 测试集 | |||
| 电池标号 | CS36 | CS35; CS37; CS38 | Cell1 | Cell3; Cell7; Cell8 | b0c31 | b0c32; b0c34; b0c35 | ||
| 循环次数 | 791 | 716; 857; 849 | 78 | 76; 77; 76 | 839 | 683; 683; 640 | ||
3.2 参与比较的方法
3.3 评价指标
(1) AIS指标.AIS指标定义为所有区间估计点的区间分数均值,可综合衡量区间覆盖率和区间宽度,其值越大越优,按下式计算.
式中:α为置信区间宽度;Ntest为测试集电池循环次数;S(α)(xi)为第i个估计区间的区间分数,定义为
式中:L(α)(xi)、U(α)(xi)分别为预测下限和上限;yi为第i个评估点的实际值;
(2) MPICD指标.MPICD表示预测区间中心位置与实际值的偏差,该值越小越优,按下式计算.
(3) MAPE指标.MAPE按下式计算,该指标可衡量预测区间的宽度信息,狭窄的区间比宽大的区间更好.
式中:Li、Ui分别为预测下限和上限.
4 实验结果与分析
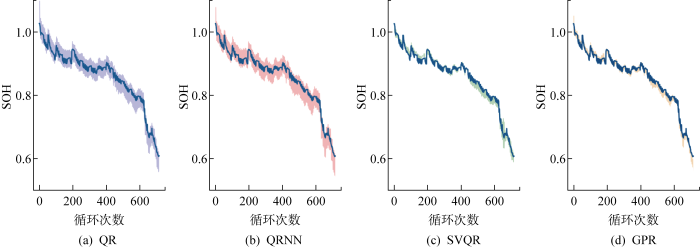
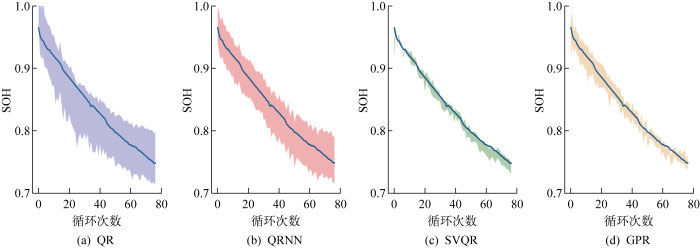
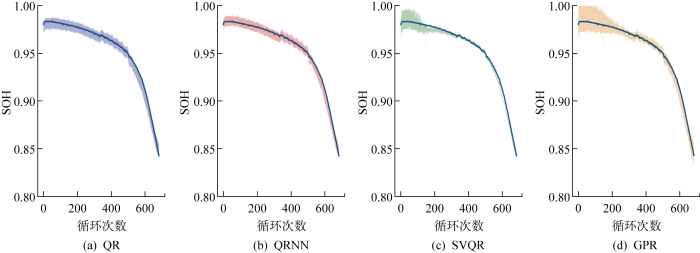
经过特征提取和交叉验证特征自动优选过程,最终对CALCE数据集选择IC曲线峰值、IC曲线峰值对应电压、IC曲线左斜率、CC充电上升到给定电压所用时间、CV充电下降到给定电流所用时间5个特征;对Oxford数据集选择IC曲线峰值、IC曲线左斜率、IC曲线右斜率3个特征;对TRI数据集选择IC曲线峰值、IC曲线右斜率、CV充电下降到给定电流所用时间3个特征.为了实验对比的公平性,其余3种方法在评估时针对不同的数据集采用与SVQR方法同样的特征参数.表3~5分别展示所提方法与QR、QRNN和GPR方法分别在CALCE、Oxford和TRI数据集中各自任选的3个单体电池上的SOH评估结果,其中用粗体标出的为最优结果.图6~8分别展示4种方法在3个数据集中CS35、Cell7、b0c32这3个电池上的SOH估计效果.
表3 CALCE数据集3个单体电池的SOH估计对比结果
Tab.3
| 单体电池 | 方法 | AIS | MPICD | MAPE |
|---|---|---|---|---|
| CS35 | QR | -0.1472 | 1.679 | 12.39 |
| QRNN | -0.1499 | 3.792 | 11.05 | |
| SVQR | -0.0582 | 0.97 | 6.62 | |
| GPR | -0.0524 | 3.109 | 16.32 | |
| CS37 | QR | -0.1211 | 1.816 | 12.07 |
| QRNN | -0.1262 | 1.575 | 10.78 | |
| SVQR | -0.0513 | 0.707 | 5.46 | |
| GPR | -0.0416 | 0.959 | 14.57 | |
| CS38 | QR | -0.1256 | 4.773 | 12.39 |
| QRNN | -0.1285 | 2.773 | 11.03 | |
| SVQR | -0.0868 | 1.64 | 7.29 | |
| GPR | -0.0567 | 2.232 | 18.1 |
表4 Oxford数据集3个单体电池的SOH估计对比结果
Tab.4
| 单体电池 | 方法 | AIS | MPICD | MAPE |
|---|---|---|---|---|
| Cell3 | QR | -1.946 | 1.91 | 105.36 |
| QRNN | -1.614 | 1.68 | 87.19 | |
| SVQR | -0.43 | 1.34 | 19.892 | |
| GPR | -0.698 | 2.49 | 32.63 | |
| Cell7 | QR | -1.904 | 11.19 | 104.17 |
| QRNN | -1.567 | 3.96 | 84.75 | |
| SVQR | -0.402 | 3.75 | 18.99 | |
| GPR | -0.651 | 2.12 | 32.48 | |
| Cell8 | QR | -1.929 | 2.709 | 105.35 |
| QRNN | -1.611 | 2.57 | 87.51 | |
| SVQR | -0.4 | 0.322 | 20.54 | |
| GPR | -0.705 | 3.218 | 32.56 |
表5 TRI数据集3个单体电池的SOH估计对比结果
Tab.5
| 单体电池 | 方法 | AIS | MPICD | MAPE |
|---|---|---|---|---|
| b0c32 | QR | -0.0312 | 1.934 | 12.39 |
| QRNN | -0.0283 | 1.2 | 11.05 | |
| SVQR | -0.0234 | 1.811 | 6.62 | |
| GPR | -0.0411 | 0.035 | 16.326 | |
| b0c34 | QR | -0.0304 | 2.274 | 12.07 |
| QRNN | -0.0273 | 1.51 | 10.78 | |
| SVQR | -0.0198 | 2.67 | 5.46 | |
| GPR | -0.0368 | 0.416 | 14.57 | |
| b0c35 | QR | -0.0362 | 3.49 | 12.39 |
| QRNN | -0.034 | 2.561 | 11.03 | |
| SVQR | -0.0331 | 3.972 | 7.29 | |
| GPR | -0.0508 | 1.13 | 18.1 |
图6
图6
4种方法在CALCE数据集CS35电池的SOH区间估计对比结果
Fig.6
Comparison of four methods for estimating SOH interval of CS35 battery in CALCE dataset
图7
图7
4种方法在Oxford数据集Cell7电池的SOH区间估计对比结果
Fig.7
Comparison of four methods for SOH interval estimation of Cell7 battery in Oxford dataset
图8
图8
4种方法在TRI数据集b0c32电池的SOH区间估计对比结果
Fig.8
Comparison of four methods in estimating SOH interval of b0c32 battery in TRI dataset
首先,从图6~8和表3~5可以看出,在所有数据集上,对于所有的评价指标QRNN与QR结果比较接近,但都远劣于SVQR;QRNN略优于QR,这印证了QR本质上是线性回归方法,其在处理锂电池SOH非线性估计上性能不足.而QRNN性能远劣于SVQR,这充分印证了在本文数据集的量级上,SVQR处理小样本非线性问题时具有更好的泛化能力.其次,在所有实验中SVQR方法的结果与GPR接近,但在多数电池上多数指标都优于GPR方法.尤其在MAPE指标方面,SVQR方法在所有数据集上全优于GPR.AIS指标方面,SVQR方法在Oxford和TRI数据集上均取得最好结果,仅在CALCE数据集上,劣于GPR方法;MPICD指标方面,SVQR方法在CALCE和Oxford数据集上除Cell7电池外,均明显优于GPR,仅在TRI数据集上略劣于GPR.文献[15]报道,GRP方法是目前处理锂电池SOH估计的最优方法.但实际上,GPR需要假设数据服从高斯分布,而实测的锂电池充放电数据涉及复杂过程和噪声干扰,很难确保满足高斯假设.本文所提SVQR则无需此假设,这可以解释上述实验中SVQR总体优于GPR的原因.另外值得指出的是,实验采用同一充电协议下的某一放电深度较深电池的全生命期循环充放电数据来训练SVQR模型,用同数据集中其他电池来测试,这与其他多数研究采用同一电池的部分充放电数据来预测其剩余循环的退化情况相比更有实际意义.上述结论充分证明本文方法在SOH估计方面的优势.
5 结论
提出一种考虑不同充电策略的锂电池剩余容量SVQR区间估计方法.该方法在离线阶段,从锂电池充放电电压、电流及容量增量曲线中获取多个特征,并采用交叉验证方法自动选择最优特征组合.选取放电程度较深的单体电池循环充放电数据训练SVQR模型.在SOH在线估计阶段,采用和训练模型相同的特征作为模型输入,对服役中的锂电池进行SOH区间估计.最后在3个采用不同充电策略的数据集验证所提方法,并与QR、QRNN和GPR方法进行对比,可得出以下结论:
(1) 在不同充电策略下,利用相同外部特征对于锂电池SOH的估计结果也不同.采用两步特征提取策略,即首先针对不同充电策略提取足够多特征,再选取针对不同电池及充电策略的个性化特征参数,可以显著提高电池SOH估计的精度,且具有良好的普适性.
(2) 神经网络类方法的训练需要较大数据集样本,但在样本量有限的锂电池充放电数据集中神经网络类算法估计效果有限.而SVQR利用SVR算法适用于小样本数据集的特点,即使是在小样本条件下也可以较好地在置信区间内估计锂电池SOH.
(3) 相较于文献报告的当前最优的GPR方法,所提SVQR方法无需原始数据服从高斯分布,可在一定置信区间内实现较好的SOH估计结果,具有更好的适应性和鲁棒性.
参考文献
锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测
[J].
Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery
[J].
基于容量增量曲线峰值区间特征参数的锂离子电池健康状态估算
[J].
State of health estimation for lithium-ion batteries based on peak region feature parameters of incremental capacity curve
[J].
基于双充电状态的锂离子电池健康状态估计
[J].
DOI:10.16183/j.cnki.jsjtu.2021.027
[本文引用: 2]

针对锂离子电池实际应用中存在不完全充放电而导致的充电起始点及截止点不确定问题,提出一种基于双充电状态因子的电池健康状态估计方法.搭建电池老化实验台架,采用8块镍钴锰锂离子电池进行老化实验;区别于传统单状态因子估计,选取不同老化阶段下恒压充电状态前端等时间差的电流平均值,以及恒流充电状态末端等幅值电压的充电时间构造健康因子;分析不同老化阶段实验电池的荷电状态-开路电压对应关系,通过理论推导及实验结果证明健康因子的正确性;建立具备强泛化能力的改进支持向量回归模型,并通过粒子群算法优化模型超参数.实验结果表明:所提双充电状态健康因子与电池老化衰减密切相关,所建立的改进支持向量回归模型可实时估计不同老化状态下的电池健康状态,具备容量局部回弹变化的表征能力,可作为一种有效的嵌入式电池管理系统健康状态估计方法.
State of health estimation of lithium-ion batteries based on dual charging state
[J].
退役动力电池健康状态特征提取及评估方法综述
[J].
Research on feature extraction and SOH evaluation methods for retired power battery
[J].
大数据驱动的动力电池健康状态估计方法综述
[J].
DOI:10.3901/JME.2023.02.151
[本文引用: 2]

动力电池健康状态估计是电池管理系统关键算法之一,对提高动力电池能量利用效率、降低电池热失控风险,以及动力电池的维保和残值评估具有重要意义。对比分析试验法、模型法、数据驱动法的优势和不足,并以数据驱动方法为核心,分别从动力电池健康状态数据集构建、健康状态特征参数提取、健康状态估计模型三个方面对现阶段健康状态估计方法的理论基础和技术方案进行综述。总结常用的大数据采集方法以及数据预处理方法,明确大数据在健康状态评估中的意义。比较现有健康状态特征提取方法,对其优劣以及适用场景做了分析。阐述不同健康状态估计模型的基本原理,提出模型融合是未来技术发展方向。最后,面向未来大数据实车应用场景,对动力电池健康状态估计方面存在的问题和发展前景进行了总结和展望。
Review on techniques for power battery state of health estimation driven by big data methods
[J].
DOI:10.3901/JME.2023.02.151
[本文引用: 2]

State of health estimation of power batteries is one of the key algorithms of the battery management systems, which is of great significance for improving power battery energy utilization efficiency, reducing thermal runaway risk, as well as power battery maintenance and residual value evaluation. Comparative analysis has been done on experimental-based, model-based and data-driven methods, and data-driven methods are elaborated from three aspects:dataset construction, health indicators extraction, model establishment. The big data collection methods and data preprocessing methods are summarized. The health indicators extraction methods are compared by their pros and cons and applicable scenarios. The basic principles of different health state estimation models are discussed. The conclusion that model fusion is the direction of future technology development is proposed. Finally, facing the future application scenarios of big data in electric vehicles, the current issue and prospective are depicted.
锂离子电池的健康状态估计综述
[C]//
A review of the estimation of the state of health of lithium-ion batteries
[C]//
Application domain extension of incremental capacity-based battery SoH indicators
[J].DOI:10.1016/j.energy.2021.121224 URL [本文引用: 1]
Battery aging assessment for real-world electric buses based on incremental capacity analysis and radial basis function neural network
[J].DOI:10.1109/TII.9424 URL [本文引用: 1]
基于证据推理规则CS-SVR模型的锂离子电池SOH估算
[J].
DOI:10.16183/j.cnki.jsjtu.2021.345
[本文引用: 2]

锂离子电池健康状态(SOH)的准确性影响电池的安全性和使用寿命.针对锂离子电池SOH估算问题,提出一种基于证据推理(ER)规则的布谷鸟搜索支持向量回归(CS-SVR)的SOH估算模型,并利用NASA Ames研究中心的锂离子电池数据集进行SOH估算试验.该方法以电池放电循环的平均放电电压和平均放电温度为模型输入,利用ER规则进行推理,得到输入数据的融合信度矩阵.将该矩阵输入CS算法优化的SVR模型得到电池SOH估算结果.结果表明,与5种估算效果较好的现有模型相比,基于ER规则的CS-SVR模型具有更良好的估算性能.
State of health estimation of lithium-ion battery using a CS-SVR model based on evidence reasoning rule
[J].
State of health estimation of lithium-ion batteries based on the constant voltage charging curve
[J].DOI:10.1016/j.energy.2018.11.008 URL [本文引用: 1]
基于锂离子电池热特性的SOH在线诊断模型研究
[J].
On-line diagnosis model of SOH based on thermal characteristics of lithium-ion battery
[J].
一种基于数据驱动与经验模型组合的锂电池在线健康状态预测方法
[J].
An online state of health prediction method for lithium batteries based on combination of data-driven and empirical model
[J].
一种基于能量建模的锂离子电池电量估算方法
[J].
A method to estimate the capacity of the lithium-ion battery based on energy model
[J].
Machine learning pipeline for battery state-of-health estimation
[J].DOI:10.1038/s42256-021-00312-3 [本文引用: 4]
Interval prediction of solar power using an improved bootstrap method
[J].DOI:10.1016/j.solener.2017.10.051 URL [本文引用: 1]
Intelligent prognostics for battery health monitoring using the mean entropy and relevance vector machine
[J].
基于多物理过程约束的锂离子电池优化充电方法
[J].
DOI:10.3901/JME.2023.02.223
[本文引用: 1]

锂离子电池在快速充电过程中极易触发内部过热,并加速寿命衰退,因此在确保快速充电的同时主动约束锂离子电池重要中间物理状态具有重要意义。因此,提出一种基于多物理过程变量约束的电池快速充电方法。建立电-热-老化综合模型,并在典型充电场景下进行电热模拟精度验证;在此基础上,设计基于模型的荷电状态与内部温度估计方法,兼顾充电速度、温度约束与寿命衰退抑制,设计基于模型预测控制的快速充电策略。试验验证结果表明,所提出的充电策略能主动限制电池内部温度始终低于预定阈值,在相似的充电速度前提下,所提出的充电策略相比优选的恒流恒压充电法具有更低的寿命衰减速率,两者200次快充-放电循环的容量衰减分别为2.12%和4.88%。所提出的快速充电策略基于模型预测控制方法实现了电池内部状态的有效约束,综合提升了锂离子电池充电过程的快速性、安全性和耐久性。
Multiphysics-constrained optimal charging of lithium-ion battery
[J].
DOI:10.3901/JME.2023.02.223
[本文引用: 1]

The lithium-ion battery(LIB) is prone to the expected over-heating and quick degradation during the fast charging.Therefore, it is of great significance to constrain the key intermediate physical states of LIB actively within a reasonable range, while pursuing the speed of charging. Motivated by this, a multiple physics-constrained fast charging strategy is proposed for the LIB. A comprehensive electro-thermal-aging model is established and validated under typical charging scenarios. On this basis, a model-based observer is designed to estimate the state of charge and internal temperature of LIB in real time. Accounting for multiple conflicting objectives, i.e., the charging speed, temperature rise and degradation rate, a model predictive control-based strategy is proposed to optimize the charging process of LIB. Experimental results suggest that the proposed charging strategy can actively constrain the internal temperature of battery below the predetermined threshold. With a comparable charging speed, the proposed charging strategy leads to a slower degradation than the widely-used constant-current-constant-voltage charging strategy. The capacity decays within 200 charge-discharge cycles are 2.12% and 4.88%, respectively, for the two strategies. Based on the model predictive control, the proposed fast charging strategy constrains the battery internal states effectively, while a comprehensive promotion in terms of rapidity, safety and life extension is realized.
电动汽车大功率充电过程动力电池充电策略与热管理技术综述
[J].
DOI:10.19799/j.cnki.2095-4239.2021.0267
[本文引用: 1]

为实现“双碳”目标,电动汽车成为了交通工具转型的重要途径。但由于充电速度影响电动汽车用户体验,一定程度上制约了电动汽车的推广应用,为此,发展大功率充电是提升电动汽车市场渗入率的重要技术途径。然而,由于大功率充电带来的动力电池加速老化以及快速产热导致的动力电池组温度分布不一致性等问题,给电动汽车快速充电策略的制定和热管理系统的设计带来了新的挑战。本文从电动汽车大功率充电策略优化和电池组热管理系统设计两个角度,归纳了目前面向电动汽车大功率充电过程的管理技术研究现状。围绕大功率充电方式对动力电池性能的影响,评价了不同充电策略和热管理系统设计方法的优缺点。在此基础上,重点分析了电动汽车大功率充电策略及热管理技术发展中面临的挑战。
Summary of charging strategy and thermal management technology of power battery in high-power charging process of electric vehicle
[J].
一种基于温度变化的动力电池智能充电策略
[J].
An intelligent charging strategy of power battery based on temperature change
[J].
Regression quantiles
[J].DOI:10.2307/1913643 URL [本文引用: 1]
Non-crossing quantile regressions by SVM
[C]//
Estimating value at risk with semiparametric support vector quantile regression
[J].DOI:10.1007/s00180-011-0283-z URL [本文引用: 3]
GACV for quantile smoothing splines
[J].DOI:10.1016/j.csda.2004.10.008 URL [本文引用: 1]
Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method
[J].DOI:10.1016/j.jpowsour.2011.08.040 URL [本文引用: 2]
Data-driven prediction of battery cycle life before capacity degradation
[J].
DOI:10.1038/s41560-019-0356-8
[本文引用: 2]

Accurately predicting the lifetime of complex, nonlinear systems such as lithium-ion batteries is critical for accelerating technology development. However, diverse aging mechanisms, significant device variability and dynamic operating conditions have remained major challenges. We generate a comprehensive dataset consisting of 124 commercial lithium iron phosphate/graphite cells cycled under fast-charging conditions, with widely varying cycle lives ranging from 150 to 2,300 cycles. Using discharge voltage curves from early cycles yet to exhibit capacity degradation, we apply machine-learning tools to both predict and classify cells by cycle life. Our best models achieve 9.1% test error for quantitatively predicting cycle life using the first 100 cycles (exhibiting a median increase of 0.2% from initial capacity) and 4.9% test error using the first 5 cycles for classifying cycle life into two groups. This work highlights the promise of combining deliberate data generation with data-driven modelling to predict the behaviour of complex dynamical systems.
Constructing prediction intervals for landslide displacement using bootstrapping random vector functional link networks selective ensemble with neural networks switched
[J].DOI:10.1016/j.neucom.2018.02.046 URL [本文引用: 1]
Landslide displacement interval prediction using lower upper bound estimation method with pre-trained random vector functional link network initialization
[J].
DOI:S0893-6080(20)30261-6
PMID:32717458
[本文引用: 1]

Interval prediction is an efficient approach to quantifying the uncertainties associated with landslide evolution. In this paper, a novel method, termed lower upper bound estimation (LUBE), of constructing prediction intervals (PIs) based on neural networks (NNs) is applied and extended to landslide displacement prediction. A random vector functional link network (RVFLN) is adopted as the NN used in the improved LUBE. A hybrid evolutionary algorithm, termed PSOGSA, that combines particle swarm optimization (PSO) and gravitational search algorithm (GSA) is utilized to train LUBE. The loss function of LUBE is redesigned by considering the quality of PI centre, which allows for a more comprehensive evaluation of PIs. The population initialization in the training process of LUBE is implemented by transferring the weights of a series of pre-trained RVFLNs. The performance of the improved LUBE method is validated by considering a comprehensive set of cases using seven benchmark datasets. In addition, a hybrid method that integrates ensemble empirical mode decomposition (EEMD) with the improved LUBE is proposed for the special case of landslide displacement prediction. Six real-world reservoir-induced landslides are considered to validate the capability and merit of the proposed hybrid method.Copyright © 2020 Elsevier Ltd. All rights reserved.
基于实时电价与支持向量分位数回归的短期电力负荷概率密度预测方法
[J].
Short-term power load probability density forecasting method based on real time price and support vector quantile regression
[J].