海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性.
本文提出一种应用于混合模型试验的环境载荷逆向识别和虚拟模型试验方法.该方法可以逆向识别截断模型试验中的环境载荷,并通过截断水深的虚拟模型试验来验证载荷分离的准确性.由于环境载荷直接从物理模型试验中分离得到,所以该载荷考虑到了平台六自由度(Six-degree-of-freedom, 6 DOF)运动之间的耦合作用、破浪砰击等非线性作用以及流体对浮体的黏性力作用.对一半潜式平台,在180°和90°方向极端海况下,分别开展风浪流模型试验.由于水池尺寸限制无法开展全水深物理模型试验,所以只对比分析截断水深物理模型试验和截断水深虚拟模型试验结果,验证环境载荷分离方法和虚拟模型试验数值模型的准确性.
1 环境载荷逆向识别与虚拟模型试验方法
定义随体坐标系G -xyz ,其原点G 位于平台重心.全局坐标系O -XYZ 初始位置与G -xyz 重合.浮体的六自由度由向量ξ 表示,则ξi (i = 1~6)分别表示纵荡、横荡、垂荡、横摇、纵摇和首摇运动.根据牛顿第二定律和达朗贝尔原理,浮体的运动方程可表示为
(1) M ξ ¨ + K ξ = F E X + F M R
式中:M 为浮体的质量矩阵;K 为回复力系数矩阵;F EX 为作用于浮体重心的整体环境载荷,包括与浮体运动相关的力,比如附加质量力和阻尼力等;F MR 为作用于浮体重心的系泊载荷,在数值计算中,系泊系统的黏性力依据规范简化为相关黏性系数来表示[7 ] .
在模型试验中可以测得基于浮体重心的六自由度运动ξ test 和加速度数据ξ ¨ t e s t F MR, test .因此该模型试验,环境载荷可表示为
(2) F E X , t e s t = M ξ ¨ t e s t + K ξ t e s t - F M R , t e s t
模型试验中,系泊缆载荷通常由单分力传感器测得,因此需要进行力的分解变换,从而获得全局坐标下的系泊系统载荷矩阵,具体可表示为
(3) F M R , t e s t = F x (t) F y ( t ) F z ( t ) M x ( t ) M y ( t ) M z ( t ) = ∑ i = 1 n T i (t) 1 0 0 0 1 0 0 0 1 0 - Z f , i ( t ) Y f , i ( t ) Z f , i ( t ) 0 - X f , i ( t ) - Y f , i ( t ) X f , i ( t ) 0 × s i n α i ( t ) c o s β i ( t ) s i n α i ( t ) s i n β i ( t ) c o s α i ( t )
式中:[Fx (t ) Fy (t ) Fz (t ) Mx (t ) My (t ) Mz (t )]T 是六自由度方向的系泊缆载荷;i (i =1~n ) 表示系泊缆编号,n 表示系泊缆总数;Ti (t )表示t 时刻第i 根系泊缆的顶端张力;α 表示相对于Z 轴的偏角;β 表示在X -Y 平面内相对于X 轴的偏角;(X f , Y f , Z f )表示基于全局坐标系的导缆孔相对于重心的坐标,可以由下式求得:
(4) X f Y f Z f = c o s ξ 5 c o s ξ 6 - c o s ξ 5 s i n ξ 6 s i n ξ 6 s i n ξ 4 s i n ξ 5 c o s ξ 6 + c o s ξ 4 s i n ξ 6 - s i n ξ 4 s i n ξ 5 s i n ξ 6 + c o s ξ 4 c o s ξ 6 - s i n ξ 4 c o s ξ 5 - c o s ξ 4 s i n ξ 5 c o s ξ 6 + s i n ξ 4 s i n ξ 6 c o s ξ 4 s i n ξ 5 s i n ξ 6 + s i n ξ 4 c o s ξ 6 c o s ξ 4 c o s ξ 5 x f y f z f
式中:(x f , y f , z f )表示基于随体坐标系的导缆孔相对于重心的坐标.在模型试验中,系泊缆的偏角测量难度较大,可以在数值模型中基于平台的运动数据对系泊缆进行强迫振荡,从而可以近似计算得到α 与β .
时域计算方程式(1)没有解析解,需要通过数值方法求得近似解.Runge-Kutta系列方法常被应用在求解非线性常微分方程中[8 ] ,为了提高计算效率,减少搜索时间步长的计算量,使用Runge-Kutta-Fehlberg 方法(RKF45)[9 ] 进行求解.在每一时间步中,RKF45 方法分别使用两种不同阶数的方法求下一时刻的数值解.若时间步合适,则两种方法求得解的差别应极小.因此,将两者的解进行比较后,若两者差值不满足要求,则减小时间步长;若其差值远小于设定的误差,则增大时间步长;若恰好满足要求,则时间步不变.首先,RKF45 方法在每一时间步需要求解下述6个分量:
(5) k 1 = h f ( t k , y k ) k 2 = h f t k + 1 4 h , y k + 1 4 k 1 k 3 = h f t k + 3 8 h , y k + 3 32 k 1 + 9 32 k 2 k 4 = h f ( t k + 12 13 h , y k + 1932 2197 k 1 - 7200 2197 k 2 + 7296 2197 k 3 ) k 5 = h f ( t k + h , y k + 439 216 k 1 - 8 k 2 + 3680 513 k 3 - 845 4104 k 4 ) k 6 = h f ( t k + 1 2 h , y k - 8 27 k 1 + 2 k 2 - 3544 2565 k 3 + 1859 4104 k 4 - 11 40 k 5 )
分别使用四阶Runge-Kutta方法和五阶Runge-Kutta方法估算方程下一刻的解,分别记为yk +1 和zk +1 :
(6) y k + 1 = y k + 25 216 k 1 + 1408 2565 k 3 + 2197 4101 k 4 - 1 5 k 5
(7) z k + 1 = y k + 16 135 k 1 + 6656 12825 k 3 + 28561 56430 k 4 - 9 50 k 5 + 2 55 k 6
最优的时间步长a Δt 可以通过现有的时间步长Δt 乘以一个系数a 进行估算,a 可由下式求得:
(8) a = e t o l Δ t 2 z k + 1 - y k + 1 1 4
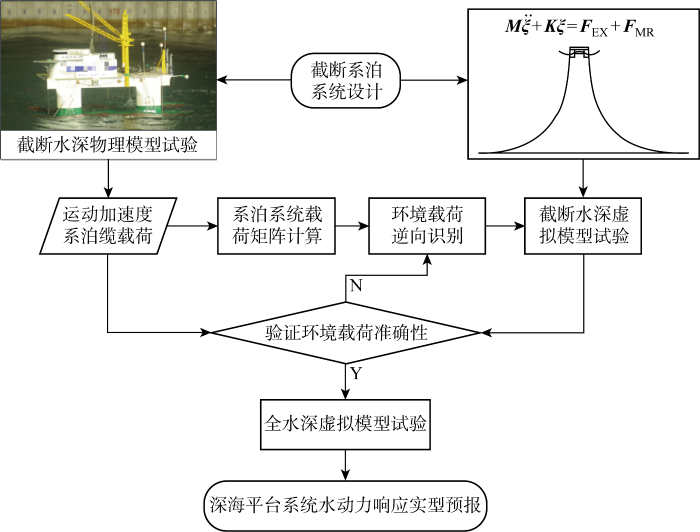
方法流程图如图1 所示,从物理模型试验中分离出环境载荷F EX, test ,F EX, test 是N ×6矩阵,其中N 表示时间步数.将F EX, test 代入到运动控制方程式(1)中, 作用在数值模型重心处,可对模型开展同环境载荷的虚拟模型试验, 通过虚拟模型试验与物理模型试验结果的对比可以验证环境载荷逆向识别方法的准确性.在同一海况下,截断模型试验和全水深模型试验中的波浪、风、流的参数设定一致,仅系泊系统存在差异,因此忽略两模型试验中的环境载荷差异.式(2)考虑了截断模型试验中的系泊载荷因素,所得环境载荷是与系泊系统的无关量.因此基于截断模型试验所得的环境载荷可以用于全水深系统的运动预报.
图1
图1
方法示意图
Fig.1
Flow chart of the proposed method
2 模型试验概述
2.1 平台与系泊系统
基于一半潜式平台开展模型试验,验证环境载荷逆向识别与虚拟模型试验方法的准确性.模型试验在上海交通大学海洋工程深水试验池中进行,模型缩比尺为1∶60,平台主体结构包括4根立柱、2个浮箱、连接立柱的4个圆形横撑和1个封闭箱型甲板,如图2 所示.平台的主要参数如表1 所示.平台采用对称系泊布置,8根系泊索,分为4组,布置在4个立柱上,系泊系统中锚链长度为 1 350 m,直径为0.147 m,湿重为373.66 kg/m,轴向刚度为1 845 MN.平台作业水深500 m,对应模型水深8.33 m.
图2
图2
半潜式平台试验模型
Fig.2
Test model of the semi-submersible platform
2.2 海洋环境与工况设计
选取12级台风以及十年一遇风浪流海况,开展平台在180° 和90° 方向的模型试验.波浪采用 JONSWAP 谱,有义波高为11.1 m, 谱峰周期为 13.6 s,谱型因子为2.4,流速为1.62 m/s,风速为 33 m/s,风浪流载荷作用方向一致.试验工况如表2 所示.模型试验中,平台重心处的六自由度运动可由非接触式光学运动捕捉系统测得;系泊缆的顶端张力可由力传感器测得;所有的数据通道都被实时数据采样系统获得,采样频率为100 Hz.
3 结果与分析
3.1 静水试验结果
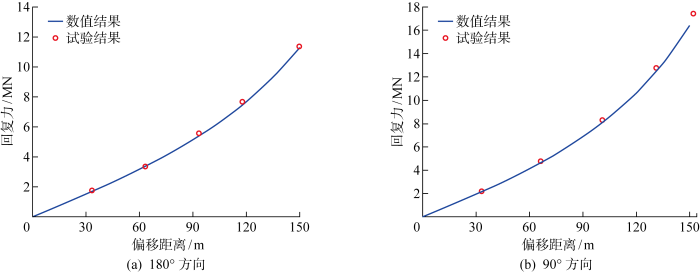
静水自由衰减试验可以得到半潜式平台的垂荡、横摇和纵摇运动的固有周期,平台自由衰减试验结果如表3 所示,固有周期的试验结果与频域计算软件HydroD[10 ] 求得的数值结果基本一致.水平刚度试验用于验证系泊系统试验模型的准确性.图3 为系泊系统水平刚度对比结果.可以看出,系泊系统试验模型的水平刚度特性在平台运动区间内与设计结果基本相同,符合试验要求.
图3
图3
系泊系统水平刚度曲线
Fig.3
Curves of horizontal stiffness of mooring system
3.2 风浪流响应结果
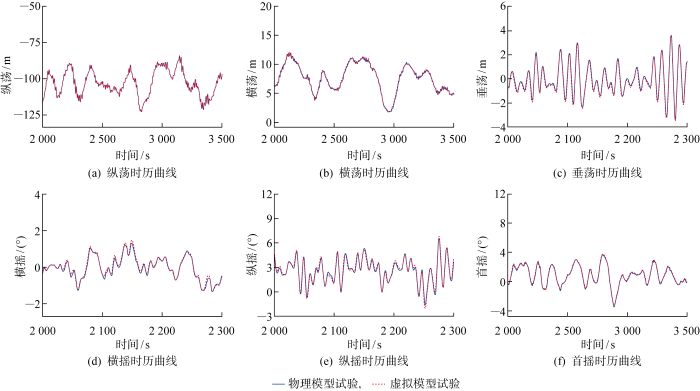
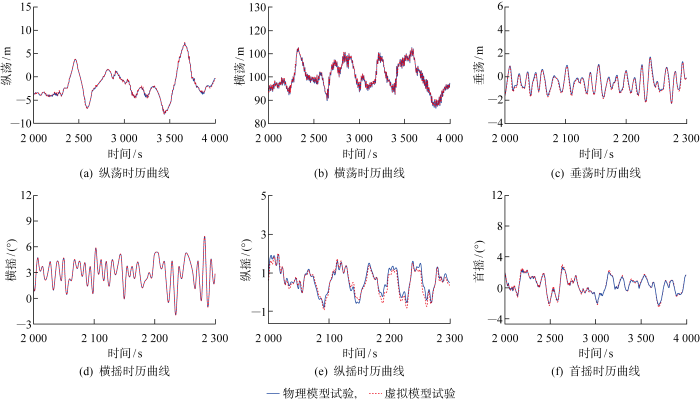
首先在深水试验池开展风浪流模型试验,然后通过环境载荷逆向识别方法将作用于平台上的环境载荷分离出来,并将其加载到虚拟水池的数值模型上,开展虚拟模型试验,试验结果对比如图4 ~5 所示.图4 为180° 风浪流方向下,平台六自由度运动物理模型试验结果和虚拟模型试验的时历曲线结果对比,可以看出,基于环境载荷逆向识别的虚拟模型试验结果与物理试验结果基本一致,从而验证了环境载荷逆向识别方法的准确性.如图4(b) 、4(f) 所示,平台横荡和首摇发生明显的流致运动(Flow-induced Motion),说明环境载荷逆向识别方法可以有效地识别出黏性力载荷.图5 为90° 风浪流方向下,平台六自由度运动物理模型试验结果和虚拟模型试验的时历曲线结果对比,虚拟模型试验结果与物理试验结果基本一致.同样,平台纵荡和首摇也发生明显的流致运动,如图5(a) 、5(f) 所示.结果显示环境载荷逆向识别方法可以准确识别多角度、风浪流联合作用下的模型试验环境载荷.
图4
图4
180° 风浪流工况下,平台六自由度运动物理模型试验和虚拟模型试验结果对比
Fig.4
Time histories of 6 DOF motions in head waves
图5
图5
90° 风浪流工况下,平台六自由度运动物理模型试验和虚拟模型试验结果对比
Fig.5
Time histories of 6 DOF motions in beam waves
4 结语
本文提出一种基于模型试验的环境载荷逆向识别和虚拟模型试验方法.将模型试验中的浮体受到的环境载荷分离出来并施加到虚拟水池中的数值模型上,进行虚拟模型试验.环境载荷直接从物理模型试验中分离得到,因此该载荷考虑到了平台六自由度运动之间的耦合作用、破浪抨击等非线性作用以及流体对浮体的黏性力作用.
基于一半潜式平台,开展180° 和90° 方向的风浪流模型试验.由物理模型试验和虚拟模型试验的对比结果可知,环境载荷逆向识别方法可以准确识别风浪流响应模型试验的环境载荷.
平台在180° 方向的响应中,横荡和首摇运动出现明显的流致运动,同样,在90° 方向的响应中,纵荡和首摇运动也出现明显的流致运动,说明环境载荷逆向识别方法可以有效地识别出黏性力载荷.
参考文献
View Option
[1]
杨晓彤 , 赵伟文 , 万德成 . 规则波下半潜式平台波浪爬升数值模拟
[J]. 水动力学研究与进展 2021 , 36 (1 ): 48 -55 .
[本文引用: 1]
YANG Xiaotong ZHAO Weiwen WAN Decheng . Numerical simulation of wave run-up of semi-submersible offshore platform under regular wave
[J]. Chinese Journal of Hydrodynamics 2021 , 36 (1 ): 48 -55 .
[本文引用: 1]
[2]
白云山 . 半潜式平台水动力性能分析与优化设计 [D]. 大连 : 大连理工大学 , 2014 .
[本文引用: 1]
BAI Yunshan . Analysis and optimization design of hydrodynamic performance of SEMI [D]. Dalian : Dalian University of Technology , 2014 .
[本文引用: 1]
[4]
魏汉迪 , 肖龙飞 , 田新亮 , 等 . 半潜式平台运动的非线性耦合数学模型研究
[J]. 中国造船 2017 , 58 : 28 -35 .
[本文引用: 1]
WEI Handi XIAO Longfei TIAN Xinliang , et al Nonlinear coupling model of semi-submersible platform under regular and irregular waves
[J]. Ship Building of China 2017 , 58 : 28 -35 .
[本文引用: 1]
[5]
WAALS O J PHADKE A C BULTEMA S . Flow induced motions on multi column floaters
[C]// International Conference on Offshore Mechanics and Arctic Engineering San Diego, California, USA : ASME , 2007 , 42673 : 669 -678 .
[本文引用: 1]
[6]
STANSBERG C T ORMBERG H ORITSLAND O . Challenges in deep water experiments: Hybrid approach
[J]. Journal of Offshore Mechaniccs Arctic Engineering 2002 , 124 (2 ): 90 -96 .
[本文引用: 2]
[7]
DET NORSKE VERITAS . Position mooring: DNVGL-OS-E301 [S]. Norway : DNV G L , 2015 .
[本文引用: 1]
[8]
STRANG G . Computational science and engineering [M]. Wellesley, USA : Wellesley-Cambridge Press , 2007 .
[本文引用: 1]
[9]
National Aeronautics Space Administration . Low-order classical Runge-Kutta formulas with stepsize control and their application to some heat transfer problems: TR R-315 [S]. Washington D.C., USA : NASA , 1969 .
[本文引用: 1]
[10]
DET NORSKE VERITAS . Sesam user manual: Wave load and stability analysis of fixed and floating structures [M]. Norway : DNV G L , 2014 .
[本文引用: 1]
规则波下半潜式平台波浪爬升数值模拟
1
2021
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
Numerical simulation of wave run-up of semi-submersible offshore platform under regular wave
1
2021
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
1
2014
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
1
2014
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
Study on the effects of mooring system stiffness on air gap response
1
2021
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
半潜式平台运动的非线性耦合数学模型研究
1
2017
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
Nonlinear coupling model of semi-submersible platform under regular and irregular waves
1
2017
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
Flow induced motions on multi column floaters
1
2007
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
Challenges in deep water experiments: Hybrid approach
2
2002
... 海上浮式结构物的水动力性能对于浮体的运动响应至关重要.目前关于浮式结构物水动力学的研究主要通过两种途径:数值计算方法和模型试验方法[1 ] .基于势流理论的数值计算方法被广泛应用于浮式结构物运动响应[2 ] 、平台气隙响应[3 ] 、平台共振特性[4 ] 等研究,势流理论基于流体无黏性假设,但是黏性力作用,比如涡激运动、驰振现象等,被证实对于平台十分重要[5 ] .模型试验方法已经被成功应用于研究和评估海洋结构物水动力性能数十年,但是随着海洋结构物的工作水深增加,在合理缩尺比范围内(1/80≤λ ≤1/60)[6 ] ,现有的深水试验池由于尺寸限制,无法开展全水深模型试验.因此,Stansberg等[6 ] 提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
... [6 ]提出混合模型试验方法.该方法主要分为3个步骤.第1步根据等效准则,设计一套与全水深系泊系统近似等效的截断系泊系统.第2步在海洋试验水池开展截断模型试验.由于截断系泊系统不可能与全水深系泊系统完全等效,所以需要第3步,即开展数值重构与数值外推,最终以数值结果预报全水深系统的实型水动力响应.数值重构为建立截断数值模型,通过调节相关的水动力参数,使得数值计算结果与模型试验结果尽可能一致.然后将验证过的截断数值模型系泊系统替换为全水深系泊系统开展计算,即为数值外推.传统基于势流理论的时域耦合数值模型,对于复杂海况下截断水深模型试验中可能存在的波浪爬升、波浪砰击、涡激运动等强非线性和黏性水动力响应,理论数值方法面临巨大困难和挑战,影响到基于数值结果进行深海平台系统水动力预报的准确性. ...
1
2015
... 式中:M 为浮体的质量矩阵;K 为回复力系数矩阵;F EX 为作用于浮体重心的整体环境载荷,包括与浮体运动相关的力,比如附加质量力和阻尼力等;F MR 为作用于浮体重心的系泊载荷,在数值计算中,系泊系统的黏性力依据规范简化为相关黏性系数来表示[7 ] . ...
1
2007
... 时域计算方程式(1)没有解析解,需要通过数值方法求得近似解.Runge-Kutta系列方法常被应用在求解非线性常微分方程中[8 ] ,为了提高计算效率,减少搜索时间步长的计算量,使用Runge-Kutta-Fehlberg 方法(RKF45)[9 ] 进行求解.在每一时间步中,RKF45 方法分别使用两种不同阶数的方法求下一时刻的数值解.若时间步合适,则两种方法求得解的差别应极小.因此,将两者的解进行比较后,若两者差值不满足要求,则减小时间步长;若其差值远小于设定的误差,则增大时间步长;若恰好满足要求,则时间步不变.首先,RKF45 方法在每一时间步需要求解下述6个分量: ...
1
1969
... 时域计算方程式(1)没有解析解,需要通过数值方法求得近似解.Runge-Kutta系列方法常被应用在求解非线性常微分方程中[8 ] ,为了提高计算效率,减少搜索时间步长的计算量,使用Runge-Kutta-Fehlberg 方法(RKF45)[9 ] 进行求解.在每一时间步中,RKF45 方法分别使用两种不同阶数的方法求下一时刻的数值解.若时间步合适,则两种方法求得解的差别应极小.因此,将两者的解进行比较后,若两者差值不满足要求,则减小时间步长;若其差值远小于设定的误差,则增大时间步长;若恰好满足要求,则时间步不变.首先,RKF45 方法在每一时间步需要求解下述6个分量: ...
1
2014
... 静水自由衰减试验可以得到半潜式平台的垂荡、横摇和纵摇运动的固有周期,平台自由衰减试验结果如表3 所示,固有周期的试验结果与频域计算软件HydroD[10 ] 求得的数值结果基本一致.水平刚度试验用于验证系泊系统试验模型的准确性.图3 为系泊系统水平刚度对比结果.可以看出,系泊系统试验模型的水平刚度特性在平台运动区间内与设计结果基本相同,符合试验要求. ...