考虑驾驶工况及老化程度的锂电池荷电状态估算

doi:10.16183/j.cnki.jsjtu.2023.168

考虑驾驶工况及老化程度的锂电池荷电状态估算

乌江^,¹^,², 张燕¹^,², 刘泽龙¹^,², 程刚¹^,², 雷冬¹^,², 焦朝勇³

1.西安工程大学电子信息学院,西安 710048

2.西安市电气设备互联感知与智能诊断重点实验室,西安 710048

3.国电南瑞科技股份有限公司,南京 211106

State of Charge Estimation of Lithium-Ion Battery Considering Operating Conditions and Aging Degree

WU Jiang^,¹^,², ZHANG Yan¹^,², LIU Zelong¹^,², CHENG Gang¹^,², LEI Dong¹^,², JIAO Chaoyong³

1. School of Electronics and Information, Xi’an Polytechnic University, Xi’an 710048, China

2. Xi’an Key Laboratory of Interconnected Sensing and Intelligent Diagnosis for Electrical Equipment, Xi’an 710048, China

3. NARI Technology Co., Ltd., Nanjing 211106, China

责任编辑: 王历历

收稿日期: 2023-05-4 修回日期: 2023-06-13 接受日期: 2023-06-16

基金资助:

陕西省科技厅自然科学基础研究重点项目(2022JZ-35)

Received: 2023-05-4 Revised: 2023-06-13 Accepted: 2023-06-16

作者简介 About authors

乌江(1986—),副教授,主要从事电池参数估计研究;E-mail:wujiang@xpu.edu.cn.

摘要

扩展卡尔曼滤波(EKF)估算电动汽车动力电池荷电状态(SOC)时,驾驶工况随机多变、电池老化等因素造成系统噪声与模型参数变化,导致估算精度降低.以NCR18650B型三元锂离子电池为研究对象,首先采用二阶RC等效电路模型并对其模型参数进行辨识;其次,以EKF算法为主体,基于极大似然估计准则,固定测量噪声协方差并自适应调整过程噪声协方差,构建自适应扩展卡尔曼滤波算法估算电池SOC;同时,应用卡尔曼滤波算法实时估算等效电路模型中欧姆内阻,最终结合形成自适应双扩展卡尔曼滤波算法(ADEKF).最后,利用自有实验数据和公开数据集验证算法性能.利用所提ADEKF算法估算恒流工况、动态应力工况与北京公交车动态应力测试工况下5组不同老化程度锂离子电池SOC,并与EKF等常见算法进行对比分析.结果表明:相比EKF算法,所提ADEKF算法对不同老化电池在3种工况下,估算结果的平均绝对误差分别下降1.868百分点、2.296百分点和2.534百分点,证明该算法有效提高在动力工况、电池老化以及二者综合因素下的锂离子电池SOC估算精度.

关键词： 锂离子电池; 荷电状态; 复杂工况; 电池老化; 自适应双扩展卡尔曼滤波

Abstract

When using the extended Kalman filter (EKF) to estimate the state of charge (SOC) of an electric vehicle power battery, the change of system noise and model parameters may lead to a reduction in estimation accuracy, due to variable operating conditions, battery aging, and other factors. The NCR18650B ternary lithium-ion battery is selected, and the second-order RC model is established with identified parameters. Then, by using EKF as the main body with a fixed measurement noise covariance and adaptively adjusting process noise covariance based on the maximum likelihood estimation criterion, an adaptive extended Kalman filter is built to estimate the SOC of the battery. Simultaneously, a Kalman filter is used to estimate the ohmic resistance in real time. Thus, an adaptive dual extended Kalman filter (ADEKF) algorithm is formed. Finally, algorithm verifications are performed with testing data and public datasets. The ADEKF proposed is used to estimate the SOC of five groups of aged lithium batteries under three operating conditions, which are constant current, dynamic stress test, and Beijing dynamic stress test, and compared with that of EKF and other algorithms. The results show that compared with EKF, the average absolute error of the estimation results of ADEKF for different aged batteries under three operating conditions decreases by 1.868 percentage points, 2.296 percentage points, and 2.534 percentage points, respectively, which proves that ADEKF algorithm can effectively improve the SOC estimation accuracy under multiple operating conditions, battery aging and the combination of the two factors.

Keywords： lithium-ion battery; state of charge(SOC); complex operating conditions; battery aging; adaptive dual extended Kalman filter (ADEKF)

PDF (2934KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

乌江, 张燕, 刘泽龙, 程刚, 雷冬, 焦朝勇. 考虑驾驶工况及老化程度的锂电池荷电状态估算[J]. 上海交通大学学报, 2024, 58(12): 1935-1945 doi:10.16183/j.cnki.jsjtu.2023.168

WU Jiang, ZHANG Yan, LIU Zelong, CHENG Gang, LEI Dong, JIAO Chaoyong. State of Charge Estimation of Lithium-Ion Battery Considering Operating Conditions and Aging Degree[J]. Journal of Shanghai Jiaotong University, 2024, 58(12): 1935-1945 doi:10.16183/j.cnki.jsjtu.2023.168

随着我国“双碳”目标的提出,发展新能源汽车已成为共识,新能源汽车在交通出行领域占据重要战略地位^[1],锂离子电池作为高效的电能存储装置在电动汽车等领域获得了广泛使用.为保证锂离子电池的安全运行,延长其使用寿命,需建立性能优良的电池管理系统(battery management system,BMS),而估算电池荷电状态(state of charge,SOC)是BMS系统其他功能实现的前提.因此,准确估算电池SOC具有十分重要的意义^[2-3].但电池SOC受到电流、温度、老化及复杂工况等因素影响^[4-5],导致SOC实时精确估算成为难点.

在目前估算SOC的方法中,扩展卡尔曼滤波(extended Kalman filter,EKF)算法在保持较高锂离子电池估算精度的前提下更易实现,是目前SOC估算中研究较多的方法^[6⇓-8].然而,在电动汽车SOC估算过程中,电池实际驾驶工况以及电池本身的老化过程给传统卡尔曼滤波算法的准确性带来巨大挑战.

首先,电动汽车驾驶工况复杂多变是造成系统噪声不稳定的重要原因之一,而使用EKF估算锂离子电池SOC时认为系统的噪声为高斯白噪声,这与实际驾驶工况不相符,会导致较大的估算误差.杨帆等^[9]提出一种无迹卡尔曼滤波(unscented Kalman filter,UKF)与反向传播(back propagation,BP)神经网络结合的联合算法,在UKF估算电池SOC基础上,采用BP神经网络预测不同噪声下UKF算法滤波的误差,再将预测出的误差从UKF估算结果中去除.He等^[10]根据测量值与估算值之间的差值来自适应调整系统的噪声,建立自适应扩展卡尔曼滤波算法(adaptive extended Kalman filter,AEKF)改善由于噪声值变化引起的估算误差大和发散等问题,在联邦城市行驶工况(federal urban driving schedule,FUDS)下验证了算法准确度,但缺少其他工况下的验证,因此算法的普适性有待商榷.

其次,EKF是基于模型的算法,锂离子电池老化过程中模型参数会发生明显变化,进而造成SOC估算准确性大幅下降.为减小由于模型参数不准确而导致的估算误差,陈玉珊等^[11]采用含遗忘因子的递推最小二乘算法实时估计电池模型参数.杜帮华等^[12]提出可变遗忘因子的递推最小二乘法,通过不断更新遗忘因子更好地实时跟踪电池特性.Xiong等^[13]提出多尺度扩展卡尔曼滤波即利用宏观尺度估计电池模型参数,利用微观尺度估计电池SOC.但在现有研究中,同时考虑锂离子电池模型参数变化与噪声调整的研究较少.

考虑到动力电池实际工作情况,将驾驶工况和电池老化两种变量结合研究更加符合客观规律.采用自适应双扩展卡尔曼滤波算法(adaptive dual extended Kalman filter,ADEKF),即在EKF算法的基础上通过极大似然估计准则,设计自适应算法,对系统噪声中的过程噪声协方差进行自适应调整,形成AEKF算法,有效地适应不同工况条件;采用单独的卡尔曼滤波(Kalman filter,KF)算法对模型参数中的欧姆内阻进行动态估算,并将之与AEKF算法结合起来形成ADEKF算法,可以在估算电池SOC的同时,实时估算电池模型参数,解决电池老化造成的模型参数不准确问题,进一步提高估算的精度.随后,在恒流工况、动态应力测试工况(dynamic stress test,DST)和北京公交车动态应力测试工况(Beijing dynamic stress test,BBDST)3种工况条件下采用该联合算法开展不同老化程度锂离子电池SOC估算实验,证明该方法的准确性和普适性.

1 锂离子电池等效电路模型及其参数辨识

1.1 等效电路模型

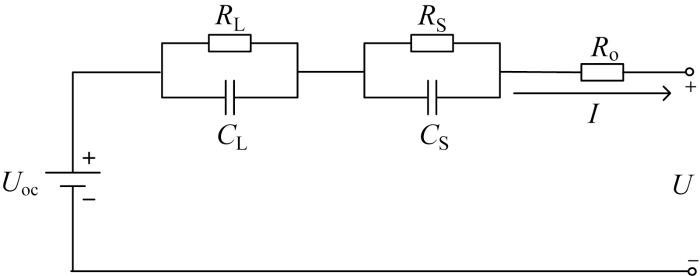
用于SOC估算的锂离子电池模型主要可分为电化学模型和等效电路模型^[14].电化学模型过于复杂,不适用于电池仿真和控制^[15].常见的等效电路模型包括Rint模型、新一代汽车协商会模型、一阶RC模型以及二阶RC模型等,采用精度较高且易建立的二阶RC模型^[16-17]用于SOC估算,该模型的电路结构如图1所示.图中:U为电池的端电压;I为电池的工作电流;R_o为电池欧姆内阻;R_L、C_L分别为电池的电化学极化电阻和电容;R_S、C_S分别为电池的浓度差极化电阻和电容;U_oc为电池的开路电压(open circuit voltage,OCV).

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 锂离子电池等效电路模型

Fig.1 Equivalent circuit model of lithium-ion battery

由安时积分法计算的SOC一般表达式为

(1)ξ_SOC(t)=ξ_SOC(t₀)-

\frac{1}{3600 C_{N}} \int_{t_{0}}^{t}

Idt

式中:ξ_SOC为荷电状态;ξ_SOC(t)为电池在t时刻的SOC值;ξ_SOC(t₀)为电池在t₀时刻的SOC值;C_N为锂离子电池的初始容量.

由电池的等效电路模型可得:

(2)

\begin{array}{l} C_{S} \frac{d U_{S}}{d t} = I - \frac{U_{S}}{R_{S}} \\ C_{L} \frac{d U_{L}}{d t} = I - \frac{U_{L}}{R_{L}} \\ U = U_{o c} - U_{S} - U_{L} - R_{o} I \end{array}\}

式中:U_S为R_S两端的电压;U_L为R_L两端的电压.

令τ_S=R_SC_S,τ_L= R_LC_L,表征电池极化过程的时间常数;将ξ_SOC、U_S、U_L作为状态变量,I作为输入变量,进行离散化处理,最终可得关于SOC的状态空间方程:

(3)

[\begin{array}{l} ξ_{S O C} (k) \\ U_{S} (k) \\ U_{L} (k) \end{array}]

[\begin{array}{l} 1 & 0 & 0 \\ 0 & e^{- \frac{Δ T}{τ_{S} (k)}} & 0 \\ 0 & 0 & e^{- \frac{Δ T}{τ_{L} (k)}} \end{array}] [\begin{array}{l} ξ_{S O C} (k - 1) \\ U_{S} (k - 1) \\ U_{L} (k - 1) \end{array}]

[\begin{array}{l} - \frac{Δ T}{3600 C_{N}} \\ R_{S} (k) (1 - e^{- \frac{Δ T}{τ_{S} (k)}}) \\ R_{L} (k) (1 - e^{- \frac{Δ T}{τ_{L} (k)}}) \end{array}]

I(k-1)

(4)U(k)=U_oc(ξ_SOC(k))-U_S(k)-U_L(k)-R_o(k)I(k)

式中:ΔT为采样时间;k为时刻.

1.2 老化锂离子电池的开路电压与SOC的关系

实验在室温25 ℃下进行,实验平台为蓝电CT2001B电池测试仪,实验对象为日本松下公司生产的额定容量为3.4 A·h的NCR18650B型三元锂离子电池.为了获得不同老化程度的锂离子电池样品,以0.5C倍率电流对4个同批次的电池进行老化实验^[18],得到健康状态(State of Health,ζ_SOH)分别为94.9%、90.8%、84.6%和79.2%的老化电池并与新电池(ζ_SOH=100%)组成本文实验样品组.

为获得不同老化程度锂离子电池的SOC-OCV曲线,以实际测得的电池实际容量为基准,用0.5C倍率分别对样品组中的5个电池进行脉冲放电实验^[19]:①将电池充满电后静置3 h获得电池ξ_SOC=100%时的开路电压;②以0.5C电流放出电池5%的电量并静置获得对应SOC下的开路电压;③重复步骤①~②直到将电池电量放完.

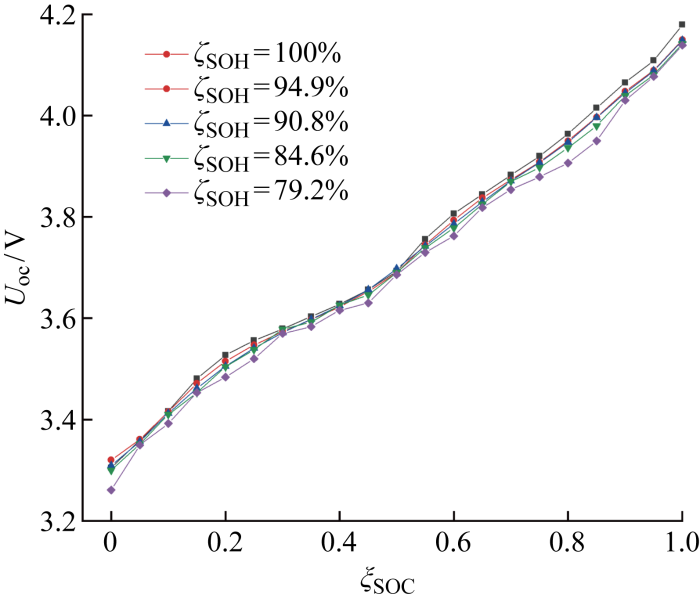
由此得到随着SOC减小开路电压的变化.对得到的SOC-OCV曲线进行9阶多项式拟合,实测数据和多项式拟合结果如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不同老化程度锂离子电池SOC-OCV放电曲线

Fig.2 Curves of lithium-ion battery SOC-OCV discharge at different aged levels

1.3 老化电池模型参数初始值辨识

电池模型建立后,需对模型中的参数进行初步离线辨识.采用最小二乘参数拟合法分别处理样品组中5个电池脉冲放电后的锂离子电池电压静置恢复曲线,结合电池二阶RC模型,获得各电池不同SOC值处模型的参数值,形成不同SOC值与电池参数的对应表.通过查表就可得到不同SOC值对应的5个等效电路模型参数值R_o、R_L、C_L、R_S、C_S.对于不在表中的SOC值,选择其临近的右侧值来代替.

2 基于卡尔曼滤波的SOC估计算法

由于电动汽车驾驶工况随机多变、电池老化等因素会造成SOC估算过程中系统噪声设置不合理、模型参数不准确的问题,所以在EKF的基础上自适应动态调整噪声协方差并采用KF实时调整电池模型参数.

2.1 自适应扩展卡尔曼滤波算法估算电池SOC

AEKF算法是针对EKF算法中将系统噪声假定为确定值与实际不相符的问题提出的改进算法,由EKF算法和自适应调整噪声协方差两部分组成.

2.1.1 EKF算法

对于任何一个非线性离散系统,其状态空间方程为

(5)

\begin{array}{l} x_{k + 1} = f (x_{k}, u_{k}) + w_{k} \\ y_{k} = g (x_{k}, u_{k}) + v_{k} \end{array}\}

式中:f为状态方程;g为观测方程;x_k为状态变量;u_k为输入变量;y_k为观测变量;w_k为系统的过程噪声;v_k为系统的量测噪声.

EKF算法将过程噪声w_k与量测噪声v_k均假设为高斯白噪声,服从以下分布:

(6)

\begin{array}{l} P (w_{k}) ~ N (0, Q) \\ P (v_{k}) ~ N (0, R) \end{array}\}

式中:P表示概率;N为高斯分布;Q为过程噪声协方差;R为量测噪声协方差.

EKF算法估算非线性系统状态量包括以下步骤.

(1) 将非线性化系统线性化处理,对非线性系统进行一阶泰勒展开,具体如下:

A_k_-1= ${\frac{d f (x_{k - 1}, u_{k})}{d x_{k - 1}}|}_{{\hat{x}}_{k - 1}}$

C_k= ${\frac{d g (x_{k / k - 1}, u_{k})}{d x_{k / k - 1}}|}_{{\hat{x}}_{k / k - 1}}$

其中A_k为状态转移矩阵;C_k为观测矩阵;k/k-1表示系统上一时刻对k时刻的估计量; ^ 表示相应变量的预测值.

(2) 算法初始化,令

(7)

\begin{array}{l} {\hat{x}}_{0} = E (x_{0}) \\ P_{0} = E ((x_{0} - {\hat{x}}_{0}) (x_{0} - {\hat{x}}_{0})^{T}) \end{array}\}

式中: ${\hat{x}}_{0}$ 为状态变量估计值的初值;x₀为状态变量;E为求期望;P₀为状态误差协方差的初值.

(3) 时间更新,由前一时刻的状态和误差协方差得到当前时刻状态量的先验估计和误差协方差

(8)

{\hat{x}}_{k / k - 1}

=f(

{\hat{x}}_{k - 1}

, u_k)

(9)P_k/k_-1=A_k_-1P_k_-1

{A^{T}}_{k - 1}

式中:P_k/k_-1为误差协方差的预测值.

(4) 量测更新,由卡尔曼滤波增益和量测值修正状态量的先验估计得到状态量的后验估计,更新误差协方差,为下一次递推做准备

(10)K_k=P_k/k_-1

{C^{T}}_{k}

(C_kP_k/k_-1

{C^{T}}_{k}

+R)^-1

(11)

{\hat{x}}_{k}

{\hat{x}}_{k / k - 1}

+K_k(y_k-g(

{\hat{x}}_{k / k - 1}

, u_k))

(12)P_k=(M-K_kC_k)P_k/k_-1

式中:M为单位矩阵;K_k为卡尔曼滤波增益.

将关于锂离子电池SOC的状态空间方程式(3)和(4)代入以上步骤进行运算,即为运用EKF算法估算电池SOC.

2.1.2 自适应调整噪声策略的选取制定

利用EKF进行SOC估算时,认为系统中的过程噪声和测量噪声都是高斯白噪声,即其对应的误差协方差Q和R为固定值.然而实际的电池系统非常复杂,与此假设并不相符,这样的处理方法忽略了噪声变化,会造成SOC估算误差.针对系统噪声不固定这一问题的改进方法是根据测量值与估算值之间的差值来自适应调整系统噪声,改善因噪声值引起的估算误差大和发散等问题^[10,20].使噪声自适应的方法有基于模糊控制的自适应卡尔曼滤波^[21]、Sage-Husa自适应方法^[22]、极大似然准则的自适应卡尔曼滤波^[23]3种.基于模糊控制的自适应卡尔曼滤波原理较为复杂,涉及到模糊控制器的设计,实现起来也相对困难;Sage-Husa自适应卡尔曼滤波法相比极大似然准则的自适应卡尔曼滤波法,未知参数更多,增加了应用实现的复杂度,因此采用极大似然准则对噪声进行自适应调整.

极大似然估计是从系统量测量出现概率最大的角度进行估计,其特点是不仅考虑新息的变化,而且考虑新息协方差矩阵的变化规律^[24],通过统计系统量测新息序列,实现对系统的噪声协方差矩阵的实时更新.具体公式如下:

(13)υ_j=y_j-y_j/j_-1

(14)S_k=

\frac{1}{m} \overset{k}{\sum_{j = k - m + 1}}

υ_j

{υ^{T}}_{j}

(15)R_k=S_k-C_kP_k/k_-1

{C^{T}}_{k}

(16)Q_k=K_kS_k

{K^{T}}_{k}

式中:υ_j为系统量测新息;y_j为从当前时刻往前算起第j个时刻系统量测值;S_k为前m个量测新息的均值;m为从当前时刻往前算起的历史信息数;R_k为k时刻量测噪声协方差;Q_k为k时刻过程噪声协方差.

由式(9)和(10)可知,过程噪声协方差Q和测量噪声协方差R都能通过影响卡尔曼滤波增益K,影响最终估算效果.Q间接影响K,Q增大,会使K增大或减小;R直接影响K,R越大,K就越小,观测值对状态预测值的反馈调整作用也就越弱.对Q、R进行自适应调整时,存在3种不同的调整策略:①同时调整Q和R^[24];②固定Q,只调整R;③固定R,只调整Q.由文献[25]可知,第1种策略的滤波过程不稳定,可能会导致滤波发散,不可取.对后两种策略,通过分析式(15)可知,R要受到观测函数的导数阵C_k的直接影响,而此处的观测函数是不连续函数,如果采用第2种策略,在自适应调整过程中,会使R在断点处出现较大波动,因此采用第3种策略更好.

现有自适应调整噪声协方差估算SOC的研究大部分都采取策略①,即同时调整Q和R,而单独调整Q或R方面的研究较少.但经过以上分析可知,单独调整Q更具优势,因此采用只调整Q的策略,并将通过实验进行验证.

在EKF算法估算SOC的同时,用以上方法自适应调整Q,就可实现AEKF算法估算电池的SOC.

2.2 卡尔曼滤波器算法KF估算内阻

电池内部参数会受到SOC、充放电电流、温度、电池寿命等因素的影响^[26]而不断变化,为了提高SOC的估算精度,需对电池模型参数进行实时在线估算.但如果对所有电池模型参数都做实时估算,算法太过复杂;而考虑到在各种影响因素中,电池寿命的影响最大,并且极化内阻、极化电容受电池寿命影响小,欧姆内阻在电池寿命初期和后期会有较大变化^[27],因此只在线估算电池欧姆内阻.

欧姆内阻随电池寿命的变化缓慢,短时间内可认为基本不变^[28],从而可以得到其状态方程:

(17)R_o_,_k=R_o_,_k_-1

式中:R_o,_k为k时刻欧姆内阻值.

再由图1中电路模型,可以得到其观测方程:

(18)U(k)=U_oc(ξ_SOC(k))-U_S(k)- U_L(k)-R_o(k)I(k)

这是一个关于欧姆内阻的线性系统,可以用KF算法估算.KF算法的运算过程与EKF类似,只是不需要对系统作线性化近似处理.

2.3 自适应双卡尔曼滤波器算法估算电池SOC

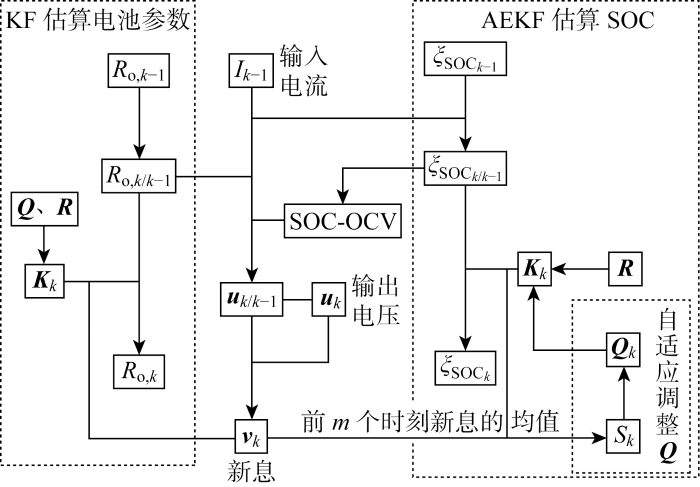
在运用AEKF估算SOC的同时运用KF估算电池欧姆内阻,就形成ADEKF估算电池SOC的算法,其算法结构如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 ADEKF算法结构图

Fig.3 Structure of ADEKF algorithm

该算法以EKF算法为基础,通过自适应调整过程噪声协方差Q改变增益,进而改善估算效果,同时使用KF实时估算欧姆内阻提高模型精度,进一步提高了估算精度.

3 实验验证与分析

在实验验证中设置分组对比实验,分别以典型工况、锂离子电池老化程度以及典型工况下老化程度为外部变量,对比分析EKF、AEKF以及所提ADEKF联合算法的准确性.在验证实验中,SOC实际初值为1,为定量研究算法的收敛性,算法中设置SOC初值ξ_SOC,0=0.7,定义算法估算结果首次收敛到误差小于2%所用时间为收敛时间.

采用平均绝对误差δ_MAE和算法收敛到2%后的最大误差δ_ME定量研究算法的准确性,δ_MAE的计算公式如下:

(19)δ_MAE=

\frac{1}{n} \overset{n}{\sum_{i = 1}} |h_{i} - x_{i}|

式中:n为估算数据总量;h_i、x_i分别为第i个点处SOC真值和估算值.

3.1 不同调整策略下的噪声自适应算法比较分析

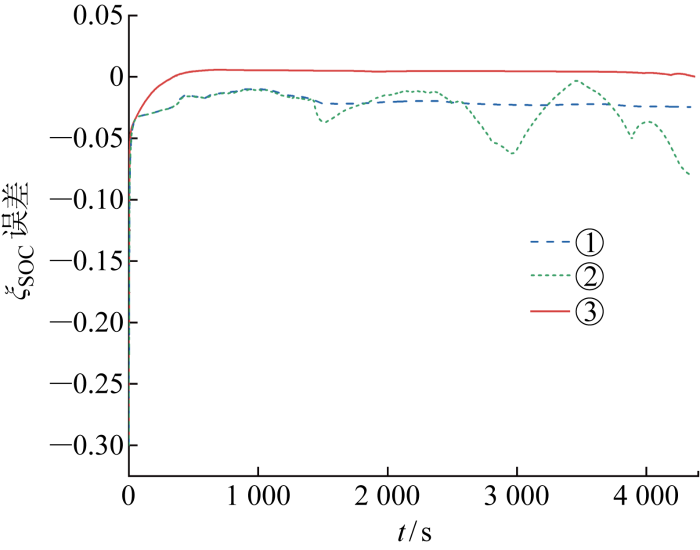
在ADEKF算法中使用AEKF估算锂离子电池的SOC时,自适应调整Q、R有3种情况:①同时自适应调整Q和R;②固定Q,自适应调整测量噪声R;③自适应调整过程噪声协方差Q,固定R.在恒流工况下,这3种情况下估算ξ_SOC的误差如图4和表1所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 自适应调整不同因子估算ξ_SOC误差

Fig.4 ξ_SOC error of adaptive estimation with different factors

表1 自适应调整不同因子估算ξ_SOC误差对比

Tab.1 Comparison of ξ_SOC error estimation with different adaptive factors

自适应因子	δ_MAE/%	δ_ME/%
③	0.461	1.958
②	2.582	7.963
①	2.022	2.955

新窗口打开| 下载CSV

对比可知,自适应调整Q比自适应调整R、同时自适应调整Q和R估算SOC的准确度高.这与2.1节中的分析相符.因此,在所提ADEKF算法中使用AEKF估算电池的SOC时选择自适应调整Q.

3.2 3种典型工况下电池SOC结果对比

为验证ADEKF算法在不同工况下的普适性,分别在恒流工况、动态应力测试工况和北京公交车动态应力测试工况下对比ADEKF、AEKF及EKF算法估算全新锂离子电池SOC的结果,对比中将ξ_{SOC, 0}均设为错误值0.7.以DST工况为例展示典型工况下不同算法估算SOC结果如图5所示,其他工况下不同估算方法的δ_MAE及δ_ME分析如表2所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 DST工况下ξ_SOC估算结果

Fig.5 ξ_SOC estimation results under DST condition

表2 典型工况下不同算法估算ξ_SOC的误差

Tab.2 Error of different algorithms for estimation of ξ_SOC under typical operating conditions

工况	ADEKF			AEKF			EKF
工况	δ_MAE/%	δ_ME/%	收敛时间/s	δ_MAE/%	δ_ME/%	收敛时间/s	δ_MAE/%	δ_ME/%	收敛时间/s
恒流	0.46	1.96	130	1.17	2.75	213	1.94	3.85	440
DST	0.41	2.64	56	2.06	4.01	1250	2.50	6.13	2776
BBDST	0.38	2.33	158	2.30	3.72	1440	2.74	4.95	2694

新窗口打开| 下载CSV

由图5可知,3种算法中,ADEKF算法在DST工况下估算误差最小,EKF算法估算曲线振荡严重,而ADEKF算法估算曲线平滑.与EKF估算结果对比,ADEKF算法δ_MAE减小2.09百分点,δ_ME减小3.49百分点且收敛时间从 2 776 s 加快到 56 s.因此,ADEKF算法有明显优势,能较好地估算DST工况下锂离子电池SOC.同时,对比表2中另外两种工况下估算误差和收敛时间数据,与DST工况有类似结论.尤其在复杂的BBDST工况下,ADEKF估算δ_MAE在3种工况中最小,表明多工况条件下ADEKF算法在估算精度与速度方面优势明显.

3.3 不同老化程度电池SOC结果对比

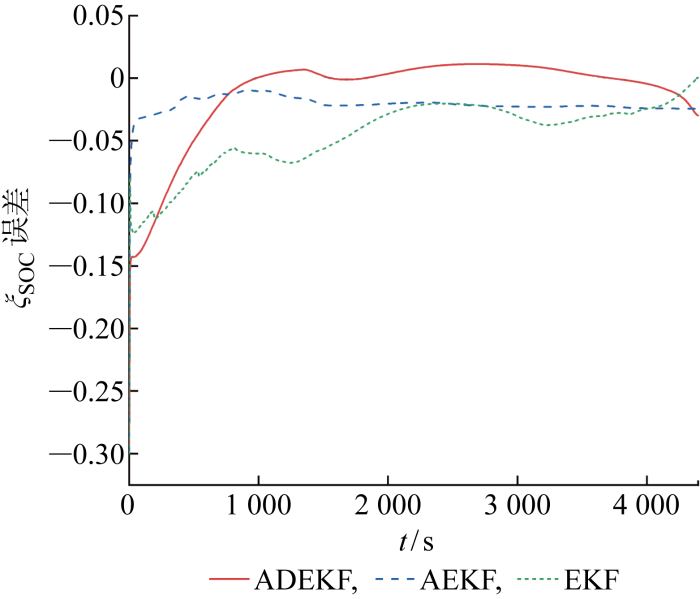
在恒流工况下,利用实验样品组中5组不同健康状态的电池分别对比ADEKF算法、 AEKF算法和EKF算法估算SOC结果. 老化程度最严重即电池寿命终止时(ζ_SOH=79.2%)的SOC估算结果对比如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 ζ_SOH=79.2%时ξ_SOC估算误差对比

Fig.6 Comparison of ξ_SOC estimation error at ζ_SOH=79.2%

由图6可见,在恒流工况下,实时估算电池R_o并固定其余4个模型参数的ADEKF算法与采用5个固定参数的AEKF或EKF相比,前者估算SOC精度更高;但在电池放电末段,ADEKF估算SOC的误差增大,这可能是由于电池放电后期内部化学反应剧烈.此外,其他不同老化程度锂离子电池估算对比结果如表3所示.

表3 不同算法估算老化电池ξ_SOC的误差对比

Tab.3 Comparison of errors of different algorithms for estimation of ξ_SOC of aged batteries

SOH/%	ADEKF		AEKF		EKF
SOH/%	δ_MAE/%	δ_ME/%	δ_MAE/%	δ_ME/%	δ_MAE/%	δ_ME/%
100	0.46	1.96	1.17	2.75	1.94	3.85
94.9	0.47	2.41	1.43	3.50	2.31	4.59
90.8	0.56	2.08	1.57	2.84	2.49	4.64
84.6	0.62	1.97	2.94	5.81	2.76	3.07
79.2	0.66	2.99	1.51	3.48	2.61	3.79

新窗口打开| 下载CSV

由表3可见,在不同老化程度下ADEKF算法δ_MAE均为最小,且随着老化程度加深,ADEKF算法估算误差变化很小.由此可以看出,在恒流工况下ADEKF算法在老化锂离子电池SOC估算中优势明显.

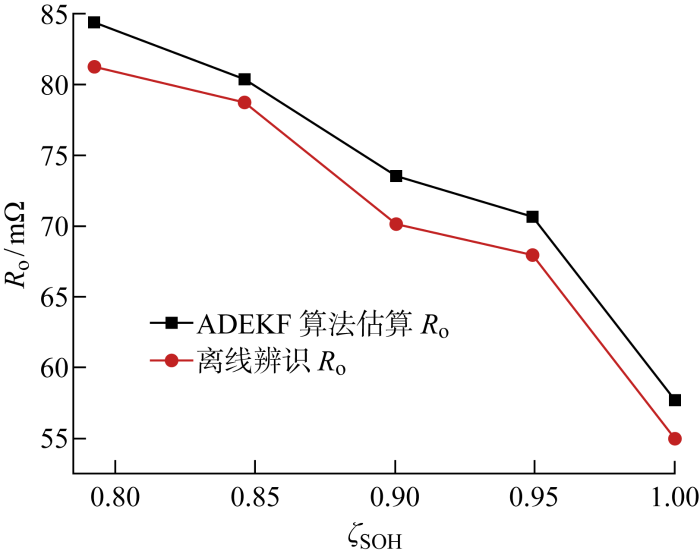
同时,为了验证等效电路模型参数实时估算的准确性与有效性,对比ADEKF算法实时估算R_o结果和离线辨识结果.如图7所示,不同老化程度电池在SOC=70%时2种结果基本吻合.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 ADEKF算法估算与离线辨识R_o结果对比

Fig.7 Comparison of R_o estimation by using ADEKF algorithm and offline identification of R_o

3.4 公开数据集下ADEKF算法验证

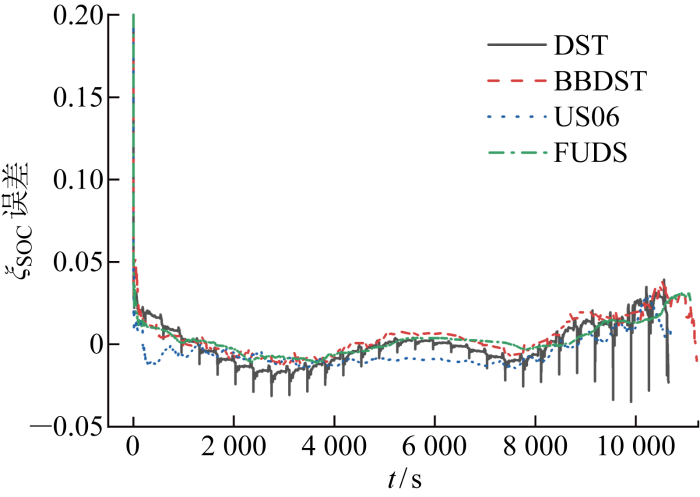
选用马里兰数据集中额定容量为2 A·h的 18 650 型三元锂离子电池数据验证复杂工况下ADEKF算法准确度,验证选择实际初始容量为 1.997 6 A·h的电池2在实验温度为25 ℃下的实验数据.数据提供了电池2的脉冲实验数据以及在4种常用电动汽车测试工况DST、BBDST、US06和FUDS的测试数据^[29].电池模型以及模型参数设置均与利用自有实验数据验证算法时相同,采用了1.1节和1.3节中所描述的方法.各工况测试中电池实际初始SOC均为80%,为验证算法收敛性,算法中取ξ_SOC.0=1. 4种工况下ADEKF算法估算误差如图8和表4所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 电池2各工况下估算ξ_SOC误差

Fig.8 Estimated ξ_SOC error of Battery 2 under different operating conditions

表4 不同算法估算电池ξ_SOC的误差对比

Tab.4 Comparison of errors in estimation of battery ξ_SOC using different algorithms

工况	ADEKF			对比算法
工况	δ_MAE/%	δ_ME/%	收敛时间/s	算法	δ_MAE/%
DST	0.92	3.93	171	CNN-GUR^[30]	1.28
BBDST	0.89	3.92	112	BP-EKF^[31]	1.17
US06	0.91	2.96	8	EMD-GUR^[32]	1.30
FUDS	0.68	3.15	57	AUKF^[16]	0.81

新窗口打开| 下载CSV

由表4分析可知,4种工况下,ADEKF算法估算锂离子电池SOC的δ_MAE均小于1%,并且在复杂工况下算法δ_MAE小、收敛时间短.在使用相同数据验证的情况下,本文算法相比于其他3种算法,在不同工况下估算精度均有一定提升.DST工况下,相比于CNN-GUR算法δ_MAE降低28.125%.BBDST工况下,在初值设置均偏离正确值的情况下,相比于BP-EKF算法δ_MAE降低23.932%.US06工况下,相比于EMD-GUR算法δ_MAE降低29.908%.FUDS工况下,相比于AUKF算法δ_MAE降低16.049%.采用马里兰数据集验证并将验证结果与其他算法对比,发现ADEKF算法兼具准确度高、鲁棒性强和工况容忍性强的优点,具有明显优势.

3.5 复杂动力工况下老化锂离子电池SOC估算结果综合对比

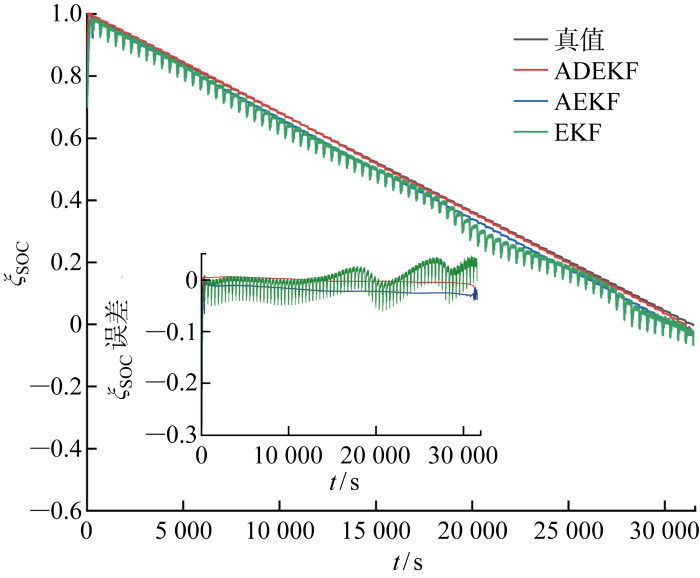
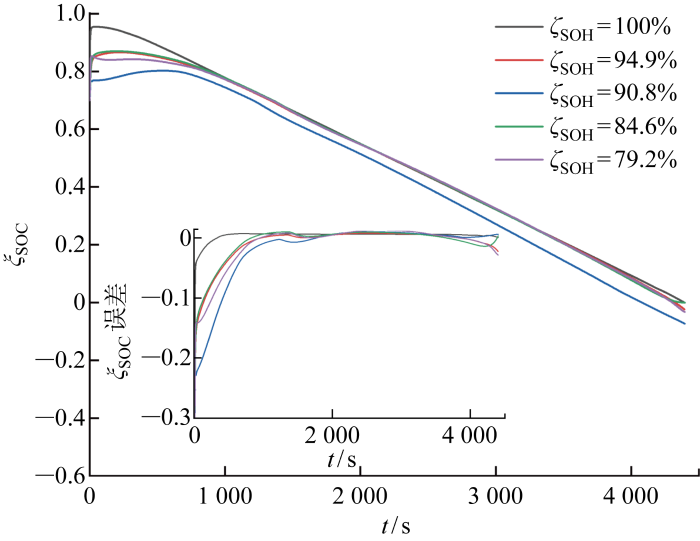
前述自有实验数据与公开数据集验证结果表明,ADEKF算法在不同工况或不同老化程度电池SOC估算中均表现出较高的估算精度,但在动力电池实际使用中,驾驶工况与电池老化两种影响因素同时存在.因此,为验证ADEKF算法在驾驶工况和电池老化综合作用下估算电池ξ_SOC的准确性,分别在恒流工况、DST工况和BBDST这3种工况下采用ADEKF算法估算不同老化程度(ζ_SOH=94.9%,90.8%,84.6%,79.2%)电池SOC,结果如图9~11所示,误差分析结果如表5所示.表中: EKF与AEKF最小误差表示在相同对比工况下,电池ζ_SOH为100%、94.9%、90.8%、84.6%、79.2%时估算结果中δ_MAE的最小值.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 恒流工况下老化电池ξ_SOC估算结果

Fig.9 ξ_SOC estimation of aged batteries under constant current condition

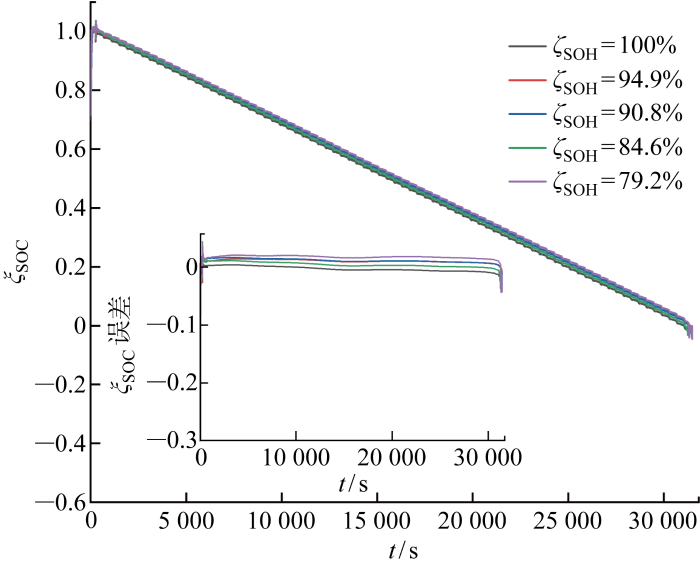
图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 DST工况下老化电池ξ_SOC估算结果

Fig.10 ξ_SOC estimation of aged batteries under DST condition

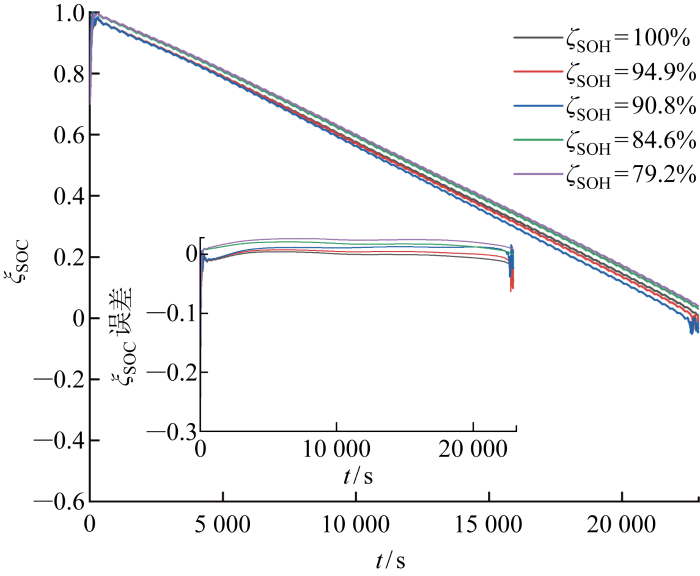
图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 BBDST工况下老化电池ξ_SOC估算结果

Fig.11 ξ_SOC estimation of aged battery under BBDST condition

表5 典型工况下ADEKF算法估算老化电池ξ_SOC的误差对比

Tab.5 Error comparison of ADEKF algorithm for estimation of ξ_SOC of aged battery under typical operating conditions

SOH	恒流			DST			BBDST
SOH	δ_MAE/%	δ_ME/%	收敛时间/s	δ_MAE/%	δ_ME/%	收敛时间/s	δ_MAE/%	δ_ME/%	收敛时间/s
100%	0.46	1.96	130	0.41	2.64	56	0.38	2.33	158
94.9%	0.47	2.41	490	0.63	4.55	56	0.47	6.34	54
90.8%	0.56	2.08	530	1.20	1.84	76	1.02	3.89	55
84.6%	0.62	1.97	445	2.45	2.85	76	1.58	2.06	110
79.2%	0.66	2.99	510	1.89	4.28	56	2.20	2.62	111
EKF最小误差		1.94			2.50			2.74
AEKF最小误差		1.17			2.06			2.29

新窗口打开| 下载CSV

由表5分析可知,在多工况与电池老化两种综合因素影响下,所提针对老化锂离子电池SOC的ADEKF算法在恒流工况下δ_MAE不超过0.66%,收敛时间不超过530 s;DST工况下δ_MAE不超过2.45%,收敛时间不超过76 s;BBDST工况下δ_MAE不超过2.20%,收敛时间不超过158 s.由此可得,在恒流工况、DST以及BBDST这3种工况下估算老化电池SOC时,所提ADEKF算法收敛速度明显加快.此外,将ADEKF估算结果δ_MAE与同工况下EKF与AEKF算法的δ_MAE进行对比,发现除DST下84.6%SOH一组数据外,ADEKF联合算法的最大δ_MAE均小于其他两种算法最小δ_MAE.通过多组实验数据对比分析可得,相比EKF算法,所提ADEKF算法对不同老化电池在3种工况下,估算结果的δ_MAE分别下降1.868百分点、2.296百分点和2.534百分点.说明在3种工况下估算老化电池SOC时,所提ADEKF算法精度更高.综上可得,经实验验证ADEKF算法在动力电池实际复杂应用条件下普适性强.

4 结论

为减小常见EKF算法估算动力电池SOC时由于复杂驾驶工况和电池老化两种因素导致的估算误差,以二阶RC模型作为锂离子电池的等效电路模型,采用ADEKF算法对三元锂离子电池在不同工况条件以及不同老化程度下进行SOC估算.研究结果表明:

(1) 仅考虑复杂工况下估算电池SOC时噪声设置不合理的问题,采用固定量测噪声协方差而只调整过程噪声协方差的方法可以明显改善SOC估算结果.分别采用自有实验数据和马里兰数据库对比验证,在较为复杂的工况条件下,估算精度相对其他算法显著提高.

(2) 仅考虑电池老化后电池模型参数会发生变化的问题,ADEKF中运用1组KF实时跟踪欧姆内阻的变化,有效提高老化锂离子电池SOC估算精度.

(3) 综合考虑驾驶工况与电池老化两种综合因素作用时的SOC估算,实验验证所提ADEKF在恒流、DST和BBDST这3种工况下估算老化锂离子电池SOC时,平均绝对误差与最大误差相比AEKF与EKF估算误差均有效减小.因此,两种因素综合作用,ADEKF算法依然具有明显的精度优势,算法普适性强,实用价值高.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李佳琪, 徐潇源, 严正.

大规模新能源汽车接入背景下的电氢能源与交通系统耦合研究综述

[J]. 上海交通大学学报, 2022, 56(3): 253-266.

DOI:10.16183/j.cnki.jsjtu.2021.464 [本文引用: 1]

新能源的大规模开发利用是实现“双碳”目标的重要手段.可再生能源发电耦合制氢技术在提高可再生能源消纳率的同时,加速了新能源汽车的普及.未来,电氢能源系统与交通系统的耦合将会更加密切.以大规模新能源汽车接入为背景,首先综述了电氢能源系统的发展现状,并对耦合系统制氢、出力波动平抑以及参与电力系统优化运行3种工作模式进行了介绍.在此基础上,从不同能源角度出发,分别对电力-交通耦合系统中的联合规划与优化运行研究现状以及氢能-交通耦合系统中的加氢站优化与氢能运输相关问题进行了总结分析.最后,结合当前研究中存在的瓶颈,从动态模型构建、不确定性因素影响等方面对未来可行研究方向进行了展望.

Jiaqi

, XU

Xiaoyuan

, YAN

Zheng

A review of coupled electricity and hydrogen energy system with transportation system under the background of large-scale new energy vehicles access

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(3): 253-266.