综合惯性控制下风力机惯性支撑能力分析及等效惯量评估

doi:10.16183/j.cnki.jsjtu.2023.161

综合惯性控制下风力机惯性支撑能力分析及等效惯量评估

周涛¹, 黄菊¹, 韩汝帅², 胡秦然^,², 权浩¹

1.南京理工大学自动化学院,南京 210094

2.东南大学电气工程学院,南京 210096

Inertial Support Capacity Analysis and Equivalent Inertia Estimation of Wind Turbines in Integrated Inertial Control

ZHOU Tao¹, HUANG Ju¹, HAN Rushuai², HU Qinran^,², QUAN Hao¹

1. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China

2. School of Electrical Engineering, Southeast University, Nanjing 210096, China

通讯作者: 胡秦然,副教授,博士生导师;E-mail:qhu@seu.edu.cn.

责任编辑: 王历历

收稿日期: 2023-04-28 修回日期: 2023-08-14 接受日期: 2023-08-17

基金资助:

江苏省自然科学基金青年项目(BK20220216)
中央高校基本科研业务费专项资金资助(30922010709)

Received: 2023-04-28 Revised: 2023-08-14 Accepted: 2023-08-17

作者简介 About authors

周涛(1991—),博士,讲师,主要研究方向为电力系统运行与控制、新型电力系统频率稳定.

摘要

针对可再生能源高占比并网所引发的新型电力系统频率安全问题,风电机组多采用综合惯性控制为电力系统提供惯量及一次调频支撑.为更好地把握系统的惯量安全水平,保障电网频率稳定,首先对采用综合惯性控制的风电机组进行动态建模,根据风力机蕴含的动能及其对电网提供的频率支撑推导出风力机的有效惯量.然后,建立综合惯性控制下包含风力机的系统频率响应模型,得到风力机调频过程中有效惯性时间常数的解析式并进行惯性支撑能力分析.根据“等面积原理”推导出综合惯性控制下风力机参与调频过程的等效惯量评估方法,该方法能够对风力机提供的惯性支撑能力进行分析并给出量化结果.最后,通过算例分析验证了所提方法的有效性和可行性,并分析了不同因素对风力机等效惯量的影响.

关键词： 新型电力系统; 风力发电; 综合惯性控制; 等效惯量; 等面积原理

Abstract

In response to the new power system frequency safety issues caused by the high percentage of renewable energy sources connected to the grid, wind turbines mostly use integrated inertia control for the inertia and primary frequency regulation support provided by the power system. In order to better improve the inertia safety of the system and guarantee the grid frequency stability, dynamic modeling of wind turbines with integrated inertia control is conducted to derive the effective inertia of the wind turbine based on the kinetic energy contained in the wind turbine and the frequency support it provides to the grid. Then, a system frequency response model of the wind turbine in integrated inertia control is established, the analytical formula of the effective inertia time constant in the process of wind turbine frequency regulation is obtained, and the inertia support capability is analyzed. Based on the “equal area principle”, the equivalent inertia evaluation method of the wind turbine in integrated inertia control is derived, which can analyze the inertial support capacity provided by the wind turbine and give quantitative results. Finally, the validity and feasibility of the proposed method is verified in a case study, and the impact of different factors on the equivalent inertia of the wind turbine is analyzed.

Keywords： new power system; wind power; integrated inertial control; equivalent inertia; equal area principle

PDF (2385KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

周涛, 黄菊, 韩汝帅, 胡秦然, 权浩. 综合惯性控制下风力机惯性支撑能力分析及等效惯量评估[J]. 上海交通大学学报, 2024, 58(12): 1915-1924 doi:10.16183/j.cnki.jsjtu.2023.161

ZHOU Tao, HUANG Ju, HAN Rushuai, HU Qinran, QUAN Hao. Inertial Support Capacity Analysis and Equivalent Inertia Estimation of Wind Turbines in Integrated Inertial Control[J]. Journal of Shanghai Jiaotong University, 2024, 58(12): 1915-1924 doi:10.16183/j.cnki.jsjtu.2023.161

我国提出“双碳”战略目标以来,传统电力系统逐渐转型升级为以新能源为主体的新型电力系统,风电、光伏、电池储能等大规模并网,传统同步机组被替代,新能源机组占比不断提高^[1⇓⇓-4].据全球风能理事会统计,2021年全球和中国新增风电装机容量分别为93.6 GW和47.57 GW,风电在中国以及全球范围内均呈现广泛且高速的发展状态,对系统的稳定运行产生愈发明显的影响^[5-6].

新能源高占比的系统因低惯量特性容易引发系统产生严重的动态频率安全隐患.当前,双馈型感应风力机作为风电场采用的主要机型,其自身惯量及对系统惯量的影响不容忽视^[7].为解决低惯量特征引起的动态频率失稳问题,引入综合惯性控制技术^[8].随着风电占比不断提高,综合惯性技术愈加广泛地应用在实际电网运行中.因此,评估全响应时间尺度下考虑综合惯性控制的风电机组有效惯量及其对系统频率调节的支撑能力,对评估新型电力系统惯量具有重要意义.

因为新型电力系统的等效惯性时间常数直接影响含有风电机组的系统动态频率特性,所以诸如系统的有功功率缺额、频率变化率、频率跌落最低点等均与之密切相关^[9-10].在实际系统应用中,同步机的惯性时间常数是确定的;但对于考虑综合惯性控制的风电机组来说,由于风速存在波动性,且其与风力机转子、转速间亦存在不确定性,风电机组的等效虚拟惯性时间常数无法确定,所以无法确定新型电力系统的等效惯性时间常数.由此可知,研究风电机组的等效惯量是研究系统惯量支撑能力的基本.

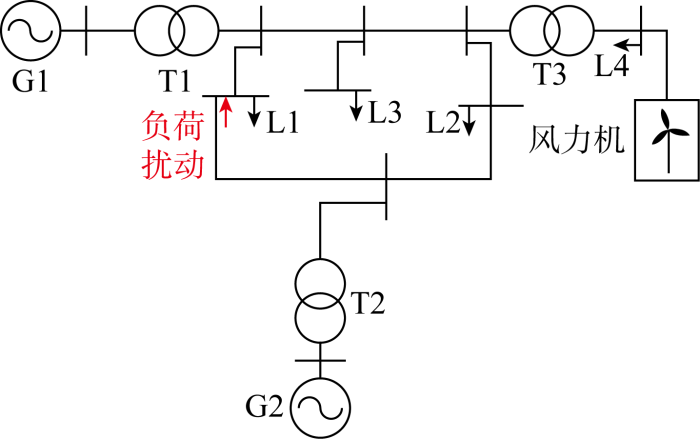
目前针对风电机组等效虚拟惯量的评估主要从风力机模型和系统辨识这两个方面入手.文献[11]中建立基于虚拟惯量控制的风电机组并网系统小信号模型,采用模态分析法分析虚拟惯量控制相关控制回路对同步发电机间机电振荡模式的影响规律;但该方法主要分析虚拟惯量控制参数对系统动态特性的影响,并没有给出有关风电机组虚拟惯量的具体求解式,不能直观地从惯量方面分析对系统动态频率的影响.文献[12]中定义了双馈型风电场等效虚拟惯性时间常数并阐明了其物理意义,建立含虚拟惯性控制的风电机组简化模型和风电场模型,计算求得虚拟惯性时间常数的频域和时域解析解;但该方法仅单独考虑虚拟惯性控制,并没有综合下垂控制进行分析,在惯量控制方法上缺乏前沿性.文献[13]中构建计及锁相环和虚拟惯量控制的风电机组转子转速时间尺度下的简化模型,理论推导了风电机组在虚拟惯量控制作用期间的等效惯量频域表达式;但仅考虑在转速时间尺度下的等效惯量,并没有分析全响应过程,时间尺度上不够全面.文献[14]中推导了含风电虚拟惯性响应的电力系统等效惯量理论表达式,利用同步相量测量单元获取发电装置节点处的有功-频率数据,然后利用受控自回归模型以及含有遗忘因子的递推最小二乘算法评估不同风电渗透率下的全网等效惯量;但该方法采用定义式求解风电机组的等效惯性时间常数问题,将系统同步机组与新能源机组容量进行简单叠加,仅代表系统自身所包含的容量,并不一定全部提供给系统进行频率调节,即并不是作为提供给系统频率调节的有效能量.文献[15]中根据能量守恒原理提出一种利用风电场公共连接点有功-频率量测数据进行计算的惯量评估方法,避免了基于系统辨识方法在评估过程中对辨识模型降阶所带来的误差,从而可以得到更高精度的惯量评估结果;但该方法仅利用转子运动方程建立风电机组与系统的转速转化,并未分析同等频率支撑能力下风电惯量与同步机惯量之间的关系.

针对以上问题,为了更好地把握系统的惯量安全水平,保障电网频率稳定,首先对采用综合惯性控制的风电机组进行动态建模,得到风力机调频下电力系统的频率响应模型,再根据风电机组本身所蕴含的动能及其对电网所提供的频率支撑能力推导出风电机组自身的有效惯量.然后,建立综合惯性控制下包含风电机组的系统频率响应模型,得到风力机调频过程风电机组有效惯性时间常数的解析式并进行惯性支撑能力分析.其次,根据“等面积原理”推导出综合惯性控制下风力机参与调频过程的等效惯量评估方法,该方法能够分析风力机提供的惯性支撑能力并给出量化结果,为保障新型电力系统安全稳定提供参考.最后,通过算例分析验证了所提方法的有效性和可行性,分析了不同风速和调频控制参数对等效惯量的影响.

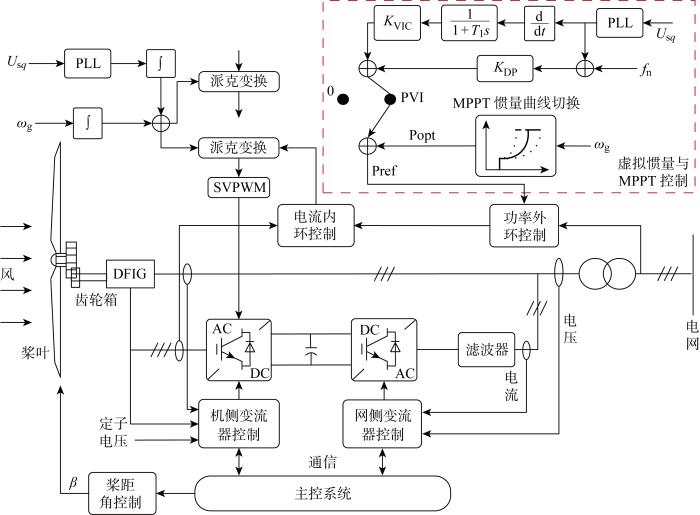
1 风电机组动态建模

以双馈感应式风电机组(doubly-fed induction generator, DFIG)作为研究对象,其控制系统^[16]如图1所示.DFIG机组主要由风力机、传动链轴系、感应电机、锁相环控制系统、风力机桨距角控制系统、转速控制系统以及四象限变流器控制系统组成^[17].图中:PLL表示锁相环;SVPWM表示空间矢量脉宽调制;MPPT表示最大功率点跟踪;β为桨距角;U_s_q为锁相环q轴输入电压;f_n为额定频率;ω_g为角速度;K_VIC为锁相环控制系数;K_DP为虚拟惯量控制系数;T₁为锁相环控制惯性时间常数;s为拉普拉斯算子;t为时间;AC、DC分别表示交流电和直流电.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 双馈风电机组控制系统框图

Fig.1 Block diagram of doubly-fed wind turbine control system

为了方便分析,建立适合于研究虚拟惯性响应的风电机组调频下电力系统的频率响应模型,详细的模型包含发电机模型、变流器简化模型以及综合惯性控制模型.

首先,发电机模型的电磁转矩表达式为

(1)T_em=

\frac{3 P L_{m}}{4 L_{s}}

(ψ_d_si_q_r-ψ_q_si_d_r)

式中:P为风电机组极对数;L_m、L_s分别为风电机组励磁电感和定子漏感;ψ_d_s、ψ_q_s分别为定子磁链在d、q轴的分量;i_d_r、i_q_r分别为转子电流在d、q轴的分量^[18].

由于采用定向矢量控制策略,所以定子磁链在q轴的分量,即ψ_q_s=0.令a₁=3PL_m/4L_s,电磁转矩可表示为

(2)T_em=

\frac{3 P L_{m}}{4 L_{s}}

ψ_d_si_q_r=a₁ψ_d_si_q_r

风力发电机转子运动方程为

(3)2H_DFIG

\frac{d ω_{r}}{d t}

=T_mech-T_em

式中:H_DFIG为风电机组的等效虚拟惯性时间常数;ω_r为风力机转速;T_mech为风电机组机械转矩.

其次,转子侧变流器模型可以简化为一个一阶惯性环节:

(4)G_q(s)=

\frac{i_{q r}}{i_{q r}^{*}}

\frac{1}{1 + τ s}

式中: $i_{q r}^{*}$ 为转子交轴电流参考值;τ为变流器响应时间常数,按照经验取0.02 s.

由τ值可知,电流内环的响应速度较机电暂态过程快得多,在此将变流器控制模型简化为一阶惯性环节来研究风电机组虚拟惯性响应暂态过程是合理的.

最后,综合惯性控制将虚拟惯量控制和下垂控制这两种策略结合,以系统的频率偏差和频率变化率作为输入,改变风力机的输出功率^[19].由此得到综合惯性控制策略产生的附加电磁转矩为

(5)Δ

T_{e m}^{*}

\frac{K_{d f} s + K_{p f}}{1 + T_{f} s}

Δω_s

式中:K_df为虚拟惯量控制系数;K_pf为下垂控制系数;T_f为滤波时间常数;Δω_s为系统角速度变化量.

2 基于综合惯性控制的风电机组频率建模及惯量分析

2.1 含风力机的系统频率响应模型

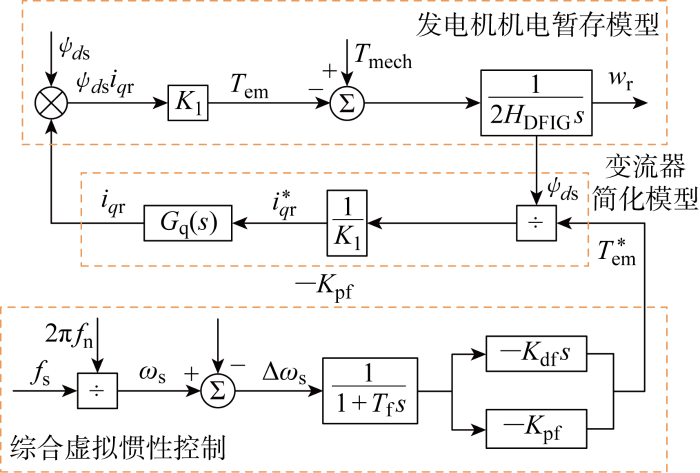
由第1节建立的与风电机组虚拟惯性响应相关的各模块控制模型可以进一步得到含综合惯性控制的风电机组的控制模型,如图2所示.图中:f_n=50 Hz;f_s为系统频率;K₁为式(2)中ψ_d_s、i_q_r的系数;w_r为风力机转速; $T_{e m}^{*}$ 为发电机电磁转矩标幺值.稳态时,系统同步角速度保持额定值不变,有Δω_s=0,Δ $T_{e m}^{*}$ =0.又由于风速保持不变,转子角速度增量Δω_r=0,电磁转矩值T_em保持不变,风电机组不进行惯性响应.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 含综合虚拟惯量控制的双馈风电机组简化模型

Fig.2 Simplified model of doubly-fed wind turbine with integrated virtual inertia control

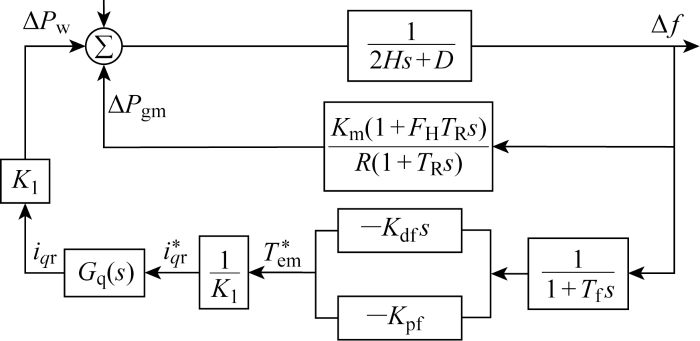
将全网所有发电机转子运动方程等值聚合为单机模型,同时针对原动机调速系统动态环节进行等值拟合处理,利用单机模型表示全系统,得到系统频率响应(system frequency response,SFR)模型.为研究考虑综合惯性控制的风电机组频率响应过程及其惯量,以SFR模型为基础,增加含综合惯量控制的风电机组简化模型的频率响应传递函数,如图3所示.图中:H为发电机惯性时间常数;D为系统的阻尼系数;T_R为再热时间常数;F_H为高压涡轮分数;K_m为与发电机功率因数和备用系数相关的系数;R为调速器调速系数;ΔP_w为系统的负荷扰动功率;ΔP_gm为一次调频增加的出力;Δf为系统频率变化量.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 考虑双馈风电机组的SFR模型

Fig.3 SFR model considering doubly-fed wind turbines

2.2 风力机有效惯量能力分析

风电机组通过改变电磁转矩实现虚拟惯性响应,电磁转矩增量决定等效惯性时间常数的大小,在此先计算风电机组惯性响应过程中的电磁转矩增量.

对于具有机电暂态时间尺度的惯性响应过程,可忽略定子磁链动态变化^[20],即满足Δψ_d_s=0,定子磁链一直保持初始稳态值不变.

因此,根据式(3),当电磁转矩增加时,有

(6)T_em+ΔT_em=K₁ψ_d_si_q_r+K₁ψ_d_sΔi_q_r

根据图2控制模型:

(7)ΔT_em=K₁ψ_d_sΔ

i_{q r}^{*}

G_q(s)=

\frac{K_{1} ψ_{d s} Δ T_{e m}^{*} G_{q} (s)}{K_{1} ψ_{d s}}

=Δ

T_{e m}^{*}

G_q(s)

由式(7)可知,求得电磁转矩参考增量Δ $T_{e m}^{*}$ 即可得到电磁转矩增量.

由前述分析和式(5)可知,电磁转矩增量为

(8)ΔT_em=-

\frac{K_{d f} s + K_{p f}}{1 + T_{f} s}

G_q(s)= -

\frac{(K_{d f} s + K_{p f})}{(1 + T_{f} s) (1 + τ s)}

设风电机组初始转速为ω_r0,初始机械转矩为T_mech0,初始电磁转矩为T_em0,忽略风电机组阻尼D.

当风电机组的转速发生变化时,转子运动方程为

(9)2H_DFIG

\frac{d (ω_{r 0} + Δ ω_{r})}{d t}

=T_mech0-(T_em0+ΔT_em)

偏差量表示的转子运动方程为

(10)2H_DFIG

\frac{d Δ ω_{r}}{d t}

=-ΔT_em

将式(10)转换为频域方程,并将式(8)代入式(10),得到:

(11)2H_DFIGΔω_rs=-ΔT_em=

\frac{(K_{d f} s + K_{p f}) Δ ω_{s}}{(1 + T_{f} s) (1 + τ s)}

进而:

(12)

\frac{Δ ω_{r}}{Δ ω_{s}}

\frac{K_{d f} s + K_{p f}}{2 H_{D F I G} s (1 + T_{f} s) (1 + τ s)}

因变流器响应速度较惯性响应、机电暂态响应过程快得多,可忽略变流器动态过程,在此取时间常数 τ=0,则由式(12)得到:

(13)

\frac{Δ ω_{r}}{Δ ω_{s}}

\frac{K_{d f} s + K_{p f}}{2 H_{D F I G} s (1 + T_{f} s)}

由于风电机组采用综合惯性控制后,风电机组与系统相耦合,即风力机转速与系统转速相耦合,响应过程中的动能变化量前后应相同,即

(14)ΔE_K-DFIG=

\frac{J_{D F I G} [(ω_{r 0} + Δ ω_{r})^{2} - ω_{r 0}^{2}]}{2 P^{2} S_{N}}

\frac{J_{w - e q u} [(ω_{s 0} + Δ ω_{s})^{2} - ω_{s 0}^{2}]}{2 P^{2} S_{N}}

式中:S_N、J_DFIG分别为额定容量、固有转动惯量;J_w-equ、ω_s0分别为含综合惯性控制的风电机组系统虚拟转动惯量、系统初始同步角速度.

整理式(14)可得:

(15)J_w-equ=J_DFIG

\frac{ω_{r 0} Δ ω_{r}}{ω_{s 0} Δ ω_{s}}

根据惯量与动能之间的关系,

(16)H=

\frac{E_{K}}{S_{N}}

\frac{J ω_{n}^{2}}{2 S_{N}}

式中:E_K为动能;J为转动惯量;ω_n为系统额定转速.

联立式(15)和式(16)得到考虑综合惯性控制的风电机组系统等效虚拟惯量:

(17)H_w-equ=H_DFIG

\frac{ω_{r 0}}{ω_{s 0}} \frac{Δ ω_{r}}{Δ ω_{s}}

将式(13)代入式(17)中,可得频域下的虚拟惯性时间常数为

(18)H_w-equ(s)=

\frac{ω_{r 0} (K_{d f} s + K_{p f})}{2 s ω_{s 0} (1 + T_{f} s)}

对其进行拉氏反变换,可得时域下的系统虚拟惯性时间常数为

(19)H_w-equ(t)=

[\frac{K_{p f}}{2} + \frac{(K_{d f} - K_{p f} T_{f}) e^{- \frac{t}{T_{f}}}}{2 T_{f}}] \frac{ω_{r 0}}{ω_{s 0}}

由式(19)可知,考虑综合惯性控制的风电机组系统的等效虚拟惯量随时间而变化,具有时变性,并不是一个恒定常数.因此,风电机组本身参数及其运行工作点都会影响风电机组对系统的有效惯量.

2.3 风力机惯量特性分析及等效惯量评估

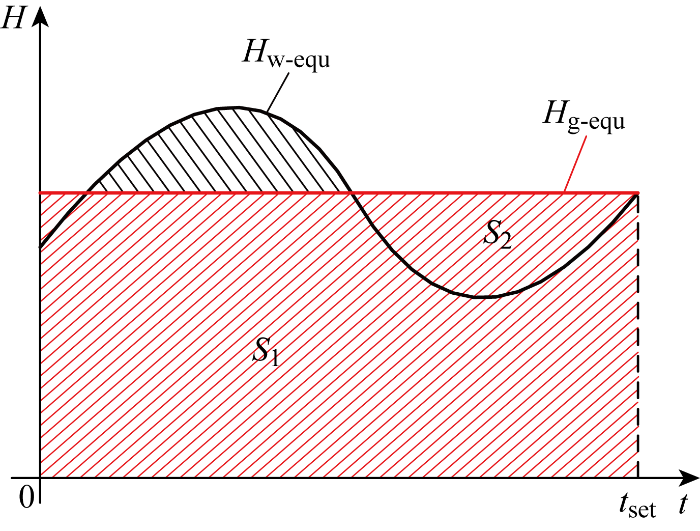
由于受到系统频率的影响,不同于同步电机的惯性时间常数固定,风电机组的虚拟惯性时间常数具有时变性,这一特性由式(19)可以看出.风电机组作为新型电力系统的重要组成部分进一步影响新型电力系统的惯量,其惯量不容忽视.量化评估风电机组的惯量,并研究其对系统频率的支撑能力,对保证新型电力系统频率安全稳定的运行具有重要意义.基于上述原理,利用“等面积原理”并采用相同时间内系统具有相同惯量支撑能力的同步电机替代风电机组.

在全响应时间范围内,在受到相同的不平衡功率扰动时,对系统表现相同的惯量支撑能力的风电机组惯量可由相同特性的同步电机惯量等效替换.基于上述原理,采用“等面积原理”,即对同步电机惯量和风电机组等效虚拟惯量进行时域积分,在相同的响应时间范围内两者相等,也即S₁=S₂,如图4所示.图中:S₁为时变的风电机组惯量在全响应时间t_set内的积分;S₂为恒定的等效同步机惯量在t_set时间内的积分;H_g-equ为同步电机惯量.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 等面积原理示意图

Fig.4 Schematic diagram of equal area principle

对同步电机惯量和风电机组等效虚拟惯量进行时域积分,如下:

(20)

\int_{0}^{t}

H_g-equdt=

\int_{0}^{t}

H_w-equdt

将式(19)代入上式中,可得:

(21)H_g-equ(t)=-

\frac{ω_{r 0}}{2 t_{s e t} ω_{s 0}}

[K_{d f} + K_{p f} (t_{s e t} - T_{f}) + (K_{p f} T_{f} - K_{d f}) e^{- \frac{t_{s e t}}{T_{f}}}]

当同步电机与具有综合惯性控制的风电机组受到同等大小的负荷扰动时,在全响应时间尺度下,两个电机在考虑一次调频的情况下,对系统的惯量支撑能力相同.

3 算例与分析

为验证所提模型和方法的正确性和有效性,在MATLAB/Simulink搭建如图5所示的3机9节点系统,其中风力机为额定功率1.5 MV·A的双馈感应式风力机,G1、G2为容量为10 MV·A的同步机组;T、L分别表示变压器和负荷.系统详细参数见文献[21],系统等效频率响应模型参数为H=8 s, D=1.风电机组以综合惯性控制参与电网调频,具体参数为K_df=1.841 5,K_pf=0.254 6.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 3机9节点系统

Fig.5 Three-machine nine-node system

3.1 风力机有效惯量验证与分析

在t=0 s时系统处于稳态,在t=40 s时在L1施加一个负荷波动Δ $P_{d}^{p . u .}$ =0.05,得到调频响应阶段的系统频率如图6所示,风力机有效惯量曲线如图7所示.由图6可见,系统频率在扰动发生后很快即可恢复稳定,频率到达nadir点的时刻为t=43.76 s,此时的电网频率为f=49.83 Hz,稳态频率为49.88 Hz.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 系统频率响应曲线

Fig.6 System frequency response curve

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 风电机组的等效惯量曲线

Fig.7 Equivalent inertia curves of wind turbines

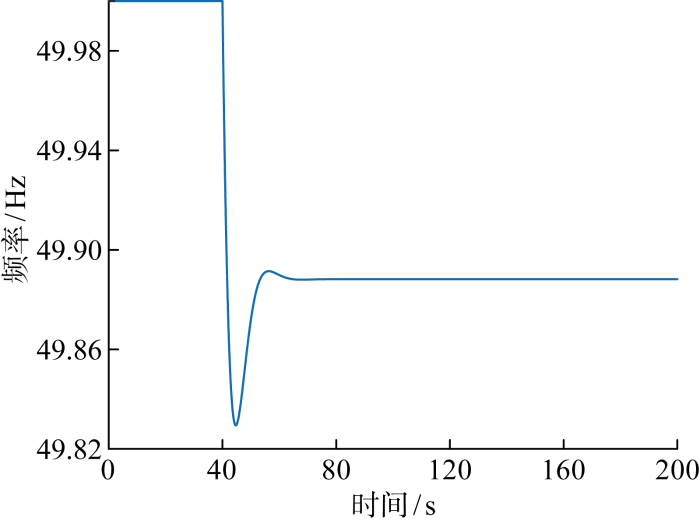
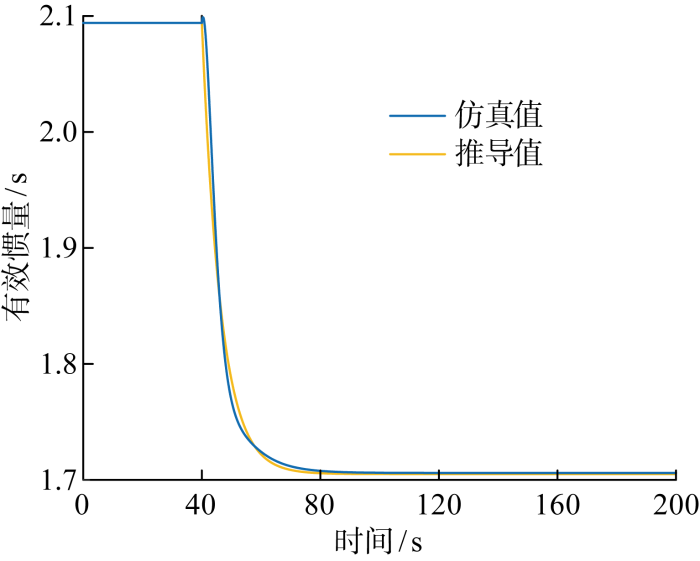
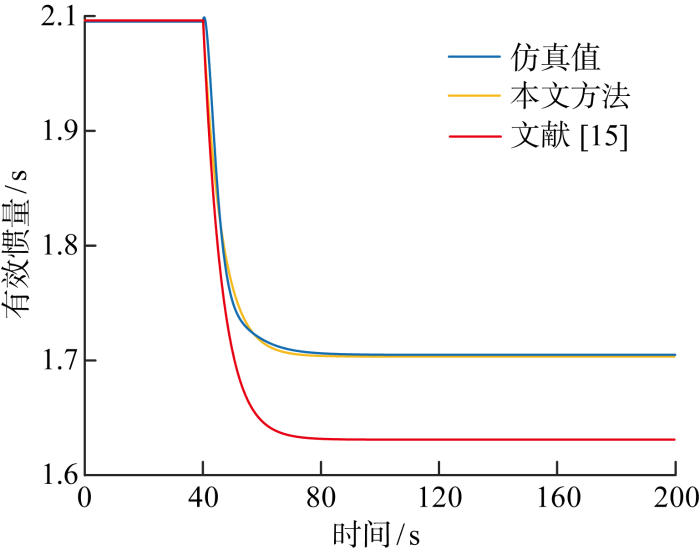
图7中,蓝色线为实际系统仿真值,黄色线为根据式(19)得到的理论推导值.由图可见,两条曲线趋势相同、数值相近,验证了所提有效惯量求解方法的正确性.惯量变化曲线具有如式(19)所述的时变特性.在初始时间,系统处于稳态,风力机惯量在恒风速条件下保持初始值不变.40 s时系统受到功率扰动,风电机组的转速首先响应,风力机出力提供功率支撑,风力机转速减小速度大于系统转速的下降速度,有效惯量减小.此后频率保持稳定,频率偏差和频率变化率均为0,风力机出力为0,风力机转速保持不变,从而惯量保持稳定不变.

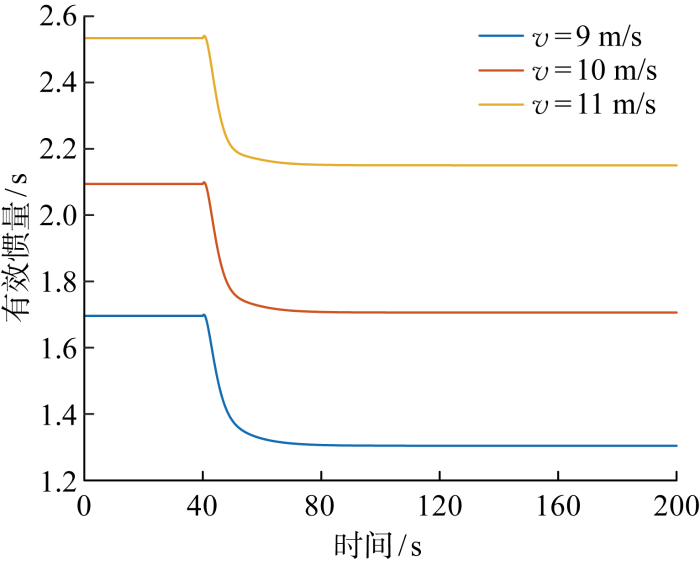
为分析风速对风力机有效惯量的影响,分别在9、10、11 m/s这3种风速(v)状态下进行系统仿真,结果如图8所示.由图可见,当v=11 m/s时,稳态时H_w-equ=2.15 s;当v=10 m/s时,稳态时H_w-equ=1.706 s;当v=9 m/s时,稳态时H_w-equ=1.304 s.由此可知,随着风速提升,由于风力机蕴含的转子动能增加,其等效惯量也在增大,所以对电网频率的支撑能力增强.风力机在高风速下具有更强的惯性响应能力,从而具有更大的等效惯量值H_w-equ.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同风速下风电机组的等效惯量对比

Fig.8 Comparison of equivalent inertia of wind turbines at different wind speeds

3.2 等效惯量验证与分析

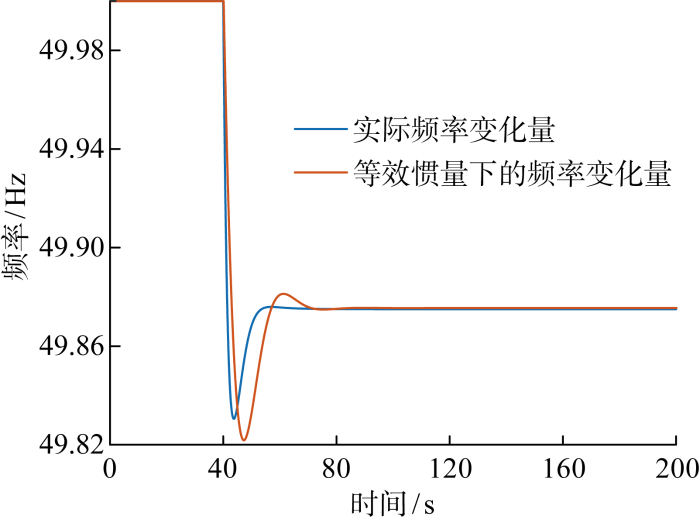
在风速v=9 m/s条件下进行仿真验证与分析,根据等面积原理求得风力机的等效同步惯量H_g-equ为 1.396 6 s.分别以风力机和等效惯量下同步电机参与电网调频,t=40 s时,向系统施加一个Δ $P_{d}^{p . u .}$ =0.05的扰动量,观察在频率达到稳态的全过程内系统频率变化量,如图9所示.由图可见,风电机组的实际频率变化量和2.2节求解得到的等效惯量的同步电机的频率支撑能力相同,验证了等效惯量评估模型的有效性.其中,实际仿真时频率达到频率最低点所需的时间早于等效惯量下系统达到频率最低点所需时间,且频率最低点频率高于采用等效惯量下的频率,这是由于综合惯性控制的输入为频率变化率和频率偏差,实际仿真系统中风力机采用综合惯量控制时能够实时计及电网的频率信息,予以系统快速的频率支撑和响应.而同步机本身具有较大惯量,其响应速度慢于采用综合惯性控制的风力机.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同情况下的频率对比曲线

Fig.9 Comparison of frequency in different cases

3.3 综合惯性控制系数对等效惯量的影响

综合惯性控制由虚拟惯量控制和下垂控制构成,因此风力机的等效惯量受到虚拟惯性控制参数和下垂控制参数共同影响.为分析综合惯性系数对等效惯量的影响,需分别考虑仅改变虚拟惯量控制系数和仅改变下垂控制系数这两种场景下的等效惯量.

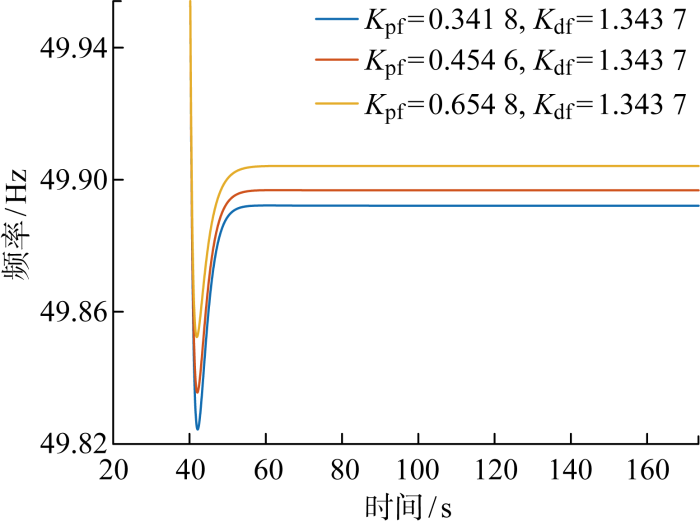
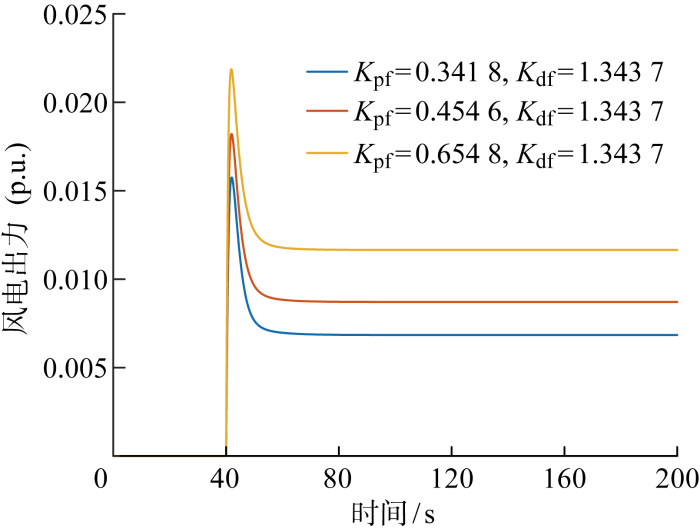
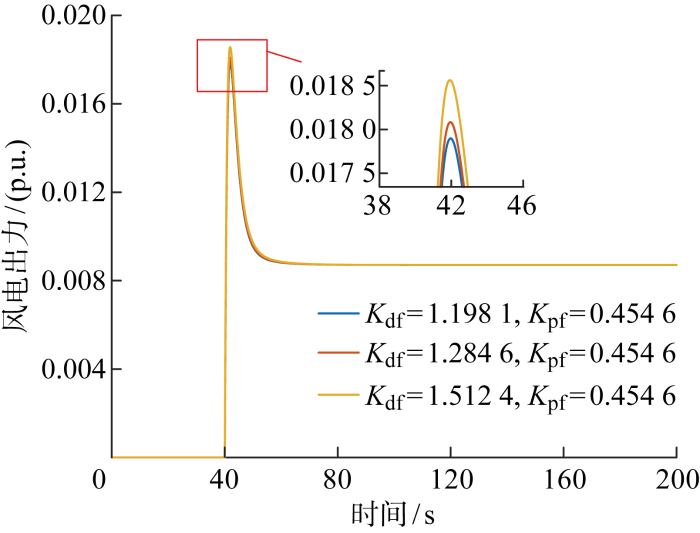
(1)场景一为虚拟惯性控制参数不变,仅改变下垂控制系数,得到系统频率曲线和风力机出力分别如图10和图11所示.由图可知,当系统受到负荷扰动时,初时频率变化率较大,虚拟惯量控制起主导作用;到频率最低点即nadir点时,频率变化率为率为0,频率偏差最大,此时下垂控制起主导作用;频率最低点即nadir点之后,频率进行恢复,虚拟惯性控制可能阻碍电网频率恢复,主要依靠下垂控制调节风力机出力.系统频率稳态值和频率最低点即nadir点频率值均随着K_pf的增加而增大,这是由于风电出力随着K_pf增加而增大,给系统提供更大功率支撑.根据文献[10]中的分析,风力机出力越大,系统最大频率偏差越小,稳态频率偏差越小,风力机调频的支撑能力增大,因此等效惯量也在增大,具体数值如表1所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同K_pf下的频率响应曲线

Fig.10 Frequency response at different K_pf values

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同K_pf下的风电出力曲线

Fig.11 Wind power output at different K_pf values

表1 不同K_pf下的等效惯量值

Tab.1 Equivalent inertia at different K_pf values

综合惯性控制参数	等效惯量/s
K_pf=0.314 8, K_df=1.343 7	1.131 4
K_pf=0.454 6, K_df=1.284 6	1.159 5
K_pf=0.454 6, K_df=1.512 4	1.342 9

新窗口打开| 下载CSV

(2) 场景二为下垂控制参数保持不变,仅改变虚拟惯性控制系数,得到系统频率曲线和风力机出力分别如图12和图13所示.由图可知,在K_pf保持不变的情况下,随着K_df增大,系统频率最低点减小,这是由于风电出力在随着K_df增加而增大,给系统提供更大的功率支撑.频率达到稳态时,频率变化率为0,此时K_df的改变对其没有影响,K_pf相同时频率稳态值相同.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同K_df下的频率响应曲线

Fig.12 Frequency response at different K_df values

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同K_df下的风电出力曲线

Fig.13 Wind power output at different K_df values

由上述分析可知,在K_pf保持不变的情况下,随着K_df增大,风力机出力也随之增大,对系统的惯量支撑能力越大, 具体数值如表2所示.虽然此时风力机频率变化率为正,提供负功率,对频率恢复略有影响,导致K_df对频率后续的恢复过程具有阻碍作用,但在全过程中,调频支撑作用还是随着K_df增大而增大,跟虚拟惯性控制系数的物理意义相符合^[22].

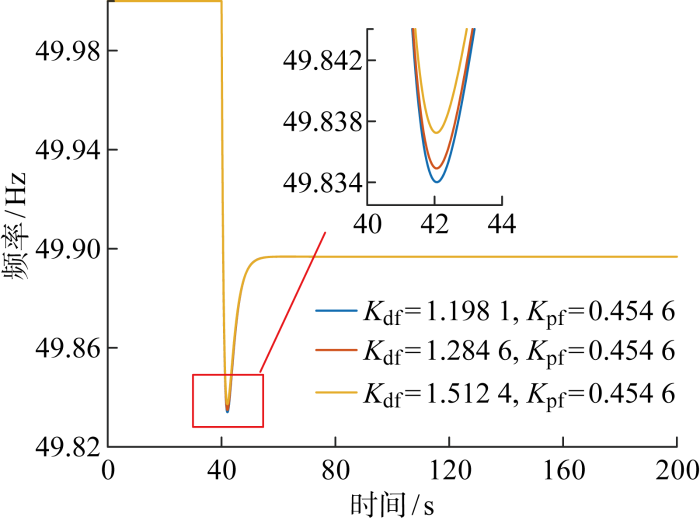
表2 不同K_df下的等效惯量值

Tab.2 Equivalent inertia at different K_df values

综合惯性控制参数	等效惯量/s
K_pf=0.454 6, K_df=1.198 1	1.193 8
K_pf=0.454 6, K_df=1.284 6	1.276 4
K_pf=0.454 6, K_df=1.512 4	1.468 7

新窗口打开| 下载CSV

由表1和表2数据可知,虚拟惯性控制系数和下垂控制系数均与风电机组等效惯量呈正相关特性,两种因素的影响差异较小.理论上应该虚拟惯性系数对等效惯量影响更大,但在实际算例中等效惯量数值受到多种因素影响,在特定场景下调节下垂控制系数和虚拟惯性系数可以缩小这种影响差异.

3.4 方法比较

文献[12]中建立了含虚拟惯性控制的双馈风电机组简化模型和风电场模型,计算求得风电场等效虚拟惯性时间常数的频域和时域解析解.文献[12]和本文均在离线场景下应用解析方法对风力机的等效惯量进行评估,分析风力机的惯量时域变化.本文在文献[12]的基础上,模型上增加下垂控制,采用综合虚拟惯性控制,并对整个过程进行惯量评估,等效出相同频率支撑能力下的同步机惯量.文献[12]中计及速度控制器,在风力机模型上更为完整,但在实际运行中其影响较小.具体对比如表3所示.

表3 方法对比

Tab.3 Comparison of methods

对比项	文献[15]	本文
能否计及虚拟惯性控制	能	能
能否计及下垂控制	否	能
能否分析惯量的时或变化	能	能
能否求解风力机等效惯量	否	能

新窗口打开| 下载CSV

现用本文系统参数对文献[12]中的模型求解风力机等效虚拟惯量的时域,如图14所示.由图可知,应用本文方法得到的风力机惯量曲线比文献[12]更接近仿真值.应用式(20)求解文献[12]中的惯量曲线,得到风力机的等效惯量为 1.118 7 s,而本文方法为 1.396 6 s.对于惯量时域曲线以及等效惯量结果,文献[12]方法得到的惯量值均比本文方法低,这是因为该方法未计及下垂控制部分提供的有效惯量.因此,本文方法对于风电机组的有效惯量评估具有更好的精确性,能够计及更为复杂的调频控制策略,有效量化风力机对系统的惯量支撑能力.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 风电机组的有效惯量曲线

Fig.14 Effective inertia of wind turbines

4 结论

风电机组以综合惯性控制参与电网一次调频,能够从频率变化率和频率偏差这两个方面进行频率调节,提高风电机组的频率响应能力.因此,对采用综合惯性控制的风电机组进行动态建模得到风力机调频下电力系统的频率响应模型,推导出风电机组的有效虚拟惯性时间常数时域解析式,对风电机组在系统中的等效惯量进行量化评估,分析不同因素对风力机等效惯量的影响,所得结论如下.

(1) 在风电机组频率响应的初始阶段,系统处于稳态,风力机惯量在恒风速条件下保持初始值不变.系统受到功率扰动后,风力机出力提供功率支撑,有效惯量减小.此后频率保持稳定,风力机转速保持不变,惯量保持稳定不变.

(2) 风电机组的实际频率变化量和参与电网调频的等效惯量下同步电机的频率支撑能力相同,验证了所提风电机组等效惯量评估模型的准确性,有效量化风电机组对系统的惯量支撑能力.其中,采用综合惯性控制的风电机组能够实时计及电网的频率信息,予以系统快速的频率支撑和响应.

(3) 对比分析风速和调频控制参数变化对等效惯量的影响可以看出,风速、虚拟惯性控制参数和下垂控制参数均与风电机组等效惯量呈正相关特性.理论上虚拟惯性系数对等效惯量影响更大,但在实际算例中等效惯量数值受到多种因素影响,两种因素的影响差异可能较小,这说明在特定场景下调节下垂控制系数和虚拟惯性系数均可以改善风力机惯量.随着风速提升,风力机的有效惯量增大,风力机在高风速下具有更强的惯性响应能力,从而具有更大的等效惯量值.

新型电力系统电网惯量显著降低,需要“源-网-荷-储”多方共同提供惯性支撑,保证电力系统的安全稳定.为精准计算风电场的惯性支撑能力,电网调控中心需要风电场和电网等多方面提供数据和信息,以确保惯量支撑能力.本文方法为新型电力系统下新能源侧的等效惯量评估提供思路和参考,实际应用中还存在局限性.本文基于采用综合惯性控制的风电机组进行动态建模得到风力机调频下电力系统的频率响应模型,进而推导出风电机组的有效虚拟惯性时间常数时域解析式,对风电机组在系统中的等效惯量进行量化评估.如果风力机采用其他调频方式例如短时超发控制和功率备用等,调频原理与综合惯性控制并不相同,虽然仍然能够给电网提供惯量支撑,但其时域模型较为复杂,本文方法可能不再适用,其惯性支撑能力有待深入研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

鲁宗相, 姜继恒, 乔颖, 等.

新型电力系统广义惯量分析与优化研究综述

[J]. 中国电机工程学报, 2023, 43(5): 1754-1776.