随着新型电力系统的加紧构建,新能源的反调峰、波动性等不利特性日益凸显,威胁电力系统稳定可靠运行.储能因能暂存电能,摆脱了传统发电机组即发即用的束缚,可进行低储高发,有效减少弃风、弃光现象,同时平滑新能源出力,利于电力系统安全[1 -2 ] .因此,大力发展电源侧储能产业已成为全球共识[3 -4 ] .
电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义.
针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失.
目前,针对储能参与电力现货市场日前-实时两阶段、多场景应用的竞标指导策略还未完全形成,但已有相关研究开展.文献[15 ]中提出一种基于风险评估的储能参与日前电能量市场、旋转备用市场以及日内平衡市场的竞标策略,计及市场价格不确定性以及备用需求不确定性,进行报价决策优化.文献[16 -17 ]中研究储能在日前电能量和辅助服务联合市场中的运行情况,并分别采用概率分布、多场景生成等方法模拟实时市场的不确定性影响,优化竞标决策方案.
进一步地,电力市场作为一个规模庞大、各市场主体关系耦合的复杂交易体系,每个个体的决策都会对市场出清产生影响.随着我国引入碳排放权交易,出于发电成本的考量,火电机组在电力现货市场中的售电报价将直接受到影响,因而引起电能量市场出清结果变动.文献[18 ⇓ -20 ]中均基于碳排放和运行经济性考虑,对能源系统进行优化调度研究.但上述研究虽然对碳交易下能源调度做了研究,但未同时计及新能源出力的不确定性.
综上所述,针对缺乏有效的能同时计及新能源出力不确定性及电-碳市场耦合性的电源侧储能参与电力市场多场景运行调度的指导策略这一问题,以风电为例,开展电源侧储能多应用场景协同运行的竞价投标策略研究,细化储能与电力交易中心之间的博弈关系,充分考虑风电出力不确定性和碳排放权交易对储能投标策略的影响,借鉴双层模型优化思路[21 ⇓ -23 ] ,构建电源侧储能参与日前电能量市场、日前备用辅助服务市场以及实时平衡市场竞价投标双层优化模型.借助Karush-Kuhn-Tucker(KKT)条件[24 ] 将上述双层模型转化为单层模型后,进一步对其线性化.最后,基于MATLAB仿真平台求解模型,仿真结果验证了所提策略在市场出清过程中指导储能优化自身决策和提升收益的有效性.
1 电源侧储能参与电力市场主从博弈竞标机制分析
1.1 主从博弈竞标机制
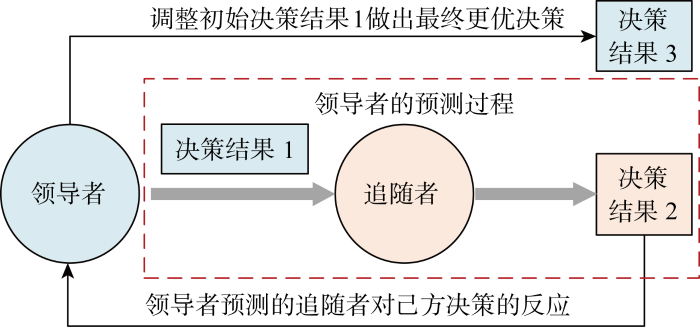
主从博弈是基于博弈论的一种动态博弈,参与博弈的各方在决策时存在先后顺序,即领导与跟随的主从关系[25 -26 ] .先做出决策的主体称为领导者,根据领导者的决策情况后做出决策的主体称为跟随者.主从博弈基本原理如图1 所示.
图1
图1
主从博弈基本原理
Fig.1
Basic principles of master-slave game
在电力市场中,电力交易中心需依托储能等各竞标方的投标数据,组织电力市场有序运行,降低电力交易成本,而关系储能收益的中标量与出清电价又受到电力交易中心的决策影响.因此,考虑到电力市场运行过程中储能与电力交易中心之间存在利益制衡,且各自追求收益最大化的特点与博弈论研究对象特点类似,故可将电源侧储能参与日前及日内电力市场竞标及市场出清过程建模为主从博弈模型.
从电源侧储能角度出发,假设储能具有优先决策权,电力交易中心跟随决策,则电源侧储能作为主从博弈的领导者,在考虑自身运行约束的基础上充分考虑市场对其自身投标计划的反应,提前对可能出现的电力市场出清情况进行预测,优化决策出最佳竞价投标方案.
1.2 考虑碳交易的电力市场机制
碳排放权交易是我国为减少温室气体排放所进行的碳排放配额(carbon emission allowance, CEA)交易机制,主要面向高碳排放的重点单位,如燃煤电厂等,交易对象为CEA.重点单位超排即配额缺额部分可向碳交易市场购买,满足自身排放需求,反之盈余部分也可向碳排放权交易市场出售进行获利.
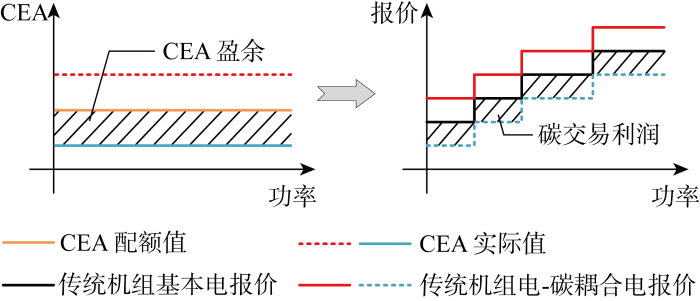
传统机组在碳排放权交易市场购买缺额后,相应单位发电成本增加,因而会选择在电力现货市场提高报价以补贴发电成本.若传统机组碳排放量未超出配额,可出售配额盈余,则单位发电成本降低,传统机组将在电力现货市场降低报价以提高竞标竞争力[27 ] .因此,可根据传统机组在碳交易市场和电力现货市场中的成本转移行为构建传统机组的电-碳耦合报价机制,其形成机理如图2 所示.
图2
图2
考虑碳排放权交易的传统机组电-碳耦合报价机制
Fig.2
Electricity-carbon coupling pricing mechanism for traditional units considering carbon trading
(1) γ g , t e c , o γ e g , t γ c g
(2) γ c g C r g C b g c
式中:γ g , t e c , o g 在电力市场t 时刻的电-碳耦合报价;γ e g , t g 在电力市场t 时刻基本的电报价;γ c g g 的碳交易成本;C r g g 的碳排放量实际值;C b g g 的碳排放量配额值;V c 为碳排放权交易市场中的碳单价.
2 电源侧储能电力市场多场景应用竞标博弈双层优化模型
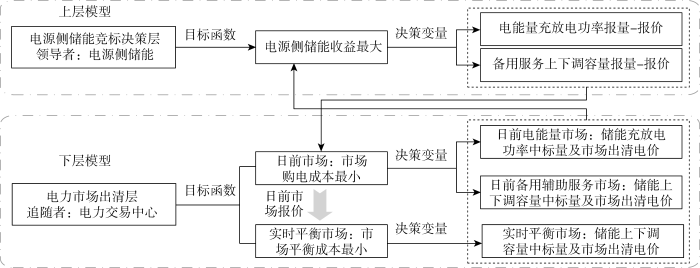
鉴于电源侧储能竞标报价与市场出清电价之间具有相互影响的耦合关系,电源侧储能参与电力市场竞标过程可具体建模为一个决策变量能在上下层间传递的双层模型,以凸显主从博弈过程.上层为电源侧储能竞标决策层,电源侧储能根据自身功率、报价等约束,追求日前与实时平衡市场综合营收最大,规划自己的量-价投标方案并报至下层电力交易中心;下层为电力市场出清层,电力交易中心统筹电源侧储能、传统机组等各交易主体上报的竞标数据,综合考虑新能源预测出力偏差带来的净负荷偏差,以及传统机组碳交易下的电-碳耦合报价,进行日前-实时平衡市场的出清,最后把电源侧储能在各市场中的中标量和市场出清电价返回给电源侧储能决策层,进而储能可优化初始投标策略,得到更优竞标方案.双层优化模型构建如图3 所示.
图3
图3
电源侧储能电力市场多场景应用竞标博弈双层优化模型
Fig.3
Two-level optimization model for participation of power side energy storage in multi-scenario application bidding games in an electricity market
2.1 上层电源侧储能竞标决策模型
(1) 目标函数.储能收益来源包括日前市场的电能量市场、备用辅助服务市场以及实时平衡市场.每个收益来源都基于储能的两种工作模式,即充电和放电.上层模型以储能在3种市场中的综合收益最大为目标建立目标函数
(3) $ \begin{array}{c} \max \sum_{t=1}^{T} \sum_{e=1}^{E}\left\{\left[\lambda_{t}^{\mathrm{e}}\left(P_{e, t}^{\mathrm{dis}}-P_{e, t}^{\mathrm{ch}}\right)\right]+\right. \\ {\left[\lambda_{t}^{\mathrm{up}}\left(S_{e, t}^{\mathrm{ch}, \text { up }}+S_{e, t}^{\text {dis, up }}\right)+\right.} \\ \left.\lambda_{t}^{\text {down }}\left(S_{e, t}^{\mathrm{ch}, \text { down }}+S_{e, t}^{\text {dis.down }}\right)\right]+ \\ \sum_{k=1}^{K} \phi_{k}\left[\lambda_{t, k}^{\mathrm{b}}\left(P_{e, t, k}^{\mathrm{ch}, \text { up }}-P_{e, t, k}^{\mathrm{ch}, \text { down }}\right)+\right. \\ \left.\left.\lambda_{t, k}^{\mathrm{b}}\left(P_{e, t, k}^{\mathrm{dis}, \mathrm{pp}}-P_{e, t, k}^{\text {dis,down }}\right)\right]\right\} \end{array}$
式中:T 、E 分别为储能调度周期和储能数量;K 、ϕk 分别为实时平衡市场中净负荷偏差不确定性场景k 的数量和对应场景出现概率;λ e t t 时刻电能量市场出清价格;λ t u p λ t d o w n t 时刻备用辅助服务市场上调备用和下调备用的市场出清价格;λ b t , k k 下t 时刻实时平衡市场中容量调用出清价格;P e , t c h P e , t d i s e 在电能量市场t 时刻中标的充、放电功率;S e , t c h , u p S e , t c h , d o w n e 在备用辅助服务市场t 时刻中标的充电状态下所提供的上、下调备用容量;S e , t d i s , u p S e , t d i s , d o w n e 在备用辅助服务市场t 时刻中标的放电状态下所提供的上、下调备用容量;P e , t , k c h , u p P e , t , k c h , d o w n e 在场景k 的实时平衡市场t 时刻中标的充电状态下所提供的上、下调容量;P e , t , k d i s , u p P e , t , k d i s , d o w n e 在场景k 的实时平衡市场t 时刻中标的放电状态下所提供的上、下调容量.
(4) U e , t c h U e , t d i s
式中:U e , t c h U e , t d i s e 充、放电动作状态0-1变量.约束式(4)的目的在于禁止储能e 同时进行充、放电.
(5) 0≤ P e , t c h , o U e , t c h P e r a t e d
(6) 0≤ S e , t c h , u p , o U e , t c h S e u p , m a x
(7) 0≤ S e , t c h , d o w n , o U e , t c h S e d o w n , m a x
(8) S e , t c h , d o w n , o P e , t c h , o U e , t c h P e r a t e d
(9) S e , t c h , u p , o P e , t c h , o
(10) 0≤ P e , t d i s , o U e , t d i s P e r a t e d
(11) 0≤ S e , t d i s , u p , o U e , t d i s S e u p , m a x
(12) 0≤ S e , t d i s , d o w n , o U e , t d i s S e d o w n , m a x
(13) S e , t d i s , u p , o P e , t d i s , o U e , t d i s P e r a t e d
(14) S e , t d i s , d o w n , o P e , t d i s , o
式中:P e , t c h , o P e , t d i s , o e 在电能量市场t 时刻申报的充、放电功率;P e r a t e d e 的额定功率;S e , t c h , u p , o S e , t c h , d o w n , o e 在备用辅助服务市场t 时刻申报的充电状态下所能提供的上、下调备用容量;S e , t d i s , u p , o S e , t d i s , d o w n , o e 在备用辅助服务市场t 时刻申报的放电状态下所能提供的上、下调备用容量;S e u p , m a x S e d o w n , m a x e 的最大上、下调节能力.约束式(5)和(10)限制储能申报的充、放电功率不超过额定值.式(6)和(7)限制储能申报的其充电模式下的上、下调备用容量不超过额定调节能力.式(8)表示储能所申报的在t 时刻以充电方式提供下调备用的容量与所申报的t 时刻的充电功率之和应不超过储能额定充电功率.式(9)表示储能申报的在t 时刻以减小充电功率方式提供的上调备用容量不应大于此时储能申报的充电功率.式(11)和(12)限制储能申报的放电模式下的上、下调备用容量不超过其最大调节能力.式(13)表示储能所申报的在t 时刻以放电模式提供上调备用的容量与申报的同一时刻的放电功率之和应不超过储能额定放电功率.式(14)表示储能申报的在t 时刻以减小放电功率方式提供的下调备用容量不应大于此时储能申报的放电功率.
(15) 0≤Ee , t ≤ E e r a t e d
(16) $ \begin{aligned} E_{e, t} & =E_{e}^{\mathrm{init}}-\left[P_{e, t}^{\mathrm{dis}}+\right. \\ & \left.\sum_{k=1}^{K} \phi_{k}\left(P_{e, t, k}^{\mathrm{dis}, \mathrm{pp}}-P_{e, t, k}^{\mathrm{dis}, \mathrm{down}}\right)\right] / \eta_{\mathrm{dis}} \Delta t+ \\ & {\left[P_{e, t}^{\mathrm{ch}}+\sum_{k=1}^{K} \phi_{k}\left(-P_{e, t, k}^{\mathrm{ch}, \mathrm{up}}+P_{e, t, k}^{\mathrm{ch}, \mathrm{down}}\right)\right] \eta_{\mathrm{ch}} \Delta t } \end{aligned}$
(17) E e i n i t e ,24
式中:Ee , t e 在t 时刻的能量值;E e r a t e d E e i n i t e 的额定能量值和在调度周期初始时刻能量值;Ee ,24 为调度周期末储能e 的能量值;η ch 、η dis 分别为储能e 的充、放电效率.约束式(15)表示储能的能量值应在额定范围内.式(16)为储能在任一时刻的能量值.式(17)表示为保证储能调度的循环进行,应当令每个调度周期末尾的能量值回到初始值.
(18) 0≤ γ e , t e , o γ e m a x
(19) 0≤ γ e , t c h , u p , o γ e , t c h , d o w n , o γ e , t d i s , u p , o γ e , t d i s , d o w n , o γ e m a x
式中:γ e , t e , o e 在电能量市场t 时刻申报的充放电价格;γ e , t c h , u p , o γ e , t c h , d o w n , o e 在备用辅助服务市场t 时刻申报的充电状态下的上、下调备用容量价格;γ e , t d i s , u p , o γ e , t d i s , d o w n , o e 在备用辅助服务市场t 时刻申报的放电状态下的上、下调备用容量价格;γ e m a x e 在电力市场的报价上限.约束式(18)和(19)用以限制储能报价非负且在限定范围之内.
2.2 下层电力市场出清模型
2.2.1 日前电力市场出清模型
(20) $ \begin{array}{l} \min \left[\sum_{e=1}^{E}\left(\gamma_{e, t}^{\mathrm{c}, 0} P_{e, t}^{\mathrm{dis}}-\gamma_{e, t}^{\mathrm{c}, 0} P_{e, t}^{\mathrm{ch}}\right)+\sum_{g=1}^{G} \gamma_{k, t}^{\mathrm{ce}, P_{k}} P_{g, t}+\right. \\ \sum_{e=1}^{E}\left(\gamma_{e, t}^{\text {ch, up }, 0} S_{e, t}^{\text {ch, up }}+\gamma_{e, t}^{\text {ch, down }, o} S_{e, t}^{\text {ch,down }}+\right. \\ \left.\gamma_{e, t}^{\text {dis, up }, o} S_{e, t}^{\text {dis. up }}+\gamma_{e, t}^{\text {dis.down } o \mathrm{o}} S_{e, t}^{\text {dis.down }}\right)+ \\ \left.\sum_{g=1}^{G} \gamma_{k, t}^{s, 0}\left(S_{g, t}^{\mathrm{up}}+S_{g, t}^{\text {down }}\right)\right] \end{array}$
式中:G 为参与电力市场的传统机组数量;γ g , t s , o g 在日前备用辅助服务市场t 时刻的报价;Pg , t g 在电能量市场t 时刻的中标电量;S g , t u p S g , t d o w n g 在备用辅助服务市场t 时刻中标的上调备用容量和下调备用容量.目标函数式(20)以市场购电成本最小为目标构建目标函数.考虑到对风电的保障性消纳,将风电作为负的负荷对待,其不参与市场报价,只在约束中对其考量.
(21) ∑ e = 1 E P e , t d i s - P e , t c h ∑ w = 1 W w , t + ∑ g = 1 G g , t = ∑ l = 1 L l , t : λ e t
式中:W 为风电场数量;Pw , t w 在t 时刻的出力;L 为负荷数量;Pl , t l 在t 时刻的功率需求值.
(22) ∑ e = 1 E S e , t c h , u p S e , t d i s , u p ∑ g = 1 G S g , t u p S t u p λ t u p
(23) ∑ e = 1 E S e , t c h , d o w n S e , t d i s , d o w n ∑ g = 1 G S g , t d o w n S t d o w n λ t d o w n
式中:S t u p S t d o w n t 时刻市场上、下调备用容量总需求.
(24) 0≤Pg , t ≤ P o g , t μ _ g , t μ - g , t
(25) 0≤ P e , t c h P e , t c h , o μ _ e , t c h μ - e , t c h
(26) 0≤ P e , t d i s P e , t d i s , o μ _ e , t d i s μ - e , t d i s
式中:P o g , t g 在电能量市场t 时刻的申报功率.约束式(24)~(26)用于限制各市场主体所中标的功率不超过其申报值.
(27) 0≤ S g , t u p S g , t u p , o μ _ g , t u p μ - g , t u p
(28) 0≤ S g , t d o w n S g , t d o w n , o μ _ g , t d o w n μ - g , t d o w n
(29) 0≤ S e , t c h , u p S e , t c h , u p , o μ _ e , t c h , u p μ - e , t c h , u p
(30) 0≤ S e , t c h , d o w n S e , t c h , d o w n , o μ _ e , t c h , d o w n μ - e , t c h , d o w n
(31) 0≤ S e , t d i s , u p S e , t d i s , u p , o μ _ e , t d i s , u p μ - e , t d i s , u p
(32) 0≤ S e , t d i s , d o w n S e , t d i s , d o w n , o μ _ e , t d i s , d o w n μ - e , t d i s , d o w n
式中:S g , t u p , o S g , t d o w n , o g 在备用辅助服务市场t 时刻的上、下调备用容量申报量.约束式(27)~(32)用于限制各市场主体中标量不超过其申报量.
(33) S g , t u p g , t ≤ P o g , t μ g , t u p
(34) S g , t d o w n g , t ≤0: μ g , t d o w n
(35) S e , t d i s , d o w n P e , t d i s μ e , t d i s , d o w n
(36) S e , t c h , u p P e , t c h μ e , t c h , u p
约束式(33)~(36)用于限制传统机组和储能各自的中标能量及其中标容量之间的耦合关系.
2.2.2 日内实时平衡市场出清模型
(37) $ \begin{array}{l} \min \left[\sum_{g=1}^{G} \gamma_{g, t}^{\mathrm{cc}, \mathrm{o}}\left(P_{g, t, k}^{\mathrm{up}}-P_{g, t, k}^{\mathrm{down}}\right)+\right. \\ \sum_{e=1}^{E} \gamma_{e, t}^{\mathrm{c}, \mathrm{o}}\left(P_{e, t, k}^{\mathrm{dis}, \mathrm{pp}}-P_{e, t, k}^{\mathrm{dis} \text { down }}\right)+ \\ \left.\sum_{e=1}^{E} \gamma_{e, t}^{\mathrm{c}, \mathrm{o}}\left(P_{e, t, k}^{\mathrm{ch}, \mathrm{up}}-P_{e, t, k}^{\mathrm{ch}, \mathrm{down}}\right)+\sum_{w=1}^{\mathrm{d}} V_{w, t} l_{w, t, k}\right] \end{array}$
式中:P g , t , k u p P g , t , k d o w n g 在场景k 下t 时刻上、下调节的中标量;Vw , t w 在t 时刻单位弃风量损失;lw , t , k w 在t 时刻的弃风量.目标函数式(37)以电力市场对净负荷偏差的不平衡调节成本最小为目标构建目标函数.
(38) $ \begin{array}{c} \sum_{e=1}^{E}\left(P_{e, t, k}^{\mathrm{ch}, \mathrm{up}}-P_{e, t, k}^{\mathrm{ch}, \mathrm{down}}\right)+\sum_{e=1}^{E}\left(P_{e, t, k}^{\mathrm{dis}, \text { up }}-P_{e, t, k}^{\mathrm{dis}, \text { down }}\right)+ \\ \sum_{g=1}^{G}\left(P_{g, t, k}^{\mathrm{up}}-P_{g, t, k}^{\mathrm{down}}\right)+l_{w, t, k}=P_{t, k}: \lambda_{t, k}^{\mathrm{b}} \end{array}$
式中:Pt , k k 下t 时刻的净负荷偏差.
(39) 0≤ P g , t , k u p S g , t u p ρ _ g , t , k u p ρ - g , t , k u p
(40) 0≤ P g , t , k d o w n S g , t d o w n ρ _ g , t , k d o w n ρ - g , t , k d o w n
约束式(39)和(40)表示为保证实时平衡市场调节容量的可调用,传统机组在实时平衡市场的中标量应小于其在该时刻中标的备用容量.
(41) 0≤ P e , t , k c h , u p S e , t c h , u p ρ _ e , t , k c h , u p ρ - e , t , k c h , u p
(42) 0≤ P e , t , k c h , d o w n S e , t c h , d o w n ρ _ e , t , k c h , d o w n ρ - e , t , k c h , d o w n
(43) 0≤ P e , t , k d i s , u p S e , t d i s , u p ρ _ e , t , k d i s , u p ρ - e , t , k d i s , u p
(44) 0≤ P e , t , k d i s , d o w n S e , t d i s , d o w n ρ _ e , t , k d i s , d o w n ρ - e , t , k d i s , d o w n
约束式(41)~(44)表示为保证实时平衡市场调节容量的可调用,储能的中标量应小于其在该时刻中标的备用容量.
(45) 0≤lw , t , k ≤Pw , t : ρ _ w , t , k ρ - w , t , k
约束式(45)旨在限制风电场w 在t 时刻的弃风量不超过其在该时刻的计划出力.
上述讨论的约束式(21)~(36)、(38)~(45)中各式冒号后的变量均为该约束式所对应的对偶变量.其中,对偶变量μ 、ρ 无实际物理意义.
3 双层优化模型求解
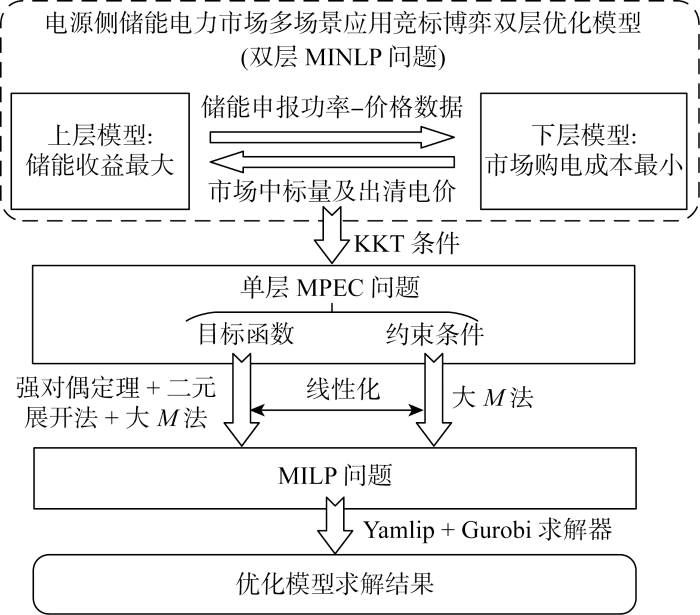
所提电源侧储能电力市场多场景应用竞标博弈双层优化模型为混合整数非线性(mixed integer nonlinear programming, MINLP)问题,直接进行求解具有难度.因此,采用KKT条件先将双层模型转化为单层模型,即变为带均衡约束的数学规划(mathematical programs with equilibrium constraints, MPEC)模型.但因该模型中含有双变量乘积项,属于非线性问题,故再进一步利用大M 法[28 ] 和二元展开法[29 ] 将MPEC模型作线性处理,最终变换成混合整数线性规划(mixed integer linear programming, MILP)模型,此时即可借助Yamlip+Gurobi专业求解器在MATLAB平台上完成模型求解.所提竞标博弈双层优化模型整体求解流程如图4 所示.
图4
图4
竞标博弈双层优化模型求解流程
Fig.4
Solution process of biding game two-level optimization model
以下将对KKT条件转化及线性化处理过程作进一步说明,因下层中实时平衡市场出清模型的处理过程与日前市场出清模型处理过程类似,所以仅以日前电力市场出清模型为例进行说明.
3.1 下层模型的KKT条件
(46) γ e , t e , o λ e t μ - e , t d i s μ _ e , t d i s μ e , t d i s , d o w n
(47) - γ e , t e , o λ e t μ - e , t c h μ _ e , t c h μ e , t c h , u p
(48) γ g , t e c , o λ e t μ - g , t μ _ g , t μ g , t u p μ g , t d o w n
(49) γ e , t d i s , u p , o λ t u p μ - e , t d i s , u p μ _ e , t d i s , u p
(50) γ e , t d i s , d o w n , o λ t d o w n μ - e , t d i s , d o w n μ _ e , t d i s , d o w n μ e , t d i s , d o w n
(51) γ e , t c h , u p , o λ t u p μ - e , t c h , u p μ _ e , t c h , u p μ e , t c h , u p
(52) γ e , t c h , d o w n , o λ t d o w n μ - e , t c h , d o w n μ _ e , t c h , d o w n
(53) γ g , t s , o λ t u p μ - g , t u p μ _ g , t u p μ g , t u p
(54) γ g , t s , o λ t d o w n μ - g , t d o w n μ _ g , t d o w n μ g , t d o w n
式(46)~(54)分别为对原模型中决策变量P e , t d i s P e , t c h Pg , t S e , t d i s , u p S e , t d i s , d o w n S e , t c h , u p S e , t c h , d o w n S g , t u p S g , t d o w n
(55) 0≤Pg , t ⊥ μ _ g , t
(56) 0≤(P o g , t g , t )⊥ μ - g , t
(57) 0≤ S g , t u p μ _ g , t u p
(58) 0≤(S g , t u p , o S g , t u p μ - g , t u p
(59) 0≤ S g , t d o w n μ _ g , t d o w n
(60) 0≤(S g , t d o w n , o S g , t d o w n μ - g , t d o w n
(61) 0≤(P o g , t g , t - S g , t u p μ g , t u p
(62) 0≤(Pg , t - S g , t d o w n μ g , t d o w n
(63) 0≤ P e , t c h μ _ e , t c h
(64) 0≤(P e , t c h , o P e , t c h μ - e , t c h
(65) 0≤ P e , t d i s μ _ e , t d i s
(66) 0≤(P e , t d i s , o P e , t d i s μ - e , t d i s
(67) 0≤ S e , t c h , u p μ _ e , t c h , u p
(68) 0≤(S e , t c h , u p , o S e , t c h , u p μ - e , t c h , u p
(69) 0≤ S e , t c h , d o w n μ _ e , t c h , d o w n
(70) 0≤(S e , t c h , d o w n , o S e , t c h , d o w n μ - e , t c h , d o w n
(71) 0≤ S e , t d i s , u p μ _ e , t d i s , u p
(72) 0≤(S e , t d i s , u p , o S e , t d i s , u p μ - e , t d i s , u p
(73) 0≤ S e , t d i s , d o w n μ _ e , t d i s , d o w n
(74) 0≤(S e , t d i s , d o w n , o S e , t d i s , d o w n μ - e , t d i s , d o w n
(75) 0≤(P e , t c h S e , t c h , u p μ e , t c h , u p
(76) 0≤(P e , t d i s S e , t d i s , d o w n μ e , t d i s , d o w n
式(55)~(76)为利用KKT理论推导的式(24)~(36)的互补松弛条件.其中,“⊥”表示其左右侧两个非负值至多有一个可以严格大于0.
经过上述KKT条件数学变换,下层模型已转化为上层模型的约束形式,即原双层模型已变换为单层模型.
3.2 模型线性化
(1) 互补松弛条件的线性化.因互补松弛约束式(55)~(76)中存在决策变量与对偶变量的乘积项,故采用大M 法对其进行精确化线性处理,在此仅以对式(55)线性化为例进行说明,结果如式下:
(77) 0≤Pg , t Mu
(78) 0≤ μ _ g , t
式中:M 为一个足够大的正数;u 为0-1二进制辅助变量.
(2) 目标函数的线性化.因单层化后的MPEC模型目标函数式(3)中存在大量双变量乘积的非线性项,所以采用强对偶定理对其进行处理
(79) $ \begin{array}{l} \max \sum_{t=1}^{T} \sum_{e=1}^{E}\left\{\lambda_{t}^{\mathrm{e}}\left(P_{e, t}^{\mathrm{dis}}-P_{e, t}^{\mathrm{ch}}\right)+\right. \\ {\left[\lambda_{t}^{\mathrm{up}}\left(S_{e, t}^{\mathrm{ch}, \mathrm{up}}+S_{e, t}^{\mathrm{dis}, \text { up }}\right)+\right.} \\ \left.\lambda_{t}^{\text {down }}\left(S_{e, t}^{\text {ch,down }}+S_{e, t}^{\text {dis.down }}\right)\right]+ \\ \sum_{k=1}^{K} \phi_{k}\left[\lambda_{t, k}^{\mathrm{b}}\left(P_{e, t, k}^{\mathrm{ch}, \text { up }}-P_{e, t, k}^{\mathrm{ch}, \text { down }}\right)+\right. \\ \left.\left.\lambda_{t, k}^{\mathrm{b}}\left(P_{e, t, k}^{\mathrm{dis}, \text { up }}-P_{e, t, k}^{\text {dis, down }}\right)\right]\right\}= \\ \max \left[-\sum_{g=1}^{G} \gamma_{g, t}^{\mathrm{cc}, \mathrm{o}} P_{g, t}-\sum_{g=1}^{G} \gamma_{g, t}^{s, 0}\left(S_{g, t}^{\mathrm{up}}+S_{g, t}^{\mathrm{down}}\right)+\right. \\ \sum_{g=1}^{G} \bar{\mu}_{g, t} P_{g, t}^{\mathrm{o}}-\sum_{\mathrm{g}=1}^{G} \bar{\mu}_{g, t}^{\mathrm{up}} S_{g, t}^{\mathrm{up}, \mathrm{o}}- \\ \sum_{g=1}^{G} \bar{\mu}_{g, t}^{\text {down }} S_{g, t}^{\text {down }, o}-\sum_{g=1}^{G} \mu_{g, t}^{\text {up }} P_{g, t}^{o}+ \\ \lambda_{t}^{e}\left(P_{g, t}-P_{w, t}\right)+\left(\lambda_{t}^{\mathrm{up}} S_{t}^{\mathrm{up}}+\lambda_{t}^{\mathrm{down}} S_{t}^{\mathrm{down}}\right)- \\ \sum_{w=1}^{W} V_{w, t} l_{w, t, k}-\sum_{g=1}^{G} \gamma_{g, t}^{\mathrm{e}, \mathrm{o}}\left(P_{g, t, k}^{\mathrm{up}}-P_{g, t, k}^{\mathrm{down}}\right)- \\ \sum_{w=1}^{W} \bar{\rho}_{w, t, k} P_{w, t}-\sum_{g=1}^{G}\left(\bar{\rho}_{g, t, k}^{\text {up }} S_{g, t}^{\text {up }}+\right. \\ \left.\left.\bar{\rho}_{g, t, k}^{\text {down }} S_{g, t}^{\text {down }}\right)+\lambda_{t, k}^{b} P_{t, k}\right] \end{array}$
然而,观察式(79)可知,其中仍存在双变量乘积项ρ - g , t . k u p S g , t u p ρ - g , t . k d o w n S g , t d o w n . 接下来以线性化ρ - g , t . k u p S g , t u p
决策变量S g , t u p S g , t , m i n u p S g , t , m a x u p u g , t u p
(80) S g , t u p S g , t , m i n u p S g , t u p ∑ i = 1 I i -1 u g , t u p
(81) Δ S g , t u p S g , t , m a x u p S g , t , m i n u p I
式中:ΔS g , t u p I 为展开项数,决定线性化的精度,以增加计算量及计算时间为代价,求解精度随着I 的增大而提升.
(82) ρ - g , t . k u p S g , t u p ρ - g , t . k u p S g , t , m i n u p ρ - g , t . k u p S g , t u p ∑ i = 1 I i -1 u g , t u p
定义变量Xρu =ρ - g , t . k u p u g , t u p
(83) ρ - g , t . k u p S g , t u p ρ - g , t . k u p S g , t , m i n u p S g , t u p ∑ i = 1 I i -1 Xρu
Xρu =ρ - g , t . k u p u g , t u p M 法进行线性化表述为
(84) 0≤ ρ - g , t . k u p ρu ≤M u g , t u p
(85) 0≤Xρu ≤M(1- u g , t u p
4 算例仿真及分析
4.1 算例设置
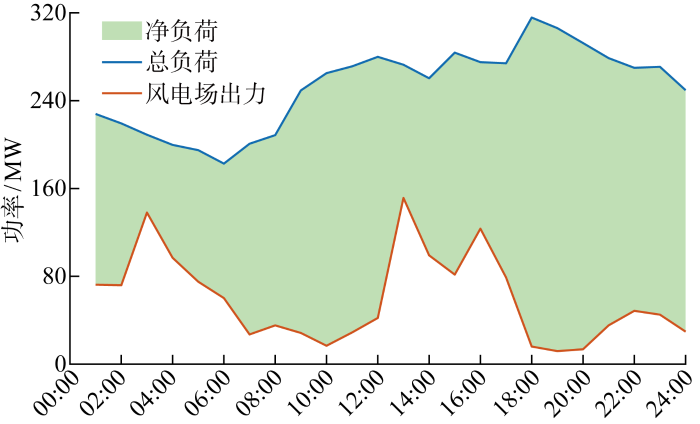
为验证所提模型的有效性,设置电力系统仿真场景进行仿真验证.系统中包含1个装机容量为200 MW的风电场W1,1个储能电站E1,5台传统机组G1~G5.其中,系统负荷需求及风电场预测出力如图5 所示.图5 中阴影区域为系统净负荷,即系统总负荷与风电场出力的差值.同时净负荷偏差考虑全部由风电场出力不确定性引起的预测偏差产生,系统通过调用日前备用辅助服务市场中标的储能及传统机组来对净负荷偏差进行消除,满足实时潮流平衡.
图5
图5
系统负荷需求及风电预测出力
Fig.5
System load demand and predicted wind power output
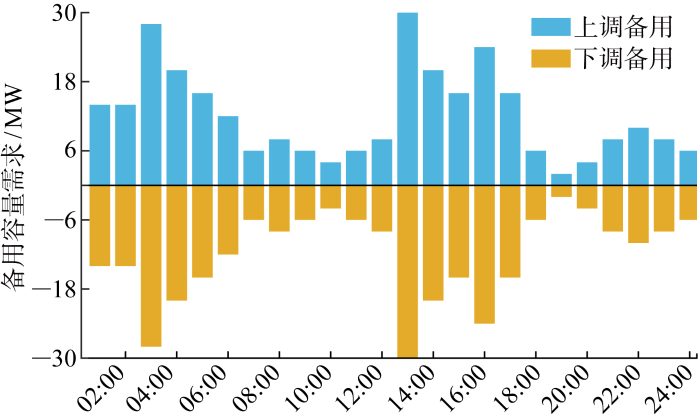
储能规模设置为40 MW/160 MW·h,最大上调备用功率S e u p , m a x S e d o w n , m a x P ch 和放电效率P dis 均为0.95,初始荷电状态E e i n i t . 2E e r a t e d . 参照文献[27 ],传统机组G1~G5的CEA配额值均为0.877 t/(MW·h),其实际CEA分别设为1.087、0.727、0.887、0.861、1.083 t/(MW·h),碳交易单价定为14 美元/t,传统机组其余参数设置如表1 所示.系统日前备用辅助服务市场上调备用和下调备用需求如图6 所示.
图6
图6
系统日前市场总备用容量需求
Fig.6
Total reserve capacity demand of the system in current market
4.2 仿真结果及分析
(1) 各竞标主体市场收益及中标总体情况.各竞标主体在电能量市场、备用辅助服务市场及实时平衡市场的总体收益情况如表2 所示.由表可见,电源侧储能与传统机组的主要收益来源均是电能量收益,这也从侧面体现电源侧发电机组作为能量供应者的基本角色定位.此外,电源侧储能综合市场与自身情况进行策略性竞标,因而在各市场中均有中标,并获得可观收益.
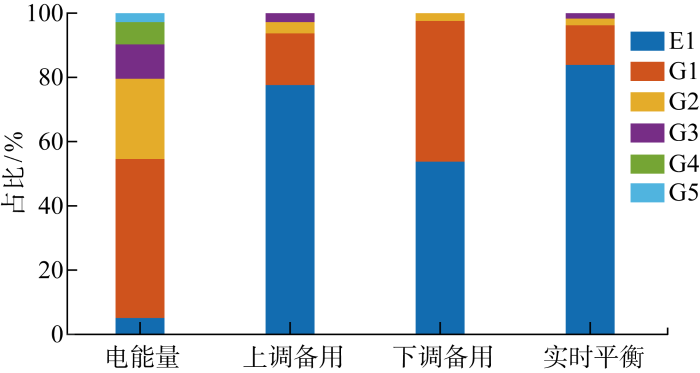
各竞标主体总体中标情况如图7 所示.由图可见,电能量市场中传统机组的中标量占绝大多数,与传统机组仍是电能量提供的主力实际情况相吻合.而在备用辅助服务市场中,储能中标量占比更大,这主要得益于储能可以通过改变自身充放电状态,灵活提供上下调备用,因而能够在市场竞争中占据优势.综合表2 与图7 可知,各主体在市场中的收益情况与其中标量表现一致,在市场统一出清下,中标量大的主体收益也更大.对于未竞标成功的机组则市场收益为0,如日前备用辅助服务市场中的机组G4、G5,结合市场出清规则来看,主要源于其高报价难以被优先安排出清,这也进一步凸显出市场主体应注重降本增效,从而可在低生产成本下得以进行较低报价,以提高中标机会.
图7
图7
各竞标主体市场总体中标情况
Fig.7
Overall winning situation of each bidding entity in electricity market
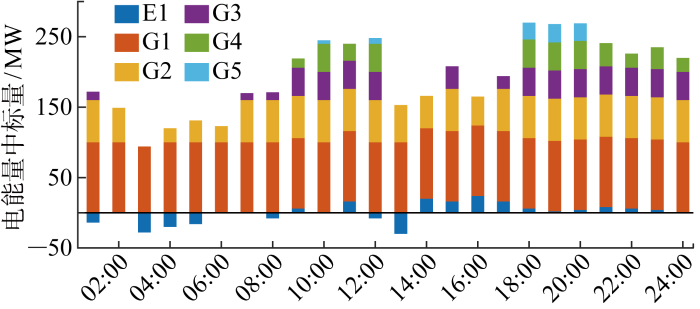
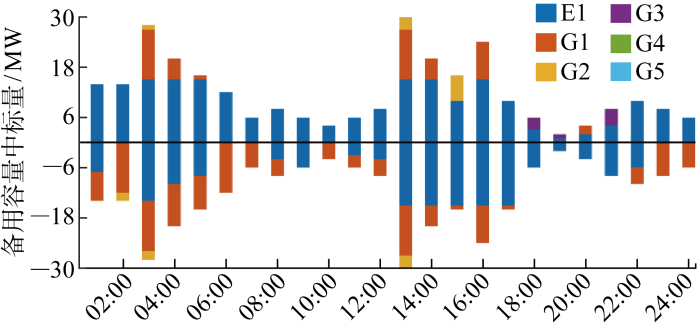
(2) 各竞标主体各时段中标情况及市场出清电价.图8 ~10 分别展示各竞标主体在不同市场各时段具体中标情况.由图8 可更清晰地看出,储能在电能量市场各时段中标量占比较少,传统机组G1的中标量则在所有竞价主体中占比最大.市场呈现此种出清表现,一方面与G1机组报价较低,得以优先出清,且其中标量已能覆盖系统的大部分能量需求有关;另一方面也源于储能容量有限且其需要对自身能量及功率进行全局规划.此外,由图8 还可看出储能能够在电能量市场适时切换放能、用能角色,以对能量进行调配,如 3:00—5:00、14:00—17:00.
图8
图8
各竞标主体电能量市场中标情况
Fig.8
Winning situation of each bidding entity in electric energy market
图9
图9
各竞标主体备用辅助服务市场中标情况
Fig.9
Winning situation of each bidding entity in reserve ancillary service market
图10
图10
各竞标主体实时平衡市场中标情况
Fig.10
Winning situation of each bidding entity in real-time balanced market
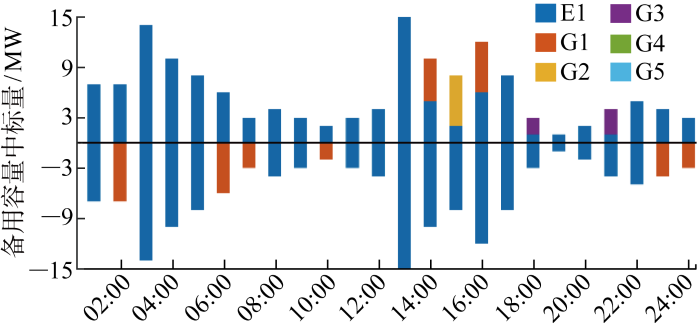
图9 和图10 则进一步体现在备用辅助服务市场中可灵活切换充放电状态的储能是调节主力.此外,对比图9 及和图10 还可看出,在备用辅助服务市场中标的备用容量未必在实时平衡市场会得到全部调用,具体调用情况取决于电力系统在实时运行过程中的实际需求.
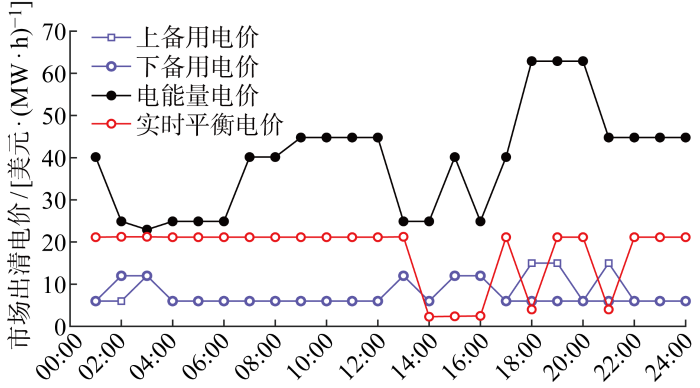
图11 所示为各时段电力市场出清电价,可看出在电力负荷需求较高、供电紧张的 9:00—12:00、18:00—20:00 时段,电能量市场出清电价也较高,充分体现供求关系下电力的商品价值属性.
图11
图11
电力市场出清电价
Fig.11
Electricity market clearing price
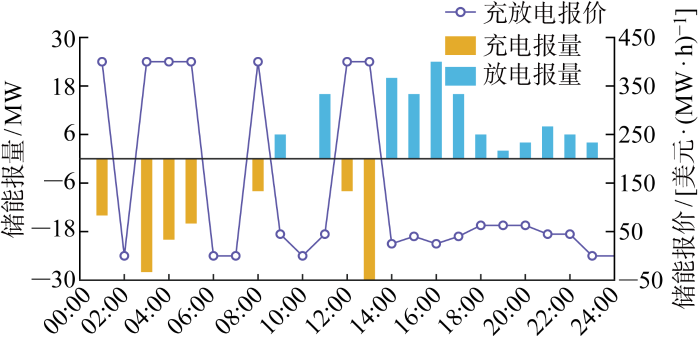
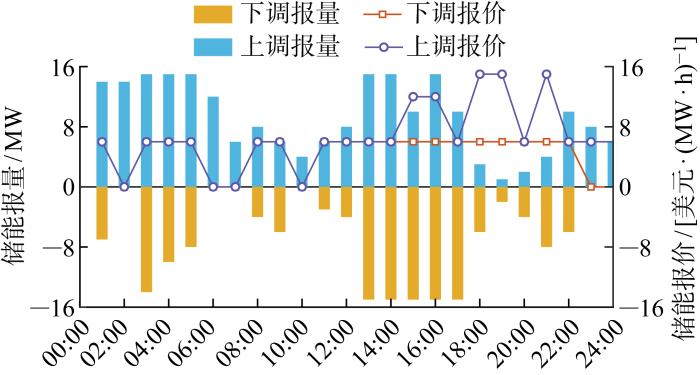
(3) 电源侧储能竞标策略.图12 和图13 所示分别为电源侧储能在电能量市场和备用辅助服务市场中的竞标策略,即时序耦合下的功率报量和能量报价.其中,由图12 可以看出,储能中标充电功率时,如 1:00、3:00—5:00、8:00、12:00—13:00,会以一个极高值进行报价,在市场对购电方报价由高到低排序作为优先出清顺序的机制下,该策略无疑可以提高充电功率中标机会.
图12
图12
电源侧储能电能量市场竞标策略
Fig.12
Bidding strategy of power side energy storage in electric energy market
图13
图13
电源侧储能备用辅助服务市场竞标策略
Fig.13
Bidding strategy of power side energy storage in reserve ancillary service market
4.3 碳单价参数灵敏度分析
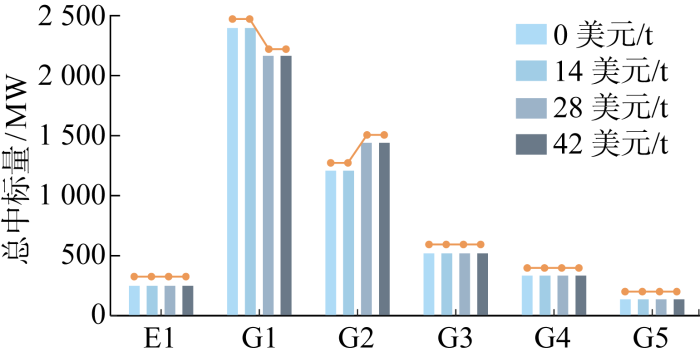
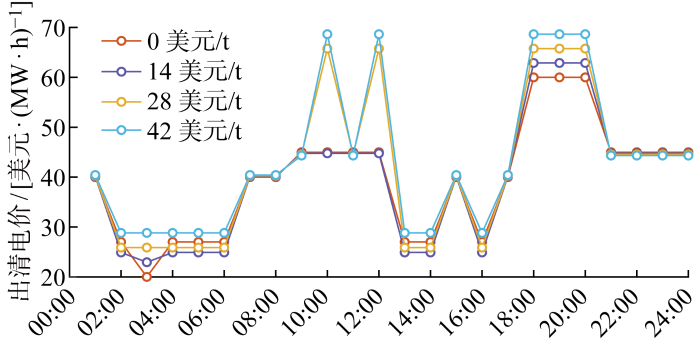
碳交易成本主要附加在传统机组电能量市场报价上,故在此分别设置碳单价为0、14、28、42 美元/t,重点研究碳单价改变引起的电能量市场运行结果变化.不同碳单价下各机组中标量及电能量市场出清电价分别如图14 和图15 所示.
图14
图14
不同碳单价下各机组电能量中标量
Fig.14
Winning bid of electric energy for each unit at different carbon unit prices
图15
图15
不同碳单价下电能量市场出清电价
Fig.15
Clearing prices in the electricity market at different carbon unit prices
随着碳单价的增加,传统机组的报价将整体发生变化,因而不同碳单价下节点边际电价呈现相近的变化趋势,电源侧储能的总中标量趋向相同,如图14 所示.但随着碳单价增加,G1中标量逐渐减小,G2中标量逐渐增加,高碳排放量的G1出力逐渐向较低碳排放量的G2发生转移;其原因是高碳排放机组报价G1随碳单价的增加而增大,而G2由于其碳排放实际值低于配额值,其报价与碳单价变化呈负相关,且当碳单价升高到一定范围,G2报价会低于G1报价,此时G2取代G1,被优先出清.机组电-碳耦合报价大小关系无改变情况下,其出清顺序也不改变.G3~G5中标总量无明显变化主要源于所测试的碳单价还未增大到一定程度,以至于其引起的附加碳交易成本还未覆盖甚至超过G3~G5之间的电能量报价差,故在负荷需求及报价大小关系不变下,G3~G5的中标总量基本不变.
由图15 可得出,当碳单价不断升高时,传统机组报价相应升高,引起市场出清电价随之升高.因此,电源侧储能在进行投标决策时应充分了解相关市场机制,紧跟市场动态,有助于己方进行更加合理且更高收益的策略竞标.
5 结论
通过分析电力市场交易机制,从电源侧储能角度出发,建立计及风电出力不确定性及碳交易的储能参与电力市场多场景应用竞标博弈双层优化模型,指导优化电源侧储能竞标策略,提升其多场景应用综合经济效益.同时,进行算例仿真并得到以下结论.
(1) 基于博弈关系所构建的双层优化模型,借助数学变换,可将复杂的多目标、非线性市场竞标优化问题转化为单一目标的线性优化求解问题,有效反映出实际出清过程中电源侧储能与市场的博弈关系.
(2) 所提模型能以电源侧储能综合收益最大为目标,兼顾社会购电成本及风电出力不确定性,完成对电源侧储能在电力市场的竞标策略优化及市场模拟出清,实现多方主体互利共赢.
(3) 因充当的市场角色不同,电源侧储能在不同市场中的竞价策略存在差异,在电能量市场中充当用能角色时会以极高报价提高充电中标概率,而充当电源角色进行放电或在备用辅助服务市场发挥调节作用时,其报价多与优化模拟的市场出清电价相近.
(4) 计及碳交易后,碳单价的改变对电源侧储能在电能量市场中的中标量无明显影响,但会使得传统机组的中标量在不同碳排放强度机组间发生转移.同时,碳单价升高会引起电能量市场出清电价升高,进而使得电源侧储能在电能量市场的中标电价同步升高.
本文基于我国负荷侧报量不报价的现行电力市场规则,在电源侧储能参与电力市场竞标博弈建模中对负荷侧的投标方式同样采用报量不报价模式.然而,随着电力市场改革的深入推进,为充分发挥市场价格发现及调控作用,势必会向负荷侧报量报价转变.因此,下一步将考虑负荷侧报量报价的竞标机制,对目前的优化模型加以改进.
参考文献
View Option
[1]
黄强 , 郭怿 , 江建华 , 等 . “双碳” 目标下中国清洁电力发展路径
[J]. 上海交通大学学报 , 2021 , 55 (12 ): 1499 -1509 .
DOI:10.16183/j.cnki.jsjtu.2021.272
[本文引用: 1]
目前,第三次能源革命已经开始,为了减少碳排放,发达国家先后制定了清洁能源发展战略,并公布了放弃火电、核电的时间表.与此同时,中国也向世界作出承诺:2030年前碳排放达峰,2060年实现碳中和.因此,在“双碳”目标下,研究清洁电力发展路径具有重要意义.分析了中国水、风、光等清洁能源储量及其特征,预测了中长期电力需求,依据电力电量平衡原理,估算了2030和2050规划水平年电力系统结构组成,并分析了未来CO<sub>2</sub>排放趋势,提出了未来中国清洁电力的发展对策与建议.结果表明:预计2027年中国电力系统将实现“碳达峰”;2030年中国清洁电力发电量将超过总发电量的50%;2050年火电、核电将被水、风、光等清洁电力全部取代,电力行业将实现CO<sub>2</sub>的“零排放”,基本全面实现电力系统的绿色转型,以响应国家的“双碳”目标.
HUANG Qiang GUO Yi JIANG Jianhua et al Development pathway of China’s clean electricity under carbon peaking and carbon neutrality goals
[J]. Journal of Shanghai Jiao Tong University , 2021 , 55 (12 ): 1499 -1509 .
[本文引用: 1]
[2]
SHI J LEE W J LIU X F Generation scheduling optimization of wind-energy storage system based on wind power output fluctuation features
[C]// 2017 IEEE/IAS 53rd Industrial and Commercial Power Systems Technical Conference. Niagara Falls , Canada : IEEE , 2017 : 1 -7 .
[本文引用: 1]
[3]
SIOSHANSI R DENHOLM P ARTEAGA J et al Energy-storage modeling: State-of-the-art and future research directions
[J]. IEEE Transactions on Power Systems , 2022 , 37 (2 ): 860 -875 .
[本文引用: 1]
[4]
李姚旺 , 张宁 , 张世旭 , 等 . 面向电力系统的多能源云储能模式:基本概念与研究展望
[J]. 中国电机工程学报 , 2023 , 43 (6 ): 2179 -2190 .
[本文引用: 1]
LI Yaowang ZHANG Ning ZHANG Shixu et al Multi-energy cloud energy storage for power systems: Basic concepts and research prospects
[J]. Proceedings of the CSEE , 2023 , 43 (6 ): 2179 -2190 .
[本文引用: 1]
[5]
陈国平 , 梁志峰 , 董昱 . 基于能源转型的中国特色电力市场建设的分析与思考
[J]. 中国电机工程学报 , 2020 , 40 (2 ): 369 -379 .
[本文引用: 1]
CHEN Guoping LIANG Zhifeng DONG Yu Analysis and reflection on the marketization construction of electric power with Chinese characteristics based on energy transformation
[J]. Proceedings of the CSEE , 2020 , 40 (2 ): 369 -379 .
[本文引用: 1]
[6]
陈启鑫 , 房曦晨 , 郭鸿业 , 等 . 储能参与电力市场机制:现状与展望
[J]. 电力系统自动化 , 2021 , 45 (16 ): 14 -28 .
[本文引用: 1]
CHEN Qixin FANG Xichen GUO Hongye et al Participation mechanism of energy storage in electricity market: Status quo and prospect
[J]. Automation of Electric Power Systems , 2021 , 45 (16 ): 14 -28 .
[本文引用: 1]
[7]
闫斯哲 , 王维庆 , 李笑竹 , 等 . 储能-机组联合调频的动态经济环境跨区灵活性鲁棒优化调度
[J]. 电力系统自动化 , 2022 , 46 (9 ): 61 -70 .
[本文引用: 1]
YAN Sizhe WANG Weiqing LI Xiaozhu et al Cross-regional flexible robust optimal scheduling in dynamic economic environment with joint frequency regulation of energy storage and units
[J]. Automation of Electric Power Systems , 2022 , 46 (9 ): 61 -70 .
[本文引用: 1]
[8]
ZHOU B FANG J K AI X M et al Storage right-based hybrid discrete-time and continuous-time flexibility trading between energy storage station and renewable power plants
[J]. IEEE Transactions on Sustainable Energy , 2023 , 14 (1 ): 465 -481 .
[本文引用: 1]
[9]
ABDELTAWAB H MOHAMED Y A R I Energy storage planning for profitability maximization by power trading and ancillary services participation
[J]. IEEE Systems Journal , 2022 , 16 (2 ): 1909 -1920 .
[本文引用: 1]
[10]
尚楠 , 陈政 , 冷媛 . 电碳市场背景下典型环境权益产品衔接互认机制及关键技术
[J]. 中国电机工程学报 , 2024 , 44 (7 ): 2558 -2577 .
[本文引用: 1]
SHANG Nan CHEN Zheng LENG Yuan Mutual recognition mechanism and key technologies of typical environmental interest products in power and carbon markets
[J]. Proceedings of the CSEE , 2024 , 44 (7 ): 2558 -2577 .
[本文引用: 1]
[11]
张巍 , 缪辉 . 基于云储能租赁服务的风储参与能量-调频市场竞价策略研究
[J]. 电网技术 , 2021 , 45 (10 ): 3840 -3850 .
[本文引用: 1]
ZHANG Wei MIAO Hui Bidding strategies of wind power and energy storage participating in energy and frequency regulation market based on cloud energy storage leasing services
[J]. Power System Technology , 2021 , 45 (10 ): 3840 -3850 .
[本文引用: 1]
[12]
孙鑫 , 魏文荣 , 李琼林 , 等 . 计及不确定性的风储联合系统多时间尺度市场参与策略
[J]. 电力自动化设备 , 2024 , 44 (2 ): 18 -25 .
[本文引用: 1]
SUN Xin WEI Wenrong LI Qionglin et al Multi-time scale market participation strategy of wind-energy storage combined system considering uncertainty
[J]. Electric Power Automation Equipment , 2024 , 44 (2 ): 18 -25 .
[本文引用: 1]
[13]
王霞 . 含储能的能量与一次调频服务市场联合优化出清研究 [D]. 武汉 : 武汉大学 , 2021 .
[本文引用: 1]
WANG Xia Research on the joint optimization clearing for eneregy and primary frequency regulation markets incorporating energy storage [D]. Wuhan : Wuhan University , 2021 .
[本文引用: 1]
[14]
葛晓琳 , 凡婉秋 , 符杨 , 等 . 基于改进柔性策略评价的风火储多主体博弈电能-调频市场联合竞价模型
[J]. 电网技术 , 2023 , 47 (5 ): 1920 -1933 .
[本文引用: 1]
GE Xiaolin FAN Wanqiu FU Yang et al Joint bidding model of electricity and frequency regulation market with wind fire storage multi-agent games based on improved soft actor-critic
[J]. Power System Technology , 2023 , 47 (5 ): 1920 -1933 .
[本文引用: 1]
[15]
KAZEMI M ZAREIPOUR H AMJADY N et al Operation scheduling of battery storage systems in joint energy and ancillary services markets
[J]. IEEE Transactions on Sustainable Energy , 2017 , 8 (4 ): 1726 -1735 .
[本文引用: 1]
[16]
MORENO R MOREIRA R STRBAC G A MILP model for optimising multi-service portfolios of distributed energy storage
[J]. Applied Energy , 2015 , 137 : 554 -566 .
[本文引用: 1]
[17]
AKHAVAN-HEJAZI H MOHSENIAN-RAD H Optimal operation of independent storage systems in energy and reserve markets with high wind penetration
[J]. IEEE Transactions on Smart Grid , 2014 , 5 (2 ): 1088 -1097 .
[本文引用: 1]
[18]
车泉辉 , 吴耀武 , 祝志刚 , 等 . 基于碳交易的含大规模光伏发电系统复合储能优化调度
[J]. 电力系统自动化 , 2019 , 43 (3 ): 76 -82 .
[本文引用: 1]
CHE Quanhui WU Yaowu ZHU Zhigang et al Carbon trading based optimal scheduling of hybrid energy storage system in power systems with large-scale photovoltaic power generation
[J]. Automation of Electric Power Systems , 2019 , 43 (3 ): 76 -82 .
[本文引用: 1]
[19]
YAN N MA G C LI X J et al Low-carbon economic dispatch method for integrated energy system considering seasonal carbon flow dynamic balance
[J]. IEEE Transactions on Sustainable Energy , 2023 , 14 (1 ): 576 -586 .
[本文引用: 1]
[20]
MU C G DING T ZHU S Y et al A decentralized market model for a microgrid with carbon emission rights
[J]. IEEE Transactions on Smart Grid , 2023 , 14 (2 ): 1388 -1402 .
[本文引用: 1]
[21]
张钧钊 , 姜欣 , 段世杰 , 等 . 虚拟电厂参与电-碳联合市场运行的竞价策略研究
[J]. 电力系统保护与控制 , 2023 , 51 (11 ): 108 -118 .
[本文引用: 1]
ZHANG Junzhao JIANG Xin DUAN Shijie et al Bidding strategy for a virtual power plant to participate in the power-carbon joint market
[J]. Power System Protection & Control , 2023 , 51 (11 ): 108 -118 .
[本文引用: 1]
[22]
马云聪 , 武传涛 , 林湘宁 , 等 . 计及碳排放权交易的光热电站市场竞价策略研究
[J]. 电力系统保护与控制 , 2023 , 51 (4 ): 82 -92 .
[本文引用: 1]
MA Yuncong WU Chuantao LIN Xiangning et al Bidding strategy for a concentrated solar power plant participating in the electricity market with the background of carbon trading
[J]. Power System Protection & Control , 2023 , 51 (4 ): 82 -92 .
[本文引用: 1]
[23]
米阳 , 赵海辉 , 付起欣 , 等 . 考虑风光不确定与碳交易的区域综合能源系统双层博弈优化运行
[J]. 电网技术 , 2023 , 47 (6 ): 2174 -2188 .
[本文引用: 1]
MI Yang ZHAO Haihui FU Qixin et al Two-level game optimal operation of regional integrated energy system considering wind and solar uncertainty and carbon trading
[J]. Power System Technology , 2023 , 47 (6 ): 2174 -2188 .
[本文引用: 1]
[24]
RUIZ C CONEJO A J Pool strategy of a producer with endogenous formation of locational marginal prices
[J]. IEEE Transactions on Power Systems , 2009 , 24 (4 ): 1855 -1866 .
[本文引用: 1]
[25]
潘虹锦 , 高红均 , 杨艳红 , 等 . 基于主从博弈的售电商多元零售套餐设计与多级市场购电策略
[J]. 中国电机工程学报 , 2022 , 42 (13 ): 4785 -4800 .
[本文引用: 1]
PAN Hongjin GAO Hongjun YANG Yanhong et al Multi-type retail packages design and multi-level market power purchase strategy for electricity retailers based on master-slave game
[J]. Proceedings of the CSEE , 2022 , 42 (13 ): 4785 -4800 .
[本文引用: 1]
[26]
姜欣 , 刘萌 , 王天梁 , 等 . 电网侧储能电站参与现货联合市场的竞价策略
[J]. 电网技术 , 2021 , 45 (9 ): 3398 -3408 .
[本文引用: 1]
JIANG Xin LIU Meng WANG Tianliang et al Bidding strategy for grid-side energy storage power stations to participate in the spot joint market
[J]. Power System Technology , 2021 , 45 (9 ): 3398 -3408 .
[本文引用: 1]
[27]
王凯 , 延肖何 , 蒋凯 , 等 . 考虑碳交易的风光储场站参与电力现货市场报价策略与调控方法
[J]. 中国电机工程学报 , 2023 , 43 (18 ): 7091 -7103 .
[本文引用: 2]
WANG Kai YAN Xiaohe JIANG Kai et al Bidding strategy and regulation method for the unified wind/photovoltaic/energy storage power stations in electricity spot market considering carbon trading
[J]. Proceedings of the CSEE , 2023 , 43 (18 ): 7091 -7103 .
[本文引用: 2]
[28]
NASROLAHPOUR E KAZEMPOUR J ZAREIPOUR H et al A bilevel model for participation of a storage system in energy and reserve markets
[J]. IEEE Transactions on Sustainable Energy , 2018 , 9 (2 ): 582 -598 .
[本文引用: 1]
[29]
TOUBEAU J F BOTTIEAU J DE GRÈVE Z et al Data-driven scheduling of energy storage in day-ahead energy and reserve markets with probabilistic guarantees on real-time delivery
[J]. IEEE Transactions on Power Systems , 2021 , 36 (4 ): 2815 -2828 .
[本文引用: 1]
“双碳” 目标下中国清洁电力发展路径
1
2021
... 随着新型电力系统的加紧构建,新能源的反调峰、波动性等不利特性日益凸显,威胁电力系统稳定可靠运行.储能因能暂存电能,摆脱了传统发电机组即发即用的束缚,可进行低储高发,有效减少弃风、弃光现象,同时平滑新能源出力,利于电力系统安全[1 -2 ] .因此,大力发展电源侧储能产业已成为全球共识[3 -4 ] . ...
Development pathway of China’s clean electricity under carbon peaking and carbon neutrality goals
1
2021
... 随着新型电力系统的加紧构建,新能源的反调峰、波动性等不利特性日益凸显,威胁电力系统稳定可靠运行.储能因能暂存电能,摆脱了传统发电机组即发即用的束缚,可进行低储高发,有效减少弃风、弃光现象,同时平滑新能源出力,利于电力系统安全[1 -2 ] .因此,大力发展电源侧储能产业已成为全球共识[3 -4 ] . ...
Generation scheduling optimization of wind-energy storage system based on wind power output fluctuation features
1
2017
... 随着新型电力系统的加紧构建,新能源的反调峰、波动性等不利特性日益凸显,威胁电力系统稳定可靠运行.储能因能暂存电能,摆脱了传统发电机组即发即用的束缚,可进行低储高发,有效减少弃风、弃光现象,同时平滑新能源出力,利于电力系统安全[1 -2 ] .因此,大力发展电源侧储能产业已成为全球共识[3 -4 ] . ...
Energy-storage modeling: State-of-the-art and future research directions
1
2022
... 随着新型电力系统的加紧构建,新能源的反调峰、波动性等不利特性日益凸显,威胁电力系统稳定可靠运行.储能因能暂存电能,摆脱了传统发电机组即发即用的束缚,可进行低储高发,有效减少弃风、弃光现象,同时平滑新能源出力,利于电力系统安全[1 -2 ] .因此,大力发展电源侧储能产业已成为全球共识[3 -4 ] . ...
面向电力系统的多能源云储能模式:基本概念与研究展望
1
2023
... 随着新型电力系统的加紧构建,新能源的反调峰、波动性等不利特性日益凸显,威胁电力系统稳定可靠运行.储能因能暂存电能,摆脱了传统发电机组即发即用的束缚,可进行低储高发,有效减少弃风、弃光现象,同时平滑新能源出力,利于电力系统安全[1 -2 ] .因此,大力发展电源侧储能产业已成为全球共识[3 -4 ] . ...
Multi-energy cloud energy storage for power systems: Basic concepts and research prospects
1
2023
... 随着新型电力系统的加紧构建,新能源的反调峰、波动性等不利特性日益凸显,威胁电力系统稳定可靠运行.储能因能暂存电能,摆脱了传统发电机组即发即用的束缚,可进行低储高发,有效减少弃风、弃光现象,同时平滑新能源出力,利于电力系统安全[1 -2 ] .因此,大力发展电源侧储能产业已成为全球共识[3 -4 ] . ...
基于能源转型的中国特色电力市场建设的分析与思考
1
2020
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
Analysis and reflection on the marketization construction of electric power with Chinese characteristics based on energy transformation
1
2020
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
储能参与电力市场机制:现状与展望
1
2021
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
Participation mechanism of energy storage in electricity market: Status quo and prospect
1
2021
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
储能-机组联合调频的动态经济环境跨区灵活性鲁棒优化调度
1
2022
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
Cross-regional flexible robust optimal scheduling in dynamic economic environment with joint frequency regulation of energy storage and units
1
2022
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
Storage right-based hybrid discrete-time and continuous-time flexibility trading between energy storage station and renewable power plants
1
2023
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
Energy storage planning for profitability maximization by power trading and ancillary services participation
1
2022
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
电碳市场背景下典型环境权益产品衔接互认机制及关键技术
1
2024
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
Mutual recognition mechanism and key technologies of typical environmental interest products in power and carbon markets
1
2024
... 电源侧储能产业的健康发展依赖于合理的市场政策与运营指导机制.然而,我国电力市场建设起步较晚,尚未形成完善的针对电源侧储能参与电力市场竞价的整体运行机制[5 -6 ] .总体而言,现阶段电源侧储能参与电力市场运行调度策略方面主要存在以下问题:一是由于缺乏成熟的商业模式,电源侧储能多参与单一应用场景运行,利用率低,营收情况不佳.目前我国电源侧储能多为新能源发电厂商兴建,主要作为辅助设施优化新能源出力[7 ] .仅参与单一应用场景使得电源侧储能非工作时段功率及容量大量闲置,未充分发挥应用潜力,运营经济性差,成本回收期长.二是缺乏具体有效的指导电源侧储能同其他市场主体竞标的策略机制.与传统发电机组仅作为市场中的发电方不同,储能在新能源电力超发阶段还可充当用能角色进行充电,且储存的电力又可参与其他应用场景[8 -9 ] .如何考虑市场动态且兼顾储能特性进行最优的市场竞标是储能良好参与电力市场的关键.三是碳交易引入下传统机组在电能量市场的报价与其碳交易成本存在耦合性[10 ] ,影响传统机组的投标策略,进而增加电力系统中能量分配的难度.因此,研究电源侧尤其是新能源侧储能在电力市场环境下的经济调度策略对于其优化运营、提高营收、降低扶持政策依赖,并促进储能参与下的电力市场健康有序发展具有重要意义. ...
基于云储能租赁服务的风储参与能量-调频市场竞价策略研究
1
2021
... 针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失. ...
Bidding strategies of wind power and energy storage participating in energy and frequency regulation market based on cloud energy storage leasing services
1
2021
... 针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失. ...
计及不确定性的风储联合系统多时间尺度市场参与策略
1
2024
... 针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失. ...
Multi-time scale market participation strategy of wind-energy storage combined system considering uncertainty
1
2024
... 针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失. ...
1
2021
... 针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失. ...
1
2021
... 针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失. ...
基于改进柔性策略评价的风火储多主体博弈电能-调频市场联合竞价模型
1
2023
... 针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失. ...
Joint bidding model of electricity and frequency regulation market with wind fire storage multi-agent games based on improved soft actor-critic
1
2023
... 针对储能多场景运行的投标策略研究中,文献[11 -12 ]中提出一种风储系统参与电能量市场和调频市场的报价策略,可指导风储系统在联合市场中竞价投标.文献[13 -14 ]中综合考虑储能调频可靠性与经济性,研究储能参与电能量和一次调频联合市场的竞价与出清机制.但是,上述针对联合市场的竞价策略研究虽然考虑了多场景应用,但在市场类型上又均只考虑日前市场,未考虑与日前市场高度耦合的实时平衡市场.缺乏对实时平衡市场不确定性考量,会使得日前决策在应对电力市场实际交割时新能源出力不确定性方面存在局限性,增加储能的机会损失. ...
Operation scheduling of battery storage systems in joint energy and ancillary services markets
1
2017
... 目前,针对储能参与电力现货市场日前-实时两阶段、多场景应用的竞标指导策略还未完全形成,但已有相关研究开展.文献[15 ]中提出一种基于风险评估的储能参与日前电能量市场、旋转备用市场以及日内平衡市场的竞标策略,计及市场价格不确定性以及备用需求不确定性,进行报价决策优化.文献[16 -17 ]中研究储能在日前电能量和辅助服务联合市场中的运行情况,并分别采用概率分布、多场景生成等方法模拟实时市场的不确定性影响,优化竞标决策方案. ...
A MILP model for optimising multi-service portfolios of distributed energy storage
1
2015
... 目前,针对储能参与电力现货市场日前-实时两阶段、多场景应用的竞标指导策略还未完全形成,但已有相关研究开展.文献[15 ]中提出一种基于风险评估的储能参与日前电能量市场、旋转备用市场以及日内平衡市场的竞标策略,计及市场价格不确定性以及备用需求不确定性,进行报价决策优化.文献[16 -17 ]中研究储能在日前电能量和辅助服务联合市场中的运行情况,并分别采用概率分布、多场景生成等方法模拟实时市场的不确定性影响,优化竞标决策方案. ...
Optimal operation of independent storage systems in energy and reserve markets with high wind penetration
1
2014
... 目前,针对储能参与电力现货市场日前-实时两阶段、多场景应用的竞标指导策略还未完全形成,但已有相关研究开展.文献[15 ]中提出一种基于风险评估的储能参与日前电能量市场、旋转备用市场以及日内平衡市场的竞标策略,计及市场价格不确定性以及备用需求不确定性,进行报价决策优化.文献[16 -17 ]中研究储能在日前电能量和辅助服务联合市场中的运行情况,并分别采用概率分布、多场景生成等方法模拟实时市场的不确定性影响,优化竞标决策方案. ...
基于碳交易的含大规模光伏发电系统复合储能优化调度
1
2019
... 进一步地,电力市场作为一个规模庞大、各市场主体关系耦合的复杂交易体系,每个个体的决策都会对市场出清产生影响.随着我国引入碳排放权交易,出于发电成本的考量,火电机组在电力现货市场中的售电报价将直接受到影响,因而引起电能量市场出清结果变动.文献[18 ⇓ -20 ]中均基于碳排放和运行经济性考虑,对能源系统进行优化调度研究.但上述研究虽然对碳交易下能源调度做了研究,但未同时计及新能源出力的不确定性. ...
Carbon trading based optimal scheduling of hybrid energy storage system in power systems with large-scale photovoltaic power generation
1
2019
... 进一步地,电力市场作为一个规模庞大、各市场主体关系耦合的复杂交易体系,每个个体的决策都会对市场出清产生影响.随着我国引入碳排放权交易,出于发电成本的考量,火电机组在电力现货市场中的售电报价将直接受到影响,因而引起电能量市场出清结果变动.文献[18 ⇓ -20 ]中均基于碳排放和运行经济性考虑,对能源系统进行优化调度研究.但上述研究虽然对碳交易下能源调度做了研究,但未同时计及新能源出力的不确定性. ...
Low-carbon economic dispatch method for integrated energy system considering seasonal carbon flow dynamic balance
1
2023
... 进一步地,电力市场作为一个规模庞大、各市场主体关系耦合的复杂交易体系,每个个体的决策都会对市场出清产生影响.随着我国引入碳排放权交易,出于发电成本的考量,火电机组在电力现货市场中的售电报价将直接受到影响,因而引起电能量市场出清结果变动.文献[18 ⇓ -20 ]中均基于碳排放和运行经济性考虑,对能源系统进行优化调度研究.但上述研究虽然对碳交易下能源调度做了研究,但未同时计及新能源出力的不确定性. ...
A decentralized market model for a microgrid with carbon emission rights
1
2023
... 进一步地,电力市场作为一个规模庞大、各市场主体关系耦合的复杂交易体系,每个个体的决策都会对市场出清产生影响.随着我国引入碳排放权交易,出于发电成本的考量,火电机组在电力现货市场中的售电报价将直接受到影响,因而引起电能量市场出清结果变动.文献[18 ⇓ -20 ]中均基于碳排放和运行经济性考虑,对能源系统进行优化调度研究.但上述研究虽然对碳交易下能源调度做了研究,但未同时计及新能源出力的不确定性. ...
虚拟电厂参与电-碳联合市场运行的竞价策略研究
1
2023
... 综上所述,针对缺乏有效的能同时计及新能源出力不确定性及电-碳市场耦合性的电源侧储能参与电力市场多场景运行调度的指导策略这一问题,以风电为例,开展电源侧储能多应用场景协同运行的竞价投标策略研究,细化储能与电力交易中心之间的博弈关系,充分考虑风电出力不确定性和碳排放权交易对储能投标策略的影响,借鉴双层模型优化思路[21 ⇓ -23 ] ,构建电源侧储能参与日前电能量市场、日前备用辅助服务市场以及实时平衡市场竞价投标双层优化模型.借助Karush-Kuhn-Tucker(KKT)条件[24 ] 将上述双层模型转化为单层模型后,进一步对其线性化.最后,基于MATLAB仿真平台求解模型,仿真结果验证了所提策略在市场出清过程中指导储能优化自身决策和提升收益的有效性. ...
Bidding strategy for a virtual power plant to participate in the power-carbon joint market
1
2023
... 综上所述,针对缺乏有效的能同时计及新能源出力不确定性及电-碳市场耦合性的电源侧储能参与电力市场多场景运行调度的指导策略这一问题,以风电为例,开展电源侧储能多应用场景协同运行的竞价投标策略研究,细化储能与电力交易中心之间的博弈关系,充分考虑风电出力不确定性和碳排放权交易对储能投标策略的影响,借鉴双层模型优化思路[21 ⇓ -23 ] ,构建电源侧储能参与日前电能量市场、日前备用辅助服务市场以及实时平衡市场竞价投标双层优化模型.借助Karush-Kuhn-Tucker(KKT)条件[24 ] 将上述双层模型转化为单层模型后,进一步对其线性化.最后,基于MATLAB仿真平台求解模型,仿真结果验证了所提策略在市场出清过程中指导储能优化自身决策和提升收益的有效性. ...
计及碳排放权交易的光热电站市场竞价策略研究
1
2023
... 综上所述,针对缺乏有效的能同时计及新能源出力不确定性及电-碳市场耦合性的电源侧储能参与电力市场多场景运行调度的指导策略这一问题,以风电为例,开展电源侧储能多应用场景协同运行的竞价投标策略研究,细化储能与电力交易中心之间的博弈关系,充分考虑风电出力不确定性和碳排放权交易对储能投标策略的影响,借鉴双层模型优化思路[21 ⇓ -23 ] ,构建电源侧储能参与日前电能量市场、日前备用辅助服务市场以及实时平衡市场竞价投标双层优化模型.借助Karush-Kuhn-Tucker(KKT)条件[24 ] 将上述双层模型转化为单层模型后,进一步对其线性化.最后,基于MATLAB仿真平台求解模型,仿真结果验证了所提策略在市场出清过程中指导储能优化自身决策和提升收益的有效性. ...
Bidding strategy for a concentrated solar power plant participating in the electricity market with the background of carbon trading
1
2023
... 综上所述,针对缺乏有效的能同时计及新能源出力不确定性及电-碳市场耦合性的电源侧储能参与电力市场多场景运行调度的指导策略这一问题,以风电为例,开展电源侧储能多应用场景协同运行的竞价投标策略研究,细化储能与电力交易中心之间的博弈关系,充分考虑风电出力不确定性和碳排放权交易对储能投标策略的影响,借鉴双层模型优化思路[21 ⇓ -23 ] ,构建电源侧储能参与日前电能量市场、日前备用辅助服务市场以及实时平衡市场竞价投标双层优化模型.借助Karush-Kuhn-Tucker(KKT)条件[24 ] 将上述双层模型转化为单层模型后,进一步对其线性化.最后,基于MATLAB仿真平台求解模型,仿真结果验证了所提策略在市场出清过程中指导储能优化自身决策和提升收益的有效性. ...
考虑风光不确定与碳交易的区域综合能源系统双层博弈优化运行
1
2023
... 综上所述,针对缺乏有效的能同时计及新能源出力不确定性及电-碳市场耦合性的电源侧储能参与电力市场多场景运行调度的指导策略这一问题,以风电为例,开展电源侧储能多应用场景协同运行的竞价投标策略研究,细化储能与电力交易中心之间的博弈关系,充分考虑风电出力不确定性和碳排放权交易对储能投标策略的影响,借鉴双层模型优化思路[21 ⇓ -23 ] ,构建电源侧储能参与日前电能量市场、日前备用辅助服务市场以及实时平衡市场竞价投标双层优化模型.借助Karush-Kuhn-Tucker(KKT)条件[24 ] 将上述双层模型转化为单层模型后,进一步对其线性化.最后,基于MATLAB仿真平台求解模型,仿真结果验证了所提策略在市场出清过程中指导储能优化自身决策和提升收益的有效性. ...
Two-level game optimal operation of regional integrated energy system considering wind and solar uncertainty and carbon trading
1
2023
... 综上所述,针对缺乏有效的能同时计及新能源出力不确定性及电-碳市场耦合性的电源侧储能参与电力市场多场景运行调度的指导策略这一问题,以风电为例,开展电源侧储能多应用场景协同运行的竞价投标策略研究,细化储能与电力交易中心之间的博弈关系,充分考虑风电出力不确定性和碳排放权交易对储能投标策略的影响,借鉴双层模型优化思路[21 ⇓ -23 ] ,构建电源侧储能参与日前电能量市场、日前备用辅助服务市场以及实时平衡市场竞价投标双层优化模型.借助Karush-Kuhn-Tucker(KKT)条件[24 ] 将上述双层模型转化为单层模型后,进一步对其线性化.最后,基于MATLAB仿真平台求解模型,仿真结果验证了所提策略在市场出清过程中指导储能优化自身决策和提升收益的有效性. ...
Pool strategy of a producer with endogenous formation of locational marginal prices
1
2009
... 综上所述,针对缺乏有效的能同时计及新能源出力不确定性及电-碳市场耦合性的电源侧储能参与电力市场多场景运行调度的指导策略这一问题,以风电为例,开展电源侧储能多应用场景协同运行的竞价投标策略研究,细化储能与电力交易中心之间的博弈关系,充分考虑风电出力不确定性和碳排放权交易对储能投标策略的影响,借鉴双层模型优化思路[21 ⇓ -23 ] ,构建电源侧储能参与日前电能量市场、日前备用辅助服务市场以及实时平衡市场竞价投标双层优化模型.借助Karush-Kuhn-Tucker(KKT)条件[24 ] 将上述双层模型转化为单层模型后,进一步对其线性化.最后,基于MATLAB仿真平台求解模型,仿真结果验证了所提策略在市场出清过程中指导储能优化自身决策和提升收益的有效性. ...
基于主从博弈的售电商多元零售套餐设计与多级市场购电策略
1
2022
... 主从博弈是基于博弈论的一种动态博弈,参与博弈的各方在决策时存在先后顺序,即领导与跟随的主从关系[25 -26 ] .先做出决策的主体称为领导者,根据领导者的决策情况后做出决策的主体称为跟随者.主从博弈基本原理如图1 所示. ...
Multi-type retail packages design and multi-level market power purchase strategy for electricity retailers based on master-slave game
1
2022
... 主从博弈是基于博弈论的一种动态博弈,参与博弈的各方在决策时存在先后顺序,即领导与跟随的主从关系[25 -26 ] .先做出决策的主体称为领导者,根据领导者的决策情况后做出决策的主体称为跟随者.主从博弈基本原理如图1 所示. ...
电网侧储能电站参与现货联合市场的竞价策略
1
2021
... 主从博弈是基于博弈论的一种动态博弈,参与博弈的各方在决策时存在先后顺序,即领导与跟随的主从关系[25 -26 ] .先做出决策的主体称为领导者,根据领导者的决策情况后做出决策的主体称为跟随者.主从博弈基本原理如图1 所示. ...
Bidding strategy for grid-side energy storage power stations to participate in the spot joint market
1
2021
... 主从博弈是基于博弈论的一种动态博弈,参与博弈的各方在决策时存在先后顺序,即领导与跟随的主从关系[25 -26 ] .先做出决策的主体称为领导者,根据领导者的决策情况后做出决策的主体称为跟随者.主从博弈基本原理如图1 所示. ...
考虑碳交易的风光储场站参与电力现货市场报价策略与调控方法
2
2023
... 传统机组在碳排放权交易市场购买缺额后,相应单位发电成本增加,因而会选择在电力现货市场提高报价以补贴发电成本.若传统机组碳排放量未超出配额,可出售配额盈余,则单位发电成本降低,传统机组将在电力现货市场降低报价以提高竞标竞争力[27 ] .因此,可根据传统机组在碳交易市场和电力现货市场中的成本转移行为构建传统机组的电-碳耦合报价机制,其形成机理如图2 所示. ...
... 储能规模设置为40 MW/160 MW·h,最大上调备用功率 S e u p , m a x S e d o w n , m a x P ch 和放电效率P dis 均为0.95,初始荷电状态 E e i n i t . 2 E e r a t e d . 参照文献[27 ],传统机组G1~G5的CEA配额值均为0.877 t/(MW·h),其实际CEA分别设为1.087、0.727、0.887、0.861、1.083 t/(MW·h),碳交易单价定为14 美元/t,传统机组其余参数设置如表1 所示.系统日前备用辅助服务市场上调备用和下调备用需求如图6 所示. ...
Bidding strategy and regulation method for the unified wind/photovoltaic/energy storage power stations in electricity spot market considering carbon trading
2
2023
... 传统机组在碳排放权交易市场购买缺额后,相应单位发电成本增加,因而会选择在电力现货市场提高报价以补贴发电成本.若传统机组碳排放量未超出配额,可出售配额盈余,则单位发电成本降低,传统机组将在电力现货市场降低报价以提高竞标竞争力[27 ] .因此,可根据传统机组在碳交易市场和电力现货市场中的成本转移行为构建传统机组的电-碳耦合报价机制,其形成机理如图2 所示. ...
... 储能规模设置为40 MW/160 MW·h,最大上调备用功率 S e u p , m a x S e d o w n , m a x P ch 和放电效率P dis 均为0.95,初始荷电状态 E e i n i t . 2 E e r a t e d . 参照文献[27 ],传统机组G1~G5的CEA配额值均为0.877 t/(MW·h),其实际CEA分别设为1.087、0.727、0.887、0.861、1.083 t/(MW·h),碳交易单价定为14 美元/t,传统机组其余参数设置如表1 所示.系统日前备用辅助服务市场上调备用和下调备用需求如图6 所示. ...
A bilevel model for participation of a storage system in energy and reserve markets
1
2018
... 所提电源侧储能电力市场多场景应用竞标博弈双层优化模型为混合整数非线性(mixed integer nonlinear programming, MINLP)问题,直接进行求解具有难度.因此,采用KKT条件先将双层模型转化为单层模型,即变为带均衡约束的数学规划(mathematical programs with equilibrium constraints, MPEC)模型.但因该模型中含有双变量乘积项,属于非线性问题,故再进一步利用大M 法[28 ] 和二元展开法[29 ] 将MPEC模型作线性处理,最终变换成混合整数线性规划(mixed integer linear programming, MILP)模型,此时即可借助Yamlip+Gurobi专业求解器在MATLAB平台上完成模型求解.所提竞标博弈双层优化模型整体求解流程如图4 所示. ...
Data-driven scheduling of energy storage in day-ahead energy and reserve markets with probabilistic guarantees on real-time delivery
1
2021
... 所提电源侧储能电力市场多场景应用竞标博弈双层优化模型为混合整数非线性(mixed integer nonlinear programming, MINLP)问题,直接进行求解具有难度.因此,采用KKT条件先将双层模型转化为单层模型,即变为带均衡约束的数学规划(mathematical programs with equilibrium constraints, MPEC)模型.但因该模型中含有双变量乘积项,属于非线性问题,故再进一步利用大M 法[28 ] 和二元展开法[29 ] 将MPEC模型作线性处理,最终变换成混合整数线性规划(mixed integer linear programming, MILP)模型,此时即可借助Yamlip+Gurobi专业求解器在MATLAB平台上完成模型求解.所提竞标博弈双层优化模型整体求解流程如图4 所示. ...