基于碳排放流模型的分布式产消者点对点电-碳交易机制

doi:10.16183/j.cnki.jsjtu.2023.139

基于碳排放流模型的分布式产消者点对点电-碳交易机制

詹博淳¹, 冯昌森², 王晓晖³, 张恒³, 马军伟⁴, 文福拴^,¹

1.浙江大学电气工程学院,杭州 310027

2.浙江工业大学信息工程学院,杭州 310023

3.国网经济技术研究院有限公司,北京 102200

4.国网山西省电力有限公司信息通信公司,太原 030001

A P2P Electricity-Carbon Trading Mechanism for Distributed Prosumers Based on Carbon Emission Flow Model

ZHAN Bochun¹, FENG Changsen², WANG Xiaohui³, ZHANG Heng³, MA Junwei⁴, WEN Fushuan^,¹

1. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China

2. College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China

3. State Grid Economic and Technical Research Institute Co., Ltd., Beijing 102200, China

4. Information and Telecommunication Company, State Grid Shanxi Electric Power Co., Ltd., Taiyuan 030001, China

通讯作者: 文福拴,教授,博士生导师,电话(Tel.):0571-87951542;E-mail:wenfs@hotmail.com.

责任编辑: 王历历

收稿日期: 2023-04-17 修回日期: 2023-07-13 接受日期: 2023-07-14

基金资助:

国家自然科学基金资助项目(U1910216)
国家电网有限公司科技项目资助(SGSXXT00JFJS2250157)

Received: 2023-04-17 Revised: 2023-07-13 Accepted: 2023-07-14

作者简介 About authors

詹博淳(1999—),硕士生,从事电力市场、区块链技术在电力系统中的应用研究.

摘要

针对配电系统层面设计分布式交易机制时,需要考虑产消者间的双边碳交易.提出一种考虑电能交易碳足迹的点对点(P2P)电-碳交易机制.首先,分析储能装置的碳排放特性,建立考虑储能装置的碳排放流模型.其次,建立基于碳排放流模型的产消者P2P电-碳交易模型,基于 Benders 分解法将原问题分解为网络约束主问题和产消者优化调度松弛子问题,采用分布式求解方法确定产消者最优P2P电-碳交易量,以保护产消者隐私.然后,建立基于纳什议价模型的产消者P2P电-碳交易结算模型,依据产消者在电-碳交易中的贡献度分配合作收益.最后,以改进的IEEE 33节点配电系统为例对所提交易模型进行验证,仿真结果表明所提机制可在保证配电网络安全运行的前提下,有效促进需求侧碳减排,并公平地分配产消者合作收益.

关键词： 碳排放流; 电能交易; 碳排放权交易; Benders分解; 纳什议价

Abstract

It is necessary to consider the carbon emission trading between prosumers when designing a distributed transaction mechanism in a distribution system. In this paper, a peer-to-peer (P2P) electricity-carbon transaction mechanism considering the carbon footprint of electricity trading is established. First, the carbon emission characteristic of energy storage system is analyzed, and a carbon emission flow model considering energy storage system is established. Next, a P2P electricity-carbon transaction model based on the carbon emission flow model is established. Based on the improved Benders decomposition method, the original problem is decomposed into the main problem considering network constraints and the subproblem of optimal scheduling for prosumers. Through distributed solutions, the optimal P2P electricity-carbon trading amount of prosumers is solved to protect the privacy of prosumers. Then, a P2P electricity-carbon trading settlement model based on the Nash bargaining model is established, and the cooperation benefit is distributed according to the contribution of prosumers in the electricity-carbon transaction. Finally, the effectiveness of the proposed model is validated by case studies on the improved IEEE 33-bus distribution system. The proposed model can not only ensure the secure operation of the distribution system, but also promote the reduction of demand-side carbon emission and fairly distribute the benefit among cooperative prosumers.

Keywords： carbon emission flow; electricity trading; carbon emission trading; Benders decomposition; Nash bargaining

PDF (1717KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

詹博淳, 冯昌森, 王晓晖, 张恒, 马军伟, 文福拴. 基于碳排放流模型的分布式产消者点对点电-碳交易机制[J]. 上海交通大学学报, 2024, 58(12): 1846-1856 doi:10.16183/j.cnki.jsjtu.2023.139

ZHAN Bochun, FENG Changsen, WANG Xiaohui, ZHANG Heng, MA Junwei, WEN Fushuan. A P2P Electricity-Carbon Trading Mechanism for Distributed Prosumers Based on Carbon Emission Flow Model[J]. Journal of Shanghai Jiaotong University, 2024, 58(12): 1846-1856 doi:10.16183/j.cnki.jsjtu.2023.139

国家能源局发布《能源碳达峰碳中和标准化提升行动计划》^[1],要求推进分布式能源就地消纳,健全能源产业链碳足迹核算标准,完善全产业链碳排放量化评估.因此,在遵循市场规律和保障电力系统安全稳定运行的前提下,有必要针对产消者分布式交易的特点建立一种公平、透明的碳足迹量化方法和电-碳交易机制,以促进分布式能源就地消纳和需求侧碳减排^[2-3].

为协调电力市场中新兴的产消者,近年来学术界已针对其分布式交易开展广泛研究.现有的分布式产消者点对点(peer-to-peer, P2P)交易模型主要分为三类:基于拍卖的交易模型、基于博弈的交易模型和基于一致性算法的交易模型.文献[4]中建立基于自适应进取性交易策略的连续双向拍卖机制.文献[5]中建立基于供需随机拆分的多段报价拍卖模型.上述基于拍卖的交易模型未考虑网络安全运行约束.文献[6]中建立基于最优反应学习算法的产消者非合作博弈竞价模型.文献[7]中建立考虑舒适度需求的住宅建筑间非合作博弈交易模型.上述基于博弈的交易模型对于实际大规模非线性的电能管理和交易问题不一定存在纳什均衡解.文献[8]中建立基于次梯度算法的产消者双边合同交易模型;文献[9]中提出基于边际电价和交替方向乘子法的P2P交易竞价一致性算法.基于一致性算法的交易模型有较高的求解效率和良好的收敛特性.本文建立一种基于Benders分解法的P2P交易模型,将集中优化问题分解为网络约束问题和产消者问题分布式优化求解,以保护产消者隐私.

针对市场主体参与碳排放权市场的交易策略已有广泛研究.文献[10]中建立基于委托拍卖的发电公司碳配额分配和交易决策模型.文献[11]中建立同时考虑碳配额和碳税的发电主体交易决策模型.文献[12]中考虑风光发电的不确定性,建立基于信息间隙决策的发电主体碳交易决策模型.上述研究针对发电侧主体建立碳排放量控制和交易策略,并未考虑需求侧终端产消费外购电能的间接碳排放.然而电能需求是源侧碳排放的内在驱动因素,已有学者针对需求侧的碳排放义务开展研究.文献[13]中建立与电力潮流对应的碳排放流(carbon emission flow, CEF)模型,量化电力网络中碳排放量的分布.文献[14]中建立基于潮流追踪法的日前日内碳排放流双向分配模型,引入网损分配系数追踪实时功率和碳流偏差.文献[15]中建立电-气-热综合能源系统的CEF模型,量化与多类型能源流耦合的碳排流.上述研究重点分析了碳排放流的计算方法.进一步地,文献[16]中针对终端用户参与电力市场和碳排放权市场,建立基于CEF模型的主动需求响应两阶段优化模型.文献[17]中建立基于改进比例共享原理的需求侧碳足迹分配模型.文献[18]中建立基于Aumann-Shapley值的源荷双层调度模型,通过调整荷侧用电需求实现源荷两侧碳排放总量控制和经济效益最优.上述研究并未考虑需求侧终端产消者间双边碳交易.基于此,建立考虑储能装置(energy storage system, ESS)的CEF模型以量化产消者从上级电网购电的间接碳排放,进而建立考虑碳排放成本的分布式产消者P2P电-碳交易优化模型.

1 考虑储能装置的CEF模型

基于CEF模型对分布式产消者电能交易进行碳足迹跟踪,量化分布式产消者从配电公司购买电能导致的间接碳排放.当储能装置闲置或放电时,可视其为发电设备,碳排放密度不变.当储能装置充电时,则可视其为吸收电能的负载.储能装置的碳排放密度为

(1)

e_{i, b e s s}^{t + 1}

\{\begin{array}{l} e_{i, b e s s}^{t}, & P_{i, c}^{t} = 0 \\ \frac{e_{i, b e s s}^{t} E_{i, b e s s}^{t} + e_{i, N}^{t} P_{i, c}^{t} Δ t}{E_{i, b e s s}^{t} + P_{i, c}^{t} Δ t}, & P_{i, d c}^{t} = 0 \end{array}

式中: $e_{i, b e s s}^{t + 1}$ 、 $e_{i, b e s s}^{t}$ 分别为时段t+1和时段t位于节点i的储能装置碳排放密度; $E_{i, b e s s}^{t}$ 为时段t节点i储能装置的电量; $P_{i, d c}^{t}$ 、 $P_{i, c}^{t}$ 分别为时段t位于节点i的产消者储能装置的放电功率和充电功率.

进而可得出考虑储能装置的节点i和线路b的碳排放密度为

(2)$ e_{i, \mathrm{~N}}^{t}=\frac{P_{i, \mathrm{dg}}^{t} e_{i, \mathrm{dg}}+P_{i, \mathrm{de} e}^{t} e_{i, \mathrm{bess}}^{t}+\sum_{b \in L_{i}^{+}}\left|P_{b}^{t}\right| e_{b, \mathrm{~B}}^{t}}{P_{i, \mathrm{dg}}^{t}+P_{i, \mathrm{rg}}^{t}+P_{i, \mathrm{dc}}^{t}+\sum_{b \in L_{i}^{+}}\left|P_{b}^{t}\right|}$

(3)$ e_{b, \mathrm{~B}}^{t}=e_{i, \mathrm{~N}}^{t}, \quad i=G_{b}$

式中: $e_{i, N}^{t}$ 、 $e_{b, B}^{t}$ 分别为时段t节点i和线路b的碳排放密度;e_i_,dg为节点i化石能源发电机组的碳排放密度; $L_{i}^{+}$ 为向节点i注入功率的线路集合; $P_{i, r g}^{t}$ 、 $P_{i, d g}^{t}$ 分别为时段t节点i的可再生能源设备和化石能源发电设备出力; $P_{b}^{t}$ 为时段t线路b的有功功率;G_b为向线路b注入功率的节点集合.

当节点i为配电网络中的变电站节点时,其碳排放密度为上级电网注入电能的碳排放密度;当节点i为参与P2P交易的分布式产消者节点时,其碳排放密度取决于配电网络的功率流和节点各设备出力;线路b的碳排放密度等于向线路b注入功率的节点的碳排放密度^[19-20].

2 分布式产消者P2P电-碳交易机制

配电侧分布式产消者通过P2P电能交易和与配电公司交易满足电能需求,通过P2P碳配额交易和碳排放权市场交易达到碳排放考核要求.P2P电能交易和碳配额交易周期分别与电力现货市场交易周期和碳排放权市场交易周期相同.为研究需求侧碳排放考核对于产消者交易决策的影响,将需求侧碳配额的分配考核周期T设定为1 d,碳排放权市场的交易周期T_c设定为6 h, 电力现货市场交易周期T_e设定为1 h.

2.1 产消者P2P电-碳交易模型

产消者本质为合作关系,通过P2P电能交易最大化消纳分布式可再生能源,减少电能交易成本和对上级电网的依赖性,在实现电能共享的同时也减少了间接碳排放量.产消者P2P电-碳交易目标为1个碳排放考核周期T内总成本最低:

(4)$ \begin{array}{c} \min C_{\text {total }}=\sum_{t \in T} \sum_{i \in A}\left[\lambda_{\mathrm{bg}}^{t} P_{i, \mathrm{bg}}^{t}-\lambda_{\text {sk }}^{t} P_{i, \mathrm{se}}^{t}+c_{i, \mathrm{rg}} P_{i, \mathrm{tg}}^{t}+\right. \\ \left.c_{i, \mathrm{bess}}\left(P_{i, \mathrm{dc}}^{t}+P_{i, \mathrm{c}}^{t}\right)+\lambda_{\mathrm{bc}}^{t} M_{i, \mathrm{bc}}^{t}-\lambda_{\mathrm{sc}}^{t} M_{i, \mathrm{sc}}^{t}\right] \end{array}$

式中:C_total为产消者碳排放考核周期T内的总成本; A为参与P2P交易的产消者集合; $λ_{b g}^{t}$ 、 $λ_{s g}^{t}$ 分别为时段t产消者向配电公司购电和售电的价格; $P_{i, b g}^{t}$ 、 $P_{i, s g}^{t}$ 分别为时段t节点i处产消者向配电公司的购电功率和售电功率;c_i_,rg、c_i_,bess分别为节点i处产消者可再生能源发电设备和储能装置的成本系数; $λ_{b c}^{t}$ 、 $λ_{s c}^{t}$ 分别为时段t碳排放权市场的碳配额购买价格和出售价格; $M_{i, b c}^{t}$ 、 $M_{i, s c}^{t}$ 分别为时段t节点i处产消者在碳排放权市场的购碳数量和售碳数量.

约束条件包括以下4个.

(1) 产消者设备出力约束:

(5)(1-h_rg)

P_{i, r g, m a x}^{t}

≤

P_{i, r g}^{t}

≤

P_{i, r g, m a x}^{t}

(6)

S_{i, b e s s}^{t}

S_{i, b e s s}^{t - 1}

(η_{i, c} P_{i, c}^{t} - \frac{1}{η_{i, d c}} P_{i, d c}^{t}) \frac{Δ t}{Q_{i, b e s s}}

(7)

S_{i, b e s s}^{m i n}

≤

S_{i, b e s s}^{t}

≤

S_{i, b e s s}^{m a x}

(8)0≤

P_{i, c}^{t}

≤

y_{i, b e s s}^{t}

P_i_,c,max

(9)0≤

P_{i, d c}^{t}

≤(1-

y_{i, b e s s}^{t}

)P_i_,dc,max

式中:h_rg为可再生能源发电的最大弃能率; $P_{i, r g, m a x}^{t}$ 为时段t节点i处产消者可再生能源设备预测最大发电功率; $S_{i, b e s s}^{t}$ 为时段t节点i处产消者辖下ESS的荷电状态, $S_{i, b e s s}^{m i n}$ 、 $S_{i, b e s s}^{m a x}$ 分别为其辖下ESS的荷电状态的下限和上限;η_i_,dc、η_i_,c分别为其辖下ESS的放电效率和充电效率;P_i_,dc,max、P_i_,c,max 分别为节点i处产消者辖下ESS的最大放电功率和最大充电功率;Q_i_,bess为其辖下ESS的额定容量; $y_{i, b e s s}^{t}$ 为其辖下ESS的时段t充放电状态的二元变量,充电和放电分别取1和0.

(2) 功率平衡约束:

(10)

P_{i, r g}^{t}

P_{i, d c}^{t}

P_{i, c}^{t}

P_{i, L}^{t}

P_{i, s m}^{t}

P_{i, s g}^{t}

P_{i, b m}^{t}

P_{i, b g}^{t}

(11)

P_{i, s m}^{t}

P_{i, s g}^{t}

≤ζ(1-

y_{i, e}^{t}

)

(12)

P_{i, b m}^{t}

P_{i, b g}^{t}

≤ζ

y_{i, e}^{t}

(13)

P_{i, s m}^{t}

P_{i, s g}^{t}

P_{i, b m}^{t}

P_{i, b g}^{t}

≥0

(14)

\sum_{i \in A} P_{i, b g}^{t}

κ_{b g}^{t}

(15)

\sum_{i \in A} P_{i, s g}^{t}

κ_{s g}^{t}

(16)

\sum_{i \in A} P_{i, s m}^{t}

\sum_{i \in A} P_{i, b m}^{t}

式中: $P_{i, L}^{t}$ 为时段节点i处产消者的负荷; $P_{i, b m}^{t}$ 、 $P_{i, s m}^{t}$ 分别为其时段t在P2P电能交易中的购电功率和售电功率; $κ_{b g}^{t}$ 、 $κ_{s g}^{t}$ 分别为时段t所有产消者向配电公司的总购电功率和总售电功率.为避免节点i处产消者时段t同时购买和出售电能, $y_{i, e}^{t}$ 为时段t节点i处产消者电能交易状态的二元变量,产消者购买电能和出售电能分别取1和0;ζ为一足够大的正数.

(3) 碳配额平衡约束:

(17)M_i_{, 0}=

M_{t o t a l}^{T} \frac{\sum_{t \in T} P_{i, L}^{t}}{\sum_{i \in A} \sum_{t \in T} P_{i, L}^{t}}

(18)M_i_{, 0}-

\sum_{t \in T} P_{i, b g}^{t} e_{i, N}^{t}

\sum_{t \in T}

(

M_{i, s m}^{t}

M_{i, s c}^{t}

M_{i, b m}^{t}

M_{i, b c}^{t}

)

(19)

M_{i, s m}^{t}

M_{i, s c}^{t}

≤ζ(1-

y_{i, c}^{t}

)

(20)

M_{i, b m}^{t}

M_{i, b c}^{t}

≤ζ

y_{i, c}^{t}

(21)

M_{i, s m}^{t}

M_{i, s c}^{t}

M_{i, b m}^{t}

M_{i, b c}^{t}

≥0

(22)

\sum_{i \in A} M_{i, b c}^{t}

κ_{b c}^{t}

(23)

\sum_{i \in A} M_{i, s c}^{t}

κ_{s c}^{t}

(24)

\sum_{i \in A} M_{i, b m}^{t}

\sum_{i \in A} M_{i, s m}^{t}

式中:M_i_{, 0}为基于预测负荷比例分配^[3]的节点i处产消者初始碳配额数量; $M_{t o t a l}^{T}$ 为考核周期T区域初始碳配额总量; $M_{i, b m}^{t}$ 、 $M_{i, s m}^{t}$ 分别为时段t节点i处产消者在P2P碳交易中购买碳配额数量和出售碳配额的数量; $κ_{b c}^{t}$ 、 $κ_{s c}^{t}$ 分别为时段t所有产消者在碳排放权市场购买碳配额总量和出售碳配额总量; $y_{i, c}^{t}$ 为时段t节点i处产消者碳配额交易状态的二元变量,产消者购买碳配额和出售碳配额分别取1和0.

(4) 网络约束:

(25)

P_{i j, F}^{t}

P_{j, S}^{t}

\sum_{k \neq i : (j, k) \in L} P_{j k, F}^{t}

+r_ij(

I_{i j}^{t}

)²

(26)

P_{i, S}^{t}

P_{i, r g}^{t}

P_{i, d c}^{t}

P_{i, c}^{t}

P_{i, L}^{t}

(27)

Q_{i j, F}^{t}

Q_{j, S}^{t}

\sum_{k \neq i : (j, k) \in L} Q_{j k, F}^{t}

+χ_ij(

I_{i j}^{t}

)²

(28)(

V_{j}^{t}

)²=(

V_{i}^{t}

)²-2(r_ij

P_{i j, F}^{t}

+χ_ij

Q_{i j, F}^{t}

)+(

r_{i j}^{2}

χ_{i j}^{2}

)(

I_{i j}^{t}

)²

(29)(

I_{i j}^{t}

)²(

V_{i}^{t}

)²=(

P_{i j, F}^{t}

)²+(

Q_{i j, F}^{t}

)²

(30)(V_i_,down)²≤(

V_{i}^{t}

)²≤(V_i_,up)²

(31)0≤(

I_{i j}^{t}

)²≤(I_ij_,up)²

式中:L为系统线路集合; $P_{i j, F}^{t}$ 、 $Q_{i j, F}^{t}$ 分别为时段t线路(i, j)的有功潮流和无功潮流; $P_{i, S}^{t}$ 、 $P_{j, S}^{t}$ 、 $Q_{j, S}^{t}$ 分别为时段t节点i注入的有功功率和节点j注入的有功、无功功率; r_ij、χ_ij分别为线路(i, j)的电阻和电抗; $I_{i j}^{t}$ 为时段t线路(i, j)的电流; $V_{i}^{t}$ 、 $V_{j}^{t}$ 分别为时段t节点i和节点j的电压模值;V_i_,up、V_i_,down分别为节点i的电压模值上限和下限;I_ij_,up为线路(i, j)的电流上限.

2.2 基于Benders分解法求解P2P交易模型

定义Δ $P_{i}^{t}$ 为时段t节点i处产消者电能交易总量,包括P2P电能交易量和与配电公司的交易量;定义Δ $M_{i}^{t}$ 为时段t节点i处产消者碳配额交易总量,包括P2P碳配额交易量和在碳排放权市场交易量,即

(32)Δ

P_{i}^{t}

P_{i, s m}^{t}

P_{i, s g}^{t}

P_{i, b m}^{t}

P_{i, b g}^{t}

P_{i, S}^{t}

(33)Δ

M_{i}^{t}

M_{i, s m}^{t}

M_{i, s c}^{t}

M_{i, b m}^{t}

M_{i, b c}^{t}

将式(14)~(16)代入式(32)、式(22)~(24)代入式(33),整理可得:

(34)

\sum_{i \in A}

P_{i}^{t}

κ_{s g}^{t}

κ_{b g}^{t}

(35)

\sum_{i \in A}

M_{i}^{t}

κ_{s c}^{t}

κ_{b c}^{t}

为保护产消者隐私,减少产消者与负责安全校验的配电公司间共享的信息,如产消者可再生能源发电数据、储能装置信息等隐私数据,基于Benders分解法^[21-22]将式(4)目标函数分解为网络安全约束主问题和产消者优化调度子问题,通过变量的交互迭代分布式求解.网络安全约束主问题决策变量为Δ $P_{i}^{t}$ 、 $P_{i, b g}^{t}$ 、 $P_{i, s g}^{t}$ 、Δ $M_{i}^{t}$ 、 $M_{i, b c}^{t}$ 和 $M_{i, s c}^{t}$ ,约束条件包括碳排放流约束式(1)~(3)、产消者电能交易总量平衡约束式(14)~(15)和式(34)、碳配额交易总量平衡约束式(22)~(23)和式(35)和网络约束式(25)~(31),即

(36)min

\sum_{t \in T}

(

λ_{b g}^{t} κ_{b g}^{t}

λ_{s g}^{t} κ_{s g}^{t}

λ_{b c}^{t} κ_{b c}^{t}

λ_{s c}^{t} κ_{s c}^{t}

)

(37)s.t. 式(1)~(3)、式(14)~(15)、式(22)~(23)、式(25)~(31)、式(34)~(35)

产消者优化调度子问题的目标函数为原目标函数中产消者设备出力相关项,约束条件包括产消者各设备出力约束式(5)~(9)、每个产消者的电能平衡约束式(10)~(13)、碳配额平衡约束式(18)~(21)和辅助变量约束式, 即

(38)min C_i=

\sum_{t \in T} [c_{i, r g} P_{i, r g}^{t} + c_{i, b e s s} (P_{i, d c}^{t} + P_{i, c}^{t})]

(39)

{\bar{X}}_{i}^{t}

X_{i}^{t}

(40)

X_{i}^{t}

\{Δ P_{i}^{t}, P_{i, b g}^{t}, P_{i, s g}^{t}, Δ M_{i}^{t}, M_{i, b c}^{t}, M_{i, s c}^{t}\}

(41)

{\bar{X}}_{i}^{t}

\{Δ {\bar{P}}_{i}^{t}, {\bar{P}}_{i, b g}^{t}, {\bar{P}}_{i, s g}^{t}, Δ {\bar{M}}_{i}^{t}, {\bar{M}}_{i, b c}^{t}, {\bar{M}}_{i, s c}^{t}\}

(42)s.t. 式(5)~(13)、式(18)~(21)

式中:C_i为第i个产消者的设备调度成本; $X_{i}^{t}$ 为主问题中相关变量集合; ${\bar{X}}_{i}^{t}$ 为子问题辅助变量集合;式(39)~(41)为辅助变量约束式.

在常规Benders分解法中,含整型变量的优化问题为主问题求解^[14].2.1节建立的产消者P2P电-碳交易模型中包括储能装置的充放电状态变量、产消者电能交易状态变量和碳配额交易状态变量,均为整型变量,且在产消者优化调度子问题中求解,因此需要对子问题进行拉格朗日松弛^[23-24].

(1) 子问题有可行解.当子问题式(38)~(42)在主问题给定 $X_{i}^{t}$ 下有最优解时,将子问题松弛并求解生成Benders切割,引入辅助变量后松弛形式的子问题可表述为

(43)

\begin{array}{l} m i n \sum_{t \in T} [c_{i, b e s s} (P_{i, d c}^{t} + P_{i, c}^{t}) + c_{i, r g} P_{i, r g}^{t} + \\ π_{i, X}^{t} ({\bar{X}}_{i}^{t} - X_{i}^{t})] \\ s . t . 式 (42) \end{array}\}

式中: $π_{i, X}^{t}$ 为约束条件式(39)中变量X的拉格朗日乘子.

基于松弛子问题的解 ${\bar{X}}_{i}^{t}$ ,可获得向主问题返回的Benders切割:

(44)η_i≥

\sum_{t \in T}

[c_i_,rg

{\bar{P}}_{i, r g}^{t}

+c_i_,bess(

{\bar{P}}_{i, d c}^{t}

{\bar{P}}_{i, c}^{t}

π_{i, X}^{t}

(

{\bar{X}}_{i}^{t}

X_{i}^{t}

)]

式中:η_i为节点i处产消者对应的子问题(简称子问题i)返回主问题的目标函数近似值参数; $\bar{}$ 表示子问题变量.

(2) 子问题无可行解.在子问题的求解中,约束条件式(39)将主问题的解赋给子问题,可能导致子问题式(38)~(42)在该解下无可行解,违反电能平衡约束式(10)和碳配额平衡约束式(18).当子问题式(38)~(42)无可行解时,为了形成有效的Benders切割,需要将约束条件式(10)和式(18)松弛:

(45)min (α+β)

(46)

P_{i, r g}^{t}

P_{i, d c}^{t}

P_{i, c}^{t}

P_{i, L}^{t}

+α=

P_{i, s m}^{t}

P_{i, s g}^{t}

P_{i, b m}^{t}

P_{i, b g}^{t}

(47)M_i_{, 0}-

\sum_{t \in T} P_{i, b g}^{t} e_{i, N}^{t}

+β=

\sum_{t \in T}

(

M_{i, s m}^{t}

M_{i, s c}^{t}

M_{i, b m}^{t}

M_{i, b c}^{t}

)

(48)s.t. 式(5)~(9)、式(11)~(13)、式(19)~(21)

式中:α、β为决策变量.

通过求解问题式(45)~(48)可获得约束条件的最小松弛和对应的乘子 $π_{i, X}^{t}$ ,进而可求解松弛子问题:

(49)

\begin{array}{l} m i n \sum_{t \in T} [c_{i, b e s s} (P_{i, d c}^{t} + P_{i, c}^{t}) + \\ c_{i, r g} P_{i, r g}^{t} + π_{i, X}^{t} ({\bar{X}}_{i}^{t} - X_{i}^{t})] \\ s . t . 式 (5) ~ (9) 、 式 (11) ~ (13) 、 \\ 式 (19) ~ (21) 、 式 (46) ~ (47) \end{array}\}

在获得可行松弛子问题的解 ${\bar{X}}_{i}^{t}$ 后,基于式(44)求解向主问题返回的Benders切割.加入Benders切割约束的主问题表述为

(50)

\begin{array}{l} m i n [\sum_{t \in T} (λ_{b g}^{t} κ_{b g}^{t} - λ_{s g}^{t} κ_{s g}^{t} + λ_{b c}^{t} κ_{b c}^{t} - λ_{s c}^{t} κ_{s c}^{t}) + \\ \sum_{i \in A} η_{i}] \\ η_{i} \geq \sum_{t \in T} {c_{i, r g} {\bar{P}}_{i, r g}^{t} (l) + c_{i, b e s s} [{\bar{P}}_{i, d c}^{t} (l) + \\ {\bar{P}}_{i, c}^{t} (l)] + π_{i, X}^{t} (l) [{\bar{X}}_{i}^{t} (l) - X_{i}^{t}]}, \\ \forall l \in {1, 2, \dots, a - 1} \\ s . t . 式 (37) \end{array}\}

在Benders分解法的第a轮迭代中,主问题基于原约束和第l轮(l=1, 2…a-1)迭代形成的Benders切割约束,求解满足网络约束的交易计划,包括产消费间P2P电-碳交易量、与配电公司的交易功率和在碳市场交易碳配额数量.子问题基于主问题最优解优化产消者设备出力,生成新的Benders切割,并添加到主问题约束中,以进一步逼近原问题最优解.基于Benders分解法求解P2P电-碳交易模型的具体流程如下.

步骤1 设置原问题的初始下界A_LB=-∞,初始上界为A_UB=∞,迭代轮次a=1,收敛偏差为ω.在没有附加切割平面的约束下求解主问题式 (36)~(37), 得到主问题的初始解 $X_{i}^{t}$ (1),基于主问题潮流计算出配电网络节点的碳排放密度,跳转至步骤3.

步骤2 基于第a-1轮迭代中子问题形成的Benders切割,求解主问题式(50),获得主问题的解 $X_{i}^{t}$ (a)和节点的碳排放密度,更新下界A_LB= $\sum_{i \in A}$ η_i(a),跳转至步骤3.

步骤3 节点i处产消者基于第a轮主问题的解 $X_{i}^{t}$ (a)和节点碳排放密度求解子问题式(38)~(42).若有可行解,则获取式(39)的拉格朗日乘子 $π_{i, X}^{t}$ ,并跳转至步骤4,否则跳转至步骤5.

步骤4 第a轮迭代子问题i有可行解,基于乘子 $π_{i, X}^{t}$ ,求解松弛子问题式(43),得到松弛子问题最优解 ${\bar{X}}_{i}^{t}$ (a),进而基于式(44)求解第a轮迭代子问题i向主问题返回的Benders切割,跳转至步骤6.

步骤5 第a轮迭代子问题i无可行解,基于式(45)~(48)求解约束条件的最小松弛和对应的乘子 $π_{i, X}^{t}$ ,进而求解松弛子问题式(49),得到松弛子问题的最优解 ${\bar{X}}_{i}^{t}$ (a),并基于式(44)求解第a轮迭代子问题i向主问题返回的Benders切割,跳转至步骤6.

步骤6 更新上界A_UB= $\sum_{i \in A}$ C_i(a),进行迭代终止判定.若A_UB-A_LB≤ω,则跳转至步骤7;否则 a=a+1, 并跳转至步骤2.

步骤7 输出P2P电-碳交易方案,包括产消者间P2P电-碳交易量、与配电公司的电能交易量和在碳排放权市场交易的碳配额数量.

3 产消者P2P电-碳交易结算模型

在2.1节建立的产消者P2P电-碳交易模型以产消者总成本最低为目标,将产消者的分布式资源优化配置,进而确定产消者最优P2P电-碳交易量.在交易结算环节,建立基于纳什议价^[25]的P2P交易结算模型,根据产消者贡献度进行收益分配.基于纳什议价的P2P交易结算模型包括P2P电能交易结算和碳配额交易结算:

(51)max

\prod_{i \in A}

{[

{C^{N}}_{i, e l e}

{C^{H}}_{i, e l e}

C_{i, e l e}^{P 2 P}

)

]^{τ_{i, e l e}}

×[

{C^{N}}_{i, c a r}

{C^{H}}_{i, c a r}

C_{i, c a r}^{P 2 P}

)

]^{τ_{i, c a r}}

}

(52)

{C^{H}}_{i, e l e}

\sum_{t \in T}

[c_i_,rg

P_{i, r g}^{t}

+c_i_,bess(

P_{i, d c}^{t}

P_{i, c}^{t}

λ_{b g}^{t} P_{i, b g}^{t}

λ_{s g}^{t} P_{i, s g}^{t}

]

(53)

{C^{H}}_{i, c a r}

\sum_{t \in T}

(

λ_{b c}^{t} M_{i, b c}^{t}

λ_{s c}^{t} M_{i, s c}^{t}

)

(54)

{C^{H}}_{i, e l e}

C_{i, e l e}^{P 2 P}

≤

{C^{N}}_{i, e l e}

(55)

{C^{H}}_{i, c a r}

C_{i, c a r}^{P 2 P}

≤

{C^{N}}_{i, c a r}

(56)

\sum_{i \in A} C_{i, e l e}^{P 2 P}

(57)

\sum_{i \in A} C_{i, c a r}^{P 2 P}

式中: ${C^{N}}_{i, e l e}$ 、 ${C^{N}}_{i, c a r}$ 分别为节点i处产消者参与集中式电-碳交易时的电能总成本和碳配额总成本,电能总成本包括产消者与配电公司的交易成本和设备发电成本,碳配额总成本为在碳排放权市场的交易成本; $C_{i, e l e}^{H}$ 为P2P交易模式下节点i处产消者的基础用电成本,包括设备发电成本和与配电公司交易成本; $C_{i, c a r}^{H}$ 为P2P交易模式下节点i处产消者在碳排放权市场的交易成本; $C_{i, e l e}^{P 2 P}$ 、 $C_{i, c a r}^{P 2 P}$ 分别为节点i处产消者的P2P电能交易结算费用和碳配额交易结算费用;τ_i,_ele、τ_i,_car分别为节点i处产消者P2P电能交易结算和碳配额交易结算的议价因子,由节点i处产消者在P2P电-碳交易中的贡献度决定,即节点i处产消者的P2P交易量权重决定,计算公式如下:

(58)τ_i_,ele=

\frac{\sum_{t \in T} (P_{i, s m}^{t} + P_{i, b m}^{t})}{\sum_{i \in A} \sum_{t \in T} (P_{i, s m}^{t} + P_{i, b m}^{t})}

(59)τ_i_,car=

\frac{\sum_{t \in T} (M_{i, s m}^{t} + M_{i, b m}^{t})}{\sum_{i \in A} \sum_{t \in T} (M_{i, s m}^{t} + M_{i, b m}^{t})}

将基于纳什议价的P2P交易结算模型目标函数式(51)取对数,转化为凸优化问题求解:

(60)

\begin{array}{l} m i n \sum_{i \in A} {- τ_{i, e l e} [{C^{N}}_{i, e l e} - ({C^{H}}_{i, e l e} + C_{i, e l e}^{P 2 P})] - \\ τ_{i, c a r} [{C^{N}}_{i, c a r} - ({C^{H}}_{i, c a r} + C_{i, c a r}^{P 2 P})]} \\ s . t . 式 (52) ~ (59) \end{array}\}

4 算例与结果

4.1 参数设置

采用改进的IEEE 33节点配电系统进行算例分析.该系统的拓扑结构如附录中图A1所示.假设参与分布式交易的产消者有12个,分别位于节点2、3、4、6、9、13、17、20、21、23、28、32,编号为产消者 a~l.假设每个产消者均配备电池储能装置和光伏发电设备,各产消者设备基本参数如附录中的表A1所示,负荷数据和可再生能源发电设备各时段最大出力取自文献[24].各时段配电公司购售电价格取自文献[16],碳排放权市场中碳配额价格取自文献[18],其他参数^[25-26]为:变电站节点的碳排放密度e_sub,N=0.85 kg/(kW·h),初始碳配额总量 ${M^{T}}_{t o t a l}$ =50 kg,收敛偏差ω=10^-3,最大弃风弃光率h_rg=0.02.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 电力现货市场、碳排放权市场和P2P交易时间尺度

Fig.1 Time scale of electricity spot market, carbon emission trading market, and P2P trading

4.2 算法计算性能分析

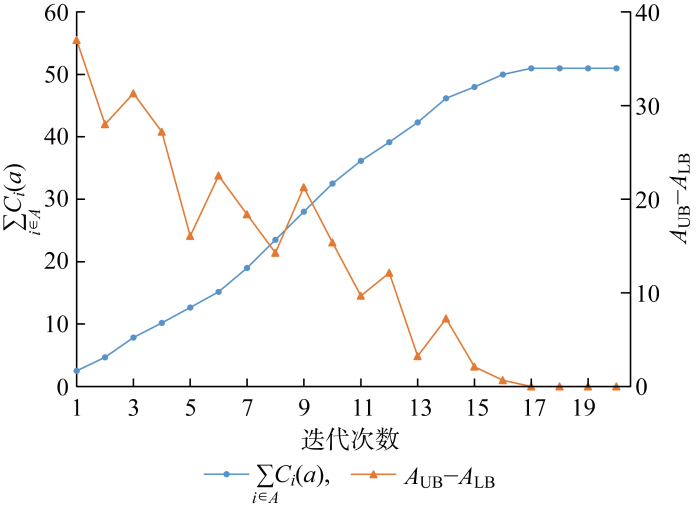
图2为Benders分解法收敛过程中相关变量的变化情况.由图可见,上下界差值作为收敛判定条件虽然在迭代过程中有明显的振荡,但产消者的总成本逐渐增加,最终在第17次迭代时稳定到收敛解处.这是因为主问题是原始优化问题的松弛形式,松弛随着子问题返回切割平面数量的增加而逐渐收紧.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Benders分解法迭代过程

Fig.2 Iterative process of improved Benders decomposition

表1比较了所提算法与交替方向乘子法 (alternating direction method of multipliers, ADMM)算法^[25]和集中式算法的计算结果.可以看出,Benders分解法能收敛到集中式算法的全局最优解,收敛到最优解所需的迭代次数少于ADMM算法,平均计算时间与ADMM算法相比缩短3.8%,也无需考虑ADMM算法中的步长敏感性问题^[25].

表1 算法计算结果比较

Tab.1 Comparison of computational performance

产消者数量/个	Benders分解			ADMM			集中式算法
产消者数量/个	迭代次数/次	总计算时间/s	最优解/元	迭代次数/次	总计算时间/s	最优解/元	总计算时间/s	最优解/元
12	17	209.78	51.04	19	218.07	51.04	6.28	51.04
20	23	577.30	76.97	28	601.58	76.97	13.42	76.97
30	36	1634.76	108.65	47	1695.74	108.65	25.76	108.65

新窗口打开| 下载CSV

表2为Benders分解法主问题和松弛子问题每轮迭代的平均计算时间.由于子问题为相互独立的产消者优化调度问题,不随产消者总体规模的增加发生改变,所以子问题的计算时间并未显著增加,迭代的平均计算时间均低于1.5 s.然而,当产消者数量增加时,主问题的平均计算时间显著增加,从2.48 s增加到77.29 s.这是因为主问题的约束条件包含网络安全约束和子问题返回的Benders切割约束,这些约束条件的数量随着产消者规模的增加而增加, 加剧主问题的计算负担.上述分析表明基于Benders分解法的布式求解算法能在保证计算效率和收敛性能的基础上,减少产消者信息共享,保护产消者隐私.

表2 算法平均计算时间

Tab.2 Average algorithm running time by iteration

产消者个数	每轮迭代平均计算时间/s
产消者个数	主问题	子问题
5	2.48	0.75
12	11.46	0.88
20	24.13	0.97
30	44.25	1.16
50	77.29	1.28
100	167.34	1.42

新窗口打开| 下载CSV

4.3 产消者P2P交易策略分析

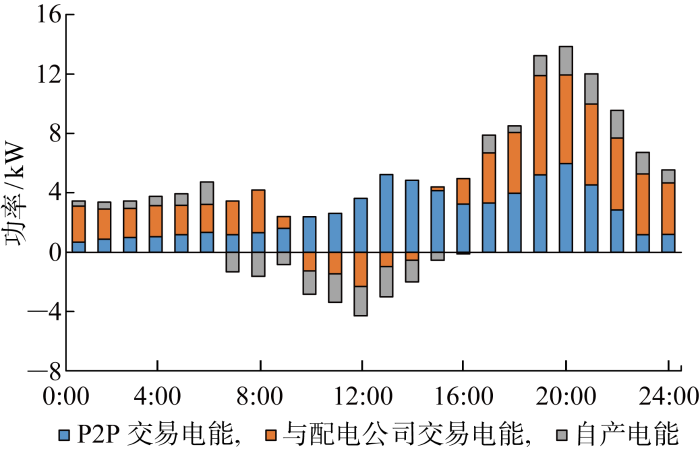
图3为各时段P2P市场交易电量、与配电公司交易电量和自产电量.与配电公司交易量为负表明产消者向配电公司售电,自产电量包括产消者可再生能源设备发电量和电池储能装置放电量,自产电量为负表明电池储能装置充电量大于可再生能源设备发电量.可以看出,自产电量最高峰时段对应可再生能源发电量高峰时段,同时也是向配电公司出售电能最多的时段.在 1:00—5:00,由于可再生能源发电量处于低谷期,P2P电能交易量在产消者电能消费结构的占比较低,产消者主要通过向配电公司购电满足用电需求.而在 10:00—15:00,可再生能源发电设备发电量增加,P2P交易量在产消者电能消费结构的占比明显提升,说明通过P2P交易促进了分布式可再生能源的消纳.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 24时段产消者电能消费结构

Fig.3 Energy consumption structure of prosumers in 24 periods

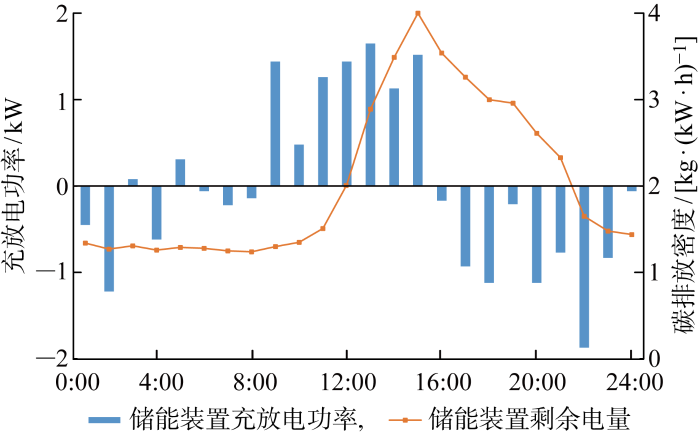
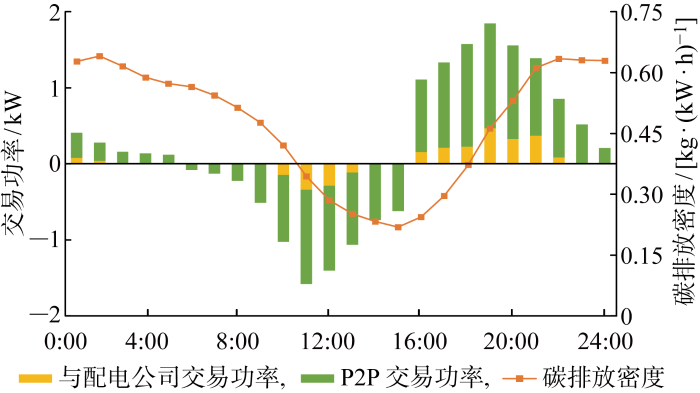
以产消者e为例进一步说明分布式产消者的交易策略.图4为各时段产消者e储能装置的调度计划,图5为各时段产消者e的电能交易计划和节点碳排放密度.可以看出,由于午间分布式光伏发电量充足,产消者e的储能装置的充电行为主要集中午间,而在晚间负荷高峰时段放电满足部分电能需求.在 6:00—15:00,产消者e将富余的电能部分出售给其余产消者和配电公司,部分存储在储能装置中,15:00 时储能装置存储电量达到上限,此时段储能装置相当于吸收可再生电能的负载,节点的碳排放密度减小;在 17:00—23:00 的用电需求高峰期,产消者e调度储能装置放电满足部分电能需求,同时由于其从配电公司购买电能比例提高,节点的碳排放密度增大. 上述分析表明建立的考虑储能装置的碳排放流模型可有效量化产消者的碳足迹.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 产消者e储能装置调度计划

Fig.4 Scheduling plans of energy storage system for Prosumer e

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 产消者e电能交易计划和节点碳排放密度

Fig.5 Energy trading plans and carbon intensity for Prosumer e

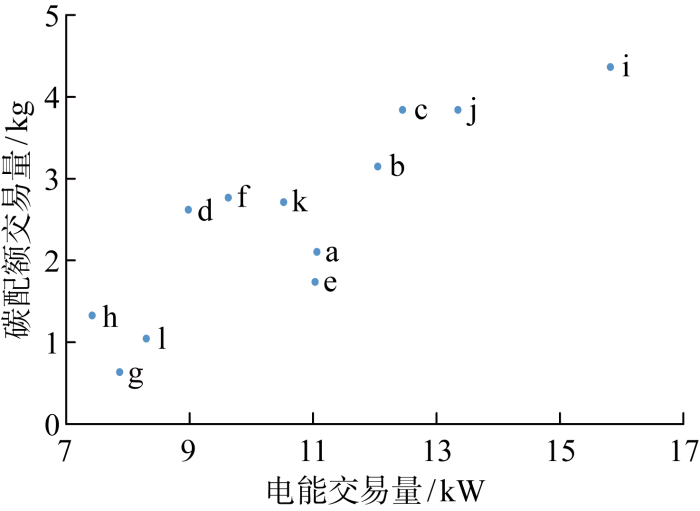
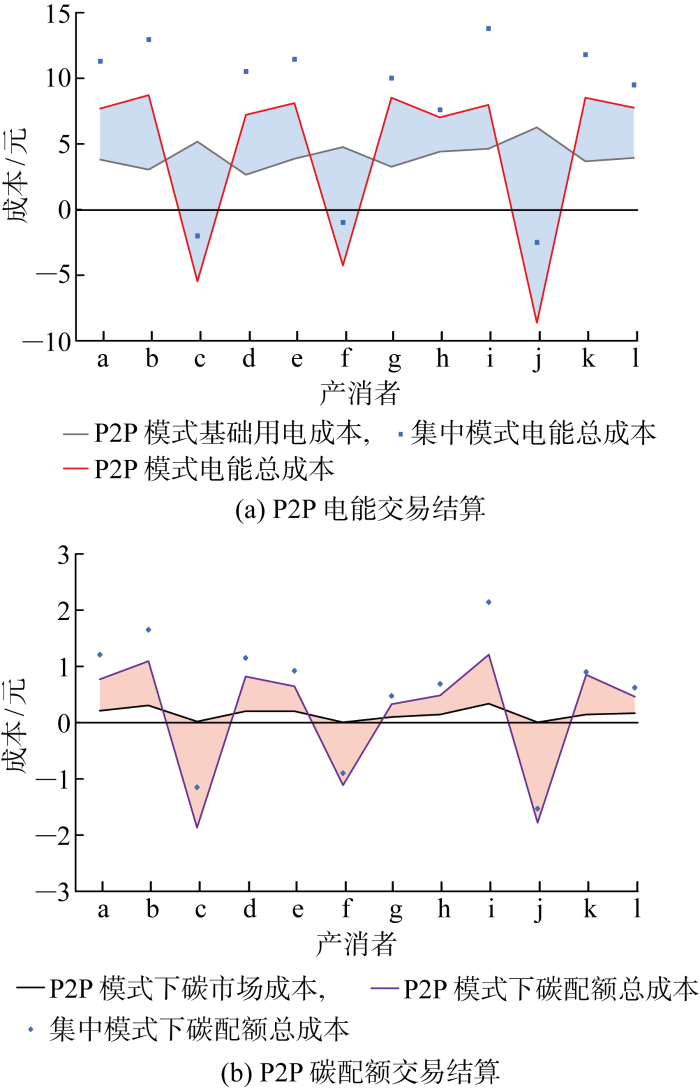
图6为各产消者24时段P2P交易总量结果,图7为基于纳什议价模型的P2P交易结算结果,其中成本为负值表示产消者出售电能或碳配额所获得的收益,图中阴影部分为各产消者的P2P电能交易结算费用和碳配额交易结算费用.可以看出,12位产消者参与直接P2P交易后用能成本均有所降低,其中产消者i的P2P电能交易量和碳配额交易量最大,因此其P2P电-碳交易贡献度和议价因子高于其他产消者,从而使其在交易结算中收益最大,与集中式交易相比其总成本降幅为47.6%,所有产消者平均成本降幅为28.9%.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 各产消者24时段P2P交易量

Fig.6 Total P2P trading amount of each prosumer in 24 periods

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 P2P交易结算费用

Fig.7 Settlement fee of P2P trading

4.4 对比分析

对比以下3种交易模式来分析所提模型对分布式产消者收益和碳排放总量的影响,进而说明所提模型的合理性和可行性.

(1) 模式1.产消者间可进行P2P电能交易和碳配额交易,考核产消者的间接碳排放量,即所提交易模式.

(2) 模式2.不考虑产消者间的电能交易和碳配额交易,考核产消者的间接碳排放量.产消者只能通过自产自消或与配电公司交易以满足电能需求,利用碳排放权市场满足碳排放权需求.

(3) 模式3.考虑产消者间P2P电能交易,但不考核产消者的间接碳排放量,产消者间无P2P碳配额交易.

表3为3种模式对比结果,其中P2P交易率定义为P2P交易量占总交易量的比率.在模式2中,0:00—24:00的交易周期里12位产消者优化调度后与配电公司的净交易电量为103.44 kW·h,电力交易成本为74.48元,设备调度成本为18.98元,电能总成本为93.46元.在碳排放权市场的碳配额交易量为32.75 kg,碳排放权交易总成本为6.37元.模式3不考核产消者的间接碳排放量,产消者总成本仅为电能成本,产消者间P2P电能交易量为43.32 kW·h,电能交易成本相较模式2降低48.5%,碳排放量降低14.9%.

表3 3种模式下得到的结果比较

Tab.3 Comparisons of results obtained in three modes

序号	产消者总成本/元		P2P交易率/%		碳排放量/kg
序号	电能成本	碳排放权成本	电能交易率	碳配额交易率	碳排放量/kg
模式1	49.21	1.83	55.44	61.78	59.42
模式2	93.46	6.37	0	0	82.75
模式3	48.17	0	38.68	0	70.44

新窗口打开| 下载CSV

在模式1中,产消者间P2P电能交易量和碳配额交易量分别为64.32 kW·h和15.23 kg,虽然考核产消者的间接碳排放量导致额外的排放权成本,但产消者总成本相较模式3而言增幅不显著,这是因为间接碳排放考核提高了产消者P2P电能交易率,减少其与配电公司的交易电量;同时,由于产消者间的碳配额交易无网络约束限制,所以模式1的P2P碳配额交易率略高于P2P电能交易率.在碳排放量方面,模式1的碳排放量相较模式2和模式3分别降低28.2%和15.6%.上述分析表明所提交易模式能有效促进产消者P2P交易,同时有助于减少碳排放量.

5 结论

构建基于Benders分解法的P2P电-碳交易模型和基于纳什议价模型进行P2P收益结算分配,对所提模型进行算例仿真分析,得出以下结论.

(1) 引入对需求侧产消者的间接碳排放量考核,基于碳排放流模型量化产消者的购电碳足迹,可有效促进产消者改变用能行为,进而促进碳减排.

(2) 基于Benders分解法求解P2P产消者电-碳交易方案,有良好的收敛性能和计算效率,同时分布式的求解方法能有效保护产消者的隐私数据信息.

(3) 基于纳什议价的P2P收益结算方案依据产消者电-碳交易总量对收益进行分配,结果表明引入P2P电-碳交易有助于降低产消者的用电成本和碳排放权成本,同时有效考虑产消者在P2P电-碳交易中的贡献度,实现收益的公平分配.

在后续研究中,拟将所提模型部署在区块链平台进行仿真分析,同时考虑分布式产消者提供辅助服务的补偿与收费方式.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2024/1006-2467/1006-2467-58-12-1846.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

中华人民共和国国家能源局.

能源碳达峰碳中和标准化提升行动计划

[EB/OL]. (2022-10-09)[2023-04-05]. http://www.nea.gov.cn/2022-10/09/c_1310668927.htm.

URL [本文引用: 1]

National Energy Administration of the People’s Republic of China.

Action plan for energy carbon peaking and carbon neutrality standardization improvement

[EB/OL]. (2022-10-09)[2023-04-05]. http://www.nea.gov.cn/2022-10/09/c_1310668927.htm.

URL [本文引用: 1]

[2]

秦博宇, 周星月, 丁涛, 等.

全球碳市场发展现状综述及中国碳市场建设展望

[J]. 电力系统自动化, 2022, 46(21): 186-199.