上海交通大学学报

上海交通大学学报, 2024, 58(11): 1745-1752 doi: 10.16183/j.cnki.jsjtu.2023.037

船舶海洋与建筑工程

水泥基材料孔隙结构随机分散模型与仿真试验

程钕1, 徐文浩1, 吴标1, 陈小文1, 侯东伟,1,2

1.上海交通大学 船舶海洋与建筑工程学院,上海 200240

2.上海市公共建筑与基础设施数字化运维重点实验室,上海 200240

Random Dispersion Model and Simulation of Model Pore Structure of Cementitious Materials

CHEN Nü1, XU Wenhao1, WU Biao1, CHEN Xiaowen1, HOU Dongwei,1,2

1. School of Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Shanghai Key Laboratory for Digital Maintenance of Building and Infrastructure, Shanghai 200240, China

通讯作者: 侯东伟,讲师;E-mail:houdw@sjtu.edu.cn.

责任编辑: 李博文

收稿日期: 2023-02-6   修回日期: 2023-05-25   接受日期: 2023-05-29  

Received: 2023-02-6   Revised: 2023-05-25   Accepted: 2023-05-29  

作者简介 About authors

程钕(1998—),硕士生,从事水泥基材料孔隙结构研究.

摘要

为描述水泥基材料的孔隙结构演变,将水泥浆体看作两相介质随机分散体系,建立了孔隙结构计算模型. 同时采用μic平台进行水泥水化仿真,与理论结果相互验证,并进一步分析理论模型的计算条件和参数变化规律. 计算结果表明:对于完全分散的新拌水泥浆体,多分散硬球模型与仿真结果一致; 考虑水化产物交错和团聚效应,单分散同心球模型计算的孔隙结构与仿真结果一致,且硬核半径比与水化度呈线性负相关. 考虑水泥颗粒絮凝效应时,单分散硬球模型与仿真结果接近.

关键词： 两相介质; 随机分散模型; μic仿真平台; 孔隙结构; 孔径分布

Abstract

In order to investigate the evolution of pore structures in cementitious materials, a statistical model is proposed by taking the cement paste as a random dispersion system of two-phase medium. Simultaneously, the μic platform is employed to simulate the cement hydration. The results obtained from the simulation and the disperse models are compared with each other, and further analysis on calculation conditions and parameters of the disperse models are conducted. The pore size distribution obtained from polydisperse hard sphere model is very close to the simulation in completely dispersion condition. Taking into account the cross and agglomeration effects of hydrated products, the calculation results of the monodisperse concentric-shell model are more consistent to the simulations. Considering the flocculation of cement particles in initial state, the monodisperse hard model is closer to the simulation results. This paper offers a new insight from the viewpoints of mathematics and physics to understand and describe the pore structures of cementitious materials.

Keywords： two-phase media; randomly disperse models; μic simulation platform; pore structure; pore size distribution

PDF (2646KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

程钕, 徐文浩, 吴标, 陈小文, 侯东伟. 水泥基材料孔隙结构随机分散模型与仿真试验[J]. 上海交通大学学报, 2024, 58(11): 1745-1752 doi:10.16183/j.cnki.jsjtu.2023.037

CHEN Nü, XU Wenhao, WU Biao, CHEN Xiaowen, HOU Dongwei. Random Dispersion Model and Simulation of Model Pore Structure of Cementitious Materials[J]. Journal of Shanghai Jiaotong University, 2024, 58(11): 1745-1752 doi:10.16183/j.cnki.jsjtu.2023.037

水泥基复合胶凝材料是一种典型的多孔介质,其孔结构通常分为3种类型:① 凝胶孔,0.5~10 nm,与徐变和收缩相关;② 毛细孔,10 nm~10 μm, 由粒径分布和水灰比决定;③ 宏观孔,由非完全堆积或引入气体形成.其中,毛细孔及其形成的孔隙网络是材料力学性能和耐久性的决定因素.孔隙结构决定材料强度,传统上通过水灰比设计混凝土强度,其本质是不同水灰比产生不同的孔隙结构[1-2];混凝土中的孔隙结构是环境中水分、气体及其他有害介质传输的通道,孔隙率、孔径分布、连通度和曲折度等孔隙特征影响着介质传输的速度[3⇓-5],决定了材料的耐久性;孔隙空间是一系列物理和化学过程的发生场所,孔隙内有害介质的浓度和含量决定着混凝土劣化的速度[6].

水泥基材料的孔隙计算模型通常基于传统的颗粒堆积理论.颗粒堆积理论通过假设颗粒的粒级分布[7]及堆积方式[8-9],采用几何推导计算孔径分布.由于水泥粒子的多尺度分布及在水中的复杂分散状态,颗粒堆积理论的假设过于严苛,计算困难,不适用于水泥基材料的孔隙结构计算.理解孔隙结构的另一个思路,是将水泥基材料看作两相介质的随机分散体系[10],孔隙结构则用水泥颗粒间的空间来表征,采用统计方法进一步建立孔隙结构的计算模型.

基于两相介质随机分散理论,以毛细孔为研究对象,建立水泥基材料的孔隙结构计算模型.同时,采用μic仿真平台[11]对浆体的微观结构演变进行模拟,统计孔径分布,并与分散模型计算结果相互验证,同时反向标定分散模型参数,分析模型参数在不同水化程度下的变化规律.该模型从数学和物理角度,揭示了水泥基材料的孔隙形成机制和演变规律,为孔隙结构计算和材料性能设计奠定了理论基础.

1 两相介质随机分散理论

水泥浆体及水化初期的水泥体系,可看作固相颗粒在水中两相介质的随机分散体系.在分散理论中,根据分散质的粒径分布特征,可分为单分散体系和多分散体系.分散质采用同心球简化模型,多分散粒子的3种分散状态如图1所示.其中,ε为粒子硬核半径比.同心球包含硬核部分和可重叠部分,如图1(a)所示,在随机投放过程中,硬核部分不可重叠,可重叠部分的交叠程度则可表示分散质的团聚情况.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   多分散粒子的3种分散状态

Fig.1   Three distribution states of polydisperse particles


在分散体系中,定义分散剂中一点与其最邻近的分散质表面的距离rp为该点的孔径[12],如图 1(a)所示,点A处的孔径即为rp.显然,分散剂中任意一点距离最邻近分散质表面的距离为rp 的概率 f(rp) 即为孔径概率密度函数,孔径不小于rp的概率 F(rp) 即为孔径累积分布函数.

在同心球模型中,根据粒子间的相互作用,可考虑两种极限情况.当ε = 1时,同心球粒子转化为硬球粒子,粒子间完全不能重叠,模型简化为硬球模型,如图1(b)所示,如其分散系中的粒子均等径,即为单分散硬球(monodisperse hard sphere model, MHS)模型.当ε = 0时,粒子间无相互作用,可任意程度重叠,属于随机球模型,如图1(c)所示,如其分散系中的粒子等径,即为单分散随机球(monodisperse randomly placed sphere model, MRPS)模型.

根据Rikvold等[13]关于两相介质随机分散理论的孔隙特征理论表达式,推导出单分散同心球模型(monodisperse concentric-shell model,MCS)的孔径累积分布函数的解析式为

$\begin{array}{l}F\left(\varepsilon, \eta \mid r_{\mathrm{p}}\right)= \\\quad \quad \exp \left\{-\frac{\left(1+r_{\mathrm{p}} /\langle r\rangle\right)^{3}-1}{1-\varepsilon \eta} \eta\right\} H\left(\varepsilon, \eta \mid r_{\mathrm{p}}\right)\end{array}$

其中

$ \begin{array}{c}H\left(\varepsilon, \eta \mid r_{\mathrm{p}}\right)=\exp \left[\frac{-3 \varepsilon \eta^{2}}{(1-\varepsilon \eta)^{3}} \times\right. \\\left.\quad\left(a_{0} \frac{r_{\mathrm{p}}}{\langle r\rangle}+a_{1} \frac{r_{\mathrm{p}}^{2}}{\langle r\rangle}+\frac{r_{\mathrm{p}}^{3}}{\langle r\rangle}\right)\right]\end{array}$
$a_{0}=3\left\{1-\varepsilon^{1 / 3}\left[1+\left(1-\varepsilon^{1 / 3}\right) \varepsilon \eta\right]\right\}$
$a_{1}=3\left[1-\frac{1}{2} \varepsilon^{1 / 3}(1+\varepsilon \eta)\right]$

式中:H、a0、a1均为系数;团粒的无量纲密度η=4π<r>3ρ/3,ρ为水泥颗粒的数密度(单位体积的粒子数);r为水泥粒子的半径;水泥粒子数量平均半径为<r>=∫0∞ rf(r)dr,随着水化时间的演变,水泥粒子的状态会由粉末粒子变为浆体粒子、水泥石粒子,其中< >在统计物理学中表示系综均值;f(r)为粒子的数量概率密度分布.

ρ与固液相的体积比相关,因此η可由液相体积分数ϕw和同心球硬核半径ε<r>确定

$\begin{array}{l}\phi_{w}(\varepsilon, \eta)=\Phi(\varepsilon, \eta) A(\varepsilon, \eta) \end{array}$
$\Phi(\varepsilon, \eta)=(1-\varepsilon \eta) \exp \left[-\frac{(1-\varepsilon)}{1-\varepsilon \eta} \eta\right]$
$\begin{array}{l}A(\varepsilon, \eta)=\exp \left\{-\frac{3 \varepsilon \eta^{2}}{2(1-\varepsilon \eta)^{3}} \times\right. \\\left.\quad\left[2-3 \varepsilon^{1 / 3}+\varepsilon-\left(3 \varepsilon^{1 / 3}-6 \varepsilon^{2 / 3}+3 \varepsilon\right) \varepsilon \eta\right]\right\}\end{array}$

式中:A( )与Φ( )为系数.

分别将ε=1及ε=0代入式(1),可得到MHS模型与 MRPS模型关于孔径累积分布函数的解析解.

对于多分散体系,同心球模型的累计孔径分布在ε=0的随机球模型(polydisperse randomly placed sphere model, PRPS)和ε=1的硬球模型(polydisperse hard sphere model, PHS)条件下存在解析解[12].

多分散随机球模型累计孔径分布函数解析表达式为

$F\left(r_{\mathrm{p}}\right)=\phi_{w}^{B\left(r_{\mathrm{p}}\right)-1}$
$\begin{array}{l}B\left(r_{\mathrm{p}}\right)=1+3 \frac{r_{\mathrm{p}}}{r_{\mathrm{s}}}+3 \frac{\langle r\rangle\left\langle r^{3}\right\rangle}{\left\langle r^{2}\right\rangle^{2}} \frac{r_{\mathrm{p}}^{2}}{r_{\mathrm{s}}^{2}}+\frac{\left\langle r^{3}\right\rangle^{2}}{\left\langle r^{2}\right\rangle^{3}} \frac{r_{\mathrm{p}}^{3}}{r_{\mathrm{s}}^{3}}\end{array}$

式中:B为系数;表面平均半径$r_{\mathrm{s}}=\left\langle r^{3}\right\rangle /\left\langle r^{2}\right\rangle ;\langle r\rangle 、 \left\langle r^{2}\right\rangle 、 \left\langle r^{3}\right\rangle$分别是多分散水泥粒子半径在原点(origin)的1次统计矩、2次统计矩及3次统计矩的期望值.

多分散硬球模型的累计孔径分布函数解析表达式为

$F\left(r_{\mathrm{p}}\right)=\exp \left[-\pi \rho\left(a_{0} r_{\mathrm{p}}+a_{1} r_{\mathrm{p}}^{2}+a_{2} r_{\mathrm{p}}^{3}\right)\right]$

其中

$a_{0}=\frac{4}{1-\eta}\left\langle r^{2}\right\rangle$
$\begin{array}{l}\begin{aligned}a_{1}= & \frac{4}{1-\eta}\langle r\rangle+\frac{12 \xi_{2}}{\left(1-\xi_{3}\right)^{2}}\left\langle r^{2}\right\rangle \end{aligned}\end{array}$
$\begin{array}{l}\begin{aligned}a_{2}= & \frac{4}{3(1-\eta)}+\frac{8 \xi_{2}}{(1-\eta)^{2}}\langle r\rangle+ \\& \frac{32}{3} \frac{\xi_{2}^{2}}{(1-\eta)^{3}}\left\langle r^{2}\right\rangle \end{aligned}\end{array}$
$\begin{array}{l}\begin{aligned}\xi_{k}= & 2^{k-3} \eta \frac{\left\langle r^{2}\right\rangle}{\left\langle r^{3}\right\rangle}, \quad k=1,2\end{aligned}\end{array}$

式中:ξ和k为系数.

2 仿真试验

2.1 μic仿真平台

μic仿真平台是Bishnoi开发的模拟水化过程中微观结构演变的程序代码[14].μic仿真平台具有很好的用户自定义性,可通过配置文件自定义水泥颗粒的粒径分布、反应物与生成物、水化动力学方程、粒子生长模型、粒子堆积方式等,且模拟结果与实验测试吻合良好,故被研究者广泛接受.

2.1.1 水化动力学模型

采用的水化动力学模型为两阶段模型,分别为反应物自由表面控制阶段与扩散控制阶段,分别如下

$\begin{aligned}\frac{\mathrm{d} r_{\text {in }}}{\mathrm{d} t} & =-3 k_{1} t^{2} \mathrm{e}^{-k_{1} t^{3}} \end{aligned}$
$\begin{aligned}\frac{\mathrm{~d} r_{\text {in }}}{\mathrm{d} t} & =\frac{-k_{\text {diff }}}{r_{\text {out }}-r_{\text {in }}}\end{aligned}$

式中:rin为粒子未水化部分的半径;rout为粒子总半径,包括产物层;k1、kdiff分别为水化反应系数;t为水化时间.

在μic中,水化动力学方程的系数与粒子的粒径建立直接联系,具有实际物理意义.除水化反应产物在水泥颗粒表面发生沉积之外,部分水化产物如氢氧化钙(CH)与水化硅酸钙(C-S-H)等还会在液相中形成新的颗粒.μic中可以通过自定义成核速率方程、最大成核数量及成核位点等来描述这一现象.

2.1.2 孔径统计方法

μic中统计孔径的方法为三维像素侵入法(voxel-erosion)[14],将整个分散体系划分为指定尺寸的像素网格,如图2所示.其中,黑色网格表示固体粒子,其他网格为孔隙空间.其统计算法为:对孔隙空间进行标记,第一步将固液相界面的像素网格标记为1,下一步将与像素网格1交界的像素网格标记为2,直至所有的孔隙像素网格都被标记.根据该算法,任意被标记的像素网格与最邻近粒子的距离即为标记值.由此可知,基于像素数标记值的孔径统计方法中对孔径概念的定义与分散理论中定义的孔径概念一致,即某个标记值的数量分数为该孔径的概率密度.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   μic中孔径统计算法示意图

Fig.2   Pore size statistical algorithm in μic platform


2.2 模型参数

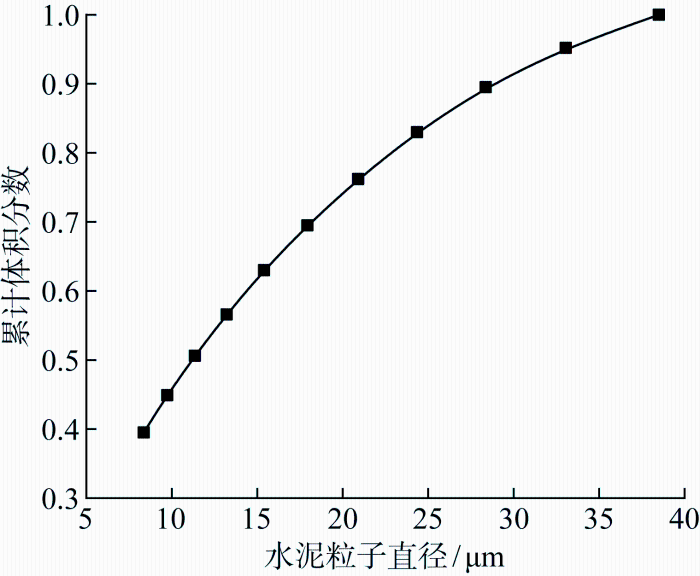
采用典型的水泥颗粒粒径分布计算水泥水化过程的微观结构变化,粒径分布曲线如图3所示.反应体系的尺寸设置为100 像素×100 像素×100像素的立方体.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   仿真中水泥粒径体积分布

Fig.3   Cement particle size distribution used in the simulations


仿真中水泥水化的反应物为硅酸三钙(C3S)、硅酸二钙(C2S)以及铝酸三钙(C3A),初始固液体积比为0.58∶1. 水化产物C-S-H一部分在反应物粒子表面沉积,以反应物粒子的固液界限为界,分为内层C-S-H与外层C-S-H;另一部分在液相内成核生长,产物CH也在液相内成核生长,钙矾石等其余产物则在反应物表面成核.各主要反应物、产物的特性以及两阶段水化系数参考文献[14]中经典仿真案例的参数设置,如表1所示.模拟的水化温湿度也与案例中保持一致,采用标准养护条件.需要说明的是,不同的水泥材料需对其水化参数进行试验标定.

表1   仿真中各物质的密度以及水化反应系数

Tab.1  Density of materials in simulation and coefficients in reaction kinetic equations

反应物/产物密度/
(g·cm-3)		k1/h-3kdiff/
(μm2·h-1)
C3S3.151.14×10-51.0
C2S3.281.14×10-41.0
C3A3.031.14×10-21.0
内层C-S-H2.20.04
外层C-S-H2.21.0
CH2.21.0

注:表中空白表示无数值.

新窗口打开| 下载CSV


3 结果与讨论

3.1 微观结构演化

μic仿真平台基于2.2节中的反应物和如图3所示的粒径分布进行初始化,按照式(15)与式(16)给定的反应动力学方程进行反应.初始化粒子的分散方式为完全分散,不允许粒子发生絮凝或重叠,对应分散系中的硬球模型,但在水化反应发生后,反应物粒子表面生成的产物层及孔隙间新增产物颗粒,将导致粒子之间不可避免地相互接触,接触区域不再产生新的产物,反应产物只可附着在未接触的颗粒表面.计算结果如图4所示,其中α为水化度.黑色球为未水化水泥颗粒,部分水化产物C-S-H以球环形式在水泥颗粒表面生成,进一步以灰度深浅将其区分为内层C-S-H与外层C-S-H,另一部分水化产物在原孔溶液中形成,包括CH颗粒与C-S-H颗粒,其密度与外层C-S-H相同.由图可知,反应物粒子的半径随水化度的增大而减小,液相中的产物颗粒发生成核生长,外层C-S-H的厚度逐渐增大.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同水化度下反应体系的微观结构

Fig.4   Microstructure of cement at different hydration degrees


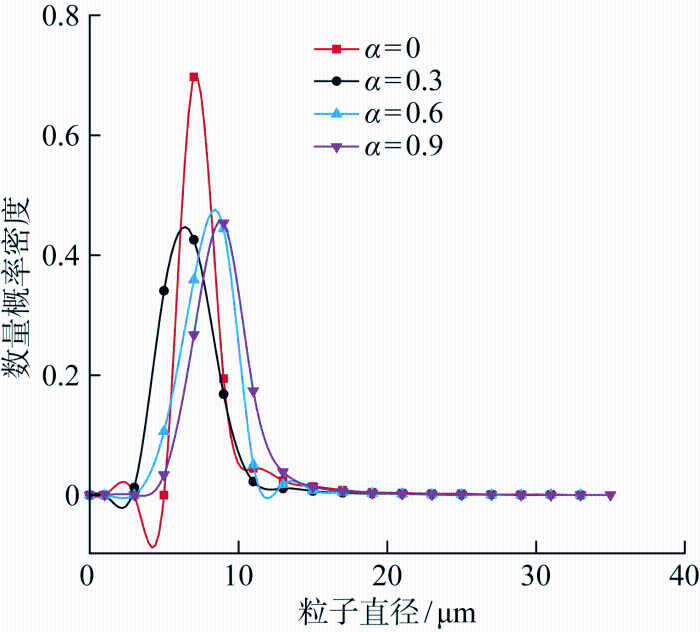
水化过程中,水泥颗粒和生成物的粒径分布及固液比的变化导致了孔隙结构的变化.同水化度时的颗粒粒径分布如图5所示.相对初始粒径,α=0.3时,粒径发生了细化,主要由于水泥颗粒表面溶解和水化导致粒径减小,同时溶液中大量小粒径的成核粒子生成. 随着水化度升高,水化控制机理由成核生长转变为扩散控制. 此时,新成核粒子不再增加,这一阶段水化度的增大主要表征为水化产层厚度的增加,进而导致粒径粗化,粒径分布曲线右移.一方面,固相生成物附着在颗粒表面使其体积增大,另一方面,成核粒子也发生聚集生长. 不同水化度时的孔径概率密度分布如图6所示,曲线与x轴形成的面积即为孔隙的体积分数.水化度增大,孔隙的体积分数随之减小,最可几孔径也减小,说明孔径细化,水泥的微观结构逐渐致密.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   水化进程中粒径分布的演变

Fig.5   Evolution of particle size distribution in hydration


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   水化进程中孔径分布的演变

Fig.6   Evolution of pore size distribution in hydration


3.2 模型计算结果与参数分析

由随机分散理论的计算模型可知,影响孔径分布的主要因素为分散体系的粒径数量分布、粒子的相互作用及固液体积比.其中,颗粒粒径的数量分布与单分散、多分散特性相关,粒子间作用势由同心球模型硬核径比或可重叠度决定,固液体积比则与水化程度相关.在应用两相介质随机分散模型计算水泥基材料孔隙结构演变时,需根据不同水化阶段的颗粒特性确定单分散模型和多分散模型的适用性及同心球的可重叠程度.

美国国家标准与技术研究所(National Institute of Science and Technology,NIST)根据粒子的分散程度,定义数量不小于90%粒子的粒径与平均粒径偏差不大于5%的分散系为单分散体系,否则为多分散体系[15]. 如果所有的水泥及水化产物颗粒都是完全分散(相互作用为硬球模型)的,则根据仿真得到的不同水化度下的粒径分布见图5,可直接判断水泥体系属于多分散系类型.但在实际情况中,初始状态的水泥浆体,水泥颗粒近似多分散体系,随着水化度的增大,颗粒及水化产物之间的接触与重叠使得多个粒子聚集为团粒.此时,颗粒粒径按团粒粒径进行统计更为准确,且团粒粒径分布更加集中,所以单分散模型更加适用.

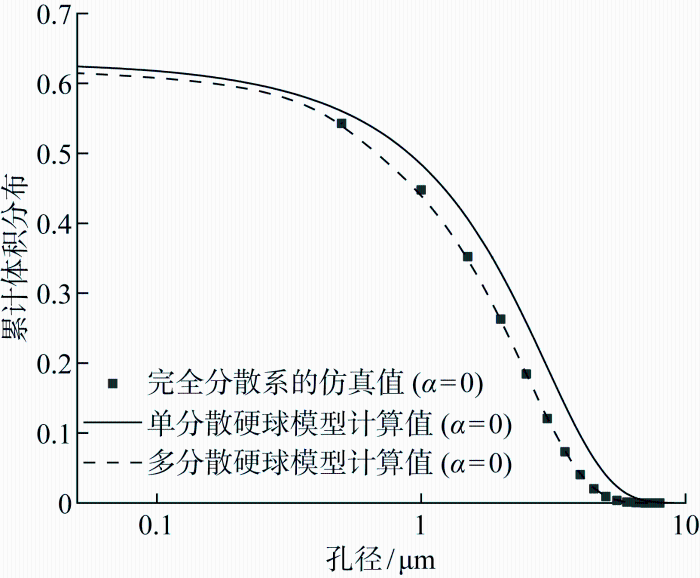
基于μic仿真输出的给定水化度下的微观结构信息,包括颗粒粒径分布、固液比等,可通过随机分散模型计算孔隙结构.模型中采用的粒径统计矩及液相体积分数如表2所示.在水化初始阶段α= 0时,水泥颗粒完全分散且不存在碰撞或重叠,此时属于硬球分散模式,分别采用多分散硬球模型与MHS模型计算初始状态的累计孔径分布,结果如图7所示.其中,散点为仿真统计结果,曲线为模型计算结果.通过对比可知,多分散硬球模型的计算结果与仿真计算一致,而 MHS模型计算的孔隙率偏高且孔径偏大.

表2   粒径统计矩以及液相体积分数

Tab.2  Statistical moments of particle radius and water/pore volume fraction

α<r>/ μm<r2>/μm2<r3>/μm3ϕw
04.1218.88105.880.63
0.33.7015.0972.670.48
0.64.2919.83103.670.35
0.94.5722.50123.500.24

新窗口打开| 下载CSV


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   粒子初始化状态孔径累计分布(α=0)

Fig.7   Cumulative volume fraction of pore size in initial dispersion (α=0)


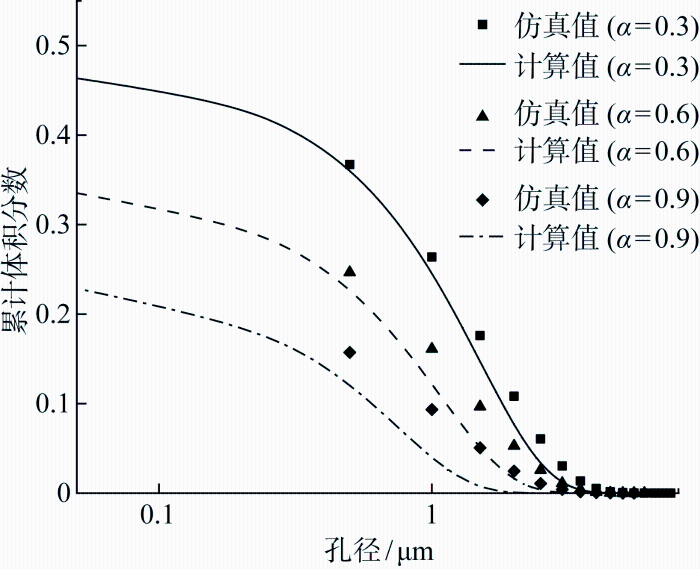
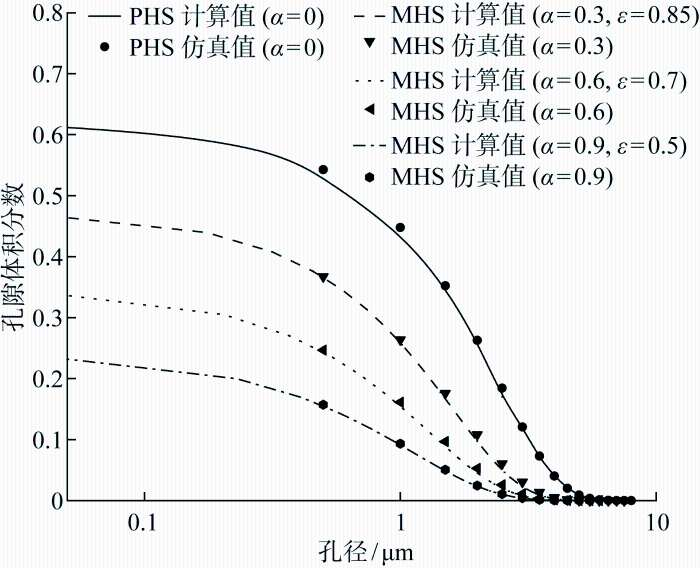
由图4可知,除水化前的初始状态外,水泥开始水化后,水化产物碰撞和接触使得颗粒间的相互作用不再满足硬球势,且团粒的形成使得粒径统计不宜采用仿真中直接获取的所有颗粒的粒径分布.计算结果表明,多分散硬球模型与仿真结果偏差较大,且会随水化度的增大而越来越大,如图8所示.考虑各水化度下的粒径分布,虽然粒径分布范围跨数量级,但是90%以上的粒径都集中在数量平均粒径<r>±1 μm范围内.颗粒间的相互碰撞与接触,尤其很多小颗粒团聚形成了较大的团粒,粒径发生较为明显的重分布.因此,水化后的水泥体系宜采用单分散同心球模型来计算孔径分布的理论解.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   多分散硬球模型关于累计孔径分布计算结果(α≠0)

Fig.8   PHS calculation results of cumulative volume fraction of pore size(α≠0)


采用单分散同心球模型进行孔径分布计算时,由于不同水化度下水泥颗粒的生长与接触程度不同,因此需要确定适合的ε.采用最小二乘法,拟合仿真得到孔径分布离散点,确定各水化度下ε的最佳取值,分散模型与仿真计算的结果对比如图9所示.由图可知,单分散同心球模型的计算结果与仿真结果一致,ε随水化度增大而逐渐减小,出水泥颗粒的接触效应随水化进程逐步增强.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   分散模型与仿真关于孔径累计分布的计算结果

Fig.9   Comparison of disperse model and simulation of calculation result


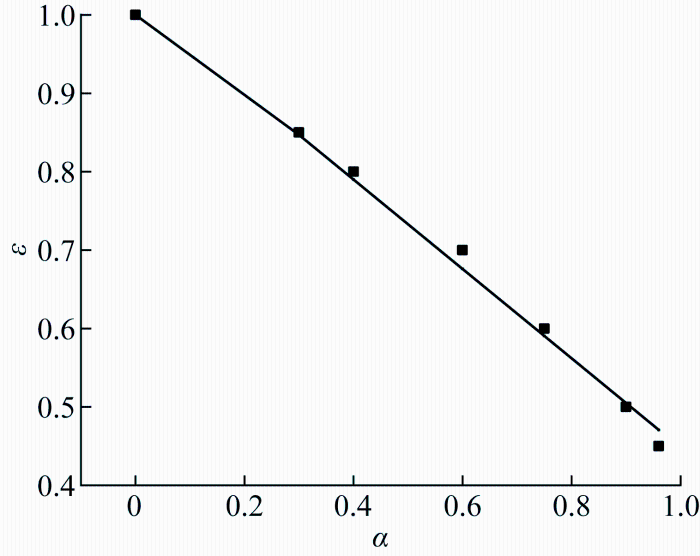
ε与α的关系如图10所示,二者呈线性负相关.采用线性拟合得到二者的关系服从式

ε=-0.59α+1

当α=0时,ε=1,此时为硬球分散模式,与前文的分析和计算结果一致;当α=1时,ε≈0.41,说明即便水泥完全水化,其水化产物也不能完全混合,而是以一定比例、在一定范围内接触和生长.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   硬核半径比ε与水化度α的关系

Fig.10   Hard core ratio ε versus hydration degree α


3.3 颗粒絮凝对孔径分布的影响

水泥浆体系中,在低水灰比或不使用减水剂等情况下,水泥颗粒并不能完全分散在水中,而是会发生一定程度的絮凝,这将对初始孔隙结构及水化后的孔径分布产生一定影响.μic仿真平台中关于絮凝的处理算法有以下4个步骤:

步骤1 对中心粒子指定距离范围内的其他粒子按絮凝因子减小距离.

步骤2 按指定的次数重复步骤1.

步骤3 对中心粒子距离范围的其他粒子围绕中心粒子随机移动很小的距离.

步骤4 一直重复步骤3,直至粒子发生重叠或移动次数达到1 000次.

考虑絮凝后水泥分散体系(α = 0)的二维截面如图11所示.与图4(a)对比可知,絮凝效应使粒子团聚的趋势更加明显,絮凝使得小颗粒形成团粒,团粒的粒径分布相较于完全分散的颗粒来说,更集中在数量均值粒径附近.因此,考虑絮凝效应时,硬球模型中的粒径分布应采用团粒粒径参数,与完全分散时的初始粒径分布不同,此时单分散模型更适用.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   考虑絮凝后粒子的分散状态

Fig.11   Disperse state in particle flocculation


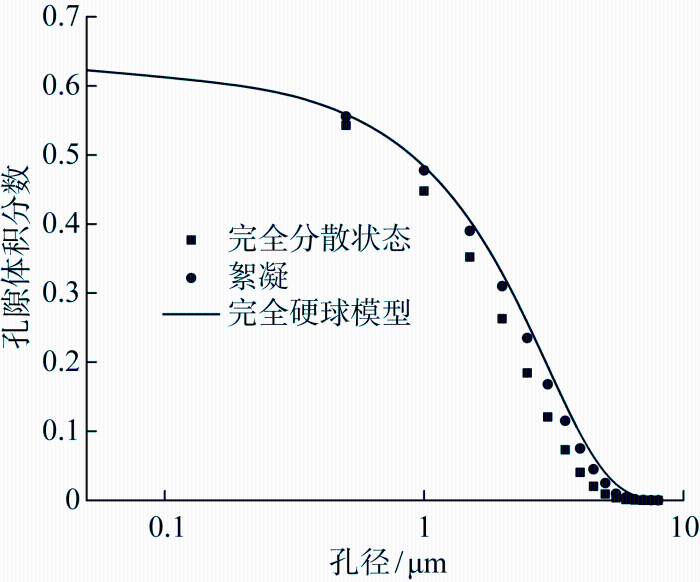
完全分散和考虑絮凝效应的孔径累计分布仿真结果对比如图12所示.由图可知,絮凝造成分散系的最可几孔径增大.采用MHS模型计算絮凝后的分散系,其中粒子半径取原粒子的数量平均粒径<r>,结果如图中实线所示,且絮凝使得分散系的孔径分布更接近于MHS模型的计算结果.絮凝造成了团粒粒径的重分布,并进一步改变了分散系的孔隙结构.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   完全分散系与絮凝分散系的孔径累计分布对比

Fig.12   Pore size distribution in random packing dispersion and flocculation


4 结论

侧重于初步建立水泥孔隙结构的理论计算模型,并尽可能对其适用性进行探索.基于两相介质的随机分散理论,将水泥体系看作两相介质,建立水泥水化过程孔径分布的计算模型.通过采用μic水泥水化仿真平台,验证基于分散模型计算孔结构演变的可行性与合理性;利用μic平台对比试验对水化条件控制的高度灵活性,深入探索分散模型在不同絮凝程度及水化全阶段的适用性.为确保仿真数据的正确性与可靠性,特地采用μic仿真平台开发者Bishnoi在经典仿真案例中的参数设置[14],该参数对应的仿真结果的可靠性在其博士论文中已经得到论证.主要结论如下:

(1) 新拌水泥浆体中的水泥颗粒,在加入足量的减水剂时或在高水灰比条件下完全分散时,满足多分散硬球体系的计算条件,计算得到的孔径分布与仿真结果高度一致.

(2) 随着水泥浆体的水化度增大,水化产物层的碰撞与新生产物颗粒的交错使得颗粒之间的相互作用不再满足硬球势,同时聚集成团粒的粒径分布趋于集中,此时水泥体系满足单分散随机球模型的计算条件.通过硬核比表征颗粒交错程度,并建立硬核比与水化度的关系,可知单分散同心球模型计算的各水化度下的孔隙结构与仿真结果吻合良好.

(3) 考虑水泥颗粒絮凝效应时,由于水泥颗粒相互接触形成团粒,团粒的粒径分布偏离原始颗粒的粒径分布,导致粒径分布范围减小,此时更接近单分散模型的计算条件.仿真结果显示,絮凝条件下孔径粗化,与MHS模型的计算结果更加吻合.

但本文在孔隙尺度计算方面存在一定局限性,在研究材料方面存在不完善性.对孔隙结构的计算主要集中在微观尺度的毛细孔层面,所以无论在理论计算还是仿真中,都对C-S-H的粒子模型进行了一定的理想化假设,暂时无法得到更复杂的凝胶粒子层间孔;研究材料方面,由于水泥孔隙结构的理论计算模型目前是空白的,故以最简单的基准水泥为研究对象进行初步建模.实际上,分散模型并不限制水泥的类型,对于组分更复杂的水泥,同样可计算出其在水化过程中各组分粒子的粒径变化、固液比变化,可通过分散模型计算任一水化度下的孔径分布特征.

参考文献

CHINDAPRASIRT P, HOMWUTTIWONG S, SIRIVIVATNANON V.

Influence of fly ash fineness on strength, drying shrinkage and sulfate resistance of blended cement mortar

[J]. Cement and Concrete Research, 2004, 34(7): 1087-1092.

[本文引用: 1]

HOU D W, LI D Y, HUA P C, et al.

Statistical modelling of compressive strength controlled by porosity and pore size distribution for cementitious materials

[J]. Cement and Concrete Composites, 2019, 96: 11-20.

[本文引用: 1]

ZHANG Y, YE G, YANG Z X.

Pore size dependent connectivity and ionic transport in saturated cementitious materials

[J]. Construction and Building Materials, 2020, 238: 117680.

[本文引用: 1]

佘安明, 马坤, 王中平, 等.

低场核磁共振低温测孔技术表征硬化水泥浆体孔结构

[J]. 建筑材料学报, 2021, 24(5): 916-920.

[本文引用: 1]

SHE Anming, MA Kun, WANG Zhongping, et al.

Characterization of pore structure in hardened cement paste by low field NMR cryoporometry

[J]. Journal of Building Materials, 2021, 24(5): 916-920.

[本文引用: 1]

谢恩慧, 周春圣.

利用低场磁共振弛豫测孔技术预测水泥基材料的水分渗透率

[J]. 硅酸盐学报, 2020, 48(11): 1808-1816.

[本文引用: 1]

XIE Enhui, ZHOU Chunsheng.

Prediction of water permeability for cement-based material from the pore size distribution achieved by low-field nuclear magnetic resonance relaxation technique

[J]. Journal of the Chinese Ceramic Society, 2020, 48(11): 1808-1816.

[本文引用: 1]

SLANIČKA Š.

The influence of fly ash fineness on the strength of concrete

[J]. Cement and Concrete Research, 1991, 21(2/3): 285-296.

[本文引用: 1]

YU A B, STANDISH N.

Estimation of the porosity of particle mixtures by a linear-mixture packing model

[J]. Industrial & Engineering Chemistry Research, 1991, 30(6): 1372-1385.

[本文引用: 1]

ALONSO M, SAINZ E, LOPEZ F A, et al.

Void-size probability distribution in random packings of equal-sized spheres

[J]. Chemical Engineering Science, 1995, 50(12): 1983-1988.

[本文引用: 1]

DODDS J A, LLOYD P J.

A model for the void structure in multi-component sphere packs applied to capillary pressure curves

[J]. Powder Technology, 1972, 5(2): 69-76.

[本文引用: 1]

TORQUATO S. Random heterogeneous materials: microstructure and macroscopic properties[M]. New York: Springer Science, 2002.

[本文引用: 1]

BISHNOI S, SCRIVENER K L.

μic: A new platform for modelling the hydration of cements

[J]. Cement and Concrete Research, 2009, 39(4): 266-274.

[本文引用: 1]

LU B L, TORQUATO S.

Nearest-surface distribution functions for polydispersed particle systems

[J]. Physical Review A, 1992, 45(8): 5530-5544.

PMID:9907651      [本文引用: 2]

RIKVOLD P A, STELL G.

D-dimensional interpenetrable-sphere models of random two-phase media: Microstructure and an application to chromatography

[J]. Journal of Colloid and Interface Science, 1985, 108(1): 158-173.

[本文引用: 1]

BISHNOI S. Vector modelling of hydrating cement microstructure and kinetics[D]. Japan: University of Tokyo, 2008.

[本文引用: 4]

MERKUS H G. Particle size measurements: fundamentals, practice, quality[M]. Dordrecht: Springer, 2009.

[本文引用: 1]

/

〈 〉