基于人工神经网络的深基坑支护结构侧移预测

doi:10.16183/j.cnki.jsjtu.2023.109

基于人工神经网络的深基坑支护结构侧移预测

徐长节^,¹^,²^,³, 李欣雨¹^,²

1.浙江大学滨海和城市岩土工程研究中心,杭州 310058

2.浙江大学平衡建筑研究中心, 杭州 310028

3.华东交通大学江西省岩土工程基础设施安全与控制重点实验室,南昌 330013

Lateral Deformation Prediction of Deep Foundation Retaining Structures Based on Artificial Neural Network

XU Changjie^,¹^,²^,³, LI Xinyu¹^,²

1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China

2. Center for Balance Architecture, Zhejiang University, Hangzhou 310028, China

3. Jiangxi Key Laboratory of Infrastructure Safety Control in Geotechnical Engineering, East China Jiaotong University, Nanchang 330013, China

责任编辑: 王一凡

收稿日期: 2023-03-27 修回日期: 2023-07-11 接受日期: 2023-07-24

基金资助:

国家自然科学基金(51878276)
浙江省自然科学基金委员会-华东院联合基金(LHZ19E080001)
浙江大学平衡建筑研究中心配套资金(20203512-10C)

Received: 2023-03-27 Revised: 2023-07-11 Accepted: 2023-07-24

作者简介 About authors

徐长节(1972—),教授,博士生导师,主要从事基坑工程支护结构方面的研究;E-mail:xucj@zju.edu.cn.

摘要

为了更精准地预测基坑开挖引起的支护结构侧移,采用支持向量机模型、传统人工神经网络模型及2种考虑时序性输入的循环神经网络模型,建立了不同基坑支护结构最大侧移、同一基坑不同工况支护结构侧移的预测模型.结果显示,人工神经网络可以根据工程实测数据实时更新和预测支护结构变形,有助于及时规划工程下一步施工工艺.在支护结构不同工况侧移的预测上,考虑了时序性输入的循环神经网络模型效果优于传统人工神经网络模型.

关键词： 基坑工程; 变形预测; 机器学习; 支护结构

Abstract

In order to more accurately predict the lateral deformation of retaining structures caused by foundation pit excavation, this paper adopts support the vector machine model, traditional artificial neural network model, and two kinds of recurrent neural network models considering temporal inputs to establish a prediction model for the maximum lateral deformation of retaining structures in different foundation pits, and for the same foundation pit under different working conditions. The results show that the artificial neural network can update and predict the deformation of the retaining structure in real time based on the measured data of the project, which is helpful for timely planning of the next construction process of the project. In the prediction of lateral deformation of retaining structures under different working conditions, the cyclic neural network model considering temporal inputs is better than the traditional artificial neural network model.

Keywords： excavation; deformation prediction; machine learning; retaining structures

PDF (2275KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

徐长节, 李欣雨. 基于人工神经网络的深基坑支护结构侧移预测[J]. 上海交通大学学报, 2024, 58(11): 1735-1744 doi:10.16183/j.cnki.jsjtu.2023.109

XU Changjie, LI Xinyu. Lateral Deformation Prediction of Deep Foundation Retaining Structures Based on Artificial Neural Network[J]. Journal of Shanghai Jiaotong University, 2024, 58(11): 1735-1744 doi:10.16183/j.cnki.jsjtu.2023.109

近年来,随着我国经济建设高速发展,地面空间的开发日益饱和,对地上空间的开发利用已经不能满足需求,越来越多的工程项目开始向地下发展,如地铁站、地下车库、地下商场、地下综合体,因此出现了大量与深基坑相关的工程.在进行基坑开挖过程中,保证基坑的稳定性及施工人员的安全性十分重要,支护结构及周围环境变形过大会引起很大的安全隐患,导致安全事故的发生.随着城市建设的愈发完善,许多工程位于人口密集、周围建筑物或管线密集的区域.基坑的支护结构除了满足自身要求外,还需要对支护结构及周围环境的变形进行控制,减小基坑工程对周围环境的影响.因此,有必要对基坑开挖过程中的变形规律进行研究,进一步形成支护结构变形预测方法,为基坑工程的支护结构设计及施工提供指导性意见.

基坑开挖过程中支护结构及周围环境的变形问题受到许多学者关注.文献[1 ⇓⇓⇓⇓⇓⇓⇓-9]中通过对土层分布、施工方法、支护方案、开挖深度等实测和模拟数据的分析,发现支护结构的最大侧移与开挖深度的关系可以由地质条件、施工方法、支护方案等条件来确定,根据不同施工条件确定的支护结构最大侧移一般为开挖深度的0.1%~0.87%.文献[10-11]中通过分析基坑开挖时桩锚支护结构的实测数据与数值模拟结果,归纳冠梁和支护桩的变形分布规律,并利用最小势能原理,推导出支护桩桩顶最大水平位移的计算公式.文献[12 ⇓⇓⇓⇓⇓-18]中通过数值模型模拟了不同的施工状态、地质条件和支护方式,动态分析了基坑开挖不同阶段支护结构、周围环境和结构的变形,为支护结构的设计选型、设计优化和施工提供了参考数据.随着机器学习技术的快速发展与普及,部分学者开始将机器学习应用于岩土工程领域.张雯超等^[19]基于70多个苏州地铁深基坑设计及监测数据,分析施工工法、地连墙厚度等8个输入参数与地连墙变形的相关性.Kung等^[20]通过对12个历史基坑开挖工程进行数值模拟,并通过人工神经网络(ANN)对基坑开挖过程中各个工况下地下连续墙的水平位移进行预测,通过对比数值模拟与ANN预测结果说明ANN算法可以准确预测软土地区基坑开挖过程中地下连续墙的变形情况.

针对基坑工程中支护结构侧移预测问题,已经有学者通过有限元模拟、经验公式总结、理论解析解推导、机器学习等方法进行了研究,但仍存在一定的局限性.经验公式和理论解析解难以准确计算基坑开挖过程中各时刻支护结构的变形,在基坑开挖过程中,可能会出现内部支护失效、周边环境变化等突发情况,通过相关公式难以充分考虑这些突发情况对围护结构变形的影响.与上述两种方法相比,数值模拟能更好地考虑围护结构周围环境参数对围护结构变形的影响,并能模拟施工各阶段的变形,但模型的建立耗时较长,建模所需的参数范围较大.建模值具有一定的随机性,难以验证仿真结果的准确性和有效性.机器学习算法在岩土工程领域得到了应用,可以有效地预测基坑开挖过程中围护结构的变形和地表沉降的情况,与上述3种预测方法相比,该方法具有学习速度快、预测模型实时更新、预测精度高等优点.但现有的预测模型大多是针对同一工程项目中不同时间序列的支护结构变形,不能预测不同基坑设计方案下支护结构的最大侧移,而且大多数考虑时间序列的变形预测模型只考虑了时间因素对变形的影响,忽略了其他因素对变形的影响,造成特征数据的浪费.

基于此,引入支持向量机模型和人工神经网络中的多层感知器模型,对基坑开挖引发的支护结构最大侧移进行了预测;引入长短期记忆(LSTM)和门循环单元(GRU)两种改进后的循环神经网络模型,对基坑开挖不同阶段的支护结构侧移进行了预测;并进一步探究了这几种模型的预测效果及输入步长对预测效果的影响.

1 机器学习模型

1.1 支持向量机模型

支持向量机(SVM)由Vapnik等^{[21⇓⇓-24]}在20世纪90年代提出.在早期,这种方法被用于统计学习领域,可以通过对小样本数据的学习,来探究样本数据之间的规律.

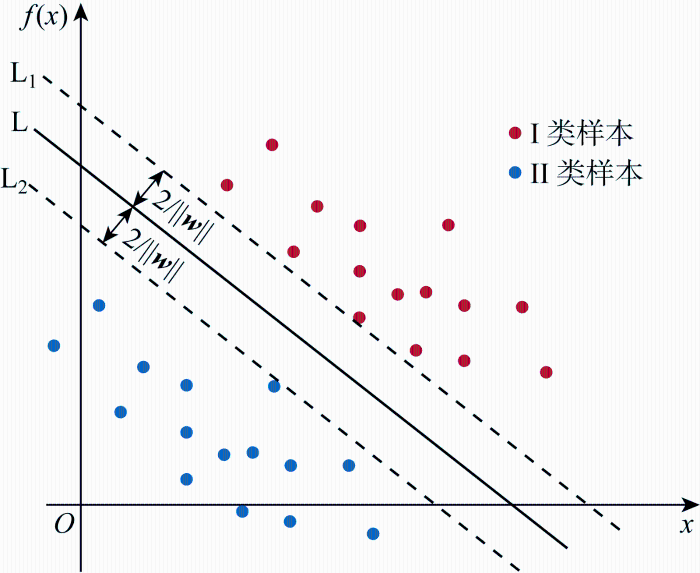
SVM的核心理论是找到数据归类的最优超平面,如图1所示.图中:f(x)为最优超平面函数;w为最优超平面的法向量;红色(I类)和蓝色(II 类)的点依次代表两类数据样本;L为分类线;L₁为穿过I类样本数据、平行于分类线且与分类线距离最近的线;L₂为穿过 II 类样本数据、平行于分类线且与分类线距离最近的线.最优超平面应该满足,L能将两组数据样本归类,且L₁与L₂的相距最大.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 SVM最优超平面示意图

Fig.1 Schematic diagram of SVM optimal hyperplane

对于回归问题,可以使用SVM中的支持向量机回归(SVR)模型,如图2所示.图中L₁、L₂为穿过样本数据、与回归线平行且相距最远的线.最优超平面应该满足,所有样本数据都在L₁与L₂之间的区域,且L₁与L₂的相距最小.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 SVR最优超平面示意图

Fig.2 Schematic diagram of SVR optimal hyperplane

对于线性可分样本,可以直接在原始空间中找到最优分类面;对于非线性可分样本,通过引入核函数,将输入特征量从低维空间变换到更高维的空间,并在新建的高维空间中找到最优分类面.最优超平面的计算公式如下:

(1)$\begin{array}{l} f(x)= \operatorname{sgn}(\boldsymbol{w} \cdot \boldsymbol{\Phi}(x)+\boldsymbol{b})= \\\operatorname{sgn}\left({ }^{\prime} a_{j} y_{j} \boldsymbol{\Phi}\left(x_{i}\right) \cdot \boldsymbol{\Phi}\left(x_{j}\right)+\boldsymbol{b}\right), \\\boldsymbol{\Phi}(x) \in \boldsymbol{H}\end{array}$

式中:y_j为x_j的类标记;w^*为最优权值向量;b^*为最优偏置向量; $a_{j}^{*}$ 为拉格朗日乘数最优解;l为数据样本集的数量;Φ(x)为特征向量;H为特征空间.

1.2 多层感知器模型

多层感知器(MLP)模型是一种基本的ANN模型.最早由Rosenblatt^[25]在20世纪60年代提出.MLP模仿人脑在处理问题时的工作机制,大脑由多个神经元连接在一起,当一个神经元接收到来自其他神经元的信号时,它会产生刺激,将信号经过处理后传输给其他神经元,神经元重复地传输信号,并且不断调整反馈输入和输出信号之间的关系.

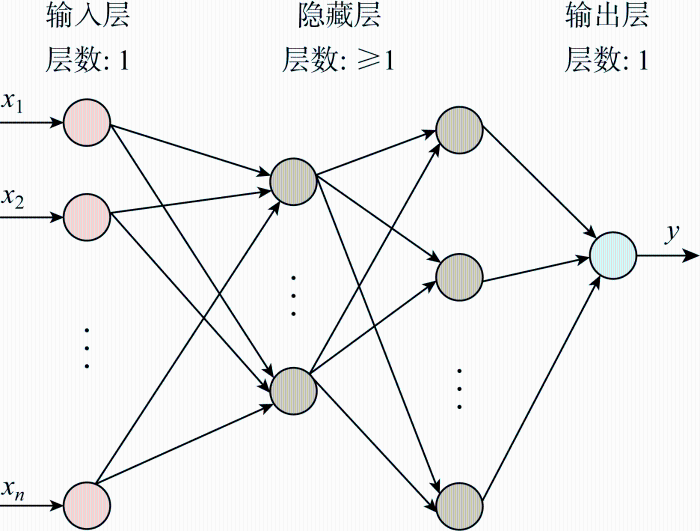
在处理回归问题时,MLP的基本结构如图3所示.神经网络由输入层、隐藏层和输出层组成.隐藏层的数量根据问题的情况而变化.特征数据通过输入层输入,输入数据由隐藏层神经元进行处理和学习,神经元的输入输出值通过决策函数进行变换,最后通过输出层输出预测结果.一般来说,隐层的层数越多,每层神经元的个数越多,模型的拟合能力越强,但过多的隐藏层和过多的神经元也可能导致过拟合.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 MLP模型示意图

Fig.3 Schematic diagram of MLP model

神经元上的决策函数模拟了人脑处理问题时激活神经元的过程,因此也叫激活函数.激活函数可以在神经元中引入非线性因素,使神经网络能够处理非线性问题.在本文中,使用ReLU激活函数,如下式所示:

(2)$f_{\max}(x)=\max\{0,x\}$

当输入值小于或等于0时,下一层中的神经元将不被激活.当输入值大于0时,下一层的神经元将被激活.这种激活函数在运算过程中收敛速度快,在机器学习领域得到了广泛的应用.

1.3 长短期记忆网络模型

LSTM最早由Hochreiter和Schmidhuber^[26]在1997年提出.LSTM模型是一种考虑时序性输入参数的人工神经网络模型,与MLP相比,该模型考虑了不同时序输出量之间的影响,在预测时序性数据时更准确.与传统的循环神经网络(RNN)模型相比,LSTM引入了门控单元,解决了传统RNN模型在输入数据过大时梯度可能消失的问题.

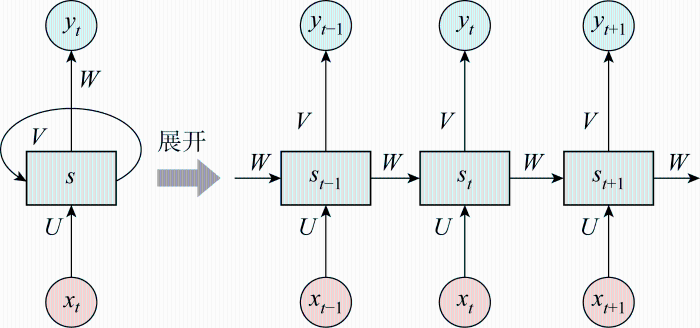
图4是传统RNN模型的示意图.图中:y_t、y_t_-1、y_t₊₁为时间t、t-1、t+1的输出值;s_t、s_t_-1、s_t₊₁分别为时间t、t-1、t+1的记忆;x_t、x_t_-1、x_t₊₁为时间t、t-1、t+1的输入值;U、V、W为权重参数.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 传统RNN模型示意图

Fig.4 Schematic diagram of traditional RNN model

时间t的输出值计算如下:

(3)$y_{t}=G\left(V s_{t}\right) $

(4)$s_{t}=F\left(U x_{t}+W s_{t-1}\right)$

式中:F(x)、G(x)为激活函数,其中F(x)通常使用tanh、ReLU、Sigmoid激活函数,G(x)通常使用Softmax激活函数.

如图5所示,LSTM单元由遗忘门、输入门、输出门组成.遗忘门通过Sigmoid函数对x_t、y_t_-1进行激活,Sigmoid函数的输出值在0~1之间,只有当σ=1时,对应的信息才会被完整的保存下来;输入门对输入值和前一个单元格的状态执行更新;输出门通过对输入值和当前单元状态的处理,得到时间t的输出值.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 LSTM单元示意图

Fig.5 Schematic diagram of LSTM unit

1.4 门循环单元模型

GRU模型是LSTM的简化模型,由Cho等^[27]于2014年首次提出.与LSTM模型相比,GRU模型结构更简单,结构参数更少,因此在同等条件下,GRU模型计算量更小,训练时间更短.

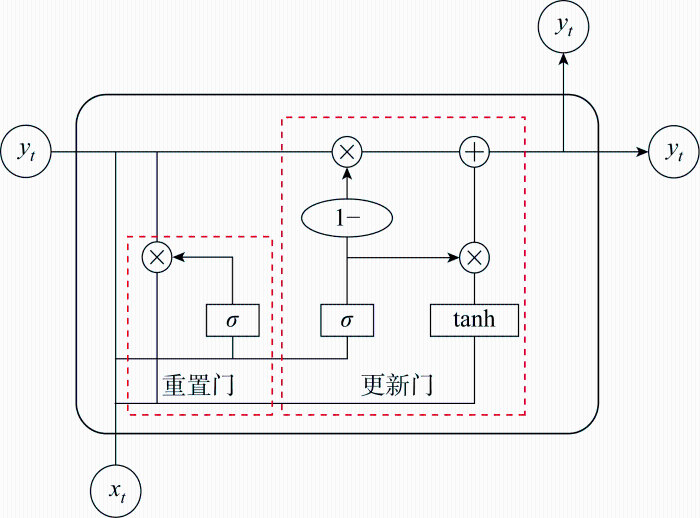
如图6所示,GRU单元由重置门、更新门组成.重置门对输入值和上个单元的隐藏状态进行激活.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 GRU单元示意图

Fig.6 Schematic diagram of GRU unit

2 支护结构最大侧移预测模型

2.1 数据集构建

支护结构最大水平位移预测模型的研究资料取自徐中华^[28]根据岩土工程领域已出版的专著、各类期刊和论文编制的上海地区基坑工程变形实测案例数据库,数据集包括上海地区的89个基坑工程的实测数据.该数据集包括水文地质参数、施工参数、基坑设计参数和测量的最大水平位移.在本节中,通过SVM和MLP模型来预测支护结构的最大侧移.随机选取总数据集70%的数据(即62个)作为模型的训练集,剩余30%的数据(即27个)作为模型的测试集.根据国内外对基坑支护结构变形影响因素的研究和数据库涉及实际工程的情况,主要关注基坑设计参数对支护结构侧移的影响,选取基坑开挖深度x₁、地下连续墙厚度x₂、支护结构长度x₃、支护结构单位长度抗弯刚度x₄、内支撑数量x₅、首道内支撑距离地面深度x₆、内支撑平均间隔x₇、支护类型x₈这8个主要因素作为模型的输入量,支护结构最大侧移y为输出量.x₈=1时对应支护结构与地下主体结构相结合的支护方式;x₈=2时对应顺作法的地下连续墙支护方式.

由于数据集的参数范围和单位的差异很大,所以需要对数据集的参数进行预处理,以加快神经网络模型的收敛速度.对于参数x₁~x₇和y使用归一化方法对数据进行预处理,使这些参数的数值分布在[0,1]的范围内.具体计算方法如下式:

(5)$x_\mathrm{norm}=\frac{x-x_\mathrm{min}}{x_\mathrm{max}-x_\mathrm{min}}$

式中:x_norm为归一化处理后的参数;x为归一化处理前的参数;x_max为归一化处理前的最大参数;x_min为归一化处理前的最小参数.

对于x₈该分类特征类型的参数,通过独热编码对数据进行预处理,并通过2位状态寄存器对2个支持类型的状态进行编码.

2.2 模型建立及训练

采用SVM和MLP模型支护结构最大侧移的预测进行训练,并随机选取样本数据的10%作为验证集,以验证训练模型的准确性.

通过随机搜索算法和参数优化经验调整模型所需的超参数.在优化过程中,通过损失函数监督神经网络的学习过程,计算预测模型在当前迭代次数下的损失.对于回归问题,经常使用均方误差损失函数,计算公式如下:

(6)$E_{\mathrm{MSE}}\left(g, g^{\prime}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(g_{i}-g_{i}^{\prime}\right)^{2}$

式中:m为样本数据数量;g为实测的输出值;g'为预测的输出值.对于同一模型,E_MSE(g, g')取值越小,模型准确度越高

在训练过程中,为了防止训练模型过拟合,增加L2正则化,并对原损失函数项和正则项比例进行加权,优化原损失函数.计算公式如下:

(7)$f_{\text {loss }}^{\prime}(x)=f_{\text {loss }}(x)+\frac{\lambda}{2 m} \sum w_{i}^{2}$

式中:f_loss(x)为原有的损失函数;f'_loss(x)为L2正则化后的损失函数;λ为正则项的权重.

最终确定SVM模型参数取值:惩罚系数为1、核函数为Gauss径向基核函数、回归精度epsilon为0.1.MLP模型参数取值:隐藏层层数为3、神经元数量为64、学习率为 0.000 5、激活函数为ReLU函数、训练步数为 5 000.

3 不同阶段支护结构侧移预测模型

3.1 数据集构建

不同阶段支护结构水平位移预测模型数据取自杭州市某高铁站基坑工程实测数据,该车站为地下三层双柱三岛式车站,基坑总长约457 m,开挖宽度22 m,开挖深度26.05 m,基坑底部主要位于粉砂层.基坑标准段采用明挖顺作法施工,支护结构由 1 m 厚的地下连续墙、7道内支撑及2个换钢支撑组成.数据集选择CX23监测点的支护结构侧移数据进行预测和分析.总共收集80期数据,因用于预测的模型考虑了时序性输入,所以按照测量时间的顺序对训练集和测试集进行分组更合理,前64期数据作为训练集,后16期数据作为测试集.由于施工过程中各监测点周围的水文地质条件及基坑设计参数保持不变,对支护结构变形的影响可以忽略不计,本节预测模型的影响因素主要考虑施工参数.根据国内外对基坑支护结构变形影响因素的研究,结合工程实际情况,选取基坑开挖深度X₁、开挖阶段X₂、第1道混凝土钢结构支撑轴力X₃、第5道混凝土钢结构支撑轴力X₄、第2道钢支撑轴力X₅、第3道钢支撑轴力X₆、第4道钢支撑轴力X₇、距离开工时间X₈、侧移变化速率X₉这9个主要因素作为模型的输入,支护结构侧移Y为输出量.

部分样本数据如表1所示.对于参数X₁~X₉和Y,使用归一化方法对数据进行预处理,使这些参数的数值分布在[0,1]的范围内.具体计算方法见式(5).

表1 不同阶段支护结构侧移预测模型部分样本数据表

Tab.1 Partial sample data for predicting lateral displacement of retaining structures in different stages

编号	X₁/m	X₂	X₃/kN	X₄/kN	X₅/kN	X₆/kN	X₇/kN	X₈/d	X₉/(mm·h^-1)	Y/mm
1	5	1	1 913.59	0	0	0	0	22	-0.22	-0.66
2	5	1	2 369.11	0	0	0	0	25	0.43	0.63
3	5	1	2 309.13	0	0	0	0	27	0.37	1.37
︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙
78	26.05	7	1 870.24	7 096.59	968.79	845.28	1 107.62	118	1.54	58.14
79	26.05	7	1 677.10	7 336.54	925.58	791.38	1 100.69	119	-1.55	56.59
80	26.05	7	2 028.95	7 431.26	978.13	870.61	1 152.58	120	-0.4	56.19

新窗口打开| 下载CSV

对于X₂该分类特征类型的参数,通过独热编码对数据进行预处理,并通过7位状态寄存器对7个施工阶段进行编码,X₂取值及对应施工阶段如表2所示.表中:h为基坑开挖深度.

表2 X₂预处理后的参数取值及对应施工阶段

Tab.2 Pre-processed parameter values of X₂ and corresponding construction stages

独热编码前的参数	独热编码后的参数	对应的施工阶段
1	1000000	h≤5 m
2	0100000	5 m<h≤10 m
3	0010000	10 m<h≤15 m
4	0001000	15 m<h<26.05 m
5	0000100	h=26.05 m
6	0000010	架设第6道支撑
7	0000001	架设第7、8道支撑

新窗口打开| 下载CSV

3.2 模型建立及训练

采用MLP、LSTM、GRU模型不同阶段支护结构侧移的预测进行训练,并随机选取样本数据的10%作为验证集,以验证训练模型的准确性.

通过随机搜索算法和参数优化经验调整模型所需的超参数.在优化过程中,利用均方误差损失函数,计算公式见式(6),来监督神经网络的学习过程,计算预测模型在当前迭代次数下的损失.为了训练模型过拟合,向损失函数添加L2正则化项以形成新的损失函数,计算公式见式(7).

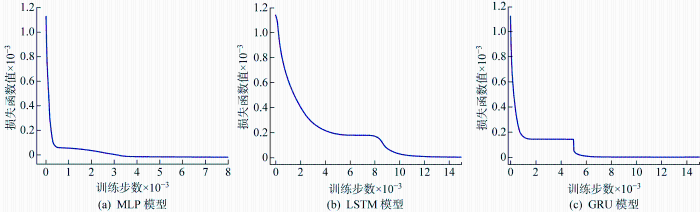
最终确定各模型参数取值如表3所示,在该参数组合下的损失函数如图7所示.由图7可知,随着训练步数的增加,训练集的损失逐渐减少.MLP模型在训练步数达到约4 500时逐渐收缩,LSTM模型在训练步数达到约13 000时逐渐收敛,GRU模型在训练步数达到约8 000时逐渐收敛,损失减小到最小值附近.LSTM和GRU模型有两个收敛平台,这可能是由于训练数据集分布不均匀,导致训练过程中出现局部最优解.在第1个收敛平台阶段,模型参数更新速度较快,但随着训练步长的增加,模型仍处于局部最优解状态,损失函数值基本不变.在第2个收敛平台中,模型参数的更新速度变慢,但随着训练步长的增加,模型跳出了局部最优解,模型的表达能力得到了提高.此时,模型具有较好的泛化能力,可用于预测新的数据.

表3 不同阶段支护结构侧移预测模型参数取值

Tab.3 Parameter values of lateral displacement prediction models for support structures in different stages

模型	隐藏层层数	神经元数量	步长	学习率	激活函数	训练步数
MLP	3	64	-	0.000 1	ReLU	4 500
LSTM	1	64	4	0.000 1	ReLU	13 000
					Sigmoid	13 000
					tanh	13 000
GRU	1	64	6	0.000 5	ReLU	8 000
					Sigmoid	8 000
					tanh	8 000

新窗口打开| 下载CSV

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 损失函数与训练步数关系

Fig.7 Relation between loss function and training steps

4 预测结果分析

4.1 支护结构最大侧移预测

基于2.2节中的最优参数值,分别采用SVM和MLP模型对不同基坑支护结构的最大侧移进行预测.训练数据来自文献[28]中随机选择的62组数据,经过训练和交叉验证,得到上述两个模型对应的预测模型,并对样本数据剩余的27组数据进行预测,图8为各模型最优参数组合下测试集回归效果对比图.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 各模型测试集回归效果

Fig.8 Regression effect of each model test set

从图8可以看出,SVM模型和MLP模型在预测支护结构最大侧移时表现较好,其中MLP模型预测值与实测值的误差主要在10%以内,SVM模型的误差范围主要在20%以内.相比之下,MLP模型在预测包络线最大位移时具有更高的准确度和精度.这是因为与SVM模型相比,MLP模型具有更好的泛化能力和更精确的预测模式,它的神经元结构具有更强的学习能力,可以学习更多的特征信息,从而提高预测精度.

表4给出了各模型预测结果的评价指标值.表中:R²为决定系数,

(8)$R^{2}\left(g, g^{\prime}\right)=1-\frac{\sum_{i=1}^{m}\left(g_{i}-g_{i}^{\prime}\right)^{2}}{\sum_{i=1}^{m}\left(g_{i}-\bar{g}\right)^{2}}$

式中: $\bar{g}$ 为实际输出值平均值.R²(g, g')取值在[0,1]的范围内,取值大小可以反映输入参数对输出参数的解释程度,值越大,模型拟合效果越好.通过比较两个模型的R²值,可以看出MLP的整体预测效果优于SVM.

表4 支护结构最大侧移预测模型评价指标

Tab.4 Evaluation indicators of maximum lateral displacement prediction model for retaining structures

模型	E_MSE	R²
SVM	4.99	0.99
MLP	36.96	0.95

新窗口打开| 下载CSV

综上所述,MLP模型在支护结构最大侧移预测的表现更好,是一个更可靠和准确的预测模型.在实际基坑工程中,可优先考虑采用基于机器学习的MLP模型,为工程的稳定性、安全性分析提供可靠的参考数据.

4.2 不同阶段支护结构侧移预测

基于表3中的最优参数值,分别使用MLP、LSTM和GRU模型预测水平位移不同阶段的包络结构.训练数据来自对应于表1中编号1~64的数据.通过训练和交叉验证得到上述3个模型对应的预测模型,并对样本数据的最后16组数据进行预测.预测结果与实测对比如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 预测结果与实测对比

Fig.9 Comparison of predicted results and actual measurements

由图9(a)可以看出,MLP模型的预测误差范围约为-1.46~1.50 mm,其中最大绝对误差值为1.50 mm,最小绝对误差值为0.15 mm.由图9(b)可以看出,LSTM模型的预测误差范围约为-1.42~1.17 mm,其中最大误差的绝对值为1.42 mm,最小误差的绝对值为0.05 mm.由图9(c)可以看出,GRU模型的预测误差范围约为-1.21~1.43 mm,其中最大绝对误差值为1.43 mm,最小绝对误差值为0.04 mm.根据3种模型的预测结果,MLP、LSTM和GRU模型的支护结构侧移的预测值与实测值一致,预测误差范围在1.5 mm以内,满足实际工程对支护结构侧移测量误差的要求.这3种模型对基坑开挖过程中不同阶段的支护结构侧移预测具有较高的精度.

表5给出了每个模型的均方误差、决定系数和预测时间.通过比较3种模型的R²值和预测用时,可以看出总体预测效果GRU>LSTM>MLP.LSTM和GRU模型考虑了时间序列对产出结果的影响.与MLP模型相比,输入参数的特征更接近基坑开挖的真实情况,预测结果更准确.通过比较3种模型的预测时间,可看出预测速度MLP>GRU>LSTM,与其他两个RNN模型相比,MLP的神经元数量较少,每个神经元之间只有一个连接,没有回路结构,在处理数据时可以并行计算每个神经元的输出.与LSTM模型相比,GRU的单元结构更简单,这使得GRU的计算量小于LSTM,此外,GRU的参数数量也比LSTM少,减少了内存消耗和大模型存储,加快了数据处理速度.

表5 不同阶段支护结构侧移预测模型评价指标

Tab.5 Evaluation indicators of lateral displacement prediction models for support structures in different stages

模型	E_MSE	R²	预测用时/min
MLP	1.01	0.96	1.7
LSTM	0.77	0.97	4.7
GRU	0.75	0.97	4.3

新窗口打开| 下载CSV

4.3 输入步长分析

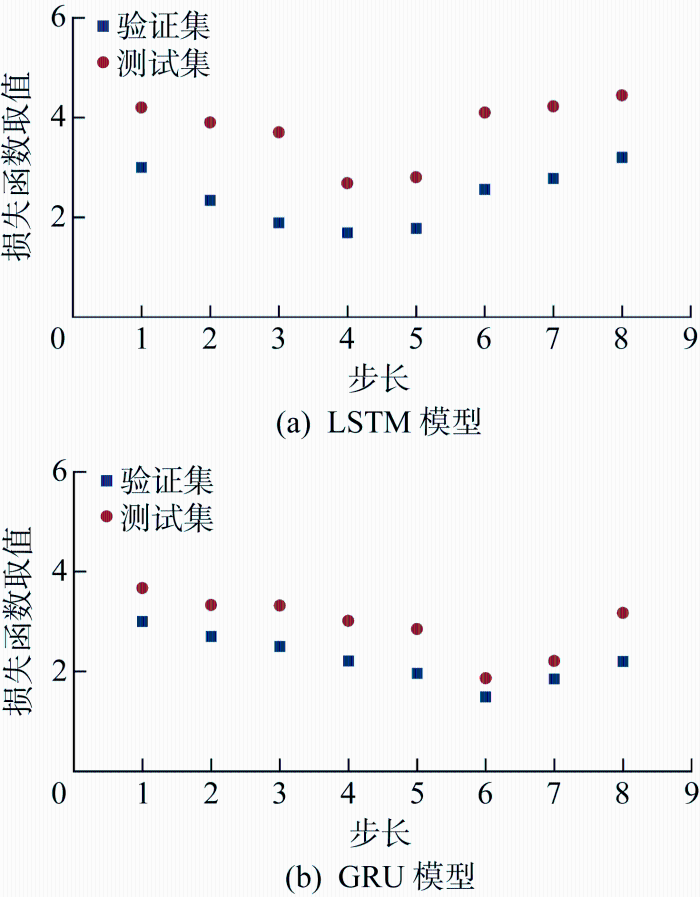
LSTM和GRU考虑了输入参数按时间序列顺序输入的影响,与MLP模型相比增加了步长参数的概念.例如,在预测时间序列t的支护结构侧移时,需要考虑从t-n到t-1时间序列的隐藏状态对时间序列t侧移的影响,其中n是输入步长参数.为了探索步长参数对预测效果的影响,在保持其他参数不变的情况下,改变模型的步长,得到不同取值的损失函数,如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同步长对应的损失函数值

Fig.10 Values of loss function corresponding to different steps

从图10(a)可以看出,对于LSTM模型,步长为4的预测模型具有最小的损失函数值;当步长小于4时,预测模型的损失函数随着步长的增大而减小,向预测模型输入更多的时间序列较小的序列数据,可以为模型带来更多的用于学习的历史数据,使得预测模型更加准确;当步长大于4时,预测模型的损失函数随着步长的增大而增大,用训练集训练的模型比用步长为4训练的模型更接近过拟合现象.从图10(b)可以看出,对于GRU模型,步长为6预测模型具有最小的损失函数值;当步长小于6时,预测模型的损失函数随着步长的增大而减小;当步长大于6时,预测模型的损失函数随步长的增大而增大.

综上所述,对于考虑时间序列的支护结构侧移预测模型,增加输入步长可以在一定程度上提高模型预测精度,但步长过大也会导致模型过拟合.对于不同的模型,最优输入步长的取值可能不同,这是因为不同的模型设置了不同的超参数,比如学习率、隐层数、神经元数等,这些参数的不同设置可能导致需要不同的输入序列长度以获得更好的性能.

5 结论

(1) SVM和MLP模型在预测不同基坑支护结构最大侧移时有较好表现,预测误差大部分在 ±20% 范围内.与SVM模型相比,MLP神经元结构具有更强的学习能力,可以学习到更多的特征信息,预测精度更高.

(2) MLP、LSTM和GRU模型对不同阶段支护结构变形的预测结果误差范围均在1.5 mm以内,3种模型均能准确预测基坑开挖过程中支护结构的变形,满足实际工程测量精度要求.与传统的神经网络MLP模型相比,LSTM和GRU两个RNN模型考虑了时间输入对输出的影响,能够捕捉到时间输入之间的依赖关系,更接近基坑开挖过程中支护结构变形的实际情况,预测效果更好.

(3) 对于考虑时间序列输入的支护结构侧移预测模型,增大输入步长可以在一定程度上提高模型的预测精度,但步长过大也会导致模型过拟合.对于不同的模型,由于模型参数的不同,最优输入步长可能不同.

(4) 提出的基于机器学习的变形预测方法与传统的有限元模拟、公式计算等变形预测方法相比,计算速度更快,并可根据工程实测数据实时更新和预测,有助于及时规划工程下一步施工工艺.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

徐中华, 王建华, 王卫东.

上海地区深基坑工程中地下连续墙的变形性状

[J]. 土木工程学报, 2008(8): 81-86.